Время на прочтение
3 мин
Количество просмотров 9.5K
Немного теории.
Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.
1 л.с. – это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.
Как известно, мощность показывает, какую работу совершает тело в единицу времени:
Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:
Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности – Ватт:
Перейдем к основной части, а именно – к техническим характеристикам автомобиля.
Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.
m = 2 тонны = 2000 кг – масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.с., но реально мощность выше – измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)
Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.
У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.
Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:
Вооружившись этими знаниями, получим конечную формулу:
Выражая отсюда t, получим итоговую формулу для вычисления разгона:
На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов. Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.
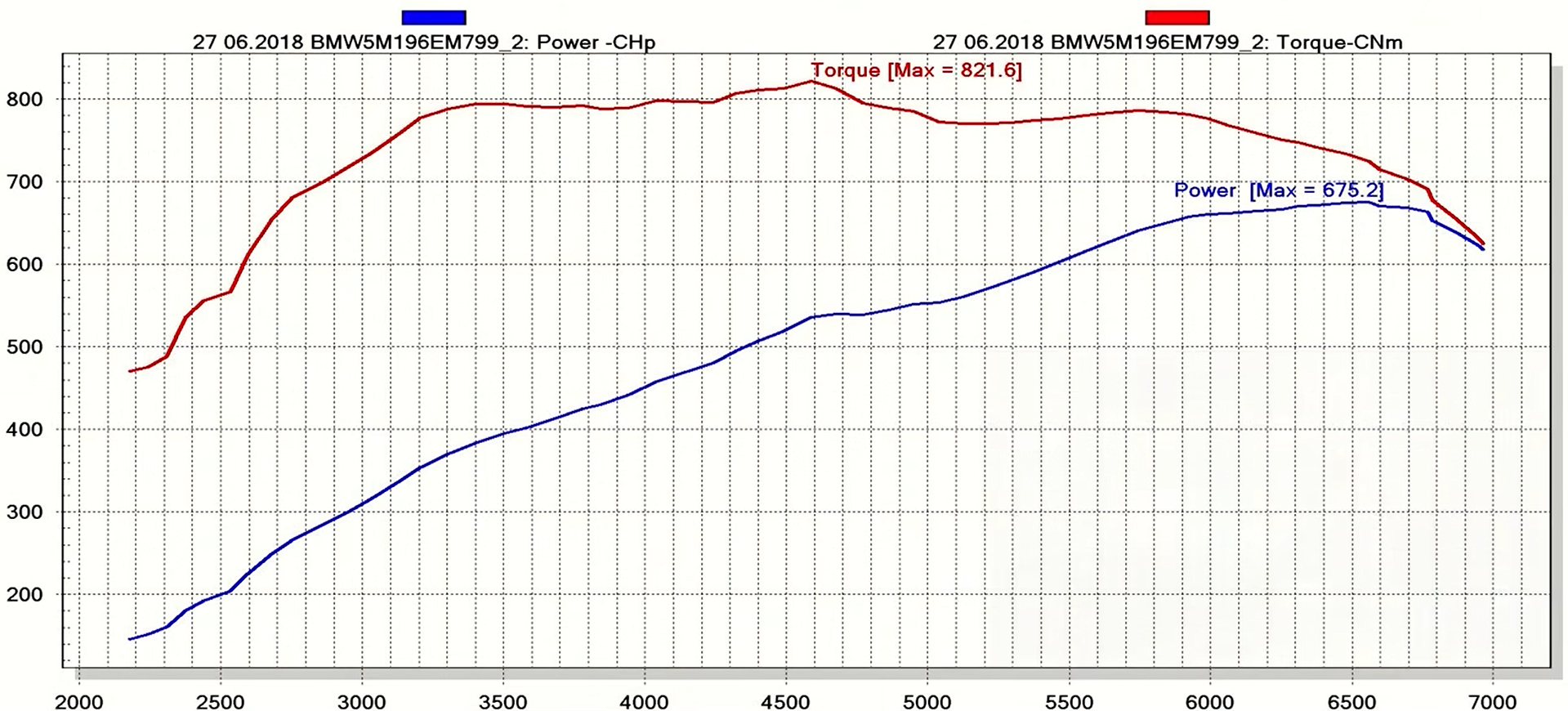
Главное, что мы должны усвоить из этого графика – мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.
Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:
При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную – 600 л.с. (7000 об/мин):
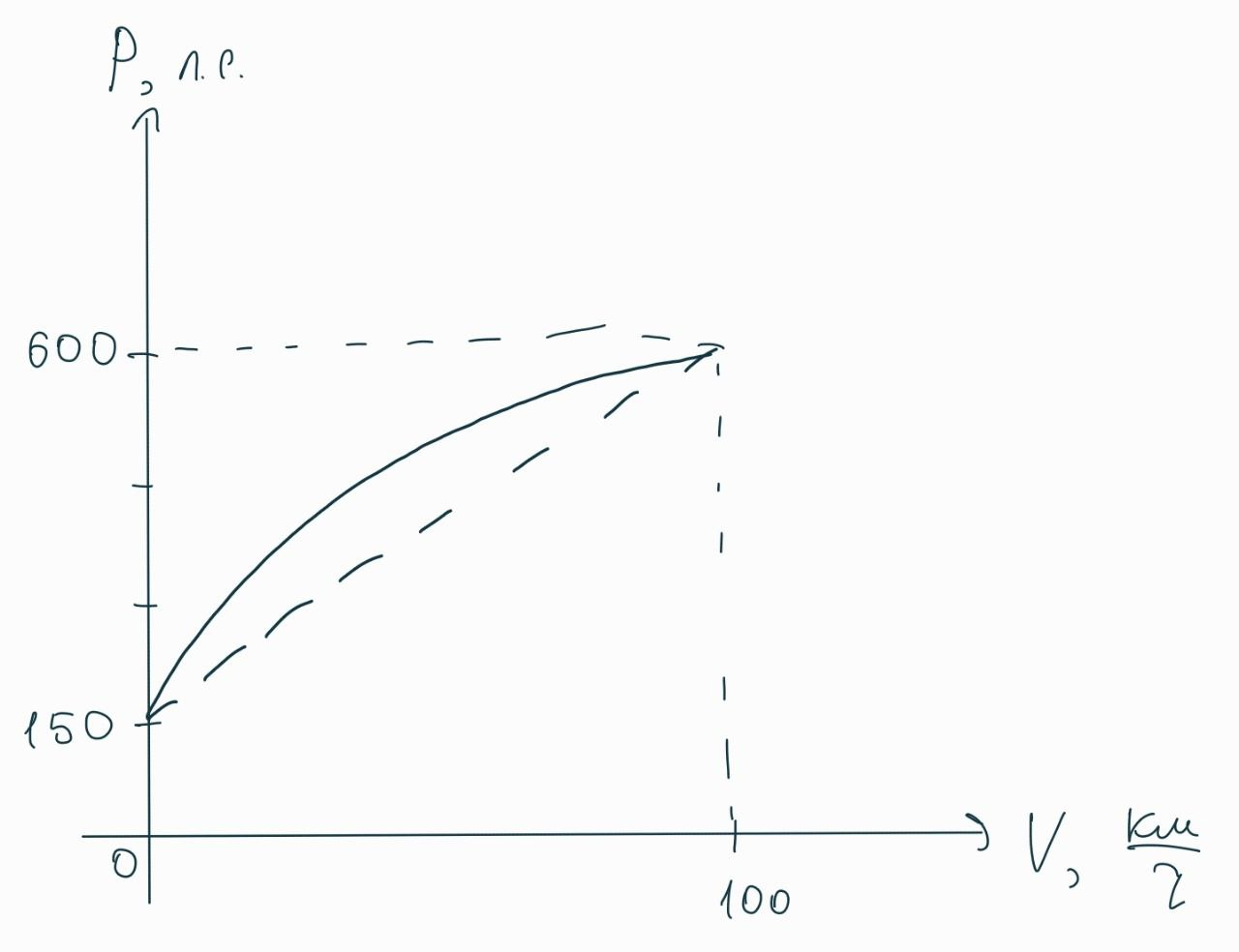
Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:
Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства. Потери мощности 20%, значит эффективность 80%=0.8:
Теперь подставляем всё в конечную формулу:
Получили довольно близкий к “паспортным” 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.
Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.
С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.
Так делать конечно же нельзя! После 2-й передачи двигатель работает на “комфортных” для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:
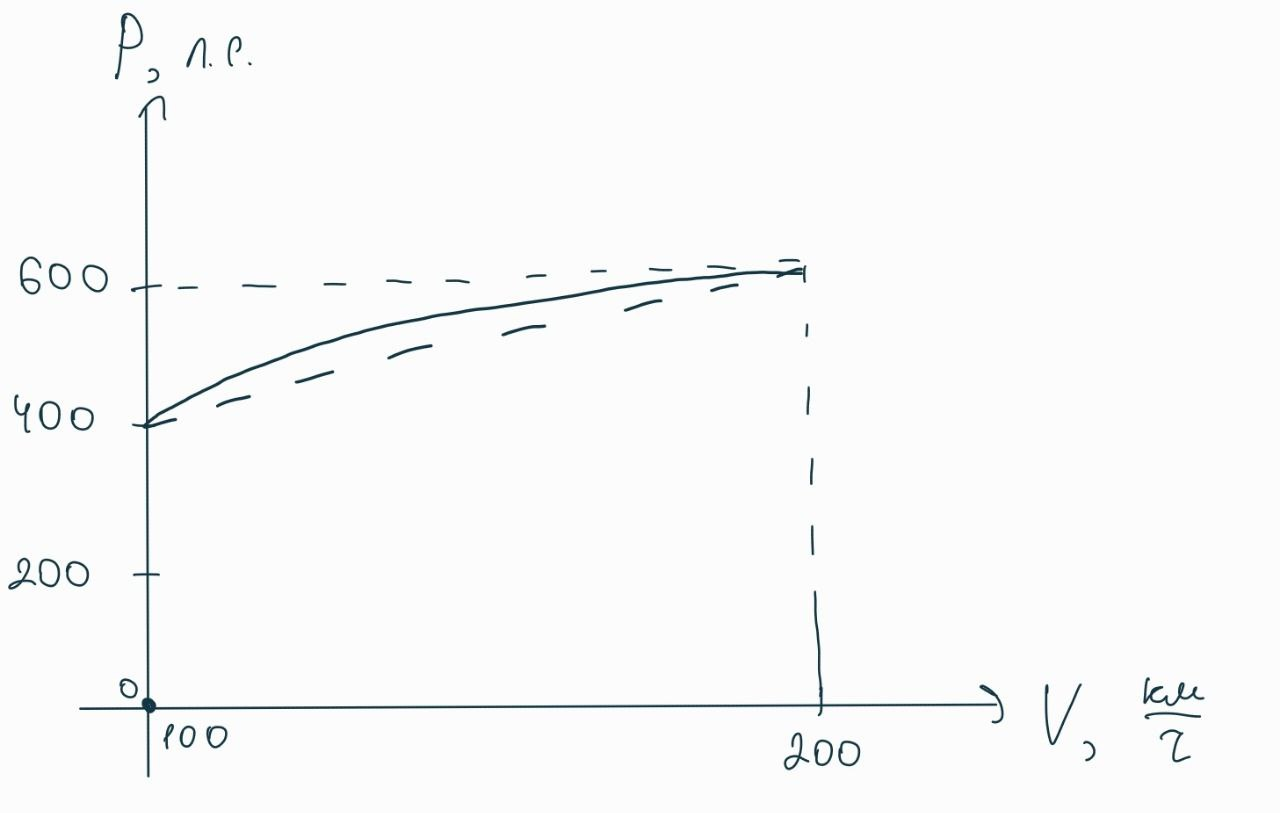
Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:
Тогда итоговое время разгона 100-200 км/ч:
Время разгона “по паспорту” 7.6 с. И снова мы оказались близко к истине!
P.S. не хочу объяснять, откуда взялось (V^2 – V_0^2), можете повыводить на досуге 🙂
Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная “школьные” формулы по физике, можно решать такие интересные задачки, связанные с жизнью.
Как рассчитать скорость в зависимости от оборотов двигателя и выбранной передачи

Немного из школьного курса математики и геометрии — как рассчитать скорость в зависимости от оборотов двигателя и выбранной передачи.
Для этого необходимо знать размерность шин и передаточные отношения главной пары и передач в коробке передач…
Формулы:
Диаметр колеса: Ширина шины, м х Профиль, % х 2 + Диаметр обода, дюймов х 2,54/100
Пример: шина 195/65R15: 0,195 х 0,65 х 2 + 15 х (2,54 / 100) = 0,63 м
Используя формулу диаметра колеса, можно посчитать на сколько изменится клиренс, поделив изменение диаметра на 2
Окружность колеса: Диаметр колеса х число Пи (3,14)
Пример: 0,63 м х 3,14 = 1,98 м
Используя формулу окружности колеса, можно посчитать на сколько процентов изменятся показания одометра и спидометра при замене дисков и/или резины, поделив новое значение окружности на старое и отняв единицу, и умножив полученное значение на сто
Скорость автомобиля при 1 000 об/мин на выбранной передаче: Окружность колеса делим на произведение передаточного отношения главной пары и передаточного отношения выбранной передачи, полученное число умножаем на 60 (минут в часе) и делим на 1 000 (метров в километре), далее полученное число умножаем на число оборотов двигателя в минуту (в нашем случае 1 000 об/мин)
Пример: [1,98 / (3,8 х 1 (пятая передача))] х (60 / 1 000) х 1 000 = 31 км/ч
Технические данные для расчетов (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):
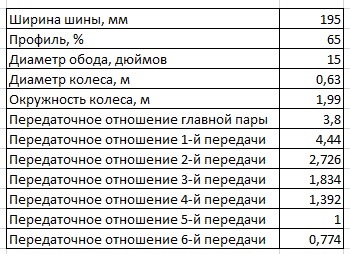
Непосредственно сами расчеты (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):
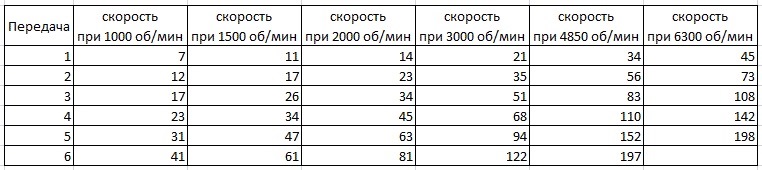
* Максимальная мощность на этом двигателе достигается при 6 300 об/мин, максимальный крутящий момент — при 4 850 об/мин
Источник
Расчет максимальной скорости автомобиля
Это будет не информационный пост как обычно, а некий мануал, калькулятор, который в зависимости от заданных типоразмеров шин, оборотов мотора и указанных передаточных чисел коробки рассчитает, какая будет скорость движения у автомобиля на передачи.

Конечно, калькулятор скорости автомобиля по передаточным числам и шинам производит расчет в идеальных (лабораторных) условиях. В реальных же условиях на конечную скорость автомобиля влияет очень много факторов, начиная от климатических условий и состояния дорожного полотна, и заканчивая настройкой мотора. Другими словами, калькулятор показывает потенциал коробки передач, до какой максимальной скорости она способна разогнать автомобиль.
Калькулятор расчет максимальной скорости автомобиля и КПП
| КПП #1 | КПП #2 |
| Диаметр (R) колеса * : | |
| Ширина колеса: | |
| Профиль колеса: | |
| Обороты двигателя: | |
| Передаточное число главной пары: | |
| Передаточное число 1 й передачи: | |
| Передаточное число 2 й передачи: | |
| Передаточное число 3 й передачи: | |
| Передаточное число 4 й передачи: | |
| Передаточное число 5 й передачи: | |
| Передаточное число 6 й передачи: |
Прогноз максимальной скорости движения авто на передаче:
| 1 я передача: | 23.68 | км/ч | 24.43 | км/ч |
| 2 я передача: | 36.34 | км/ч | 41.52 | км/ч |
| 3 я передача: | 52.47 | км/ч | 58.01 | км/ч |
| 4 я передача: | 69.1 | км/ч | 73.3 | км/ч |
| 5 я передача: | 90.21 | км/ч | 93.04 | км/ч |
| 6 я передача: | нет | км/ч | нет | км/ч |
* Для сликов маркированных в дюймах вводите только R колеса (вводить ширину и профиль не надо).
По умолчанию в калькуляторе расчета передаточных чисел КПП указаны характеристики коробок S4C (КПП #1) и S9B (КПП #2). Выбрал эти коробки не случайно, т.к. первая устанавливалась на Civic EK9, а вторая считается самой длинной МКПП для Б-моторов.
На форуме есть несколько тем, посвященных Honda коробкам, из которых Вы можете узнать передаточные числа для калькулятора. Информация еще не полная, но со временем, усилиями сообщества обновим топики и сделаем полную подборку характеристик:
 — КПП и передаточные числа для моторов B серии;
— КПП и передаточные числа для моторов B серии;
— КПП и передаточные числа для моторов K серии;
— КПП и передаточные числа для моторов H серии;
— КПП и передаточные числа для моторов F серии.
—
В завершении поста, хочу заметить, что при установке на автомобиль дисков большего диаметра или шин отличных от стокового типоразмера, спидометр будет выдавать не совсем корректные данные. Единицы отдают его на калибровку, чтобы снимать точные показания, в 99.999% случаев автовладельцы оставляют все как есть. Чтобы узнать, насколько спидометр «обманывает» Вас, в блоге есть еще один полезный инструмент:
Источник
#Про максимальные скорости. Немного матчасти для сказочников и интересующихся.

нет, сколько можно читать одно и то-же:
» у меня 1,6 115 лс, едет 220 км/ч»
» Opel Astra GTC Z18XER 140 лс, валит 230 км/ч, дальше не разгонялся, страшно»
» Гольфы вообще валят, у бати 170 лс дизель, прёт 250″.
Подобные высказывания очень часто встречаются в интернете и на драйве. Из-за неправильно запрограммированного периметра колёс в ЭБУ и забегающего вперед спидометра.
Что из этого правда?
Огорчу всех, ни-че-го.

Для того, почему к сожалению собственное эго придется немного поубавить и некоторым придется все-же подойти поближе к писсуару, поскольку у них не такой длиный хер пенис как им кажется, попытаюсь вам немного рассказать сегодня.

Сперва заявим, что как правило заявленая мощность и момент производителя соответствуют действительности.
Правило R85 министерства автотранстпорта, сроительства и развития (Германия):
«при окончательной проверки продукции мощность обязана мерится при друх различных оборотах двигателя S1 +S2, которые служили как эталон замера мощности и макс. момента при контрольного образца допуска транспортного средства к эксплуатации. При этих оборотах S1 +S2 как минимум в одной точке измереные значения не имеют превышать или быть ниже показателей образца допуска дтс на 5%».
То есть показания мощности и момента с завода уже не могуть превышать заявленные на более чем 5 %.
Во вторых заявим, что спидометры никогда, никогда не имеют права показывать меньшую скорость чем настоящую. Но бОльшую могут- и показывают, так положено.
При скорости в 250 км/ч скорость может отличатся от реальной на до 30 км/ч!
Особенно негативно влияет неправильный индекс в эбу приборки. Ведь чем МЕНЬШЕ периметр колес, чем запрограммировано, тем бОльшую скорость показывает спидометр. На Астре H например есть 4 группы, которые программируются. Но никто из моих знакомых не парится с ними.
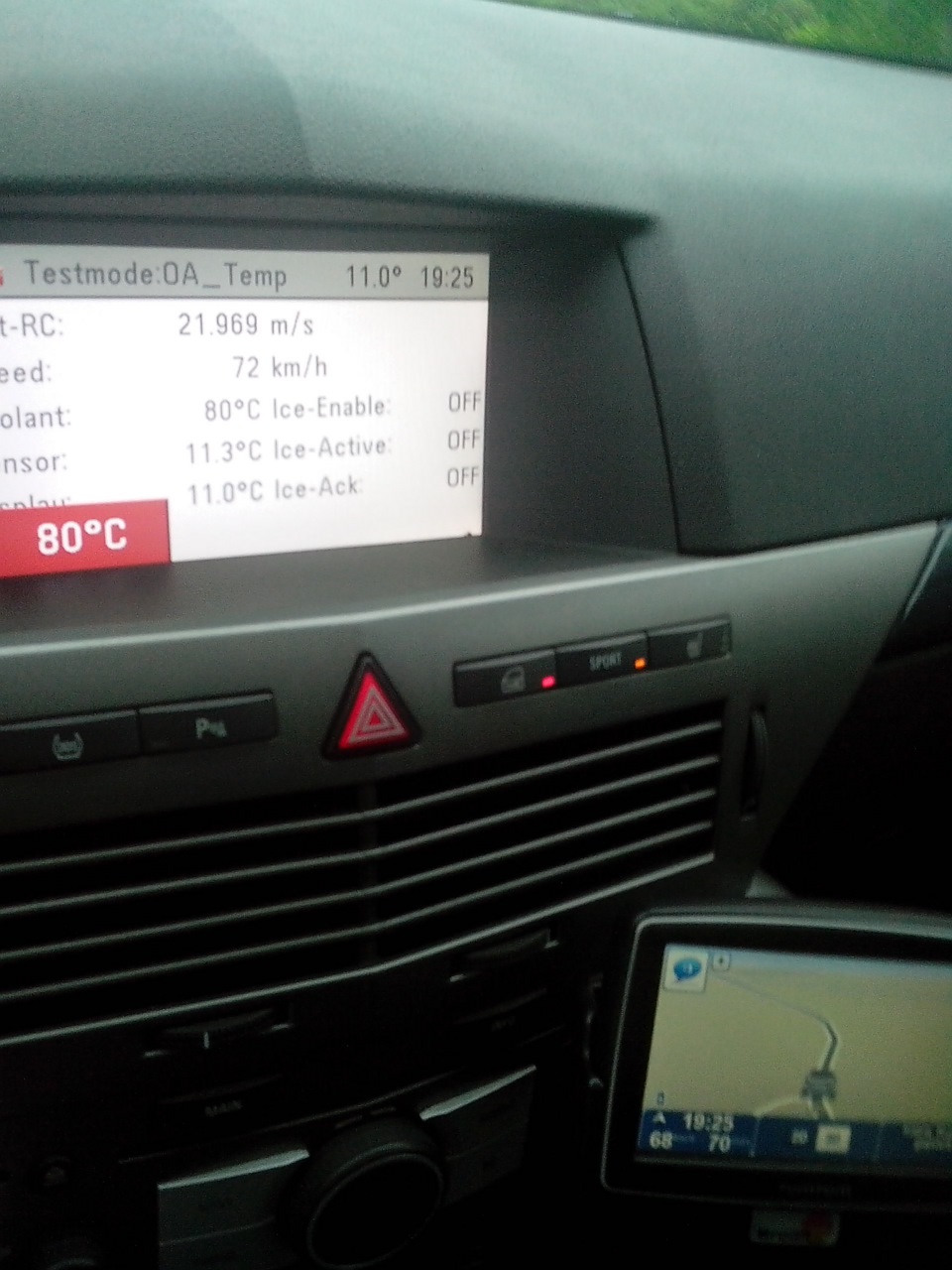
Проверяйте скорость по GPS. Это в данный момент более точный метод чем приборка. P-Box например делает очень точные замеры, основанные на GPS- для беглого взгляда хватит просто мобильного навигатора.

Но ведь есть еще много влияющих на скорость фактов.
Сопротивление воздуха.
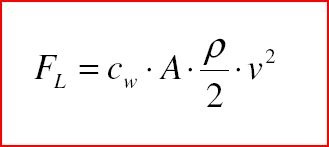
Fl — сопротивление воздуха (N)
Cw — коэффициент лобового сопротивления
A- площадь лобовой поверхности
p — плотность воздуха (кг/м³)
v — скорость (м/с)
Дорожное сопротивление
На этом месте я упущу полное описание дорожного сопротивления. Кто хочет знать об этом точно, погуглите лекцию профессора Отта «Kraftfahrzeuge 1». Тут я лишь укажу примерно точную формулу коэффициента дорожного сопротивления на сухой дороге.
Коэффициент дорожного сопротивления fr:

Дорожное сопротивление FR — исходное от коэффициента и давления на ДП, которое производит ТС из-за своего веса.
FR — сила дорожного сопротивления (N)
Fn — сила давления ДП
fr — коэффициент дорожного сопротивления, бездименсионный.
Это сумма дорожного и воздушного сопротивления.
Диаграмма общего сопротивления:
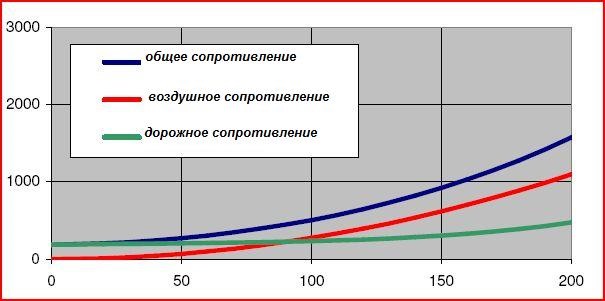
С помощью этих даных и знания диаграммы КПП и момента мотора является возможным вычислить макс. допустимую скорость автомобиля.
Следующая диаграмма показывает Audi A3 1.8 T (8L). Автомобиль заявлен с 217 км/ч.
Линии сопротивления перекрещивается с линией силы тяги (нм) на 216 км/ч. Так что эта форма вычисления довольно точна.
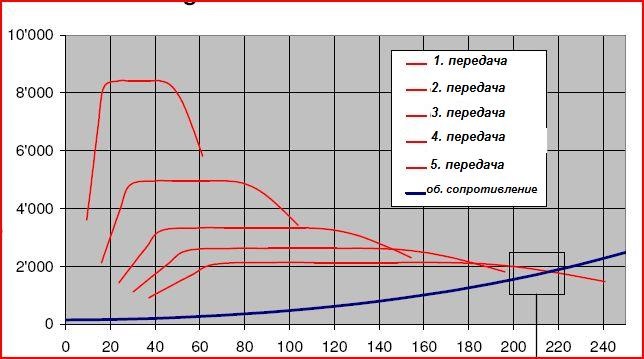
И учитывайте — коэффициент сопротивления после 40 км/ч растет почти в квадрате к скорости!
С помощью так называемого short-cut- метода это можно вычислить быстрее и почти так-же точно. При этом методе используются уже известные данные автомобиля, чтобы вычислить неизвестные. С этой помощью можно просто вычислить фиктивную возможную скорость или нужную мощность для набора определённой скорости.
Силу воздушного сопротивления я уже описывал:
FL — сопротивление воздуха
Сw — коэффициент лобового сопротивления
A- площадь лобовой поверхности
pho — плотность воздуха (кг/м³)
v — скорость
Необходимая мощность — это сила F * расстояние s / время t
Cкорость v — это расстояние s / время t

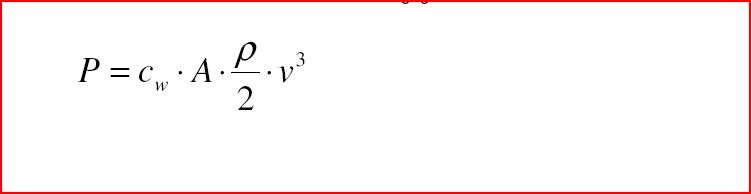
Теперь можно вывести значения мозности для 2 разных скоростей:
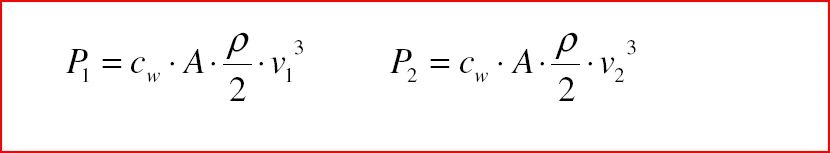
Если сейчас поделить мощность1 на мощность2, то получим формулу для высчета фиктивной макс. скорости.

И как её использовать и вообще о чем это в реальной жизни?
А вот так оно выглядит:
Исходное ТС- ауди а3 (8L), 1.6, 102лс, Vmax — 189 км/ч
-Сколько мощности необходимо, чтобы она поехала 202 км/ч?
-По формуле 125 лс.
Ауди а3 1.8/125 лс заявлена с 202 км/ч
-Сколько мощности необходимо, чтобы она поехала 217 км/ч?
-По формуле 154 лс.
Ауди а3 1.8Т/150 лс заявлена с 217 км/ч
-Сколько мощности необходимо, чтобы она поехала 228 км/ч?
-По формуле 179 лс.
Ауди а3 1.8/180 лс заявлена с 228 км/ч
Как видите, довольно точно…
Кому этого всего много и голова пухнет от формул, и с математикой и физикой возится не хочется, выкладываю готовую таблицу exсel, любезно предоставленную клубом kaoscrew.
Просто задавайте площадь сопротивления, коэффициент и желаемую скорость или мощность и вы увидите, сколько лошадей необходимо иметь для достижения определенной скорости или какую скорость можно достичь. Для площади сопротивления, если она не известна, можете примерно помножить высоту*ширину авто.
И помните — подойдите поближе… Он не такой длинный как вам кажется )
Я надеюсь, что помог чуть развеять миф о валящих 240 км/ч гольфах и фокусах с 140 лс. ) )
Источник
Максимальная скорость, аэродинамика, мощность и момент (мат. часть)

Доброго времени суток, в прошлой записи Максималки Astra G на которую меня сподвигло большое количество сказочников я пропустил мимо практически всю физику. Видимо зря. Не то, чтобы меня это сильно беспокоило, но ввиду свободного времени в выходной и плохой погоды — решил состряпать статейку из нескольких копи-паст (источники вконце) и немножко отсебятины.
Всем остальным для общего развития не помешает почитать и подчерпнуть какие-то знания, или уточнить что-то, что вызывало сомнения. Возможно пригодится кому-то, чтобы объяснить своему товарищу, что » вы, батенька, пиздите » он не прав и немножко привирает. Потому что, даже грамотные и уважаемые люди после прошлой записи немного недопонимали основного. Цитата » Тебя сейчас бомбанет если я напишу что мой нексиевский 8миклоп с длинным коробасом 200 поедет, только скорость буду набирать примерно минут 20» Не бомбануло, он поедет столько-же сколько и с «коротким коробасом», почему? читаем про мощность и момент.
Часть 1. Коэффициент аэродинамического сопротивления Cx
Наверное, каждый слышал о том, что сила сопротивления воздуха пропорциональна квадрату скорости – столь быстро нарастает противодействие движению в процессе разгона. Впечатляет, но как это соотнести с параметрами автомобиля? Для этого нужно лишь перейти в термины механической работы, и тогда получится, что отбираемая от двигателя мощность находится аж в кубической зависимости от скорости! Только представьте, с каким трудом даются автомобилю последние десятки километров в час. В таких условиях даже значительная прибавка мощности мотора не в состоянии существенно увеличить максимальную скорость.
Таким образом, задача снижения лобового сопротивления – приоритетная задача не только для аэродинамики, но, в свете борьбы за экологию, и для всего автомобилестроения в целом.

Решение можно искать по двум направлениям. Первое – это уменьшение площади поперечного сечения автомобиля, иными словами, создание более узкого и низкого кузова. Путь весьма эффективный, ибо сопротивление воздуха напрямую зависит от размеров объекта, но, к сожалению, совершенно расходящийся с нынешней тенденцией к увеличению габаритов автомобилей. И увеличению, стоит отметить, немалому, ведь в моду активно входят кроссоверы, вторгающиеся даже в совершенно чуждый им сегмент спортивных, скоростных автомобилей, где требования к аэродинамике предельно высоки.
А значит остается второй и единственный вариант – оптимизация процесса обтекания кузова, критерием совершенства которого как раз и является коэффициент аэродинамического сопротивления Cx (или Cw, как иногда встречается в литературе).
Величина Cx определяется опытным путем. Факторов, влияющих на Cx автомобиля, несколько: во-первых, это внутреннее сопротивление, возникающее при прохождении воздуха через подкапотное пространство и салон, во-вторых, сопротивление трения между воздушным потоком и поверхностью кузова, и, в-третьих, сопротивление формы, проявляющееся главным образом в избыточном давлении перед автомобилем и разряжением позади него.
Внутреннее сопротивление составляет около 12% от общей величины, и пока особых успехов в этой области не наблюдается: напротив, все более и более мощные моторы современных автомобилей требуют все больше воздуха для охлаждения. Например, в пределе 300-сильный бензиновый двигатель выделяет в виде тепла около 450кВт – этого хватило бы для отопления нескольких особняков! Соответственно, растут размеры радиаторов, уплотняются моторные отсеки, увеличивается сопротивление воздуха… Существенные же улучшения здесь возможны лишь при переходе на более эффективные электродвигатели, но пока они так и остаются технологией будущего.
Сопротивление поверхностного трения так же вносит свой 10-процентный вклад в величину Cx. Вообще, наличие столь ощутимого трения между воздухом и кузовом может показаться странным, но оно действительно имеет место: прилегающий к поверхности слой воздуха сталкивается с микронеровностями покрытия и тормозиться — образуется так называемый пограничный слой. Пока это течение находится в ламинарном состоянии, то есть все его частицы движутся в одном направлении, толщина пограничного слоя невелика (около нескольких миллиметров) и сопротивление трения небольшое. Но с переходом в турбулентное состояние, когда поток «спотыкается» о более крупное препятствие, и траектории его частиц становятся хаотичными, пограничный слой расширяется, а вместе с ним увеличивается и трение – воздух словно становится более вязким. Таким образом, от разработчиков в данном случае требуется обеспечение гладкости кузова, дабы пограничный слой дольше оставался ламинарым. А для этого нужно уменьшать зазоры кузовных элементов, закрывать уплотнителями щели между деталями. Помогает и придание поверхностям небольшой кривизны – прилегающий поток ускоряется, давление в нем падает, и траектории частиц упорядочиваются. К сожалению, в целях экономии этими мерами в последнее время частично пренебрегают, например, уплотнители по периметру лобового стекла или вокруг фар сейчас встретишь нечасто.
И, наконец, сопротивление формы или сопротивление давления – главный фактор, определяющий значение Cx. Причина его возникновения понятна – спереди на автомобиль давит набегающий поток воздуха, а позади его «оттягивает» назад зона разряжения, образующаяся в результате отрыва потока от резко заканчивающегося кузова. Решение проблемы тоже, казалось бы, очевидно – нужно придать автомобилю такую форму, чтобы он плавно рассекал воздух и опять-таки плавно, без отрыва потока от поверхности, позволял ему сойтись позади себя. Но загвоздка в том, что в соответствии с такими требованиями автомобиль должен напоминать дирижабль (точнее, его половину, отрезанную в продольной плоскости), то есть иметь минимум граней и, главное, очень длинную, постепенно сужающуюся заднюю часть. Разумеется, о рациональной компоновке в данном случае говорить трудно.
Немножко о Cx ВАЗов.
Что может стандартный ВАЗовский двигатель и чего он не может.
Скоростные характеристики.
ВАЗ 2108-09-99-2115: Cx — 0,468; S (площадь лобового сопротивления) — 1,8
1100 карб. (39,7 кВт/54,4 л.с.) — 139, 35 км/ч.
1300 карб. (47 кВт/64,4 л.с.) — 147,42 км/ч.
1500 карб. (51,5 кВт/71,6 л.с.) — 152 км/ч.
1500 инж. (60 кВт/82,2 л.с) — 159,92 км/ч.
ВАЗ 2110: Cx — 0,348; S (площадь лобового сопротивления) — 1,93
1500 инж. 8-кл. (56 кВт/76,7 л.с.) — 168,54 км/ч.
1500 инж. 16-кл. (69 кВт/94,5 л.с.) — 180,69 км/ч
Для достижения «зубилом» скоростного барьера в 200 км/ч. необходима мощность двигателя 160 л.с, «десятке» потребуется поменьше — 130 л.с. Другие «контрольные точки» —
170 км/ч — 100 л.с (2108)/ 80 л.с (2110)
180 км/ч — 120 л.с (2108)/ 95 л.с (2110)
190 км/ч — 140 л.с (2108)/110 л.с (2110)
Будьте реалистами. Законы физики обмануть невозможно. Для преодоления каждых «лишних» 10 км/ч на максимальных скоростях «зубилкам» требуется около 20 л.с, «матрешкам» — 15 (Дальше — еще больше: сопротивление растет пропорционально квадрату скорости) Хвастливые утверждения о достижении на стандартных авто ВАЗ скорости 200 (300) км/ч. могут вызвать лишь улыбку. Cx Нивы 0.536 поэтому я дико ржал с мифического родственника одного из коментаторов, который 170 на ней ехал. 137 максималка НИВЫ.

Барьер 300 км/час требует от двигателя минимум 390 лошадиных сил и двигаться на таких скоростях могут только спортивные авто либо седаны огромной по 600+лс мощности.
400 км/час. Даже имея двигатель мощностью 1000 лошадиных сил не каждый суперкар может развить эту скорость ведь сопротивление воздуха на таких скоростях так велико что для преодоления каждых 10 км/час приходиться добавлять к мощности двигателя около 100 лошадей.

Часть 2. Мощность и крутящий момент
Часто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал.
Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F.
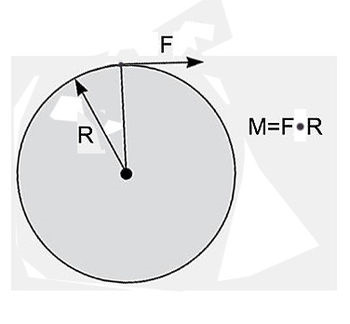
Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2πR – и выполнит работу: А = F • R • 2π = М • 2π. А работа за n оборотов: А = М • 2π • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2πn /60.
Выражение 2π n /60 = 0,1047 n = ω – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]).
Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]).
Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое.
Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того
Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя. Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде.
Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.

Величины мощности N1 … N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.
Главные враги любителя скорости – не гаишники, а силы, тормозящие движение, – от этих не откупишься! Мощность сопротивления воздуха вкупе с мощностью шинных потерь показаны на рис. 1 линией Nсопр.
(Желающие посчитать, могут воспользоваться следующими формулами. Nсопр. = Nw + Nf. Мощность аэродинамических потерь Nw для автомобиля весом 15000 Н при плотности воздуха 1,25 кг/м3, Сх = 0,3 и лобовой площади S = 2 • м2 составляет: Nw = (0,3 • 2 • 1,25)/2 • v3 = 0,375 v3 Вт. А мощность шинных потерь Nf = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч Nсопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)
Колеса автомобиля, борясь с мощностями сил сопротивления, при максимальной скорости полностью расходуют мощность, получаемую от двигателя. Но ее характеристика (например, показанная кривой N4 на рис.1) при полностью открытом дросселе похожа на гору с округлой макушкой, тогда как характеристика мощности сопротивлений Nсопр. поднимается как крутая парабола. Чтобы полностью использовать арсенал мощности двигателя – и получить максимум скорости V4 (на горизонтальной трассе, без ветра), передаточное число трансмиссии и размер шин подбирают так, чтобы кривая Nсопр пересекла кривую N4 возле вершины. Максимальные скорости на третьей и пятой передачах (V3 и V5) существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.
Другие враги скорости – подъем дороги и встречный ветер. Подъем с углом всего 1,5% добавит к потерям в шинах еще столько же. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, – и уже эту сумму в расчете затрат мощности надо возвести в куб! При скорости по спидометру 36 км/ч (10 м/сек) и ровном встречном ветре 5 м/сек мощность Nсопр вырастет лишь на 0,9 кВт, а вот при 180 км/ч (50 м/сек) – аж на 15,5 кВт

Так зависит крутящий момент (М1…М5) или тяговая сила (Fтяг 1 …Fтяг 5) на ведущей оси от включенной передачи. При коэффициенте сцепления шин с дорогой 0,7 ведущая ось, нагруженная половиной веса машины (Gавтом = 15000 н), может создать реальную тяговую силу не больше Fмакс. доп. = 5250 Н.
На рис.2 величины крутящего момента М1…М5, а заодно и теоретические тяговые силы F1…F5 на ведущей оси, показаны одними и теми же кривыми, – ведь тяговые силы пропорциональны моментам. Величины сил – на вертикальной оси справа. Но тут важно учесть следующее.
Разгоняет машину не вся тяговая сила, а лишь избыточная – то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать – считать, что машину разгоняет полная сила Fтяг.1. Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Если, например, ведущая ось несет половину веса машины – 7500 Н, то при коэффициенте сцепления φ = 0,7 тяговая сила не может превысить 35% ее веса. Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!).
Если избыточная сила (на первой передаче, например) слишком велика, машина «шлифует» дорогу. Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие – тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы (или моменты) на колесах. Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее.
Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там. Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению. То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов — оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. Почему?
А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: «Человек совершенно может не иметь понятие про мощность.А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать.» Ясно, что на динамику автомобиля оказывают большое влияние и передаточные числа КПП. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.
При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона (по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени). Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов (дальше водитель двигатель раскручивает редко). И что выходит? А выходит, что «низовой», моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль. А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.
Проповедующие формулировку «скорость определяется мощностью, а динамика разгона — моментом двигателя» могут убедиться в своем заблуждении, решив простую задачу.
Вводные
1. Равномерный подъем на некоторую высоту равносилен равномерному ускорению, поскольку увеличивает потенциальную энергию тела mgh*. (что можно объяснить — чем с большей высоты упадет, тем сильней ударится).
2. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.
3. Имеется черный ящик, в котором спрятан мотор неизвестной природы и, возможно, редуктор с КПД=1.
Вопросы.
1. Какая мощность должна быть в моторе, спрятанном внутри черного ящика?
2. Какой момент должен быть в моторе, спрятанном внутри черного ящика?
Подъем указанного груз на нужную высоту за время аналогичен разгону по горизонтали той же массы с ускорением g в 0.5 степени или корень из g.
Если ускорение определяется моментом — просто назовите цифру
Если ускорение определяется мощностью — тоже просто назовите цифру
Если цифру назвать не удается, значит параметр может быть самым разным и роли не играет.
Вы можете разгонять тело с заданным ускорением (или поднимать его вверх), меняя крутящий момент по своей прихоти (и устанавливая каждый раз соответствующий редуктор). Вы можете отталкиваться от параметров редуктора, и всякий раз требуемый момент будет меняться и зависеть от передаточного отношения этого редуктора. Но всегда мощность будет оставаться одной и той же, неизменной величиной — для подъема груза 75 кг на 1 м за 1с понадобится ровно одна лошадиная сила или 0,73549875 кВт
Это практически ответ на цитату про «длинный коробас».
Касаемо тех-же астр, если воткнуть коробку F18 с 2.0 вместо F13 на какой-нибудь 1.2 или 1.4 двигатель, максималка не увеличится, а скорее даже и снизится, потому что передаточные числа подобраны оптимально для более мощного двигателя и с ними не будет достигнута оптимальная мощность на более слабом двигателе.
Повторюсь: будьте реалистами. Законы физики обмануть невозможно.
Если дочитали до конца, то молодцы. Надеюсь кому-нибудь когда нибудь пригодится этот материал. Можно кидать на него ссылку особо упёртым в своей правоте гонщикам))) Хотя таких людей ничего не переубедит.
Источник
Немного из школьного курса математики и геометрии — как рассчитать скорость в зависимости от оборотов двигателя и выбранной передачи.
Для этого необходимо знать размерность шин и передаточные отношения главной пары и передач в коробке передач…
Формулы:
Диаметр колеса: Ширина шины, м х Профиль, % х 2 + Диаметр обода, дюймов х 2,54/100
Пример: шина 195/65R15: 0,195 х 0,65 х 2 + 15 х (2,54 / 100) = 0,63 м
Используя формулу диаметра колеса, можно посчитать на сколько изменится клиренс, поделив изменение диаметра на 2
Окружность колеса: Диаметр колеса х число Пи (3,14)
Пример: 0,63 м х 3,14 = 1,98 м
Используя формулу окружности колеса, можно посчитать на сколько процентов изменятся показания одометра и спидометра при замене дисков и/или резины, поделив новое значение окружности на старое и отняв единицу, и умножив полученное значение на сто
Скорость автомобиля при 1 000 об/мин на выбранной передаче: Окружность колеса делим на произведение передаточного отношения главной пары и передаточного отношения выбранной передачи, полученное число умножаем на 60 (минут в часе) и делим на 1 000 (метров в километре), далее полученное число умножаем на число оборотов двигателя в минуту (в нашем случае 1 000 об/мин)
Пример: [1,98 / (3,8 х 1 (пятая передача))] х (60 / 1 000) х 1 000 = 31 км/ч
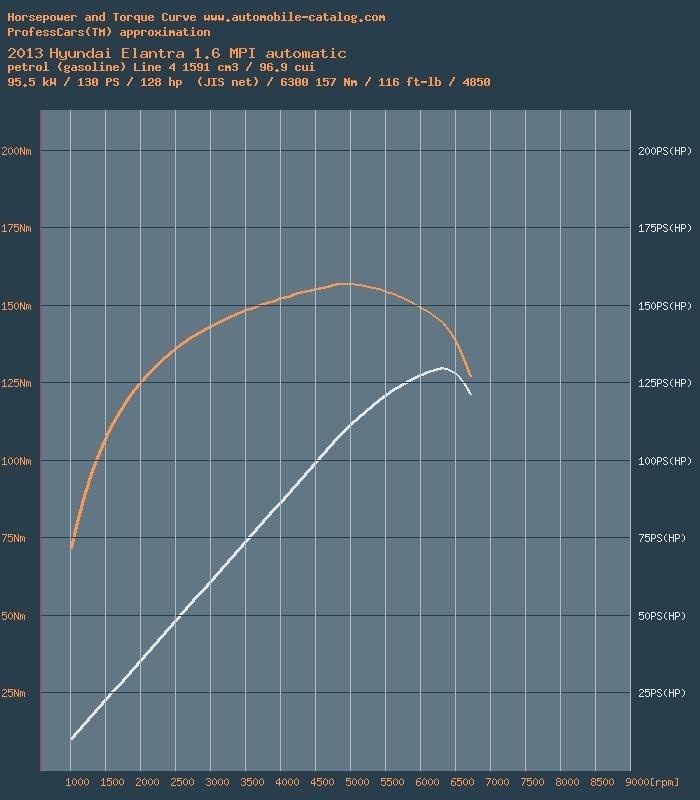
Технические данные для расчетов (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):

Непосредственно сами расчеты (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):

* Максимальная мощность на этом двигателе достигается при 6 300 об/мин, максимальный крутящий момент — при 4 850 об/мин
Запчасти на фото: KH130, 55006000
Технические характеристики для расчетов взяты с этого сайта www.automobile-catalog.com
Цена вопроса: 0 €
Пробег: 7 600 км
Для
всех ступеней коробки передач и
дополнительной коробки рассчитываются
значения
скорости движения автомобиля в зависимости
от частоты вращения коленчатого вала
двигателя (по согласованию с руководителем
расчёт может производиться только
для высшей ступени дополнительной
коробки).
Расчёт
ведётся по формуле
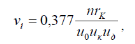
где
v
–
скорость автомобиля, км/ч;
n
–
частота вращения коленчатого вала
двигателя, об/мин;
rК
–
радиус качения, м;
и0
–
передаточное число главной передачи;
ик
–
передаточное число рассчитываемой
ступени коробки передач;
ид
–
передаточное число рассчитываемой
ступени дополнительной (раздаточной)
коробки.
Значения
частоты вращения коленчатого вала
берутся теми же, что и при построении
внешней скоростной характеристики.
Рассчитанные
значения vt
заносятся
в столбец 4 табл. 2.1. Графики зависимости
скорости движения автомобиля от частоты
вращения коленчатого вала двигателя
представляют собой серию лучей, выходящих
под разными углами из начала координат
рисунок 2.2.
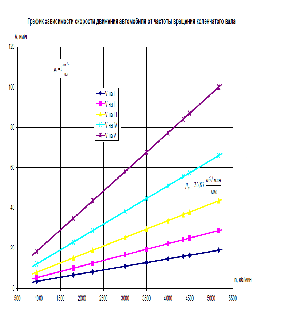
Рис.
2.2 Зависимости скорости движения
автомобиля от частоты вращения коленчатого
вала по передачам.
2.6. Тяговая характеристика и тяговый баланс автомобиля
Тяговая
характеристика представляет собой
зависимость силы тяги автомобиля от
скорости движения по передачам. Значения
силы тяги РТ
рассчитываются
в отдельных точках по формуле
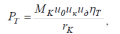
(2.26)
где
МК
–
крутящий момент двигателя, Нм;
ηТ
–
КПД трансмиссии.
Результаты
расчёта РТ
заносятся
в столбец 7 табл. 2.1, и по ним строятся
графики зависимости РТ
=f(V)
по
передачам.
Тяговый
баланс автомобиля описывается уравнением
тягового или силового баланса
РТ
=
Рд
+
Рв
+
Ри
,
(2.27)
где
РТ
–
сила тяги автомобиля, Н;
Рд
–
суммарная сила сопротивления дороги,
Н;
Рв
–
сила сопротивления воздушной среды, Н;
Ри
–
сила инерции автомобиля, Н.
Величина
Рд
определяется
по выражению
Рд
= Gaψ, (2.28)
где
Ga
– полный
вес автомобиля, Н; ψ
– суммарный
коэффициент сопротивления дороги.
Суммарный
коэффициент сопротивления дороги
является величиной, зависящей от
скорости автомобиля. Однако учёт этой
зависимости сильно осложняет
выполнение тягового расчёта и в то же
время не даёт важного для практики
уточнения. Поэтому при выполнении
тягового расчёта рекомендуется принять
значение ψ
постоянным,
равным тому значению, которое было
рассчитано для максимальной скорости
движения автомобиля при определении
мощности двигателя, необходимой для
движения на режиме максимальной
скорости, т.е. принять везде ψ=ψv.
При
каком-то одном выбранном значении ψ
величина
Рд
остаётся
постоянной для всех расчётных точек
на всех передачах. Поэтому значение Рд
подсчитывается
один раз и в таблицу не заносится. На
графике тяговой характеристики
зависимость PТ=f(v)
представляется
в виде прямой, параллельной оси абсцисс.
Рис.
2.3 Тяговая характеристика автомобиля.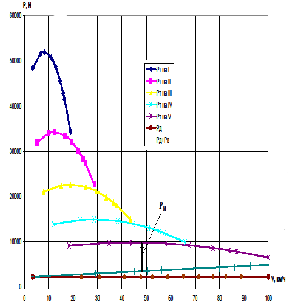
Сила
сопротивления воздушной среды Рв
составляет
величину
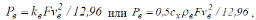 (2.29)
(2.29)
где
сх
– коэффициент
продольной аэродинамической силы;
рв
– плотность
воздуха, кг/м3
;
кв
– коэффициент
обтекаемости, кг/м3;
F
– лобовая
площадь автомобиля, м ;
vв
– скорость
воздушного потока относительно
автомобиля, км/ч.
При
расчёте можно задать ρв=1,225
кг/м . Скорость воздушного потока обычно
принимается равной скорости движения
автомобиля.
Значения
Рв
рассчитываются
для всех точек и заносятся в столбец 5
табл. 2.1. График зависимости Рв
от
скорости представляет собой параболу,
проходящую через начало координат.
Для
удобства дальнейшего анализа этот
график смещают вверх на величину,
равную Рд
(в
принятом для сил масштабе). Фактически
при таком построении этот график выражает
зависимость (Pв+Pd)=f(v).
Сила
инерции автомобиля Ри
после
расчёта Рд
и
Рв
может
быть определена как замыкающее слагаемое
силового баланса
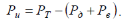 (2.30)
(2.30)
На
графике значение Ри
определяется
отрезком прямой, проведённой для нужного
значения скорости параллельно оси
ординат, между точками пересечения этой
прямой графиков PТ=f[v)
и
(Pд+Pв)=f(v).
Если
заданная скорость может быть обеспечена
на нескольких передачах, то каждой из
этих передач будет соответствовать
своё значение силы инерции. Рассчитанные
значения Ри
следует
занести в столбец 6 табл. 2.1.
Значение
РТ
заносится в столбец 7 табл. 2.1. Тяговая
характеристика автомобиля представлена
на рис. 2.3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти скорость зная силу и мощность ?
ксюша моторина
Ученик
(188),
на голосовании
11 лет назад
Голосование за лучший ответ
Александр Тюльдиков
Знаток
(464)
11 лет назад
скорость равна мощность делённая на силу
sage_kih
Ученик
(123)
3 года назад
V=P/F
Похожие вопросы
