Как для высказывания найти предикат

Как для высказывания найти предикат

Высказывания и предикаты. Кванторы

  1. Высказывания
  2. Предикаты
  3. Кванторы
  4. Примеры

п.1. Высказывания

Высказывание – это повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно.

Например:
«Число 13 – нечётное» – высказывание, истинное
«2 + 2 = 5» – высказывание, ложное
«Мы живём в XXI веке» – высказывание, истинное
«Который час?» – не высказывание, т.к. вопросительное предложение
«Вася Пупкин – хороший человек» – не высказывание, т.к. неоднозначно. Но, если определить множество людей, которые оцениваются, и правила их оценки так, что предложение приобретёт однозначность, оно станет высказыванием.

Высказывания обозначают большими латинскими буквами (A, B, C, X, Y, Z, …)

Например:
A: натуральное число a делится на 2;
B: натуральное число a чётное.
Заметим, немного забегая наперёд, что в данном случае из А следует В, и из В следует А. Говорят, что эти высказывания эквивалентны: A ⇔ B.

п.2. Предикаты

Предикат – это предложение с переменной P(x), которое становится высказыванием при подстановке определённого значения переменной.
Предикат P(x) является функцией, которая определена на некотором множестве значений {x}, и ставит ему в соответствие два значения {0; 1} – истина или ложь.

Например:
P(x): x – объект с четырьмя ногами
При x = слон – предикат становится истинным высказыванием, P(“слон” )=1
При x = муравей – предикат становится ложным высказыванием, т.к. у муравья 6 ног, P(муравей)=0
При x = стол – предикат становится истинным высказыванием, P(“стол” )=1
При x = человек – предикат становится ложным высказыванием, т.к. у человека 2 ноги, P(человек)=0

Множество значений переменной, на котором предикат становится истинным, называют множеством истинности предиката.
Предикат, который при любых значениях переменной, является истинным, называют тождественным предикатом или тождеством.

Например:
P(x):|x| ≥ 0 – выполняется при любом значении x, это тождественный предикат.
(mathrm{P(x)=1, forall xin mathbb{R}})

Предикат может быть функцией нескольких переменных, в этом случае его называют многоместным предикатом.

Например:
P(x, y): x делится на y – двуместный предикат, который становится истинным высказыванием на парах значений переменных (15;5), (14;7), (16;4) и т.д.
P(a, b):(a + b)2 = a2 + 2ab + b2 – является тождественным двуместным предикатом, т.к. выполняется для любых a и b.

п.3. Кванторы

Квантор – логическая операция, ограничивающая область истинности предиката и создающая высказывание.

Вид квантора

Обозначение

Читается

Всеобщности

∀

«для любого…», «для всех…», «любой…»

Существования

∃

«существует…», «найдётся…»

Единственности и существования

∃!

«существует точно одно такое, что…», «существует и единственно…»

Пусть P(x) – одноместный предикат. Чтобы установить истинность высказывания (∃x)P(x), достаточно найти хотя бы один такой x*, что P(x* ) становится истинным высказыванием.

Например:

Высказывание

Формула

Доказательство истинности

Существуют натуральные числа, которые делятся на 13

(mathrm{(exists xin mathbb{N})x : 13})

Например x = 26

Существуют треугольники, у которых все углы равны

(∃ΔABC) ∠A = ∠B = ∠C

Например, равносторонний треугольник со стороной 1

Пусть P(x) – одноместный предикат. Чтобы установить ложность высказывания (∀x)P(x), достаточно найти хотя бы один такой x*, что P(x* ) становится ложным высказыванием.

Например:

Высказывание

Формула

Доказательство ложности

Любое натуральное число делится на 5

(mathrm{(forall xin mathbb{N})x : 5})

Например x = 6 на 5 не делится

У любого выпуклого четырехугольника диагонали перпендикулярны

(∀ABCD) AC ⊥ BD

Например, у прямоугольника со сторонами 3 и 4 угол между диагоналями ≈ 74° ≠ 90°

Пусть P(x) – одноместный предикат. Чтобы установить истинность высказывания (∀x)P(x), необходимо доказать, что предикат P(x) является тождеством.

Например:

Высказывание

Формула

Доказательство истинности (тождественности)

Разность квадратов двух любых выражений равна произведению суммы и разности

(mathrm{(forall x,y)x^2-y^2=(x+y)(x-y)})

Сумма углов любого треугольника равна 180°.

(∀ABC) ∠A + ∠B + ∠C = 180°

Третий класс задач (теорема) – самый сложный, т.к. требует не просто одного примера, а доказательства в общем случае.

п.4. Примеры

Пример 1. Запишите по два высказывания (A – истинное, B – ложное), относящиеся к
а) физике
A: Плотность равна отношению массы тела к его объему.
B: КПД механизма может быть больше 1.
б) химии
A: Гидроксид натрия – сильное основание.
B: Сульфат натрия – нерастворимая соль.
в) географии
A: На Земле шесть материков.
B: На Земле три океана.

Пример 2. Запишите по два предиката, относящиеся к
а) физике
A(h): Потенциальная энергия прямо пропорциональна высоте h.
B(v): Сила лобового сопротивления прямо пропорциональна квадрату скорости v2.
б) химии
A(x,y): Между основанием x и кислотой y проходит реакция нейтрализации.
B(x): Металл x вытесняет водород из HCl.
в) географии
A(x,y,z): День x является днём y солнцестояния в z полушарии.
B(x,y): Река x впадает в море y.

Пример 3. С каким из кванторов предикат x2 + 4 = 12 станет истинным высказыванием?
Если запишем (∀x) x2 + 4 = 12 – это ложное высказывание, т.к., например, при x=0 оно не выполняется.
Если запишем (∃x) x2 + 4 = 12 – это истинное высказывание, т.к., например, при (mathrm{x=2sqrt{2}}), оно выполняется.
Если запишем (∃x!) x2 + 4 = 12 – это ложное высказывание, т.е. решений у данного уравнения не одно, а два: (mathrm{x_{1,2}=2sqrt{2}})
Ответ: квантор существования ∃.

Пример 4. Найдите область истинности предиката: $$ P(x): left{ begin{array}{ l } mathrm{x^2-11x+28geq 0} & \ mathrm{x^2-11x+18lt 0} & end{array}right. $$ Решаем систему: $$ left{ begin{array}{ l } mathrm{(x-4)(x-7)geq 0} & \ mathrm{(x-2)(x-9)lt 0} & end{array}right. $$ Пример 4
Область истинности предиката: x ∈ (2;4] ∪ [7;9)
P(x) = 1 приx ∈ (2;4] ∪ [7;9)

Источник

1. Высказывания и предикаты. Отрицание высказывания

Относительно
понятий и отношений между ними можно
высказы­вать
различные суждения. Языковой формой
суждений являются повествовательные
предложения. Предложения,
используемые в математике, могут быть
записаны как в словесной форме, так и в
символической. Предложения могут нести
верную или ложную информацию.

Высказыванием
называется любое повествовательное
предложение, которое может быть либо
истинным, либо ложным.

Пример.
Следующие предложения являются
высказываниями:

1)
Все студенты МГПУ – отличники (ложное
высказывание),

2)
На Кольском полуострове водятся крокодилы
(ложное высказывание),

3)
Диагонали прямоугольника равны (истинное
высказывание),

4)
Уравнение
не имеет действительных корней (истинное
высказывание),

5)
Число 21 – четное (ложное высказывание).

Следующие
предложения не являются высказываниями:

  1. Какая
    погода будет завтра?

  2. х
    – натуральное
    число,

  3. 745
    + 231 – 64.

Высказывания
принято обозначать большими буквами
латинского алфавита: А,
В, С,…, Z.

«Истина»
и «ложь» называются значениями
истинности высказывания.
Каждое высказывание либо истинно, либо
ложно, одновременно быть и тем, и другим,
оно не может.

Запись
[А]
= 1 означает,
что высказывание
А
– истинно.

А
запись [А]
= 0 означает,
что высказывание
А
– ложно.

Предложение
не является высказыванием, так как о
нем невозможно сказать: истинно оно или
ложно. При подстановке конкретных
значений переменнойх
оно обращается в высказывание: истинное
или ложное.

Пример.
Если
,
то– ложное высказывание, а если,
то– истинное высказывание.

Предложение
называетсяпредикатом
или высказывательной
формой. Оно
порождает множество высказываний одной
и той же формы.

Предикатом
называется
предложение с одной или несколькими
переменными, обращающееся в высказывание
всякий раз при подстановке вместо
переменных их значений.

В
зависимости от числа переменных, входящих
в предложение, различают одноместные,
двухместные, трехместные и т.д. предикаты,
которые обозначаются:
и т.д.

Пример.
1)
– одноместный предикат,

2)
«Прямая х
перпендикулярна прямой у»
– двухместный предикат.

Также
в предикатах переменные могут содержаться
неявно. В предложениях: «Число четное»,
«две прямые пересекаются» переменных
нет, но они подразумеваются: «Число х
– четное», «две прямые х
и у
пересекаются».

При
задании предиката указывают его область
определения
– множество,
из которого выбираются значения
переменных, входящих в предикат.

Пример.
Неравенство
можно рассматривать на множестве
натуральных чисел, а можно считать, что
значение переменной выбирается из
множества действительных чисел. В первом
случае областью определения неравенствабудет множество натуральных чисел, а
во втором – множество действительных
чисел.

Одноместным
предикатом,
заданным на множестве Х,
называется предложение с переменной,
которое обращается в высказывание при
подстановке в него переменной из
множества Х.

Множеством
истинности
одноместного предиката называется
множество тех значений переменной из
области ее определения, при подстановке
которых предикат обращается в истинное
высказывание.

Пример.
Множеством истинности предиката
,
заданном на множестве действительных
чисел, будет промежуток.
Множество истинности предиката,
заданном на множестве целых неотрицательных
чисел, состоит из одного числа 2.

Множество
истинности
двухместного предиката
состоит из всех таких парпри подстановке которых в этот предикат
получается истинное высказывание.

Пример.
Пара
принадлежит множеству истинности
предиката,
т.к.– истинное высказывание, а паране принадлежит, т.к.– ложное высказывание.

Высказывания
и предикаты могут быть как простыми,
так и сложными (составными). Сложные
предложения
образуются из простых с помощью логических
связок –
слов «и»,
«или»,
«если…,
то…»,
«тогда и
только тогда, когда…».
С помощью
частицы «не»
или
словосочетания
«неверно,
что» можно
из данного предложения получить новое.
Предложения, не являющиеся составными,
называют элементарными.

Примеры.
Составные предложения:

  1. Число
    42 – четное и делится на 7. Образовано
    из двух элементарных предложений: Число
    42 четное, число 42 делится на 7 и составлено
    с помощью логической связки «и».

  2. Число
    х
    больше или равно 5. Образовано из двух
    элементарных предложений: Число х
    больше 5 и число х
    равно 5 и составлено с помощью логической
    связки «или».

  3. Число
    42 не делится на 5. Образовано из
    предложения: Число 42 делится на 5 с
    помощью частицы «не».

Значение
истинности элементарного высказывания
определяют, исходя из его содержания с
опорой на известные знания. Чтобы
определить значение истинности составного
высказывания, надо знать смысл логических
связок, с помощью которых оно образовано
из элементарных, и уметь выявлять
логическую структуру высказывания.

Пример.
Выявим логическую структуру предложения:
«Если углы вертикальны, то они равны».
Оно состоит из двух элементарных
предложений: А
– углы вертикальные, В
– углы равны. Соединены они в одно
составное предложение с помощью
логической связки «если…,
то…». Данное
составное предложение имеет логическую
структуру (форму): «если
А, то В».

Выражение
«для любого х»
или «для всех х»
или «для каждого х»
называется квантором
общности
и обозначается
.

Высказывание,
полученное из высказывания или предиката
при помощи квантора общности, обозначается:и читается: «Для любого значениях
из множества Х
имеет место
».

Выражение
«существует х»
или «для некоторых х»
или «найдется такое х»
называется квантором
существования и
обозначается
.

Высказывание,
полученное из высказывания или предиката
при помощи квантора существования,
обозначается:и читается: «Для некоторыхх
из множества Х
имеет место
»
или «Существует (найдется) такое значениех
из Х,
что имеет место
».

Кванторы
общности и существования употребляются
не только в математических выражениях,
но и в повседневной речи.

Пример.
Следующие высказывания содержат квантор
общности:

а)
Все стороны квадрата равны; б) Каждое
целое число является действительным;
в) В любом треугольнике медианы
пересекаются в одной точке; г) У всех
студентов есть зачетная книжка.

Следующие
высказывания содержат квантор
существования:

а)
Существуют числа, кратные 5; б) Найдется
такое натуральное число
,
что;
в) В некоторых студенческих группах
учатся кандидаты в мастера спорта; г)
Хотя бы один угол в треугольнике острый.

Высказывание
являетсяистинным
тогда и только тогда, когда предикат
–
тождество, т.е. принимает истинные
значения при подстановке в него любых
значений переменной.

Пример.
Высказывание
истинно.

Высказывание
ложно,
если при некотором значении переменной
х
предикат
превращается в ложное высказывание.

Пример.
Высказывание
ложно, т.к. припредикатпревращается в ложное высказывание.

Высказывание
являетсяистинным
тогда и только тогда, когда предикат
не является тождественно ложным, т.е.
при некотором значении переменнойх
предикат
превращается в истинное высказывание.

Пример.
Высказывание
истинно, т.к. припредикатпревращается в истинное высказывание.

Высказывание
ложно,
если предикат
является противоречием, т.е. тождественно
ложным высказыванием.

Пример.
Высказывание
ложно, т.к. предикатявляется тождественно ложным.

Пусть
предложение А
– высказывание.
Если перед сказуемым данно­го
предложения поставить частицу «не»
либо перед всем предложением поставить
слова «неверно,
что»,
то получится новое предложение, кото­рое
называется отрицанием
данного
и обозначается:
А или

(читают:
«не
А»
или
«неверно,
что
А»).

Отрицанием
высказывания А
называется
высказыва­ние

или

А,
которое ложно, когда высказывание А
истинно, и истинно, когда
высказывание А
– ложно.

Таблица
истинности отрицания:

А

1

0

0

1

Пример.
Если высказывание А:
«Вертикальные углы равны», то отрицание
этого высказывания
А:
«Вертикальные
углы не равны».
Первое из этих высказываний истинное,
а второе – ложное.

Для
построения отрицания высказываний с
кванторами надо:

  1. квантор
    общности заменить квантором существования
    или наоборот;

  2. высказывание
    заменить его отрицанием (поставить
    перед глаголом частицу «не»).

На
языке математических символов это
запишется так:

или
.

Соседние файлы в папке Логика

  • #

    09.02.20163.5 Mб201.rtf

  • #
  • #
Источник

Логика предикатов

Предикаты вслед за высказываниями являются следующим важным предметом, исследуемым математической логикой. Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики. В настоящей главе рассматриваются основы теории предикатов.

Понятие предиката

В высказывании все четко: это — конкретное утверждение о конкретных объектах — истинное или ложное. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно. Дадим точное определение.

Определение 18.1. Определенным на множествах M_1,M_2,ldots,M_n n-местным предикатом называется предложение, содержащее n переменных x_1,x_2,ldots,x_n, превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств M_1,M_2,ldots,M_n соответственно.

Для n-местного предиката будем использовать обозначение P(x_1,x_2,ldots,x_n). Переменные x_1,x_2,ldots,x_n называют предметными, а элементы множеств M_1,M_2,ldots,M_n, которые эти переменные пробегают, — конкретными предметами. Всякий n-местный предикат P(x_1,x_2,ldots,x_n), определенный на множествах M_1,M_2,ldots,M_n, представляет собой функцию п аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также функцией-высказыванием.

Рассмотрим пример. Предложение “Река x впадает в озеро Байкал” является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной x название “Баргузин”, получим высказывание “Река Баргузин впадает в озеро Байкал”. Это высказывание истинно. Подставив вместо предметной переменной x название “Днепр”, получим ложное высказывание “Река Днепр впадает в озеро Байкал”.

Другой пример. Предложение (выражение) “x^2+y^2 leqslant 9” является двухместным предикатом, заданным над множествами mathbb{R},mathbb{R}. Множества, на которых задан двухместный предикат, совпадают (говорят, что “двухместный предикат задан на множестве mathbb{R}^2“). Пара действительных чисел 2, 2 превращает данный предикат в истинное высказывание: “2^2+2^2 leqslant 9“, а пара чисел 2, 3 — в ложное: “2^2+3^2 leqslant 9“.

Отметим еще один подход к понятию предиката. Как отмечалось, предикат P(x_1,x_2,ldots,x_n), определенный на множествах M_1,M_2,ldots,M_n, превращается в конкретное высказывание P(x_1,x_2,ldots,x_n), если вместо предметных переменных x_1,x_2,ldots,x_n подставить в него конкретные предметы (элементы a_1,a_2,ldots,a_n) из множеств M_1,M_2,ldots,M_n соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию n аргументов, заданную на множествах M_1,M_2,ldots,M_n принимающую значение в двухэлементном множестве {0;1}. Иногда эту функцию и называют предикатом.

Классификация предикатов

Определение 18.2. Предикат P(x_1,x_2,ldots,x_n), заданный на множествах M_1,M_2,ldots,M_n, называется:

а) тождественно истинным, если при любой подстановке вместо переменных x_1,x_2,ldots,x_n любых конкретных предметов a_1,a_2,ldots,a_n из множеств M_1,M_2,ldots,M_n соответственно он превращается в истинное высказывание P(a_1,a_2,ldots,a_n);

б) тождественно ложным, если при любой подстановке вместо переменных x_1,x_2,ldots,x_n любых конкретных предметов из множеств M_1,M_2,ldots,M_n соответственно он превращается в ложное высказывание;

в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов a_1,a_2,ldots,a_n из множеств M_1,M_2,ldots,M_n соответственно, при подстановке которых вместо соответствующих предметных переменных в предикат P(x_1,x_2,ldots,x_n) последний превратится в истинное (ложное) высказывание P(a_1,a_2,ldots,a_n).

Приведем примеры предикатов.

Одноместный предикат “Город x расположен на берегу реки Волги”, определенный на множестве названий городов, является выполнимым, потому что существуют города, названия которых превращают данный предикат в истинное высказывание, или, иначе, удовлетворяют этому предикату (например, Ульяновск, Саратов и т. д.). Но данный предикат не будет тождественно истинным, потому что существуют города, названия которых превращают его в ложное высказывание, или, иначе, не удовлетворяют этому предикату (например, Прага, Якутск и т.д.). Этот же предикат являет собой пример опровержимого, но не тождественно ложного предиката (продумайте!).

В другом примере одноместный предикат “sin^2x+cos^2x=1“, определенный на множестве действительных чисел, тождественно истинный. Наконец, двухместный предикат “x^2+y^2<0“, заданный также на множестве действительных чисел, является тождественно ложным предикатом, потому что любая пара действительных чисел превращает его в ложное высказывание (не удовлетворяет ему).

Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов (рекомендуется осмыслить их):

1) каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2) каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3) каждый не тождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4) каждый не тождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.

Множество истинности предиката

Определение 18.3. Множеством истинности предиката P(x_1,x_2,ldots,x_n), заданного на множествах M_1,M_2,ldots,M_n, называется совокупность всех упорядоченных n-систем (a_1,a_2,ldots,a_n), в которых a_1in M_1,a_2in M_2,ldots,a_nin M_n, таких, что данный предикат обращается в истинное высказывание P(a_1,a_2,ldots,a_n) при подстановке x_1=a_1,x_2=a_2,ldots,x_n=a_n. Это множество будем обозначать P^{+}. Таким образом,

P^{+}= bigl{(a_1,a_2,ldots,a_n)colon, lambda bigl(P(a_1,a_2, ldots, a_n)bigr)= 1bigr}.

Множество P^{+} истинности “-местного предиката P(a_1,a_2,ldots,a_n) представляет собой n-арное отношение между элементами множеств M_1,M_2,ldots,M_n. Если предикат P(x) — одноместный, заданный над множеством M, то его множество истинности P^{+} является подмножеством множества Mcolon, P^{+}subseteq M.

Например, множеством истинности двухместного предиката “Точка x принадлежит прямой y“, заданного на множестве E всех точек плоскости и на множестве F всех прямых этой плоскости, является бинарное отношение принадлежности (инцидентности) между точками и прямыми плоскости. Другой пример. Множество истинности двухместного предиката S(x,y)colon~ x^2+y^2=9, заданного на множестве mathbb{R}^2, есть множество всех таких пар действительных чисел, которые являются координатами точек плоскости, образующими окружность с центром в начале координат и радиуса 3. Наконец, если A(x)colon “|a|>2” — одноместный предикат над mathbb{R}, то A^{+}= (-infty;-2)cup(2;+infty), или A^{+}= mathbb{R} setminus[-2;2].

В терминах множества истинности легко выразить понятия, связанные с классификацией предикатов (определение 18.2). В самом деле, n-местный предикат P(x_1,x_2,ldots,x_n), заданный на множествах M_1,M_2,ldots,M_n, будет:

а) тождественно истинным тогда и только тогда, когда P^{+}=M_1times M_2times ldotstimes M_n;
б) тождественно ложным тогда и только тогда, когда P^{+}=varnothing;
в) выполнимым тогда и только тогда, когда P^{+}nevarnothing;
г) опровержимым тогда и только тогда, когда P^{+}ne M_1times M_2times ldotstimes M_n.

На языке множеств истинности еще более отчетливо проясняются закономерности взаимосвязей между предикатами различных типов, отмеченные в конце предыдущего пункта. Проанализируйте их еще раз.

Равносильность и следование предикатов

Определение 18.4. Два n-местных предиката P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n), заданных над одними и теми же множествами M_1,M_2,ldots,M_n, называются равносильными, если набор предметов (элементов) a_1in M_1, a_2in M_2, ldots, a_nin M_n превращает первый предикат в истинное высказывание P(a_1,a_2,ldots,a_n) в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание Q(a_1,a_2,ldots,a_n).

Другими словами (на языке множеств истинности), предикаты P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n) равносильны тогда и только тогда, когда их множества истинности совпадают. P^{+}=Q^{+}.

Утверждение о равносильности двух предикатов P и Q символически будем записывать так: PLeftrightarrow Q. Отношение равносильности предикатов является отношением эквивалентности, так что совокупность всех n-местных предикатов, определенных на множествах M_1,M_2,ldots,M_n, распадается на непересекающиеся классы равносильных предикатов (все они определяют одну и ту же функцию, заданную на множествах M_1,M_2,ldots,M_n и принимающую значения в двухэлементном множестве {0;1}). Переход от предиката P_1 к равносильному ему предикату P_2 называется равносильным преобразованием первого. Это понятие очень важно для школьной математики, потому что изучаемые в ней уравнения и неравенства представляют собой частные виды предикатов. Решение уравнения и неравенства есть поиск их множеств истинности. При таком поиске мы проделываем над уравнением и неравенством различные преобразования, и здесь важно, чтобы эти преобразования были равносильными, т. е. чтобы найденное множество оказалось бы множеством истинности именно исходного уравнения или неравенства. Аналогична ситуация при решении систем уравнений или неравенств.

Рассмотрим простой пример. Пусть требуется решить уравнение (найти множество истинности предиката): 4x-2=-3x-9. Преобразуем его равносильным образом:

4x-2=-3x-9quad Leftrightarrowquad 4x+3x=-9+2quad Leftrightarrowquad x=-1

Ответ: {-1} — множество всех решений данного уравнения (множество истинности данного предиката).

Отметим следующее немаловажное обстоятельство: может быть так, что два предиката равносильны, если их рассматривать над одним множеством, и неравносильны, если их рассматривать над другим (в частности, объемлющим первое) множеством. Такова, например, ситуация с предикатами: sqrt{xcdot y}=15 и sqrt{x}cdotsqrt{y}=15.

Определение 18.5. Предикат Q(x_1,x_2, ldots,x_n), заданный над множествами M_1,M_2, ldots, M_n, называется следствием предиката P(x_1,x_2,ldots,x_n), заданного над теми же множествами, если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат P(x_1,x_2,ldots,x_n).

Другими словами (в терминах множеств истинности), можно сказать, что предикат Q является следствием предиката P тогда и только тогда, когда P^{+}subseteq Q^{+}.

Утверждение о том, что предикат Q является следствием предиката P, будем символически записывать так: PRightarrow Q.

Например, одноместный предикат, определенный на множестве натуральных чисел, “n делится на 3″ является следствием одноместного предиката, определенного на том же множестве, “n делится на 6″. Из двух предикатов, упомянутых перед последним определением, первый будет следствием второго, если считать, что оба предиката заданы на множестве mathbb{Z} целых чисел.

Язык множеств истинности позволяет установить взаимосвязь между понятиями равносильности и следования предикатов: два предиката, определенные на одних и тех же множествах, равносильны тогда и только тогда, когда каждый из них является следствием другого. Кроме того, этот же язык дает возможность без труда установить следующие простые теоремы.

Теорема 18.6. Каждые два тождественно истинных (тождественно ложных) предиката, заданных на одних и тех же множествах, равносильны. Обратно, всякий предикат, равносильный тождественно истинному (тождественно ложному) предикату, сам является тождественно истинным (тождественно ложным) предикатом.

Теорема 18.7. Каждый тождественно истинный n-местный предикат является следствием любого другого n-местного предиката, определенного на тех же множествах. Каждый n-местный предикат является следствием любого тождественно ложного n-местного предиката, определенного на тех же множествах.

Теорема 18.8. Пусть P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n) — два n-местных предиката, определенные на одних и тех же множествах, такие, что Q(x_1, x_2, ldots, x_n) есть следствие P(x_1,x_2,ldots,x_n). Тогда:

а) если P(x_1,x_2,ldots,x_n) тождественно истинный (выполнимый), то и Q(x_1, x_2, ldots, x_n) тождественно истинный (выполнимый);

б) если Q(x_1,x_2,ldots,x_n) тождественно ложный (опровержимый), то и P(x_1, x_2, ldots, x_n) тождественно ложный (опровержимый).

Доказательство теоремы 18.8:

а) Поскольку PRightarrow Q, поэтому P^{+}subseteq Q^{+}. Если теперь P тождественно истинный предикат, то

P^{+}= M_1times M_2times ldotstimes M_n (где M_1,M_2,ldots,M_n — множества, на которых определены n-местные предикаты P и Q).

Но Q^{+}subseteq M_1times M_2times ldotstimes M_n. Поэтому Q^{+}= M_1times M_2times ldotstimes M_n, а, значит, предикат Q — тождественно истинный предикат. Если же P — выполнимый предикат, то P^{+}nevarnothing. Но P^{+}subseteq Q^{+}. Тогда Q^{+}nevarnothing и Q — выполнимый предикат.

б) Пусть Q — тождественно ложный предикат. Тогда Q^{+}=varnothing. Но P^{+}subseteq Q^{+}, поэтому P^{+}=varnothing. Следовательно, предикат P — тождественно ложный. Наконец, пусть Q — опровержимый предикат. Тогда Q^{+}ne M_1times M_2times ldotstimes M_n. Поскольку, кроме того,

P^{+}subseteq Q^{+} и P^{+}subseteq M_1times M_2times ldotstimes M_n, то P^{+}ne M_1times M_2times ldotstimes M_n.

Следовательно, предикат P — опровержимый.

Отыщите самостоятельно в настоящем и предыдущем пунктах данной лекции утверждения, обосновывающие остальные сформулированные теоремы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Аннотация: Рассматриваются основные понятия и сведения алгебры высказываний и предикатов – высказывания, предикаты, аксиомы, логические выражения и функции, эквивалентные выражения и приведение к эквивалентному выражению, другие сопутствующие понятия и факты логики, а также инфологические задачи.

Информатика, как было рассмотрено выше, изучает знаковые (алфавитные) системы. Алгебра – наиболее адекватный математический аппарат описания действий в них, поэтому алгебраический аппарат наилучшим образом подходит для описания информационных систем общей природы, отвлеченно от их предметной направленности. Информационные процессы хорошо формализуются с помощью различных алгебраических структур.

Алгеброй A называется некоторая совокупность определенных элементов X, с заданными над ними определенными операциями f (часто определяемые по сходству с операциями сложения и умножения чисел), которые удовлетворяют определенным свойствам – аксиомам алгебры.

Операция f называется n-местной, если она связывает n операндов (объектов – участников этой операции).

Совокупность операций алгебры A называется ее сигнатурой, а совокупность элементов алгебры – носителем алгебры.

Утверждение ( высказывательная форма )
– основная единица, неделимая с точки зрения отражения смысла информации (семантики).

Высказывание
– некоторое повествовательное утверждение, про которое можно однозначно сказать (“сразу посмотрев на него”), истинно оно или ложно. Эти два значения всевозможных высказываний обозначаются “истина” и “ложь”, “true” и “fаlse” или “1” и “0”.

Переменная, значениями которой могут быть лишь значения “1” или “0”, называется логической переменной или булевой переменной.

Пример. Рассмотрим словосочетания:

  1. Москва – столица США.
  2. Житель города Москва.
  3. 5 – 7 + 8.
  4. 5 – 9 + 28 = 4.
  5. В пятую неделю зимы было очень холодно.
  6. В Антарктиде живут тигры.

Высказывание должно быть однозначно истинным или однозначно ложным, поэтому высказываниями являются только утверждения 1), 4), 6).

Пример. Не является высказыванием и “парадокс лжеца” (Эвбулид, учитель Демосфена, около 350 лет до н.э.): “То, что я сейчас утверждаю, – ложно”, ибо если оно истинно – то оно ложно, а если допустить, что оно ложно, то оно истинно. Это неопределенная высказывательная форма. Аналогичный пример принадлежит известному математику, логику Гёделю (1931 г.): “То, что утверждается в этом предложении, не может быть доказано”. Если его можно опровергнуть, то его нельзя доказать, а если его нельзя опровергнуть, то его можно доказать. Предложения такого рода не могут быть доказаны или опровергнуты в пределах того языка (той теории, алгебры ), с помощью которой они сформулированы. Известны многие подобные парадоксы.

Рассматривая высказывания, мы не обращаем внимания на их внутреннюю структуру и можем разлагать их на структурные части, равно как и объединять их.

Пример. Построим из ниже заданных простых высказываний составные, сложные высказывания, принимающие значение “истина”, “ложь”:

  1. “Зима – холодное время года”.
  2. “Пальто – теплая одежда”.
  3. “Камин – источник тепла”.

Истинным будет, например, сложное высказывание: “Зима – холодное время года и зимой носят пальто”, а ложным будет, например, высказывание: “Некоторые ходят в пальто, поэтому на улице зима”. Придумайте другие примеры.

Предикат
– высказывательная форма с логическими переменными (множество значений этих переменных вполне определено), имеющая смысл при любых допустимых значениях этих переменных. Количество переменных в записи предиката называется его местностью.

Простые высказывания или предикаты
не зависят от других высказываний или предикатов (“не разбиваемы на более простые”), а сложные – зависят хотя бы от двух простых.

Пример. Выражение “х = у” – предикат, “х > 5” – предикат, а “7 > 5” – высказывание. Утверждение “Хорошо” не является высказыванием, утверждение “Оценка студента А по информатике – хорошая” – простое высказывание, утверждение “Вчера была ясная погода, я был вчера на рыбалке” – сложное высказывание, состоящее из двух простых.

Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой аргумент х – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f) = {1,0}.

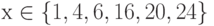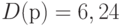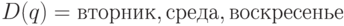Пример. Заданы предикаты вида р = “число х делится нацело на 3” и q = “у – день недели”. Найдем множество истинности предикатов р и q, если х in {1, 4, 6, 16, 20, 24}, у in {первый, вторник, среда, 1999, зима, выходной, праздник, воскресенье}. Получаем, что D(р)={6, 24}, D(q) = {вторник, среда, воскресенье}.

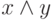Множество логических переменных х,y in Х с определенными над ним операциями: overline{x} – отрицания или инверсии, x lor y – логического сложения или дизъюнкции, x land y – логического умножения или конъюнкции
называется алгеброй предикатов (и высказываний )
, если эти операции удовлетворяют следующим аксиомам:

  1. Аксиома двойного отрицания:

    overline{overline{x}}=x

  2. Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции ):

    x land y = yland x, x lor y = y lor x

  3. Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов):

    (x land y) land z = x land (y land z), (x lor y) lor z = x lor (y lor z)

  4. Аксиомы одинаковых операндов:

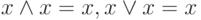
    xland x = x, x lor x = x

  5. Аксиомы поглощения (множителем — множителя-суммы или слагаемым — слагаемого-произведения):

    x land (x lor y) = x, x lor (x land y) = x

  6. Аксиомы распределения операции ( дизъюнкции относительно конъюнкции и наоборот):

    x land (y lor z) = (x land y) lor (x land z), x lor (y land z) = (x lor y) land (x lor z)

  7. Аксиомы де Моргана (перенесения бинарной операции на операнды):

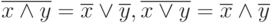
    overline{xland y} = overline{x}loroverline{y}, overline{xlor y}=overline{x}landoverline{y}

  8. Аксиомы нейтральности (взаимноинверсных множителей или слагаемых):

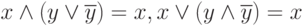
    xland(yloroverline{y})=x, xlor(ylandoverline{y})=x

  9. Аксиома существования единицы ( истина, true, 1) и нуля ( ложь, false, 0), причем,

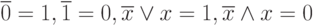
    overline{0}=1, overline{1}=0, overline{x}lor x=1, overline{x}land x = 0

Из этих аксиом следует ряд полезных соотношений, например,

xland1=x,\xlor0=x,\xlor1=1,\xland0=0,\ overline{x}lor x=1,\ overline{x}land x=0

Источник
Автор статьи

Татьяна Шкляр

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Понятие предиката

Определение 1

Предикат – утверждение, которое содержит переменные, принимающие значение $1$ или $0$ (истинно или ложно) в зависимости от значений переменных.

Пример 1

Например, выражение $x=x^5$ является предикатом, т.к. оно является истинным при $x=0$ или $x=1$ и ложным при всех остальных значениях $x$.

Определение 2

Множество, на котором предикат принимает только истинные значения, называется множеством истинности предиката $I_p$.

Замечание 1

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

$P (x_1, dots, x_n)=1$

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

$P (x_1, dots, x_0)=0$

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Т.к. предикаты могут принимать только два значения (истинно/ложно или $0/1$), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.

Примеры предикатов

Пусть предикат $R(x, y)$: $«x = y»$ обозначает отношение равенства, где $x$ и $y$ принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных $x$ и $y$.

Другой пример предиката — РАБОТАЕТ($x, y, z$) для отношения «$x$ работает в городе y в компании $z$».

Еще один пример предиката — НРАВИТСЯ($x, y$) для «x нравится y» для $x$ и $y$, которые принадлежат $M$ — множеству всех людей.

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

«Предикаты и кванторы» 👇

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Определение 3

Конъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает истинное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает истинное значение, а ложное значение — во всех остальных случаях. Множество истинности $T$ предиката — пересечение множеств истинности предикатов $A(x)$ и $B(x)$. Например: предикат $A(x)$: «$x$ — чётное число», предикат $B(x)$: «$x$ делится на $5$». Таким образом, предикатом будет выражение «$x$ — чётное число и делится на $5$» или «$x$ делится на $10$».

Определение 4

Дизъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает ложное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката — объединение областей истинности предикатов $A(x)$ и $B(x)$.

Определение 5

Отрицание предиката $A(x)$ — предикат, который принимает истинное значение при всех значениях $x$ из $T$, при которых предикат $A(x)$ принимает ложное значение и наоборот. Множество истинности предиката $A(x)$ — дополнение $T’$ к множеству $T$ в множестве $x$.

Определение 6

Импликация предикатов $A(x)$ и $B(x)$ — предикат , который является ложным при тех и только тех значениях $x$ из $T$, при которых $A(x)$ — истинно, а $B(x)$ — ложно, и принимает истинное значение во всех остальных случаях. Читается: «Если $A(x)$, то $B(x)$».

Пример 2

Пусть $A(x)$: «Натуральное число $x$ делится на $3$»;

$B(x)$: «Натуральное число $x$ делится на $4$».

Составим предикат: «Если натуральное число $x$ делится на $3$, то оно делится и на $4$».

Множество истинности предиката — объединение множества истинности предиката $B(x)$ и дополнения к множеству истинности предиката $A(x)$.

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Определение 7

Кванторы — логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания.

Определение 8

Квантор — логические операции, которые ограничивают область истинности предиката и создают высказывание.

Чаще всего используют кванторы:

  • квантор всеобщности (обозначается символом $forall x$) — выражение «для всех $x$» («для любого $x$»);

  • квантор существования (обозначается символом $exists x$) — выражение «существует $x$ такое, что… »;

  • квантор единственности и существования (обозначается $exists !x$) — выражение «существует точно одно такое $x$, что… ».

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

Пусть — предикат «$x$ кратно $7$».

С помощью квантора всеобщности можно записать следующие ложные высказывания:

  1. любое натуральное число делится на $7$;

  2. каждое натуральное число делится на $7$;

  3. все натуральные числа делятся на $7$;

который будет иметь вид:

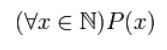
Рисунок 1.

Для записи истинных высказываний используем квантор существования:

  1. существуют натуральные числа, которые делятся на $7$;

  2. найдётся натуральное число, которое делится на $7$;

  3. хотя бы одно натуральное число делится на $7$.

Запись будет иметь вид:

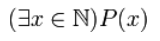
Рисунок 2.

Пусть на множестве $x$ простых чисел задан предикат : «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, $2$ является простым четным числом).

Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число , которое является нечетным» (например, $x=3$ ).

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

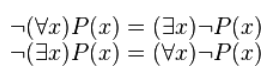
Рисунок 3.

Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

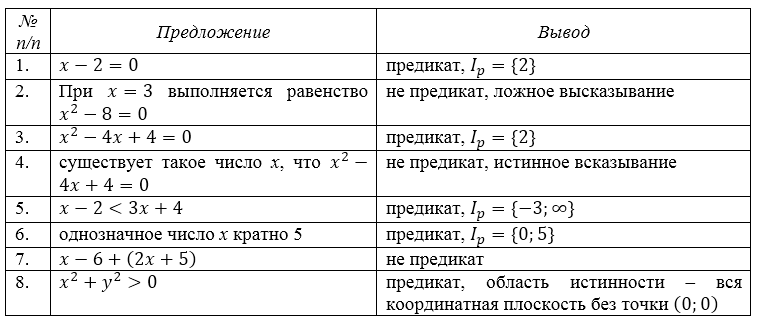
Рисунок 4.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Добавить комментарий