Как найти координаты центра тяжести кривой

Как найти координаты центра тяжести кривой

Статические моменты и координаты центра тяжести

Вычисление статических моментов и координат центра тяжести кривой

а) Пусть материальная точка A массы m отстоит от оси ell на расстоянии d. Статическим моментом этой точки относительно оси ell называют число md. Статическим моментом системы материальных точек A_1,A_2,ldots,A_n, расположенных по одну сторону от оси ell, массы которых равны m_1,m_2,ldots,m_n, а расстояния от оси ell равны d_1,d_2,ldots,d_n называют число

S_{ell}= sumlimits_{k=1}^{n}m_kd_k,.

Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.

Поэтому если точки A_1,A_2,ldots,A_n расположены на координатной плоскости,

A_k=A_k(x_k;y_k), то S_x=sumlimits_{k=1}^{n}m_ky_k,,~~ S_y=sumlimits_{k=1}^{n}m_kx_k,,

где S_x — статический момент относительно оси Ox и S_y — относительно оси Oy.

б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой Gamma или по некоторой области lambda. Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.

Начнем со случая кривой линии Gamma, задаваемой уравнением y=f(x),~a leqslant x leqslant b, причем предположим, что функция f(x) непрерывна и неотрицательна.

Как обычно, разобьем отрезок [a;b] на части точками a=x_0<x_1< ldots<x_n=b и обозначим через m_k и M_k наименьшее и наибольшее значения функции f(x) на отрезке [x_k;x_{k+1}], Этому разбиению соответствует разбиение дуги Gamma на части gamma_0,ldots, gamma_{n-1} (рис. 60). Из физических соображений ясно, что статический момент S_k части gamma_k относительно оси абсцисс заключен между m_kell_k и M_kell_k, где ell_k—длина этой части, ell_k=ell(gamma_k) (напомним, что мы положили линейную плотность дуги равной единице). Таким образом,

Разбиение отрезка на части точками

m_kcdotell_k leqslant S_k leqslant M_kcdotell_k. Поэтому sumlimits_{k=0}^{n-1} m_kell_k leqslant S_x leqslant sumlimits_{k=0}^{n-1}M_kell_k, то есть

sumlimits_{k=0}^{n-1}m_k intlimits_{x_k}^{x_{k+1}} sqrt{1+(y')^2},dx leqslant S_x leqslant sumlimits_{k=0}^{n-1}M_k intlimits_{x_k}^{x_{k+1}} sqrt{1+(y')^2},dx,.

Так как на отрезке [x_k;x_{k+1}] выполняется неравенство

m_kcdot sqrt{1+(y')^2} leqslant ycdot sqrt{1+(y')^2} leqslant M_kcdot sqrt{1+(y')^2},,

то в тех же границах, что и S_x, заключен интеграл intlimits_{a}^{b} ysqrt{1+(y')^2},dx. Значит,

S_x= intlimits_{a}^{b}ysqrt{1+(y')^2},dx,.

(1)

Этот интеграл обозначают также следующим образом: intlimits_{Gamma}y,dell или intlimits_{0}^{ell}y,dell.

Физики обычно заменяют проведенное рассуждение более коротким. Они берут “бесконечно малый участок дуги” dell. Его статический момент равен y,dell. А статический момент всей дуги равен сумме элементарных статических моментов, т. е. intlimits_{a}^{b} y,dell. Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое “бесконечно малый участок дуги”, или как еще говорят, “элемент дуги”. При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что

S_y=intlimits_{a}^{b}xsqrt{1+(y')^2},dx= intlimits_{0}^{ell}x,dell,.

(2)

Как формула (1), так и формула (2) верны и в случае, когда кривая Gamma пересекает оси координат.

в) Введем понятие центра тяжести.

Определение. Центром тяжести тела называется такая точка C, что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через xi и eta расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

S_x= ellcdoteta= intlimits_{0}^{ell}y,dell,;qquad S_y=ellcdotxi= intlimits_{0}^{ell}x,dell,.

Разрешая полученные равенства относительно xi и eta, найдем координаты центра тяжести плоской кривой Gamma:

xi=frac{1}{ell} intlimits_{0}^{ell} x,dell,;qquad eta=frac{1}{ell} intlimits_{0}^{ell}y,dell,.

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью Ox. Тогда статический момент полуокружности относительно диаметра выразится формулой

S_x=intlimits_{0}^{ell} y,dell, где dell=sqrt{1+(y')^2},dx — дифференциал дуги кривой y=f(x).

В выбранной системе координат уравнение полуокружности запишется так: y=sqrt{R^2-x^2}. Тогда

y'=-frac{x}{sqrt{R^2-x^2}},~~1+(y')^2= frac{R^2}{R^2-x^2} и потому dell=frac{R,dx}{sqrt{R^2-x^2}}.

Следовательно,

S_x=intlimits_{-R}^{R}! sqrt{R^2-x^2}cdot frac{R,dx}{sqrt{R^2-x^2}}= 2R intlimits_{0}^{R}dx= 2R^2.

Пример 2. Найдем центр тяжести четверти окружности x^2+y^2=4, расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому xi=eta. Достаточно найти только xi=frac{1}{ell} intlimits_{0}^{ell} x,dell.

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

begin{cases}x=2cos{t},,\ y=2sin{t},,end{cases} 0 leqslant t leqslant frac{pi}{2},.

Отсюда находим, что x'_t=-2sin{t},~ y'_t=2cos{t} и

dell= sqrt{(x'_t)^2+(y'_t)^2},dt= sqrt{4sin^2t+4cos^2t},dt= 2,dt,.

Поскольку длина ell четверти данной окружности равна frac{1}{4}cdot 2picdot2=pi, то

xi=frac{1}{pi} intlimits_{0}^{2pi} 2cos{t}cdot2,dt= left.{frac{4}{pi} sin{t}}right|_{0}^{pi/2}= frac{4}{pi},.

Вычисление статических моментов и координат центров тяжести плоских фигур

Найдем статический момент прямоугольника со сторонами k и ell относительно стороны k. Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны k и dy (рис. 61). Масса элементарного прямоугольника равна его площади k,dy (напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен ky,dy, а статический момент всего прямоугольника равен

Разбиение прямоугольника на элементарные прямоугольники

intlimits_{0}^{ell} ky,dy= left.{frac{k}{2},y^2}right|_{0}^{ell}= frac{kell^2}{2},.

(1)

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой y=f(x), где f(x) — непрерывная и неотрицательная функция на отрезке [a;b], снизу осью абсцисс, а с боков прямыми x=a,~ x=b.

Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно dx и высота y. Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен frac{y^2}{2},dx, а потому статический момент всей криволинейной трапеции равен frac{1}{2}intlimits_{a}^{b} y^2,dx. В случае, когда не выполняется предположение о неотрицательности функции y=f(x), эту формулу надо заменить такой:

S_x=frac{1}{2} intlimits_{a}^{b} y|y|,dx

(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в S_x).

Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу intlimits_{a}^{b} |y|,dx, а потому ордината центра тяжести этой трапеции выражается формулой

eta=frac{intlimits_{a}^{b} y|y|,dx}{2 intlimits_{a}^{b} |y|,dx},.

Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно x. Поэтому его статический момент равен x|y|,dx, а статический момент всей трапеции выражается формулой

S_y=intlimits_{a}^{b} x|y|,dx. Следовательно, абсцисса центра тяжести выражается так: xi=frac{intlimits_{a}^{b} x|y|,dx}{intlimits_{a}^{b} |y|,dx}.

Пример 3. Найти статический момент (относительно оси Ox) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:

begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}),end{cases} 0leqslant tleqslant2pi,.

Решение. Так как параметр t одной арки циклоиды изменяется от 0 до 2pi, то

begin{aligned}S_x&= frac{1}{2} intlimits_{0}^{2pi} a^2(1-cos{t})^2a(1-cos{t}),dt= frac{a^3}{2} intlimits_{0}^{2pi} (1-cos{t})^3,dt=\ &= left.{frac{a^3}{2}! left[t-3sin{t}+ frac{3}{2}! left(t+frac{1}{2} sin2tright)- left(sin{t}-frac{1}{3} sin^3tright)right] }right|_{0}^{2pi}=\ & =frac{a^3}{2}! left(2pi+frac{3}{2}cdot 2piright) = frac{5}{2},pi a^3.end{aligned}

Пример 4. Найти центр тяжести фигуры, ограниченной осью Ox и одной полуволной синусоиды y=sin{x}.

Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой x=frac{pi}{2}, то центр тяжести лежит на этой прямой и, следовательно, xi=frac{pi}{2}. Ордината eta центра тяжести находится по формуле eta=frac{1}{2S} intlimits_{0}^{pi} y^2,dx.

Так как S=intlimits_{0}^{pi} sin{x},dx= Bigl.{-cos{x}}Bigr|_{0}^{pi}=2, то eta=frac{1}{4} intlimits_{0}^{pi}sin^2x,dx = frac{pi}{8}.

Итак, центр тяжести данной фигуры находится в точке left(frac{pi}{2}; frac{pi}{8}right).

Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}).end{cases}.

Решение. Данная фигура расположена симметрично относительно прямой x=pi a, следовательно, центр тяжести ее находится на этой прямой, и потому xi=pi a. Найдем eta по формуле eta=frac{1}{2S} intlimits_{a}^{b} y^2,dx.

Площадь S данной фигуры была вычислена раньше, она равна 3pi a^2. Следовательно,

eta=frac{1}{6pi a^2} intlimits_{0}^{2pi} a^3(1-cos{t})^3,dt= frac{5}{6},a,.

Центр тяжести данной фигуры находится в точке left(pi a; frac{5}{6},aright).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° 206, 207. При решении задач рекомендуется помнить, что если кривая расположена симметрично относительно некоторой прямой, то центр тяжести кривой лежит на этой прямой.

592. Найти центр тяжести дуги цепной линии:

содержащейся между точками, для которых х = — а х = а.

Решение. Так как рассматриваемая дуга расположена симметрично относительно оси Oyt то центр тяжести дуги лежит на оси Oy и, следовательно,Найдем ординату, пользуясь формулой

Так как

и, следовательно,

593. Найти центр тяжести одной арки циклоиды:

Решение. Так как арка циклоиды расположена симметрично относительно прямой х = па, то центр тяжести дуги циклоиды лежит на этой прямой и, следовательно,

Ордината центра тяжести будет: ? ( ~ е [а I а

Ц – – Ie _L_£

1 a(e*~-)Ja 2 f


I = Jt а.

Найдем ординату центра тяжести по формуле:

Длина дуги одной арки циклоиды равна 8а (см. задачу

Найдем ординату центра тяжести:

594. Найти центр тяжести дуги кривой»

содержащейся между точками, для которых Решение. Найдем

(см. задачу 491).

Найдем абсциссу центра тяжести:

3 + 2 In 2

4

Найдем ординату центра тяжести:

2

595. Найти центр тяжести однородной треугольной пластинки.

ч

3 (3 + 2 In 2)

Решение. Разбиваем данную пластинку прямыми, параллельными одной из сторон, на бесконечно тонкие полоски. Центр тяжести каждой полоски находится в ее середине и лежит, таким образом, на медиане, а следовательно, и центр тяжести всей треугольной пластинки лежит на этой медиане. Так как это рассуждение применимо к любой стороне, то центр тяжести треугольника находится в точке пересечения его медиан.

Тот же результат получаем вычислением. Площадь полоски, отстоящей на расстояние х от данной стороны

Ь, равна dS = —(h—х) А я, где А —высота, опущенная h

на эту сторону, а Дл; — ширина полоски, следовательно, расстояние центра тяжести от этой стороны равно: н н

I*= — [ xdS — Г— (h—х) xdx =

SJ bh J h 9

A1 2 3 J I о 3 Таким образом, центр тяжести треугольника находится на расстоянии, равном — высоты от соответствующей

З

стороны, т. е. в точке пересечения его медиан, ибо это— е&инственная точка, обладающая таким свойством.

596. Найти центр тяжести площади, ограниченной осью Ox и одной полуволной синусоиды

Решение. Так как площадь одной полуволны синусоиды расположена симметрично относительно прямой

, то центр тяжести лежит на этой прямой и, сле

довательно, . Ордината центра тяжести находится

по формуле

Так как

то

Итак, центр тяжести данной площади находится в точке

597. Найти координаты центра тяжести площади, ограниченной параболами

Решение. Данные параболы, пересекающиеся в точках О (0, 0) и А (а; а), ограничивают площадь, расположенную симметрично относительно биссектрисы Следовательно, центр тяжести данной площади лежит на биссектрисе, а отсюда

Так как площадь ограничена двумя кривыми


и, то абсцисса центра тяжести площади на-

ходится по формуле:


найдем:

точке

598. Найти центр тяжести площади, ограниченной осью абсцисс и одной аркой циклоиды:

Таким образом, центр тяжести площади находится в

Решение. Данная площадь расположена симметрично относительно прямой, следовательно, центр тяжести ее находится на этой прямой и отсюда

Найдем ц по формуле. Площадь S данной

фигуры была вычислена (см.Задачу 467):Сле

довательно,

Центр тяжести данной площади находится в точке

599. Пользуясь теоремой Гюльдена, вычислить поверхность тора, образованного вращением круга радиуса а вокруг оси, расположенной в его плоскости и отстоящей от центра его на расстояние

Решение. Так как длина данной окружности равна , а длинаокружности, описанной центром тяжести ее, равна, то поверхность тора по первой теореме Гюльдена равна:

600. Пользуясь теоремой Гюльдена, вычислить объем и боковую поверхность прямого кругового конуса.

Решение. Боковая поверхность конуса с высотой, образующейИ радиусом основанияПолучается при вращении гипотенузы длинойВокруг катета длиной. Центр тяжести гипотенузы находится на ее середине и

удален от оси вращения на. Поэтому по первой теореме Гюльдена боковая поверхность равна:

Площадь треугольника равна, центр тяжести его, находясь на пересечении медиан, отстоит от катета А на расстояние, равноеВысоты, опущенной на этот катет, т. е., следовательно, по второй теореме Гюльдена объем конуса равен:

601. На цилиндре, имеющем 6 см в диаметре, кругом вдоль поверхности вырезан канал, имеющий поперечным сечением равносторонний треугольник со стороной в 0,5 сж. Вычислить объем срезанного материала.

Решение. Искомый объем есть объем тела, получаемого при вращении равностороннего треугольника со стороной в 0,5 см вокруг оси, параллельной основанию и удаленной от него на 3 ел, причем вершина лежит между основанием и осью (рис. 26).

Высота треугольника равна

площадь его равна

Расстояние центра тяжести от оси ОС = OA — AC =

(AC равно

высоты). По второй теореме Гюльдена имеем:

602. Длина одной арки циклоиды

РавнаА поверхность, образуемая вращением ее вокруг оси Oxt равна. Вычислить поверхность, образуемую вращением той же арки циклоиды вокруг касательной в верхней ее точке.

Решение. Пусть— расстояние центра тяжести от оси Oxi тогда по первой теореме Гюльдена:

, откуда

Наибольшая ордината кривой соответствуетИ рав

на 2а, причем касательная в этой точке параллельна оси Ох следовательно, расстояние центра тяжести от этой

касательной равно

Таким образом, искомая поверхность, образуемая’ вращением той же арки циклоиды вокруг касательной в верхней ее точке равна:

603. Найти центр тяжести дуги, составляющей четверть окружности радиусаРасположенной в первом квадранте.

604. Найти центр тяжести расположенной в первом квандранте дуги гипоциклоиды x = acosst, у = a sin31.

605. Найти центр тяжести половины площади эллипса, опирающейся на большую ось.

606. Найти центр тяжести площади, заключенной

– L – L. L между параболой х2 – J – у2 = а 2 и осями координат.

607. Найти центр тяжести плоской фигуры, ограниченной кривой at/2 = Jc3 и прямой х = а {а > 0).


608. Найти центр тяжести площади, ограниченной кривыми

у = ах3, х = а, у = 0.

609. Найти центр тяжести площади, ограниченной эллипсом jc2 -)- 4у2 = 4 и окружностью х2– у2 = 4 и расположенной в первом квадранте.


610. Найти центр тяжести фигуры, ограниченной замкнутой кривой у2 = ах3 — х*.

< Предыдущая   Следующая >
Источник
Автор статьи

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Задача 1

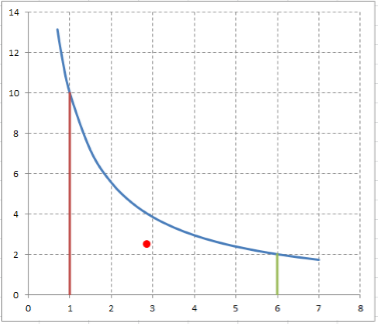
Найти координаты центра тяжести (КЦТ) материальной плоской фигуры в виде криволинейной трапеции (КрТ), образованной кривой $y=frac{150}{12cdot x+3} $ между точками с абсциссами $x=1$ и $x=6$. Поверхностную плотность фигуры считать величиной постоянной. Выполнить графические построения.

График данной криволинейной трапеции:

Координаты центра тяжести

КЦТ материальной плоской фигуры в виде КрТ, образованной кривой $y=yleft(xright)$ на промежутке $left[a,; bright]$, вычисляют по формулам $x_{C} =frac{int limits _{a}^{b}xcdot yleft(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } $ и $y_{C} =frac{frac{1}{2} cdot int limits _{a}^{b}y^{2} left(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } $.

Продолжение задачи 1

Находим интеграл $I_{1} =int limits _{a}^{b}yleft(xright)cdot dx $:

[I_{1} =int limits _{1}^{6}frac{150}{12cdot x+3} cdot dx =frac{150}{12} cdot left[ln left|12cdot x+3right|right]_{1}^{6} =]

[=frac{150}{12} cdot left(ln left|12cdot 6+3right|-ln left|12cdot 1+3right|right)=]

[=12,5cdot left(ln 75-ln 15right)=12,5cdot ln frac{75}{15} =12,5cdot ln 5approx 12,5cdot 1,609approx 20,11; ]

Находим интеграл $I_{2} =frac{1}{2} cdot int limits _{a}^{b}y^{2} left(xright)cdot dx $:

[I_{2} =frac{1}{2} cdot int limits _{1}^{6}frac{150^{2} }{left(12cdot x+3right)^{2} } cdot dx =frac{150^{2} }{2} cdot int limits _{1}^{6}left(12cdot x+3right)^{-2} cdot dx =]

[=frac{150^{2} }{2cdot 12} cdot left[frac{left(12cdot x+3right)^{-2+1} }{-2+1} right]_{1}^{6} =-frac{150^{2} }{24} cdot left[frac{1}{12cdot x+3} right]_{1}^{6} =]

[=-frac{150^{2} }{24} cdot left(frac{1}{12cdot 6+3} -frac{1}{12cdot 1+3} right)=-frac{150^{2} }{24} cdot left(frac{1}{75} -frac{1}{15} right)=]

[=-frac{150^{2} }{24} cdot frac{1-5}{75} =frac{150^{2} }{24} cdot frac{4}{75} =frac{150^{2} }{6cdot 75} =50.]

Находим интеграл $I_{3} =int limits _{a}^{b}xcdot yleft(xright)cdot dx $:

[I_{3} =int limits _{1}^{6}xcdot frac{150}{12cdot x+3} cdot dx =int limits _{1}^{6}frac{150cdot x}{12cdot x+3} cdot dx =]

[=int limits _{1}^{6}frac{12cdot 150cdot x}{12cdot left(12cdot x+3right)} cdot dx =int limits _{1}^{6}frac{12cdot 150cdot x+150cdot 3-150cdot 3}{12cdot left(12cdot x+3right)} cdot dx =]

[=int limits _{1}^{6}frac{150cdot left(12cdot x+3right)-150cdot 3}{12cdot left(12cdot x+3right)} cdot dx =int limits _{1}^{6}frac{150cdot left(12cdot x+3right)}{12cdot left(12cdot x+3right)} cdot dx -]

[-int limits _{1}^{6}frac{150cdot 3}{12cdot left(12cdot x+3right)} cdot dx =frac{150}{12} cdot int limits _{1}^{6}dx -frac{3}{12} cdot int limits _{1}^{6}frac{150}{12cdot x+3} cdot dx =]

[=frac{150}{12} cdot left[xright]_{1}^{6} -frac{3}{12} cdot I_{1} approx 12,5cdot left(6-1right)-frac{3}{12} cdot 20,11approx 62,5-5,03approx 57,47.]

Вычисляем КЦТ:

[x_{C} =frac{int limits _{a}^{b}xcdot yleft(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } =frac{I_{3} }{I_{1} } approx frac{57,47}{20,11} approx 2,86;]

[y_{C} =frac{frac{1}{2} cdot int limits _{a}^{b}y^{2} left(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } =frac{I_{2} }{I_{1} } approx frac{50}{20,11} approx 2,49.]

Центр тяжести отмечен на рисунке красной точкой.

Задача 2

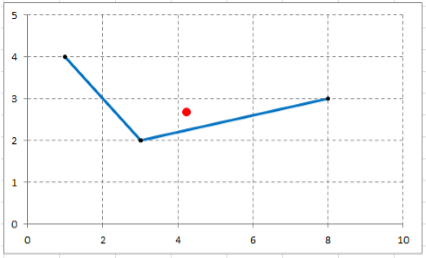
Найти КЦТ материальной кривой в виде ломаной линии, проходящей последовательно через заданные точки $Mleft(1,; 4right)$,~$Nleft(3,; 2right)$ и $Kleft(8,; 3right)$. Линейную плотность ломаной считать величиной постоянной. Выполнить графические построения.

График данной ломаной:

Координаты центра тяжести

Формулы для вычисления КЦТ плоской кривой имеют вид $x_{C} =frac{int limits _{a}^{b}xcdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } $ и $y_{C} =frac{int limits _{a}^{b}yleft(xright)cdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } $.

Продолжение задачи 2

Находим уравнения прямых, учитывая, что общее уравнение прямой имеет следующий вид:

$Acdot x+Bcdot y+C=0$, где $A=y_{2} -y_{1} $, $B=x_{1} -x_{2} $, $C=-Acdot x_{1} -Bcdot y_{1} $.

  1. Для прямой $MN$ имеем такие значения коэффициентов:

    2. [A=y_{2} -y_{1} =2-4=-2; B=x_{1} -x_{2} =1-3=-2;]

    [C=-Acdot x_{1} -Bcdot y_{1} =2cdot 1+2cdot 4=10.]

    Уравнение прямой $MN$: $-2cdot x-2cdot y+10=0$ или $-x-y+5=0$.

  2. Для прямой $NK$ имеем такие значения коэффициентов:

    3. [A=y_{2} -y_{1} =3-2=1; B=x_{1} -x_{2} =3-8=-5; ]

    [C=-Acdot x_{1} -Bcdot y_{1} =-1cdot 3+5cdot 2=7.]

Уравнение прямой $NK$: $x-5cdot y+7=0$.

Находим выражение $sqrt{1+y’^{2} } $ для данных прямых:

  1. для прямой $MN$ $y=-x+5$, $y’=-1$, $sqrt{1+y’^{2} } =sqrt{2} approx 1,41$.
  2. для прямой $NK$ $y=frac{1}{5} cdot x+frac{7}{5} $, $y’=frac{1}{5} $, $sqrt{1+y’^{2} } =frac{sqrt{26} }{5} approx 1,02$.

Находим интеграл $I_{1} =int limits _{a}^{b}xcdot sqrt{1+y’^{2} } cdot dx $ вдоль всей ломаной:

[I_{1} =1,41cdot int limits _{1}^{3}xcdot dx +1,02cdot int limits _{3}^{8}xcdot dx =1,41cdot left[frac{x^{2} }{2} right]_{1}^{3} +1,02cdot left[frac{x^{2} }{2} right]_{3}^{8} =]

[=frac{1,41}{2} cdot left(3^{2} -1^{2} right)+frac{1,02}{2} cdot left(8^{2} -3^{2} right)=frac{1,41}{2} cdot 8+frac{1,02}{2} cdot 55approx 33,69.]

Находим интеграл $I_{2} =int limits _{a}^{b}ycdot sqrt{1+y’^{2} } cdot dx $ вдоль всей ломаной:

[I_{2} =1,41cdot int limits _{1}^{3}left(-x+5right)cdot dx +1,02cdot int limits _{3}^{8}left(frac{1}{5} cdot x+frac{7}{5} right)cdot dx =]

[=1,41cdot left[-frac{x^{2} }{2} +5cdot xright]_{1}^{3} +1,02cdot left[frac{1}{5} cdot frac{x^{2} }{2} +frac{7}{5} cdot xright]_{3}^{8} =1,41cdot 6+1,02cdot frac{125}{10} approx 21,21.]

Находим интеграл $I_{3} =int limits _{a}^{b}sqrt{1+y’^{2} } cdot dx $ вдоль всей ломаной:

[I_{3} =1,41cdot int limits _{1}^{3}dx +1,02cdot int limits _{3}^{8}dx =1,41cdot 2+1,02cdot 5approx 7,92.]

Находим КЦТ ломаной линии:

[x_{C} =frac{int limits _{a}^{b}xcdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } =frac{I_{1} }{I_{3} } approx frac{33,69}{7,92} approx 4,25; ]

[y_{C} =frac{int limits _{a}^{b}yleft(xright)cdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } =frac{I_{2} }{I_{3} } approx frac{21,21}{7,92} approx 2,68.]

Центр тяжести отмечен на рисунке красной точкой.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Пусть на плоскости Oxy дана
система материальных точек  , , …, с массами  

координаты центра
тяжести в данном случае будут определяться по формулам

,

Центр
тяжести плоской линии

Пусть
задана кривая АВ уравнением , , и пусть эта кривая представляет собой материальную
линию.

Координаты центра
тяжести данной линии

 

Центр
тяжести плоской фигуры.

Пусть данная фигура,
ограниченная линиями ,, , , представляет собой материальную плоскую фигуру.

Координаты центра
тяжести такой фигуры

 

Пример:

Вычислить
координаты центра масс однородной плоской фигуры, ограниченной линиями  и  

Координаты центра
тяжести такой фигуры

Данное значение координаты  можно получить
из соображений симметрии.

Источник

Определение координат центра тяжести фигур

Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести:

  1. Аналитический (путем интегрирования).
  2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
  3. Экспериментальный. (метод подвешивания тела).
    Этот способ подходит в основном для плоских и линейных тел.
  4. Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.

    Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
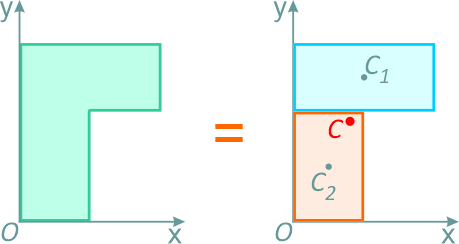
    Определение координат центра тяжести разбиением

    Рисунок 1.8

    Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
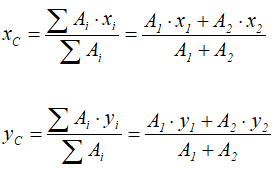
    Формулы для расчета координат центра тяжести

  5. Дополнение (Метод отрицательных площадей или объемов).
    Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

    Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
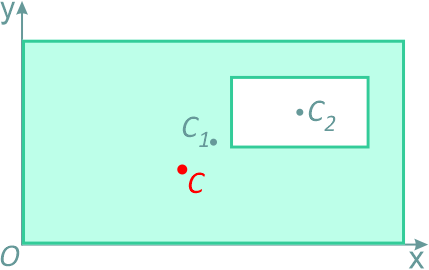
    Метод отрицательных площадей или объемов

    Рисунок 1.9

    Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
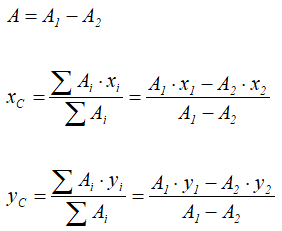
    Формула определения центра тяжести

При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Пример определения координат центра тяжести плоской фигуры

Задача
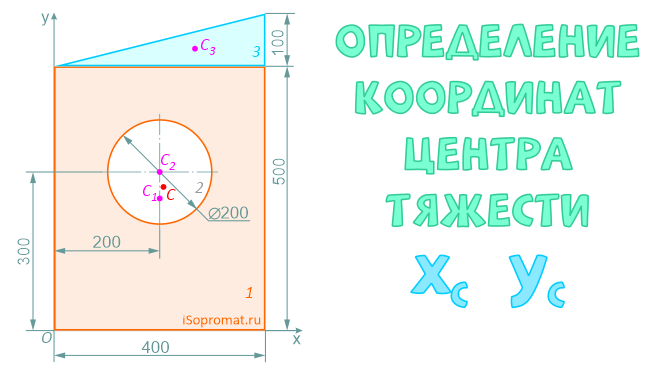
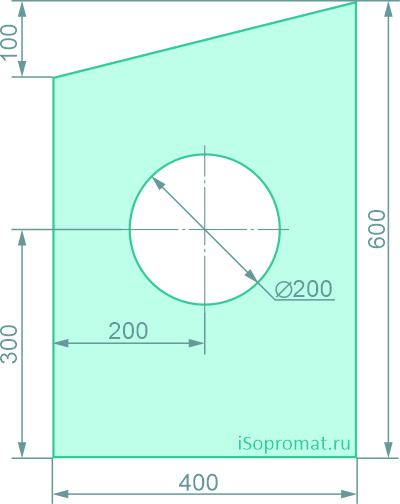
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Сложное сечение
Решение
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
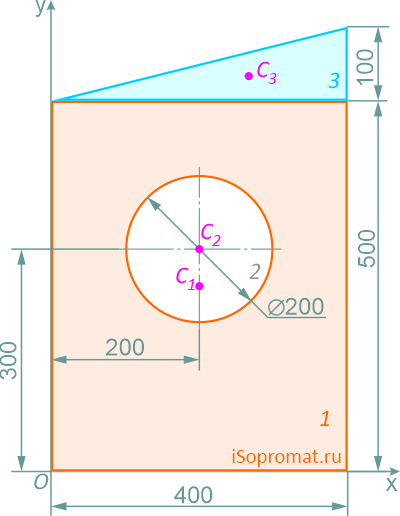
Разбивка сечения
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
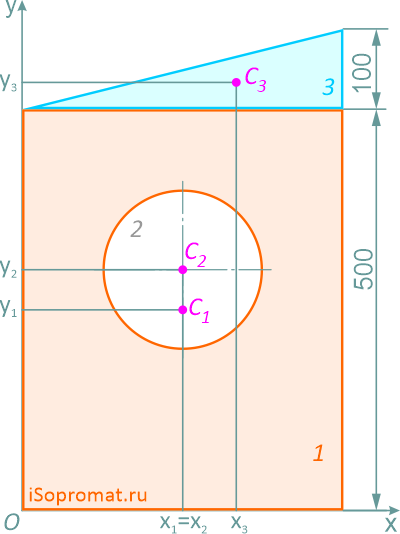
Центры тяжести частей фигуры
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм

Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм

Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
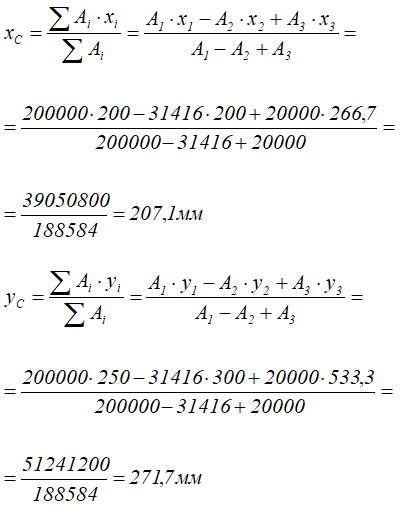
Расчет координат центра тяжести
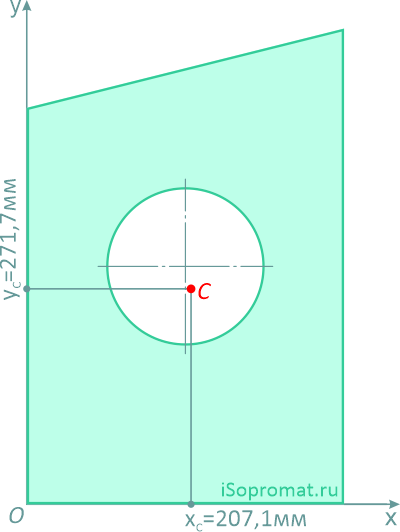
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Координаты центра тяжести

Другие примеры решения задач >
Центры тяжести простейших фигур >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Добавить комментарий