Продольные
силы в поперечных сечениях
Под растяжением
(сжатием)понимают такой вид
нагружения, при котором в поперечных
сечениях стержня возникают только
продольные силы![]() ,
,
а прочие силовые факторы равны нулю.
Рассмотрим однородный прямолинейный
стержень длиной ![]() и площадью поперечного сеченияА,
и площадью поперечного сеченияА,
на двух концах которого приложены
две равные по величине и противоположно
направленные центральные продольные
силыР(рис. 2.2,а).
Продольная сила– внутреннее
усилие, равное сумме проекций всех
внешних сил,взятых с одной стороны
от сечения, на ось стержня. Примем
следующееправило знаков для
продольной силы: растягивающая
продольная сила положительна, сжимающая
– отрицательна (рис. 2.1).

Рис.2.1
Поместим начало плоской системы координат
yzв центре тяжести левого сечения,
а ось![]() направим
направим
вдоль продольной оси стержня.
Для определения величин внутренних
усилий воспользуемся методом сечений.
Задавая некоторое сечение на расстояние
z(![]() )
)
от начала системы координат и рассматривая
равновесие левой относительно заданного
сечения части стержня (рис. 2.2,б),
приходим к следующему уравнению:
![]() ,
,
откуда следует,
что
![]() .
.
Следовательно, продольная сила в сечении
численно равна сумме проекций на ось
стержня всех сил, расположенных по одну
сторону сечения
![]() (2.1)
(2.1)
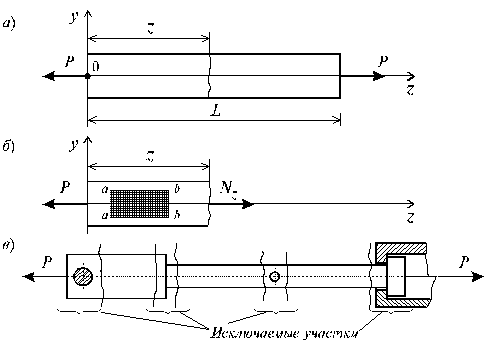
Рис. 2.2
Для наглядного представления о характере
распределения продольных сил по длине
стержня строится эпюра
продольных сил ![]() .
.
Осью абсцисс служит ось стержня. Каждая
ордината графика – продольная сила (в
масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком
сечении действует максимальное внутреннее
усилие (например, найти Nmaxпри растяжении-сжатии). Сечение, где
действует максимальное усилие будем
называтьопасным.
Рассмотрим несколько примеров определения
внутренних сил.
Пример 1.
Пусть имеется стержень постоянного
поперечного сечения, нагруженный силами
2Ри 3Рвдоль продольной оси
стержня, показанный на рис.2.3. Определить
величину внутренних сил.
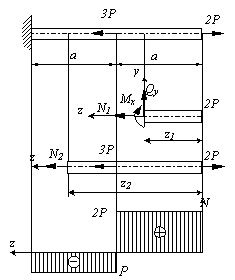
Рис.2.3
Решение.
Стержень может быть разделен на два
участка, граничными точками которых
являются точки приложения сосредоточенных
сил и точка закрепления. Если начало
координат расположить на правом конце
стержня, а ось zнаправить справа налево, то, используя
метод сечений,рассекаяпоследовательно
участки,отбрасываялевую часть,заменяяее действие внутренними
усилиямиN,Qy,
Mx
иуравновешиваяоставшуюся часть,
получим:
Iучасток:![]()
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
![]() ,
,![]()
Как
видно, при
растяжении в поперечных сечениях стержня
возникает только один внутренний силовой
фактор – нормальная сила N.
IIучасток:![]()
![]() ,
,![]() .
.
Таким образом, нормальная сила равна
алгебраической сумме проекций сил,
приложенных к отсеченной части на
продольную ось
![]() .
.
Полученные результаты для большей
наглядности удобно представить в виде
графика, (эпюры N),
показывающего изменение продольной
силы вдоль оси стержня (рис.2.3). Построим
на первом участке линию параллельную
осиzна высоте 2Р,
на втором участке – линию со значением
–Р. Области ограниченные графиком
и осьюzпринято
штриховать и обозначать знак этой
области. Видно, что наибольшая продольная
сила возникает на первом участке стержня
и, как следствие, при прочих равных
условиях, он скорее может разрушиться,
чем второй участок.
Пример
2.
Построить
эпюру продольных сил для жестко
защемленной балки (рис.2.4).
Решение:
1.
Намечаем характерные сечения, нумеруя
их от свободного конца стержня к заделке.
2.
Определяем продольную силу
![]() в
в
каждом характерном сечении. При этом
рассматриваем всегда ту отсеченную
часть, в которую не попадает жесткая
заделка.
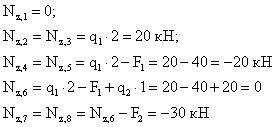
3. По
найденным значениям строим эпюру
![]() .
.
Положительные значения откладываются
(в выбранном масштабе) над осью эпюры,
отрицательные – под осью.
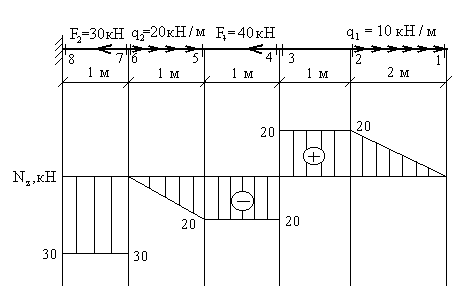
Рис.2.4
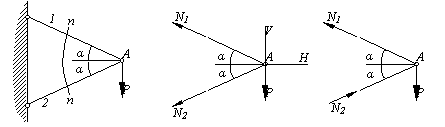
Пример 3.
Два стержня, соединенные в т. А,
находятся под действием силыР(рис.2.5,а). Определить усилия,
действующие в стержнях.
а)
б) в)
Рис.2.5
Решение.
Воспользуемся методом сечений. Рассечемстержни в произвольном месте сеченияn–n.Отбросимлевую отсеченную часть.Заменимотброшенную часть, приложив
усилияN1иN2в сечениях
к правой части. Направление усилий
целесообразно выбрать так чтобы они
растягивали отсеченные части (рис.2.5,б).
Уравновесимотсеченную часть,
запишем уравнения![]() ;
;![]() .
.

Решая, из первого уравнения получим
![]() ,
,
из второго уравнения окончательно имеем
![]() ;
;![]() .
.
Так как величина силы N2
< 0, то
её направление следует изменить на
противоположное (рис.2.5,в). Согласно
рисунку нормальная силаN1растягивает отсеченную часть стержня
1 – она положительна, силаN2
сжимает отсеченную часть стержня
2 – она отрицательна.
Пример 4.
Абсолютно жесткий брус подвешен на двух
стержнях и находится под действием силы
Р(рис.2.6,а). Определить усилия
в стержнях.
Решение.
Используя метод сечений, получим
отсеченную часть, показанную на рис.2.6,
б.
Запишем уравнения равновесия
![]() и
и
![]() :
:
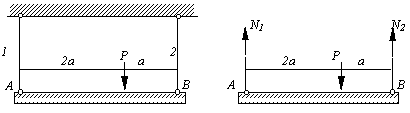
Рис.2.6
Решая систему уравнений, получим
![]() ;
;![]() .
.
Напряжение
в поперечных сечениях стержня
Нормальная сила
![]() приложена в центре тяжести сечения,
приложена в центре тяжести сечения,
является равнодействующей внутренних
сил в сечении и, в соответствии с
этим, определяется следующим образом:
![]() .
.
Но из этой формулы нельзя найти закон
распределения нормальных
![]() напряжений в поперечных сечениях
напряжений в поперечных сечениях
стержня. Для этого обратимся к анализу
характера его деформирования.
Если на боковую поверхность этого
стержня нанести прямоугольную сетку
(рис. 2.2, б), то после нагружения
поперечные линииа–а,
b–bи т.д.
переместятся параллельно самим себе,
откуда следует, что все поверхностные
продольные волокна удлинятся одинаково.
Если предположить также, что и внутренние
волокна работают таким же образом, то
можно сделать вывод о том, что поперечные
сечения в центрально растянутом стержне
смещаются параллельно начальным
положениям, что соответствует гипотезе
плоских сечений(гипотезе
Бернулли).
Значит, все продольные волокна стержня
находятся в одинаковых условиях, а
следовательно, нормальные напряжения
во всех точках поперечного сечения
должны быть также одинаковы и равны
![]() ,
,
(2.2)
где A-площадь
поперечного сечения стержня.
В сечениях, близких к месту приложения
внешних сил, гипотеза Бернулли нарушается:
сечения искривляются, и напряжения в
них распределяются неравномерно. По
мере удаления от сечений, в которых
приложены силы, напряжения выравниваются,
и в сечениях, удаленных от места приложения
сил на расстояние, равное наибольшему
из размеров поперечного сечения,
напряжения можно считать распределенными
по сечению равномерно. Это положение,
называемое принципом
Сен-Венана, позволяет при определении
напряжений в сечениях, достаточно
удаленных от мест приложения внешних
сил, не учитывать способ их приложения,
заменять систему внешних сил статически
эквивалентной системой. Например,
экспериментально установлено, что во
всех трех случаях нагружения стержня
(рис. 2.7,а) значения напряжений в
сечениях, удаленных от крайних сечений
на расстояние не менее высоты сечения![]() ,
,
одинаковы:![]() (рис. 2.7,б), а в сечениях, близких к
(рис. 2.7,б), а в сечениях, близких к
местам приложения внешних сил,
распределения напряжений по сечению
существенно различны (рис. 2.7,в).
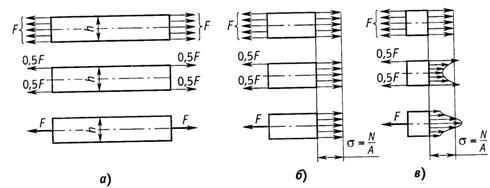
Рис.2.7
Высказанное предположение о равномерном
распределении нормальных напряжений
в поперечном сечении справедливо для
участков, достаточно удаленных от мест:
резкого изменения площади поперечного
сечения (рис. 2.2, в); скачкообразного
изменения внешних нагрузок; скачкообразного
изменения физико-механических
характеристик конструкций.
Нормальные напряжения при сжатии
определяют также, как и при растяжении,
но считают отрицательными.
Следует помнить, что длинные (тонкие)
стержни, нагруженные сжимающими силами,
могут потерять устойчивость. Расчет
стержней на устойчивость рассмотрен в
разделе «Устойчивость».
В инженерных сооружениях встречаются
растянутые или сжатые элементы, имеющие
отверстия. В сечениях с отверстием
определяют осредненные нормальные
напряжения по формуле
![]() ,
,
(2.3)
где
![]() -площадь
-площадь
поперечного сечения нетто;![]() –
–
площадь поперечного сечения брутто;![]() –
–
площадь его ослабления.
Деформации
и перемещения. Закон Гука
Рассмотрим однородный стержень с одним
концом, жестко заделанным, и
другим – свободным, к которому
приложена центральная продольная
сила Р(рис. 2.8). До нагружения
стержня его длина равнялась![]() – после нагружения она стала равной
– после нагружения она стала равной![]() (рис. 2.8). Величину
(рис. 2.8). Величину![]() называютабсолютным
называютабсолютным
удлинениемстержня.
Рис. 2.8
Если в нагруженном стержне напряженное
состояние является однородным, т.е. все
участки стержня находятся в одинаковых
условиях, деформация
![]() остается одной и той же по длине стержня
остается одной и той же по длине стержня
и равной
![]() .
.
(2.4)
Если же по длине стержня возникает
неоднородное напряженное состояние,
то для определения его абсолютного
удлинения необходимо рассмотреть
бесконечно малый элемент длиной dz(рис. 2.8). При растяжении он увеличит
свою длину на величину![]() и его деформация составит:
и его деформация составит:
![]() .
.
(2.5)
В пределах малых деформаций при простом
растяжении или сжатии закон Гука
записывается в следующем виде (нормальные
напряжения в поперечном сечении прямо
пропорциональны относительной линейной
деформации
![]() ):
):
![]() .
.
(2.6)
Величина Епредставляет собой
коэффициент пропорциональности,
называемый модулем упругости материала
первого рода (модуль продольной
упругости). Его величина постоянна для
каждого материала. Он характеризует
жесткость материала, т.е. способность
сопротивляться деформированию под
действием внешней нагрузки.
Из совместного рассмотрения уравнений
(2.5) и (2.6) получим:
![]() ,
,
откуда с учетом того, что
![]() и
и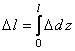 ,
,
окончательно получим:
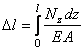 .
.
(2.7)
Если стержень изготовлен из однородного
изотропного материала с Е =const,
имеет постоянное поперечное сечениеA =constи
нагружен по концам силойР, то из
(2.7) получим
![]() .
.
(2.8)
Зависимость (2.8) также выражает закон
Гука. Знаменатель EAназываетсяжесткостью при растяжении
– сжатииили продольной жесткостью.
При решении многих практических задач
возникает необходимость, наряду с
удлинениями, обусловленными действием
механических нагрузок, учитывать
также удлинения, вызванные температурным
воздействием. В этом случае пользуются
принципом независимости действия
сил, и полные деформации рассматривают
как сумму силовой и температурной
деформаций:
![]() ,
,
(2.9)
где
![]() -коэффициент
-коэффициент
температурного расширения материала;t-перепад
температуры тела. Для однородного
стержня, нагруженного по концам
продольными силамиРи равномерно
нагретого по длине, получим:
![]() .(2.10)
.(2.10)
Потенциальная
энергия деформации
Внешние силы, приложенные к упругому
телу и вызывающие изменение геометрии
тела, совершают работу Wна соответствующих перемещениях.
Одновременно с этим в упругом теле
накапливается потенциальная энергия
его деформированияU. При действии
динамических внешних нагрузок часть
работы внешних сил превращается в
кинетическую энергию движения частиц
телаК.Приняв энергетическое
состояние системы до момента действия
данных сил равным нулю, и в условиях
отсутствия рассеивания энергии, уравнение
баланса энергии можно записать в
следующем виде:
W = U + K.(2.11)
При действии статических нагрузок
К = 0, следовательно,
W = U.(2.12)
Это означает, что при статическом
нагружении работа внешних сил полностью
преобразуется в потенциальную энергию
деформации. При разгрузке тела
производится работа за счет потенциальной
энергии деформации, накопленной телом.
Таким образом, упругое тело является
аккумулятором энергии. Это свойство
упругого тела широко используется в
технике, например, в заводных пружинах
часовых механизмов, в амортизирующих
рессорах и др. В случае простого
растяжения (сжатия) для вывода необходимых
расчетных зависимостей потенциальной
энергии деформации рассмотрим решение
следующей задачи.
На рис. 2.9, аизображен
растягиваемый силойРстержень,
удлинение которого соответствует
отрезку![]() ,
,
ниже показан график изменения величины
удлинения стержня![]() в зависимости от силыР(рис. 2.9,б).
в зависимости от силыР(рис. 2.9,б).
В соответствии с законом Гука этот
график носит линейный характер.
Пусть некоторому значению силы Рсоответствует удлинение стержня![]() .Дадим некоторое приращение силеDР-соответствующее
.Дадим некоторое приращение силеDР-соответствующее
приращение удлинения составит![]() .Тогда элементарная работа на этом
.Тогда элементарная работа на этом
приращении удлинения составит:
![]() ,
,
(2.13)
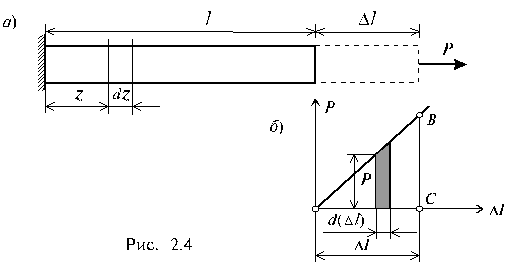
Рис.2.9
вторым слагаемым, в силу его малости,
можно пренебречь, и тогда
![]() .
.
(2.14)
Полная работа равна сумме элементарных
работ, тогда, при линейной зависимости
“нагрузка -перемещение”,
работа внешней силыРна перемещении![]() будет равна площади треугольникаОСВ(рис. 2.9), т.е.
будет равна площади треугольникаОСВ(рис. 2.9), т.е.
![]() .
.
(2.15)
В свою очередь, когда напряжения
![]() и деформации
и деформации![]() распределены по объему телаVравномерно (как в рассматриваемом
распределены по объему телаVравномерно (как в рассматриваемом
случае) потенциальную энергию
деформирования стержня можно записать
в виде:
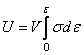 .
.
(2.16)
Поскольку, в данном случае имеем, что
![]() ,
,![]() и
и![]() ,
,
то
 ,
,
(2.17)
т.е. подтверждена справедливость (2.12).
С учетом (2.8) для однородного стержня с
постоянным поперечным сечением и
при Р = constиз (2.17) получим:
![]() .
.
(2.18)
Единицей измерения потенциальной
энергии деформации является 1Hм = 1Дж.
Напряженное
и деформированное состояние при
растяжении и сжатии
Рассмотрим более подробно особенности
напряженного состояния, возникающего
в однородном растянутом стержне.
Определим напряжения, возникающие на
некоторой наклонной площадке, составляющей
угол ![]() с плоскостью нормального сечения (рис.
с плоскостью нормального сечения (рис.
2.10,а).
Из условия
![]() ,
,
записанного для отсеченной части стержня
(рис. 2.10,б), получим:
![]() ,
,
(2.19)
где A-площадь
поперечного сечения стержня,![]() -площадь
-площадь
наклонного сечения. Из (2.19) легко
установить:
![]() .
.
(2.20)
Раскладывая напряжение рпо нормали
и касательной к наклонной площадке
(рис. 2.10,в), с учетом (2.20) получим:
![]() ;
;![]() .
.
(2.21)

Рис. 2.10
Полученные выражения показывают, что
для одной и той же точки тела величины
напряжений, возникающих в сечениях,
проходящих через эту точку, зависят
от ориентации этой площадки, т.е. от угла
![]() .
.
При![]() из (2.21) следует, что
из (2.21) следует, что![]() ,
,![]() .
.
При![]() ,
,
т.е. на продольных площадках,![]() .
.
Это означает, что продольные слои
растянутого стержня не взаимодействуют
друг с другом. Касательные напряжения![]() принимают наибольшие значения при
принимают наибольшие значения при![]() ,
,
и их величина составляет![]() .
.
Важно отметить, что![]() .
.
Следовательно, в любой точке тела на
двух взаимно перпендикулярных площадках
касательные напряжения равны между
собой по абсолютной величине. Это условие
является общей закономерностью любого
напряженного состояния и носит названиезакона парности касательных
напряжений.
Теперь перейдем к анализу деформаций
в растянутом стержне. Наблюдения
показывают, что его удлинение в продольном
направлении сопровождается
пропорциональным уменьшением поперечных
размеров стержня (рис. 2.11).
Если обозначить:
![]() ;
;![]() ;
; ,
,
то, как показывают эксперименты,
![]() = constдля данного материала и является
= constдля данного материала и является
безразмернымкоэффициентом
Пуассона. Величина![]() является важной характеристикой
является важной характеристикой
материала и определяется экспериментально.
Для реальных материалов![]() принимает значения 0,1…0,45.
принимает значения 0,1…0,45.
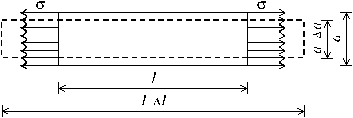
Рис. 2.11
При растяжении стержня возникают не
только линейные, но и угловые деформации.
Рассмотрим прямой угол АВС(рис. 2.12,а), образованный
отрезкамиАВиАС, в
недеформированном состоянии.
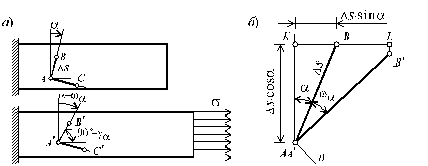
Рис. 2.12
При растяжении стержня точки А, ВиСзаймут положениеА¢,
B¢,C¢соответственно. Величина
![]()
называется
угловой деформацией или угловым сдвигом
в точке А.
Совместим точки АиА¢и рассмотрим взаимное расположение
отрезковАВиА¢B¢
(рис. 2.12,б). На этом рисунке
отметим вспомогательные точкиKиLи прямуюn, перпендикулярную
отрезкуА¢B¢.
Из рис. 2.12,бимеем:
![]() ;
;![]() ,
,
откуда с учетом
![]() получим:
получим:
![]()
![]() .
.
(2.22)
Для определения
![]() спроектируем ломаную
спроектируем ломаную![]()
на осьn
![]() ,
,
откуда, учитывая малость угла
![]() ,
,
т.е.![]() ,
,![]() ,
,
получим:
![]() .
.
(2.23)
В результате совместного рассмотрения
(2.22) и (2.23) получим:
![]() .
.
Откуда
![]() .
.
Следовательно,
![]() .
.
(2.24)
Сопоставляя выражение
![]() с выражением
с выражением![]() из (2.21) окончательно получим закон
из (2.21) окончательно получим закон
Гука для сдвига:
![]() (2.25)
(2.25)
где величина
![]() называется модулем сдвига или модулем
называется модулем сдвига или модулем
упругости материала второго рода.
Расчеты
на прочность и жесткость при растяжении
(сжатии)
Основной задачей расчета конструкции
является обеспечение ее безопасной
эксплуатации. Важнейшим условием,
обеспечивающим безопасную эксплуатацию
конструкции, является условие прочности.
Существуют различные методы обеспечения
прочности конструкций. Мы чаще всего
будем пользоваться одним из этих методов
– расчетом по допускаемым напряжениям.
Согласно этому методу для конструкций,
работающих на растяжение-сжатие, условие
прочности, составленное для опасного
сечения, можно записать в таком виде:
![]() (2.26)
(2.26)
где
![]() – максимальное напряжение в конструкции;
– максимальное напряжение в конструкции;![]() –
–
характеристика материала, называемаядопускаемым напряжением.
Допускаемое напряжение находится по
формуле
![]() .
.
(2.27)
где
![]() – предельное напряжение, при достижении
– предельное напряжение, при достижении
которого в стержне наступаетпредельное
состояние материала: появляются
пластические деформации, если материал
стержня – пластичный, или происходит
разрушение, если стержень выполнен из
хрупкого материала;n
– нормируемый коэффициент запаса
прочности.
Кроме формулы (2.26), возможен второй
вариант условия прочности
![]() ,
,
(2.28)
где
![]() (2.29)
(2.29)
называется действительным коэффициентом
запаса прочности, показывающим во
сколько раз надо увеличить максимальное
напряжение в стержне, чтобы материал
стержня оказался в опасном (предельном)
состоянии.
Условие прочности в зависимости от цели
поставленной задачи позволяет выполнять
расчеты на прочность двух видов: проектный
и проверочный. Для спроектированного
стержня можно также определять допускаемую
нагрузку.
Проектный расчетвыполняют с целью определения размеров
поперечных сечений элемента конструкции
при известных рабочих нагрузках и
материале (допускаемых напряжений).
Площадь поперечного сечения определяют
из выражения
![]() .
.
(2.30)
Форма сечения стержня не влияет на его
прочность при растяжении (сжатии). Форму
сечения стержня необходимо знать только
для определения размеров сечения при
известном значении площади.
Зная площадь сечения и его форму, находят
размеры сечения.
Проверочный расчетвыполняют для спроектированной
конструкции с целью проверки ее прочности.
При проверочном расчете должны быть
известны площадь опасного сечения,
нагрузка и материал (допускаемое
напряжение). Проверочный расчет выполняют
по формуле (2.26).
Определение
допускаемой нагрузкидля
спроектированного элемента конструкции,
размеры поперечного сечения которого
и материал (допускаемые напряжения)
известны. Условие прочности в этом
случае записывают в виде
![]() .
.
(2.31)
Зная значение
![]() ,
,
определяют допускаемую нагрузку![]() .
.
Так как допускаемые напряжения не имеют
точного значения, а выбираются приближенно,
то при проверочном расчете максимальные
рабочие напряжения могут превышать
допускаемые на 5%. По этой же причине
можно округлять полученные в расчетах
значения площади опасного поперечного
сечения или допускаемой нагрузки так,
чтобы максимальные напряжения отличались
от допускаемых не более чем на 5%. По этой
же причине можно округлять полученные
в расчетах значения площади опасного
поперечного сечения или допускаемой
нагрузки та, чтобы максимальные напряжения
отличались от допускаемых не более чем
на 5%.
При проектировании элементов конструкций
стремятся сделать их во всех сечениях
равнопрочными.
Рассмотренные три вида расчетов на
прочность можно выполнять не только
при растяжении или сжатии, а при любом
виде деформации (сдвиге, кручении,
изгибе).
При проектировании строительных
конструкций расчет на прочность стальных
элементов, подверженных центральному
растяжению или сжатию, следует выполнять
по формуле
![]() (2.32)
(2.32)
где
![]() –коэффициент условий работы,
–коэффициент условий работы,
принимаемый по СНИП (см. табл.2.1) или
другим нормам.
Таблица 2.1
|
Элементы конструкции |
|
|
Колонны общественных зданий и опор Элементы а) сжатых б) растянутых Сплошные Сечения
Сжатые элементы из одиночных уголков, |
0,95 0,95 0,95 1,1 1,1 0,75 |
Примечание:
В случаях, не оговоренных в настоящих
нормах, в формулах следует
принимать
![]() .
.
Для хрупких строительных материалов
условия прочности принимают вид:
при растяжении:
![]() ,
,![]() ;
;
при сжатии:
![]() ,
,![]() (2.33)
(2.33)
где
![]() и
и![]() – допускаемые напряжения при растяжении
– допускаемые напряжения при растяжении
и сжатии;ntиnc– нормативные коэффициенты запаса
прочности по отношению к пределу
прочности (nt, nc>1).
Для центрально сжатых бетонных элементов
формула (2.33) записывается в виде:
![]() (2.34)
(2.34)
где
![]() – коэффициент, принимаемый для бетона
– коэффициент, принимаемый для бетона
тяжелого, мелкозернистого и легкого
равным 1,00; для ячеистого автоклавного
– 0,85; для ячеистого неавтоклавного –
0,75.
В некоторых случаях работоспособность
элемента конструкции определяется не
только его прочностью, но и жесткостью,
т.е. способностью элемента воспринимать
нагрузки без недопустимых упругих
деформаций. При расчетах на жесткость
определяют максимальные перемещения
сечений и сопоставляют их с допускаемыми
перемещениями.
Условие жесткости, ограничивающее
изменение длины элемента, имеет следующий
общий вид:
![]() ,
,
где
![]() – изменение размеров детали;
– изменение размеров детали;
![]() – допускаемая величина этого изменения.
– допускаемая величина этого изменения.
Учитывая, что при растяжении (сжатии)
абсолютное удлинение в общем виде
определяется как алгебраическая сумма
величин
![]() по участкам
по участкам
![]() ,
,
(2.35)
условие жесткости при растяжении
(сжатии) запишем следующим образом:
![]() .
.
(2.36)
Так как перемещение, согласно закону
Гука, зависит от нагрузки и размеров
поперечного сечения, условие жесткости
позволяет решать те же три вида задач,
что и условие прочности.
Расчеты
статически определимых стержней
Статически определимый стержень– это стержень, который можно рассчитать,
используя только уравнения равновесия
(уравнения статики).
В
любой науке, которая называется «точной»
и в которой используются аналитические
методы описания состояний и явлений,
не обойтись без моделей. В нашем случае
при решении различных задач мы каждый
раз будем выбирать для рассматриваемого
объекта расчетную схему.
Расчетная
схема –
это упрощенная схема конструкции или
ее элементов, освобожденная от
несущественных в данной задаче
особенностей. При этом расчетная схема
должна отражать все наиболее существенное
для характера работы данной конструкции
и не содержать второстепенных факторов,
мало влияющих на результаты ее расчета.
Построение и обоснование расчетной
схемы – ответственный этап проектирования
и расчета конструкции.
Перейдем
к рассмотрению конкретных примеров.
Пример
5.
Чугунная
труба-стойка высотой
![]()
с наружным диаметром
![]()
и внутренним диаметром
![]()
нагружена сжимающей силой
![]() ,
,
модуль упругости чугуна
![]() .
.
Найти напряжение
![]()
в поперечном сечении колонны, абсолютное
![]()
и относительное укорочения
![]() .
.
Решение.
Как
уже говорилось выше, решение задачи
начинается с выбора расчетной схемы. В
данном случае стойка изображается как
вертикальный стержень длиной
![]() ,
,
жестко закрепленный в нижней части
(условное изображение фундамента или
земли). К верхней части стержня приложена
сосредоточенная сжимающая сила
(направление к стержню). При этом линия
действия силы должна совпадать с осью
стержня. Кроме того, рядом необходимо
изобразить поперечное сечение стойки
с указанием основных размеров. В данном
примере – это кольцо. Расчетная схема
для решения задачи изображена на рис.
2.13, а.
Далее строим эпюру продольной силы и
определяем максимальное внутреннее
усилие, возникающее в колонне. Поскольку
внешняя нагрузка постоянна по высоте,
то возникает только одна сжимающая
продольная сила
![]() .
.
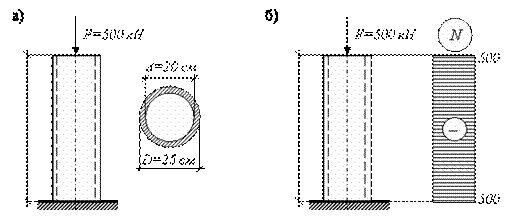
Рис.
2.13.
Максимальное нормальное напряжение
![]() определяется по формуле:
определяется по формуле:
![]()
где
![]()
– площадь трубы:
![]() .
.
тогда:
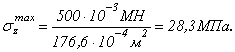
Абсолютное
и относительное укорочения стойки
определяем по формулам:
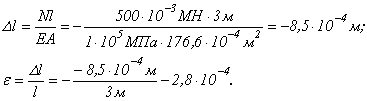
Знак “минус” обозначает уменьшение
размера (укорочение).
Пример
6.
Стальной
стержень круглого сечения растягивается
усилием
![]() .
.
Относительное удлинение не должно
превышать
![]() ,
,
а напряжение –![]() .
.
Найти наименьший диаметр, удовлетворяющий
этим условиям, если модуль упругости
стали
![]() .
.
Решение.
Как
и ранее, решение задачи начинается с
изображения расчетной схемы и построения
эпюра продольных сил (рис. 2.14).
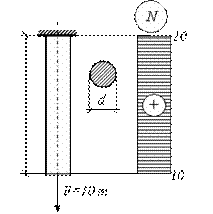
Рис.2.14
По условию задачи напряжение не должно
превышать
![]() ,
,
в связи с чем данная величина может быть
принята за расчетное сопротивление
материала стойки на растяжение, то есть
![]() .
.
По аналогии заданное относительное
удлинение можно принять за предельно
допустимое для данной стойки, то есть![]() .
.
В результате необходимо подобрать
диаметр стойки, удовлетворяющий условию
прочности и условию жесткости.
Продольное
растягивающее усилие равно по величине
внешней нагрузке, действующей на стержень
![]()
Требуемая
площадь поперечного сечения колонны
из условия прочности будет определяться
выражением:
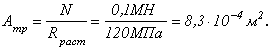
Зная
требуемую площадь, выразим необходимый
из условия прочности диаметр:
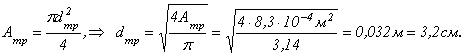
Условие жесткости при центральном
растяжении-сжатии:
![]()
![]()
![]()
Выражаем
из предельного неравенства требуемую
из условия жесткости площадь поперечного
сечения:
![]()
Диаметр
стойки из условия жесткости определим
по формуле:
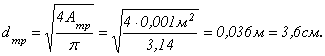
Окончательно принимаем из двух диаметров
больший,
![]()
Пример
7.
Определить
грузоподъемность и удлинение балки,
если
![]() .
.
Расчетная
схема бруса и эпюра продольных сил
изображены на рис. 2.15.

Рис.2.15
Решение.
Грузоподъемность бруса– это
максимальная нагрузка, которую он может
выдержать, не разрушаясь. Таким образом,
необходимо определить требуемую нагрузку
из условия прочности:
![]()
Согласно эпюре
![]() ,
,
тогда условие прочности примет вид:
![]()
Отсюда грузоподъемность бруса будет
равна:
![]()
![]()
Для определения удлинения стержня
![]() разбиваем его на участки. Каждый участок,
разбиваем его на участки. Каждый участок,
должен иметь постоянную жесткость
![]() и величину продольной силы. Таким
и величину продольной силы. Таким
образом, для данного бруса получаем три
участка (на рис. 2.15 они обозначены
римскими цифрами), тогда абсолютная
деформация в общем виде будет определяться
выражением:
![]() ,
,
в котором каждое слагаемое определяется
отдельно:
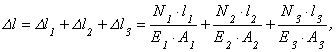
где
![]()
– значения продольных сил соответственно
на первом, втором и третьем участках;
![]()
– длины соответственно первого, второго
и третьего участков;
![]()
– значения модулей упругости материалов
бруса для каждого участка;
![]()
– площади поперечных сечений стержня
на первом, втором и третьем участках.
Поскольку
жесткости всех трех участков одинаковые
(балка изготовлена из одного материала
и имеет постоянное по всей длине
поперечное сечение), можно обозначить
![]()
и вынести этот множитель за скобки. В
результате получим выражение в виде:
![]()
![]()
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пример
8.
Проверить прочность чугунного бруса
(рис.2.16, а). Принять![]() =150
=150
МПа;![]() =650
=650
МПа, допускаемый коэффициент запаса
прочности![]() =
=
4.
Решение.
Строим эпюры продольных сил
![]() и
и
нормальных напряжений![]() (рис.2.16,б ив).
(рис.2.16,б ив).
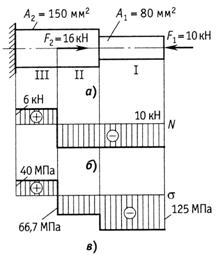
Рис.2.16
Напряжения на участках бруса
![]()
![]()
![]()
Так как материал бруса имеет различную
прочность при растяжении и сжатии,
проверку прочности следует выполнять
для сжатого и растянутого участков,
несмотря на то, что на участке
![]() напряжение
напряжение
значительно больше по абсолютному
значению.
Коэффициенты запаса прочности
![]()
– прочность обеспечена;
![]()
– прочность обеспечена.
Из решения задачи можно сделать следующие
выводы:
1) прочность стержня не обеспечена, так
как на одном его участке коэффициент
запаса прочности меньше требуемого;
2) на участках
![]() и
и![]() коэффициент запаса прочности завышен,
коэффициент запаса прочности завышен,
следовательно, эти участки бруса можно
сделать меньшего диаметра. При
проектировании элементов конструкций
следует стремиться к тому, чтобы во всех
сечениях коэффициент запаса прочности
был равен или близок к требуемому.
Проверку прочности бруса можно было
выполнить, используя условие прочности
в виде
![]() ,
,
определив предварительно допускаемые
напряжения по формулам
![]() ;
;![]() .
.
Учет
собственного веса при растяжении и
сжатии
Подбор
сечений с учетом собственного веса (при
растяжении и сжатии)
При установлении внешних сил, растягивающих
или сжимающих элементы конструкций, мы
до сих пор игнорировали собственный
вес этих элементов. Возникает вопрос,
не вносится ли этим упрощением расчета
слишком большая погрешность? В связи с
этим подсчитаем величины напряжений и
деформаций при учете влияния собственного
веса растянутых или сжатых стержней.
Пусть вертикальный стержень (рис.2.17, а)
закреплен своим верхним концом; к нижнему
его концу подвешен грузР. Длина
стержняl, площадь поперечного
сеченияF, удельный вес материала
![]() и модуль упругостиЕ. Подсчитаем
и модуль упругостиЕ. Подсчитаем
напряжения по сечениюАВ, расположенному
на расстоянии
![]() от свободного конца стержня.
от свободного конца стержня.
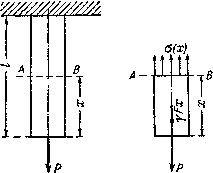
а)
б)
Рис.2.17.
Рассечем стержень сечением АВи
выделим нижнюю часть длиной
![]() с
с
приложенными к ней внешними силами
(рис.2.17,б) — грузомРи ее
собственным весом
![]() .
.
Эти две силы уравновешиваются напряжениями,
действующими на площадьАВ от
отброшенной части. Эти напряжения будут
нормальными, равномерно распределенными
по сечению и направленными наружу от
рассматриваемой части стержня, т. е.
растягивающими. Величина их будет равна:
![]()
Таким образом, при учете собственного
веса нормальные напряжения оказываются
неодинаковыми во всех сечениях. Наиболее
напряженным, опасным, будет верхнее
сечение, для которого
![]() достигает наибольшего значенияl;
достигает наибольшего значенияl;
напряжение в нем равно:
![]()
Условие прочности должно быть выполнено
именно для этого сечения:
![]()
Отсюда необходимая площадь стержня
равна:
![]()
От формулы, определяющей площадь
растянутого стержня без учета влияния
собственного веса, эта формула отличается
лишь тем, что из допускаемого напряжения
вычитается величина
![]() .
.
Чтобы оценить значение этой поправки,
подсчитаем ее для двух случаев. Возьмем
стержень из мягкой стали длиной 10 м; для
него![]() ,
,
а величина![]() .
.
Таким образом, для стержня из мягкой
стали поправка составит
![]() т. е. около 0,6%. Теперь возьмем кирпичный
т. е. около 0,6%. Теперь возьмем кирпичный
столб высотой тоже 10м; для него![]() ,
,
а величина![]() Таким образом, для кирпичного столба
Таким образом, для кирпичного столба
поправка составит 18/1,2, т.е. уже 15%.
Вполне понятно, что влиянием собственного
веса при растяжении и сжатии стержней
можно пренебрегать, если мы не имеем
дела с длинными стержнями или со стержнями
из материала, обладающего сравнительно
небольшой прочностью (камень, кирпич)
при достаточном весе. При расчете длинных
канатов подъемников, различного рода
длинных штанг и высоких каменных
сооружений (башни маяков, опоры мостовых
ферм) приходится вводить в расчет и
собственный вес конструкции.
В таких случаях возникает вопрос о
целесообразной форме стержня. Если мы
подберем сечение стержня так, что дадим
одну и ту же площадь поперечного сечения
по всей длине, то материал стержня будет
плохо использован; нормальное напряжение
в нем дойдет до допускаемого лишь в
одном верхнем сечении; во всех прочих
сечениях мы будем иметь запасв
напряжениях, т. е. излишний материал.
Поэтому желательно так запроектировать
размеры стержня,чтобы во всех его
поперечных сечениях (перпендикулярных
к оси) нормальные напряжения были
постоянны,
Такой стержень называется стержнем
равного сопротивлениярастяжению
или сжатию. Если при этом напряжения
равны допускаемым, то такой стержень
будет иметь наименьший вес.
Возьмем длинный стержень, подверженный
сжатию силой Ри собственным весом
(рис.2.18). Чем ближе к основанию стержня
мы будем брать сечение, тем больше будет
сила, вызывающая напряжения в этом
сечении, тем большими придется брать
размеры площади сечения. Стержень
получит форму, расширяющуюся книзу.
Площадь сеченияFбудет изменяться
по высоте в зависимости от
![]() ,
,
т. е.
![]() .
.
Установим этот закон изменения площади
в зависимости от расстояния сечения
![]() от верха стержня.
от верха стержня.
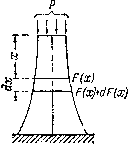 Рис.2.18.
Рис.2.18.
Площадь верхнего сечения стержня
![]() определится из условия прочности:
определится из условия прочности:
![]() и
и![]()
где
![]() —
—
допускаемое напряжение на сжатие;
напряжения во всех прочих сечениях
стержня также должны равняться величине
![]()
Чтобы выяснить закон изменения площадей
по высоте стержня, возьмем два смежных
бесконечно близких сечения на расстоянии
![]() от верха стержня; расстояние между
от верха стержня; расстояние между
сечениями
![]() ;
;
площадь верхнего назовем
![]() ,
,
площадь же смежного![]() .
.
Приращение площади
![]() при переходе от одного сечения к другому
при переходе от одного сечения к другому
должно воспринять вес![]() элемента
элемента
стержня между сечениями. Так как на
площади![]() он
он
должен вызвать напряжение, равное
допускаемому![]() ,
,
то![]() определится
определится
из условия:
![]()
Отсюда:
![]()
После интегрирования получаем:
![]()
При
![]() площадь
площадь
![]() ;
;
подставляя эти значения, имеем:
![]() и
и![]()
Отсюда
![]() ,
,
![]()
Если менять сечения точно по этому
закону, то боковые грани стержня получат
криволинейное очертание (рис.2.18), что
усложняет и удорожает работу. Поэтому
обычно такому сооружению придают лишь
приближенную форму стержня равного
сопротивления, например в виде усеченной
пирамиды с плоскими гранями. Приведенный
расчет является приближенным. Мы
предполагали, что по всему сечению
стержня равного сопротивления передаются
только нормальные напряжения; на самом
деле у краев сечения напряжения будут
направлены по касательной к боковой
поверхности.
В случае длинных канатов или растянутых
штанг форму стержня равного сопротивления
осуществляют тоже приближенно, разделяя
стержень по длине на ряд участков; на
протяжении каждого участка сечение
остается постоянным (рис.2.19) — получается
так называемый эквивалентный ступенчатый
стержень.
 Рис.2.19.
Рис.2.19.
Определение площадей
![]() ,
,
![]() …
…
при выбранных длинах производится
следующим образом. Площадь поперечного
сечения первого нижнего участка будет
по формуле равна:
![]()
Чтобы получить площадь поперечного
сечения второго участка, надо нагрузить
его внешней силой Ри весом первого
участка
![]() :
:
![]()
Для третьего участка к внешней силе
добавляются веса первого и второго
участков. Подобным же образом поступают
и для других участков.
Деформации
при действии собственного веса
При определении влияния собственного
веса на деформацию при растяжении и
сжатии стержней придется учесть, что
относительное удлинение различных
участков стержня будет переменным, как
и напряжение
![]() .
.
Для вычисления полного удлинения стержня
постоянного сечения определим сначала
удлинение бесконечно малого участка
стержня длиной
![]() ,
,
находящегося на расстоянии
![]() от конца стержня (рис.2.20).
от конца стержня (рис.2.20).
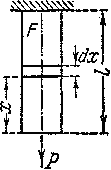 Рис.2.20.
Рис.2.20.
Абсолютное удлинение этого участка
равно
![]()
Полное удлинение стержня
![]() равно:
равно:
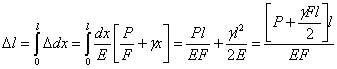
Величина
![]() представляет
представляет
собой полный вес стержня. Таким образом,
для вычисления удлинения от действия
груза и собственного веса можно
воспользоваться прежней формулой:
![]()
подразумевая под Sвнешнюю силу и
половину собственного веса стержня.
Что же касается деформаций стержней
равного сопротивления, то, так как
нормальные напряжения во всех сечениях
одинаковы и равны допускаемым
![]() ,
,
относительное удлинение по всей длине
стержня одинаково и равно
![]()
Абсолютное же удлинение при длине
стержня lравно:
![]()
Деформацию ступенчатых стержней следует
определять по частям, выполняя подсчеты
по отдельным призматическим участкам.
При определении деформации каждого
участка учитывается не только его
собственный вес, но и вес тех участков,
которые влияют на его деформацию,
добавляясь к внешней силе. Полная
деформация получится суммированием
деформаций отдельных участков.
Пример 9.
Определить объем кладки мостовой опоры
высотой 42 м, нагруженной сжимающей
силой F=400 т, для двух вариантов:
1 вариант– опора постоянного сечения;
2 вариант– опора ступенчатая из трех
частей одинаковой высоты.
Объемный вес материала кладки
![]() ,
,
расчетное сопротивление материала
кладки на сжатие
![]() .
.
Решение.
Объем кирпичной кладки вычисляется по
формуле:
![]() ,
,
где
![]() – площадь поперечного сечения столба;
– площадь поперечного сечения столба;
![]() – высота столба.
– высота столба.
Таким образом, для решения задачи
необходимо знать площади поперечных
сечений мостовой опоры.
1.Вариант.
Расчетная схема и эпюра внутренних
усилий для данного варианта изображена
на рис. 2.21.
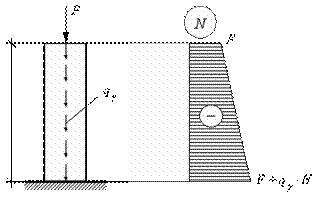
Рис.2.21
Максимальная сжимающая продольная сила
возникает у основания опоры и определяется
выражением (для удобства будем подставлять
значения внутренних усилий по абсолютной
величине):
![]()
![]()
Записываем условие прочности:
![]()
Подставляя в это выражение значение
![]() получим:
получим:
![]()
Отсюда требуемая площадь из условия
прочности кладки на сжатие равна:
![]()
Объем кладки для первого варианта будет
равен:
![]()
2 вариант.
Расчетная схема и эпюра внутренних
усилий для данного варианта изображена
на рис. 2.22.
Мостовая опора состоит из трех ступеней,
высота каждой
![]() .
.
Площади поперечных сечений ступеней
соответственно
![]() ,
,
![]() ,
,
![]() ,
,
в связи с чем в пределах каждой ступени
от действия собственного веса будут
возникать различные по величине
продольные силы и напряжения.
Таким образом, для решения задачи
необходимо рассмотреть условие прочности
для каждой ступени отдельно.
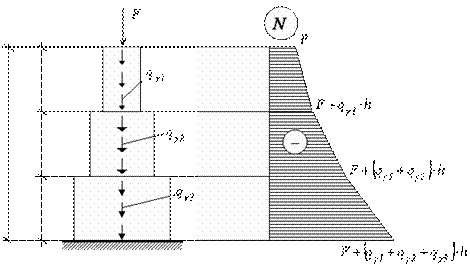
Рис.2.22
1-я ступень. Максимальная сжимающая
продольная сила для первой ступени
(рис. 2.22):
![]()
![]() .
.
По аналогии с вариантом 1, записываем
для первой ступени условие прочности
и подставляем в него исходные данные:
![]()
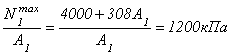 .
.
Отсюда требуемая площадь первой ступени
равна:
![]()
2-я ступень. Максимальная сжимающая
продольная сила для второй ступени
(рис. 2.22):
![]()
![]() .
.
Записываем для второй ступени условие
прочности и подставляем в него исходные
данные:
![]()
 .
.
Отсюда требуемая площадь второй ступени
равна:
![]()
3-я ступень. Максимальная сжимающая
продольная сила для третьей ступени
(рис. 2.22):
![]()
![]() .
.
Записываем для третьей ступени условие
прочности, из которого по аналогии с
предыдущими записями определяем
требуемую площадь поперечного сечения:
![]()
![]()
Объем кладки мостовой опоры для второго
варианта определяется выражением:
![]() .
.
Таким образом, мостовая опора, состоящая
из ступеней различной площади, выгоднее
по расходу материала, чем опора постоянного
по всей высоте сечения.
Пример 10.
Определить полное удлинение стержня,
с учетом собственного веса, а также
перемещение сечения m-n. Площадь
поперечного сечения –А, модуль
упругости –Е, объемный вес материала
–
![]() Расчетная схема стержня изображена на
Расчетная схема стержня изображена на
рис. 2.23.
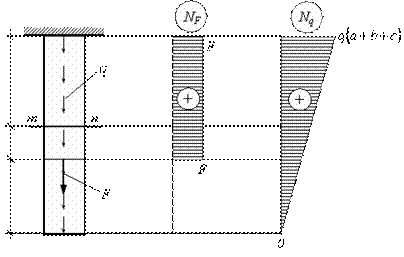
Рис.2.23
Решение.
Для решения задачи используем принцип
независимости действия сил, а именно:
отдельно построим эпюры продольных сил
от действия сосредоточенной силы
![]() и от действия собственного веса, то есть
и от действия собственного веса, то есть
от равномерно распределенной продольной
нагрузки
![]() .
.
Расчетная схема и эпюры продольных сил
![]() и
и
![]() изображены на рис. 2.23.
изображены на рис. 2.23.
Полное удлинение стержня
![]() будет складываться из удлинения,
будет складываться из удлинения,
полученного стержнем от действия
сосредоточенной силы
![]() и от действия собственного веса:
и от действия собственного веса:
![]() .
.
Или в другом виде:
![]() .
.
Для того, чтобы определить перемещение
сечения m-nотбрасываем часть стержня
ниже сеченияm-n,а ее действие заменяем
сосредоточенной силой
![]() ,
,
равной продольной силе в сеченииm-n:
![]() .
.
В результате получаем новую расчетную
схему, которая приведена на рис. 2.24.

Рис.2.24.
А теперь решаем новую задачу о нахождении
полного удлинения
![]() уже для данного стержня (рис. 2.23):
уже для данного стержня (рис. 2.23):
![]() ,
,
![]() .
.
Расчет
статически определимых стержневых
систем
Статически
определимая стержневая система
– это система, в которой все неизвестные
реакции опор и внутренние усилия можно
определить из уравнений равновесия
(статики).
Для
«решения» любой стержневой системы
необходимо выделить в ней объект
равновесия. В связи с этим, все системы
можно разделить на два типа:
1 тип
– системы, состоящие из абсолютно
жестких (недеформируемых) стержней и
одиночных невесомых (деформируемых)
стержней. Для стержневых систем этого
типа объектами равновесия являются
недеформируемые стержни.
2
тип –
системы, состоящие из нескольких
деформируемых стержней, соединенных в
одной точке. Точки соединения двух и
более стержней называются узлами,
которые и являются объектами равновесия
для систем 2-го типа.
Все
соединения в элементах систем шарнирные,
однако существуют определенные правила,
по которым вводятся реакции и усилия в
стержнях:
–
в шарнире, соединяющем абсолютно жесткий
элемент системы с «землей» или с другой
конструкцией, всегда возникают две
реакции – горизонтальная
![]()
и вертикальная
![]() ;
;
– в шарнире, соединяющем деформируемый
стержень с абсолютно жестким стержнем
или с другой конструкцией, всегда
возникает одна реакция, направленная
вдоль этого стержня и равная по величине
усилию, возникающему в нем.
В абсолютно жестких стержнях никогда
не возникает внутренних усилий, они не
деформируются!
– в шарнире, соединяющем несколько
деформируемых стержней (узловой шарнире),
возникают усилия, направленные вдоль
этих стержней и сходящиеся в этом узле.
Порядок решения большинства задач о
проверке прочности статически определимых
стержневых систем при расчете по
допускаемым напряжениям сводится к
следующим этапам:
1) находим внутренние усилия (продольную
силу при растяжении-сжатии) и выявляем
опасные сечения;
2) определяем напряжения;
3) после выявления максимальных напряжений
используем условие прочности (формулы
(2.26), (2.28), (2.32)) при растяжении-сжатии).
Пример 11.
Абсолютно жесткий брус
![]() поддерживается стальным стержнем
поддерживается стальным стержнем![]() ,
,
имеющим площадь поперечного сечения
100 мм2(рис.2.25,а). Определить
из условия прочности стержня![]() допускаемую
допускаемую
нагрузку![]() и проверить, обеспечена ли жесткость
и проверить, обеспечена ли жесткость
системы, если допускается перемещение
сечения![]() бруса под действием силы
бруса под действием силы![]() не более 2 мм. Допускаемое напряжение
не более 2 мм. Допускаемое напряжение
принять равным![]() =150
=150
МПа, модуль упругости![]() Па.
Па.
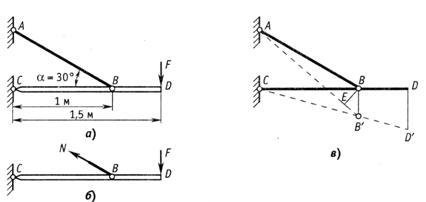
Рис.2.25
Решение.
Используя метод сечений, определим
соотношение между продольной силой
![]() в стержне
в стержне![]() и нагрузкой
и нагрузкой![]() .
.
Из условия равновесия сил (рис.2.25,б)
находим
![]() ;
;![]() ;
;![]() .
.
Допускаемая продольная сила
![]() для стержня
для стержня![]() из условия его прочности
из условия его прочности
![]()
Допускаемая нагрузка на систему
![]()
При нагружении системы стержень
![]() удлиняется на
удлиняется на![]() ,
,
а абсолютно жесткий брус поворачивается,
оставаясь прямолинейным. Система после
деформации стержня![]() показана штриховой линией на рисунке
показана штриховой линией на рисунке
2.25,в. Из треугольника![]() определяем длину
определяем длину![]() стержня
стержня![]() :
:![]() м.
м.
На основании принципа начальных размеров
принимаем, что значение угла
![]() не изменяется, а точки
не изменяется, а точки![]() и
и![]() перемещаются по вертикали.
перемещаются по вертикали.
Из прямоугольного треугольника
![]() находим
находим
![]() ;
;
так как![]() ,
,![]() ,
,
то
![]()
Перемещение точки
![]() определяем из подобия треугольников
определяем из подобия треугольников![]() и
и![]()
![]() ;
;![]()
Жесткость
системы не обеспечена.
Следует заметить, что нельзя повысить
жесткость системы, применив для стержня
![]() более прочную сталь, так как характеристикой
более прочную сталь, так как характеристикой
свойств материала, влияющей на жесткость,
является модуль упругости, значение
которого для всех марок сталей примерно
одинаково. Повысить жесткость системы
можно, либо увеличив площадь поперечного
сечения стержня![]() ,
,
либо уменьшив его длину.
Пример 12.
Определить допускаемую нагрузку
![]() для системы из двух стержней, изготовленных
для системы из двух стержней, изготовленных
из дюралюминиевых труб одинакового
поперечного сечения (рис.2.26,а).
Допускаемое напряжение принять![]() =
=
100 МПа.
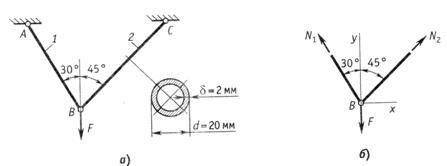
Рис.2.26
Решение.
Используя метод сечений, вырезаем узел
![]() и из уравнений равновесия сил
и из уравнений равновесия сил
![]() ;
;![]() ;
;
![]() ;
;![]()
находим
неизвестные продольные силы, возникающие
в стержнях, через нагрузку![]() (рис.2.26,б)
(рис.2.26,б)
![]() ;
;![]() .
.
Допускаемую нагрузку
![]() определяем из условия прочности наиболее
определяем из условия прочности наиболее
нагруженного стержня1:
![]()
![]()
Следует отметить, что стержень 2
недогружен. Напряжение в нем
![]()
что примерно
на 30% ниже допускаемого. Для стержня 2
можно использовать трубу меньшего
поперечного стержня.
Пример 13.
Рассмотрим стержневую систему, состоящую
из абсолютно жесткого (недеформируемого)
стержня
![]() ,
,
шарнирно закрепленного в точке
![]() и невесомого (деформируемого) стержня
и невесомого (деформируемого) стержня
![]() ,
,
шарнирно закрепленного по концам,
загруженную в точке
![]() сосредоточенной силой
сосредоточенной силой
![]() (рис. 2.27).
(рис. 2.27).
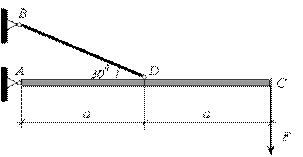
Рис.2.27
Решение.
Объектом равновесия в данном случае
будет являться стержень
![]() ,
,
для которого и будем составлять уравнения
равновесия.
Под действием внешней нагрузки, на
основании введенных выше правил, в
точке![]() будут возникать две реакции
будут возникать две реакции![]() и
и![]() ,
,
а в стержне![]() возникает усилие
возникает усилие![]() ,
,
направленное по стержню (рис. 2.28).
Определим несущую способность
(грузоподъемность) заданной системы,
то есть допустимую нагрузку
![]() ,
,
если площадь сечения стержня![]() ,
,
расчетное сопротивление материала
стержня![]() .
.
Для этого можно составить следующие
уравнения равновесия:
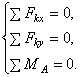
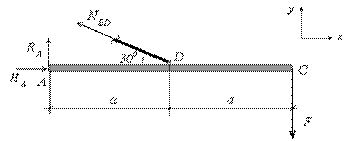
Рис.2.28
Поскольку в конечном итоге решение
задачи будет сводиться к определению
усилия в стержне
![]() ,
,
то оставляем в рассмотрении уравнение
равновесия, содержащее только
![]() ,
,
то есть уравнение моментов относительно
точки
![]() .
.
Распишем данное уравнение:
![]()
отсюда неизвестное усилие
![]() .
.
Записываем условие прочности для стержня
![]() и
и
выражаем нагрузку
![]() :
:
 ,
,
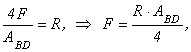
![]() .
.
Пример 14.
Определить необходимые размеры поперечных
сечений металлических тяг в стержневой
системе из условия прочности, если тяга
№ 1 – из стали, расчетное сопротивление
![]() ,
,
поперечное сечение – швеллер; тяга № 2
– из алюминия, расчетное сопротивление
![]() ,
,
круглого поперечного сечения. Стержневая
система изображена на рис. 2.29.

Рис.2.29
Решение.
Под действием внешней нагрузки в точках
опор системы
![]() ,
,
![]() и
и
![]() возникают реакции
возникают реакции
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Кроме того, в тягах возникают усилия
соответственно
![]() и
и
![]() .
.
Для решения данной задачи необходимо
по очереди рассмотреть равновесие двух
абсолютно жестких стержней. Сначала
рассекаем систему сечением 1-1по
тяге № 1 и рассматриваем равновесие
нижнего бруса (рис. 2.30,б), а
затем – равновесие верхнего бруса
(рис. 2.30,а). Из условий равновесия
для нижней части будем находить усилие
в первой тяге
![]() ,
,
а из условия равновесия для верхней –
![]() (при этом усилие
(при этом усилие
![]() считается уже известным).
считается уже известным).
Для определения усилия
![]() необходимо записать уравнение моментов
необходимо записать уравнение моментов
относительно точки
![]() (рис. 2.30,б):
(рис. 2.30,б):
![]()
отсюда
![]() – усилие растяжения.
– усилие растяжения.
Теперь, считая усилие
![]() известным, необходимо рассмотреть
известным, необходимо рассмотреть
равновесие средней части, для чего
записать уравнение моментов относительно
точки
![]() (рис. 2.30,а):
(рис. 2.30,а):
![]()
![]() .
.
отсюда
![]() – усилие растяжения.
– усилие растяжения.
а)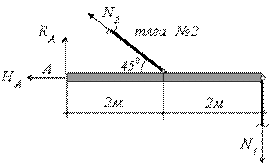
б)
Рис.2.30
Далее, для каждой тяги записываем условие
прочности и выражаем площади поперечных
сечений
![]() – площадь тяги № 1,
– площадь тяги № 1,
![]() – площадь тяги № 2.
– площадь тяги № 2.
Тяга № 1:
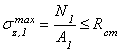 ,
,
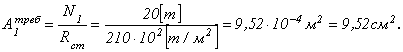
По сортаменту принимаем швеллер [ №10,
![]()
Фактическая площадь сечения должна
быть не меньше требуемой!
Тяга № 2:
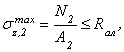
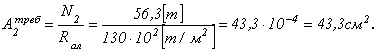
Алюминиевая тяга имеет круглое сечение,
тогда требуемый диаметр:
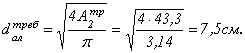
Фактическая площадь круглого сечения:
![]()
Пример 15.
Определить усилия, возникающие в стержнях
системы (рис. 2.31) под действием внешней
нагрузки.
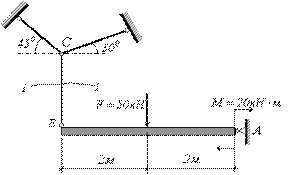
Рис.2.31
Решение.
Под действием внешней нагрузки в точке
опоры системы Авозникают реакции![]() ,
,![]() ,
,
а также усилия в стержнях![]() ,
,![]() ,
,![]() .
.
В качестве объектов равновесия в этой
задаче выступают абсолютно жесткий
брус ABи узелC.
Поэтому, для определения неизвестных
усилий сначала рассекаем системусечением 1-1по стержнюBCи рассматриваем равновесие нижней части
(рис. 2.32,б), а затем рассматриваем
равновесие узлаC(рис. 2.32,а).
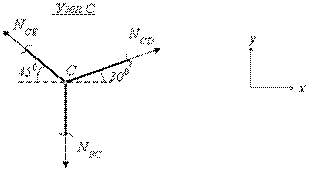
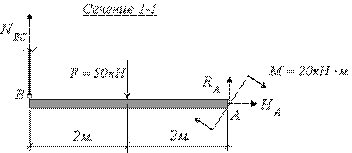
Рис.2.32
Для определения усилия
![]() необходимо записать уравнение моментов
необходимо записать уравнение моментов
относительно точки
![]() (рис. 2.32,б):
(рис. 2.32,б):
![]() ,
,
отсюда
![]() кН
кН
– усилие растяжения.
Теперь, считая усилие
![]() известным, необходимо рассмотреть
известным, необходимо рассмотреть
равновесие узлаС, для чего записать
уравнения сумм проекций всех сил на
вертикальную и горизонтальную оси (рис.
2.32,а):

![]() ,
,
![]() .
.
В результате получаем систему двух
уравнений с двумя неизвестными:

Решая систему определяем усилия в
стержнях
![]() и
и![]() :
:
 .
.
Пример 16.
Два стальных (Е= 2·105МПа)
стержня, шарнирно соединенные в точкеА, находятся под действием силыР(рис. 2.33). Первый стержень имеет длину
си площадь поперечного сеченияF, второй длинуаи площадь –2F.
1)
Найти величины нормальных напряжений,
действующих в стержнях.
2) Найти абсолютную и относительную
деформации стержней.
Дано: Р= 130 кН,с= 1,5 м,а= 2 м,F= 12 см.
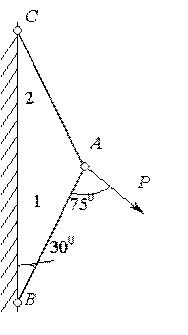
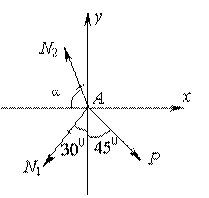
Рис.2.33Рис.2.34
Решение.
Стержни прикреплены к стене и соединены
между собой шарнирами (точках В,СиА). Шарниры предполагаются
идеальными, т. е. такими, трение в которых
отсутствует. НагрузкаРприложена
в узлеА. Поэтому стержни будут
испытывать только продольные (растягивающие
или сжимающие) усилия, т.е. в поперечных
сечениях стержней возникает
только один внутренний силовой фактор
– продольная силаN.
1. Для определения усилий рассмотрим
равновесие узла А(рис. 2.34), к которому
приложены нагрузкаРи два неизвестных
усилияN1, иN2,
действующие со стороны стержнейАВиАСи направленные вдоль их
осей.
При определении неизвестных усилий
в стержнях обычно принято считать их
растянутыми и соответственно этому
направлять векторы сил от узла. Знак
плюс в решении для усилия будет
подтверждать правильность сделанного
предположения о направлении усилия, а
знак минус укажет на то, что в
действительности усилие направлено
противоположно и соответствующий
стержень сжат.
Полагая оба стержня растянутыми, направим
усилия N1, иN2так, как показано на рис.2.34. Для
плоской системы сил, пересекающихся в
одной точке, как известно из курса
теоретической механики, можно составить
только два независимых уравнения
равновесия – в виде сумм проекции всех
сил на две оси, не параллельные друг
другу.
В качестве таких осей выберем осиХиY(рис. 2.34). Тогда
уравнения равновесия представятся в
виде:
![]() ;
;
![]() .
.
(1)
Из этой системы (1) можно было бы определить
неизвестные усилия N1,
иN2, если бы
были известны значения![]() и
и![]() .
.
Определим эти величины. Для этого
рассмотрим данную стержневую систему
(рис. 2.34). Из точкиАопустим
перпендикулярАDна прямуюВС, получим два прямоугольных
треугольника![]() и
и![]() .
.
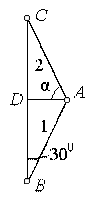
Рис.2.35
Из
треугольника ABDопределимAD:
![]() м.
м.
Из
треугольника ADG
получим:
![]()
![]() .
.
Теперь определим неизвестные усилия
N1, иN2из системы двух линейных уравнений (1).
Перепишем уравнения в следующем виде:
![]() ;
;
![]() .
.
Решим
эту систему используя метод Крамера
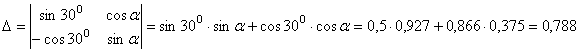 .
.
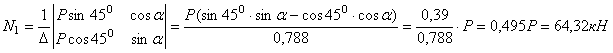 .
.
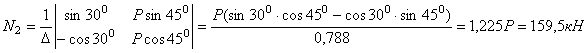 .
.
2. Определим нормальные напряжения,
действующие в стержнях.
Напряжения
в стержнях определяются по формуле
![]() .
.
Для
первого стержня
![]() ,
,
для
второго стержня
![]() .
.
3. Найдем
абсолютную и относительную деформации
стержней.
Абсолютная
деформация стержня длиной lравна:
![]() .
.
Абсолютная
деформация первого стержня
![]() .
.
Абсолютная
деформация второго стержня
![]() .
.
Относительную
деформацию определим из закона Гука
![]() .
.
Относительная
деформация первого стержня
![]() ,
,
Относительная
деформация второго стержня
![]() .
.
Понятие
о статически неопределимых системах
Основные
положения. Связи необходимые и
дополнительные.
Для решения задач сопротивления
материалов необходимо знать все внешние
силы, действующие на конструкцию, включая
реакции наложенных на нее связей. Из
теоретической механики известно, что
для равновесия твердого тела, нагруженного
плоской системой сил, достаточно наложить
на тело три связи, а нагруженного
пространственной системой сил – шесть
связей. Соответственно для таких систем
можно составить три и шесть независимых
уравнений равновесия. Если при рассмотрении
заданной системы, находящейся в
равновесном состоянии от действия
заданных внешних нагрузок, все реакции
в связях закрепления можно определить
с помощью уравнений равновесия, без
использования дополнительных условий,
то такая система называется статически
определимой.
В реальной практике встречаются такие
конструкции, при расчете которых
одних лишь уравнений равновесия
оказывается недостаточно, в связи с
чем требуется формулирование
дополнительных уравнений, связанных
с условиями деформирования конструкции.
Системы, в которых количество наложенных
связей больше, нежели число независимых
уравнений равновесия, называются
статически неопределимыми.
В машиностроении и строительных
конструкциях такие системы находят
широкое применение. В одних случаях
статическая неопределимость является
сущностью самой конструкции.
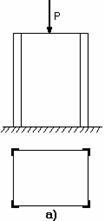
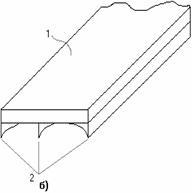
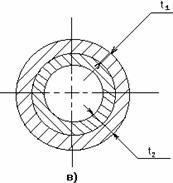
Рис.
2.36
Примерами таких конструкций могут быть:
армированные уголками стойки (рис.2.36,
а); панель крыла самолета, состоящая
из обшивки 1 с продольными ребрами 2
(рис. 2.36,б); составной цилиндр,
полученный путем напряженной посадки
двух труб из различных материалов (рис.
2.36, в). В других случаях, с целью
повышения жесткости и надежности
системы, вводятся дополнительные
связи сверх тех минимально необходимых,
которые обеспечивают ее кинематическую
неизменяемость. Наложение на систему
дополнительных связей превращает ее в
статически неопределимую. Напомним,
что кинематическая неизменяемость
плоской системы обеспечивается
тремя, а пространственной – шестью
связями.
Конструкции, состоящие из стержней,
соединенных шарнирами, называются
шарнирно-стержневыми. В этих
конструкциях есть стержни, которые
обеспечивают геометрическую неизменяемость
конструкции и при удалении которых
система превращается в механизм. Такие
стержни будем называтьнеобходимыми.
Если же при удалении некоторых стержней
геометрическая неизменяемость конструкции
не нарушается, то такие стержни назовемлишними. Лишними такие связи
называются только потому, что они не
являются необходимыми для обеспечения
равновесия конструкции и ее
геометрической неизменяемости, хотя
постановка их диктуется условиями
эксплуатации. По условиям прочности и
жесткости конструкции лишние связи
могут оказаться необходимыми.
В статически определимой системе есть
только необходимые стержни, в статически
неопределимой – число лишних стержней
равно степени статической неопределимости.
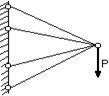
а)
б) в)
Рис. 2.37
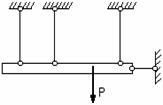
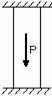
На рис.2.37 приведены схемы 3-х плоских
систем с «лишними» связями: а–
стержневой подвески;б – стержня,
закрепленного обоими концами;в–
стержневого кронштейна. В схеме,
показанной на рис. 2.37,в, вся
система состоит из упругих звеньев.
Подсчет числа наложенных связей
производится в этом случае следующим
образом. Каждый стержень связан с опорной
поверхностью двумя связями. Всего таких
связей 8. Шарнир, соединяющий концы
стержней, снимает связи, ограничивающие
относительный или взаимный их поворот.
При соединении двух стержней одним
шарниром снимается одна связь, трех
стержней – две связи, четырех – три и
т.д. В данном случае снимаются три связи.
Следовательно, всех связей, наложенных
на эту систему оказывается пять, две из
которых могут считаться «лишними».
Статически неопределимые конструкции
характеризуются рядом особенностей,
по сравнению со статически определимыми
системами. Заключаются они в том, что
в элементах статически неопределимых
систем напряжения возникают не только
от действия внешних сил, но и в результате
изменения температуры, неточности
изготовления деталей, неточностей
их сборки, смещения мест опорных креплений
и ряда других причин. Объясняется это
тем, что деформация одного из элементов
в статически неопределимой системе
приводит к деформации и других ее
элементов.
Например, если один из стержней системы
(рис. 2.37, в) изготовлен по длине
неточно, то соединение концов стержней
одним шарниром возможно только путем
деформации всех стержней.
Сила, возникающая при деформации одного
из стержней, вызывает усилия в других
стержнях, находящихся с ним в шарнирном
соединении. Смонтированная система
приходит в равновесие, следовательно,
совокупность сил системы обеспечивает
ее равновесие. Эти силы вызывают
соответствующие, называемые начальными,
напряжения в стержнях.
В статически неопределимых конструкциях
при изменении температуры ее элементов
по сравнению с температурой, при которой
осуществлялась сборка, возникают
дополнительные усилия и напряжения,
которые принято называть температурными.
Распределение усилий между элементами
системы зависит от их жесткости. Если
увеличить жесткость какого- либо
элемента, то он примет на себя большее
усилие. Изменяя соотношение жесткостей
элементов конструкций, можно менять
распределение усилий между ними.
Эти особенности статически неопределимых
конструкций должны учитываться при
проектировании или применении таких
систем.
Статически неопределимые системы
обладают повышенной «живучестью».
Разрушение одного или нескольких
элементов (в зависимости от числа
дополнительных связей) не вызывает
потерю несущей способности конструкции
в целом. Так разрушение даже двух стержней
в системе, показанной на рис. 2.37, вне приводит к потере способности
воспринимать силу P оставшимися двумя
стержнями, конечно, при условии их
достаточной прочности.
Степень
статической неопределимости. Методика
ее определения.
Статически
неопределимые системы характеризуются
степенью
статической неопределимости,
которая равна числу «лишних» связей и
может быть вычислена как разность
между числом неизвестных сил и числом
независимых уравнений равновесия. По
числу единиц этой разности системы
бывают 1,2,3….n
раз статически неопределимыми.
Для
расчетов составляется силовая схема
заданной системы, на которой указываются
все известные и неизвестные силовые
факторы.
При
составлении силовой схемы в случае
определения внутренних силовых факторов
применяется метод сечений, согласно
которому каждое звено системы разделяется
на две части в произвольном сечении,
затем отбрасываются части, примыкающие
к опорным элементам, а их действие на
оставшиеся части заменяется продольными
силами. После этого на схеме показываются
все заданные внешние силы и реакции
опор.
Затем
по этой схеме устанавливается возможное
число независимых уравнений равновесия.
Степень статической неопределимости
подсчитывается, как разность между
числом неизвестных сил и числом
независимых уравнений равновесия.
На рис.2.38, аизображен кронштейн,
состоящий из двух стержней, шарнирно
скрепленных между собой. В связи с тем,
что на конструкцию действует лишь
вертикальное усилиеР, а система
является плоской (т.е. все элементы
конструкции и вектор внешних сил лежат
в одной плоскости), получается, что
усилия в стержнях легко определяются
из условий равновесия узла![]() ,
,
т.е.
![]() ,
,![]() .
.
(2.37)
Раскрывая эти уравнения, получаем
замкнутую систему линейных уравнений
относительно неизвестных усилий N1иN2 в которой количество
уравнений равно количеству неизвестных:
![]() ;
;![]() .
.
Если конструкцию кронштейна усложнить,
добавив еще один стержень (рис.2.38, б),
то усилия в стержняхN1, N2иN3 прежним способом определить
уже не удастся, т.к. при тех же двух
уравнениях равновесия (2.37) имеются уже
три неизвестных усилия в стержнях.
В таких случаях говорят, что система
один раз статически неопределима.
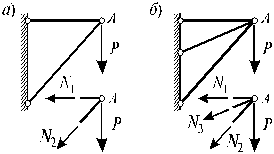
Рис.2.38
На рис.2.39 приведены примеры статически
неопределимых систем. В стержне с жестко
заделанными концами (рис.4.2, а)
возникают две реакции, а уравнение
равновесия можно составить только одно,
следовательно, конструкция один раз
статически неопределима. Не нарушая
равновесия стержня, можно отбросить
одну из опор.
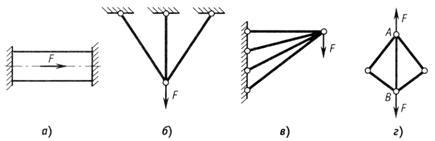
Рис.2.39
Для системы из трех стержней (рис.2.39, б)
можно составить два уравнения равновесия,
а неизвестных сил в системе три,
следовательно, система один раз статически
неопределима. Один из стержней не нужен
для равновесия системы, и его можно
отбросить. Рассуждая аналогично, можно
установить, что система из четырех
стержней (рис.2.39,в) дважды статически
неопределима.
Для определения внутренних сил в системе
из пяти стержней (рис.2.39, г) необходимо
вырезать и рассмотреть раздельно
равновесие узлов![]() и
и![]() .
.
К каждому узлу примыкают три стержня
(всего пять стержней и, следовательно,
пять неизвестных сил), а уравнений
равновесия для каждого узла можно
составить два, т.е. всего четыре уравнения.
Система один раз статически неопределима.
Напомним, что для пространственной
системы сил можно составить шесть
независимых уравнений равновесия: три
уравнения, выражающие сумму проекций
всех сил на три взаимно перпендикулярные
оси (![]() ,
,![]() ,
,![]() ),
),
и три – сумму моментов всех сил относительно
этих же осей (![]() ,
,![]() ,
,![]() ).
).
Для общего случая сил, лежащих в одной
плоскости- три независимых уравнения
(например:![]() ,
,![]() ,
,![]() ). В частных случаях плоской системы
). В частных случаях плоской системы
можно составить два независимых уравнения
равновесия: для системы параллельных
сил (например:![]() ,
,![]() )
)
и для системы сил, линии действия которых
пересекаются в одной точке (![]() ,
,![]() ).
).
Для сил, линии действия которых лежат
на одной прямой, можно записать только
одно независимое уравнение (например:![]() ).
).
На рис. 2.40 показаны примеры составления
силовых схем и определения степени
статической неопределимости по формуле
![]() ,
,
где n– общее число
неизвестных сил, включая реакции опор;m – число возможных
для данной системы независимых уравнений
статики.
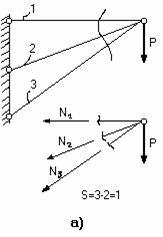
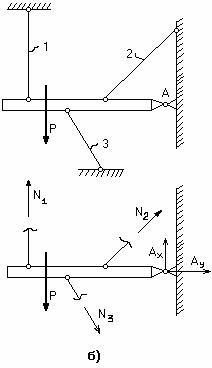
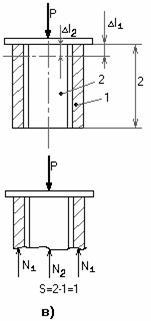
Рис.2.40
Раскрытие
статической неопределимости
Операции по определению неизвестных
силовых факторов в статически неопределимых
системах принято называть раскрытием
статической неопределимости. Производятся
они следующим образом. В начале исходя
из силовой схемы составляются уравнения
равновесия.
При решении любых задач число уравнений
должно быть равно числу неизвестных.
Для определения сил в стержнях статически
неопределимых систем следует составлять
уравнения, дополняющие уравнения
равновесия до числа неизвестных сил.
Дополнительные уравнения, называемые
уравнениями совместности перемещений
или деформаций,составляют, определяя
перемещения отдельных стержней системы
и устанавливая между ними связь.
Принцип совместности деформирования
выражает условие, заключающееся в том,
что конструкция должна деформироваться
без разъединения и непредусмотренного
взаимного перемещения отдельных ее
звеньев.
Для облегчения записей уравнений
перемещений строят схему деформаций
всех упругих элементов или схему
деформированной системы. Для любой
статистически неопределимой системы
всегда можно составить столько
дополнительных уравнений, сколько раз
система статически неопределима.
В силу различной взаимозависимости
элементов, различия накладываемых
связей и условий деформирования,
уравнения совместности деформаций
систем записываются по разному. Но все
они выражают соотношения деформаций
(перемещений) отдельных упругих элементов
системы. Например, на схеме,
на рис. 2.40, в
![]()
а на рис. 2.40, г.
![]()
т. к. весь
стержень не может не удлиниться, ни
укоротиться. На схеме (рис. 2.40, а)
можно установить геометрическое
соотношение деформаций стержней 1, 2 и
3.
После получения указанных геометрических
соотношений величины абсолютных
изменений, длины стержней
![]() заменяют по закону Гука их выражениями
заменяют по закону Гука их выражениями
через усилия![]() :
:
![]()
Полученные
таким образом уравнения, содержащие в
качестве неизвестных продольные силы,
и являются дополнительными уравнениями.
Они включают также показатели жесткости
отдельных звеньев конструкции, вводя
тем самым зависимость распределения
сил внутри системы от жесткости ее
элементов. Вместе с уравнениями статистики
общее число уравнений равно числу
неизвестных сил. Решая их, определяют
неизвестные внутренние (продольные)
силы.
В заключение может быть выполнена
энергетическая проверка решения задачи.
Она заключается в составлении и
удовлетворении равенства работы внешних
сил Аи суммы потенциальной энергии
деформации элементов системыU.
Сложные статически неопределимые
системы, в том числе статически
неопределимые фермы (элементы ферм
работают на растяжение, сжатие) и
статически неопределимые рамы,
рассматриваются в курсе строительной
механики стержневых систем. В курсе
сопротивления материалов рассматриваются
обычно простейшие статически неопределимые
системы, к которым относятся:
а) прямые стержни постоянного,
кусочно-постоянного и переменного
сечений, закрепленные с двух сторон, от
нагрузки действующей вдоль оси стержня;
б) системы шарнирно соединяемых стержней
с возможным включением жестких
недеформируемых элементов.
При решении статически неопределимых
систем, в стержнях которых действуют
продольные силы, можно отметить основные
этапы:
1) анализ работы конструкции с указанием
действующих силовых факторов и выяснением
деформации ее элементов, определение
степени статической неопределимости;
2) статическая
стороназадачи – составляют
уравнения равновесия для системы или
отсеченных ее частей;
3) геометрическая
стороназадачи – выясняют, как
деформируются стержни системы, изображают
систему в деформированном виде,
устанавливают связи между перемещениями
отдельных элементов системы, составляют
уравнения совместности перемещений;
4) физическая
стороназадачи – выражает
деформации элементов, согласно закону
Гука, через действующие в них неизвестные
усилия;
5) синтез – определяют неизвестные силы,
решая совместно систему уравнений
равновесия и перемещений.
Статически неопределимые конструкции
характеризуются рядом особенностей,
по сравнению со статически определимыми
системами. Так, при эксплуатации
конструкции возможно изменение ее
температуры, вызванное условиями работы
или сменой времен года. С изменением
температуры изменяются линейные размеры
элементов конструкции: увеличиваются
при нагреве, уменьшаются при охлаждении
на величину
![]() ,
,
(2.38)
где
![]() –
–
температурный коэффициент линейного
расширения (см. раздел «Справочные
данные»);![]() –
–
длина элемента;![]() –
–
изменение температуры, (0С).
В статически определимых системах длина
стержня может свободно изменяться при
их нагреве или охлаждении (рис.2.41, а,б).
Рис.2.41
В статически неопределимых системах
при изменении температуры возникают
дополнительные силы. Если нагреть
стержень, жестко закрепленный по концам
(рис.2.42, а), то его длина не может
изменяться: этому препятствуют жесткие
заделки. В опорах (заделках) возникают
реакции, сжимающие стержень.
Так как неизвестных сил две, а уравнение
равновесия можно составить только одно:
![]() ,
,
то система один раз статически
неопределима.
Решая геометрическую часть задачи,
составляем уравнение перемещений.
Отбросим одну из опор и заменим ее
действие неизвестной силой
![]() .
.
Теперь стержень при нагреве может
удлиниться на величину![]() (рис.2.42,б).
(рис.2.42,б).
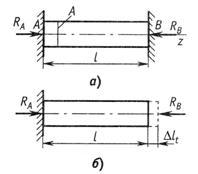
Рис.2.42
Так как длина стержня остается неизменной,
перемещение сечения
![]() должно быть равно нулю, следовательно,
должно быть равно нулю, следовательно,
сила![]() должна
должна
сжать стержень на величину, равную его
удлинению при нагреве:
![]() .
.
Решая физическую часть задачи, с учетом
равенства
![]() получаем
получаем
![]() .
.
Тогда продольная сила в сечениях стержня
![]() ;
;
напряжение в стержне
![]() .
.
Отметим, что напряжение в стержне не
зависит от площади сечения.
Элементы конструкций изготовляют с
определенной точностью. При сборке
статически неопределимых систем, имеющих
неточно изготовленные стержни, стержни
приходится деформировать (удлинять или
укорачивать), при этом в них возникают
напряжения, называемыми начальными или
монтажными.
Рассмотрим систему, один из стержней
которой изготовлен короче, чем требуется,
на величину
![]() (рис.2.43,а). Определим внутренние
(рис.2.43,а). Определим внутренние
силы и напряжения, возникающие в стержнях
системы при ее сборке. Стержни имеют
одинаковые размеры и изготовлены из
одного материала.
Рис.2.43
При сборке системы все три стержня
необходимо удлинить, приложив к ним
растягивающие силы. В собранном виде
система показана штриховыми линиями
(см. рис.2.43, а). Вырежем узел![]() (рис.2.43,б), составим уравнения
(рис.2.43,б), составим уравнения
равновесия сил
![]() ,
,
откуда
![]() ;
;
![]() .
.
Система один раз статически неопределима.
Рассмотрим геометрическую часть задач
и составим уравнение перемещений. Из
схемы, представленной на рис.2.43, а,
следует, что
![]() ,
,
где![]() .
.
Уравнение перемещений принимает вид
![]() .
.
Используя закон Гука, выразим удлинение
через неизвестные силы в стержнях
![]() .
.
Решив уравнение перемещений совместно
с уравнениями равновесия, получим
![]() ;
;![]() .
.
Начальные напряжения часто специально
создают в статически неопределимых
системах, таких, например, как соединения
с натягом и резьбовые соединения.
Создавая в элементах статически
неопределимой системы начальные
напряжения, знак которых противоположен
знаку напряжения от внешних сил, можно
повысить прочность конструкции или
увеличить допускаемую для нее нагрузку.
Распределение усилий между элементами
системы зависит от их жесткости. Если
увеличить жесткость какого- либо
элемента, то он примет на себя большее
усилие. Изменяя соотношение жесткостей
элементов конструкций, можно менять
распределение усилий между ними.
Эти особенности статически неопределимых
конструкций должны учитываться при
проектировании или применении таких
систем.
Статически неопределимые системы
обладают повышенной «живучестью».
Разрушение одного или нескольких
элементов (в зависимости от числа
дополнительных связей) не вызывает
потерю несущей способности конструкции
в целом. Так разрушение даже двух стержней
в системе, показанной на рис.2.39, вне приводит к потере способности
воспринимать силуPоставшимися
двумя стержнями, конечно, при условии
их достаточной прочности.
В заключение отметим следующие основные
свойства статически неопределимых
систем.
1. Статически неопределимая система
ввиду наличия добавочных лишних связей,
по сравнению с соответствующей статически
определимой системой оказывается
более жесткой, а при идентичном характере
нагружения значения усилий получаются
меньшими. Следовательно, и более
экономичными.
2. Разрушение лишних связей в нагруженном
состоянии, не ведет к разрушению всей
системы в целом, так как удаление этих
связей приводит к новой геометрически
неизменяемой системе, в то время как
потеря связи в статически определимой
системе приводит к изменяемой системе.
3. Для расчета статически неопределимых
систем необходимо предварительно
задаваться геометрическими характеристиками
поперечных сечений элементов, т.е.
фактически их формой и размерами, так
как их изменение приводит к изменению
усилий в связях и новому распределению
усилий во всех элементах системы.
4. При расчете статически неопределимых
систем необходимо заранее выбрать
материал конструкции, так как необходимо
знать его модули упругости.
5. В статически неопределимых системах
температурное воздействие, осадка опор,
неточности изготовления и монтажа
вызывают появление дополнительных
усилий.
Решение статически неопределимых систем
можно вести, используя три метода:
– расчет по упругой стадии деформации
(допускаемым напряжениям);
– расчет по разрушающим нагрузкам;
– расчет по предельному пластическому
состоянию.
В машиностроении отдается предпочтение
первому методу, а в строительстве –
второму и третьему.
Если в качестве физических уравнений
используется закон Гука, то такой способ
расчета носит название расчета по
упругой стадии деформаций. После
определения внутренних усилий –
продольных сил в стержнях статически
неопределимой системы – встает задача
обеспечения ее прочности. При расчете
по упругой стадии деформаций считается,
что предельное состояние конструкции
наступает тогда, когда один, наиболее
напряженный, стержень переходит в
предельное состояние (разрушится или
потечет). Поэтому после определения
усилий по этому способу находим напряжения
в стержнях и выбираем стержень, в котором
действует максимальное напряжение. Из
условия прочности этого наиболее
напряженного стержня либо вычисляем
допускаемую нагрузку, либо подбираем
сечения стержней. Следует отметить, что
в большинстве статически неопределимых
конструкций в результате расчета по
этому способу только в одном стержне
напряжения будут равны допускаемым,
остальные же стержни будут недогружены.
Достичь равенства напряжений во всех
элементах конструкции и, следовательно,
добиться выполнения требования, чтобы
напряжения во всех стержнях равнялись
допускаемым, в общем случае невозможно.
Второй способ расчета статически
неопределимых стержневых систем носит
название расчета по предельному
пластическому состоянию. Благодаря
наличию лишних стержней в статически
неопределимой системе, наступление
состояния текучести в одном (наиболее
напряженном) стержне еще не приводит к
нарушению геометрической неизменяемости
всей конструкции. Остальные стержни,
оставаясь упругими, препятствуют
пластическим деформациям этого стержня.
Конструкция продолжает выполнять свое
назначение, перейдя из упругой стадии
работы в упругопластическую. При
увеличении нагрузки в пластическую
стадию работы вовлекаются все новые
стержни. И только тогда, когда в системе
потекутвсе
лишние
стержни и хотя быодин необходимый,
конструкция превращается в механизм и
не может выполнять свои функции. Это
состояние и считается предельным при
расчете по предельному пластическому
состоянию. Таким образом, расчет по
предельному пластическому состоянию
сводится к следующему:
1) определяем, сколько стержней должно
потечь, чтобы конструкция превратилась
в механизм. Дальнейший расчет возможен
по двум вариантам:
– если в предельном состоянии текут все
стержни системы, то, составляя уравнения
равновесия конструкции в предельном
состоянии, находим из него значение
предельной нагрузки
![]() ;
;
– если в предельном состоянии течет
только часть стержней, то, не определяя
порядка перехода стержней в пластическое
состояние, рассматриваем все кинематически
возможные варианты предельного состояния
конструкции. Находим из уравнений
равновесия предельную нагрузку для
каждого варианта. Выбираем из всех
вариантов минимальное значение предельной
нагрузки
![]() ;
;
2) из условия прочности конструкции по
предельному состоянию
![]() либо вычисляем допускаемую нагрузку,
либо вычисляем допускаемую нагрузку,
либо подбираем сечения стержней.
Отметим, что расчет по предельному
пластическому состоянию является более
экономичным, чем расчет по упругой
стадии деформаций. Поэтому при сравнении
результатов расчета по двум способам
должно получиться, что допускаемая
нагрузка, найденная расчетом по
предельному пластическому состоянию,
всегда не меньше нагрузки, полученной
расчетом по упругой стадии деформации.
Соответственно площади сечений стержней,
найденные расчетом по предельному
состоянию, должны быть не больше площадей
сечений, полученных расчетом по упругой
стадии деформаций.
Примеры
типовых расчетов статически неопределимых
систем
Рассмотрим
основные этапы расчета статически
неопределимых систем на примере
простейших конструкций.
Пример 17.
Определить продольные силы в сечениях
ступенчатого стержня, жестко закрепленного
по концам (рис.2.44, а).

Рис.2.44
Решение.
Под действием силы
![]() в заделках возникают опорные реакции
в заделках возникают опорные реакции![]() и
и![]() .
.
Единственное уравнение равновесия
имеет вид
![]() ,
,
следовательно, система один раз статически
неопределима. Для раскрытия статической
неопределимости отбросим одну из опор,
например верхнюю (рис.2.44, б), и составим
для стержня уравнение совместности
перемещений. Так как длина стержня не
изменяется (он жестко закреплен по
концам), удлинение верхней части стержня
должно быть равно укорочению нижней,
т.е. перемещение сечения![]()
![]() .
.
Уравнение совместности перемещений
можно записать в ином виде, определив
перемещение верхнего сечения![]() под действием сил
под действием сил![]() и
и![]() .
.
Так как это сечение закреплено, его
перемещение равно нулю
![]() .
.
Очевидно, оба уравнения совместности
перемещений равнозначны.
На основании закона Гука, уравнение
совместности перемещений запишем в
виде
![]() .
.
Решив совместно уравнение равновесия
и уравнение перемещений, получим
![]() ;
;![]() .
.
Используя метод сечений, находим
![]() ;
;![]() .
.
Отметим, что в более жесткой нижней
части стержня возникает бóльшая по
абсолютному значению продольная сила.
Пример
18.
К стержню, закрепленному обоими концами,
приложена осевая сила Р(рис.2.45).
Определить опорные реакцииR1иR2, если известныl1, l2
иР.
Решение.

Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Обозначения в формулах:
σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.
Закон Гука:
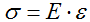
Формула для расчета напряжений в поперечном сечении стержня
Условие прочности (проверочный расчет) при растяжении-сжатии
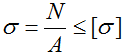
Расчет минимальной площади поперечного сечения бруса
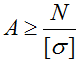
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
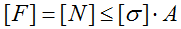
Формула для расчета абсолютных деформаций
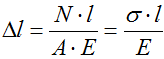
Расчет перемещения сечений
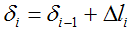
Здесь: δi — перемещение рассматриваемого сечения,
δi-1 — перемещение предыдущего сечения,
Δli — деформация участка между указанными сечениями.
Напряжения в наклонных сечениях
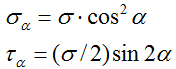
Здесь α — угол отклонения сечения от поперечного.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Как рассчитать пружину
Под понятием расчета пружины скрывается большое число параметров, таких как диаметр прутка, его свойства по материалу и его обработке. Поэтому полный расчет пружины – очень сложная операция, выполняемая с помощью специальных компьютерных программ. К основным характеристикам относят жесткость пружины, максимальную силу сжатия (растяжения), максимальную деформацию, высоту пружины в сжатом и свободном состоянии и шаг пружины.

Вам понадобится
- динамометр, линейка, весы.
Инструкция
Возьмите произвольную пружину и измерьте с помощью линейки ее длину. Это будет высота пружины в свободном состоянии. Затем максимально сожмите ее, подействовав с некоторой силой. Снова измерьте длину пружины. Это будет высота пружины в сжатом состоянии. Все измерения проводите в метрах.
Посчитайте количество витков пружины, затем поделите на это число высоту пружины в свободном состоянии. Результатом будет шаг пружины в свободном состоянии. Проделайте ту же операцию для пружины в сжатом состоянии и получите шаг пружины в сжатом состоянии.
Чтобы найти максимальную деформацию сжатой пружины, отнимите от ее высоты в свободном состоянии, высоту в сжатом состоянии. Это будет деформация на сжатие. Чтобы найти максимальную деформацию на растяжение, закрепите один из концов пружины, начинайте растягивать ее за другой конец, используя одновременно динамометр. Показания динамометра должны увеличиваться пропорционально удлинению пружины, как только показания динамометра начали нарастать быстрее, чем происходит деформация, растяжение нужно прекратить. Измерьте длину пружины и отнимите от нее длину пружины в свободном состоянии, получите максимальную деформацию на растяжение. Показания динамометра в этот момент будут отвечать максимальной силе растяжения.
Чтобы найти максимальную силу сжатия, нагружайте пружину до того момента, когда она полностью сожмется. На весах измерьте массу груза и умножьте ее на ускорение свободного падения (число 9,81). Массу выразите в килограммах, тогда силу получите в ньютонах.
Чтобы найти жесткость пружины, закрепите один из ее концов, а к другому прикрепите динамометр, придайте пружине небольшую деформацию (10-20 %). Измерьте ее длину в деформированном состоянии в метрах, и снимите показания динамометра в ньютонах. Отнимите длину деформированной пружины от длины пружины в свободном состоянии. Затем на полученное значение разделите силу, измеренную динамометром k=F/Δx. Результат получите в ньютонах на метр.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Жесткость пружины
Опубликовано 14 Июн 2015
Рубрика: Механика | 57 комментариев
 Максимальная сила сжатия или растяжения пружины не зависит от количества рабочих витков! Это означает, что если взять, например, цилиндрическую пружину сжатия, а затем разрезать её на две неравные по высоте части, то максимальное усилие при полном сжатии…
Максимальная сила сжатия или растяжения пружины не зависит от количества рабочих витков! Это означает, что если взять, например, цилиндрическую пружину сжатия, а затем разрезать её на две неравные по высоте части, то максимальное усилие при полном сжатии…
…обеих образовавшихся пружин будет одинаковым. Более того – максимальная сила останется такой же, как у исходной пружины!
В чем же тогда различие между тремя рассмотренными выше пружинами? Ответ на этот вопрос – в высотных размерах и жесткостях.
Меньшая пружина самая жесткая. У нее самый малый ход от свободного состояния до полного сжатия. Исходная пружина (до разделения) – самая мягкая. У нее самый большой ход.
Жесткость пружины (C) является ключевым параметром, определяющим силу сжатия или растяжения (Fi) при определенной величине деформации (L0— Li):
Fi=C*(L0— Li)
В свою очередь сама жесткость пружины (C) зависит только от жесткости одного витка (C1) и числа рабочих витков (N):
C=C1/N
Обратите внимание – жесткость одного витка всегда больше жесткости всей пружины! Причем, чем больше в пружине витков, тем она мягче.
Расчет в Excel жесткости витка пружины.
Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.
C1=G*X4/(Y*(D1— B)3)
В этой формуле:
G – модуль сдвига материала проволоки
Для пружинной стали:
G≈78500 МПа ±10%
Для пружинной бронзы:
G≈45000 МПа ±10%
X – минимальный размер сечения проволоки
Для круглой проволоки – это её диаметр:
X=D
Для прямоугольной проволоки:
X=H при H<B
X=B при B<H
H – высота сечения проволоки в направлении параллельном оси навивки пружины
B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины
Для круглой проволоки:
H=B=D
D1— наружный диаметр пружины
(D1— B) – средний диаметр пружины
Y – параметр жесткости сечения проволоки
Для круглой проволоки:
Y=8
Для прямоугольной проволоки:
Y=f(H/B)
Что это за функция — f (H/B)? В литературе она всегда задана в виде таблицы, что не всегда удобно, особенно для промежуточных значений H/B, которых попросту нет.
 Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
На графиках, представленных ниже, Excel нашел три уравнения для определения параметра Y при различных значениях аргумента — отношения высоты проволоки к ширине – H/B. Красные точки – это заданные значения из таблицы (столбец №2), черные линии – это графики найденных аппроксимирующих функций. Уравнения этих функций Excel вывел непосредственно на поля графиков.

В таблице в столбце №3 размещены посчитанные по полученным формулам значения параметра жесткости сечения проволоки Y, а в столбцах №4 и №5 — абсолютные Δабс и относительные Δотн погрешности аппроксимации.
Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R2 очень близка к 1 и относительная погрешность не превышает 2,7%!
Применим на практике полученные результаты.
Расчет пружины сжатия из проволоки прямоугольного сечения.

Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.
Представленная ниже программа является переработанной версией программы расчета цилиндрических пружин из круглой проволоки, подробное описание которой вы найдете, перейдя по ссылке. Прочтите эту статью, и вам проще будет разобраться в алгоритме.
Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C1), задающей жесткость пружины (C) в целом.
Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.
Внимание!!!
После выполнения расчета по программе выполняйте проверку касательных напряжений!!!

4. I=(D1/B)-1
5. При 1/3<H/B<1: Y=5,3942*(H/B)2-0,3572*(H/B)+0,5272
При 1<H/B<2: Y=5,4962*(H/B)(-1.715)
При 2<H/B<6: Y=3,9286*(H/B)(-1.2339)
6. При H<B: C1=(78500*H4)/(Y*(D1— B)3)
При H>B: C1=(78500*B4)/(Y*(D1— B)3)
8. Tnom=1,25*(F2/C1)+H
9. Tmax=π*(D1— B)*tg (10°)
11. S3=T— H
12. F3=C1*S3
14. Nрасч=(L2— H)/(H+F3/C1— F2/C1)
16. C=C1/N
17. L0=N*T+H
18. L3=N*H+H
19. F2=C*L0— C*L2
21. F1=C*L0— C*L1
22. N1=N+1,5
23. A=arctg (T/(π*(D1— H)))
24. Lразв=π*N1*(D1— H)/cos (A)
25. Q=H*B*Lразв*7,85/106
Заключение.
Значение модуля сдвига (G) материала проволоки в существенной мере влияющее на жесткость пружины (C) в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.
Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, и придерживаясь правила: «угол подъема в градусах близок значению индекса пружины», мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…
Ссылка на скачивание файла с программой: raschet-pruzhiny-szhatiya-iz-pryamougolnoy-provoloki (xls 94,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
§1. Продольные силы в поперечных сечениях
§1. Продольные силы в поперечных сечениях
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
При растяжении или сжатии осевыми силами стержней из однородного материала поперечные сечения, достаточно удаленные от точек приложения внешних сил ,остаются плоскими и перемещаются поступательно в направлении деформации. Это положение называют – гипотезой плоских сечений. На основании указанного можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. Их значения найдем, разделив продольную силу N на площадь А: σ=N/A
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
где N – абсолютное продольной силы в сечении;
А – площадь поперечного сечения;
[σ] – допускаемое напряжение пр растяжении или сжатии для материала стержня.
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
Превышение рабочего (расчетного) напряжения не должно быть больше 5% , иначе прочность рассчитываемой детали считается недостаточной.
В случаях, когда рабочее напряжения значительно ниже допускаемых σ<<[σ], получаются неэкономичные конструкции чрезмерным необоснованным расходом материала. Такие решения являются нерациональными. Следует стремится к максимальному использованию прочности материала и снижения материалоемкости конструкций.
2. Подбор сечения (проектный расчет). Исходя из условия прочности можно определить необходимые размеры сечения, зная продольную силу N и допускаемое напряжение [σ]:
A≥N/[σ]
3. Определение допускаемой продольной силы. Допускаемое значение продольной силы в поперечном сечении стержня можно найти по формуле: [N]≤ [σ]·A
Значения допускаемых напряжение для некоторых материалов приведены в табл. 1.
Допускаемые напряжения назначаются на основе результатов механических испытаний образцов соответствующих материалов.
§4. Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим – свободным, к которому приложена центральная продольная сила Р (рис. 4). До нагружения стержня его длина равнялась l – после нагружения она стала равной
(рис. 4). Величину называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).
Рис. 4. Абсолютное удлинение стержня
Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация
остается одной и той же по длине стержня и равной ε = Δl/l
Величина ε называется относительной продольной деформацией.
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации
): σ=Eε
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки. Так как величина ε безразмерная, то E – измеряется в тех же единицах измерения то и напряжение, т. е. в Паскалях (Па). Значения модуля упругости E для некоторых конструкционных материалов приведены в табл. 2.
Δl=Nl/EA
Выведенное соотношение показывает, что удлинение (укорочение) при растяжении (сжатии) зависит от величины продольной силы N, поперечного сечения А стержня, его длины l и модуля продольной упругости Е. Произведение ЕА называется жесткостью сечения стержня при растяжении (сжатии).
При растяжении и сжатии изменяются и поперечные размеры стержня. Поперечный размер, первоначально равный a , уменьшается до a1. Изменение поперечно размера Δ a= a- a1, а поперечная деформация равна ε┴= Δ a/ a.
Экспериментально установлено что отношение поперечной деформации к продольной при упругом растяжении или сжатии есть величина постоянная и обозначается µ: µ= ε┴/ ε
Следует учитывать, что продольные и поперечные деформации всегда противоположны по знаку. Иными словами, при растяжении, когда продольный размер стержня увеличивается, его поперечный размер уменьшается, и, наоборот , при сжатии продольный размер уменьшается, а поперечный –увеличивается .
Величина µ называется коэффициентом поперечной деформации, или коэффициентом Пуассона. Коэффициент поперечной деформации для некоторых материалов имеет следующие значения:
сталь ….024-032,
медь….031-035,
бронза..032-035,
резина , каучук…047.
