Как после перегорания одной лампочки в гирлянде можно определить способ соединения и починить ее? Попробуем разобраться.
Анфиса обнаружила на балконе старую гирлянду. Включив ее в розетку, девочка заметила, что горят все лампочки, кроме зеленых. Внимательно изучив провода, Анфиса увидела, что все зеленые лампочки соединены последовательно друг за другом.
Последовательное соединение проводников
При последовательном соединении конец первого проводника соединяют с началом второго, конец второго — с началом третьего и т. д.
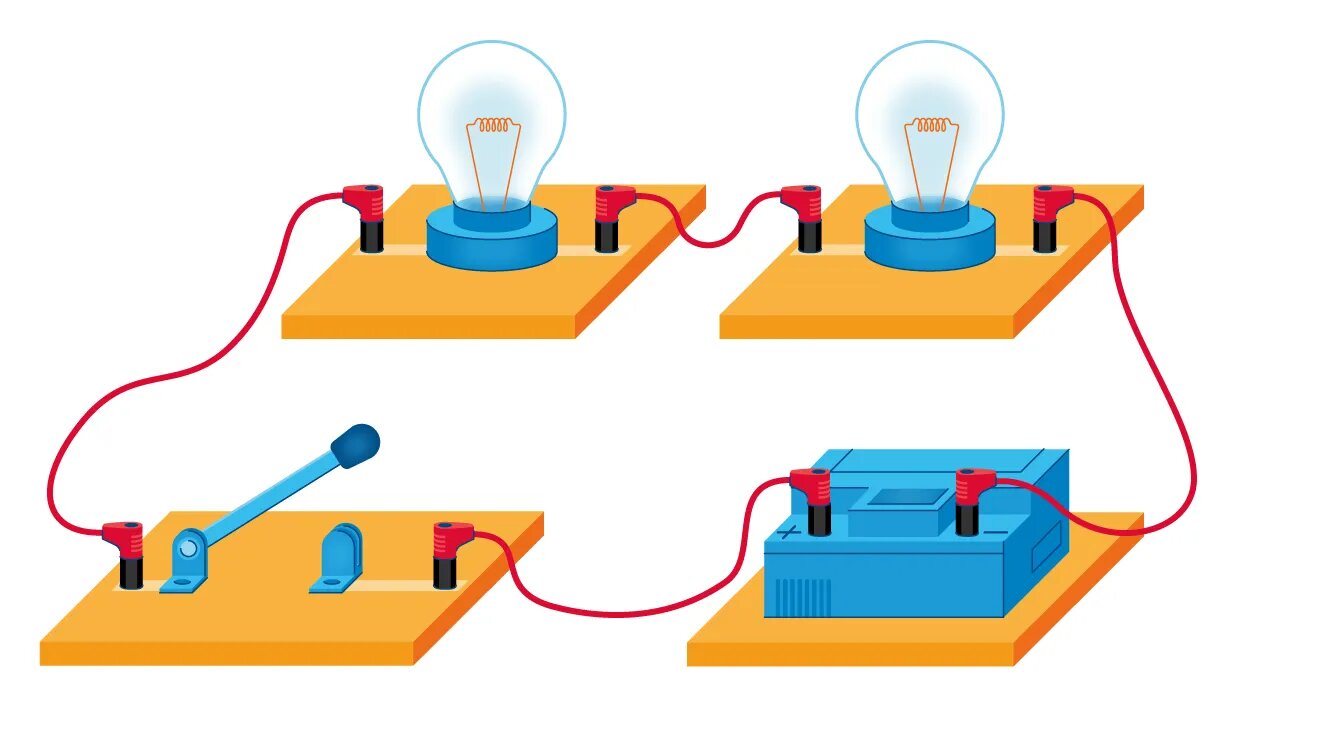
Последовательное подключение обычно используется в тех случаях, когда необходимо целенаправленно включать или выключать определенный электроприбор. Например, для работы школьного электрического звонка требуется соединить его последовательно с источником тока и ключом.
Вот некоторые примеры использования схемы последовательного соединения:
- освещение в вагонах поезда или трамвая;
- простейшие елочные гирлянды;
- карманный фонарик;
- амперметр для измерения силы тока в цепи.
Законы последовательного соединения проводников
-
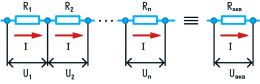
При последовательном соединении сила тока в любых частях цепи одна и та же:
I = I1 = I2 = … = In.
Если в цепи с последовательным способом соединения одна из ламп выйдет из строя и через нее не будет протекать электрический ток, то и через оставшиеся лампы ток проходить не будет. Вспомним Анфису и ее гирлянду: когда одна из зеленых лампочек перегорела, то ток, проходящий через нее, стал равен нулю. Следовательно, и другие зеленые лампочки, включенные последовательно, не загорелись. Чтобы починить гирлянду, нужно определить перегоревшую лампочку и заменить ее.
-
При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводников:
Rэкв = R1 + R2 + … + Rn.
-
При последовательном соединении общее напряжение цепи равно сумме напряжений на отдельных участках:
Uэкв = U1 + U2 + … + Un.
Пример решения задачи
В цепь с напряжением 220 В включена лампа, через нее протекает ток силой 20 А. Когда к лампе последовательно подключили реостат, сила тока в цепи уменьшилась до 11 А. Чему равно сопротивление реостата?
Решение.
-
По закону Ома определим сопротивление лампы:
R1 = U / I1 = 220 / 20 = 11 Ом.
-
Также по закону Ома определим общее сопротивление цепи при включенном реостате:
R = U / I2 = 220 / 11 = 22 Ом.
-
При последовательном соединении сопротивления лампы и реостата складываются:
R = R1 + R2.
-
Зная общее сопротивление цепи и сопротивление лампы, определим искомое сопротивление реостата:
R2 = R − R1 = 22 − 11 = 11 Ом.
Ответ: сопротивление реостата равно 11 Ом.
К сожалению, последовательное соединение не всегда оказывается удобным. Например, в торговом центре «Ашан» работает с 9:00 до 23:00, кинотеатр — с 10:00 до 02:30, а магазины — с 10:00 до 22:00. При последовательном соединении цепи свет должен будет гореть во всем ТЦ с 9:00 до 02:30. Согласитесь, что такой режим работы экономически невыгоден даже при минимальном тарифе на электроэнергию. В этом случае удачным решением будет использование параллельного соединения.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Параллельное соединение проводников
При параллельном соединении начала всех проводников соединяются в одной общей точке электрической цепи, а их концы — в другой.
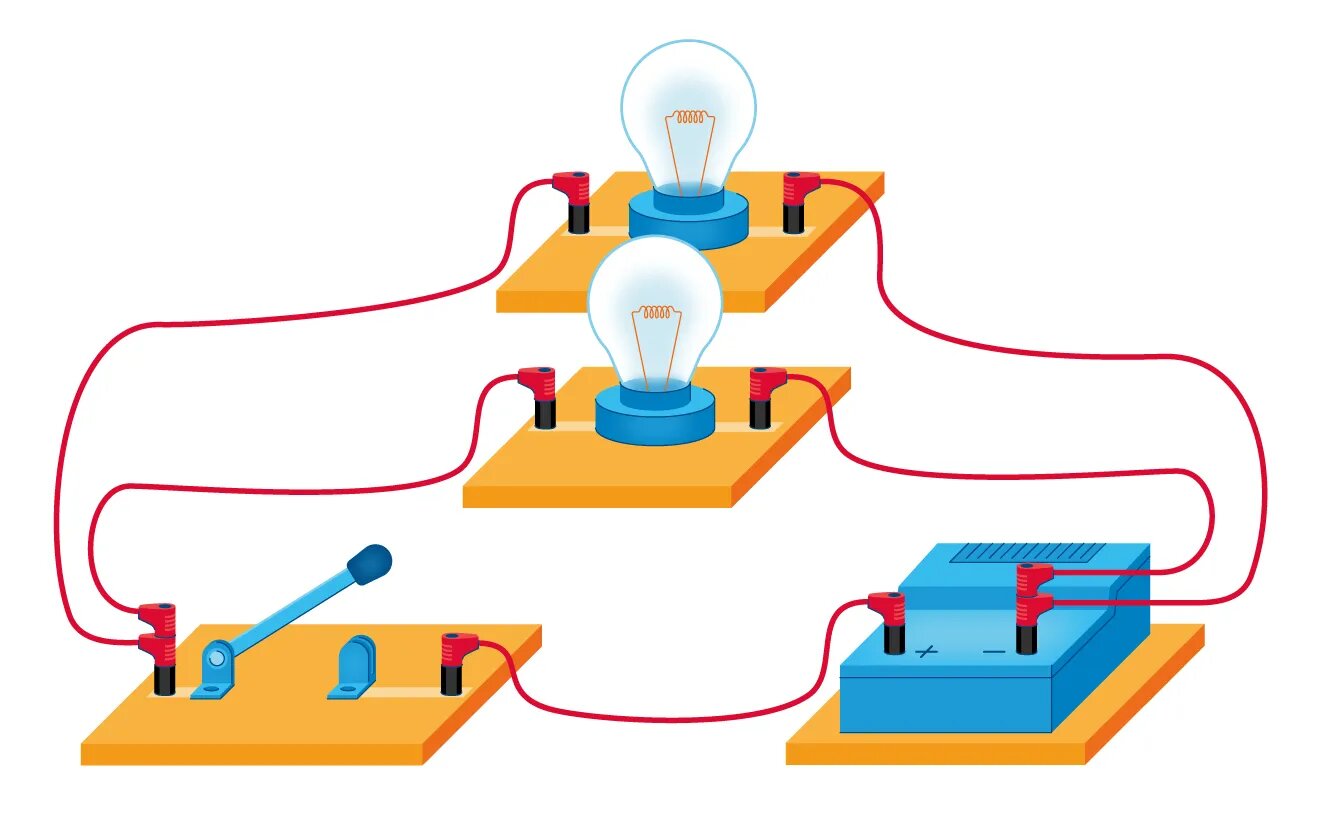
Параллельное соединение используют в тех случаях, когда необходимо подключать электроприборы независимо друг от друга. Например, если отключить чайник, то холодильник будет продолжать работать. А когда в люстре перегорает одна лампочка, остальные все так же освещают комнату.
Приведем еще несколько примеров применения параллельного способа соединения:
- освещение в больших торговых залах;
- бытовые электроприборы в квартире;
- компьютеры в кабинете информатики;
- вольтметр для измерения напряжения на участке цепи.
Параллельное соединение проводников: формулы
-
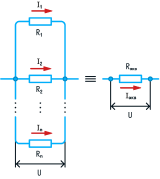
Напряжение при параллельном соединении в любых частях цепи одинаково:
U = U1 = U2 = … = Un.
Как вы помните, все бытовые электроприборы рассчитаны на одинаковое номинальное напряжение 220 В. Да и согласитесь, куда проще делать все розетки одинаковыми, а не рассчитывать напряжение для каждого прибора при их последовательном соединении.
-
Сила тока при параллельном соединении (в неразветвленной части цепи) равна сумме сил тока в отдельных параллельно соединенных проводниках:
Iэкв = I1 + I2 + … + In.
Электрический ток растекается по ветвям обратно пропорционально их сопротивлениям. Если сопротивления в ветвях равны, то и ток при параллельном соединении делится между ними поровну.
-
Общее сопротивление цепи определяется по формуле:
1 / Rэкв = 1 / R1 + 1 / R2 + … + 1 / Rn.
Для двух параллельно соединенных проводников формулу можно записать иначе:
Rэкв = (R1 · R2) / (R1 + R2).
Если n одинаковых проводников, каждый из которых имеет сопротивление R1, соединены параллельно, то общее сопротивление участка цепи можно найти, разделив сопротивление одного из проводников на их количество:
Rэкв = R1 / n.
Вернемся к Анфисе и ее гирлянде. Мы уже разобрались, почему перестали гореть все зеленые лампочки. Пришло время узнать, почему продолжили гореть все остальные. В современных гирляндах используют параллельное и последовательное соединение одновременно. Например, лампочки одного цвета соединяют последовательно, а с другими цветами — параллельно. Таким образом, отключение ветви с зелеными лампочками не повлияло на работу остальной части цепи.
Пример решения задачи
Два резистора с сопротивлениями 10 Ом и 11 Ом соответственно соединены параллельно и подключены к напряжению 220 В. Чему равна сила тока в неразветвленной части цепи?
Решение.
-
Определим общее сопротивление при параллельном соединении проводников:
R = (R1 · R2) / (R1 + R2) = (10 · 11) / (10 + 11) = 110 / 21 Ом ≈ 5,24 Ом.
-
По закону Ома определим силу тока в цепи:
I = U / R = 220 / (110 / 21) = 42 А.
Ответ: сила тока в неразветвленной части цепи равна 42 А.
Смешанное соединение проводников
Зачастую реальные электрические схемы оказываются сложнее, поэтому используют различные комбинации последовательного и параллельного способов соединения. Такой способ соединения называется смешанным. Смешанное соединение проводников предполагает использование последовательного и параллельного способов соединения в одной цепи.
Алгоритм решения задач со смешанным соединением проводников:
-
Прочитать условие задачи, начертить схему электрической цепи, при необходимости пронумеровать проводники.
-
Проанализировать схему, т. е. найти участки, где используется только последовательное или только параллельное соединение проводников. Определить сопротивление на этих участках.
-
Выяснить вид соединения участков между собой. Найти общее сопротивление всей цепи.
-
С помощью закона Ома и законов последовательного и параллельного соединения проводников найти распределения токов и напряжений в цепи.
Пример решения задачи
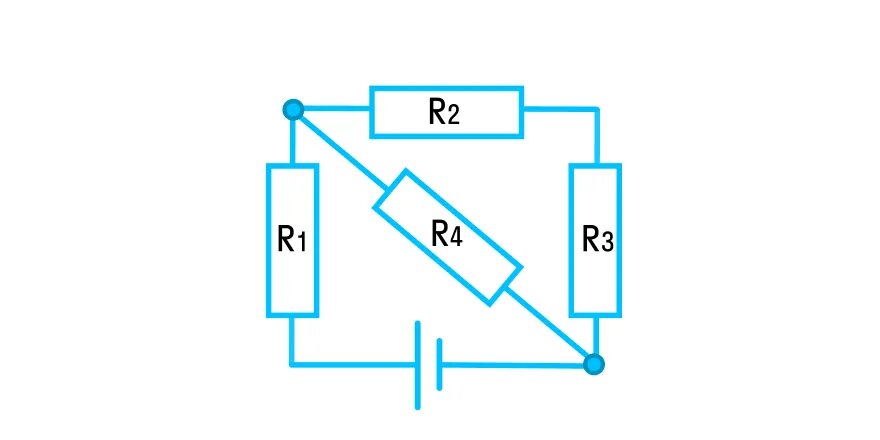
На рисунке показана схема электрической цепи. Сопротивления резисторов одинаковы и равны 12 Ом. Напряжение источника — 100 В. Какова сила тока, протекающего через резистор R4?
Решение.
-
Проанализируем данную схему. Резисторы R2 и R3 соединены между собой последовательно, а с резистором R4 — параллельно. Весь этот участок соединен последовательно с источником тока и резистором R1.
-
Определим сопротивление последовательно соединенных резисторов R2 и R3:
R23 = R2 + R3 = 12 + 12 = 24 Ом.
-
Найдем общее сопротивление резистора R4 и участка 2–3, соединенных параллельно:
R234 = (R23 · R4) / (R23 + R4) = (24 · 12) / (24 + 12) = 8 Ом.
-
Определим общее сопротивление всей цепи как сумму включенных последовательно резистора R1 и участка 2–3–4:
Rэкв = R1 + R234 = 12 + 8 = 20 Ом.
-
По закону Ома найдем силу тока в неразветвленной части цепи:
I = U / Rэкв = 200 / 20 = 5 А.
-
По закону Ома определим напряжение на участке, состоящем из резисторов R2, R3, R4:
Uэкв1 = I · R234 = 5 · 8 = 40 В.
-
Поскольку при параллельном соединении напряжение одинаково, то напряжение на резисторе R4 также равно 40 В. По закону Ома найдем силу тока, протекающего через резистор R4:
I4 = Uэкв1 / R4 = 40 / 12 ≈ 3,3 А.
Ответ: через резистор R4 протекает ток силой приблизительно 3,3 А.
Мы разобрали довольно много формул последовательного и параллельного подключения проводников. А запомнить их можно с помощью вот таких схем:
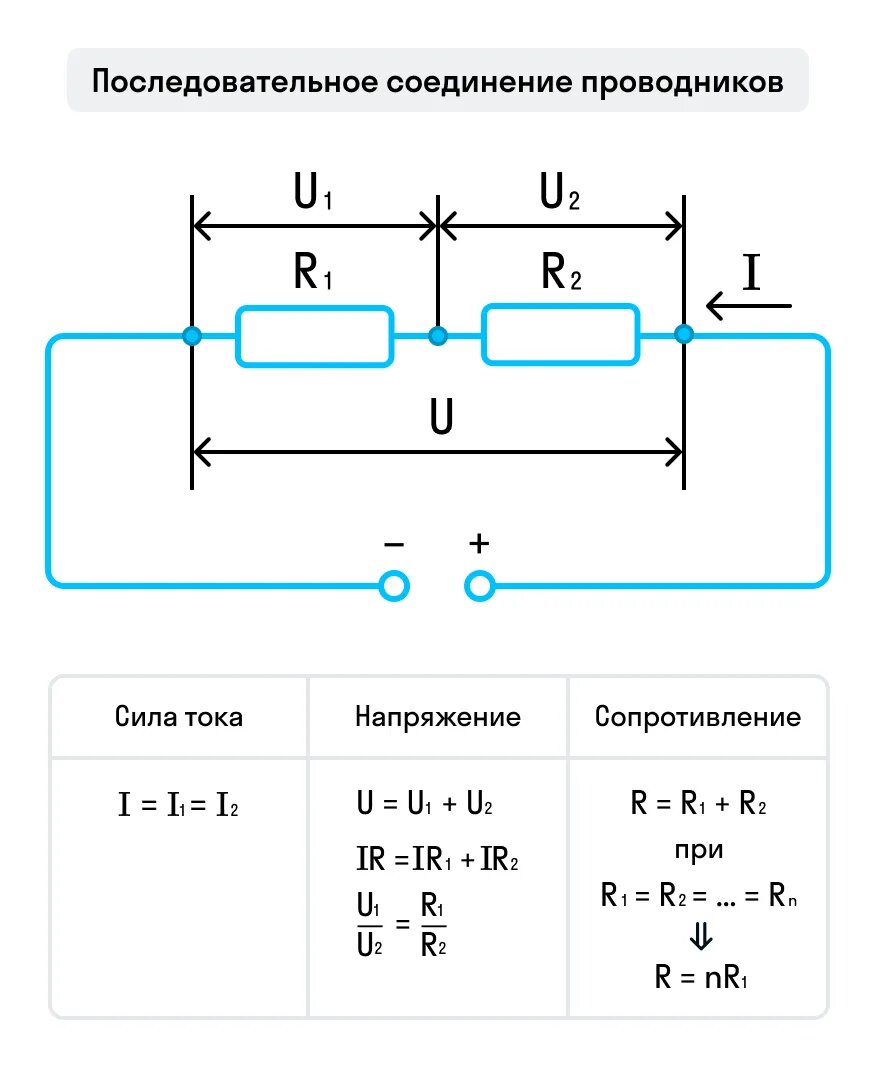
Скачать шпаргалку
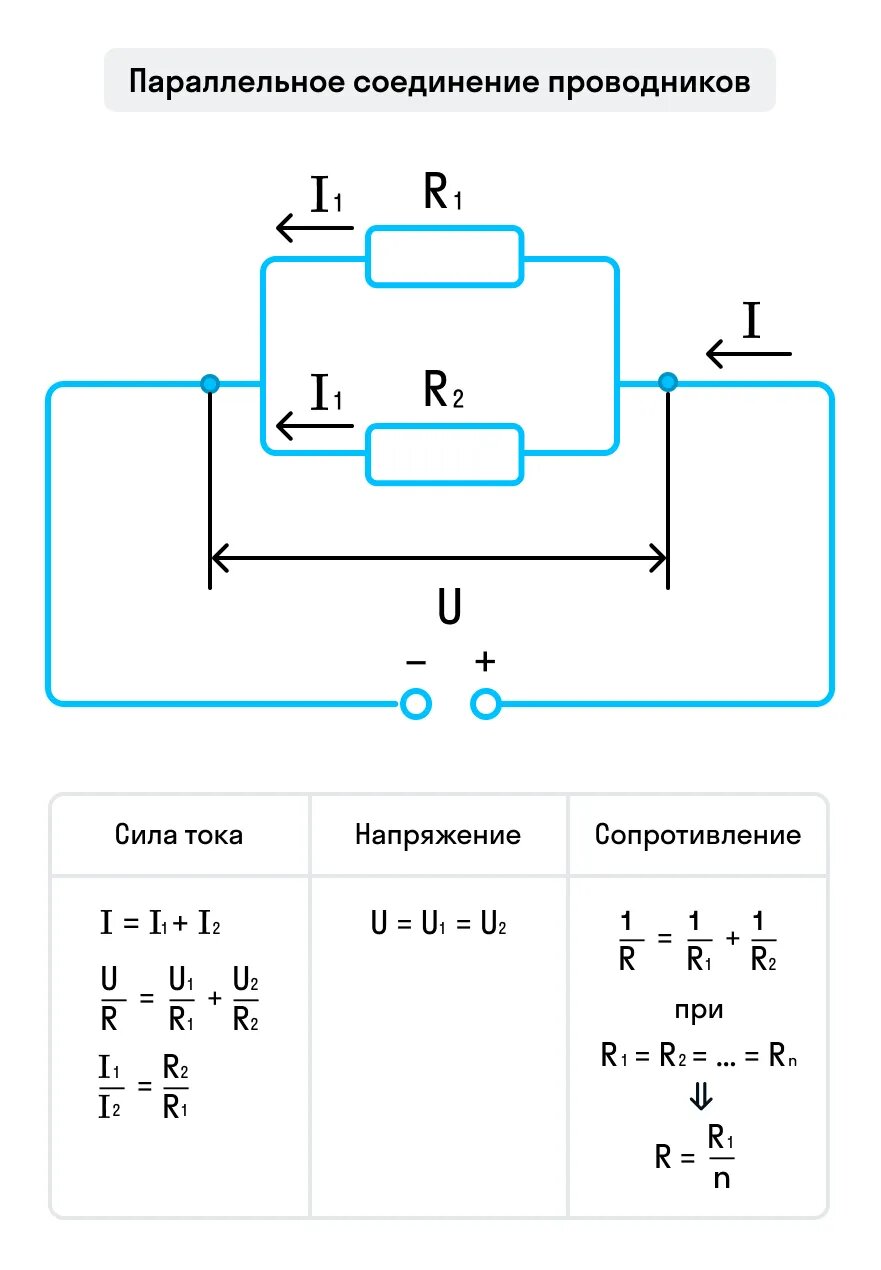
Скачать шпаргалку
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы научитесь составлять самые разнообразные электрические цепи и решать задачи с ними, а также узнаете об их применении в жизни. Ждем вас!
Загрузить PDF
Загрузить PDF
Нужно вычислить сопротивление последовательной, параллельной или комбинированной цепей? Нужно, если вы не хотите сжечь плату! В этой статье мы расскажем вам, как это сделать. Перед чтением, пожалуйста, уясните, что у резисторов нет «начала» и нет «конца». Эти слова вводятся для облегчения понимания изложенного материала.
-

1
Определение. В последовательной цепи резисторы подключены один за другим: начало одного крепится к концу другого и так по цепочке. Каждый следующий резистор в цепи добавляет некоторое сопротивление к общему сопротивлению цепи.[1]
- Формула для вычисления общего сопротивления последовательной цепи: Req = R1 + R2 + …. Rn где n — общее количество резисторов в цепи, соединенных последовательно. Таким образом, сопротивления всех резисторов просто суммируются. Например, найдем сопротивление цепи, показанной на рисунке.[2]
- В этом примере резисторы R1 = 100 Ом и R2 = 300 Ом соединены последовательно. Req = 100 Ом + 300 Ом = 400 Ом
Реклама
- Формула для вычисления общего сопротивления последовательной цепи: Req = R1 + R2 + …. Rn где n — общее количество резисторов в цепи, соединенных последовательно. Таким образом, сопротивления всех резисторов просто суммируются. Например, найдем сопротивление цепи, показанной на рисунке.[2]
-

1
Определение. Параллельное соединение резисторов — цепь, у которой начала всех резисторов соединены между собой и концы всех резисторов соединены между собой.[3]
- Формула для вычисления сопротивления параллельной цепи:
Req = 1/{(1/R1)+(1/R2)+(1/R3)..+(1/Rn)} где n — общее количество резисторов в цепи, соединенных параллельно.[4]
- Допустим, даны резисторы с сопротивлениями R1 = 20 Ом, R2 = 30 Ом, and R3 = 30 Ом.
- Тогда общее сопротивление цепи для 3 резисторов, соединенных параллельно: Req = 1/{(1/20)+(1/30)+(1/30)} = 1/{(3/60)+(2/60)+(2/60)} = 1/(7/60) = 60/7 Ом = 8,57 Ом (примерно).
- Формула для вычисления сопротивления параллельной цепи:
-

1
Определение. Комбинированная цепь — соединение последовательной и параллельной цепей между собой.[5]
Например, найдем сопротивление комбинированной цепи, показанной на рисунке.- Резисторы R1 и R2 соединены последовательно. Поэтому их общее сопротивление (обозначим его Rs) равно: Rs = R1 + R2 = 100 Ом + 300 Ом = 400 Ом.
- Резисторы R3 и R4 соединены параллельно. Поэтому их общее сопротивление (обозначим его Rp1) равно: Rp1 = 1/{(1/20)+(1/20)} = 1/(2/20)= 20/2 = 10 Ом
- Резисторы R5 и R6 также соединены параллельно. Поэтому их общее сопротивление (обозначим его Rp2) равно: Rp2 = 1/{(1/40)+(1/10)} = 1/(5/40) = 40/5 = 8 Ом
- Мы получили цепь с четырьмя резисторами Rs, Rp1, Rp2 и R7, которые соединены последовательно. Поэтому вам нужно просто сложить их сопротивления для вычисления общего сопротивления. Сопротивление R7 нам известно изначально. Req = 400 Ом + 10 Ом + 8 Ом + 10 Ом = 428 Ом.
Реклама
Некоторые факты
- Каждый электропроводный материал имеет некоторое сопротивление, являющееся сопротивляемостью материала электрическому току.
- Сопротивление измеряется в Омах. Символ единицы измерения Ом — Ω.
- Разные материалы имеют разные значения сопротивления.
- Например, сопротивление меди 0.0000017 Ом/см3
- Сопротивление керамики около 1014 Ом/см3
- Чем больше значение сопротивления, тем выше сопротивляемость электрическому току. Медь, которая часто используется в электрических проводах, имеет очень малое сопротивление. С другой стороны, сопротивление керамики очень велико, что делает ее прекрасным изолятором.
- Работа всей цепи зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
- U=IR. Это закон Ома, установленный Георгом Омом в начале 1800-х. Если вам даны любые две из этих переменных, вы легко найдете третью.
- U=IR. Напряжение (U) есть результат умножения силы тока (I) * на сопротивление (R).
- I=U/R. Сила тока есть частное от напряжение (U) ÷ сопротивление (R).
- R=U/I. Сопротивление есть частное от напряжение (U) ÷ сила тока (I).
Советы
- Запомните: при параллельном соединении существует несколько путей прохождения тока по цепи, поэтому в такой цепи общее сопротивление будет меньше сопротивления каждого отдельного резистора. При последовательном соединении ток проходит через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
- Общее сопротивление в параллельной цепи всегда меньше сопротивления одного резистора с самым низким сопротивлением в этой цепи. Общее сопротивление в последовательной цепи всегда больше сопротивления одного резистора с самым высоким сопротивлением в этой цепи.
- Чтобы закрепить материал, рассчитайте сопротивление по закону Ома:
- U = R * I
- P = U * I, где U можно заменить на RI
- P = RI * I
- P = R I^2
- Пример: дана лампа на 75 Вт, рассчитанная на напряжение в 220 В. Как найти ее сопротивление?
- P = U * I
- I = P/U => 75/220 = 0,34 Ом
- P = RI^2
- 75 Вт = R * 0,34^2
- R = 75/0,1156 = 648 A
- А теперь давайте проверим наш ответ с помощью другой формулы:
- U = R * I
- R = U/I
- R = 220/0,34 = 647 A. Ответы практически совпадают.
Реклама
Об этой статье
Эту страницу просматривали 161 202 раза.
Была ли эта статья полезной?
Главная » Справочник » Последовательное соединение резисторов. Схема соединения и примеры расчета
Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.

Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:
R = R1 + R2 + R3
То есть, в нашем случае общее сопротивление цепи будет равно:
R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм
Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.

Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.
Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).

Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:

Используя закон Ома для участка цепи, напряжение на отдельных резисторов может быть вычислена следующим образом:

В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.
В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:

Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:

Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:

Пример № 2
Необходимо рассчитать падение напряжения на выводах «А» и «В»:
а) без подключенного резистора R3
б) с подключенным резистором R3

Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).

Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Вы уже знаете, что есть два типа соединения элементов электрической цепи: последовательный и параллельный. Последовательно мы подключали в цепь амперметр, а параллельно — вольтметр.
На данном уроке мы более подробно рассмотрим последовательное соединение. Мы будем использовать сразу несколько потребителей электроэнергии и узнаем, каким закономерностям подчиняются уже известные нам величины (сила тока, сопротивление и напряжение) при таком соединении элементов в цепи.
Последовательное включение элементов в электрическую цепь
Соберем электрическую цепь. Последовательно соединим две электролампы, два источника тока и ключа (рисунок 1).
Обратите внимание, что при таком подключении аккумуляторов соблюдается определенная полярность подключения: провод, идущий от положительного полюса одного аккумулятора необходимо соединить с отрицательным полюсом другого аккумулятора. И, наоборот, провод идущий от отрицательного полюса одного аккумулятора соединяется с положительным полюсом другого.
Если в такой цепи попытаться выключить только одну лампу, то погаснет и вторая.
Схема этой электрической цепи показана на рисунке 2.
В такую цепь мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества последовательно подключенных в цепь проводников.
Сила тока в цепи при последовательном соединении проводников
При изучении силы тока мы измеряли ее на различных участках электрической цепи (рисунок 3). Полученные с помощью амперметра значения силы тока были одинаковы.
При этом все элементы у нас были соединены последовательно. Сделаем вывод.
При последовательном соединении сила тока в любых частях цепи одна и та же:
$I = I_1 = I_2 = … = I_n$.
Сопротивление в цепи при последовательном соединении проводников
Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
Давайте порассуждаем. В цепи был один проводник с определенным сопротивлением. Мы последовательно подключаем второй. Представим эти два проводника в виде одного элемента цепи. Тогда получается, что, подсоединив второй проводник, мы увеличили длину первого.
Сопротивление же зависит от длины проводника. Поэтому суммарное сопротивление цепи будет точно больше сопротивления одного проводника.
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
$R = R_1 + R_2 + … + R_n$.
На схемах электрических цепей последовательное соединение нескольких проводников изображается так, как показано на рисунке 4.
Напряжение в цепи при последовательном соединении проводников
Используя закон Ома для участка цепи, мы можем найти напряжение и на концах этих участков:
$U_1 = IR_1$,
$U_2 = IR_2$,
…
$U_n = IR_n$.
Получается, что напряжение будет тем больше, чем больше сопротивление на участках цепи. Сила тока же везде будет одинакова.
Как найти напряжение участка цепи, состоящего из последовательно соединенных проводников, зная напряжение на каждом?
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
$U = U_1 + U_2 + … + U_n$.
Полное напряжение в цепи и закон сохранения энергии
Давайте вспомним, что напряжение определяется работой электрического тока. Эта работа совершается при прохождении по участку цепи электрического заряда, равного $1 space Кл$:
$U = frac{A}{q}$.
За счет чего совершается эта работа? Мы уже говорили, что электрическое поле обладает некоторой энергией. Именно за счет нее и идет совершение работы.
Такая работа совершается на каждом участке цепи, которую мы рассматриваем. Пользуясь законом сохранения энергии, мы можем сделать следующий вывод.
Энергия, израсходованная на всей цепи, равна сумме энергий, которые расходуются на отдельных ее участках (проводниках).
Пример задачи
Два проводника сопротивлением $R_1 = 2 space Ом$ и $R_2 = 3 space Ом$ соединены последовательно. Сила тока в цепи равна $1 space А$. Определите сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Так как проводники соединены последовательно, мы будем использовать формулы, полученные на данном уроке.
Дано:
$R_1 = 2 space Ом$
$R_2 = 3 space Ом$
$I = 1 space А$
$R — ?$
$U_1 — ?$
$U_2 — ?$
$U — ?$
Решение:
Общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников:
$R = R_1 + R_2$.
Рассчитаем его:
$R = 2 space Ом + 3 space Ом = 5 space Ом$.
Сила тока на всех участках цепи будет одинакова и равна $1 space А$.
Запишем закон Ома для участка цепи с первым проводником и выразим из него напряжение на концах первого проводника:
$I = frac{U_1}{R_1}$,
$U_1 = IR_1$.
Рассчитаем его:
$U_1 = 1 space А cdot 2 space Ом = 2 space В$.
Так же рассчитаем напряжение на концах второго проводника:
$I = frac{U_2}{R_2}$,
$U_2 = IR_2$,
$U_2 = 1 space А cdot 3 space Ом = 3 space В$.
При последовательном соединении проводников полное напряжение в цепи мы можем рассчитать двумя способами.
Способ №1
Напряжение на всей цепи равно сумме напряжений на концах проводников в этой цепи:
$U = U_1 + U_2$,
$U = 2 space В + 3 space В = 5 space В$.
Способ №2
Мы уже знаем общее сопротивление двух проводников. Получается, что эти два проводника мы можем представить как один целый. Используем закон Ома для участка цепи:
$I = frac{U}{R}$,
$U = IR$,
$U = 1 space А cdot 5 space Ом = 5 space В$.
Ответ: $R = 5 space Ом$, $U_1 = 2 space В$, $U_2 = 3 space В$, $U = 5 space В$.
Упражнения
Упражнение №1
Цепь состоит из двух последовательно соединённых проводников, сопротивление которых $4 space Ом$ и $6 space Ом$. Сила тока в цепи равна $0.2 space А$. Найдите напряжение на каждом из проводников и общее напряжение.
Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$
$I = 0.2 space А$
$U_1 — ?$
$U_2 — ?$
$U — ?$
Показать решение и ответ
Скрыть
Решение:
Используя закон Ома для участка цепи, мы рассчитаем значения напряжения на концах первого и второго проводников. Сила тока на всех участках цепи одинакова.
Напряжение на концах первого проводника:
$I = frac{U_1}{R_1}$,
$U_1 = IR_1$,
$U_1 = 0.2 space А cdot 4 space Ом = 0.8 space В$.
Напряжение на концах второго проводника:
$I = frac{U_2}{R_2}$,
$U_2 = IR_2$,
$U_2 = 0.2 space А cdot 6 space Ом = 1.2 space В$.
Общее напряжение будет равно сумме напряжений на концах каждого проводника:
$U = U_1 + U_2$,
$U = 0.8 space В + 1.2 space В = 2 space В$.
Ответ: $U_1 = 0.8 space В$, $U_2 = 1.2 space В$, $U = 2 space В$.
Упражнение №2
Для электропоездов применяют напряжение, равное $3000 space В$. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение $50 space В$ каждая?
Такие лампы можно соединить последовательно в одну цепь. Главное, чтобы их суммарное напряжение не превышало общее. Рассчитаем количество таких ламп, которое мы можем включить в цепь.
Дано:
$U = 3000 space В$
$U_1 = 50 space В$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Все лампы будут иметь одинаковое напряжение в $50 space В$. Напряжение на всей цепи равно сумме напряжений на каждой лампе. Тогда:
$n = frac{U}{U_1}$,
$n = frac{3000 space В}{50 space} = 60$.
Получается, что в таком электропоезде мы можем разместить 60 ламп для освещения вагонов, соединив их последовательно.
Ответ: при последовательном соединении мы можем использовать $n = 60$ ламп.
Упражнение №3
Две одинаковые лампы, рассчитанные на $220 space В$ каждая, соединены последовательно и включены в сеть с напряжением $220 space В$. Под каким напряжением будет находиться каждая лампа?
Дано:
$U = 220 space В$
$U_1 — ?$
$U_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Лампы соединены последовательно. Значит, $U = U_1 + U_2$.
Если лампы одинаковые, то они имеют одинаковые сопротивления $R$. Сила тока тоже одинакова в каждой лампе. Из этого мы можем сделать вывод, что напряжение на лампах будет одинаковым:
$U_1 = IR$, $U_2 = IR$, $U_1 = U_2$.
Тогда мы можем записать следующее:
$U = U_1 + U_2 = 2U_1$.
Рассчитаем напряжение на одной лампе:
$U_1 = U_2 = frac{U}{2}$,
$U_1 = U_2 = frac{220 space В}{2} = 110 space В$.
Ответ: $U_1 = U_2 = 110 space В$.
Упражнение №4
Электрическая цепь состоит из источника тока — батареи аккумуляторов, создающей в цепи напряжение, равное $6 space В$, лампочки от карманного фонаря с сопротивлением в $13.5 space Ом$, двух спиралей c сопротивлением $3 space Ом$ и $2 space Ом$, ключа и соединительных проводов. Все детали цепи соединены последовательно. Начертите схему цепи. Определите силу тока в цепи, напряжение на концах каждого из потребителей тока.
Схема такой цепи изображена на рисунке 5.
Дано:
$U = 6 space В$
$R_1 = 13.5 space Ом$
$R_2 = 3 space Ом$
$R_3 = 2 space Ом$
$I — ?$
$U_1 — ?$
$U_2 — ?$
$U_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем общее сопротивление на всей цепи:
$R = R_1 + R_2 + R_3$,
$R = 13.5 space Ом + 3 space Ом + 2 space Ом = 18.5 space Ом$.
Теперь используем закон Ома для того, чтобы рассчитать силу тока в цепи:
$I = frac{U}{R}$,
$I = frac{6 space В}{18.5 space Ом} approx 0.32 space А$.
Сила тока на каждом участке цепи при последовательном соединении элементов будет одинакова. Теперь мы будем использовать закон Ома отдельно для каждого проводника.
Рассчитаем напряжение на лампочке от карманного фонаря:
$U_1 = IR_1$,
$U_1 = 0.32 space А cdot 13.5 space Ом approx 4.3 space В$.
Рассчитаем напряжение на первой спирали:
$U_2 = IR_2$,
$U_2 = 0.32 space А cdot 3 space Ом approx 1 space В$.
Рассчитаем напряжение на второй спирали:
$U_3 = IR_3$,
$U_3 = 0.32 space А cdot 2 space Ом approx 0.6 space В$.
Ответ: $I approx 0.32 space А$, $U_1 approx 4.3 space В$, $U_2 approx 1 space В$, $U_3 approx 0.6 space В$.
Проводники и другие элементы цепи могут соединяться как параллельно, так и последовательно.
Последовательное соединение – соединение, при котором конец первого проводника соединяется с началом второго.
Параллельное соединение – соединение, при котором начало первого проводника соединяется с началом другого, а конец первого – с концом второго.
От способа соединения элементов зависит сила тока, напряжение и сопротивление отдельных участков цепи и всей цепи в целом. Эту зависимость отобразим в таблице на примере двух резисторов сопротивлениями R1 и R2.
Зависимость силы тока, напряжения и сопротивления от способа соединения
| Способ соединения резисторов | Последовательное | Параллельное |
| Схема |  |
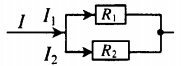 |
| Полная сила тока |
I=I1=I2 |
I=I1+I2 |
| Полное напряжение |
U=U1+U2 |
U=U1=U2 |
| Полное сопротивление |
R=R1+R2 |
1R=1R1+1R2 |
| Полное сопротивление с n одинаковыми резисторами |
R=nR0 |
R=R0n |
Пример №1. Чему равно сопротивление участка цепи, изображенного на рисунке?
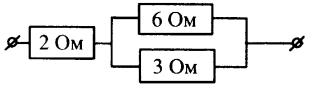
Участок цепи представляет собой последовательно соединенный резистор R1 = 2 Ом с параллельным участком, состоящим из двух резисторов R2 = 6 Ом и R3 = 3 Ом.
Сначала найдем сопротивление параллельно соединенных резисторов:
1R23=1R2+1R3
R23=R2R3R2+R3=6·36+3=2 (Ом)
Теперь нужно сложить это сопротивление с сопротивлением последовательно соединенного с ним первого резистора:
R=R1+R23=2+2=4 (Ом)
Алгоритм решения задач на расчет силы тока
Приведем алгоритм решения задач на расчет силы тока на примере конкретной задачи:
Через участок цепи (см. рисунок) течет постоянный ток I. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь.
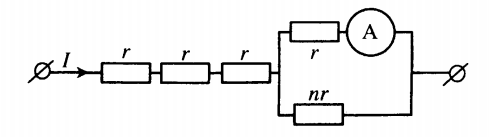
| Шаги | Действия |
| 1. Определите полное сопротивление параллельного участка цепи. |
1Rпар=1r+1nr=n+1nr |
| 2. Найдите напряжение на параллельном участке цепи. |
Uпар=Uверх+Uниж |
| 3. Вычислите силу тока на верхнем участке параллельного соединения. |
Iверх=Uпарr |
| 4. Определите силу тока на нижнем участке параллельного соединения. |
Iниж=Uпарnr |
| 5. Определите общую силу тока для параллельного участка цепи |
Iпар=Iверх+Iниж |
| 6. Определите общую силу тока для полного участка цепи. |
I=Iпар |
Пример №2. Через участок цепи (см. рисунок) течет постоянный ток I = 4 А. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь.
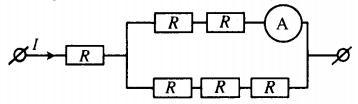
Так как первый резистор соединен с параллельным участком цепи последовательно, то сила тока параллельного участка тоже равна 4 А.
Iпар=I
Сила тока параллельного участка цепи равна сумме верхней и нижней силы тока:
Iпар=Iверх+Iниж
Так как это параллельный участок, верхнее и нижнее напряжения равны:
Uпар=Uверх+Uниж
Амперметр расположен в верхнем участке параллельного соединения. Следовательно, сила тока этого участка равна отношению напряжения параллельного участка цепи к суммарному сопротивлению верхней части параллельного участка:
Iверх=UпарR+R=Uпар2R
Если бы амперметр находился внизу, то он показал бы:
Iниж=UпарR+R+R=Uпар3R
Отсюда:
Uпар2R+Uпар3R=4
5Uпар6R=4
Uпар=24R5
Iверх=Uпар2R=24R5
12R=125=2,4 (А)
Задание EF17634
Участок цепи состоит из четырёх последовательно соединённых резисторов, сопротивления которых равны 10 Ом, 20 Ом, 30 Ом и 40 Ом. Каким должно быть сопротивление пятого резистора, добавленного в этот участок последовательно к первым четырём, чтобы суммарное сопротивление участка увеличилось в 3 раза?
Ответ:
а) 100 Ом
б) 200 Ом
в) 300 Ом
г) 400 Ом
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для определения полного сопротивления участка цепи при последовательном соединении.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Сопротивление первого резистора: R1 = 10 Ом.
• Сопротивление первого резистора: R2 = 20 Ом.
• Сопротивление первого резистора: R3 = 30 Ом.
• Сопротивление первого резистора: R4 = 40 Ом.
Чтобы суммарное сопротивление цепи увеличилось втрое, нужно добавить пятый резистор, сопротивление которого можно вычислить, решив следующую систему уравнений:
R1+R2+R3+R4+R5=3R
R1+R2+R3+R4=R
Вычислим суммарное сопротивление четырех резисторов R:
R=10+20+30+40=100 (Ом)
Следовательно:
R+R5=3R
R5=2R=100·2=200 (Ом)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17529
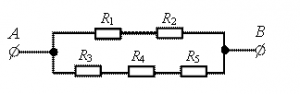 Сопротивление каждого резистора в схеме участка цепи на рисунке равно 100 Ом. При подключении участка к источнику постоянного напряжения 12 В выводами A и B напряжение на резисторе R2 равно
Сопротивление каждого резистора в схеме участка цепи на рисунке равно 100 Ом. При подключении участка к источнику постоянного напряжения 12 В выводами A и B напряжение на резисторе R2 равно
Ответ:
а) 2,4 В
б) 4 В
в) 6 В
г) 12 В
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Сопротивление каждого и резисторов: R1 = R2 = R3 = R4 = R5 = 100 Ом.
• Напряжение на всем участке цепи: U = 12 В.
Так как цепь состоит из двух параллельных цепочек, то напряжение на каждой из них одинаковое и равно 12 В. Но нас интересует напряжение только на втором резисторе в верхней цепочке, который соединен последовательно с первым резистором.
При последовательном соединении:
I1=I2=I
U1+U2=U
Применим для нашего случая:
I1=I2=I12
U1+U2=U12=U
Согласно закону Ома для участка цепи:
U=IR
Следовательно:
U1=I12R1=I12R
U2=I12R2=I12R
Отсюда:
U2=U1
Так как их сумма равна 12 В, то каждый из них равен 6 В. Следовательно, U2 = 6 В.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22543
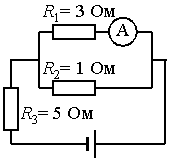 В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.
В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.
Ответ:
а) 23 В
б) 25 В
в) 27 В
г) 29 В
Алгоритм решения
1.Записать исходные данные.
2.Записать закон Ома для полной цепи.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Сила то на первом резисторе: I1 = 1 А.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сопротивление первого резистора: R1 = 3 Ом.
• Сопротивление первого резистора: R2 = 1 Ом.
• Сопротивление первого резистора: R3 = 5 Ом.
Закон Ома для полной цепи:
I=εR+r
R — полное сопротивление внешней цепи. Цепь состоит из последовательно соединенного третьего резистора с параллельным участком цепи, состоящим из первого и второго резисторов. Вычислим сопротивление параллельного участка цепи:
1R12=1R1+1R2
R12=R1R2R1+R2
Полное сопротивление внешней цепи равно:
R=R12+R3=R1R2R1+R2+R3
Следовательно, ЭДС источника тока равен:
ε=I(R+r)=I(R1R2R1+R2+R3+r)
Полная сила тока равна силе тока параллельного участка цепи, так как I = I3 = I12. А сила тока параллельного участка цепи равна сумме силы тока на первом и втором резисторе:
I12=I1+I2=I
Сначала найдем напряжение на первом резисторе, используя закон Ома для участка цепи:
U1=I1R1
Так как это параллельный участок, то:
U1=U2=U12
Следовательно, сила тока на втором резисторе равна:
I2=U2R2=I1R1R2
Сила тока на всем участке цепи равна:
I=I12=I1+I1R1R2=I1(1+R1R2)
Теперь можем вычислить ЭДС источника тока:
ε=I1(1+R1R2)(R1R2R1+R2+R3+r)
ε=1(1+31)(3·13+1+5+1)=6,75·4=27 (В)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.7k
