Математика
6 класс
Урок № 73
Бесконечные периодические десятичные дроби
Перечень рассматриваемых вопросов:
– понятие бесконечной периодической десятичной дроби;
– преобразование обыкновенных дробей в бесконечные периодические дроби;
– действия с периодическими дробями.
Тезаурус
Бесконечная периодическая десятичная дробь – это дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.
Любое рациональное число p/q можно разложить в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Обыкновенную дробь можно разложить в конечную десятичную, если в знаменателе нет простых множителей, кроме 2 и 5.
Вы уже знаете, как это сделать.
1. Умножить числитель и знаменатель на одно и то же число, чтобы привести к знаменателю 10, 100, 1000 и т. д.;
2. Выполнить деление числителя на знаменатель.
Пример 1. Умножили числитель и знаменатель на 2.
Пример 2. Сначала сократили дробь.
Пример 3. Выполнили деление 3 на 125.
Рассмотрим примеры, когда привести к знаменателю 10, 100 и т. д. нельзя. Возможно только деление числителя на знаменатель.

Заметим, что при делении получаются повторяющиеся остатки и, соответственно, повторяющиеся цифры в частном. Из-за этого процесс деления бесконечен. Отсюда происходит бесконечная десятичная дробь.
Рассмотрим другие примеры.
Повторяющиеся цифры 3; 27; 6 называют периодом дроби. Бесконечные десятичные дроби 0,333…; 0,2727…; 0,1666… называют периодическими.
Записывают так:
0,(3)
0,(27)
0,1(6)
Читают так:
«Нуль целых и три в периоде»
«Нуль целых и 27 в периоде»
«Нуль целых одна десятая и шесть в периоде»
Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби).
Отметим, что любое рациональное число p/q разлагается в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Замечание. При делении уголком десятичное разложение с периодом 9 не возникает.
Далее рассмотрим, как выполняются действия с периодическими дробями?
1. Сравните дроби
1/3 и 0,3
Запишем дробь 1/3 в виде бесконечной периодической дроби 0,333…
Запишем дробь 0,3 в следующем виде 0,300… Приписывая бесконечно много нулей, мы превращаем конечную дробь в равную ей бесконечную периодическую дробь с периодом 0.
Теперь можем сравнить: 0,333… > 0,300…
2. Разложите обыкновенную дробь в бесконечную периодическую десятичную дробь, округлите до десятых.
1/3 = 0,333… ≈ 0,3
5/9 = 0,555… ≈ 0,6
Разбор заданий тренировочного модуля
Задание 1
Представьте в виде периодической дроби. В ответе укажите её период.
период 6
период 4
период 18
период 6
Ответ: 6; 4; 18; 6.
Задание 2
Используя предыдущие задания, запишите периодическую дробь в виде обыкновенной дроби: 0,(3); 0,(5); 0,(6).
0,(3)
0,(5)
0,(6)
Ответ:
Задание 3 ⃰ (повышенного уровня сложности)
Задача: периодическую дробь 0,(1) записать в виде обыкновенной дроби.
Пусть х = 0,(1) = 0,111…
Умножим обе части на 10.
Получим
10 ∙ х = 1,111…
Найдём разность
10 ∙ х – х = 1,111… – 0,111…
Получим
9 ∙ х = 1
Значит,
Ответ:.
Периодические десятичные дроби
10 февраля 2012
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
Периодическая десятичная дробь — это любая десятичная дробь, у которой:
- Значащая часть состоит из бесконечного количества цифр;
- Через определенные интервалы цифры в значащей части повторяются.
Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
![]()
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
![]()
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
![]()
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
![]()
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
![]()
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:
- В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
- В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
- Сначала разделится целая часть, если она есть;
- Возможно, будет несколько чисел после десятичной точки;
- Через некоторое время цифры начнут повторяться.
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:
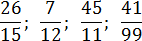
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
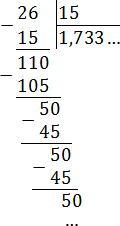
Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).
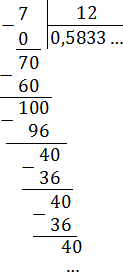
В итоге получается дробь: 0,5833 … = 0,58(3).
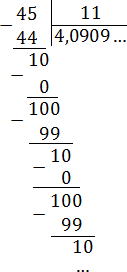
Записываем в нормальном виде: 4,0909 … = 4,(09).
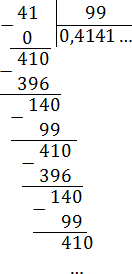
Получаем дробь: 0,4141 … = 0,(41).
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь X = abc(a1b1c1). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
- Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
- Найдите значение выражения X · 10k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
- Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
- В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.
Задача. Приведите к обыкновенной неправильной дроби числа:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Работаем с первой дробью: X = 9,(6) = 9,666 …
В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10k = 101 = 10. Имеем:
10X = 10 · 9,6666 … = 96,666 …
Вычитаем исходную дробь и решаем уравнение:
10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …
Период k = 2, поэтому умножаем все на 10k = 102 = 100:
100X = 100 · 32,393939 … = 3239,3939 …
Снова вычитаем исходную дробь и решаем уравнение:
100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10k = 101 = 10;
10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.
Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
k = 4 ⇒ 10k = 104 = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.
Смотрите также:
- Сравнение дробей

- Тест к уроку «Десятичные дроби» (2 вариант)

- Четырехугольная пирамида в задаче C2

- Как сдать ЕГЭ по математике

- Задача B5: площадь сектора

- Задача B4: тарифы на сотовую связь

Бесконечные периодические десятичные дроби – это дроби, у которых одна цифра или группа цифр повторяются.
Примеры: 0,66666666666666…; 0,33333333333333…; 0,68181818181818…
Повторяющаяся группа цифр называется периодом и записывается в скобках.
Примеры: 0,(6); 0,(3); 0,6(81).
Получить периодическую дробь можно тогда, когда при делении числителя на знаменатель получаются повторяющиеся остатки. Именно повторяющиеся остатки делают процесс деления бесконечным, что приводит к появлению бесконечной периодической дроби.
Пример 1. Разделить 1 на 3: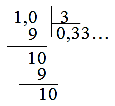 При делении мы постоянно получаем остаток 1, затем приписываем к нему 0 и делим 10 на 3. Эта операция повторяется снова и снова. В результате мы каждый раз получаем повторяющиеся остатки. Поэтому деление 1 на 3 будет выполняться бесконечно. В результате этого образуется бесконечная десятичная дробь.
При делении мы постоянно получаем остаток 1, затем приписываем к нему 0 и делим 10 на 3. Эта операция повторяется снова и снова. В результате мы каждый раз получаем повторяющиеся остатки. Поэтому деление 1 на 3 будет выполняться бесконечно. В результате этого образуется бесконечная десятичная дробь.
- Записывается. Обычно бесконечные периодические дроби записывают сокращенно: сначала записывают целую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
- Читается. Бесконечные периодические дроби читаются так: «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11:
При делении мы постоянно получаем остаток 5 или 6. Затем приписываем к остатку 0 и делим 50 или 60 на 11. В результате мы получаем повторяющиеся остатки, поэтому деление 5 на 11 будет выполняться бесконечно.
- Записывается: 0,(45).
- Читается: «ноль целых и сорок пять в периоде»
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смешанные.
- Чистые — дроби, у которых период начинается сразу после запятой.
Примеры: 0,(3); 0,(5); 0,(6). - Смешанные — дроби, у которых период начинается после некоторого количества не повторяющихся цифр.
Примеры: 0,52(3); 0,16(5); 0,31(6)
Чтобы записать периодическую дробь в виде десятичной дроби, нужно округлить эту дробь до нужного разряда. Как округлять, можно прочитать в статье «Правила округления чисел«
Примеры округления:
Округлить 0,(3) до сотых. Получаем 0,333333…≈ 0,33.
Округлить 6,31(6) до тысячных. Получаем 6,31666666… ≈ 6,317
Перевод периодической дроби в обыкновенную
✅ Для чистой периодической дроби
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно
➤ в числитель обыкновенной дроби записать период периодической дроби,
➤ в знаменатель обыкновенной дроби записать некоторое количество девяток, при этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
Пример 1: перевести 0,(3) в обыкновенную дробь.
В периодической дроби 0,(3) период состоит из одной цифры 3, поэтому в числителе записываем одну тройку, а в знаменателе — одну девятку. Полученную дробь можно сократить на 3, тогда получим обыкновенную дробь 1/3.
Пример 2. Перевести 0,(45) в обыкновенную дробь.
В периодической дроби 0,(45) период состоит из двух цифр, поэтому в числителе записываем 45, а в знаменателе — 99. Полученную дробь можно сократить на 9, тогда получим обыкновенную дробь 5/11.
✅ Для смешанной периодической дроби
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно
- в числителе записать разность:
- уменьшаемое — все цифры, стоящие после запятой, в том числе в периоде,
- вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
- в знаменателе записать некоторое количество девяток и нулей.
- количество девяток должно быть равно количеству цифр в периоде периодической дроби,
- количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Пример 3: перевести 0,31(6) в обыкновенную дробь.
➤ В числителе запишем разность разность:
уменьшаемое — все цифры, стоящие после запятой, включая и период = 316
вычитаемое — цифры, стоящие между запятой и периодом = 31
получаем числитель = (316-31).
➤ В знаменателе запишем некоторое количество девяток и нулей.
количество девяток равно количеству цифр в периоде периодической дроби 0,31(6) — одна девятка
количество нулей равно количеству цифр между запятой и периодом — два нуля.
получаем знаменатель = 900. Получили дробь, которую можно сократить.
|
316-31 900 |
= |
285 900 |
= |
285:15 900:15 |
= |
19 60 |
Пример 4. перевести 0,72(62) в обыкновенную дробь.
➤ В числителе: уменьшаемое = 7262, вычитаемое = 72, получаем числитель = (7262-72).
➤ В знаменателе: 2 цифры в периоде (99), две цифры между запятой и периодом (00), получаем 9900.
Получили дробь, которую можно сократить.
|
7262-72 9900 |
= |
7190 9900 |
= |
7190:10 9900:10 |
= |
719 990 |
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Бесконечные десятичные дроби
Десятичные дроби после запятой могут содержать бесконечное количество цифр.
Бесконечные десятичные дроби — это десятичные дроби, в записи которых находится бесконечное число цифр.
Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.
Пример 1
Например, $0,443340831dots ; 3,1415935432dots ; 135,126730405dots ; 4,33333333333dots ; 676,68349349dots$.
Рассмотрим последние две бесконечные десятичные дроби. В дроби $4,33333333333dots$ бесконечно повторяется цифра $3$, а в дроби $676,68349349dots$ с третьего знака после запятой повторяется группа цифр $3$, $4$ и $9$. Подобные бесконечные десятичные дроби называются периодическими.
Периодические десятичные дроби
Периодические десятичные дроби (или периодические дроби) — это бесконечные десятичные дроби, в записи которых с некоторого знака после запятой бесконечно повторяется какая-нибудь цифра или их группа, которая называется периодом дроби}.
Пример 2
Например, период периодической дроби $4,33333333333dots$ — цифра $3$, а период дроби $676,68349349dots$ — группа цифр $349$.
Для краткости записи бесконечных периодических десятичных дробей принято период записывать один раз, заключив его в круглые скобки. Например, периодическую дробь $4,33333333333dots$ записывают $4,(3)$, а периодическую дробь $676,68349349dots$ записывают $676,68(349)$.
Бесконечные десятичные периодические дроби получают при переводе обыкновенных дробей, знаменатели которых содержат простые множители, кроме $2$ и $5$, в десятичные дроби.
Любая конечная десятичная дробь (и целое число) может быть записана в виде периодической дроби, для чего достаточно справа дописать бесконечное количество цифр $0$.
«Периодические десятичные дроби» 👇
Пример 3
Например, конечная десятичная дробь $45,12$ может быть записана в виде периодической дроби как $45,12(0)$, а целое число $(74)$ в виде бесконечной периодической десятичной дроби будет иметь вид $74(0)$.
В случае периодических дробей, которые имеют период 9, используют переход к другой записи периодической дроби с периодом $0$. Только для этого период 9заменяют периодом $0$, при этом значение следующего по старшинству разряда увеличивается на $1$.
Пример 4
Например, периодическую дробь $7,45(9)$ можно заменить периодической дробью $7,46(0)$ или равной ей десятичной дробью $7,46$.
Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.
Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби
В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями $10, 100, dots$.
В некоторых случаях исходную обыкновенную дробь можно легко привести к знаменателю $10$, $100$ или $1 000$, после чего можно полученную дробь представить в виде десятичной дроби.
Пример 5
Чтобы дробь $frac{3}{5}$ }привести к дроби со знаменателем $10$, нужно числитель и знаменатель дроби умножить на $2$, после чего получим $frac{6}{10}$, которую не составит труда перевести в десятичную дробь $0,6$.
Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную}:
-
числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;
-
разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).
Пример 6
Перевести обыкновенную дробь $frac{621}{4}$ в десятичную дробь.
Решение.
Число $621$ в числителе представим в виде десятичной дроби. Для этого добавим десятичную запятую и для начала два нуля после нее. Далее при необходимости можно буде добавить нули еще. Итак, получили $621,00$.
Выполним деление числа $621,00$ на $4$ в столбик:
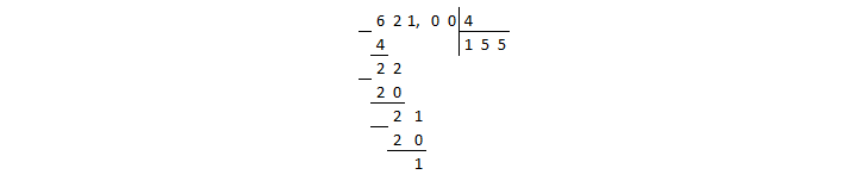
Рисунок 1.
Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:
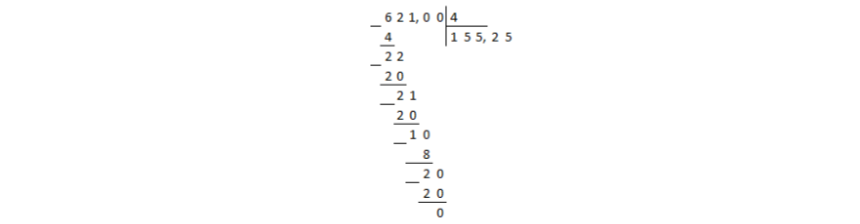
Рисунок 2.
В остатке получили нуль, значит деление окончено.
Ответ: $155,25$.
Возможен случай, когда при делении числителя и знаменателя обыкновенной дроби в остатке $0$ так и не получается. В этом случае деление можно продолжать бесконечно. Начиная с определенного момента остатки от деления периодически повторяются, а значит повторяются и цифры в частном. Из этого можно сделать вывод, что данная обыкновенная дробь переведется в бесконечную периодическую десятичную дробь.
Пример 7
Перевести обыкновенную дробь $frac{19}{44}$ в десятичную дробь.
Решение.}
Для перевода обыкновенной дроби в десятичную выполним деление в столбик:

Рисунок 3.
При делении повторяются остатки $8$ и $36$, а в частном также повторяются цифры $1$ и $8$. Итак, исходную обыкновенную дробь $frac{19}{44}$ перевели в периодическую дробь $frac{19}{44}=0,43181818dots =0,43(18)$.
Ответ: $0,43(18)$.
Общий вывод о переводе обыкновенных дробей в десятичные:
-
если знаменатель можно разложить на простые множители, среди которых будут присутствовать только числа $2$ и $5$, то такую дробь можно перевести в конечную десятичную дробь;
-
если кроме чисел $2$ и $5$ в разложении знаменателя присутствуют другие простые числа, то такая дробь переводится в бесконечную десятичную периодическую дробь.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Определение
Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же
последовательности, называется периодической десятичной дробью.
Например. $0,1234444444 ldots ; 12,453737373737 ldots$
Повторяющиеся цифры – период – для сокращения записи пишут в круглых скобках.
Например. $0,12344444444 ldots=0,123(4)$ ;
$12,453737373737 ldots=12,45(37)$
Определение
Чистой периодической дробью называется периодическая дробь, у которой период начинается сразу после запятой.
Например. $2,4949 ldots=2,(49)$
Определение
Смешанной периодической дробью называется такая десятичная дробь, у которой между запятой и
периодом есть не менее одной неповторяющейся бесконечное число раз цифры.
Например. $0,11232323 ldots=0,11(23)$ ;
$1,54444 . .=1,5(4)$
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период,
а в знаменателе записать столько девяток, сколько цифр в периоде.
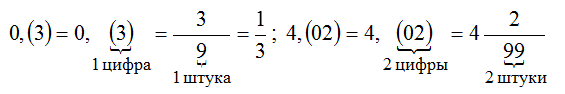
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго
периода вычесть число, стоящее до первого периода, результат записать в
числителе; в
знаменатель записать
число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между
запятой и периодом.
Например. Запишем дробь $2,34(2)$ в виде обыкновенной

Читать первую тему – понятие дроби и виды дробей,
раздела дроби.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
