Как найти полезную работу в термодинамике

Разность
работ расширения и сжатия называется
полезной работой цикла L_ц:

L_ц
= L_расш
– L_сж
.
(4.1)

Работа цикла в
координатах “p-υ
” изображается
площадью, описываемой круговым процессом
1-а-2-б-1.

Из приведенного
анализа цикла следует, что для получения
полезной работы в круговом процессе
необходимо иметь:

– горячий источник
(теплоотдатчик), отдающий рабочему телу
теплоту при его расширении;

– рабочее тело,
которое совершает работу при расширении;

– холодный источник
(холодильник), который воспринимает
теплоту от рабочего тела, при его сжатии
(рис. 4.1,в).

Связь между
теплотой, подведённой к рабочему телу
q₁
и отведённого от него q₂
и работой цикла L_ц
можно
установить, применив первый закон
термодинамики к процессам, составляющим
цикл:

– для процесса
расширения
q₁
= ΔU₁₂
+ L_расш;

– для процесса
сжатия –q₂
= –ΔU₂₁
– L_сж.

Суммируя эти
уравнения и учитывая, что ΔU₁₂
= –ΔU₂₁,
получим:

q₁
– |q₂|
= ‌‌ L_расш
– L_сж
= L_ц
. (4.2)

Таким образом,
полезная работа цикла пропорциональна
разности подведённой к рабочему телу
и отведённой от него теплоты. То есть
количество работы, совершённой
термодинамической системой за цикл,
должно равняться количеству теплоту
полученной системой в течение того же
цикла. Можно говорить, что в рассмотренном
круговом процессе произошло превращение
теплоты q_ц
= q₁
– |q₂|
в механическую работу L_ц.

q_ц
= L_ц
= q₁
– |q₂|
(4.3)

Рассмотренный
цикл совершается в тепловых двигателях,
а сам цикл называется термодинамическим
циклом или просто циклом тепловых
двигателей.

На рис. 4.2. изображена
схема, отображающая принципиальные
условия работы теплового двигателя:

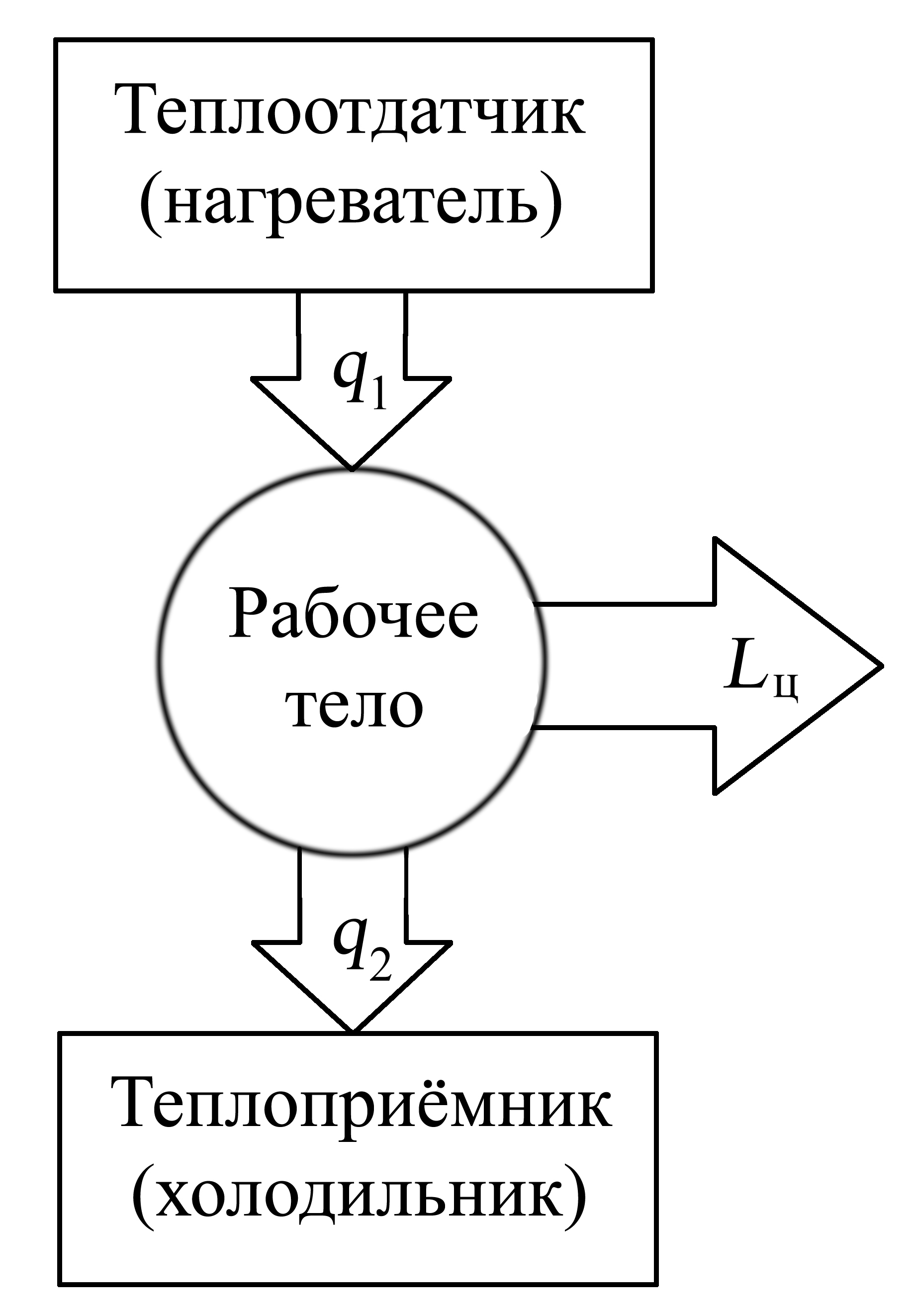
Рис. 4.2. Принципиальная
схема работы теплового двигателя

Термодинамическая
система, обеспечивающая циклическое
действие теплового двигателя в течение
необходимого достаточно продолжительного
времени, должна включать:

– рабочее тело (газ
или пар), получающее теплоту и переводящее
её в работу цикла L_ц;

– теплоотдатчик
(горячий источник тепла), сообщающий за
цикл каждой единице массы рабочего тела
теплоту q₁.

Теплоприемник
(холодный источник тепла), куда от единицы
массы рабочего тела отводится за цикл
теплота q₂.

Очевидно, что для
получения положительной работы цикла
должно быть q₁
> q₂.
Следовательно, в тепловом двигателе
только часть теплоты, получаемой от
теплоотдатчика (от горячего источника),
преобразуется в полезную работу.

А теплота q₂,
поступающая в теплообменник (холодильник),
утрачивает свою ценность как энергия,
которая может быть преобразована в
работу.

Степень преобразования
теплоты в работу в тепловом двигателе
оценивается термическим КПД.

Термическим
КПД цикла
η_t
называется отношение тепла, превращённого
в работу цикла, ко всему подведенному
за цикл теплу:

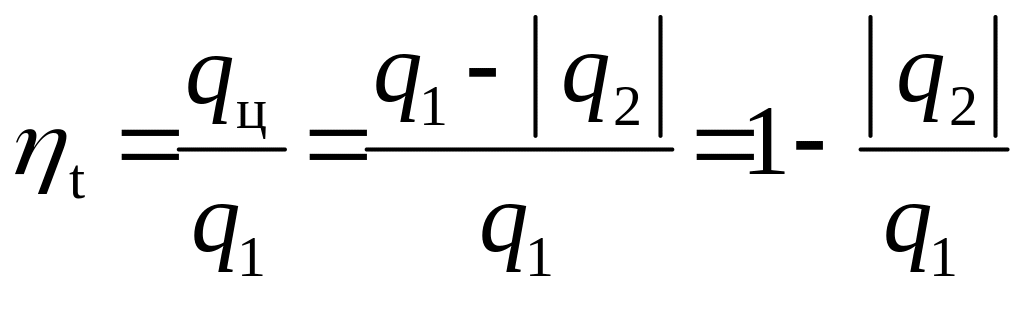
(4.4)

Термический
КПД цикла характеризует совершенство
цикла теплового двигателя с точки зрения
преобразования, в полезную работу
подведённого к рабочему телу тепла.

Значение КПД цикла
зависит от условий, в которых происходит
подвод и отвод теплоты, а также от
характера (типа) термодинамических
процессов, из которых составлен конкретный
цикл. При прочих равных условиях
наибольшее значение термического КПД
будет иметь такие циклы, в которых все
процессы являются равновесными
(обратимыми).

Цикл являются
обратимым, если он состоит только из
обратимых термодинамических процессов.
Если хотя бы один термодинамический
процесс в цикле является, необратимым,
цикл также будет необратимым. Процессы,
протекающие в реальных технических
устройствах, необратимы. Следовательно,
необратимы все циклы реализуемые в
тепловых машинах.

Согласно формуле
(4.4) для всех тепловых двигателей, в том
числе и идеальных всегда
η_t
< 1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вычисление полезной работы через КПД

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.

Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.

Aполез = Qнагревателя – Qхолодильника

Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.

Если всё это подставим в формулу для КПД, то получим

[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]

После подстановки численных значений будем иметь

η = (20 – 10)/20*100% = 50%

Теперь ясно, как определить полезную работу в физике термодинамической системы.

Формула полезной работы в физике электродинамической системы

Очень важный класс явлений. Каждый день все пользуются самыми разными электрическими устройствами: телевизором, компьютером, телефоном и т. д. Но мы рассмотрим случай попроще. Вычислим КПД электрического чайника. Допустим воде было передано 22176 Дж тепла за 2 мин. Напряжение в электросети стандартное 220 В. Сила тока равняется 1,4 А.

Решение:

Aполез будем считать работу, которая пошла на нагрев воды. Хотя она нам и дана из условия, формулу вспомнить всё равно не будет лишним.

• Q = cm(tконечная-tначальная)
• Q — количество теплоты [Дж]
• c — удельная теплоёмкость вещества [Дж/кг*˚C]
• m — масса [кг]
• tконечная — конечная температура [˚C]
• tначальная — начальная температура [˚C]
• Работа тока вычисляется по формуле
• A = (I^2)*Rt = (U^2)/R *t = UIt
• A — работа электрического тока [Дж]
• I — сила тока [А]
• U — напряжение [В]
• R — сопротивление [Ом]
• t — время [c]

В нашем примере она примет вид

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды и, подставляя численные значения, получаем

η = 22176/220*1,4*120 *100% = 60%

Формула полезной работы электродинамической системы будет:

КПД измеряется в процентах или указывается как десятичная дробь от 0 до 1. КПД 50% (или, что тоже самое– 0,5) означает, что только половина энергии используется для выполнения работы. Остальная рассеивается в окружающем пространстве, как правило, в форме тепла.

КПД в формулах обозначают греческой буквой $eta$ (эта).

$eta = frac{A_п}{A_з}$

, где $A_п$ – полезная работа, $A_з$ – затраченная.

Полезная работа и потери энергии

“Полезность” выполняемой работы – величина субъективная, связанная с человеческим восприятием, поэтому о КПД говорят чаще всего применительно к искусственно созданным системам. Несмотря на то, что технологии совершенствуются, избежать потерь в рукотворных системах инженерам не удастся:

• в механических устройствах часть затрачиваемой энергии всегда тратится на преодоление сил трения между соприкасающимися деталями (эти силы уменьшают за счет более тщательной обработки и смазки);
• в электрических системах часть энергии рассеивается в виде тепла при преодолении сопротивления проводников (явление сверхпроводимости еще не применимо к практике и требует низких температур);
• в нагревательных приборах утечки происходят в силу дефектов теплоизоляции и т.п.

Таким образом,

$A_з$ > $A_п$

, где $A_з$ – работа затраченная, $A_п$ – работа полезная.

«Формула полезной работы в физике для КПД» 👇

Потери энергии можно сводить к минимуму, но полностью исключить их невозможно. Какое бы совершенное устройство мы не придумали, КПД никогда не достигнет единицы в силу второго закона термодинамики, действие которого исключает создание механизмов с КПД равным или большим 100%.

КПД различных физических процессов

Методики подсчета КПД разнятся в зависимости от физической природы явлений, задействованных в преобразующих энергию системах.

При практических расчетах, связанных с движением, знаменатель формулы КПД удобнее представить не как работу (произведение силы на расстояние), а как затраченную энергию, выделившуюся, например, при сжигании топлива:

$eta = frac{A_п}{Q}$

, где $A_п$ — выполненная системой полезная работа, $Q$ — затраченная системой энергия.

Например, зная сколько бензина истрачено двигателем автомобиля (количество выделившегося в результате тепла можно легко подсчитать), а также массу, скорость и пройденное расстояние, легко найти КПД.

Если речь идет не об автомобиле с двигателем внутреннего сгорания, а об электромобиле, то затраты энергии в знаменателе можно подсчитать как произведение средних тока и напряжения за время движения рассматриваемого транспортного средства.

Поскольку мощность представляет собой работу, выполняемую в единицу времени, КПД иногда бывает удобно посчитать как соотношение входной и выходной мощностей системы:

$eta = frac{P_{out}}{P_{in}}$

, где $P_{in}$ – мощность на входе системы, $P_{out}$ – на выходе.

Такой подход удобен, например, при расчете КПД солнечных батарей. В знаменателе в этом случае будет мощность светового излучения, падающего на их поверхность, в числителе – мощность генерируемого тока.

Работа в термодинамике

В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.

Рассмотрим работу газа при изобарическом расширении.

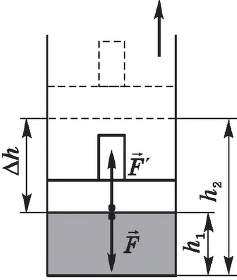
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:

$A’=F’∆h=pS∆h=p∆V$

Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.

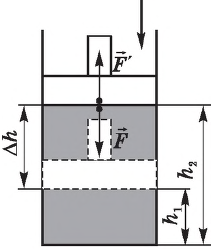
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:

$A=-A’=-p∆V$

Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.

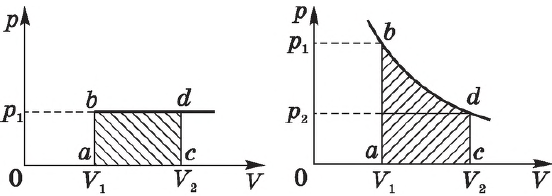
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.

Первый закон термодинамики

Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.

Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).

Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.

Первый закон термодинамики формулируется так:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

$∆U=A+Q$

где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.

Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.

При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.

Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:

$Q=∆U+A’$

где $А’$ — работа, совершаемая системой ($А’=-А$).

Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.

Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.

Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.

Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.

Применение первого закона термодинамики к различным процессам

Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.

Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.

Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.

Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.

При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,

$∆U=Q$

т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.

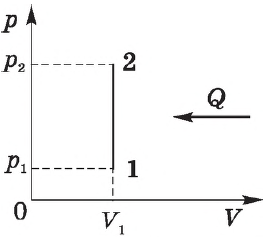
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.

Изотермический процесс графически изображается изотермой.

Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.

Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:

$Q=A’$

При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.

Изобарный процесс на термодинамической диаграмме изображается изобарой.

Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.

Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.

При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:

$Q=∆U+A’$

Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).

Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.

Адиабатический процесс

Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).

Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.

Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе

$∆U=A$

где $А$ — работа внешних сил.

При адиабатном расширении газа $А < 0$.

Следовательно,

$∆U={i}/{2}·{m}/{M}R∆T < 0,$

что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.

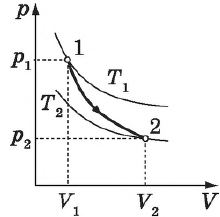
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.

Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).

Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.

Принцип действия тепловых двигателей

Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.

Таким образом, основными элементами любого теплового двигателя являются:

1. рабочее тело (газ или пар), совершающее работу;
2. нагреватель, сообщающий энергию рабочему телу;
3. холодильник, поглощающий часть энергии от рабочего тела.

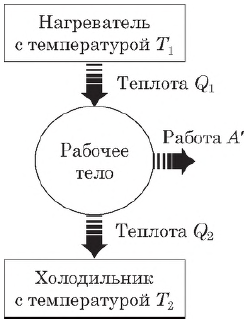
Коэффициент полезного действия теплового двигателя

Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:

$A’=|Q_1|-|Q_2|$

где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.

Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:

$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$

Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.

КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 – T_2=0$ двигатель не может работать.

Цикл Карно

Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.

Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».

Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.

Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.

Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.

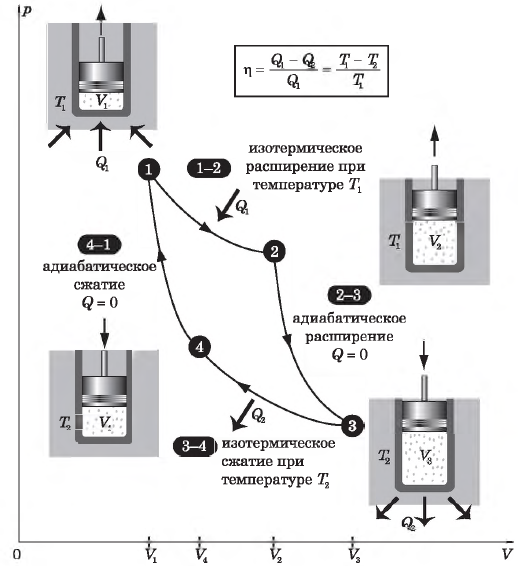
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:

$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:

$A_{23}=-∆U_{23}$

Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:

$A_{34}=Q_2,$

Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.

Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:

$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$

Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.

В термодинамике, работа, выполняемая системой, – это энергия переносится системой в свое окружение с помощью механизма, с помощью которого система может спонтанно воздействовать макроскопическими силами на свое окружение, где эти силы и их внешние воздействия могут быть измерены. В окружающей среде, через подходящие пассивные связи, вся работа, выполняемая такими силами, может поднять вес. Кроме того, именно через такие механизмы энергия может передаваться из окружающей среды в систему; в знаковом соглашении, используемом в физике (хотя в химии используется противоположное знаковое соглашение), такая передача энергии считается отрицательным объемом работы, выполняемой системой над своим окружением.

Внешне измеряемые силы и внешние воздействия могут быть электромагнитными, гравитационными, давлением / объемом или другими макроскопически механическими переменными. Для термодинамической работы эти измеряемые извне величины точно соответствуют значениям или вкладам в изменения макроскопических внутренних переменных состояния системы, которые всегда происходят в сопряженных парах, например, давление и объем или плотность магнитного потока и намагничивание.

Внешняя система, которая находится в окружении, не обязательно термодинамическая система, как строго определено обычными переменными термодинамического состояния, иначе, чем перенос вещества, можно сказать, что работа выполняется над термодинамическим система. Часть такой работы, определяемой окружением, может иметь такой же механизм, как и определенная системой термодинамическая работа, выполняемая системой, в то время как остальная часть такой определяемой окружающей средой работы представляется термодинамической системе, а не как отрицательный объем термодинамической работы, выполняемой системой. это, а, скорее, как передаваемое ему тепло. Эксперименты Джоуля с лопастным перемешиванием предоставляют пример, иллюстрирующий концепцию изохорной (или постоянного объема) механической работы, в этом случае иногда называемой работой вала. Такая работа не является термодинамической работой, как определено здесь, потому что она действует через трение внутри и на поверхности термодинамической системы и не действует через макроскопические силы, которые система может спонтанно оказывать на свое окружение, описываемые ее переменными состояния.. Работа, определяемая окружением, также может быть немеханической. Примером может служить Джоулев нагрев, потому что он происходит за счет трения, когда электрический ток проходит через термодинамическую систему. Когда это делается изохорически и независимо от того, переносится ли вещество, такая передача энергии рассматривается как передача тепла в интересующую систему.

Термодинамическая работа – это специализированная версия концепции работы по физике. В системе измерения SI работа измеряется в джоулях (символ: J). Скорость выполнения работы: мощность.

Содержание

• 1 История
  • 1,1 1824
  • 1,2 1845
• 2 Обзор
  • 2.1 Сохранение энергии
  • 2.2 Почти обратимая передача энергии за счет работы в окружающей среде
  • 2.3 Работа, выполняемая простой термодинамической системой и над ней
  • 2.4 Процессы, не описываемые макроскопической работой
  • 2.5 Открытые системы
  • 2.6 Вымышленные обратимые термодинамические «процессы»
  • 2.7 Джоулевое нагревание и трение
• 3 Формальное определение
• 4 Условные обозначения
• 5 Работа давление – объем
  • 5.1 Зависимость от траектории
• 6 Другие механические виды работы
  • 6.1 Вращательная работа
  • 6.2 Работа пружины
  • 6.3 Работа, выполняемая с упругими сплошными стержнями
  • 6.4 Работа, связанная с растяжением жидкой пленки
• 7 Свободная энергия и эксергия
• 8 Немеханические формы работы
• 9 Гравитационная работа
• 10 См. Также
• 11 Источники

История

1824

Работа, то есть «вес, поднимаемый через высоту», был первоначально определен в 1824 году Сади Карно в его знаменитом па согласно Размышления о движущей силе огня, где он использовал термин движущая сила для работы. В частности, согласно Карно:

Мы используем здесь движущую силу, чтобы выразить полезный эффект, который двигатель способен производить. Этот эффект всегда можно сравнить с подъемом веса на определенную высоту. Как мы знаем, он имеет в качестве меры произведение веса, умноженное на высоту, на которую он поднимается.

1845

Аппарат Джоуля для измерения механического эквивалента тепла

В 1845 году, английский физик Джеймс Джоул написал статью «О механическом эквиваленте тепла» для собрания Британской ассоциации в Кембридже. В этой статье он сообщил о своем самом известном эксперименте, в котором механическая сила, высвобождаемая в результате действия «веса, падающего с высоты», использовалась для поворота гребного колеса в изолированной бочке с водой.

В этом эксперименте движение лопастного колеса посредством перемешивания и трения, нагревает водный объект, так что его температура. Регистрировались как изменение температуры ∆T воды, так и высота падения ∆h груза mg. Используя эти значения, Джоуль смог определить механический эквивалент тепла. Джоуль оценил механический эквивалент тепла в 819 фут-фунт-сила / БТЕ (4,41 Дж / кал). Современные определения тепла, работы, температуры и энергии имеют отношение к этому эксперименту. При такой компоновке устройства никогда не происходит обратного процесса, когда вода приводит в движение лопасти, чтобы поднять вес даже немного. Механическая работа выполнялась аппаратом падающего груза, шкивом и лопастями, которые лежали в воде. Их движение почти не повлияло на объем воды. Работа, которая не изменяет объем воды, называется изохорной; это необратимо. Энергия, полученная при падении груза, передавалась в воду в виде тепла.

Обзор

Сохранение энергии

Предполагаемый руководящий принцип термодинамики – это сохранение энергии. Полная энергия системы – это сумма ее внутренней энергии, ее потенциальной энергии как целой системы во внешнем силовом поле, такого как гравитация, и ее кинетической энергии как всей движущейся системы. Термодинамика уделяет особое внимание передаче энергии от материального тела, такого как, например, паровой цилиндр, к окружающей среде с помощью механизмов, посредством которых тело оказывает макроскопические силы на свое окружение, чтобы поднять груз. там; такие механизмы, как говорят, опосредуют термодинамическую работу.

Помимо передачи энергии в виде работы, термодинамика допускает передачу энергии в виде тепла. Для процесса в замкнутой (без переноса вещества) термодинамической системе первый закон термодинамики связывает изменения внутренней энергии (или другого Кардинальная энергетическая функция, зависящая от условий передачи) системы на те два режима передачи энергии, как работа и как тепло. Адиабатическая работа совершается без переноса вещества и без теплопередачи. В принципе, в термодинамике для процесса в замкнутой системе количество переданного тепла определяется величиной адиабатической работы, которая потребуется, чтобы вызвать изменение в системе, вызванное теплопередачей. В экспериментальной практике теплопередачу часто оценивают калориметрически путем изменения температуры известного количества калориметрического материального вещества.

Энергия также может передаваться в систему или из системы посредством передачи материи. Возможность такой передачи определяет систему как открытую, в отличие от закрытой. По определению, такая передача не является ни работой, ни теплом.

Изменения потенциальной энергии тела в целом по отношению к силам в его окружении и кинетической энергии тела, движущегося в целом по отношению к его окружению, по определению исключаются из кардинальная энергия (примеры – внутренняя энергия и энтальпия).

Практически обратимая передача энергии при работе в окружающей среде

В окружающей термодинамической системе, внешней по отношению к ней, все различные механические и немеханические макроскопические формы работы могут быть преобразованы в друг друга без принципиальных ограничений в соответствии с законами термодинамики, так что эффективность преобразования энергии в некоторых случаях может приближаться к 100%; такое преобразование должно происходить без трения и, следовательно, адиабатическим. В частности, в принципе, все макроскопические формы работы могут быть преобразованы в механическую работу по поднятию тяжести, которая была исходной формой термодинамической работы, рассмотренной Карно и Джоулем (см. Раздел «История» выше). Некоторые авторы считали эту эквивалентность поднятию тяжести определяющей характеристикой работы. Например, с устройством эксперимента Джоуля, в котором через шкивы груз, опускающийся в окружающей среде, приводит в движение перемешивание термодинамической системы, спуск груза может быть отклонен путем изменения расположения шкивов, так что он поднимает другой вес в окружающей среде, вместо перемешивания термодинамической системы.

Такое преобразование можно идеализировать как почти без трения, хотя оно происходит относительно быстро. Обычно это происходит с помощью устройств, которые не являются простыми термодинамическими системами (простая термодинамическая система представляет собой однородное тело материальных веществ). Например, снижение веса в эксперименте с перемешиванием Джоуля снижает общую энергию груза. Он описывается как потеря гравитационной потенциальной энергии грузом из-за изменения его макроскопического положения в гравитационном поле, в отличие, например, от потери внутренней энергии груза из-за изменений его энтропии, объема и химического состава.. Хотя это происходит относительно быстро, поскольку энергия остается почти полностью доступной для работы в той или иной форме, такое отвлечение от работы в окружающей среде можно идеализировать как почти обратимое или почти совершенно эффективное.

Напротив, преобразование тепла в работу в тепловом двигателе никогда не может превышать КПД Карно, как следствие второго закона термодинамики.. Такое преобразование энергии за счет относительно быстрой работы, выполняемой в практическом тепловом двигателе термодинамической системой в его окружении, не может быть идеализировано, даже близко, как обратимое.

Термодинамическая работа, выполняемая термодинамической системой в ее окружении, определяется таким образом, чтобы соответствовать этому принципу. Исторически термодинамика заключалась в том, как термодинамическая система может воздействовать на свое окружение.

Работа, выполняемая простой термодинамической системой и над ней

Работа, выполняемая и выполняемая термодинамической системой, должна различаться посредством рассмотрения их точных механизмов. Работа, выполняемая в термодинамической системе устройствами или системами в окружающей среде, выполняется такими действиями, как сжатие, и включает работу вала, перемешивание и трение. Такая работа, совершаемая за счет сжатия, является термодинамической работой, как здесь определено. Но работа на валу, перемешивание и трение не являются термодинамическими, как здесь определено, в том смысле, что они не изменяют объем системы по сравнению с ее сопротивляющимся давлением. Работа без изменения объема известна как изохорная работа, например, когда какой-либо агент в окружении системы вызывает фрикционное действие на поверхности или внутри системы.

В процессе передачи энергии от термодинамической системы или к ней, изменение внутренней энергии системы теоретически определяется количеством адиабатической работы, которая была бы необходима для достижения конечного результата от первоначального Состояние, при этом такая адиабатическая работа может быть измерена только с помощью измеряемых извне механических переменных или переменных деформации системы, которые предоставляют полную информацию о силах, действующих на систему со стороны окружающей среды в процессе. В случае некоторых измерений Джоуля процесс был устроен так, что некоторый нагрев, происходивший вне системы (в веществе лопастей) в результате трения, также приводил к передаче тепла от лопастей в систему во время процесса, поэтому что количество работы, выполняемой окружающими элементами в системе, можно рассчитать как работу вала, внешнюю механическую переменную.

Количество энергии, передаваемой в качестве работы, измеряется посредством величин, определяемых извне для интересующей системы, и таким образом принадлежащий своему окружению. В важном знаковом соглашении, предпочитаемом в химии, работа, добавляющая к внутренней энергии системы, считается положительной. С другой стороны, по историческим причинам, часто встречающееся знаковое соглашение, предпочтительное в физике, состоит в том, чтобы рассматривать работу, выполняемую системой над ее окружением, как положительную.

Процессы, не описываемые макроскопической работой

Одним из видов теплопередачи через прямой контакт между замкнутой системой и ее окружением являются микроскопические тепловые движения частиц и связанный с ними межмолекулярный потенциал энергии. Микроскопическое описание таких процессов является делом статистической механики, а не макроскопической термодинамики. Другой вид передачи тепла – излучение. Излучательный перенос энергии необратим в том смысле, что он происходит только от более горячей системы к более холодной, и никогда наоборот. Существует несколько форм диссипативной трансдукции энергии, которые могут происходить внутри системы на микроскопическом уровне, например, трение, включая объемную и сдвиговую вязкость химическую реакцию, неограниченное расширение, как в Джоулевом расширении и в диффузии и фазовом переходе.

Термодинамическая работа не учитывает какую-либо энергию, передаваемую между системами в виде тепла или путем передачи материи.

Открытые системы

Для открытой системы первый закон термодинамики допускает три формы передачи энергии: работа, тепло и энергия, связанная с переносимой материей. Последние нельзя однозначно разделить на тепловую и рабочую составляющие.

Односторонняя конвекция внутренней энергии является формой переноса энергии, но не является, как иногда ошибочно предполагают (пережиток теории калорий тепла), передача энергии в виде тепла, потому что односторонняя конвекция – это перенос вещества; и это не передача энергии как работа. Тем не менее, если стена между системой и ее окружением толстая и содержит жидкость, в присутствии гравитационного поля конвективную циркуляцию внутри стены можно рассматривать как косвенно опосредованную передачу энергии в виде тепла между системой и ее окружением, хотя источник и назначение передаваемой энергии не находятся в прямом контакте.

Вымышленные обратимые термодинамические «процессы»

Для целей теоретических расчетов термодинамической системы можно представить фиктивные идеализированные термодинамические «процессы», которые происходят так медленно, что не вызывают трения внутри или на поверхности системы; тогда их можно рассматривать как практически обратимые. Эти фиктивные процессы протекают по траекториям на геометрических поверхностях, которые точно описываются характеристическим уравнением термодинамической системы. Эти геометрические поверхности являются локусами возможных состояний термодинамического равновесия для системы. Действительно возможные термодинамические процессы, происходящие с практической скоростью, даже если они происходят только в результате работы, оцениваемой в окружающей среде как адиабатическая, без теплопередачи, всегда вызывают трение внутри системы и поэтому всегда необратимы. Пути таких реально возможных процессов всегда отходят от этих геометрических характерных поверхностей. Даже когда они возникают только в результате работы, которая оценивается в окружающей среде как адиабатическая, без передачи тепла, такие отклонения всегда влекут за собой производство энтропии.

Джоулева нагревание и трение

Определение термодинамической работы выражается в изменениях переменных состояния обширной деформации системы (и химических составляющих и некоторых других), таких как объем, молярный химический состав, или электрическая поляризация. Примерами переменных состояния, которые не являются обширной деформацией или другими подобными переменными, являются температура T и энтропия S, как, например, в выражении U = U (S, V, {N j }). Изменения таких переменных фактически невозможно физически измерить с помощью единственного простого адиабатического термодинамического процесса; это процессы, которые не происходят ни за счет термодинамической работы, ни за счет переноса вещества, и поэтому говорят, что они происходят за счет передачи тепла. Количество термодинамической работы определяется как работа, выполняемая системой над ее окружением. Согласно второму началу термодинамики такая работа необратима. Чтобы получить фактическое и точное физическое измерение количества термодинамической работы, необходимо принять во внимание необратимость, вернув систему к ее начальному состоянию, запустив цикл, например цикл Карно, который включает целевую работу в качестве шаг. Работа, выполняемая системой с окружающей средой, рассчитывается на основе величин, составляющих весь цикл. Для фактического измерения работы, выполняемой окружением в системе, потребуется другой цикл. Это напоминание о том, что трение о поверхность системы кажется действующим в окружающей среде натирающим средством как механическая, хотя и не термодинамическая работа, выполняемая с системой, а не как тепло, а воспринимается системой как тепло, передаваемое системе, а не как термодинамическая работа. Выработка тепла при трении необратима; исторически это было свидетельством отказа от калорийной теории тепла как сохраняемого вещества. Необратимый процесс, известный как Джоулев нагрев, также происходит за счет изменения переменной экстенсивного состояния, не связанной с деформацией.

Соответственно, по мнению Лавенды, работа – не такое примитивное понятие, как тепло, которое можно измерить калориметрическим методом. Это мнение не отменяет теперь обычного термодинамического определения тепла в терминах адиабатической работы.

Известная как термодинамическая операция, инициирующий фактор термодинамического процесса во многих случаях представляет собой изменение проницаемости стенки между системой и окружающей средой. Трение – это не изменение проницаемости стены. В заявлении Кельвина о втором законе термодинамики используется понятие «неодушевленный материальный фактор»; это понятие иногда считают загадочным. Запуск процесса трения может происходить только в окружающей среде, но не в термодинамической системе в ее собственном состоянии внутреннего термодинамического равновесия. Такой запуск можно описать как термодинамическую операцию.

Формальное определение

В термодинамике количество работы, выполняемой замкнутой системой в ее окружении, определяется факторами, строго ограниченными взаимодействием окружения с системой и окружением окружающей среды. система, например, расширенное гравитационное поле, в котором находится система, то есть по отношению к вещам, внешним по отношению к системе.

Главная проблема термодинамики – свойства материалов. Термодинамическая работа определяется для целей термодинамических расчетов материальных тел, известных как термодинамические системы. Следовательно, термодинамическая работа определяется в терминахвеличин, которые описывают состояния материалов, которые появляются как обычные переменные термодинамического состояния, такие как объем, давление, температура, химический состав и электрическая поляризация. Например, чтобы измерить давление внутри системы извне, которая может перемещаться на измеритель в ответ на разницу давления между внутренней системой и окружающей средой. В этом смысле определения термодинамической системы является ограничивающей ее стенок.

Особенно важны несколько видов термодинамической работы. Один простой пример – работа давления и объема. Обеспокоенность вызывает давление, оказываемое окружением на поверхность системы, а интересующий объем отрицательным приращением объема, полученного системой из окружения. Обычно предусмотрено, что давление, оказываемое окружающей средой на поверхности, четко определено и равно дав, оказываемую систему на основе окружающей среды. Это устройство для передачи энергии в виде работы может изменяться особым образом, что зависит от строго механической природы работы давление-объем. Вариант состоит в том, что связь между системой и окружающей средой осуществляется посредством жесткого стержня, который связывает поршни различные области для системы и окружающей среды. Затем для заданного количества переданной работы обмен объемами включает различные давления, обратно пропорциональные площадям поршня, для механического равновесия. Это не может быть выполнено для передачи энергии в виде тепла из-за его немеханической природы.

Другой важный вид работы – это изохорная работа, то есть работа, которая не предполагает общего общего изменения системы между начальным и конечным состоянием процесса. Примерами являются трение о поверхности системы, как в эксперименте Рамфорда; работа вала, такая как в экспериментах Джоуля; перемешивание системы магнитной лопастью внутри нее, управляемый движущимся магнитным полем из окружающей среды; и вибрационное воздействие на систему, которое оставляет ее конечный объем неизменным, но включает трение внутри системы. Изохорическая механическая работа для тела в его собственном состоянии внутреннего термодинамического равновесия выполняется только окружающей средой на теле, а не телом в окружающей среде, так что знак изохорной механической работы с физическим соглашением о знаках всегда отрицательный.

Когда работа, например работа давления и объема, выполняется в окружающей среде замкнутой системой, потому что она ограничена адиабатической стенкой, эта работа называется адиабатической для системы, а также для окружающей среды. Когда механическая работа выполняется в такой адиабатически замкнутой среде окружающей среды, может случиться так, например, в эксперименте Джоуля с лопастями, приводящими в движение падающий груз, которые перемешивают систему. Такая работа является адиабатической для окружающей среды, даже если она занимается с трением внутри системы. Такая работа может быть или не быть изохорной для системы, в зависимости от системы и ее ограничивающих стенок. Если он оказывается изохорным для системы (и в конечном итоге не изменяет другие переменные состояния системы, такие как намагниченность), это проявляется как передача тепла системе и не кажется адиабатической для системы.

Знаковое соглашение

В ранней истории термодинамики положительный объем работы, выполняемой системой с окружающей средой, приводит к потере энергии системой. Это историческое соглашение о знаках использовалось во многих учебниках физики и используется в настоящей статье.

Согласно первому закону термодинамики для замкнутой системы, любое чистое изменение внутренней энергии U должно быть полностью учтено., по теплу Q, поступающему в систему, и работе W, совершенной системой:

Δ U = Q – W. { displaystyle Delta U = QW. ;}

Альтернативное соглашение о знаках – рассматривать работу, выполняемую в системе ее окружением, как положительную. Это приводит к изменению знака работы, так что Δ U = Q + W { displaystyle Delta U = Q + W ,}. Это соглашение исторически использовалось в химии, но было принято в нескольких современных учебниках физики.

Это уравнение отражает тот факт, что передаваемое тепло и проделанная работа не сохраняет свойства системы. Учитывая только начальное и конечное состояние системы, можно сказать только то, каково было изменение внутренней энергии, а не сколько энергии ушло в виде тепла, а сколько в виде работы. Резюмируя это, можно сказать, что тепло и работа не являются функциями состояния системы. Это контрастирует с классической механикой, где сетевая работа, создаваемая частицей, является функцией состояния.

Работа «давление – объем»

Работа «давление – объем» (или работа PV) происходит, когда объем V системы изменяется. Работа PV часто измеряется в единицах литр-атмосфера, где 1 л · атм = 101,325 Дж. В системе единиц СИ, которая измеряет P в Паскалях (Па), V в м и PV в Джоулях (Дж), литр-атмосфера не является признанной единицей в системе единиц., где 1 Дж = 1 Па · м. Фотоэлектрические работы – важная тема в химической термодинамике.

. Для процесса в закрытой системе протекающего достаточно медленно для точного определения давления на внутренней стороне стенки системы, которая движется и передает силу. в среде, описываемой как квазистатическая, работа представлена ​​следующим уравнением между дифференциалами :

δ W = P d V { displaystyle delta W = PdV ,}

где

δ W { displaystyle delta W}обозначает бесконечно малое приращение работы, выполняемой системой, по передаче энергии в окружающей среде;

P { displaystyle P}обозначает давление внутри системы, которое она оказывает на движущуюся стену, которая передает силу окружающим. В альтернативном соглашении о знаках правая часть имеет отрицательный знак.

d V { displaystyle dV}обозначает бесконечно малое приращение объема системы.

Кроме того,

W = ∫ V i V f P d V. { displaystyle W = int _ {V_ {i}} ^ {V_ {f}} P , dV.}

, где

W { displaystyle W}обозначает проделанную работу системой в течение всего обратимого процесса.

Первый закон термодинамики может быть выражен как

d U = δ Q – P d V. { displaystyle dU = delta Q-PdV ,.}

(В альтернативном соглашении о знаках, где W = работа, выполненная в системе, δ W = – P d V { displaystyle delta W = – PdV ,}. Однако d U = δ Q – P d V { displaystyle dU = delta Q-PdV ,}без изменений.)

Зависимость от пути

Работа PV является зависимой от пути и, следовательно, является термодинамической функцией процесса. В общем, член P dV не является точным дифференциалом. Утверждение, что процесс обратим и адиабатичен, дает инструкцию по процессу, но не определяет несколько однозначно, потому что путь может быть включен в себя медленных движений назад и вперед по объему, пока нет передачи энергии как тепла. первый закон термодинамики утверждает, что d U = δ Q – δ W { displaystyle dU = delta Q- delta W}. Для адиабатического процесса δ Q = 0 { displaystyle delta Q = 0}, и, таким образом, общий объем проделанной работы равен минус изменению внутренней энергии. Для обратного адиабатического процесса интегральный объем работы, выполняемой в ходе процесса, зависит только от начального и конечного состояния процесса и является одним и тем же для каждого промежуточного пути.

Если бы процесс пошел по пути, отличному от адиабатического, работа была бы другой. Это было бы возможно только в том случае, если бы тепло поступало в / из системы. В неадиабатическом процессе существует бесконечно много путей между начальным и конечным состояниями.

В текущих математических обозначениях дифференциал δ W { displaystyle delta W}является неточным дифференциалом.

В других обозначениях δW записывается как đW (с линией через d). Это обозначение означает, что đW не является точной однократной формой. Линия является просто флагом, предупреждающим нас, что на самом деле нет функции (0-форма ) W, которая является потенциалом đW. Если бы эта функция W действительно существовала, мы могли просто использовать теорему Стокса для оценки этой предполагаемой функции, дополнительной функции đW, на границе пути, которая есть начальная и конечная точка, и поэтому работа будет функция состояния. Такая невозможность согласуется с тем, что не смысла ссылаться на работу над точкой на PV диаграмме; работа предполагает путь.

Другие виды механической работы

Есть несколько способов выполнения механической работы, из которых так или иначе связан с каждой силой, действующей на расстоянии. В данной механике работа, совершенная постоянная сила F над телом, перемещается на постоянную силу в направлении силы, определяется выражением

W = F s { displaystyle W = Fs ,}

Если сила не является постоянной величиной, выполненная работа получается интегрированным способом измерения объема работы,

W = ∫ 1 2 F ds. { displaystyle W = int _ {1} ^ {2} F , ds.}

Вращательная работа

Передача энергии с помощью вращающегося вала очень распространена в инженерной практике. Часто крутящий момент T, приложенный к валу, является постоянным, что означает, что приложенная сила F постоянна. Для заданного постоянного крутящего момента работа, выполняемая за n оборотов, создается следующим образом: сила F, действующая через плечо r, создающий момент T

T = F r { displaystyle T = Fr ,}→F = T r { displaystyle F = { frac {T} {r}}}

Эта сила действует на расстоянии s, которое связано с используемом r управлением

s = 2 (r π n) { displaystyle s = 2 left (r pi n right)}

Затем работа вала определяется по формуле:

W s = F s = 2 π n T { displaystyle W_ {s} = Fs = 2 pi nT}

Мощность, передаваемая через вал, – это работа вала, совершаемая за единицу времени, которая выражается как

Вт ˙ s = 2 π T n ˙ { displaystyle { dot {W}} _ {s} = 2 pi T { dot {n}}}

Работа пружины

Когда к пружине прилагается сила, и длина пружины изменяется на дифференциала dx, выполненная работа:

∂ ws = F dx { displaystyle partial w_ {s} = Fdx}

Для линейных упругих пружин смещение x пропорционально приложенной силе

F = K x { displaystyle F = Kx},

где K – sp постоянная кольца и единицу Н / м. Смещение x измеряется от невозмущенного положения пружины (то есть есть X = 0, когда F = 0). Подставляя два уравнения

W s = 1 2 k (x 1 2 – x 2 2) { displaystyle W_ {s} = { frac {1} {2}} k left (x_ {1} ^ {2 } -x_ {2} ^ {2} right)},

где x 1 и x 2 – начальное и конечное смещение пружины соответственно, измеренное от ненарушенное положение пружины.

Работа, выполняемая с упругими сплошными стержнями

Твердые тела часто моделируются как линейные пружины, потому что под действием силы они сжимаются или удлиняются, а когда сила снимается, они возвращаются к своей первоначальной длине, как пружина. Это до тех пор, пока сила находится в недостаточной упругости, чтобы вызвать остаточную или пластическую деформацию. Следовательно, уравнения, приведенные для линейной пружины, можно также использовать для упругих сплошных стержней. С другой стороны, мы можем определить работу, связанную с расширением или сжатием упругого сплошного стержня, заменив давление P его эквивалентом в твердых телах, нормальное напряжение σ = F / A в рабочем расширении

W = ∫ 1 2 F dx. { Displaystyle W = int _ {1} ^ {2} F , dx.}

W = ∫ 1 2 A σ d x. { displaystyle W = int _ {1} ^ {2} A sigma , dx.}

где A – площадь поперечного сечения стержня.

Работа, связанная с растяжением жидкой пленки

Рассмотрим жидкую пленку, такую ​​как мыльная пленка, подвешенная на проволочном каркасе. Требуется некоторая сила, чтобы растянуть эту пленку подвижной частью проволочного каркаса. Эта сила используется для преодоления микроскопических сил между молекулами на границе раздела жидкость-воздух. Эти микроскопические силы перпендикулярны любой линии на поверхности, и сила, создаваемая этими силами на единицу длины, называется поверхностным натяжением σ, единицей измерения которого является Н / м. Следовательно, работа, связанная с растяжением пленки, называется работой поверхностного натяжения и определяется из

W s = 1 2 σ s d A. { displaystyle W_ {s} = int _ {1} ^ {2} sigma _ {s} , dA.}

где dA = 2b dx – изменение площади поверхности пленки. Коэффициент 2 связан с тем, что у пленки две поверхности, контактирующие с воздухом. Сила, действующая на подвижный провод в результате эффектов поверхностного натяжения, равна F = 2b σ, где σ – сила поверхностного натяжения на единицу длины.

Свободная энергия и эксергия

Количество полезной работы, которая может быть извлечена из термодинамической системы, определяется вторым законом термодинамики. Во многих практических ситуациях это может быть представлено функцией термодинамической доступности или Exergy. Два важных случая: в термодинамических системах, где температура и объем поддерживаются постоянными, мерой достижимой полезной работы является функция свободной энергии Гельмгольца ; а в системах, где температура и давление поддерживаются постоянными, мерой достижимой полезной работы является свободная энергия Гиббса.

Немеханические формы работы

Немеханическая работа в термодинамике определяется работой дальнодействующими силами, проникающими в систему в виде силовых полей. Действие таких сил может быть инициировано событиями в окружении системы или термодинамическими операциями на экранирующих стенках системы. Дальнодействующие силы – это силы в обычном физическом смысле слова, а не так называемые «термодинамические силы» в терминологии неравновесной термодинамики.

Немеханическая работа дальнодействующих сил может иметь как положительный, так и отрицательный знак, работа, совершаемая системой над окружающей средой, или наоборот. Работа, выполняемая дальнодействующими силами, может выполняться бесконечно медленно, чтобы приблизиться к фиктивному обратимому квазистатическому идеалу, в котором энтропия не создается в системе в процессе.

В термодинамике немеханическую работу следует противопоставлять механической работе, которая выполняется силами в непосредственном контакте между системой и ее окружением. Если предполагаемую «работу» процесса нельзя определить ни как длительную, ни как контактную работу, то иногда термодинамический формализм вообще не может ее описать как работу. Тем не менее, термодинамический формализм допускает передачу энергии между открытой системой и ее окружением с помощью процессов, работа которых не определена. Примером может служить тот случай, когда стена между системой и ее окружением не считается идеализированной и исчезающе тонкой, поэтому внутри стены могут происходить процессы, такие как трение, влияющее на перенос вещества через стену; в этом случае силы передачи не являются ни строго дальнодействующими, ни строго связанными с контактом между системой и ее окружением; тогда перенос энергии можно рассматривать как конвекцию, а в сумме оценивать как передачу внутренней энергии. Это концептуально отличается от передачи энергии в виде тепла через толстую заполненную жидкостью стенку в присутствии гравитационного поля между закрытой системой и ее окружением; в этом случае внутри стены может происходить конвективная циркуляция, но процесс все же можно рассматривать как передачу энергии в виде тепла между системой и ее окружением; если вся стена перемещается за счет приложения силы из окружающей среды, без изменения объема. Таким образом, чтобы изменить систему объема, она одновременно передает энергию как работу. Химическая реакция внутри системы электрического тока, который передает энергию в виде работы между системой и окружающей средой, хотя сами химические системы реакции (за исключением особого предельного, когда они проходят через устройство в окружающей среде так), чтобы происходило по линии термодинамического равновесия) всегда необратимы и не взаимодействуют напрямую с окружающей средой системы.

Немеханическая работа контрастирует с работой давления – объема. Работа давление – объем – один из двух основных видов механической контактной работы. Сила действует на перегородку между окружающей средой. Сила возникает из-за давления, оказываемого внутри системы на граничную стенку; Это внутреннее состояние системы, но должным образом измеряется внешними устройствами на стене. Работа с изменением системы за счет расширения или сжатия системы. В данной статье говорится, что если система расширяется, она оказывает положительное воздействие на окружающую среду. Если система сжимается, в данной статье говорится, что она отрицательно воздействует на окружение. Работа давления и объема – это своего рода контактная работа, потому что она происходит через прямой контактный материал с окружающей стенкой или материей на границе системы. Он точно описывается изменениями параметров системы, таких как динамика изменений давления и объема системы во времени. Объем системы классифицируется как «переменная деформация» и должным образом измеряется вне системы, в окружающей среде. Работа давление – объем может иметь как положительный, так и отрицательный знак. Давление – объем, выполняемая достаточно медленно, приблизиться к фиктивному обратимому квазистатическому идеалу.

Немеханическая работа также контрастирует с работой вала. Работа вала – это еще один из двух основных видов механической контактной работы. Он передает через вращение, но в итоге не меняет форму или объем системы. Это не изменяет объем системы, это не измеряется как работа давление – объем называется изохорной работой. Рассматриваемая исключительно с точки зрения возможной разницы между исходной и конечной формой и объемами системы, работа вала не меняется. В процессе работы вала, например, вращения лопасти, форма системы лилически изменяется, но это не приводит к конечному изменению формы или объема системы. Работа вала – это своего рода контактная работа, потому что она происходит за счет прямого контакта материала с окружающим веществом на границе системы. Система, которая изначально находится в состоянии термодинамического равновесия, не может инициировать какое-либо изменение своей внутренней энергии. В частности, он не может инициировать работу вала. Это объясняет любопытное использование фразы «неодушевленное материальное действие» Кельвином в одном из его утверждений о втором законе термодинамики. Считается, что термодинамические операции или изменения в среде окружающей среды вызывают сложные изменения, такие как неограниченное продолжительное, изменяющееся или прекращенное вращение ведущего вала, в то время как система запускается в состоянии термодинамического равновесия, является неодушевленной и не может этого спонтанно делать. Таким образом, знак работы вала всегда отрицательный, работа над системой выполняется окружающими. Работа вала вряд ли может выполняться бесконечно медленно; следовательно, он всегда производит энтропию в системе, потому что для ее передачи используется трение или вязкость внутри системы. Приведенные выше комментарии о работе вала применимы только в том случае, если игнорировать то, что система может сохранять угловой момент и связанную с ним энергию.

Примеры немеханических режимов работы включают

• Электрические работы – где сила определяется напряжением окружающей среды (электрическим потенциалом), а общее смещение представляет собой изменение пространственного распределения электрического заряда
• Магнитная работа – где сила определяется напряжённостью магнитного поля окружающей среды, а обобщенное смещение – это изменение общего магнитного дипольного момента
• Работа электрической поляризации – где сила определяется окружающей ‘напряжённостью электрического поля, а обобщенное смещение представляет собой изменение поляризации среды (сумма электрических дипольных моментов молекул)

Гравитационная работа

Гравитационная работа определяется силой, измеряемой в окружающем ‘гравитационном поле. Это может вызвать общее смещение в виде изменения пространственного распределения вещества внутри системы. Система получает внутреннюю энергию (или другое соответствующее кардинальное количество энергии, например энтальпию) за счет внутреннего трения. С точки зрения окружающей среды такая работа трения выглядит как механическая работа, совершаемая над системой, но с точки зрения системы она проявляется как передача энергии в виде тепла. Когда система находится в собственном состоянии внутреннего термодинамического равновесия, ее температура везде одинакова. Если объем и другие переменные экстенсивного состояния, помимо энтропии, поддерживаются постоянными в течение всего процесса, то переданное тепло должно проявляться как повышенная температура и энтропия; в однородном гравитационном поле давление системы будет больше внизу, чем вверху.

По определению, соответствующая кардинальная функция энергии отличается от гравитационной потенциальной энергии системы в целом; последнее также может измениться в результате гравитационной работы, совершаемой окружением в системе. Гравитационная потенциальная энергия системы является составной частью ее общей энергии, наряду с другими ее компонентами, а именно ее основной термодинамической (например, внутренней) энергией и ее кинетической энергией в целом движущейся системы.

См. Также

• Электротехнические работы
• Электрохимический компрессор водорода
• Химические реакции
• Микростатическое состояние (статистическая механика) – включает определение работы под микроскопом

Ссылки