Погрешности радиовысотомеров в измерении истинной высоты полета: неучет наличия и высоты искусственных сооружений (телевышек, труб, ЛЭП), отдельных деревьев и т. п.; измерение над редким лесом высоты относительно земной поверхности, а над густым— от вершин деревьев; неправильные показания истинной высоты при полете вертолета с креном. Над горной местностью и участками с резкими изменениями рельефа показания радиовысотомера становятся ошибочными и пользоваться ими в этих условиях не рекомендуется.
Измеряется истинная высота только непосредственно под вертолетом, хотя летчику важно знать и то, как она будет изменяться по направлению его движения. Перечисленные погрешности РВ следует учитывать при построении профиля полета.
Погрешности барометрических высотомеров в измерении высоты подразделяются на методические, аэродинамические и инструментальные.
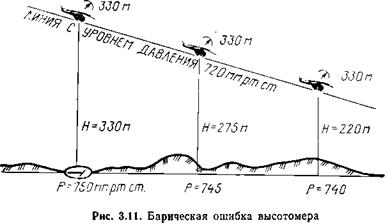
Методические’’ погрешности возникают вследствие несовпадения и неполного учета фактического состояния атмосферы с принятыми в расчет шкал высотомера, неучета рельефа местности. Прибор измеряет давление в слое атмосферы, окружающей вертолет, от начального уровня р0, устанавливаемого на приборе летчиком; не учитывает фактическую температуру наружного воздуха на высоте полета; измеряет барометрическую высоту, а не высоту над пролетаемой местностью.
Погрешность за счет изменения атмосферного давления у земли Д#б возникает, если давление над пролетаемой местностью не совпадает с давлением ро. В этом случае показание высотомера (при отсутствии других ошибок) не будет соответствовать истинной высоте полета: при его понижении по пути движения вертолета истинная высота будет меньше показания прибора, а при повышении — больше (рис. 3.11). Величина погрешности в измерении ВЫСОТЫ в метрах определяется ПО формуле ДЯбар=11Ар, где 11—барометрическая ступень — значение высоты, соответствующее изменению давления на 1 мм рт. ст. в приземном слое;
Ар — разность давления в точке, над которой определяется высота, и давления, установленного на высотомере.
Погрешности от изменения атмосферного давления у земли устраняются летчиком: перед вылетом — установкой стрелок высотомера на нуль; перед посадкой — установкой давления аэродрома посадки, которое сообщается летчику по радио; при выполнении перелетов на высотах ниже нижнего эшелона — установкой на шкале давлений высотомера минимального приведенного давления по маршруту; при расчете высот — учетом поправки ДЯбаР.
Для расчета высоты полета по маршруту с установкой на высотомере давления аэродрома взлета поправка в показание высотомера на падение атмосферного давления определяется по формуле
Л^бар = (Рприв. аэр — Рприв. мин) 11, (3.8 )
где Рприв. аэр, Рприв. мин — давление на аэродроме взлета и минимальное по маршруту, приведенные к уровню моря, определяемые на синоптической карте.
При длительном перелете ниже нижнего эшелона незнание или неучет падения атмосферного давления по маршруту может привести к опасному сближению с земной (водной) поверхностью, так как истинная высота уменьшается при неизменных показаниях барометрического высотомера. Ориентируясь по завышенному показанию высотомера, летчик может ослабить контроль за истинной высотой полета, что особенно недопустимо в условиях ограниченной видимости.
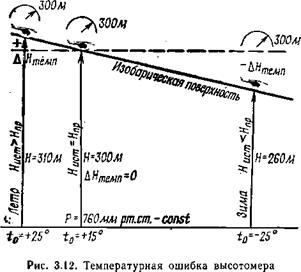
Погрешность за счет изменения температуры воздуха АЯтемп возникает вследствие несовпадения фактической средней температуры. воздуха с принятой при тарировке шкалы. Из формулы (3.7) видно, что большему значению Гср соответствует большая истинная высота и наоборот, т. е. летом высотомер будет давать заниженные показания, а зимой завышенные, что особенно опасно при полетах вблизи земной поверхности и в горных районах.
Величину методической температурной погрешности в измерении высоты можно получить после логарифмирования формулы (3.7) с последующим дифференцированием по Гср и переходом к конечным приращениям ДптеМп = (АГо/Г0)#пр или, для упрощения видоизменив формулу
Д//темп=[ (Л> 15)/300)]#пр, (3.9)
где ДГо — отклонение средней фактической температуры от расчетной;
Го — абсолютная средняя расчетная температура у земли, равная 288 К;
(to—15)—отклонение фактической температуры от расчетной (+15° С);
#щ) — показание высотомера.
Высота с учетом температурной поправки называется исправленной ЯИСЩ).
В практике для малых высот считают, что каждые 3° отклонения фактической температуры воздуха от стандартной вызывают ошибку в 1% измеряемой высоты. Величину температурной погрешности высотомера находят приближенным расчетом по формуле (3.9) или (для высот более 400 м) учитывают с помощью НЛ-10М, используя шкалы 7, 5, 9. Зимой и в горных районах эта погрешность может достигать значительной величины, пренебрегать ею нельзя (рис. 3.12). Она учитывается в случаях, когда следует пройти заданную точку (пуска ракет, бомбометания и т. п.) на заданной истинной высоте и при определении показания высотомера, соответствующего минимальной безопасной высоте полета.
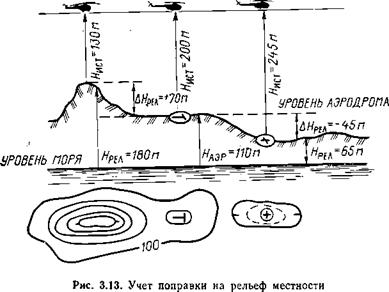
Погрешность за изменение рельефа местности ДЯрел возникает по той причине, что высотомер указывает барометрическую высоту //бар (от уровня давления, установленного на его шкале) и не реагирует на изменение рельефа местности, над которой пролетает вертолет, хотя превышение рельефа ведет к уменьшению истинной высоты, а принижение — к ее увеличению (рис. 3.13). Для учета изменения рельефа находят на полетной карте с помощью горизонталей абсолютные высоты рельефа Ярел в точке пуска ракет (бомбометания) или в полосе маршрута (при расчете безопасной высоты) и аэродрома ЯаЭр, затем рассчитывают поправку на изменение рельефа по формуле
АЯреЛ = Ярел Яаэр. (3.10)
Высота с учетом поправки на рельеф называется относительной //отн*
Аэродинамическая погрешность АНа возникает
из-за искажения воздушного потока, обтекающего приемник воздушных давлений. В результате этого статическое давление измеряется неточной Величина этой погрешности на вертолетах невелика, зависит от скорости и высоты полета и для различных типов вертолетов различна. Определяется она при летных испытаниях, указывается в формулярах. На самолетах эта погрешность в зависимости от скорости и высоты достигает сотен метров.
~^200п 200п 200п
Инструментальная погрешность АЯинстр возникает из-за изменения упругих свойств анероидного блока, износа деталей, неточности регулировки прибора. Каждый прибор имеет свою погрешность. Определяют ее периодически на контрольной установке в лаборатории, сводят совместно с аэродинамической в суммарную поправку АЯсум и показания прибора с учетом АН сум заносят в таблицу для учета (табл. 3.1), которая размещается в кабине вертолета. Для учета суммарной поправки следует по показанию высотомера войти в таблицу его поправок (графу 3), затем в графе 1 отсчитать эшелон полета (показанию 320 м соответствует эшелон 300 м). Показание высотомера, исправленное на величину суммарной поправки, представляет собой точное показание прибора #т. пр=#щ>+А#Сум. Значение Ят. пр устанавливается (снимается) на шкале 9 НЛ-10М.
Для использования барометрического высотомера в полете необходимо знать и уметь учитывать его погрешности. Учету подлежат, как правило, погрешности, имеющие существенное значение
![]()
Учет суммарных поправок высотомера
Высотомер,, тип… № …
Вертолет,, тип… № …
Дата проверки… тип ПВД…
|
Заданная высота эшелона Яэш, м |
Приборная скорость 1/пр, км/ч |
Показания высотомера с учетом суммарной поправки //пр» м |
|
1 |
2 |
3 |
|
0 |
180 |
10 |
|
300 |
180 |
320 |
|
600 |
180 |
610 |
|
900 |
180 |
920 |
|
1200 |
180 |
1210 |
|
1600 |
180 |
1610 |
|
1800 |
180 |
1820 |
|
2100 |
160 |
2120 |
|
2400 |
160 |
2420 |
|
2700 |
160 |
2750 |
|
3000 |
150 |
3070 |
в условиях полета. Порядок их учета при расчете высоты будет показан ниже. Высотомеру присущи запаздывания показаний в наборе высоты и на снижении. Это надо учитывать при маневрах в вертикальной плоскости: вывод из пикирования следует начинать до прихода показаний прибора на высоту вывода, а при наборе высоты заканчивать его при показаниях, меньших намеченной высоты набора.
Несмотря на погрешности, присущие барометрическим высотомерам, они нашли широкое применение из-за простоты устройства и удобства в пользовании. Однако только умелый учет их погрешностей позволяет избежать ошибок при определении и выдерживании высот. Барометрический высотомер используется в комплексе с радиовысотомером: первый — для выдерживания заданной высоты полета, а второй — для определения и контроля истинной высоты.
Случайные погрешности в лабораторных работах по физике можно оценивать только с использованием калькулятора
О теории случайных погрешностей
Теория случайных погрешностей была создана К.Ф.Гауссом в первой половине XIX в. в связи с его занятиями астрономией и геодезией.
Напомним, что случайные погрешности δi = xi – a проявляются при проведении серии измерений одной и той же физической величины в неизменных условиях одним и тем же методом.
Одним из фундаментальных положений теории Гаусса является “принцип арифметической середины”. В соответствии с этим принципом за истинное значение величины а принимается среднее значение
![]()
при n → ∞, если метод не сопровождается систематическими погрешностями.
Для случайных погрешностей характерны следующие свойства:
- Положительные и отрицательные случайные погрешности встречаются с одинаковой вероятностью, т. е. одинаково часто.
- Среднее арифметическое из алгебраической суммы случайных погрешностей при неограниченном возрастании числа наблюдений стремится к нулю, т. е.

- Малые по абсолютной величине случайные погрешности встречаются с большей вероятностью, чем большие.
Основная идея теории Гаусса может быть выражена следующим образом
Возможные конкретные значения случайной погрешности, как и сам результат измерения, предсказать невозможно. Однако после того как экспериментатор определил измеряемый параметр и метод его измерения, сразу “возник” объективный закон, неизвестный исследователю. Этот закон определяет совокупность случайных погрешностей, которые возникают в процессе измерений.
Всегда можно эмпирически (на конкретных опытах) выявить закон распределения случайных погрешностей, который обычно выражается в виде так называемой функции распределения f(δ). Этот закон позволяет определить вероятность, с которой погрешность может оказаться в интервале от δ1 до δ2. Вероятность эта равна площади заштрихованной криволинейной трапеции, представленной на графике функции распределения.

Гауссу удалось определить универсальный закон распределения, которому подчиняется огромный класс случайных погрешностей измерений самых разных величин различными методами.
Этот закон носит название нормального закона распределения. Конечно, существуют измерения, погрешность которых не распределена по нормальному закону. Однако всегда можно определить степень их отклонения от нормального закона.
Функция распределения φ(δ), открытая Гауссом, имеет следующие свойства:

1) Функция δ(φ) четная, т. е. δ-(φ-)δ(φ), и в силу этого симметрична относительно оси координат.
2) Функция δ(φ) имеет максимум при значениях случайной погрешности, равных нулю.
3) Функция δ(φ) имеет две точки перегиба, расположенные симметрично относительно оси координат. Координаты точек перегиба равны ±σ.
4) Касательные к кривой δ(φ) в точках перегиба отсекают на оси абcцисс отрезки, равные ±2σ.
5) Максимальное значение функции δ(φ) равно
![]()
6) Площадь под всей кривой δ(φ) стремится к 1. Площадь криволинейной трапеции, ограниченной прямыми, проходящими через точки δ1,2 = ±σ, составляет 0,68 от всей площади; если прямые проходят через точки δ3,4 = ±2σ, то площадь составляет 0,95; площадь криволинейной трапеции, ограниченной прямыми δ5,6 = ±3σ, равна 0,99.
Параметр σ, определяющий все фундаментальные свойства нормального закона, называется средним квадратическим отклонением. Этот параметр может быть определен после получения достаточно большой серии результатов измерений x1, х2, х3, …, хn. Тогда

Важность параметра σ состоит в том, что он позволяет определить границы случайных погрешностей. Действительно, вероятность получения случайных погрешностей, превосходящих по абсолютной величине 3σ, равна 1%.
При обычной организации измерений не представляется возможности провести не только бесконечно большое число измерений, но и провести просто большое их число.
Специальные исследования показали, что такая граница может быть определена при небольшом числе опытов в серии.
В такой серии из k измерений находят так называемую среднюю квадратичную погрешность

Затем Δхкв увеличивают в S раз.
Число S называется коэффициентом Стьюдента (коэффициент был предложен в 1908 г. английским математиком В. С. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент – студент). Коэффициент Стьюдента позволяет определить границу случайной погрешности серии: Δхслуч = S Δхкв.
Таблица коэффициентов S для различного числа опытов в серии

Погрешность среднего арифметического
После проведения серии равноточных измерений и нахождения хср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [хср ± 3σ], если в серии достаточно много измерений, и имеет вид [хср ± S Δхкв] при небольшом числе опытов. Это означает, что 3σ (или S Δхкв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σх или ΔSкв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около хср, чем [xcp ± 3σх].
Понять, почему должно быть именно так, помогут следующие рассуждения
Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение хср. Таких средних значений получается N: хср1, хср2, …, xcpN. Для этой совокупности средних определяется среднее квадратичное отклонение
![]()
Величина σх ср характеризует предельное распределение средних значений, это и есть величина, которая позволяет найти интервал, в котором находится истинное значение измеряемой в опыте величины [хср ± 3σх ср]. На практике такая процедура никогда не реализуется не только потому, что это очень трудоемко, но и потому, что теория погрешностей позволяет по результатам одной серии определить погрешность среднего. Это делается на основе фундаментального результата теории погрешностей:
стандартное отклонение среднего σх ср в ![]() раз меньше стандартного отклонения каждого опыта серии σх, т.е.
раз меньше стандартного отклонения каждого опыта серии σх, т.е.
![]()
Итак, если в серии с достаточно большим числом опытов определено хср, то граница случайной погрешности среднего равна
![]()
Если в серии небольшое число опытов, то граница случайной погрешности среднего находится по формуле:

Все расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел “Статистические расчеты”), следуя методическим рекомендациям, приведенным ниже.
Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей
- Включаем калькулятор, клавиша [ON]
- Нажимаем клавишу [SHIFT](SETUP)
- Входим в режим статистики. Нажимаем клавишу [2]
- Выбираем режим 1-Variable. Нажимаем клавишу [1]
- Заполняем таблицу
- Нажимаем клавишу [OPTN]
- Выбираем режим 1-Variable. Нажимаем клавишу [3]
- На дисплее получаем ряд характеристик
8.1. Первая сверху – значение среднего значения
8.2. Вторая снизу – случайная погрешность каждого опыта серии σх - Вычисляем погрешность среднего

- Находим границу случайной погрешности среднего

Пример
Измерялась скорость тела, брошенного горизонтально. В десяти опытах были получены следующие значения дальности полета L (в мм): 250, 245, 250, 262, 245, 248, 262, 260, 260, 248. Дальность полета тела измерялась линейкой с основной погрешностью Δ1 = 1мм. Высота, с которой брошено тело, в опыте равнялась Н = 1 м и измерялась мерной лентой с основной погрешностью Δ2 = 1 см и ценой деления С2 =1 см.

Решение
Сначала определим среднее значение дальности полета тела и вычислим его начальную скорость. Для этого сведем все данные в таблицу и проведем их первичную обработку.

Так как

Легко определить среднее значение скорости по результатам серии опытов:
![]()
Граница относительной погрешности измерения скорости:

В этой формуле ΔL – граница абсолютной погрешности измерения дальности полета, Δg – погрешность округления g, ΔН – погрешность прямого однократного измерения высоты.
ΔН = 1 см + 0,5 см = 1,5 см
ΔL складывается из погрешности линейки Δ1 и случайной погрешности ΔLслуч.:
ΔL = Δ1 + ΔLслуч.
Так как ΔLкв = 7мм, то при оценке ΔLслуч. нет смысла учитывать погрешность линейки Δ1 = 1мм.
Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для εv следует вместо ∆L подставить его границу ∆L = S ∆Lкв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).
Имеем:
![]()
Первое слагаемое в этой сумме равно 0,09; слагаемое в скобках (0,01 + 0,0075) = 0,0175. Следовательно, εv = 0,09. Граница абсолютной погрешности каждого опыта серии не превосходит
εv = ε0 = 0,565 ∙ 0,09 = 0,05 м/с
Это значит, если на данной установке провести еще один опыт, то гарантировать можно, что значение скорости, рассчитанное по его результатам, будет принадлежать интервалу [(0,56 – 0,05)м/с; (0,56 + 0,05)м/с].
Найдем границу случайной погрешности среднего значения скорости тела, брошенного горизонтально. Для этого в формулу для εv следует вместо ∆L подставить границу случайной погрешности среднего:
![]()
Таким образом,
![]()
Относительная погрешность среднего равна
0,027 + 0,01 + 0,0075
Последним слагаемым в этой сумме можно пренебречь. Итак, ср = 0,04 = 4%. Мы видим, что погрешность среднего в два раза меньше погрешности каждого опыта. Граница абсолютной погрешности среднего равна:
![]()
Таким образом, из серии 10 опытов по измерению скорости можно сделать вывод о том, что в любой другой такой серии из 10 опытов на данной установке среднее значение скорости будет находиться в интервале [(0,56 – 0,02)м/с; (0,56 + 0,02)м/с]. Этому же интервалу принадлежит неизвестное значение скорости, которое получится, если проделать серию с очень большим числом опытов, т. е. такое значение, которое можно назвать истинным значением.
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим:  . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
 (5.1)
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0  0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
 и указывает на качество измерения. Ее можно выразить в процентах.
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
- Для линейки 1:
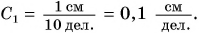
- Для линейки 2:
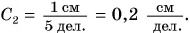
- Для линейки 3:
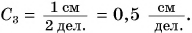
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:


А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы  ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления
), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления  ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:
1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10°  определенный по средней шкале с точностью до 5°
определенный по средней шкале с точностью до 5°  определенный по верхней шкале с точностью до 1°
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Министерство образования Республики Беларусь Учреждение образования
«МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ»
Кафедра физики
ИСПОЛЬЗОВАНИЕ ТЕОРИИ ОШИБОК ПРИ ОБРАБОТКЕ РЕЗУЛЬТАТОВ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЙ
Методические указания к лабораторной работе № 0 по разделу “Механика и молекулярная физика” курса общей физики
для студентов всех специальностей дневной и заочной формы обучения
Могилев 2011
1

Рассмотрены и рекомендованы к изданию
на заседании кафедры физики Протокол № 9 от 12 мая 2011 г.
Составители: ассистент Пусовская Т.И.
Рецензент:
кандидат физико математических наук, доцент УО МГУП В.Л.Малышев.
УДК 532.516 ©УО «Могилевский государственный
университет продовольствия», 2011
2

ЛАБОРАТОРНАЯ РАБОТА № 0
ИСПОЛЬЗОВАНИЕ ТЕОРИИ ОШИБОК ПРИ ОБРАБОТКЕ РЕЗУЛЬТАТОВ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЙ
ЦЕЛЬ РАБОТЫ: определение плотности твердого тела правильной геометрической формы; расчет абсолютной и относительной погрешностей измерений.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: весы, разновесы, штангенциркуль, образец исследуемого вещества (цилиндр).
1ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
При проведении экспериментальных исследований и обработке
результатов измерений получаемые значения величин в большинстве случаев являются приближенными.
Измерением называется нахождение значения определяемой величины опытным путем с помощью специальных технических средств, устройств или приборов. Измерения делятся на прямые и косвенные.
Прямым измерением называется измерение, при котором значение определяемой величины находится непосредственно считыванием по шкале измерительного инструмента или прибора. Например, измерение длины линейкой или времени секундомером.
Косвенное измерение – это измерение, при котором значение величины находится путем расчета по формуле, в которой фигурируют величины, определяемые путем прямых измерений. Например, необходимо определить объем параллелепипеда. Для этого можно воспользоваться формулой V a b c . Вычисление объема тела относится к косвенным измерениям, так как искомая величина объема V задается как функция величин, определяемых путем прямых измерений, в нашем случае длины а, ширины b и высоты c параллелепипеда.
1.1 Погрешности измерений
При выполнении любых измерений получают не абсолютно точные, а приближенные значения искомых величин. Иными словами, результаты измерений имеют погрешность (ошибку) измерений.
Погрешности делятся на приборные, случайные и промахи. Промахи – ошибки, вызванные чаще всего внезапной поломкой прибора или невнимательностью экспериментатора. Результаты, которые не попали в доверительный интервал при очень высокой вероятности, например р=0,99, являются промахами. Этот результат в расчетах обычно не учитывается (отбрасывается).
3
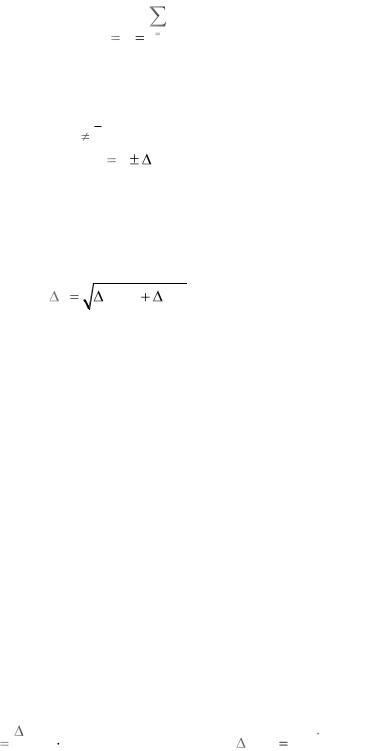
За истинное значение измеряемой величины, как правило, принимают среднее значение. Если x – измеряемая величина, то
|
n |
||||||
|
xi |
||||||
|
xср. x |
i 1 |
, |
(1) |
|||
n
где n– число измерений, i – порядковый номер измерения.
1.2 Абсолютная погрешность
В большинстве случаев xi x , поэтому считают
где x – абсолютная погрешность, которая показывает отклонение измеряемой величины от ее среднего значения.
В соответствии с теорией ошибок причинами появления абсолютной погрешности могут быть приборные и случайные ошибки. Вычисление абсолютной погрешности осуществляется по формуле
|
x |
x |
2 |
x 2 |
, |
(3) |
|
приб. |
сл. |
где xприб.– приборная погрешность, т.е. погрешность прибора, которым выполняют прямое измерение;
xсл. – случайная погрешность.
1.3Определение приборных погрешностей xприб.
1.3.1 В отдельных случаях значение xприб. указано на шкале прибора, в инструкции по его эксплуатации или известно из ГОСТов. Если такой возможности нет, то значение xприб. может осуществляется различными способами.
1.3.2В приборах с дискретным (прерывистым, скачкообразным) измерением (секундомер, пересчетные устройства и т.п.)
за xприб. принимают цену деления прибора.
Цена деления – минимальная разница между соседними делениями шкалы прибора.
1.3.3В приборах непрерывного измерения (линейка, рулетка,
термометр)
за xприб. принимают ½ цены деления прибора.
1.3.4На электроизмерительных приборах обычно указан класс точности (КТ). КТ указывается в процентах и определяется формулой:
|
xприб. |
КТ x |
|||||
|
КТ |
100% |
. Следовательно |
x |
max |
, |
|
|
xmax |
приб. |
100% |
||||
где xmax – предел измерения прибора (максимальная величина, которую можно измерить данным прибором)
4

1.4 Ошибка округления
Если значение используемой при расчетах косвенно измеряемой величины х задано некоторым числом, то при вычислении погрешности следует учитывать ошибку округления. Данная ошибка определяется как единица последнего разряда числа, деленная пополам.
|
Пример 1. При использовании в расчетах числа |
взятого с точностью |
|
до двух знаков 3,14 ошибка округления составляет |
=0,01/2=0,005. Если |
|
ускорение свободного падения g принять равным |
9,8 м/с2, то ошибка |
|
округления составит ∆g= 0,05 м/с2. |
1.5 Случайная погрешность
Случайная погрешность xсл. вычисляется по формуле:
|
n |
( x )2 |
, |
(4) |
|
xсл. n, p |
i |
||
|
i 1 |
n(n 1) |
||
|
где τn,p – коэффициент Стьюдента (находится по таблице), |
|||
|
n – число измерений, |
|||
|
р – доверительная вероятность, которая показывает |
вероятность того, |
что результат отдельного измерения отличается от истинного значения на величину, не большую, чем x.
Коэффициент Стьюдента определяется по таблице в зависимости от доверительной вероятности и числа измерений. При проведении лабораторных исследований в учебном процессе доверительная вероятность р принимается равной 0,95. Если число измерений равно 3, то в таблице находим значение коэффициента Стьюдента равное 4,3.
1.6 При прямых измерениях, если опыт проводится 1 раз, случайная погрешность xсл =0, следовательно, исходя из формулы (3), абсолютная
|
погрешность |
x = |
xприб.. |
|||||||||
|
Если опыт проводится 2 и более раз, тогда необходимо использовать |
|||||||||||
|
формулу (3). |
|||||||||||
|
Пример 2. Высоту h |
измерили 3 раза линейкой. Получили h1 , h2, h3. |
||||||||||
|
Используя формулу (3), находим абсолютную погрешность: |
|||||||||||
|
h |
h |
2 |
h |
2 . |
|||||||
|
приб. |
сл. |
||||||||||
|
Приборная погрешность |
hприб = 0,5∙10-3 (м). |
||||||||||
|
Случайная погрешность определяется, исходя из формулы (4): |
|||||||||||
|
h |
2 |
h |
2 |
h |
2 |
||||||
|
hсл. |
4, 3 |
1 |
2 |
3 |
, |
||||||
|
3(3 |
1) |
||||||||||
где ∆h1= h h1 ,
∆h2= h h2 , ∆h3= h h3 .
5

1.7 Относительная погрешность
Абсолютная погрешность измерения не несет в себе всей полноты информации о точности метода (например, одинаковые ∆x=0.1 м при изготовлении мебели и измерении расстояния между населенными пунктами имеют существенно различный смысл). Поэтому используется
относительная погрешность измерения Е.
Относительная погрешность (Е) прямого измерения определяется по формуле:
|
E |
x |
100% , |
(5) |
|
|
x |
||||
где ∆x – абсолютная погрешность измерения, сравнивается со значением измеряемой величины x ,
x – среднее значение измеряемой величины.
Пусть величина x задана формулой
|
x |
anbm |
. |
|||||||||||||
|
ck |
|||||||||||||||
|
Вычисление величины x – косвенное измерение, |
тогда его относительная |
||||||||||||||
|
погрешность (Е) определяется по формуле: |
|||||||||||||||
|
x |
a 2 |
b 2 |
c |
2 |
|||||||||||
|
E |
n |
m |
k |
(6) |
|||||||||||
|
x |
a |
b |
c |
||||||||||||
|
Пример 3 |
Необходимо |
рассчитать |
относительную погрешность |
||||||||||||
|
измерения площади S |
прямоугольника. |
Так |
как площадь фигуры |
||||||||||||
|
определяется по формуле |
|||||||||||||||
|
S = a b, |
где a – длина прямоугольника, м; b – ширина, м,
то относительная погрешность Е ,исходя из формулы (6), рассчитывается как
|
S |
a 2 |
b |
2 |
|||||||
|
E |
. |
|||||||||
|
S |
a |
b |
||||||||
Пример 4 Площадь S круга находится по формуле
|
S |
d 2 |
, |
|
|
4 |
|||
где d – диаметр круга, м.
Относительная погрешность измерения его площади
|
E |
S |
2 |
2 |
d |
2 . |
|||
|
S |
d |
|||||||
6

Применим эти теоретические знания к лабораторной работе.
Цель работы – определить плотность вещества, из которого изготовлен цилиндр, и рассчитать погрешность. Как известно, плотность тела
|
определяется по формуле: |
|||||
|
m |
, |
(7) |
|||
|
V |
|||||
|
где m – масса тела, кг; |
|||||
|
V – объем тела, м3. |
|||||
|
Объем цилиндра V равен |
|||||
|
V = S h, |
(8) |
||||
|
где h – высота цилиндра, м; |
|||||
|
S – площадь основания цилиндра , м2. |
|||||
|
Площадь основания S цилиндра – круг, следовательно |
|||||
|
S |
D2 |
, |
(9) |
||
|
4 |
|||||
где D – диаметр цилиндра, м.
Подставим формулы (8) и (9) в формулу (7), получаем рабочую формулу:
где m – масса тела, кг;
D – диаметр цилиндра, м; h – высота цилиндра, м.
Используя теоретическое введение, получим формулу для подсчета относительной погрешности измерения Е:
|
E |
, |
(11) |
||||||||||
|
где |
– среднее значение плотности материала, из которого изготовлен |
|||||||||||
|
цилиндр. |
||||||||||||
|
4m |
, |
(12) |
||||||||||
|
D 2 h |
||||||||||||
где m – масса тела, кг;
h – среднее значение высоты цилиндра, м; D – среднее значение диаметра цилиндра, м.
Следовательно,
|
E |
m 2 |
2 |
2 |
D 2 |
h |
2 . |
(13) |
|||||||
|
m |
D |
h |
||||||||||||
|
7 |

2 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1С помощью аналитических весов 1 раз измеряем массу цилиндра
2Поворачивая цилиндр вокруг своей оси, штангенциркулем измеряем 3 раза высоту цилиндра h . Находим среднее значение h . Данные
|
h1, h2, h3 и |
h заносим в таблицу 1. |
||||||||||||||||||||
|
3 В разных сечениях измеряем штангенциркулем 3 раза диаметр |
|||||||||||||||||||||
|
цилиндра |
D . Находим |
среднее |
значение |
D . Данные |
D1,D2,D3 и D |
||||||||||||||||
|
записываем в таблицу 1. |
|||||||||||||||||||||
|
Таблица 1 – Вычисление средней плотности |
|||||||||||||||||||||
|
m |
D |
D |
h |
h |
(кг/м3) |
||||||||||||||||
|
(кг) |
(м) |
(м) |
(м) |
(м) |
|||||||||||||||||
|
4 |
Все средние значения h и |
D подставляем в формулу (12) и |
||||
|
вычисляем среднее значение плотности |
металла, из которого изготовлен |
|||||
|
данный цилиндр. |
||||||
|
5 |
Определяем абсолютную погрешность измерений. |
5.1 Рассчитываем погрешность единичных измерений высоты и диаметра цилиндра (смотри Пример 2, стр.5)
|
, |
||||||
|
hi |
h |
hi |
||||
|
Di |
D |
Di |
, |
Результаты расчетов записываем в таблицу 2.
Таблица 2 – Результаты расчетов погрешностей измерений
|
№ |
hi |
hсл. |
hпр. |
h |
Di |
Dсл. |
Dпр. |
D |
1
2
3
8

5.2 Вычисляем случайные ошибки измерения высоты и диаметра:
|
h 2 |
||||||||||||||||||
|
hсл. |
tn, p |
i |
, |
|||||||||||||||
|
n(n |
1) |
|||||||||||||||||
|
D 2 |
||||||||||||||||||
|
D |
t |
i |
, |
|||||||||||||||
|
n, p |
||||||||||||||||||
|
сл. |
n(n |
1) |
||||||||||||||||
|
где коэффициент Стьюдента tn,p=4,3, если число измерений n=3. |
||||||||||||||||||
|
Полученные значения |
hсл. и Dсл. подставляем в таблицу 2. |
|||||||||||||||||
|
5.3 |
Определяем полную абсолютную погрешность высоты и диаметра |
|||||||||||||||||
|
цилиндра. |
||||||||||||||||||
|
h |
h |
2 |
h |
2 |
, |
|||||||||||||
|
сл. |
приб. |
|||||||||||||||||
|
D |
D |
2 |
D |
2 , |
||||||||||||||
|
сл. |
приб. |
|||||||||||||||||
|
где |
hпр. |
и |
Dпр. |
– |
приборные погрешности штангенциркуля (0,1 мм |
|||||||||||||
|
либо 0,05 мм). |
||||||||||||||||||
|
5.4 Массу цилиндра измеряли 1 раз, следовательно, абсолютная |
||||||||||||||||||
|
погрешность |
измерения |
массы |
m |
mприб. . Приборная погрешность |
||||||||||||||
|
аналитических весов |
m |
составляет |
m |
=5∙10-5кг. |
||||||||||||||
|
приб. |
приб. |
6 Рассчитываем относительную погрешность определения плотности материала цилиндра Е по формуле (13).
При выполнении расчетов принимаем =3,14, а ошибку округления
 =0,005.
=0,005.
7 Вычисляем абсолютную погрешность определения плотности: 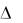 =
=  E .
E .
8Окончательный результат представляем в виде:
9Для того, чтобы определить из какого материала изготовлен цилиндр, сравниваем полученное значение плотности вещества 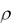 с данными
с данными
из таблицы 3.
Таблица 3 – Плотности некоторых твердых тел
|
Вещество |
Плотность |
|
(кг/м3) |
|
|
Алюминий |
2600 |
|
Медь |
8600 |
|
Свинец |
11300 |
|
Сталь |
7700 |
|
Олово |
7200 |
|
9 |
При выполнении расчетов необходимо пользоваться правилами приближенных вычислений ( смотри приложение 1).
3 КОНТРОЛЬНЫЕ ВОПРОСЫ
1Какие измерения называются прямыми, а какие косвенными?
2Приборные погрешности и возможности определения приборных погрешностей.
3Определение абсолютной погрешности при прямых измерениях.
4Определение относительной погрешности при прямых измерениях.
5Определение относительной погрешности при косвенных измерениях.
6Как определяется абсолютная погрешность при однократном измерении величины?
7Как определяется случайная ошибка?
4 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1Трофимова Т.И. Курс физики/Т.И. Трофимова. – М.: Высшая школа, 2008. -558c.
2Детлаф А.А. Курс физики: учеб. пособие/. А.А Детлаф, Б.М. Яворский . – 4-е изд., испр.- М.: Академия, 2005 – 720 с.
3Савельев И. В. Курс общей физики: учеб. пособие. В 5 кн. Кн. 1. Механика/ И. В. Савельев. – М.: АСТ, Астрель, 2006 – 336 с.
4Е.М.Гершензон А.Н.Мансуров. Лабораторный практикум по общей и экспериментальной физике. Москва, Академия, 2004 –
10
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) – это истинное значение, а (triangle a) – погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? 
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
