Площадь поверхности конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности конуса
Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Площадь боковой поверхности конуса
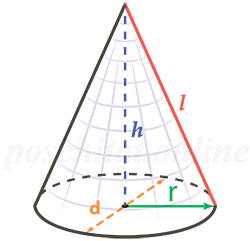
=
=
Sб.пов =
0
Округление числа π: Округление ответа:
Площадь полной поверхности конуса
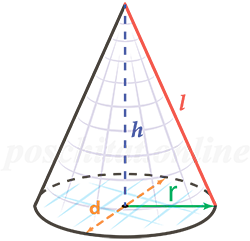
=
=
Sп.пов =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Площадь боковой поверхности конуса через образующую
Чему равна площадь боковой поверхности конуса Sб.пов, если образующая l, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ l
через диаметр:
Sб.пов = π ⋅ l ⋅ d⁄2
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sб.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²
Площадь боковой поверхности конуса через высоту
Чему равна площадь боковой поверхности конуса Sб.пов, если высота h, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ √r² + h²
через диаметр:
Sб.пов = π ⋅ d⁄2 ⋅ √(d/2)² + h²
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sб.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²
Площадь полной поверхности конуса через образующую
Чему равна площадь полной поверхности конуса Sп.пов, если образующая l, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + l)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + l)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sп.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²
Площадь полной поверхности конуса через высоту
Чему равна площадь полной поверхности конуса Sп.пов, если высота h, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + √r² + h²)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + √(d/2)² + h²)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sп.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²
См. также
Конус — это совокупность всех лучей, которые исходят из какой-либо точки пространства и пересекают плоскую поверхность.
Онлайн-калькулятор площади поверхности конуса
Точка, которая является началом этих лучей, называется вершиной конуса. В случае когда в основании конуса лежит многоугольник, конус превращается в пирамиду.
Конус состоит из некоторых элементов, знать которые необходимо для решения задач.
Образующая — отрезок, соединяющий точку, лежащую на окружности круга, который является основанием, и вершину конуса.
Высота — расстояние от плоскости основания до точки вершины конуса.
Виды конуса
Конус может быть нескольких видов:
Прямым, если его основанием является эллипс или круг. Причем вершина должна точно проектироваться в центр основания.
Косым — это тот случай, когда центр фигуры, лежащей в основании, не совпадает с проекцией вершины на это основание.
Круговым — соответственно, если основание — круг.
Усеченным — область конуса, которая будет лежать между основанием и сечением плоскости, параллельной основанию и пересекающей этот конус.
Формула площади поверхности конуса
Для нахождения полной площади поверхности конуса нужно найти сумму площади основания (или оснований, если конус усеченный) конуса и площади его боковой поверхности:
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь основания (оснований) конуса;
SбокS_{text{бок}} — площадь боковой поверхности конуса.
Рассмотрим примеры нахождения площади поверхности обычного прямого кругового конуса, а также усеченного этого же конуса.
Формула площади поверхности кругового конуса
Sосн=π⋅r2S_{text{осн}}=picdot r^2
Sбок=π⋅r⋅lS_{text{бок}}=picdot rcdot l
rr — радиус круга (основания) кругового конуса;
ll — длина образующей этого конуса.
Найти площадь поверхности кругового конуса, если радиус основания равен 3 (см.), а высота hh треугольника, путем вращения которого образовался данный конус, равна 4 (см.)
Решение
r=3r=3
h=4h=4
Образующую можно найти, если рассмотреть треугольник, катетами которого являются радиус и высота, а гипотенузой – сама образующая ll. По теореме Пифагора имеем:
l2=r2+h2l^2=r^2+h^2
l2=32+42l^2=3^2+4^2
l2=25l^2=25
l=5l=5
Вычислим площадь основания конуса:
Sосн=π⋅r2=π⋅32≈28.26S_{text{осн}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅r⋅l=π⋅3⋅5≈47.10S_{text{бок}}=picdot rcdot l=picdot 3cdot 5approx47.10 (см. кв.)
Полная площадь
S=Sосн+Sбок≈28.26+47.10=75.36S=S_{text{осн}}+S_{text{бок}}approx28.26+47.10=75.36 (см. кв.)
Ответ: 75.36 см. кв.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
Sбок=π⋅l⋅(r+r′)S_{text{бок}}=picdot lcdot (r+r’)
ll — длина образующей конуса;
rr — радиус основания;
r′r’ — радиус круга, получаемый при усечении кругового конуса.
Условие возьмем из предыдущей задачи, добавив к нему только лишь радиус второго основания r′r’. Пусть он будет равен 2 (см.). Требуется вычислить полную площадь поверхности этого усеченного конуса.
Решение
l=5l=5
r=3r=3
r′=2r’=2
Оснований у нас теперь два, поэтому полная площадь оснований будет равна сумме площадей этих оснований с радиусами rr и r′r’:
Sосн=Sосн r+Sосн r’S_{text{осн}}=S_{text{осн r}}+S_{text{осн r’}}
Площадь основания радиуса rr:
Sосн r=π⋅r2=π⋅32≈28.26S_{text{осн r}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь основания радиуса r′r’:
Sосн r’=π⋅r′2=π⋅22≈12.56S_{text{осн r’}}=picdot r’^2=picdot 2^2approx12.56 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50S_{text{бок}}=picdot lcdot (r+r’)=picdot 5cdot (3+2)approx78.50 (см. кв.)
Полная площадь:
S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32S=S_{text{осн}}+S_{text{бок}}=S_{text{осн r}}+S_{text{осн r’}}+S_{text{бок}}approx28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Тест по теме «Площадь поверхности конуса»
Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
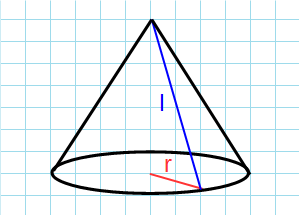
Формула боковой поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Боковая поверхность через радиус и высоту
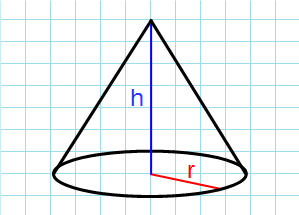
Формула боковой поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Расчет приведен для прямого кругового конуса (подробное описание внизу страницы)
Площадь основания конуса равна:
Площадь боковой поверхности конуса равна:
Полная площадь конуса равна:
Как рассчитать площадь поверхности прямого кругового конуса по радиусу основания и его высоте?
Площадь поверхности прямого кругового конуса равна сумме площадей основания конуса и боковой поверхности конуса.
Прямой круговой конус — конус в основании которого лежит круг и центр симметрии совпадает с центром этого круга (то есть это обычный, в простом понимании, конус).
Площадь основания конуса определяется по формуле:
Sо = Π*r2
Площадь боковой поверхности конуса, если известна высота, определяется по формуле:
Sб = П*r*(√(r2+h2))
Полная площадь поверхности конуса равна:
Sп = Sо + Sб = Π*r2 + П*r*(√(r2+h2)), где
h — высота конуса;
Π = 3.1415926535 — математическая постоянная, равная отношению длины окружности к её диаметру;
r — радиус основания конуса.
Полная площадь поверхности конуса равна сумме площадей основания конуса и боковой поверхности конуса.
Если радиус и высота конуса измерены в см (сантиметрах), то площадь конуса равна:
Sсм2(п) = Π*rсм2 + П*rсм*(√(rсм2+hсм2))
Sм2(п) = (Π*r2см + П*rсм*(√(rсм2+hсм2)))/10 000
Зная площадь основания конуса, можно рассчитать радиус, диаметр и периметр основания конуса, преобразовав стандартные формулы.
r=√(S_(осн.)/π)
d=2√(S_(осн.)/π)
P=2πr=2√(πS_(осн.) )
Высота, образующая и радиус конуса соединяются в прямоугольный треугольник, из которого по теореме Пифагора можно найти любое значение, зная остальные два. Угол наклона конуса можно найти из этого же треугольника через отношение тангенса, а уже через него во втором, равнобедренном треугольнике вычислить угол раствора конуса. (рис.40.1,40.2)
l=√(h^2+r^2 )=√(h^2+S_(осн.)/π)
tanβ=h/r
α=180°-2β
Вычислить площадь боковой поверхности конуса через площадь основания и высоту можно, заменив радиус и образующую конуса в формуле на соответствующие выражения. Чтобы найти площадь полной поверхности конуса, следует поступить аналогично.
S_(б.п.)=πrl=√(πS_(осн.) (h^2+S_(осн.)/π) )
S_(п.п.)=S_(осн.)+√(πS_(осн.) (h^2+S_(осн.)/π) )
Объем конуса в стандартном виде представляет собой отношение произведения высоты и площади основания к трем, поэтому его можно вычислить сразу через площадь основания и высоту, заданные в условии.
V=1/3 hS_(осн.)
Чтобы найти радиус сферы, вписанной в конус, нужно умножить высоту на выражение, найденное для радиуса, и разделить это на сумму образующей и радиуса. Радиус сферы, описанной около конуса, будет равен образующей во второй степени, деленной на удвоенную высоту. (рис. 40.3, 40.4)
r_1=hr/(l+r)=(h√(S_(осн.)/π))/(√(h^2+S_(осн.)/π)+√(S_(осн.)/π))
R=(h^2+r^2)/2h=(h^2+S_(осн.)/π)/2h
