Рис.
6
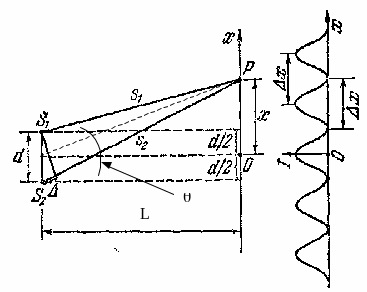
Сделаем рисунок. Здесь (рис.6) приняты
обозначения: L – расстояние от источников
до экрана,
– угол наблюдения, d – расстояние между
источниками.
В
точке O наблюдается так называемый
нулевой максимум, т.к. в эту точку волны
от обоих источников приходят в одинаковой
фазе. Для того чтобы интерференционная
картина была отчетливо различима,
необходимо выполнение условия
![]()
.
Тогда из рисунка можно определить, что
![]()
![]()
.
Здесь
xm
расстояние от центра интерференционной
картины до максимума с номером «m».
Следовательно,
![]()
.
Подстановка
значения
дает, что максимум
интенсивности будет
наблюдаться при значениях:
![]()
.
Величина xm
также определяет расстояние от «0»
максимума до максимума с номером «m».
Координаты
минимума
интенсивности определяются
из условия:
![]()
,
где m=0,1,2,…
Назовем расстояние
между двумя соседними максимумами
интенсивности расстоянием
между интерференционными полосами,
а расстояние между соседними минимумами
интенсивности
шириной
интерференционной полосы.
Видно, что расстояние между полосами и
ширина полосы имеют одинаковое значение,
равное
![]()
.
Данное значение легко можно получить,
если посчитать расстояние между двумя
соседними максимума или минимумами.
Рекомендуется расчет провести студентам
самостоятельно. Из приведенного выражения
следует, что для получения отчетливой
интерференционной картины необходимо,
чтобы выполнялось условие
,
о чем и говорилось выше.
Ширина
интерференционных полос и расстояние
между ними зависят от длины волны .
Только в центре картины при x=0, совпадут
максимумы всех длин волн. Если в установке
Юнга источник испускает белый цвет, то
только нулевой (главный) максимум
окажется белым (здесь совпадут максимумы
всех длин волн), все остальные максимумы
будут окрашены. По мере удаления от
центра максимумы разных длин волн
(разных цветов) смещаются друг относительно
друга все больше и больше. Это приводит
к смазыванию интерференционной картины
при наблюдении ее в белом цвете. В
монохроматическом свете (монохроматическим
называется свет, которому соответствует
дона определенная длина волны) число
различимых полос интерференции заметно
возрастает.
Измерив
расстояние между полосами x
и зная значения L и d, можно вычислить .
Именно из опытов по интерференции света
были впервые определены длины волн для
световых лучей разного цвета.
Оранжево-красному участку спектра
соответствуют более длинные волны
(к=780-600нм),
а сине-фиолетовому – более короткие
(ф=480-420нм).
.52.4. Интерференция в тонких пленках.
Наиболее типичным
и распространенным примером интерференции
света в природе является интерференция
в тонких пленках (мыльные пузыри, радужная
пленка нефти на воде и т.д.).
Пусть на прозрачную
тонкую пластинку толщиной d падает
плоская световая волна под углом
(рис.7). Разность хода, приобретенная
лучами 1 и 2 до того, как они сойдутся в
точке С будет равна:
![]()

Рис.
7
,
где
S1=ВС;
S2=АО+ОС.
Но
АО=ОС=d/cos,
поэтому S2=2d/cos.
В
свою очередь ВС=АСsin,
а АС=2АД=2dtg,
поэтому S1=2dtgsin.
Воспользовавшись
приведенными равенствами и соотношением
![]()
,
получим, что

Для
получения окончательной разности хода
необходимо учесть, что световые волны,
как и всякие другие волны, отражаясь от
оптически более
плотной
среды (луч 1 в точке С) получают
дополнительную разность фаз равную ,
т.е. возникает добавочная разность хода
равная /2.
При отражении от среды оптически менее
плотной (точка О) скачка фазы не происходит.
Таким
образом, при падении на пластинку плоской
волны образуются две отраженные волны,
разность хода которых определяется
формулой:
![]()
В
предположении, что лучи 1 и 2 когерентны,
в результате падения на плоскопараллельную
пленку пучка лучей в отраженном и
проходящем свете на экране получаются
чередующиеся темные и светлые полосы
в случае монохроматического света и
цветные полосы в случае белого света.
ДОПОЛНЕНИЕ 1.
Строго
говоря, лучи 1 и 2 (или две плоские
отраженные волны, распространяющиеся
в одном направлении) смогут интерферировать,
если будут соблюдены условия временной
и пространственной когерентности.
Вспомним, что
когерентностью называется согласованное
протекание нескольких колебательных
или волновых процессов. Степень
согласованности может быть различной.
Соответственно можно ввести понятие
степени
когерентности
двух волн.
Различают
временную и пространственную когерентность.
Понятие когерентности является
относительным: две волны могут вести
себя как когерентные при наблюдении с
одним прибором (с малой инерционностью)
и как некогерентные при наблюдении с
другим прибором (с большой инерционностью).
Для характеристики когерентных свойств
волн вводится время
когерентности
tког.,
которое определяет такое время, за
которое случайное изменение фазы
достигает значения ~.
За время tког.
колебание как бы забывает свою
первоначальную фазу и становится
некогерентным по отношению к самому
себе.
Воспользовавшись
понятием когерентности, можно сказать,
что когда tприбора>>tког.,
то прибор не зафиксирует интерференцию.
Если же tприбора<<tког.,
то прибор (глаз, фотопластинка и пр.)
обнаружит четкую интерференционную
картину.
Соответственно,
длиной когерентности называется
расстояние
![]()
,
на которое перемещается волна за время
tког..
Длина когерентности есть то расстояние,
на котором случайное измерение фазы
достигает значения ~.
Для получения интерференционной картины
путем деления естественной волны на
две части необходимо, чтобы оптическая
разность хода была меньше, чем длина
когерентности. Это требование ограничивает
число видимых интерференционных полос.
С увеличением номера полосы “m” разность
хода растет, поэтому четкость полос
делается все хуже и хуже.
При
интерференции немонохроматических
волн время когерентности и длина
когерентности определяются выражениями:
![]()
и

.
Пространственная
когерентность.
П

Рис.
8
усть источник имеет угловые размеры
(рис.8). Если
![]()
,
то можно наблюдать интерференцию. Отсюда
следует, что наибольшее расстояние,
между щелями, при котором можно наблюдать
интерференцию от источника с угловым
размером ,
определяется из условия
![]()
;
Будем
называть длиной пространственной
когерентности или радиусом когерентности
некое расстояние ког.,
при смещении на которое вдоль некой
волновой поверхности случайное изменение
фазы достигает значения ~.

.
Для Солнца, например, ~0,01рад;
~0,5мкм
ког.=0,05мкм.
По мере удаления от источника степень
пространственной когерентности
возрастает.
Вследствие
ограничений, накладываемых временной
и пространственной когерентностями,
интерференция
при освещении тонкой пластинки наблюдается
только в том случае, если толщина
пластинки не
превышает нескольких сотых долей
миллиметра.
При освещении светом с большой степенью
когерентности интерференция наблюдается
и при отражении от более толстых пластинок
и пленок.
Рассмотрим
теперь интерференцию монохроматического5
света при падении на пленку или пластинку
расходящегося пучка лучей (например,
при падении сферической волны).
В
этом случае результаты интерференции
отраженного (и проходящего) света в
различных точках пластинки зависят от
углов падения
лучей. Лучи, падающие под одинаковым
углом 1,
создадут на экране совокупность одинаково
освещенных точек, образующих криволинейную
темную (или светлую) полосу. Каждой из
этих полос соответствует определенное
значение угла .
Поэтому они называются полосами
равного наклона.
При нарушении плоскопараллельности
пленки или пластинки форма полос равного
наклона искажается. Этим используются
при проверке качества шлифовки
плоскопараллельных стеклянных пластин,
причем обнаруживают отклонение от
плоскопараллельности, равное 0,01мкм.
Справка 3.
![]()
–
временная когерентность
Т.к. оптические разности хода для
проходящего и и отраженного света
отличаются на
![]()
,
максимум интерференции в отраженном
свете будет соответствовать минимуму
в проходящем и наоборот.
С
увеличением толщины (d) плоскопараллельной
пластины влияние угла наклона становится
все менее заметным, полосы равного
наклона становятся все ближе и ближе
друг к другу. И при больших толщинах
плоскопараллельных пластин интерференцию
света в них наблюдать не удается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Расчет интерференционной картины можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу.
Щели S₁ и S₂ находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l ≫ d. Начало отсчета выбрано в точке О, симметричной относительно щелей.
Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода D = s₂ – s₁ Из рисунка видим, что
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равной
Она не зависит от порядка интерференции (величины m) и является постоянной для данных l, d и l₀. Согласно последнему результату, при большом расстоянии между источниками, например при d , отдельные полосы становятся неразличимыми. Для видимого света четкая, доступная для визуального наблюдения интерференционная картина имеет место при l≫d (это условие и принималось при расчете). По измеренным значениям l, d и ширины интерференционной полосы, можно экспериментально определить длину волны света. Интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m = 0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (m = 1), второго (m = 2) порядков и т. д.
Описанная картина, однако, справедлива лишь при освещении монохроматическим светом (λ = const). Если использовать белый свет, представляющий собой непрерывный набор длин волн от 0,4 мкм (фиолетовая граница спектра) до 0,76 мкм (красная граница спектра), то интерференционные максимумы для каждой длины волны будут смещены друг относительно друга и иметь вид радужных полос. Только для m = 0 максимумы всех длин волн совпадают, и в середине экрана будет наблюдаться белая полоса, по обе стороны которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т. д. (ближе к белой полосе будут находиться зоны фиолетового цвета, дальше – зоны красного цвета).
Спасибо за внимание! Ставьте лайки, подписывайтесь и комментируйте 🙂
Примеры решения расчетных задач:
Задача 1.В опыте Юнга два когерентных источника S1 и S2 расположены на расстоянии d = 1 мм друг от друга. На расстоянии L = 1 м от источника помещается экран. Найдите расстояние между соседними интерференционными полосами вблизи середины экрана (точка А), если источники посылают свет длины волны λ = 600 нм.
Решение:
Интерференционная картина на экране состоит из чередующихся темных и светлых полос, параллельных щелям S1 и S2. Интерференционная картина симметрична относительно центральной полосы, проходящей через точку А (рис. 1). Центральная полоса светлая, она соответствует разности хода Δ = 0.

В точках интерференционных максимумов оптическая разность хода
Δ= λ , где
λ , где  =0, 1, 2,… ; (1)
=0, 1, 2,… ; (1)
Условие интерференционных минимумов имеет вид:
 ; (2)
; (2)
Предположим, что в точке В находится k-й максимум на расстоянии ykот центральной полосы. Ему соответствует разность хода Δ= r2 — r1= k λ .
Из треугольника S1BC видно, что  , а из треугольника S2BD видно, что
, а из треугольника S2BD видно, что  .
.
Из двух последних уравнений получим:
 .
.
Учтём , что  ;
;  . Тогда
. Тогда  , откуда:
, откуда:
 ; (3)
; (3)
Используя для максимумов условие (1), получим:
 ;
;
где k = 1, 2, 3, … соответствуют интерференционным максимумам, расположенным выше точки А, а максимумам, расположенным ниже точки А, соответствуют k = -1, -2, -3, … Точке А соответствует центральный максимум (k = 0).
Используя условие интерференционных минимумов (2), можно найти их расстояния от центральной полосы по формуле (3):
 ;
;
Расстояние между соседними интерференционными максимумами (минимумами) называется шириной полосы и соответствует изменению k на единицу, то есть :
 ;
;
Ширина темных и светлых полос одинакова.
Ответ:
 ;
;
Задача 2. В опыте Юнга интерференционная картина по мере удаления от середины размывается, и при k = 4 полосы исчезают. Почему?
Решение:
В опыте Юнга интерференционная картина представляет чередование интерференционных максимумов и минимумов в виде полос, параллельных щелям S1 и S2. В центре интерференционной картины расположена светлая полоса (k = 0). По обе стороны от центральной полосы расположены максимумы ±1, ±2, ±3, ±4 порядков интерференции. Разность хода между интерферирующими волнами по мере удаления от центральной полосы увеличивается. При этом по мере удаления от центра ухудшается видность и четкость интерференционной картины, полосы размываются и исчезают, по условию последний максимум наблюдается при k = 4. Исчезновение полос означает, что колебания, пришедшие от двух источников S1 и S2, некогерентны. Пока их разность хода не превышала 4 λ, они были когерентны. Следовательно, максимальная разность хода, при которой наблюдается интерференция, будет равна:
 ;
;
Величина  называется длиной когерентности. Если оптическая разность хода превышает длину когерентности, интерференционная картина не наблюдается.
называется длиной когерентности. Если оптическая разность хода превышает длину когерентности, интерференционная картина не наблюдается.
Задача 3.Покажите, что при преломлении в призме с малым преломляющим углом α и показателем преломления n луч отклоняется на угол δ ≈(n — 1)α независимо от угла падения, если угол падения также мал. Призма находится в воздухе, n0 = 1.
Решение:
По построению δ-внешний угол треугольника DCB (рис. 2), он равен сумме внутренних углов, не смежных с ним:
δ= φ- β+ β1— φ1;

Согласно закону преломления,
 .
.
По условию угол φ, а значит и β малы, то есть Sinφ≈φ, Sinβ≈β, (выраженному в радианах), тогда nβ=φ, nφ1=β1. Подставив значения φ и β1 в формулу для δ, получим :
 .
.
Из треугольника СВК: β+φ1=α (α- внешний угол, равный преломляющему углу призмы по построению). Таким образом,
 .
.
Задача 4. Найдите число полос интерференции N, получающихся с помощью бипризмы, если показатель преломления бипризмы n = 1,5, преломляющий угол  рад, длина волны источника λ=600 нм. Расстояние от источника до бипризмы равно а = 1 м, расстояние от бипризмы до экрана равно b = 4 м.
рад, длина волны источника λ=600 нм. Расстояние от источника до бипризмы равно а = 1 м, расстояние от бипризмы до экрана равно b = 4 м.
Решение:
Лучи от источника S, падающие на бипризму, после преломления отклоняются от первоначального направления на угол δ≈α(n-1) (см. Задача 3). Продолжение этих лучей до точки пересечения дает изображение двух мнимых источников S1 и S2 (рис. 3). Они являются когерентными источниками, поэтому в области перекрытия АВ когерентных волн, распространяющихся от этих источников, на экране наблюдается интерференционная картина в виде чередующихся темных и светлых полос, как и в опыте Юнга. Центральный максимум интерференционной картины (k = 0) проходит через точку О экрана. Максимумы более высоких порядков находятся на расстоянии yk от центра (см. Задача 1).

Ширина полосы :
 .
.
Здесь L=a+b расстояние от источников до экрана, d — расстояние между мнимыми источниками. Из треугольника SS1K:
 .
.
Тогда ширина интерференционной полосы:
 .
.
Число интерференционных полос в области интерференции АВ равно:
 .
.
Величину области перекрытия АВ найдем из подобных треугольников CS1S и СОВ:
 .
.
Число наблюдаемых полос интерференции будет равно:
 .
.
Ответ:  .
.
Задача 5. В опыте Ллойда (рис. 4) световая волна, исходящая непосредственно из источника S (узкой щели), интерферирует с волной, отраженной от зеркала 3. В результате на экране Э образуется система интерференционных полос. Расстояние от источника до экрана L = 100 см. При некотором положении источника ширина интерференционной полосы на экране Δу = 0,25 мм, а после того как источник отодвинули от плоскости зеркала на h = 0,6 мм, ширина полос уменьшилась в η= 1,5 раза. Найдите длину λ световой волны.

Решение: В точке М интерферируют две когерентные волны 1 и 2, исходящие из источника S. По построению волну 2 можно считать исходящей из источника ,  , являющегося мнимым изображением источника S в зеркале 3. Они симметрично расположены относительно плоскости зеркала, обозначим расстояние между ними
, являющегося мнимым изображением источника S в зеркале 3. Они симметрично расположены относительно плоскости зеркала, обозначим расстояние между ними  . Если зеркало S отодвинуть на h, то новое расстояние между
. Если зеркало S отодвинуть на h, то новое расстояние между  равно
равно  (рис. 5). Для определения длины волны λ используем выражение для ширины полосы из опыта Юнга, применив его для двух расстояний между источниками.
(рис. 5). Для определения длины волны λ используем выражение для ширины полосы из опыта Юнга, применив его для двух расстояний между источниками.

Δ y = λL / d; (4).
 ; (5).
; (5).
По условию Δ y = η Δ y1, тогда  . Выразим от сюда
. Выразим от сюда
 ; (6)
; (6)
Подстановка (6) в (4) дает:
 ;
;
Ответ: .
.
Задача 6.На рис. 6 показана схема интерферометра для измерения показателей преломления прозрачных веществ. Здесь S — узкая щель, освещаемая монохроматическим светом λ = 589 нм, К — коллиматор, дающий параллельный пучок лучей, 1 и 2 — две одинаковые трубки с воздухом, длина каждой из которых  см, Д — диафрагма с двумя щелями S1 и S2 . Когда воздух в трубке 1 заменили аммиаком, то интерференционная картина на экране Э сместилась вверх на N = 17 полос. Показатель преломления воздуха n = 1,000277. Определите показатель преломления аммиака.
см, Д — диафрагма с двумя щелями S1 и S2 . Когда воздух в трубке 1 заменили аммиаком, то интерференционная картина на экране Э сместилась вверх на N = 17 полос. Показатель преломления воздуха n = 1,000277. Определите показатель преломления аммиака.

Решение: Волны, распространяющиеся от щелей S1 и S2, являются когерентными. На экране Э наблюдается интерференционная картина чередующихся темных и светлых полос. Центральная светлая полоса проходит через точку О и соответствует оптической разности хода Δ = 0, если трубки 1 и 2 заполнены воздухом. Если в трубке 1 воздух заменить аммиаком, показатель преломления n1 которого больше n, то центр интерференционной картины сместится вверх на N полос в точку, соответствующую разности хода, равной нулю, то есть
 .
.
Отсюда
 .
.
Заметим, что интерференционный метод определения показателя преломления является высокоточным методом.
Ответ: .
.
Задача 7.Собирающая линза с фокусным расстоянием F = 10 см разрезана пополам и половинки раздвинуты на расстояние d = 0,5 мм (билинза Бийе). Оцените число интерференционных полос на экране, расположенном за линзой на расстоянии D = 60 см, если перед линзой имеется точечный источник монохроматического света с длиной волны λ= 500 нм, удаленный от нее на расстояние а = 15 см.
Решение:
Каждая из половинок билинзы Бийе дает изображение источника S. Верхняя половина дает изображение S1, нижняя дает изображение S2 (рис. 7). Чтобы получить изображение S1, выберем два луча: первый луч SC после преломления в линзе пересечет фокальную плоскость РР в точке К, получившейся от пересечения с фокальной плоскостью побочной оптической оси О1О1, параллельной лучу SC. Второй луч SA проходит, не преломляясь, через точку А до пересечения с первым лучом в точке S1, являющейся изображением S в верхней половине билинзы Бийе. Аналогично построим изображение S2.

Источники S1 и S2 когерентны, поэтому в области пересечения световых волн от этих источников на экране получим интерференционную картину как в опыте Юнга.
Число полос на экране будет равно :
 .
.
Ширина полосы  (см. Задача 1) ,), где L = D — b. Величину b найдем из формулы линзы
(см. Задача 1) ,), где L = D — b. Величину b найдем из формулы линзы  , откуда
, откуда  , где а — расстояние от источника S до линзы, b — расстояние от линзы до изображения S1, F — фокусное расстояние линзы.
, где а — расстояние от источника S до линзы, b — расстояние от линзы до изображения S1, F — фокусное расстояние линзы.
Из подобия треугольников SAB и SS1S2 получим:

откуда  .
.
Подставляя d1 и L в формулу для Δy, получим:
 .
.
Треугольники SAB и SMK подобны, отсюда величина области перекрытия волн
 .
.
Тогда число наблюдаемых полос
 .
.
Ответ: .
.
Задачи для самостоятельной работы
1. В опыте Юнга отверстия S1 и S2 освещались монохроматическим светом с длиной волны λ=600нм. Расстояние d между отверстиями равно 1 мм. Найдите положение трех первых светлых полос на экране, расположенном на расстоянии L = 3 м от отверстий.
Ответ: 1,8 мм; 3,6 мм; 5,4 мм.
2. В опыте Юнга отверстия S1 и S2 освещались монохроматическим светом с длиной волны λ=600нм. На пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка, вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает перпендикулярно к поверхности пластинки, показатель преломления которой n = 1,5. Какова толщина l пластинки?
Ответ: l = 6 10-3 мм.
3. На пути одного из двух параллельных лучей, распространяющихся в вакууме, поставили плоскопараллельную стеклянную пластинку (n = 1,5) толщиной 6 см. Чему будет равно время запаздывания τ этого луча?
Ответ: τ = 0,1 нс.
4. Во сколько раз изменится расстояние между соседними светлыми (темными) полосами на экране в опыте Юнга, если зеленый светофильтр (λ1=650нм).
Ответ: в 1,3 раза увеличится.
|
3 / 3 / 0 Регистрация: 01.11.2011 Сообщений: 26 |
|
|
1 |
|
Определить расстояние между третьей и шестой соседними интерференционными полосами в опыте Юнга11.09.2012, 10:52. Показов 6848. Ответов 2
Определить расстояние между третьей и шестой соседними интерференционными полосами
0 |
|
2356 / 1463 / 125 Регистрация: 20.12.2011 Сообщений: 2,223 |
|
|
14.09.2012, 17:55 |
2 |
|
Решение
Определить расстояние между третьей и шестой соседними интерференционными полосами Такое расстояние можно найти из условия минимума интерференционной картины от двух когерентных волн в опыте Юнга:
3 |
|
3 / 3 / 0 Регистрация: 01.11.2011 Сообщений: 26 |
|
|
17.09.2012, 08:14 [ТС] |
3 |
|
Спасибо за помощь!
0 |

 Сообщение было отмечено как решение
Сообщение было отмечено как решение

