Матрица линейного оператора примеры
Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
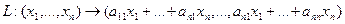
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 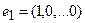 , найдём его образ, это будет вектор
, найдём его образ, это будет вектор 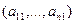 . Для этого в формуле, задающей образ вектора, полагаем
. Для этого в формуле, задающей образ вектора, полагаем 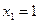 ,
, 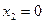 ,…,
,…, 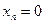 . Аналогично находим образы для
. Аналогично находим образы для 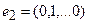 ,…,
,…, 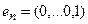 . Из координат образа вектора
. Из координат образа вектора 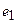 составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.
составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.
Пример 1. Пусть оператор задан с помощью формулы:
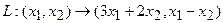 .
.
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
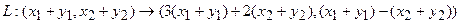 Теперь каждую координату получившегося вектора можем преобразовать:
Теперь каждую координату получившегося вектора можем преобразовать:
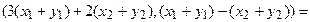
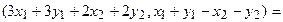
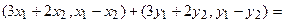
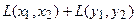 .
.
Аналогично для умножения на константу:
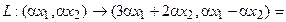
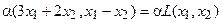
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
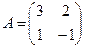 .
.
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. 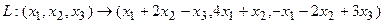 .
.
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
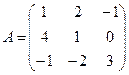 .
.
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система 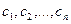 из n векторов, образующих базис, и какая-нибудь произвольная система n векторов
из n векторов, образующих базис, и какая-нибудь произвольная система n векторов 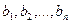 (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.
(возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть 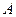 – матрица оператора в базисе
– матрица оператора в базисе 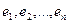 . По условию,
. По условию, 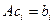 для всех индексов
для всех индексов 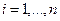 . Данные n равенств можно записать в виде одного матричного равенства:
. Данные n равенств можно записать в виде одного матричного равенства: 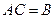 , при этом столбцы матрицы
, при этом столбцы матрицы 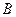 – это векторы
– это векторы 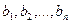 , а столбцы матрицы
, а столбцы матрицы 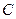 – векторы
– векторы 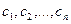 . Тогда матрица
. Тогда матрица 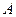 может быть найдена в виде
может быть найдена в виде 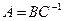 .
.
Пример. Найти матрицу линейного оператора, отображающего базис
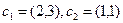 в систему векторов
в систему векторов 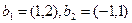 .
.
Здесь 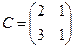 ,
, 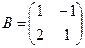 ,
, 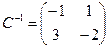 , и получаем:
, и получаем:
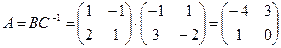 .
.
Проверка осуществляется умножением получившейся матрицы на каждый вектор: 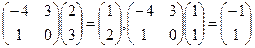 .
.
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 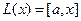 и
и 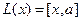 . Построим матрицу одного из этих операторов,
. Построим матрицу одного из этих операторов, 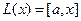 . Для этого найдём образы всех трёх базисных векторов линейного пространства.
. Для этого найдём образы всех трёх базисных векторов линейного пространства.
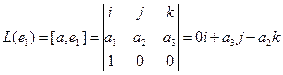 .
.
Аналогично, 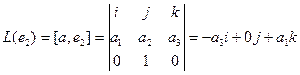 ,
,
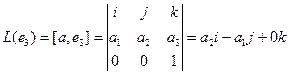 .
.
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица оператора: 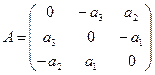 .
.
Аналогично можно построить матрицу линейного оператора 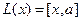 :
:
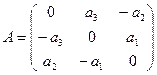 .
.
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы 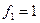 ,
, 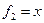 ,
, 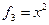 ,…,
,…, 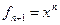 .
.
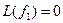 ,
, 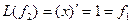 ,
, 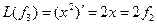 , аналогично получим
, аналогично получим 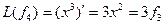 ,…,
,…, 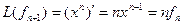 .
.
Матрица этого линейного оператора:
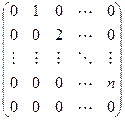
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 –  | 7588 –
| 7588 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
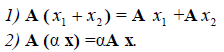
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать
Заметим, что каждый вектор 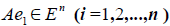 , следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.
, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.
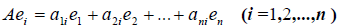
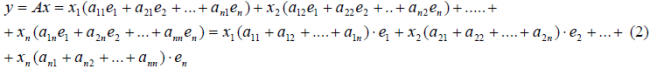
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
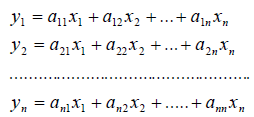
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
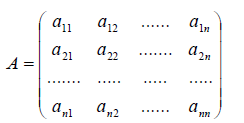
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
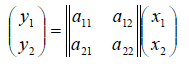
связывающее вектор-прообраз 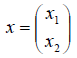 с вектором-образом
с вектором-образом 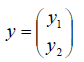
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
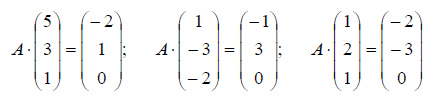
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
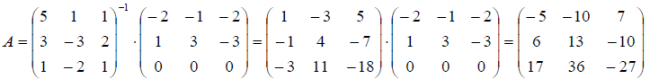
Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 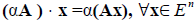 .
.
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
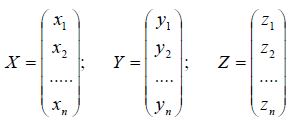
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 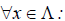
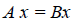 . Равенство операторов обозначается как A = B .
. Равенство операторов обозначается как A = B .
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 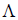 он ставит в соответствие тот же самый элемент, то есть
он ставит в соответствие тот же самый элемент, то есть 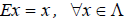
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 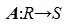 , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.
, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы  и
и  соответственно. Пусть задано отображение
соответственно. Пусть задано отображение
где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов  и
и  в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.
в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.
Пусть x − произвольный элемент в R. Тогда
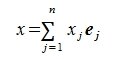 |
(3) |
является разложением x в по базису  .
.
Применим оператор A к базисным векторам  :
:
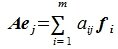 |
(4) |
где aij − координаты полученного вектора в базисе  .
.
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
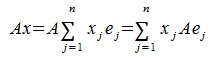
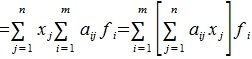
Сделаем следующее обозначение:
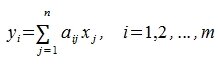 |
(6) |
Тогда равенство (5) примет следующий вид:
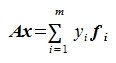 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе  имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2. n.
имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2. n.
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах  и
и  .
.
2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 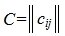 ,где i=1,2. m, j=1,2. n, т.е.
,где i=1,2. m, j=1,2. n, т.е.
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Ядро и образ линейного отображения
Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:
Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или
Заметим, что символ следует отличать от — мнимой части комплексного числа.
Примеры ядер и образов линейных отображений
1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.
2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).
3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .
4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .
Свойства ядра и образа линейного отображения
1. Ядро любого линейного отображения является подпространством: .
В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что
т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:
Следовательно, множество является линейным подпространством пространства .
2. Образ любого линейного отображения является подпространством: .
В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .
Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.
Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .
3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).
В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .
4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .
Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).
5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .
6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.
Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:
Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .
Во-первых, , так как образ любого вектора линейно выражается через векторы
Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:
то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.
Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).
Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).
Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):
Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.
Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).
Линейные операторы
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 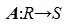 , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.
, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы  и
и  соответственно. Пусть задано отображение
соответственно. Пусть задано отображение
где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов  и
и  в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.
в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.
Пусть x − произвольный элемент в R. Тогда
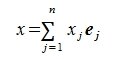 |
(3) |
является разложением x в по базису  .
.
Применим оператор A к базисным векторам  :
:
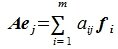 |
(4) |
где aij − координаты полученного вектора в базисе  .
.
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
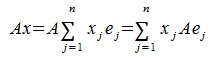
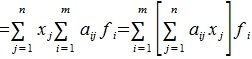
Сделаем следующее обозначение:
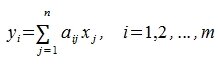 |
(6) |
Тогда равенство (5) примет следующий вид:
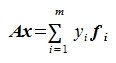 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе  имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2. n.
имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2. n.
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах  и
и  .
.
2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 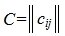 ,где i=1,2. m, j=1,2. n, т.е.
,где i=1,2. m, j=1,2. n, т.е.
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
[spoiler title=”источники:”]
http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya
http://matworld.ru/linear-algebra/linear-operator.php
[/spoiler]
Содержание:
Векторы на плоскости и в пространстве:
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
Вектором называется направленный отрезок 
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например:
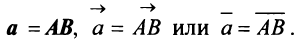
Длиной (или модулем) 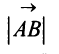 вектора
вектора 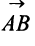 называется число, равное длине отрезка
называется число, равное длине отрезка 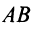 , изображающего вектор.
, изображающего вектор.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коминеарными.
Если начало и конец вектора совпадают, например 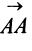 , то такой вектор называют нулевым и обозначают
, то такой вектор называют нулевым и обозначают 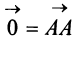 . Длина нулевого вектора равна нулю:
. Длина нулевого вектора равна нулю: 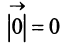 . Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
Произведением вектора 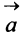 на число
на число 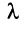 называется вектор
называется вектор 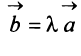 , имеющий длину
, имеющий длину 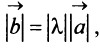 направление которого совпадает с направлением вектора
направление которого совпадает с направлением вектора 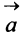 , если
, если 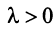 , и противоположно ему, если
, и противоположно ему, если 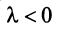 (рис. 3.2).
(рис. 3.2).
Противоположным вектором 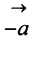 называется произведение вектора
называется произведение вектора 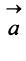 на число
на число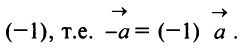
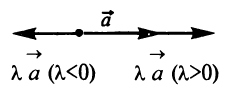
Рис. 32
Суммой двух векторов  и
и  называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец с концом вектора
, а конец с концом вектора  при условии, что начало вектора
при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  (рис. 3.3) (правило треугольника).
(рис. 3.3) (правило треугольника). 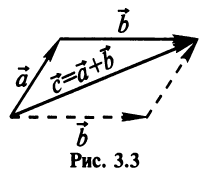
Очевидно, что вектор  в этом случае представляет диагональ параллелограмма, построенного на векторах
в этом случае представляет диагональ параллелограмма, построенного на векторах  и
и  (рис. 3.3) (правило параллелограмма).
(рис. 3.3) (правило параллелограмма).
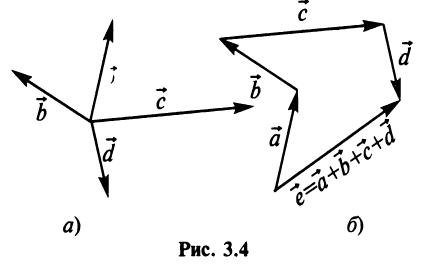
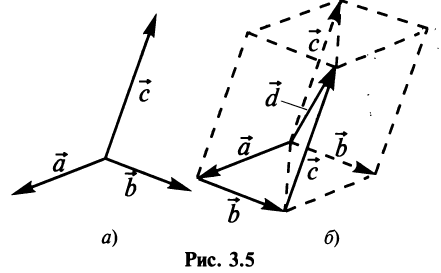
Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов 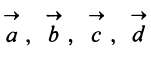 (рис. 3.4а) есть вектор
(рис. 3.4а) есть вектор 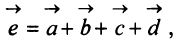 начало которого совпадает с началом вектора
начало которого совпадает с началом вектора  , а конец — с концом вектора
, а конец — с концом вектора 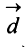 (правило многоугольника) (рис. 3.4 б).
(правило многоугольника) (рис. 3.4 б).
Нетрудно убедиться. что вектор 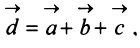 определяемый таким образом, представляет диагональ параллелепипеда, построенного на векторах
определяемый таким образом, представляет диагональ параллелепипеда, построенного на векторах  ,
, и
и 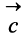 , не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда) (рис. 3.5).
, не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда) (рис. 3.5).
Разностью двух векторов  и
и  называется сумма вектора
называется сумма вектора  и вектора
и вектора  , противоположного
, противоположного  (рис. 3.6).
(рис. 3.6).
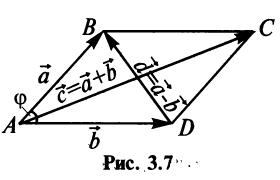
Легко убедиться в том, что в параллелограмме, построенном на векторах  и
и одна диагональ — вектор —представляет сумму векторов
одна диагональ — вектор —представляет сумму векторов  и
и  , а другая диагональ — вектор
, а другая диагональ — вектор  — их разность (рис. 3.7).
— их разность (рис. 3.7).
Перенесем вектор  параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора
параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора  называются координаты его конечной точки. Так, вектор
называются координаты его конечной точки. Так, вектор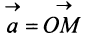 на плоскости
на плоскости  являются два числа
являются два числа 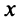 и
и 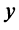 (
( 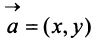 — рис. 3.8.), а в пространстве
— рис. 3.8.), а в пространстве 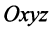 — три числа
— три числа 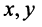 и
и 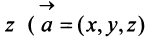 — рис. 3.9).
— рис. 3.9).
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов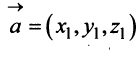 и
и 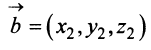 являются соответственно векторы
являются соответственно векторы
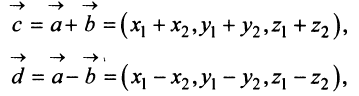 ,
,
а произведение вектора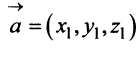 на число
на число 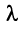 есть вектор
есть вектор 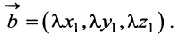 На рис. 3.8 и 3.9 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
На рис. 3.8 и 3.9 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
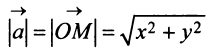 или
или
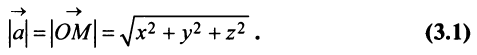
Определение. Скалярным произведением 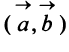 двух векторов
двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 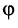 между ними:
между ними:
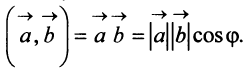
Выразим скалярное произведение через координаты векторов  и
и  .
.
Из треугольника  (рис. 3.7), сторонами которого являются векторы
(рис. 3.7), сторонами которого являются векторы 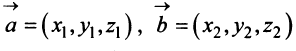 и
и 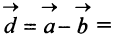
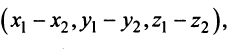 по теореме косинусов следует, что
по теореме косинусов следует, что
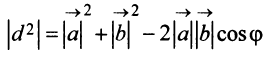 , откуда
, откуда 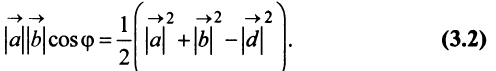
Учитывая формулу длины вектора (3.1) найдем
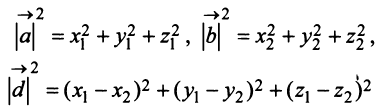 и после преобразования выражения (3.2) получим
и после преобразования выражения (3.2) получим
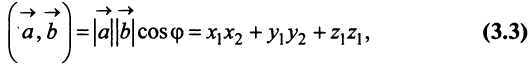
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Заметим, что при 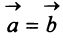 угол
угол 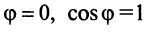 и
и
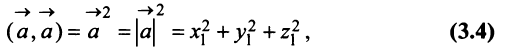
т.е. скалярный квадрат вектора равен квадрату его длины.
В частности, расстояние 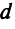 между двумя точками плоскости
между двумя точками плоскости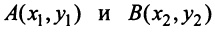 можно рассматривать как длину вектора
можно рассматривать как длину вектора 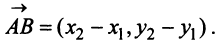
Поэтому 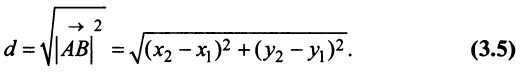
Угол между векторами и
и  определяется по формуле
определяется по формуле
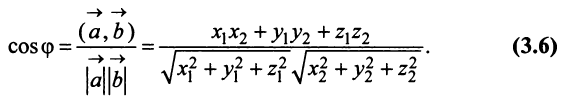
Пример:
Даны векторы 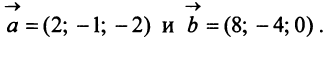
Найти: а)векторы 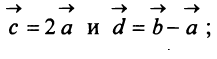 б)длины векторов
б)длины векторов 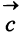 и
и 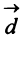 ; в) скалярный квадрат вектора
; в) скалярный квадрат вектора 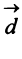 ; г) скалярное произведение векторов
; г) скалярное произведение векторов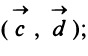 д)угол между векторами
д)угол между векторами 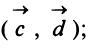
Решение:
а) По определению 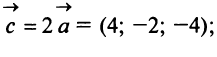
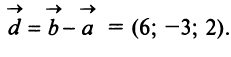
б) По формуле (3.1) найдем длины векторов 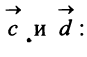
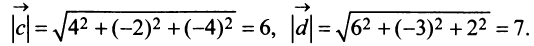
в) По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.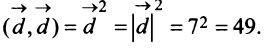
г) По формуле (3.3) скалярное произведение
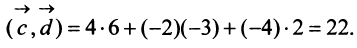
д) По формуле (3.6) угол между векторами 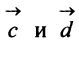 определяется равенством:
определяется равенством:
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение. -мерным вектором называется упорядоченная совокупность
-мерным вектором называется упорядоченная совокупность 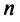 действительных чисел, записываемых в виде
действительных чисел, записываемых в виде 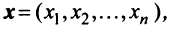 где
где 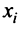 —
— 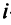 -я компонента вектора
-я компонента вектора 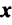 .
.
Понятие  -мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором
-мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором 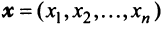 , а соответствующие цены — вектором
, а соответствующие цены — вектором 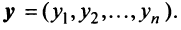
Два  -мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е.
-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. 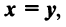 если
если 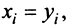
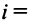
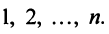
Суммой двух векторов одинаковой размерности п называется вектор 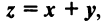 компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е.
компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. 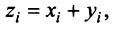
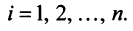
Произведением вектора  на действительное число
на действительное число 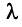 называется вектор
называется вектор 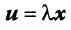 , компоненты
, компоненты 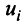 которого равны произведению
которого равны произведению 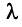 на соответствующие компоненты вектора
на соответствующие компоненты вектора  , т.е.
, т.е. 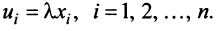
Линейные операции над любыми векторами удовлетворяют следующим свойствам:
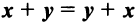 — коммутативное (переместительное) свойство суммы:
— коммутативное (переместительное) свойство суммы: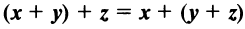 — ассоциативное (сочетательное) свойство суммы;
— ассоциативное (сочетательное) свойство суммы;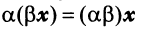 — ассоциативное относительно числового множителя свойство;
— ассоциативное относительно числового множителя свойство;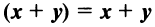 — дистрибутивное (распределительное) относительно суммы векторов свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;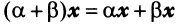 —дистрибутивное относительно суммы числовых множителей свойство;
—дистрибутивное относительно суммы числовых множителей свойство;- Существует нулевой вектор
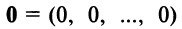 такой, что
такой, что 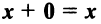 для любого вектора
для любого вектора  (особая роль нулевого вектора);
(особая роль нулевого вектора); - Для любого вектора
 существует противоположный вектор
существует противоположный вектор 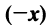 такой, что
такой, что 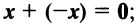
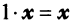 для любого вектора
для любого вектора  (особая роль числового множителя 1).
(особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под  можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа 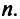 Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу
Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу  , не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже
, не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже  . А множество многочленов степени не выше
. А множество многочленов степени не выше  , но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
, но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора  на действительное число 0 и существование для каждого вектора
на действительное число 0 и существование для каждого вектора 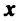 единственного противоположного вектора (—
единственного противоположного вектора (—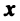 ), равного произведению этого вектора на действительное число (- 1).
), равного произведению этого вектора на действительное число (- 1).
Размерность и базис векторного пространства
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано в § 1.6 для строк матрицы.
Определение. Вектор 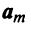 называется линейной комбинацией векторов
называется линейной комбинацией векторов  векторного пространства
векторного пространства 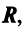 если он равен сумме произведений этих векторов на произвольные действительные числа:
если он равен сумме произведений этих векторов на произвольные действительные числа:
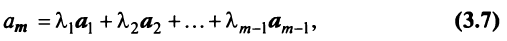
где 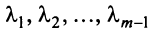 — какие угодно действительные числа.
— какие угодно действительные числа.
Определение. Векторы  векторного пространства
векторного пространства 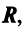 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 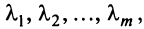 не равные одновременно нулю, что
не равные одновременно нулю, что
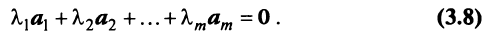
В противном случае векторы  называются линейно независимыми.
называются линейно независимыми.
Из приведенных выше определений следует, что векторы  линейно независимы, если равенство (3.8) справедливо лишь при
линейно независимы, если равенство (3.8) справедливо лишь при 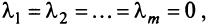 и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел
и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 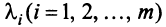 отлично от нуля.
отлично от нуля.
Можно показать (аналогично § 1.6), что если векторы  линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
Примером линейно независимых векторов являются два не-коллинеарных, т.е. не параллельных одной прямой, вектора 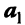 и
и 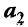 на плоскости. Действительно, условие (3.8)
на плоскости. Действительно, условие (3.8) 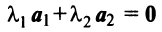 будет выполняться лишь в случае, когда
будет выполняться лишь в случае, когда 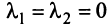 , ибо если, например,
, ибо если, например, 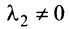 , то
, то 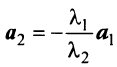 , и векторы
, и векторы 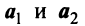 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
коллинеарны. Однако любые три вектора плоскости линейно зависимы.
Отметим некоторые свойства векторов линейного пространства:
- Если среди векторов
 имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например,
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например, 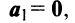 то равенство (3.8) справедливо при
то равенство (3.8) справедливо при 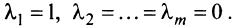
- Если часть векторов
 являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы
являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы 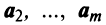 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 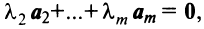 в котором не все числа равны нулю. Но тогда с теми же числами
в котором не все числа равны нулю. Но тогда с теми же числами 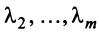 и
и 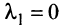 будет справедливо равенство (3.8).
будет справедливо равенство (3.8).
Пример:
Выяснить, являются ли векторы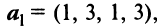
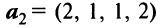 и
и 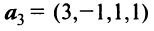 линейно зависимыми.
линейно зависимыми.
Решение:
Составим векторное равенство 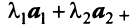
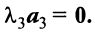 Записывая
Записывая 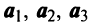 в виде вектор-столбцов, получим
в виде вектор-столбцов, получим 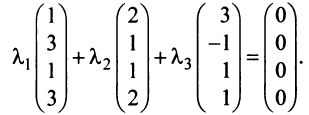
Задача свелась таким образом к решению системы:
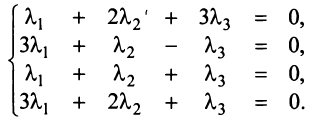
Решая систему методом Гаусса (см. § 2.3), приведем ее к виду:
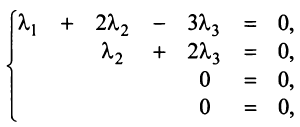
откуда найдем, бесконечное множество ее решений 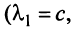
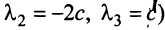 , где с — произвольное действительное число.
, где с — произвольное действительное число.
Итак, для ‘данных векторов условие (3.8) выполняется не только при 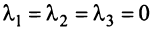 (а, например, при
(а, например, при 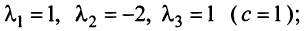 при
при 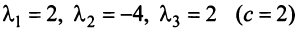 и т.д.), следовательно, эти векторы — линейно зависимые. ►
и т.д.), следовательно, эти векторы — линейно зависимые. ►
Определение. Линейное пространство  называется
называется 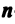 -мерным, если в нем существует я линейно независимых векторов, а любые из
-мерным, если в нем существует я линейно независимых векторов, а любые из 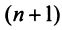 векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число
векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число  называется размерностью пространства
называется размерностью пространства  и обозначается
и обозначается 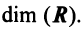
Определение. Совокупность  линейно независимых векторов
линейно независимых векторов  -мерного пространства
-мерного пространства  называется базисом. Справедлива следующая теорема.
называется базисом. Справедлива следующая теорема.
Теорема. Каждый вектор  линейного пространства
линейного пространства  можно представить
можно представить 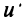 притом единственным способом в виде линейной комбинации векторов базиса.
притом единственным способом в виде линейной комбинации векторов базиса.
 Пусть векторы
Пусть векторы 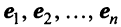 образуют произвольный базис
образуют произвольный базис  -мерного пространства
-мерного пространства  . Так как любые из (
. Так как любые из ( +1) векторов
+1) векторов  -мерного пространства R зависимы, то будут зависимы, в частности, векторы
-мерного пространства R зависимы, то будут зависимы, в частности, векторы 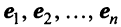 и рассматриваемый вектор
и рассматриваемый вектор  . Тогда существуют такие не равные одновременно нулю числа
. Тогда существуют такие не равные одновременно нулю числа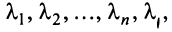 что
что
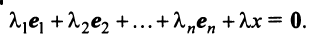
При этом 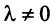 , ибо в противном случае, если
, ибо в противном случае, если 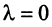 и хотя бы одно из чисел
и хотя бы одно из чисел 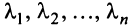 было бы отлично от нуля, то векторы
было бы отлично от нуля, то векторы 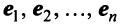 были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,
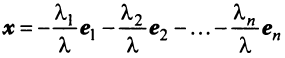 или
или
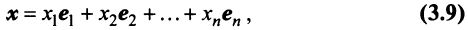
где 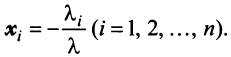
Это выражение 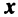 через
через  единственное, так как если допустить какое-либо другое выражение, например,
единственное, так как если допустить какое-либо другое выражение, например,
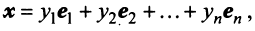 то, вычитая из него почленно (3.9), получим
то, вычитая из него почленно (3.9), получим
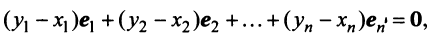 откуда из условия линейной независимости векторов
откуда из условия линейной независимости векторов следует, что ‘
следует, что ‘
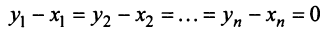 или
или
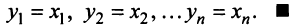
Равенство (3.9) называется разложением вектора  по базису
по базису  , а числа
, а числа 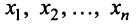 — координатами вектора
— координатами вектора  относительно этого базиса. В силу единственности разложения (3.9) каждый вектор однозначно может быть определен координатами в некотором базисе.
относительно этого базиса. В силу единственности разложения (3.9) каждый вектор однозначно может быть определен координатами в некотором базисе.
Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.
Важное значение имеет следующая теорема.
Теорема. Если  — система линейно независимых векторов пространства
— система линейно независимых векторов пространства  и любой вектор
и любой вектор 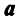 линейно выражается через
линейно выражается через  , то пространство
, то пространство  является n-мерным, а векторы
является n-мерным, а векторы  — его базисом.
— его базисом.
 Возьмем произвольные
Возьмем произвольные 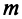 векторов пространства
векторов пространства  , где
, где 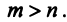 По условию каждый из них можно линейно выразить через
По условию каждый из них можно линейно выразить через  :
:
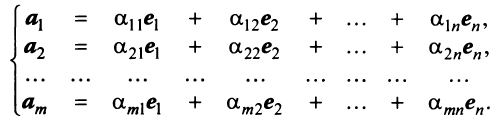 Рассмотрим матрицу
Рассмотрим матрицу 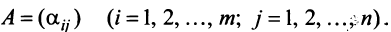
Ранг этой матрицы не превосходит 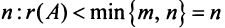 , следовательно, среди ее строк не более
, следовательно, среди ее строк не более 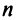 линейно независимых. Так как
линейно независимых. Так как 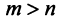 , то
, то 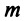 строк этой матрицы, а значит, и
строк этой матрицы, а значит, и 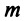 векторов
векторов 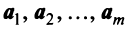 линейно зависимы. Таким образом, пространство
линейно зависимы. Таким образом, пространство 
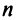 -мерно и
-мерно и  — его базис. ■
— его базис. ■
Пример:
В базисе 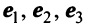 заданы векторы
заданы векторы 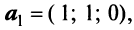
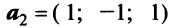 и
и 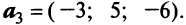 Показать, что векторы
Показать, что векторы 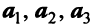 образуют базис.
образуют базис.
Решение:
Векторы 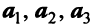 образуют базис, если они линейно независимы. Составим векторное равенство:
образуют базис, если они линейно независимы. Составим векторное равенство: 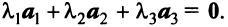 Решая его аналогично примеру 3.2, можно убедиться в единственном нулевом его решении:
Решая его аналогично примеру 3.2, можно убедиться в единственном нулевом его решении: 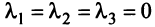 , т.е. векторы
, т.е. векторы 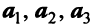 образуют систему линейно независимых векторов и, следовательно, составляют базис. ►
образуют систему линейно независимых векторов и, следовательно, составляют базис. ►
Переход к новому базису
Пусть в пространстве  имеются два базиса: старый
имеются два базиса: старый  и новый
и новый 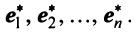 Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса: 
Полученная система означает, что переход от старого базиса  кновому
кновому 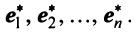 задается матрицей перехода
задается матрицей перехода 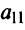 и тд.
и тд. 
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 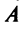 — неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса
— неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 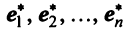 к старому базису
к старому базису 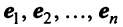 осуществляется с помощью обратной матрицы
осуществляется с помощью обратной матрицы 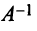 .
.
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 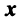 имеет координаты
имеет координаты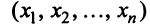 относительно старого базиса и координаты
относительно старого базиса и координаты 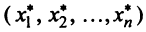 относительно нового базиса, т.е.
относительно нового базиса, т.е.
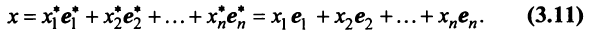
Подставив значения 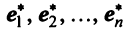 из системы (3.10) в левую часть равенства (3.11), получим после преобразований:
из системы (3.10) в левую часть равенства (3.11), получим после преобразований:
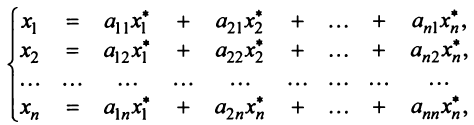
т.е. в матричной форме
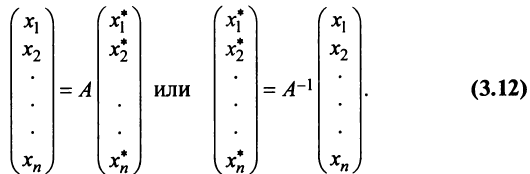
Пример:
По условию примера 3.3 вектор 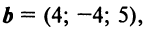 заданный в базисе
заданный в базисе 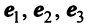 , выразить в базисе
, выразить в базисе 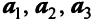 .
.
Решение:
Выразим связь между базисами: 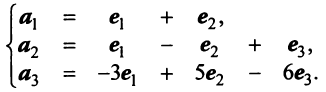
Матрица перехода от базиса  к базису
к базису  имеет вид
имеет вид 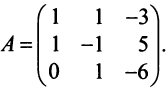 Вычисляем
Вычисляем 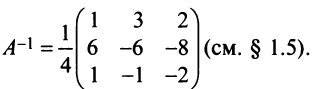 Теперь по (3.12)
Теперь по (3.12) 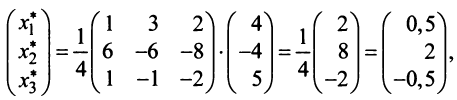
т.е. новые координаты вектора 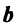 в базисе
в базисе 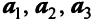 есть 0,5; 2 и -0,5 и вектор
есть 0,5; 2 и -0,5 и вектор 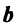 может быть представлен в виде:
может быть представлен в виде: 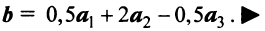
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение. Скалярным произведением двух векторов 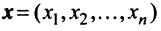 и
и 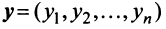 называется число
называется число
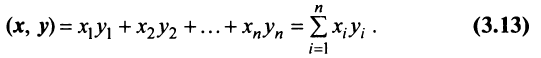
Скалярное произведение имеет экономический смысл. Если 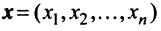 есть вектор объемов различных товаров, а
есть вектор объемов различных товаров, а 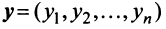 вектор их цен, то скалярное произведение
вектор их цен, то скалярное произведение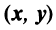 выражает суммарную стоимость этих товаров.
выражает суммарную стоимость этих товаров.
Скалярное произведение имеет следующие свойства:
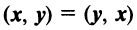 — коммутативное свойство;
— коммутативное свойство;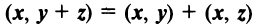 — дистрибутивное свойство;
— дистрибутивное свойство;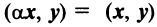 — для любого действительного числа;
— для любого действительного числа;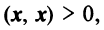 если
если 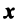 — ненулевой вектор;
— ненулевой вектор; 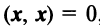 , если
, если 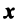 — нулевой вектор.
— нулевой вектор.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора 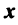 в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
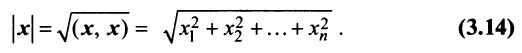
Имеют место следующие свойства длины вектора:
1. 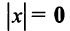 тогда и только тогда, когда
тогда и только тогда, когда 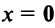 ;
;
2. 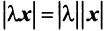 , где
, где 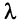 — действительное число;
— действительное число;
3. 
(неравенство Коши—Буняковского);
4. 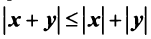 (неравенство треугольника).
(неравенство треугольника).
Угол 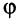 между двумя векторами
между двумя векторами  и
и 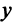 определяется равенством
определяется равенством
 где
где 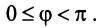
Такое определение вполне корректно, так как согласно неравенству Коши—Буняковского (3.15) 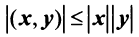 , т.е.
, т.е. 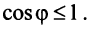
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен 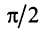 (ибо
(ибо 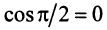 ).
).
Векторы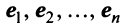
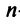 -мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, и ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если
-мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, и ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если 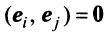 при
при 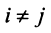 и |
и |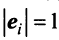 при
при 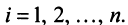
Для установления корректности приведенного определения необходимо убедиться в том, что входящие в него векторы 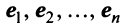 образуют один из базисов рассматриваемого
образуют один из базисов рассматриваемого 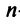 -мерного пространства
-мерного пространства  (т.е.
(т.е. 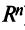 ). Для этого достаточно показать, что векторы
). Для этого достаточно показать, что векторы 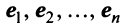 линейно независимы, т.е. равенство
линейно независимы, т.е. равенство
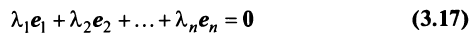
справедливо лишь при 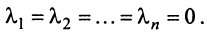
Действительно, умножая скалярно равенство (3.17) на любой вектор 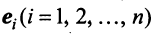 , получим
, получим
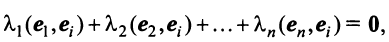
откуда, учитывая, что 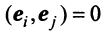 при
при 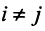 и
и 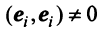 при всех
при всех 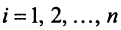 , вытекает, что
, вытекает, что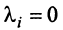 при всех
при всех 
Сформулируем теперь (без доказательства) основную теорему.
Теорема. Во всяком 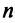 -мерном евклидовом пространстве существует ортонормированный базис.
-мерном евклидовом пространстве существует ортонормированный базис.
Примером ортонормированного базиса является система  единичных векторов
единичных векторов 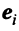 у которых
у которых 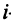 -я компонента равна единице, а остальные компоненты равны нулю:
-я компонента равна единице, а остальные компоненты равны нулю: 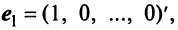
Линейные операторы
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства:  размерности
размерности 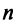 и
и  размерности
размерности 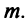
Определение. Если задан закон (правило), по которому каждому вектору  пространства
пространства  ставится в соответствие единственный вектор у пространства
ставится в соответствие единственный вектор у пространства  , то говорят, что задан оператор (преобразование, отображение)
, то говорят, что задан оператор (преобразование, отображение) 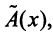 действующий из
действующий из  в
в  , и записывают
, и записывают 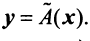
Оператор (преобразование) называется линейным, если для любых векторов  и
и 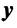 пространства
пространства  и любого числа
и любого числа 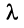 выполнился соотношения:
выполнился соотношения:
- 1.
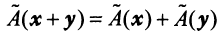 — свойство аддитивности оператора;
— свойство аддитивности оператора; - 2.
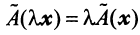 — свойство однородности оператора.
— свойство однородности оператора.
Вектор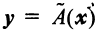 называется образом вектора
называется образом вектора  , а сам вектор
, а сам вектор  — прообразом вектора
— прообразом вектора 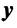 .
.
Если пространства  и
и  совпадают, то оператор
совпадают, то оператор  отображает пространство
отображает пространство  в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
Выберем в пространстве  базис eh
базис eh  и, учитывая (3.9), запишем разложение произвольного вектора
и, учитывая (3.9), запишем разложение произвольного вектора 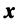 по данному базису:
по данному базису:
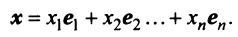
В силу линейности оператора  получаем
получаем
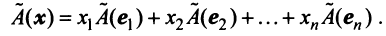
Поскольку 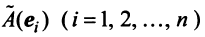 — также вектор из
— также вектор из  , то его можно разложить по базис
, то его можно разложить по базис . Пусть
. Пусть
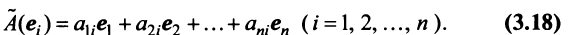
Тогда
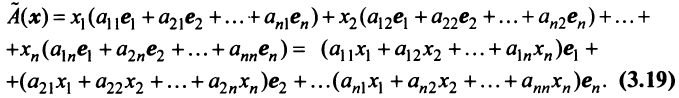
С другой стороны, вектор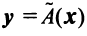 , имеющий в том же базисе
, имеющий в том же базисе  координаты
координаты 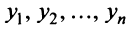 , можно записать так:
, можно записать так:
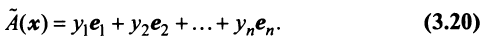
Ввиду единственности разложения вектора по базису равны правые части равенства (3.19) и (3.20), откуда
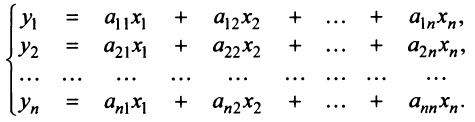
Матрица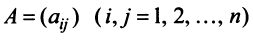 называется матрицей оператора
называется матрицей оператора  в базисе
в базисе  , а ранг
, а ранг 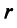 матрицы
матрицы 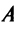 — рангом оператора
— рангом оператора  .
.
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 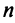 -го порядка соответствует линейный оператор
-го порядка соответствует линейный оператор 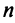 -мерного пространства.
-мерного пространства.
Связь между вектором 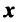 и его образом
и его образом 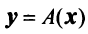 можно выразить в матричной форме уравнением
можно выразить в матричной форме уравнением

где 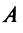 — матрица линейного оператора,
— матрица линейного оператора, 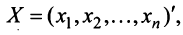
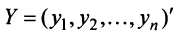 – матрицы-столбцы из координат векторов
– матрицы-столбцы из координат векторов  и
и 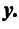
Пример:
Пусть в пространстве 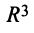 линейный оператор
линейный оператор  в базисе
в базисе 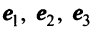 задан матрицей
задан матрицей 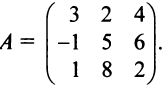 Найти образ
Найти образ 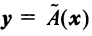 вектора
вектора 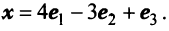
Решение:
По формуле (3.21) имеем 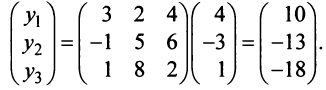
Следовательно, 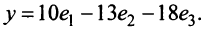 ►
►
Определим действия над линейными операторами.
Суммой двух линейных операторов 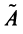 и
и 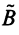 называется оператор
называется оператор 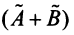 , определяемый равенством:
, определяемый равенством: 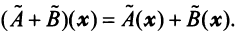
Произведением линейного оператора  на число
на число 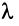 называется оператор
называется оператор 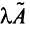 , определяемый равенством
, определяемый равенством 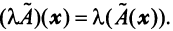
Произведением линейных операторов 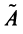 и
и 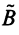 называется оператор
называется оператор 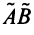 , определяемый равенством:
, определяемый равенством: 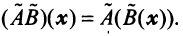
Можно убедиться в том, что операторы , полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
, полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
Определим нулевой оператор  , переводящий все векторы пространства
, переводящий все векторы пространства  в нулевые векторы
в нулевые векторы  , и тождественный оператор
, и тождественный оператор 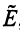 , действующий по правилу:
, действующий по правилу: 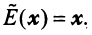
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы  и
и 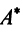 линейного оператора
линейного оператора  в базисах
в базисах 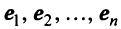 и
и 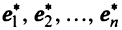 связаны соотношением
связаны соотношением

где 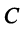 — матрица перехода от старого базиса к новому.
— матрица перехода от старого базиса к новому.
 При воздействии линейного оператора
При воздействии линейного оператора  вектор
вектор  пространства
пространства 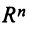 переводится в вектор
переводится в вектор 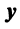 этого пространства, т.е. справедливо равенство (3.21) (в старом базисе) и равенство
этого пространства, т.е. справедливо равенство (3.21) (в старом базисе) и равенство

(в новом базисе). Так как 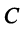 — матрица перехода от старого базиса к новому, то в соответствии с (3.12)
— матрица перехода от старого базиса к новому, то в соответствии с (3.12)

Умножим равенство (3.24) слева на матрицу  , получим
, получим 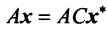 или с учетом (3.21)
или с учетом (3.21) 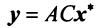 . Заменив левую часть полученного выражения в соответствии с (3.25), имеем:
. Заменив левую часть полученного выражения в соответствии с (3.25), имеем: 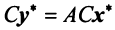 или
или 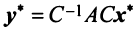 . Сравнивая найденное выражение с (3.23), мы получим доказываемую формулу (3.22).
. Сравнивая найденное выражение с (3.23), мы получим доказываемую формулу (3.22). 
Пример:
В базисе 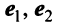 оператор (преобразование)
оператор (преобразование)  имеет матрицу
имеет матрицу 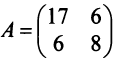 . Найти матрицу оператора
. Найти матрицу оператора  в базисе
в базисе 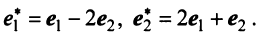
Решение:
Матрица перехода здесь 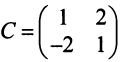 , а обратная к ней матрица
, а обратная к ней матрица 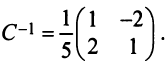 Следовательно, по (3.22)
Следовательно, по (3.22)
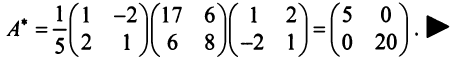
Собственные векторы и собственные значения линейного оператора
Определение. Вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если найдется такое число
, если найдется такое число 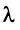 , что
, что

Число 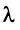 называется собственным значением оператора
называется собственным значением оператора  (матрицы
(матрицы  ), соответствующим вектору
), соответствующим вектору 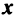 .
.
Из определения следует, что собственный вектор под действием линейного оператора  переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
Равенство (3.26) можно записать в матричной форме:

где вектор 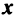 представлен в виде вектора-столбца, или в развернутом виде
представлен в виде вектора-столбца, или в развернутом виде
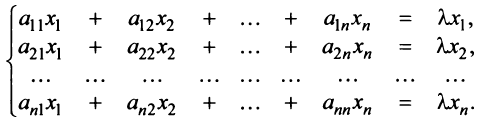
Перепишем систему так, чтобы в правых частях были нули:
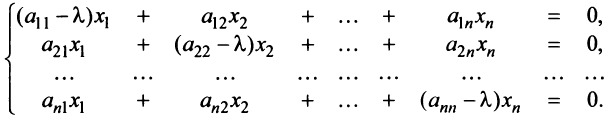
или в матричном виде
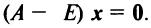
Полученная однородная система всегда имеет нулевое решение 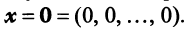 Для существования ненулевого решения (см. § 2.5) необходимо и достаточно, чтобы определитель системы
Для существования ненулевого решения (см. § 2.5) необходимо и достаточно, чтобы определитель системы
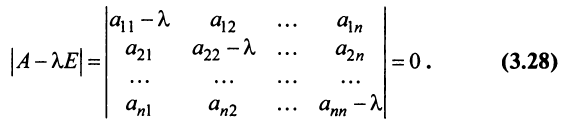
Определитель 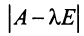 является многочленом
является многочленом 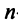 -й степени относительно
-й степени относительно 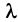 . Этот многочлен называется характеристическим многочленом оператора
. Этот многочлен называется характеристическим многочленом оператора  или матрицы
или матрицы  , а уравнение (3.28) — характеристическим уравнением оператора
, а уравнение (3.28) — характеристическим уравнением оператора  или матрицы
или матрицы  .
.
Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен 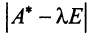 полученный в новом базисе
полученный в новом базисе 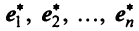 , если известна матрица
, если известна матрица 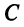 перехода от старого базиса
перехода от старого базиса 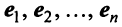 к новому. С учетом (3.22) получим
к новому. С учетом (3.22) получим
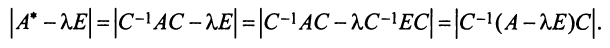
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц (см. §1.4), получим
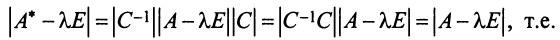
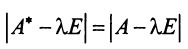 независимо от выбора базиса.
независимо от выбора базиса.
Пример:
Найти собственные значения и собственные векторы линейного оператора 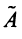 , заданного матрицей
, заданного матрицей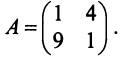
Решение:
Составляем характеристическое уравнение 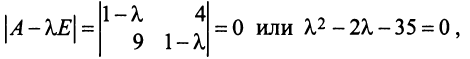
откуда собственные значения линейного оператора 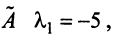
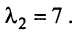
Находим собственный вектор 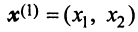 , соответствующий собственному значению
, соответствующий собственному значению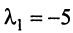 . Для этого решаем матричное уравнение
. Для этого решаем матричное уравнение
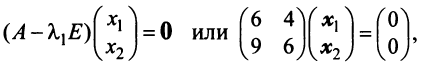 откуда находим
откуда находим 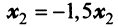 . Положив
. Положив 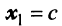 , получим, что векторы
, получим, что векторы 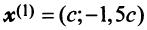 при любом
при любом 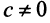 являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 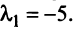
Аналогично можно убедиться в том, что векторы 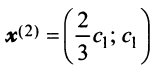 при любом
при любом 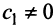 являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 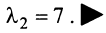
Наиболее простой вид принимает матрица 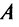 линейного оператора
линейного оператора  , имеющего
, имеющего 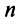 линейно независимых собственных векторов
линейно независимых собственных векторов 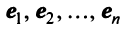 с собственными значениями, соответственно равными
с собственными значениями, соответственно равными 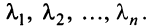 Векторы
Векторы 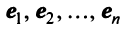 примем за базисные. Тогда
примем за базисные. Тогда 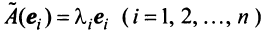 или с учетом (3.18)
или с учетом (3.18)
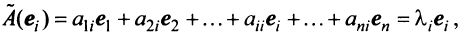
откуда 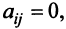 если
если 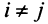 , и
, и 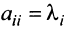 ,если
,если 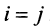 . Таким образом, матрица оператора
. Таким образом, матрица оператора  в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
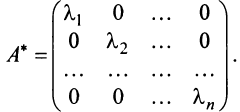 Верно и обратное: если матрица
Верно и обратное: если матрица 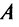 линейного оператора
линейного оператора  в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора
в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора  .
.
Можно доказать, что если линейный оператор имеет 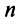 попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
- Заказать решение задач по высшей математике
Пример:
Привести матрицу 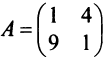 линейного оператора
линейного оператора  к диагональному виду.
к диагональному виду.
Решение:
В примере 3.7 были найдены собственные значения матрицы 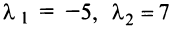 и соответствующие им собственные векторы
и соответствующие им собственные векторы 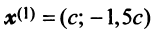 и
и 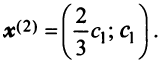 Так как координаты векторов
Так как координаты векторов 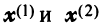 не пропорциональны, то векторы
не пропорциональны, то векторы 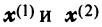 линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов
линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов 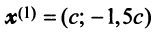 и
и 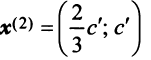 (т.е. при любых
(т.е. при любых 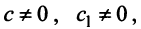 например при
например при 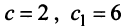 из векторов
из векторов 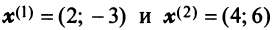 и т.д.), матрица
и т.д.), матрица 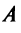 будет иметь диагональный вид:
будет иметь диагональный вид: 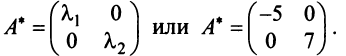 Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы
Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы 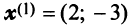 и
и 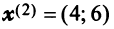 . Действительно, матрица
. Действительно, матрица 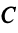 перехода от старого базиса к новому в этом случае будет иметь вид
перехода от старого базиса к новому в этом случае будет иметь вид 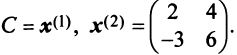 Тогда в соответствии с (3.22) матрица
Тогда в соответствии с (3.22) матрица 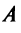 в новом базисе
в новом базисе 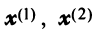 примет вид:
примет вид:
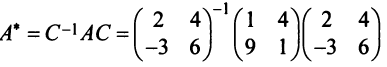
или после вычислений (которые мы опускаем) 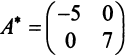
т.е. получим ту же диагональную матрицу, элементы которой по главной диагонали равны собственным значениям матрицы 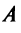 . ►
. ►
Квадратичные формы
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение. Квадратичной формой 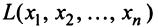 от
от 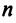 переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
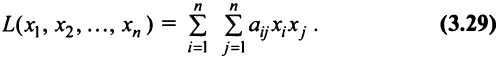
Предполагаем, что коэффициенты квадратичной формы 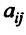 — действительные числа, причем
— действительные числа, причем 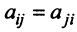 . Матрица
. Матрица 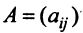
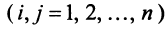 , составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:
, составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:

где 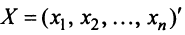 — матрица-столбец переменных. В самом деле :
— матрица-столбец переменных. В самом деле : 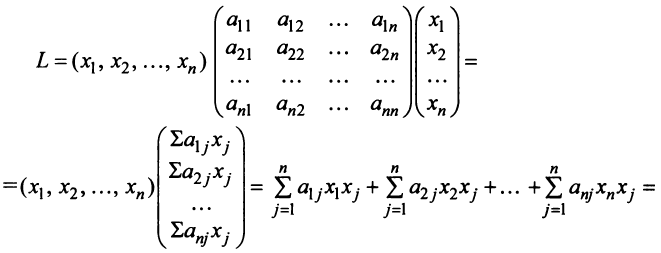
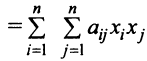 и эквивалентность формул (3.29) и (3.30) установлена.
и эквивалентность формул (3.29) и (3.30) установлена.
Пример:
Дана квадратичная форма 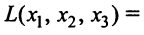
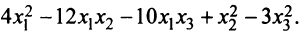 Записать ее в матричном виде.
Записать ее в матричном виде.
Решение:
Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, -3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
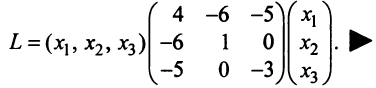
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных 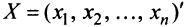 и
и 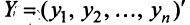 связаны линейным соотношением
связаны линейным соотношением 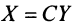 , где,
, где, 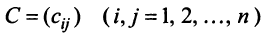 есть некоторая невырожденная матрица
есть некоторая невырожденная матрица 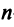 -го порядка. Тогда квадратичная форма
-го порядка. Тогда квадратичная форма
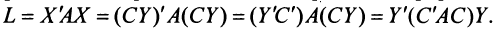
, Итак, при невырожденном линейном преобразовании 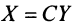 матрица квадратичной формы принимает вид:
матрица квадратичной формы принимает вид:

Пример:
Дана квадратичная форма 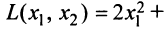
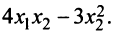 Найти квадратичную форму
Найти квадратичную форму 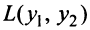 , полученную из данной линейным преобразованием
, полученную из данной линейным преобразованием 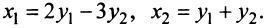
Решение:
Матрица данной квадратичной формы 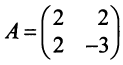 , а матрица линейного преобразования
, а матрица линейного преобразования 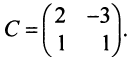
Следовательно, по (3.31) матрица искомой квадратичной формы 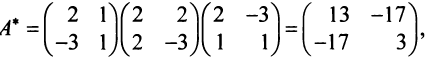 а квадратичная форма имеет вид
а квадратичная форма имеет вид 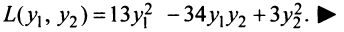
Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Квадратичная форма 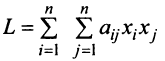 , называется канонической (или имеет канонический вид), если все ее коэффициенты
, называется канонической (или имеет канонический вид), если все ее коэффициенты 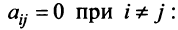
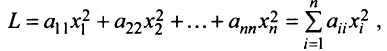
а ее матрица является диагональной. Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Пример:
Привести к каноническому виду квадратичную форму
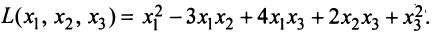
Решение:
Вначале вьделим полный квадрат при переменной 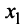 , коэффициент при квадрате которой отличен от нуля:
, коэффициент при квадрате которой отличен от нуля:
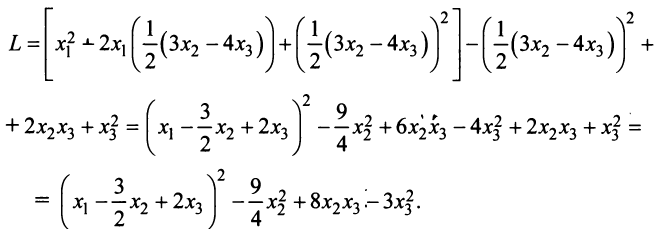
Теперь выделяем полный квадрат при переменной 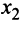 , коэффициент при которой отличен от нуля:
, коэффициент при которой отличен от нуля:
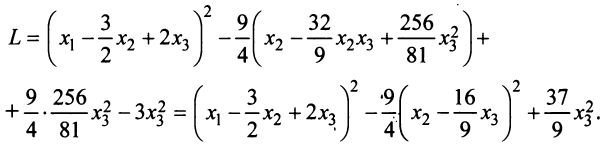 Итак, невырожденное линейное преобразование
Итак, невырожденное линейное преобразование
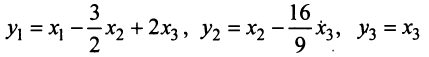
приводит данную квадратичную форму к каноническому виду
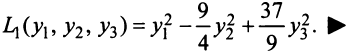
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Например, квадратичную форму 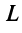 в примере 3.10 можно было привести к виду
в примере 3.10 можно было привести к виду
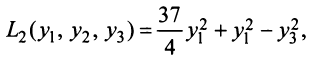
применив невырожденное линейное преобразование
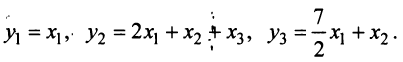
Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма 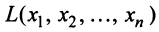 называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
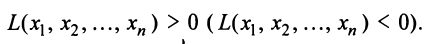
Так, например, квадратичная форма 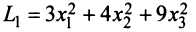 является положительно определенной, а форма
является положительно определенной, а форма 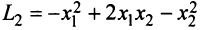 — отрицательно определенной.
— отрицательно определенной.
Теорема. Для того чтобы квадратичная форма 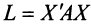 была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения
была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 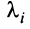 матрицы
матрицы 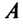 были положительны (отрицательны).
были положительны (отрицательны).
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 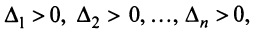 где
где
 Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка. ‘
Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка. ‘
Пример:
Доказать, что квадратичная форма 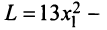
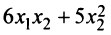 является положительно определенной.
является положительно определенной.
Решение:
Первый способ. Матрица  квадратичной формы имеет вид
квадратичной формы имеет вид 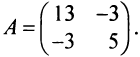 Для матрицы
Для матрицы характеристическое
характеристическое
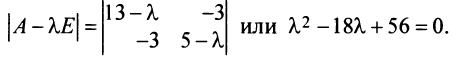
Решая уравнение, найдем 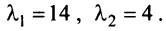 Так как корни характеристического уравнения матрицы
Так как корни характеристического уравнения матрицы  положительны, то на основании приведенной теоремы квадратичная форма
положительны, то на основании приведенной теоремы квадратичная форма 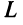 — положительно определенная.
— положительно определенная.
Второй способ. Так как главные миноры матрицы 
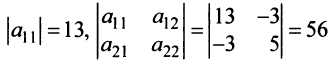 положительны, то по критерию Сильвестра данная квадратичная форма
положительны, то по критерию Сильвестра данная квадратичная форма 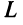 положительно определенная. ►
положительно определенная. ►
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется 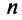 стран
стран 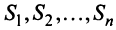 , национальный доход каждой из которых равен соответственно
, национальный доход каждой из которых равен соответственно 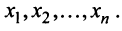 Обозначим коэффициентами
Обозначим коэффициентами 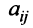 долю национального дохода, которую страна
долю национального дохода, которую страна  тратит на покупку товаров у страны
тратит на покупку товаров у страны  . Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
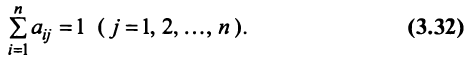
Рассмотрим матрицу 
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы 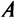 равна 1.
равна 1.
Для любой страны 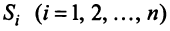 выручка от внутренней и внешней торговли составит:
выручка от внутренней и внешней торговли составит: 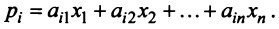
Для сбалансированной торговли необходима бездефицитность торговли каждой страны 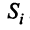 , т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
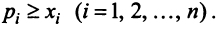
Если считать, что 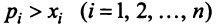 , то получаем систему неравенств
, то получаем систему неравенств
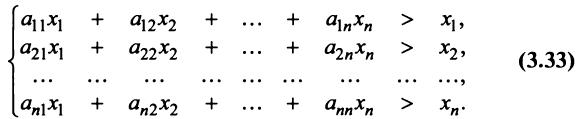
Сложив все неравенства системы (3.33), получим после группировки 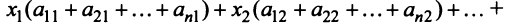
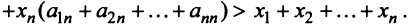
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
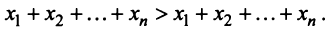
Таким образом, неравенство 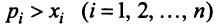 невозможно, и условие
невозможно, и условие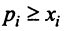 , принимает вид
, принимает вид 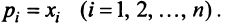 (С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
(С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
Вводя вектор  национальных доходов стран, получим матричное уравнение
национальных доходов стран, получим матричное уравнение

В котором вектор х записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы  отвечающего собственному значению
отвечающего собственному значению
Пример:
Структурная матрица торговли трех стран  имеет вид:
имеет вид:
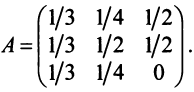
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный вектор 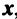 , отвечающий собственному значению
, отвечающий собственному значению 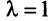 , решив уравнение
, решив уравнение 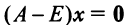 или систему
или систему
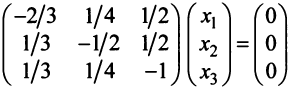
методом Гаусса. Найдем 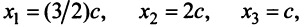 т.е.
т.е. 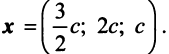 Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
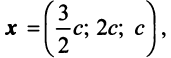 т.е. при соотношении национальных доходов стран
т.е. при соотношении национальных доходов стран 
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
Содержание:
- Линейные преобразования. Собственные векторы и собственные числа линейного оператора
- Собственные векторы и собственные числа линейного оператора: определение, свойства
- Нахождение собственных чисел и собственных векторов
- Базис пространства из собственных векторов линейного оператора
- Линейная модель обмена (модель международной торговли)
Линейные преобразования. Собственные векторы и собственные числа линейного оператора
Линейные преобразования (линейные операторы). Матрица линейного преобразования 
Пусть задано  -мерный пространство
-мерный пространство  . Если каждому вектору
. Если каждому вектору  поставлено в соответствие единственный вектор
поставлено в соответствие единственный вектор

этого же пространства, говорится, что в векторном пространстве  задано преобразование
задано преобразование  , или оператор
, или оператор  .
.
Вектор  – результат линейного преобразования – называют образом вектора
– результат линейного преобразования – называют образом вектора  , а выходной вектор
, а выходной вектор  – прообразом вектора
– прообразом вектора  .
.
Преобразование  называется линейным преобразованием, или линейным оператором, если для произвольных векторов
называется линейным преобразованием, или линейным оператором, если для произвольных векторов  и произвольного действительного скаляра
и произвольного действительного скаляра  выполняются условия:
выполняются условия:

То есть линейный оператор преобразует пространство  в то самое пространство. Это записывается следующим образом:
в то самое пространство. Это записывается следующим образом:

Примерами простейших линейных преобразований являются:
тождественное преобразование:  , когда каждый
, когда каждый  -мерный вектор пространства превращается в самого себя, то есть остается без изменения;
-мерный вектор пространства превращается в самого себя, то есть остается без изменения;
нулевой оператор  , когда каждый
, когда каждый  -мерный вектор пространства превращается в ноль-вектор этого же пространства, то есть
-мерный вектор пространства превращается в ноль-вектор этого же пространства, то есть 
Линейное преобразование  , с помощью которого осуществляется восстановление вектора
, с помощью которого осуществляется восстановление вектора  по его образу
по его образу  , называется обратным к
, называется обратным к  линейным преобразованием. В отличие от матрицы оператор записывают
линейным преобразованием. В отличие от матрицы оператор записывают  каллиграфическим
каллиграфическим шрифтом.
шрифтом.
Рассмотрим задачу об отыскании координат образа вектора  .
.
Пусть в пространстве  выбрано базис
выбрано базис  (не обязательно ортонормированный) и
(не обязательно ортонормированный) и  есть координатами вектора
есть координатами вектора  в этом базисе. Обозначим через
в этом базисе. Обозначим через  координаты вектора
координаты вектора  в выбранном базисе. по условию
в выбранном базисе. по условию  , тогда согласно линейностью оператора
, тогда согласно линейностью оператора  получим :
получим :

Но образы  тоже являются векторами с
тоже являются векторами с  , поэтому иx можно разложить по тому же базисом. Пусть
, поэтому иx можно разложить по тому же базисом. Пусть

где  коэффициенты разложения вектора
коэффициенты разложения вектора  по базису
по базису 
С учетом (5.5) соотношение (5.4) принимает вид:

Группируя члены правой части относительно векторов базиса, имеем:

С другой стороны, если  являются координатами вектора
являются координатами вектора  в базисе
в базисе  то его можно представить следующим образом:
то его можно представить следующим образом:

Сопоставляем (5.8) из (5.7) и получаем координаты вектора  :
:

Следовательно, при линейном преобразовании:

координаты образа вектора являются линейными комбинациями координат прообраза, коэффициенты при которых составляют матрицу  -го порядка (обозначим ее через
-го порядка (обозначим ее через  ):
):

Матрица  , которая в произведении (слева) с вектором с
, которая в произведении (слева) с вектором с  определяет координаты его образа при линейном преобразовании
определяет координаты его образа при линейном преобразовании  , Называется матрицей линейного преобразования
, Называется матрицей линейного преобразования  в базисе
в базисе  и пишут:
и пишут:

Каждый –  -й – столбец матрицы
-й – столбец матрицы  составляют коэффициенты разложения вектора
составляют коэффициенты разложения вектора  по базису
по базису  каждая –
каждая –  -я – строка определяет коэффициенты разложения координат вектора
-я – строка определяет коэффициенты разложения координат вектора  по координатам вектора
по координатам вектора  .
.
Обратите внимание, что  – нераздельный символ (обозначение вектораобраза), а
– нераздельный символ (обозначение вектораобраза), а  – произведение матрицы с вектором (прообразом).
– произведение матрицы с вектором (прообразом).
Каждому линейном оператору  -мерного пространства отвечает матрица
-мерного пространства отвечает матрица  -го порядка в данном базисе. И наоборот, каждой матрицы
-го порядка в данном базисе. И наоборот, каждой матрицы  -го порядка отвечает линейный оператор
-го порядка отвечает линейный оператор  -мерного пространства с определенным базисом.
-мерного пространства с определенным базисом.
Например, с помощью оператора линейных преобразований можно описать поворот произвольного вектора с пространства  вокруг начала координат на угол
вокруг начала координат на угол  против часовой стрелки. Формулы поворота осей координат (формулы перехода от исходных координат
против часовой стрелки. Формулы поворота осей координат (формулы перехода от исходных координат  и
и  к новым
к новым  и
и  , и наоборот ) определяют алгебраическую форму изображения линейного оператора поворота осей:
, и наоборот ) определяют алгебраическую форму изображения линейного оператора поворота осей:

где  оператор перехода от исходных (новых) координат к новым (исходных);
оператор перехода от исходных (новых) координат к новым (исходных);
 векторы, началом которых является точка
векторы, началом которых является точка  , а концами –
, а концами –
точки  и
и  , соответственно.
, соответственно.
По соотношению (5.12) матрица линейного преобразования}  , Описывающий поворот произвольного вектора из пространства
, Описывающий поворот произвольного вектора из пространства  вокруг начала координат на угол
вокруг начала координат на угол  против часовой стрелки, имеет вид:
против часовой стрелки, имеет вид:

а матрица обратного линейного преобразования  , то есть такого, что описывает поворот произвольного вектора из пространства
, то есть такого, что описывает поворот произвольного вектора из пространства  вокруг начала координат на угол
вокруг начала координат на угол  по часовой стрелке, имеет вид:
по часовой стрелке, имеет вид:

Теорема 5.1 (о связи между матрицами оператора в различных базисах).
Матрицы  и
и  линейного оператора
линейного оператора  в разных базисах
в разных базисах  и
и  связаны между собой соотношением:
связаны между собой соотношением:

где  матрица перехода от исходного к новому базису.
матрица перехода от исходного к новому базису.
Доказательство. Пусть линейный оператор  превращает вектор
превращает вектор  пространства
пространства  в вектор
в вектор  того самого пространства. Тогда в матричной форме связь между вектором
того самого пространства. Тогда в матричной форме связь между вектором  и его образом
и его образом  в исходном базисе можно записать как
в исходном базисе можно записать как  , а в новом – как
, а в новом – как  . Поскольку
. Поскольку  является матрицей перехода от исходного базиса к новому, то в соответствии с (4.18) имеем:
является матрицей перехода от исходного базиса к новому, то в соответствии с (4.18) имеем:

Умножим равенство (5.14) слева на матрицу  и получим
и получим  . Отсюда по определению линейного оператора имеем:
. Отсюда по определению линейного оператора имеем:  . С учетом (5.15):
. С учетом (5.15):

Сравнив соотношение  и
и  , получаем
, получаем 
Две квадратные матрицы  и
и  называются подобными, если существует такая невырожденная матрица
называются подобными, если существует такая невырожденная матрица  , матрицы
, матрицы  и
и  связанные соотношениями:
связанные соотношениями:

Соответствующие линейные операторы называются преобразованиями сходства.
Подобные матрицы описывают то же линейное преобразование, но в разных базисах, а матрица  является матрицей перехода от одного базиса к другому.
является матрицей перехода от одного базиса к другому.
Подобные матрицы имеют те же ранги, суммы элементов главной диагонали и определители.
В базисе  и
и  задана матрица линейного оператора
задана матрица линейного оператора  :
:

Определим матрицу  , которая отвечает том же оператору в базисе векторов
, которая отвечает том же оператору в базисе векторов  и
и  есть матрица
есть матрица  подобна матрице
подобна матрице  .
.
Предоставим расписание векторов нового базиса по векторам исходного базиса:  . Соответственно, матрица перехода от исходного к новому базису имеет вид:
. Соответственно, матрица перехода от исходного к новому базису имеет вид:

Ее определитель  , то есть матрица
, то есть матрица  невырожденная и имеет обратную:
невырожденная и имеет обратную:

По теореме 5.1 определяем матрицу оператора  в новом базисе:
в новом базисе:

Обратите внимание, что в новом базисе матрица оператора  оказалась диагональной.
оказалась диагональной.
Собственные векторы и собственные числа линейного оператора: определение, свойства
Рассмотрим  -мерных линейный пространство
-мерных линейный пространство  с определенным базисом и матрицу
с определенным базисом и матрицу  , некоторого линейного оператора
, некоторого линейного оператора  пространства.
пространства.
Ненулевой вектор  называют собственным, или характеристическим вектором линейного оператора
называют собственным, или характеристическим вектором линейного оператора  (или матрицы
(или матрицы  ), если существует такое действительное число
), если существует такое действительное число  , имеет место равенство:
, имеет место равенство:

Скаляр  называется собственным, или характеристическим, числом матрицы
называется собственным, или характеристическим, числом матрицы  , или ее собственным значением, соответствует собственному вектору
, или ее собственным значением, соответствует собственному вектору  :
:
Согласно определениями собственного числа и собственного вектора имеем:
1) Если  , то каждый ненулевой вектор из
, то каждый ненулевой вектор из  является собственным вектором матрицы
является собственным вектором матрицы  , при этом
, при этом  , ведь по свойству единичной матрицы имеем
, ведь по свойству единичной матрицы имеем  ;
;
2) любой ненулевой  -мерный вектор является собственным вектором нулевой матрицы
-мерный вектор является собственным вектором нулевой матрицы  , при этом
, при этом  , так как
, так как  .
.
Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы 
Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы



Запишем матричное уравнение (5.17) в развернутом виде:
Таким образом, задача сводится к решению однородной системы  линейных уравнений с
линейных уравнений с  неизвестными. Нас интересуют (по определению собственного вектора) только ненулевые векторы, то есть нетривиальные решения системы, поэтому определитель системы (5.18) должен быть равен нулю:
неизвестными. Нас интересуют (по определению собственного вектора) только ненулевые векторы, то есть нетривиальные решения системы, поэтому определитель системы (5.18) должен быть равен нулю:

Раскрытие определителя в соотношении (5.19) дает многочлен степени  относительно
относительно  , который называется характеристическим многочленом матрицы
, который называется характеристическим многочленом матрицы  , а соотношение (5.19), которое можно представить в виде
, а соотношение (5.19), которое можно представить в виде  , определяет уравнение для нахождения собственных чисел, которое называют характеристическим уравнением матрицы
, определяет уравнение для нахождения собственных чисел, которое называют характеристическим уравнением матрицы  .
.
По основной теореме алгебры уравнения  любой матрицы
любой матрицы  имеет
имеет  корней, если каждый из них считать столько раз, какова его кратность. Характеристическое уравнение матрицы может иметь только действительные, но и комплексные корни, то есть числа вида
корней, если каждый из них считать столько раз, какова его кратность. Характеристическое уравнение матрицы может иметь только действительные, но и комплексные корни, то есть числа вида  где
где  действительные числа,
действительные числа,  мнимая единица.
мнимая единица.
Множество всех собственных чисел матрицы называют спектром матрицы. Если в спектре матрицы то же собственное число повторяется  раз, то говорят, что кратность этого собственного числа равна
раз, то говорят, что кратность этого собственного числа равна  .
.
Теорема 5.2 (о единственности собственного чucлa, что соответствует собственному вектору). Если  – собственный вектор матрицы
– собственный вектор матрицы  , то существует единственный скаляр
, то существует единственный скаляр  , который удовлетворяет условие
, который удовлетворяет условие  .
.
Доказательство. Предположим, что кроме собственного числа  существует еще один
существует еще один
скаляр  , такой, что
, такой, что  . Тогда должно выполняться равенство
. Тогда должно выполняться равенство  . Поскольку по определению собственный вектор является ненулевым, то есть
. Поскольку по определению собственный вектор является ненулевым, то есть  , получим
, получим  .
.
Согласно теореме 5.2 говорят, что собственный вектор  из матрицы
из матрицы  принадлежит собственному числу
принадлежит собственному числу  .
.
Теорема 5.3 (о множестве собственных векторов, принадлежащих собственному числу). Если матрица имеет собственный вектор, принадлежащий собственному числу  , то таких векторов бесконечно много.
, то таких векторов бесконечно много.
Доказательство базируется на определении собственного вектора и свойствах ассоциативности и коммутативности операции умножения матрицы на скаляр.
Действительно, пусть  собственный вектор матрицы
собственный вектор матрицы  , тогда
, тогда  . Привлечем к рассмотрению вектор
. Привлечем к рассмотрению вектор  , коллинеарный вектору
, коллинеарный вектору  , то есть
, то есть  , где
, где  , и покажем, что в также является собственным вектором матрицы
, и покажем, что в также является собственным вектором матрицы  :
:

Поскольку равенство (5.19) выполняется для произвольного  , то существует множество собственных векторов, принадлежащих данному собственному числу.
, то существует множество собственных векторов, принадлежащих данному собственному числу.
Теорема 5.4 (критерий существования собственного вектора  , соответствующего собственному числу
, соответствующего собственному числу  ). Вектор
). Вектор  тогда и только тогда является собственным вектором матрицы
тогда и только тогда является собственным вектором матрицы  , соответствующим собственному числу
, соответствующим собственному числу  , когда его координаты
, когда его координаты  образуют ненулевое решение однородной квадратной системы линейных алгебраических уравнений
образуют ненулевое решение однородной квадратной системы линейных алгебраических уравнений 
 или
или 
Доказательство сводится к тождественных преобразований матричных уравнений.
Необходимость уже доказано переходом от соотношения  , к однородной системе линейных уравнений
, к однородной системе линейных уравнений  , представленной в развернутом виде (5 18).
, представленной в развернутом виде (5 18).
Достаточность. На основании свойств действий над матрицами с учетом условия  , осуществит переход от однородной системы уравнений в матричной форме с соотношением
, осуществит переход от однородной системы уравнений в матричной форме с соотношением  :
:

Теорема 5.5 (пpo линейную независимость собственных векторов). Собственные векторы, принадлежащие различным собственным числам, является линейно независимыми.
Доказательство проведем методом от противного. Пусть  два произвольные собственные векторы, принадлежащие соответственно собственным числам
два произвольные собственные векторы, принадлежащие соответственно собственным числам  и
и 
 . Необходимо показать, что линейная комбинация этих собственных векторов
. Необходимо показать, что линейная комбинация этих собственных векторов  ноль-вектор только тогда, когда
ноль-вектор только тогда, когда  , то есть
, то есть

Предположим обратное. Пусть (5.23) выполняется при условии, что одно из чисел  не является нулем, например,
не является нулем, например, 
Умножим левую и правую части (5.23) на собственное число  . Тогда
. Тогда

Левую и правую части равенства (5.23) умножим на матрицу  слева, и, учитывая свойства операций над матрицами, получим:
слева, и, учитывая свойства операций над матрицами, получим:

Сравним (5.25) и (5.24). Получаем:

По условию теоремы  . По определению вектор
. По определению вектор  является ненулевым, поэтому равенство (5.26) возможно только при
является ненулевым, поэтому равенство (5.26) возможно только при  , то есть предположение о линейной зависимости векторов
, то есть предположение о линейной зависимости векторов  и
и  ошибочно.
ошибочно.
Если есть более двух собственных векторов, принадлежащих попарно различным собственным числам, доведение аналогичное (с использованием метода математической индукции).
Заметим, что собственные векторы, принадлежащих различным собственным числам, можно использовать как базисные векторы пространства  .
.
Теорема 5.6 (пpo сумму и произведение собственных чисел). Если  собственные числа матрицы
собственные числа матрицы  , то:
, то:
1) сумма собственных чисел равна сумме элементов главной диагонали матрицы  :
:

2) произведение собственных чисел равна определителю матрицы  :
:

Доказательство основывается на формулах Виета, которые описывают соотношение между корнями и коэффициентами многочлена  -гo степени в случае, когда его старший коэффициент равен единице.
-гo степени в случае, когда его старший коэффициент равен единице.
Рассмотрим простейший случай  . Запишем характеристическое уравнение в развернутом виде:
. Запишем характеристическое уравнение в развернутом виде:

С (5.29) по теореме Виета (для квадратного уравнения) имеем:

Сумму всех диагональных элементов матрицы называют следом (от нем. spur – след) этой матрицы и обозначают  .
.
Для квадратной матрицы произвольного порядка  теорему 5.6 в символьном виде можно записать так:
теорему 5.6 в символьном виде можно записать так:

при этом собственное число  берем столько раз, какова его кратность как корня характеристического уравнения (5.29).
берем столько раз, какова его кратность как корня характеристического уравнения (5.29).
Нахождение собственных чисел и собственных векторов
Рассмотрим алгоритм нахождения собственных чисел матрицы  и собственных векторов, которые им принадлежат.
и собственных векторов, которые им принадлежат.
Согласно соотношениями (5.18) и (5.19) имеем такой порядок отыскания собственных чисел и собственных векторов матрицы.
1. Составляем по исходной матрицей  характеристическое уравнение (5.18) и решаем его, то есть находим спектр собственных чисел.
характеристическое уравнение (5.18) и решаем его, то есть находим спектр собственных чисел.
2. Подставляем поочередно каждое собственное число в систему (5.18) и находим все ее нетривиальные решения, что и дает множество собственных векторов, принадлежащих соответствующему собственному числу.
Замечания. Множество всех собственных векторов, принадлежащих определенному собственному числу, можно представить как линейную комбинацию фундаментальных решений однородной системы уравнений согласно (4.19), гл. 4.
Найдем собственные числа и собственные векторы матрицы

Характерным уравнением этой матрицы является квадратное уравнение:

Решив его, получим собственные числа  и
и 
Теперь описываем множества  и
и  всех собственных векторов, принадлежащих найденным собственным числам.
всех собственных векторов, принадлежащих найденным собственным числам.
Для этого в матрицу  вместо
вместо  подставим поочередно значения собственных чисел, запишем соответствующую систему однородных линейных уравнений (5.18) и решим ее:
подставим поочередно значения собственных чисел, запишем соответствующую систему однородных линейных уравнений (5.18) и решим ее:

Предоставляя параметру  произвольных значений, для данного собственного числа
произвольных значений, для данного собственного числа  получим совокупность коллинеарных между собой собственных векторов.
получим совокупность коллинеарных между собой собственных векторов.
Теорема 5.7 (про собственные числа и собственные векторы симметричной матрицы).
Симметричная матрица  имеет только действительные собственные числа. Собственные векторы, принадлежащие разным собственным числам, ортогональны и линейно независимы.
имеет только действительные собственные числа. Собственные векторы, принадлежащие разным собственным числам, ортогональны и линейно независимы.
Теорема приводим без доказательства.
Проиллюстрируем прав выводов данной теоремы на примере.
Пусть имеем симметричную матрицу

Найдем собственные числа и собственные векторы этой матрицы и докажем ортогональность собственных векторов, соответствующих различным собственным числам.
1. Составим характеристическое уравнение матрицы

2. Найдем корни полученного кубического уравнения относительно  . С элементарной алгебры известно, если многочлен со старшим коэффициентом, равным единице, имеет целые корни, то их следует искать среди делителей свободного члена. Перебирая делители числа 36, убеждаемся, что
. С элементарной алгебры известно, если многочлен со старшим коэффициентом, равным единице, имеет целые корни, то их следует искать среди делителей свободного члена. Перебирая делители числа 36, убеждаемся, что  является корнем уравнения (5.30).
является корнем уравнения (5.30).
Нахождение других двух корней сводится к решению квадратного уравнения:

3. Опишем множества  и
и  собственных векторов, принадлежащих найденным собственным числам.
собственных векторов, принадлежащих найденным собственным числам.
Для этого в матрицу  вместо
вместо  подставляем поочередно значения собственных чисел, записываем соответствующую систему однородных линейных уравнений (5.17) и решаем ее методом Жордана-Гаусса:
подставляем поочередно значения собственных чисел, записываем соответствующую систему однородных линейных уравнений (5.17) и решаем ее методом Жордана-Гаусса:

Аналогично находим собственные векторы  и
и 

Система векторов  и
и  является линейно независимой, поскольку
является линейно независимой, поскольку

Убеждаемся, что векторы  и
и  – попарно ортогональны.
– попарно ортогональны.
Для этого определим их скалярные произведения:

Поскольку скалярные произведения векторов равны нулю, то векторы попарно ортогональны.
Если в выражениях (5.31-5.33) положить  , то получим систему векторов:
, то получим систему векторов:

которая использовалась как базис пространства  в примере после теоремы
в примере после теоремы 
 и
и  . В таком базисе, то есть базисе из собственных векторов, матрица оператора
. В таком базисе, то есть базисе из собственных векторов, матрица оператора  оказалась диагональной, ее ненулевыми элементами являются собственные числа матрицы
оказалась диагональной, ее ненулевыми элементами являются собственные числа матрицы  .
.
Теорема 5.8 (о преобразовании матрицы к диагональному виду). Матрица линейного оператора  в базисе
в базисе  имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы
имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы  .
.
Теорему наводим без доказательств
Заметим, что при нахождении собственных чисел для заданной матрицы самой задачей является решение алгебраического уравнения  -й степени, что во многих случаях сделать невозможно без использования приближенных методов. Изучение приближенных методов выходит за пределы программы. Поэтому предлагаем воспользоваться известными программами MatLab, MathCad, Maple и др.
-й степени, что во многих случаях сделать невозможно без использования приближенных методов. Изучение приближенных методов выходит за пределы программы. Поэтому предлагаем воспользоваться известными программами MatLab, MathCad, Maple и др.
Следующий пример был решен в пакете MatLab, в котором конечный результат вычислений предоставляется без промежуточных выкладок.
Найдем собственные числа и соответствующие им собственные векторы матрицы

Характерным уравнением для нахождения собственных чисел является уравнение

корнями которого будут числа  а соответствующие им собственные векторы имеют вид:
а соответствующие им собственные векторы имеют вид:

Собственные числа и собственные векторы матриц имеют широкий спектр использования, в частности, в аналитической геометрии (Раздел 2), в задачах различных отраслей естественных наук и эконометрики.
Базис пространства из собственных векторов линейного оператора
По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Возникает вопрос, при каких условиях существует базис линейного пространства  , построенный из собственных векторов матрицы.
, построенный из собственных векторов матрицы.
Лема. Если  является собственным числом матрицы
является собственным числом матрицы  , то множество собственных векторов матрицы
, то множество собственных векторов матрицы  содержит
содержит  линейно независимых векторов, где
линейно независимых векторов, где  – ранг матрицы
– ранг матрицы  .
.
Доказательство. Согласно теореме 5.4 множество собственных векторов совпадает с множеством всех решений однородной системы линейных уравнений:

где  – собственный вектор матрицы
– собственный вектор матрицы  , что соответствует собственному числу
, что соответствует собственному числу  . По теореме 4.4 такая система имеет фундаментальную систему решений, количество векторов которой равна
. По теореме 4.4 такая система имеет фундаментальную систему решений, количество векторов которой равна  , то есть содержит
, то есть содержит  – линейно независимых векторов.
– линейно независимых векторов.
Теорема 5.9 (о существовании базиса из собственных векторов матрицы). Пусть числа  образуют множество всех различных собственных чисел матрицы
образуют множество всех различных собственных чисел матрицы  . Если сумма рангов матриц
. Если сумма рангов матриц  равна
равна  , то в пространстве
, то в пространстве  существует базис из собственных векторов матрицы
существует базис из собственных векторов матрицы  .
.
Доказательство. Согласно лемме каждое множество собственных векторов, соответствующих уравнению  , содержит независимые векторы в количестве
, содержит независимые векторы в количестве  . По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Тогда для матрицы
. По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Тогда для матрицы  общее количество линейно независимых собственных векторов составляет:
общее количество линейно независимых собственных векторов составляет:

Поскольку собственные векторы матрицы  в совокупности составляют систему
в совокупности составляют систему  линейно независимых векторов, то они образуют базис пространства
линейно независимых векторов, то они образуют базис пространства  .
.
Теорема 5.10 (о существовании базиса из собственных векторов симметричной матрицы). Если матрица  линейного оператора симметрична, то в пространстве
линейного оператора симметрична, то в пространстве  существует базис, образованный из собственных векторов матрицы
существует базис, образованный из собственных векторов матрицы  .
.
Теорему принимаем без доказательств.
Построим ортонормированный базис пространства  , состоящий из собственных векторов матрицы
, состоящий из собственных векторов матрицы

линейного преобразования  , и найдем матрицу
, и найдем матрицу  заданного преобразования в этом базисе.
заданного преобразования в этом базисе.
Согласно теореме 5.9 такой базис существует, поскольку матрица  является симметричной матрицей. Составим характеристическое уравнение матрицы
является симметричной матрицей. Составим характеристическое уравнение матрицы  :
:

и решим его:  (собственное значение кратности
(собственное значение кратности  ) и
) и 
Для каждого из двух различных собственных чисел матрицы определим фундаментальную систему решений однородной системы уравнений:  . При
. При  в результате элементарных преобразований основной матрицы системы получаем:
в результате элементарных преобразований основной матрицы системы получаем:

По последним шагом элементарных преобразований матрицы записываем общее решение системы:

Определяем фундаментальную систему решений однородной системы уравнений 

Собственные векторы  и
и  являются ортогональными, поскольку их скалярное произведение равно нулю:
являются ортогональными, поскольку их скалярное произведение равно нулю: 
При  в результате элементарных преобразований основной матрицы системы получаем:
в результате элементарных преобразований основной матрицы системы получаем:

По последнем шагом элементарных преобразований матрицы записываем общее решение системы:

Возлагаем  и получаем фундаментальный решение однородной системы уравнений
и получаем фундаментальный решение однородной системы уравнений 

Поскольку  и
и  , то все три вектора попарно ортогональны. Объединив полученные фундаментальные системы решений, иметь систему собственных векторов матрицы
, то все три вектора попарно ортогональны. Объединив полученные фундаментальные системы решений, иметь систему собственных векторов матрицы  . Они образуют ортогональный базис пространства
. Они образуют ортогональный базис пространства  . После нормирования векторы приобретают вид:
. После нормирования векторы приобретают вид:

Это и есть ортогональный базис пространства  , состоящий из собственных векторов матрицы
, состоящий из собственных векторов матрицы  .
.
По соотношению (5.13) определим матрицу  , что соответствует оператору
, что соответствует оператору  в базисе из собственных векторов. Согласно теореме 5.8 эта матрица будет иметь диагональный вид, а элементами ее главной диагонали будут собственные числа этой матрицы. Заключим с собственными векторами
в базисе из собственных векторов. Согласно теореме 5.8 эта матрица будет иметь диагональный вид, а элементами ее главной диагонали будут собственные числа этой матрицы. Заключим с собственными векторами  ,
,  и
и  матрицу
матрицу  перехода к новому базису и найдем обратную к ней матрицу
перехода к новому базису и найдем обратную к ней матрицу  :
:

По матричным уравнением (5.13) находим матрицу  , что соответствует оператору
, что соответствует оператору  в базисе из собственных векторов:
в базисе из собственных векторов:

Следовательно, мы получили диагональную матрицу третьего порядка, элементами главной диагонали которой есть собственные числа матрицы  .
.
Далее приведен пример применения собственных векторов и собственных чисел в одной из многих задач экономики.
Линейная модель обмена (модель международной торговли)
Практически все страны кроме внутреннего товарообмена осуществляют внешний товарообмен, то есть занимаются внешней торговлей. Торговля считается сбалансированной, или бездефицитной, если для каждой страны прибыль от торговли не меньше объем средств, которые она вкладывает в товарооборот (внутренний и внешний).
Постановка задачи. Несколько стран осуществляют взаимный товарообмен. Известную долю бюджетных средств, тратит каждая страна на закупку товаров у другой страны, учитывая и внутренний товарооборот. Определить, каким должно быть соотношение бюджетов партнеров для того, чтобы обеспечить бездефицитность торговли.
Построение математической модели. Введем обозначения количественных характеристик, описывающих торговлю между странами, и определим связь между этими характеристиками. Пусть  – страны, участвующие в международной торговле. Доли средств, которые тратит страна
– страны, участвующие в международной торговле. Доли средств, которые тратит страна  на закупку товаров в стране
на закупку товаров в стране  , учитывая и внутренний товарооборот
, учитывая и внутренний товарооборот  , обозначим через
, обозначим через  . Понятно, что
. Понятно, что

Матрицу  , элементами которой являются числа
, элементами которой являются числа  , называют структурной матрицей торговли:
, называют структурной матрицей торговли:

Эта матрица описывает взаимодействие стран в процессе международной торговли. Соотношение (5.34) означает, что сумма элементов каждого столбца матрицы равна
1. Если объем средств, которые тратит каждая страна на торговлю, обозначить через  , соответственно, то прибыль
, соответственно, то прибыль  страны
страны  от внутренней и внешней торговли составит
от внутренней и внешней торговли составит

Чтобы торговля каждой страны была сбалансированной, по определению должно выполняться условие  , и
, и  , то есть прибыль от торговли не должна быть меньше расходов. Однако соблюдение этого требования в виде неравенства невозможно для всех стран в совокупности. Действительно, добавим левые и правые части указанных неровностей, изменяя
, то есть прибыль от торговли не должна быть меньше расходов. Однако соблюдение этого требования в виде неравенства невозможно для всех стран в совокупности. Действительно, добавим левые и правые части указанных неровностей, изменяя  от единицы до
от единицы до  :
:

Группируя в левой части слагаемые, содержащие каждое из  , получим:
, получим:

Учитывая соотношение (5.20), получим:

Отсюда следует, что сбалансированная торговля возможна только в случае знака равенства. Это, полагаем, понятно не только на основании аналитических выкладок, но и с экономической точки зрения (и даже просто с точки зрения здравого смысла): все страны в совокупности не могут получить прибыль. Более того, для одной из стран не может выполняться знак строгого неравенства  .
.
Итак, условием сбалансированной торговли является равенства  , и
, и  , из которых получим:
, из которых получим:

Введем в рассмотрение вектор (бюджетных) средств  и подадим систему (5.39) в матричной форме:
и подадим систему (5.39) в матричной форме:

С (5.40) следует, что при условии сбалансированности торговли между странами вектор средств  должен быть собственным вектором структурной матрицы торговли
должен быть собственным вектором структурной матрицы торговли  , который принадлежит собственному числу
, который принадлежит собственному числу  . Таким образом, решение задачи сводится к нахождению этого собственного вектора
. Таким образом, решение задачи сводится к нахождению этого собственного вектора  , компоненты которого устанавливают соотношение между бюджетами стран, участвующих в товарообмене.
, компоненты которого устанавливают соотношение между бюджетами стран, участвующих в товарообмене.
Рассмотрим товарообмен между тремя странами. Пусть структурная матрица торговли стран  , имеет вид:
, имеет вид:

Найдем вектор средств, компонентами которого являются доли от общего объема торговли, должна вкладывать каждая из стран во внешней товарооборот для того, чтобы торговля была сбалансированной.
Искомый вектор средств является собственным вектором структурной матрицы, принадлежащий собственному значению  . Его компоненты образуют ненулевое решение однородной СЛАУ:
. Его компоненты образуют ненулевое решение однородной СЛАУ:

Поскольку система является однородной, то расширенная матрица эквивалентна основной матрицы системы. Осуществим элементарные преобразования основной матрицы этой системы уравнений:

Находим общее решение системы, в котором  – базисные переменные,
– базисные переменные,  – свободная переменная:
– свободная переменная:

Отсюда следует, что для сбалансированности торговли необходимо, чтобы средства, которые вкладывает в внешний товарооборот каждая страна, соотносились как 
Лекции:
- Разложение в ряд Фурье четных и нечетных функций
- Функции многих переменных
- Наибольшее и наименьшее значение функции
- Уравнение плоскости
- Экстремум функции трёх переменных
- Как найти вероятность: пример решения
- Свойства определенного интеграла
- Комбинаторика
- Однородные дифференциальные уравнения
- Простейшие задачи аналитической геометрии
Собственные числа и собственные векторы матрицы.
Определение 9.3. Вектор х
называется собственным вектором
матрицы А, если найдется такое число
λ, что выполняется равенство: Ах
= λх, то есть результатом
применения к х линейного
преобразования, задаваемого матрицей
А, является умножение этого вектора
на число λ. Само число λ называется
собственным числом матрицы А.
Подставив в формулы (9.3) x`j
= λxj,
получим систему уравнений для определения
координат собственного вектора:
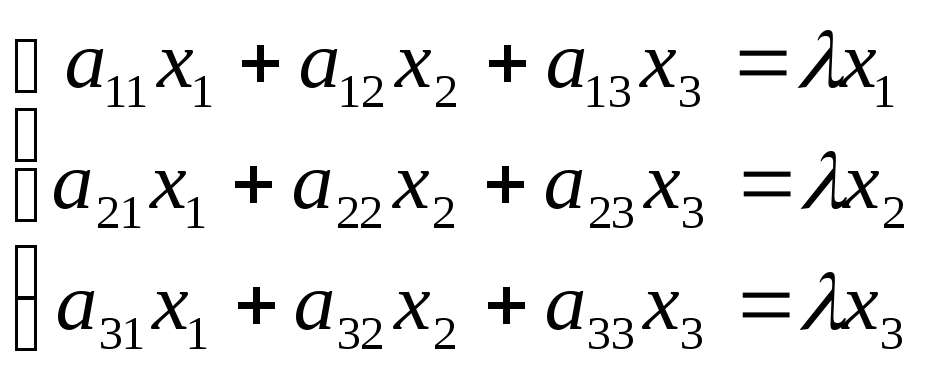 .
.
Отсюда
 .
.
(9.5)
Эта линейная однородная система будет
иметь нетривиальное решение только в
случае, если ее главный определитель
равен 0 (правило Крамера). Записав это
условие в виде:
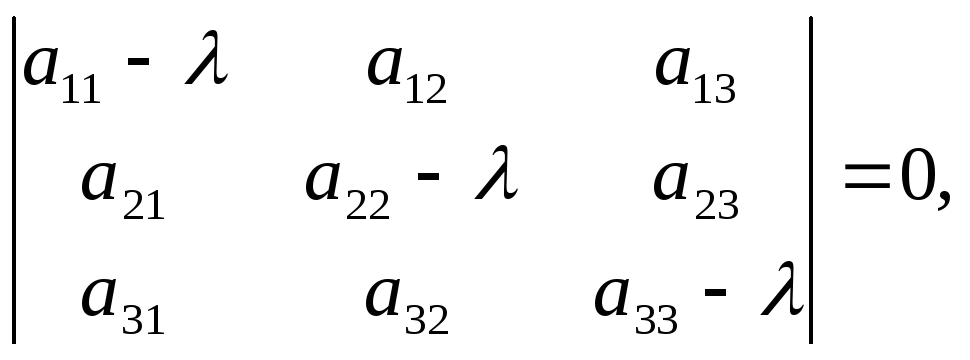
получим уравнение для определения
собственных чисел λ, называемое
характеристическим уравнением.
Кратко его можно представить так:
| A
– λE
| = 0,
(9.6)
поскольку в его левой части стоит
определитель матрицы А-λЕ. Многочлен
относительно λ | A
– λE| называется
характеристическим многочленом
матрицы А.
Свойства характеристического
многочлена:
-
Характеристический многочлен линейного
преобразования не зависит от выбора
базиса.
Доказательство.
 (см.
(см.
(9.4)), но
 следовательно,
следовательно,
 .
.
Таким образом,

не зависит от выбора базиса. Значит, и
|A-λE|
не изменяется при переходе к новому
базису. -
Если матрица А линейного преобразования
является симметрической (т.е.
аij=aji),
то все корни характеристического
уравнения (9.6) – действительные числа.
Свойства собственных чисел и
собственных векторов:
-
Если выбрать базис из собственных
векторов х1,
х2, х3,
соответствующих собственным значениям
λ1, λ2, λ3
матрицы А, то в этом базисе линейное
преобразование А имеет матрицу
диагонального вида:

(9.7)
Доказательство
этого свойства следует из определения
собственных векторов.
-
Если собственные значения преобразования
А различны, то соответствующие им
собственные векторы линейно независимы. -
Если характеристический многочлен
матрицы А имеет три различных корня,
то в некотором базисе матрица А
имеет диагональный вид.
Пример.
Найдем собственные числа и собственные
векторы матрицы

Составим характеристическое уравнение:

(1- λ)(5 –
λ)(1 – λ) + 6 – 9(5 – λ) – (1 – λ) –
(1 – λ) = 0, λ³ – 7λ² + 36 = 0, λ1
= -2, λ2 = 3, λ3 = 6.
Найдем координаты собственных векторов,
соответствующих каждому найденному
значению λ. Из (9.5) следует, что если
х(1)={x1,x2,x3}
– собственный вектор, соответствующий
λ1=-2, то

– совместная, но неопределенная система.
Ее решение можно записать в виде
х(1)={a,0,-a},
где а – любое число. В частности, если
потребовать, чтобы |x(1)|=1,
х(1)=![]()
Подставив в систему (9.5) λ2=3,
получим систему для определения координат
второго собственного вектора –
x(2)={y1,y2,y3}:
 ,
,
откуда х(2)={b,-b,b}
или, при условии |x(2)|=1,
x(2)=![]()
Для λ3 = 6 найдем собственный
вектор x(3)={z1,
z2, z3}:
 ,
,
x(3)={c,2c,c}
или в нормированном варианте
х(3) =
![]() Можно
Можно
заметить, что х(1)х(2)
= ab – ab
= 0, x(1)x(3)
= ac – ac
= 0, x(2)x(3)
= bc – 2bc
+ bc = 0. Таким
образом, собственные векторы этой
матрицы попарно ортогональны.
Лекция 10.
Квадратичные формы и их связь с
симметричными матрицами. Свойства
собственных векторов и собственных
чисел симметричной матрицы. Приведение
квадратичной формы к каноническому
виду.
Определение 10.1. Квадратичной
формой действительных переменных
х1, х2,…,хn
называется многочлен второй степени
относительно этих переменных, не
содержащий свободного члена и членов
первой степени.
Примеры квадратичных форм:
![]()
(n = 2),
![]()
(n = 3). (10.1)
Напомним данное в прошлой лекции
определение симметрической матрицы:
Определение 10.2. Квадратная матрица
называется симметрической, если
![]() ,
,
то есть если равны элементы матрицы,
симметричные относительно главной
диагонали.
Свойства собственных чисел и
собственных векторов симметрической
матрицы:
-
Все собственные числа симметрической
матрицы действительные.
Доказательство (для n
= 2).
Пусть матрица А имеет вид:
 .
.
Составим характеристическое уравнение:
![]()
(10.2) Найдем дискриминант:
![]()
следовательно, уравнение имеет только
действительные корни.
-
Собственные векторы симметрической
матрицы ортогональны.
Доказательство (для n
= 2).
Координаты собственных векторов
![]()
и
![]()
должны удовлетворять уравнениям:
![]()
Следовательно, их можно задать так:
![]() .
.
Скалярное произведение этих векторов
имеет вид:
![]()
По теореме Виета из уравнения (10.2)
получим, что
![]()
Подставим эти соотношения в предыдущее
равенство:
![]()
Значит,
![]() .
.
Замечание. В примере, рассмотренном в
лекции 9, были найдены собственные
векторы симметрической матрицы и
обращено внимание на то, что они оказались
попарно ортогональными.
Определение 10.3. Матрицей квадратичной
формы (10.1) называется симметрическая
матрица
 .
.
(10.3)
Таким образом, все собственные числа
матрицы квадратичной формы действительны,
а все собственные векторы ортогональны.
Если все собственные числа различны,
то из трех нормированных собственных
векторов матрицы (10.3) можно построить
базис в трехмерном пространстве. В этом
базисе квадратичная форма будет иметь
особый вид, не содержащий произведений
переменных.
Соседние файлы в папке лекции, 1 сем.
- #
- #
