Длина окружности
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).
Ответ: 12,56 см 2 .
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 · | 7 2 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см 2 ). |
| 4 |
Ответ: 38,465 см 2 .
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
Длина окружности

О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
[spoiler title=”источники:”]
http://www.resolventa.ru/demo/diaggia6.htm
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
[/spoiler]
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое окружность?
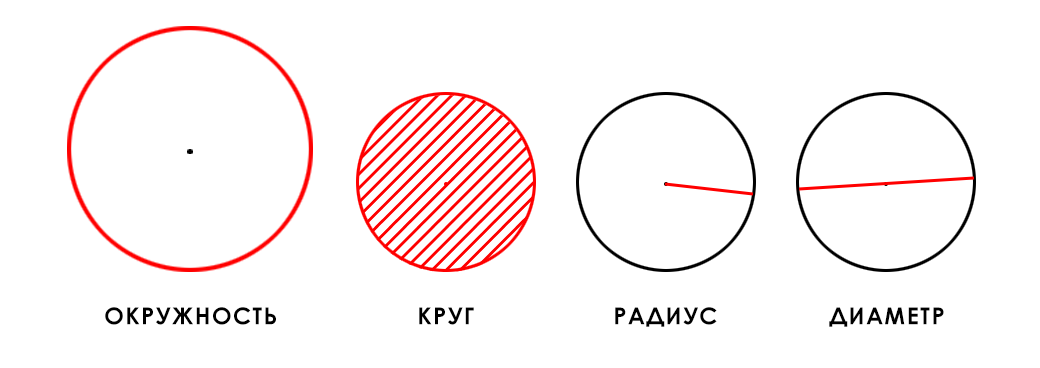
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
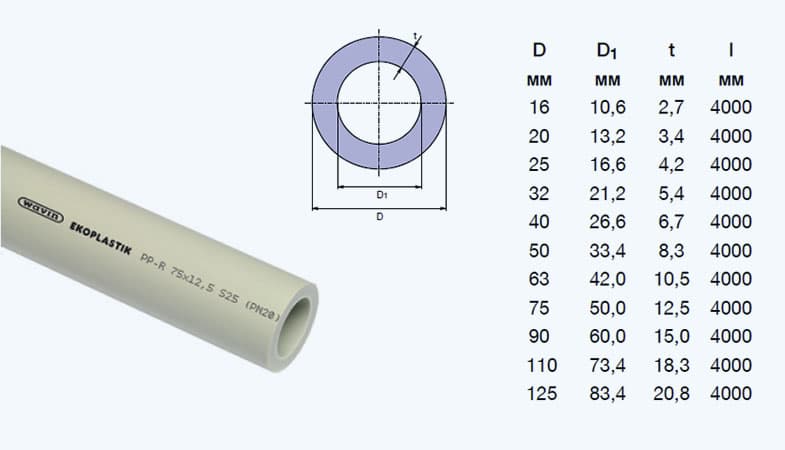
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.

Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Загрузить PDF
Загрузить PDF
Окружность – это плоская замкнутая кривая, все точки которой равноудалены от центральной точки.[1]
Длина окружности (С) – это длина замкнутой кривой, которая и образует окружность.[2]
Площадь круга (А) – это величина пространства, которое ограничено окружностью.[3]
Площадь круга и длина окружности вычисляются по формулам, в которых присутствует радиус (или диаметр) окружности и число «пи».
-

1
Формула для вычисления длины окружности. Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14)[4]
, r – радиус окружности, d – диаметр окружности.[5]
- Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
- Длина окружности измеряется в любых единицах измерения длины: в метрах, сантиметрах, миллиметрах и так далее.
-

2
Величины формулы. В формулу для нахождения длины окружности входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.
- Радиус окружности (r) – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
- Диаметр окружности (d) – это отрезок, проходящий через центр окружности и соединяющий любые две точки, лежащие на окружности.[6]
- Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.[7]
В большинстве математических вычислений число «пи» округляется до 3,14.
-

3
Измерьте радиус или диаметр окружности. Совместите начало линейки с любой точкой на окружности и сделайте так, чтобы линейка соприкасалась с центром окружности. Измерьте расстояние от точки до центра окружности, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.
- В большинстве математических задач радиус или диаметр будет дан.
-

4
Подставьте значения величин в формулу. Найдя радиус и/или диаметр окружности, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой C = 2πr, а если диаметр, формулой C = πd.
- Пример: найдите длину окружности, радиус которой равен 3 см.
- Напишите формулу: C = 2πr
- Подставьте данное значение в формулу: C = 2π3
- Перемножьте: C = (2*3*π) = 6π = 18,84 см
- Пример: найдите длину окружности, диаметр которой равен 9 м.
- Напишите формулу: C = πd
- Подставьте данное значение в формулу: C = 9π
- Перемножьте: C = (9*π) = 28,26 м
- Пример: найдите длину окружности, радиус которой равен 3 см.
-

5
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите длину окружности с диаметром 5 м.
- C = πd = 5π = 15,7 м
- Найдите длину окружности с радиусом 10 м.
- C = 2πr = C = 2π10 = 2*10* π = 62,8 м
Реклама
- Найдите длину окружности с диаметром 5 м.
-

1
Формула для вычисления площади круга. Площадь круга можно вычислить по двум формулам, включающим диаметр или радиус: A = πr2 или A = π(d/2)2[8]
, где π – число «пи» (математическая константа, приблизительно равная 3,14)[9]
, r – радиус круга, d – диаметр круга.- Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
- Площадь круга измеряется в любых единицах измерения длины, возведенных в квадрат: в квадратных метрах (м2), в квадратных сантиметрах (см2), в квадратных миллиметрах (мм2) и так далее.
-

2
Величины формулы. В формулу для нахождения площади круга входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.
- Радиус круга (r) – это отрезок, соединяющий центр круга с любой точкой, лежащей на окружности, которая ограничивает этот круг.
- Диаметр круга (d) – это отрезок, проходящий через центр круга и соединяющий любые две точки, лежащие на окружности, которая ограничивает этот круг.[10]
- Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.[11]
В большинстве математических вычислений число «пи» округляется до 3,14.
-

3
Измерьте радиус или диаметр круга. Совместите начало линейки с любой точкой на окружности, ограничивающей круг, и сделайте так, чтобы линейка соприкасалась с центром круга. Измерьте расстояние от точки до центра круга, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.
- В большинстве математических задач радиус или диаметр будет дан.
-

4
Подставьте значения величин в формулу. Найдя радиус и/или диаметр круга, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой A = πr2, а если диаметр, формулой A = π(d/2)2.
- Пример: найдите площадь круга с радиусом 3 м.
- Напишите формулу: A = πr2
- Подставьте данное значение: A = π32
- Возведите радиус в квадрат: r2 = 32 = 9
- Умножьте на число «пи»: A = 9π = 28,26 м2
- Пример: найдите площадь круга с диаметром 4 м.
- Напишите формулу: A = π(d/2)2
- Подставьте данное значение: A = π(4/2)2
- Разделите диаметр на 2: d/2 = 4/2 = 2
- Результат возведите в квадрат: 22 = 4
- Умножьте на число «пи»: A = 4π = 12,56 м2
- Пример: найдите площадь круга с радиусом 3 м.
-

5
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с диаметром 7 м.
- A = π(d/2)2 = π(7/2)2 = π(3,5)2 = 12,25 * π= 38,47 м2.
- Найти площадь круга с радиусом 3 м.
- A = πr2 = π32 = 9 * π = 28,26 м2
Реклама
- Найдите площадь круга с диаметром 7 м.
-

1
Найдите радиус или диаметр окружности. В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.
- Пример: вычислите длину окружности с радиусом (х + 1).
-

2
Напишите формулу с данным значением. Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.
- Пример: вычислите длину окружности с радиусом (х + 1).
- Напишите формулу: C = 2πr
- Подставьте данное значение: C = 2π(х + 1)
-

3
Вычислите длину окружности так, как если бы переменная была представлена числом. На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.
- Пример: вычислите длину окружности с радиусом (х + 1).
- C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
- Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.
-

4
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с радиусом 2х.
- A = πr2 = π(2x)2 = π4x2 = 12,56x2
- Найдите площадь круга с диаметром (х + 2).
- A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π
Реклама
- Найдите площадь круга с радиусом 2х.
Об этой статье
Эту страницу просматривали 212 638 раз.
Была ли эта статья полезной?
Содержание:
- Формула
- Примеры вычисления периметра круга
Формула
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
$l=2 pi r$ или $l=pi d$
где $r$ и $d$ соответственно радиус и диаметр круга, а
$pi approx 3,1415926535 ldots$. Радиусом окружности называется отрезок,
соединяющий центр окружности с точкой окружности. Диаметр – это отрезок, который соединяет две точки окружности и проходящий
через её центр. Число $pi$ – математическая константа,
выражающая отношение длины окружности к длине её диаметра.
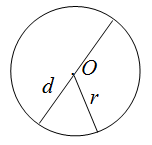
Примеры вычисления периметра круга
Пример
Задание. Найти периметр круга, радиус которого равен 2 см.
Решение. Периметр круга – это не что иное, как длина ограничивающей его окружности. Так как
нам задан радиус круга, то для вычисления длины окружности будем использовать формулу:
$l=2 pi r$
Получим:
$P_{k}=l=2 cdot pi cdot 2=4 pi approx 12,56$ (см)
Ответ. $P_{k}=4 pi approx 12,56$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Круг вписан в квадрат со стороной
$a=5$ мм. Найти периметр круга.
Решение. Сторона квадрата для круга является диаметром, то есть $a=d=5$ мм. Периметр круга равен длине окружности его
ограничивающей. Вычислим указанную длину по формуле:
$l=pi d$
Тогда искомый периметр равен:
$P_{k}=l=5 pi approx 15.7$ (мм)
Ответ. $P_{k}=l=5 pi approx 15.7$ (мм)
Читать дальше: как найти длину окружности.
Начнем с того, что определим окружность, как замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки. Эта заданная точка является центром окружности. Прямой отрезок, который проходит через центр окружности и соединяет 2 точки на ее границе, называется диаметром. А радиусом будет являться прямой отрезок, которые соединяем точку на границе окружности и ее центр.
Так как окружность – это граница круга, то длина окружности является частным случаем периметра.
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
Длина окружности круга
Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C к ее диаметру d всегда будет равно одному и тому же числу. Это число – всем известное число π («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа π, как отношение длины окружности C к двум ее радиусам r. Исходя из этого, выводится формула длины окружности C, которая равна произведения числа π и диаметра d окружности или 2-м ее радиусам r.
С=2πr
С= πd
π=C/d
Для примера решим простую задачу, где нужно найти длину окружности, у которой известен радиус r=2 см.
C= πd
d=2r=4 см
С=4*3,14=12,56
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.
Площадь круга
Площадь круга S, как и длина окружности, вычисляется с помощью константы π и радиуса окружности r.
Так же можно получить значение площади S круга с помощью диаметра d.
Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!
Пример вычисления: найти площадь круга, радиус которого равен 1 см.
Спасибо, что прочитали статью. Не забывайте про подписку на канал, а также рекомендую почитать канал наших друзей:
https://zen.yandex.ru/fgbnuac — последние научные достижения и лучшие образовательные практики.
https://zen.yandex.ru/id/5e164c941febd400ae3b4705 — ЕВРОПЕЙСКОЕ ВЫСШЕЕ ОБРАЗОВАНИЕ. Международная компания, оказывающая консультационные, сопроводительные и информационные услуги в сфере высшего образования в Европе. Официальный сайт – https://eurounis.com.
Хорошего дня и не болейте.
