Для
установления относительной важности
элементов иерархии используется шкала
отношений. Данная шкала позволяет ЛПР
ставить в соответствие степеням
предпочтения одного сравниваемого
объекта перед другим некоторые числа
(таблица 2).
Таблица
2. Шкала отношений
|
Степень |
Определение |
Объяснение |
|
1 |
Одинаковая |
Два |
|
3 |
Некоторое |
Существуют |
|
5 |
Существенная |
Имеются |
|
7 |
Очевидная |
Убедительное |
|
9 |
Абсолютная |
Свидетельства |
|
2, |
Промежуточные |
Ситуация, |
|
Обратные |
Если |
Если |
При
использовании указанной шкалы ЛПР,
сравнивая два объекта в смысле достижения
цели, расположенной на вышележащем
уровне иерархии, должен поставить число
в интервале от 1 до 9 или обратное значение.
Для
этого в иерархии выделяют элементы двух
типов: элементы – родители и
элементы – потомки.
Элементы – потомки воздействуют
на соответствующие элементы вышестоящего
уровня иерархии, являющиеся по отношению
к первым элементами – родителями.
Матрицы парных сравнений строятся для
всех элементов – потомков,
относящихся к определенному родителю.
Парные сравнения производятся в терминах
доминирования одного элемента над
другим в соответствии со шкалой отношений.
Если
элемент Е1
доминирует над элементом Е2,
то клетка матрицы, соответствующая
строке Е1
и столбцу Е2,
заполняется целым числом, а клетка,
соответствующая строке Е2
и столбцу Е1,
заполняется обратным к нему числом.
При
проведении парных сравнений следует
отвечать на вопросы: какой из двух
сравниваемых элементов важнее или имеет
большее воздействие, какой более вероятен
и какой предпочтительнее.
При
сравнении критериев обычно спрашивают,
какой из критериев более важен; при
сравнении альтернатив по отношению к
критерию – какая из альтернатив более
предпочтительна или более вероятна.
Рассмотрим
процесс построения матрицы парных
сравнений не примере.
Пример.
Провести анализ провайдеров на предмет
их желательности с точки зрения
определенного человека. Этот человек,
руководствуется пятью независимыми
(будем считать что это так) характеристиками:
тарифы, скорость сети, доступность сети,
удобство оплаты, дополнительные услуги.
В качестве альтернатив человек
рассматривает следующие компании:
Comstar,
Зебра Телеком, РОЛ и МТУ.
Иерархическая
схема может быть представлена следующим
образом (рисунок 5):
Удовлетворение
провайдером


Тарифы
Скорость
Доступность
Оплата
Услуги








Comstar
Зебра
РОЛ
МТУ
Рис. 5.
Иерархическая схема проблемы выбора
провайдера
После
построения иерархии строятся матрицы
парных сравнений. При сравнении элементов,
принадлежащих одному уровню иерархии,
ЛПР выражает свое мнение, используя
одно из приведенных в таблице 2 определений.
В матрицу сравнений заносится
соответствующее число.
Начнем
построение матриц парных сравнений с
матрицы «Удовлетворение провайдером»,
которая покажет относительную важность
характеристик при выборе компании.
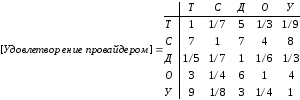
При
построении матрицы человек задавался
вопросом, какая характеристика для него
наиболее важна при выборе провайдера.
При
сравнении любого критерия с самим собой
не возникает вопросов о доминирующем
воздействии одного из критериев, т.е.
соответствующая позиция в матрице
заполняется единицей, что соответствует
одинаковой степени значимости критериев
(см. таблицу 2 – шкала отношений).
Рассмотрим
первую строку матрицы. В позиции один
два, при сравнении важности тарифов и
скорости, ЛПР поставил значение равное
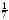 .
.
Это означает, что скорость доминирует
по предпочтению над тарифами. «При
выборе провайдера для меня скоростьво
много крат важнее
чем тарифы» – говорит ЛПР. Семерка
отвечает очевидной или очень сильной
значимости одного сравниваемого объекта
по сравнению с другим, согласно шкале
отношений.
Цифра
пять в позиции один три говорит о том,
что для ЛПР тарифы важней
доступности сети, в то время
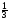 на пересечении строки тарифов и столбца
на пересечении строки тарифов и столбца
оплаты отвечает случаю, когда удобство
оплаты для ЛПРнемного
важнее
расценок провайдера.
Иерархию
в какой-либо рассматриваемой проблеме
можно выявить посредством анкетирования,
синтезировать результат и продолжить
дело с помощью анкеты для выявления
суждений.
Рассмотрим,
как могут быть получены матрицы суждения
для одной матрицы. Тот же метод может
быть применен для иерархии. В качестве
примера возьмем иерархическую структуру,
представленную на рисунке 6.
Новый
сотрудник


Образование
Опыт
Зарплата
Вписывается
ли в коллектив





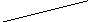


А1
А3
А2
Рис. 6
Иерархическая схема задачи выбора
нового сотрудника
Обозначим
значения шкалы, располагая их в ряд от
одного крайнего значения к равенству
и затем вновь повышая до второго крайнего
значения (таблица 3). В левом столбце
перечисли все альтернативы, которые
нужно сравнивать по степени превосходства
с другими альтернативами из правого
столбца. Эксперты должны отметить
суждения, которые выражают превосходство
элемента из левого столбца над
соответствующим элементом из правого
столбца, расположенном в той же строке.
Если такое превосходство в действительности
имеет место, то одна из позиций левее
равенства будет отмечена. В противном
случае будет отмечено равенство или
некоторая позиция справа.
Таблица
3. Сравнение альтернатив относительно
критерия “образование”
|
Абсолютное |
Очень |
Сильное |
Слабое |
Равенство |
Слабое |
Сильное |
Очень |
Абсолютное |
||
|
А1 |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
А2 |
|
А1 |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
А3 |
|
А2 |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
А3 |
Такая
таблица составляется и заполняется для
каждого критерия (четыре анкеты для
сравнения альтернатив по каждому из
критериев) и для сравнения критериев
относительно цели (одна анкета в которой
ЛПР решает какие критерии для него
наиболее значимые).
После
заполнения экспертами анкет, по ним
составляются матрицы парных сравнений.
Например анкета имеет вид, представленный
в таблице 4:
Таблица
4. Сравнение альтернатив относительно
критерия “образование”, составленное
первым экспертом по резюме кандидатов
|
Абсолютное |
Очень |
Сильное |
Слабое |
Равенство |
Слабое |
Сильное |
Очень |
Абсолютное |
||
|
А1 |
_ |
х |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
А2 |
|
А1 |
_ |
_ |
_ |
х |
_ |
_ |
_ |
_ |
_ |
А3 |
|
А2 |
_ |
_ |
_ |
_ |
_ |
_ |
х |
_ |
_ |
А3 |
Матрица
парных сравнений для анкеты из таблицы
4 имеет вид:
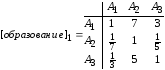
Для
агрегирования мнений экспертов
принимается среднегеометрическое,
вычисляемое по следующей формуле:

Логичность
критерия становится очевидной, если
два равноценных эксперта указывают при
сравнении объектов соответственно
оценки
 и
и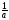 ,
,
что при вычислении агрегированной
оценки дает единицу и свидетельствует
об эквивалентности сравниваемых
объектов.
В
достаточно ответственных задачах при
оправданных задачах на экспертизу
осреднение суждений экспертов проводится
с учетом их квалификации. Для определения
весовых коэффициентов экспертов
используют иерархическую структуру
критериев, представленную на рисунке 7.
Наилучший
эксперт

Профессиональный уровень
Независимость суждений
Порядочность





Эксперт
1
Эксперт
3
Эксперт
2

Рис. 7
Иерархия для ранжирования экспертов
Расчет
агрегированной оценки в случае привлечения
 экспертов, имеющих различную значимость,
экспертов, имеющих различную значимость,
осуществляется по формуле:

Пример.
Предположим, что в случае с выбором
нового кандидата на работу, первый
эксперт, которым мог быть начальник
отдела управления кадрами, по результатам
резюме заполнил анкету, которая приведена
в таблице 4. Во время проведения
собеседования с каждым из претендентов,
второй эксперт, например один из
директоров, заключил, что по уровню
образования кандидатам соответствует
анкета, заполненная следующим образом
(таблица 5):
Таблица
5. Сравнение альтернатив относительно
критерия “образование”, составленное
вторым экспертом по результатам
собеседования с кандидатами
|
Абсолютное |
Очень |
Сильное |
Слабое |
Равенство |
Слабое |
Сильное |
Очень |
Абсолютное |
||
|
А1 |
_ |
х |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
А2 |
|
А1 |
_ |
_ |
х |
_ |
_ |
_ |
_ |
_ |
_ |
А3 |
|
А2 |
_ |
_ |
_ |
_ |
_ |
х |
_ |
_ |
_ |
А3 |
Матрица
парных сравнений для анкеты в таблице
5, имеет вид:
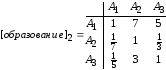
Для
объединения оценок суждений двух
экспертов строится матрица с средним
геометрическим оценок. В данной задаче
такой подход не совсем правомерен.
Однако, будем считать что суждения двух
экспертов обладают одинаковой степенью
значимости. Результирующая матрица
имеет вид:
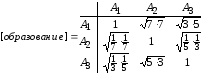
При
построении матриц парных сравнений
важным вопросом является согласованность,
или однородность матрицы. Согласованность
– это следование логике при высказывании
суждений экспертом. Для более наглядной
иллюстрации понятия «согласованности»
приведем пример.
Пример.
Предположим, что имеется три фрукта:
яблоко, апельсин и ананас. Некто,
предположим ребенок, говорит следующее:
«Ананас в три раза вкуснее апельсина,
а апельсин в два раза вкуснее яблока».
Следующим высказыванием ребенка на
вопрос о его любви к яблокам и ананасам,
он говорит, что ананас в пять раз лучше
яблока. В таких высказываниях ребенка
несогласованности практически нет,
несмотря на то, что исходя из его первого
предложения ананас в шесть раз
предпочтительнее яблока. Однако,
нарушения логики могло быть гораздо
более серьезным и даже привести к
нетранзитивности. Так, второе высказывание
могло звучать: «Мне яблоки нравятся
больше чем ананасы».
В
практических задачах количественная
и транзитивная (порядковая) однородность
нарушается, поскольку человеческие
ощущения нельзя выразить точной формулой.
Для улучшения однородности в числовых
суждениях, какая бы величина
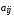 ни была взята для сравнения
ни была взята для сравнения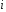 -го
-го
элемента с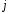 -ым,
-ым,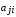 приписывается значение обратной
приписывается значение обратной
величины, т.е.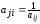 .
.
Определение.
Квадратную матрицу
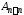 в которой все элементы
в которой все элементы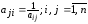 ,
,
называют обратносимметрической.
При
построении матриц парных сравнений не
следует искусственно выстраивать
матрицу исходя из условий согласованности.
Такой подход может исказить предпочтения
ЛПР. Однако во многих задачах, однородность
матриц должна быть высокой. Для оценки
однородности используют то свойство,
что при нарушении однородности ранг
матрицы отличен от единицы и она имеет
несколько собственных значений. При
небольших отклонениях суждения от
однородности одно из собственных
значений будет существенно большие
остальных и приблизительно равно порядку
матрицы. Это свойство вытекает из
следующих двух теорем.
Теорема 1.
В положительной обратносимметрической
квадратной матрице
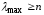 .
.
Теорема 2.
Положительная обратносимметрическая
квадратная матрица А согласованна тогда
и только тогда, когда
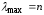 .
.
Таким
образом, для оценки однородности суждений
эксперта можно использовать отклонение
величины максимального собственного
значения
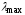 от порядка матрицы
от порядка матрицы .
.
Согласованность
суждения оценивается индексом однородности
(индексом согласованности) или отношением
однородности (отношением согласованности)
в соответствии со следующими формулами:
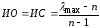
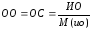
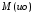 –
–
среднее значение индекса однородности
случайным образом составленной матрицы
парных сравнений, которое основано на
экспериментальных данных. Значение
есть табличная величина, входным
параметром выступает размерность
матрицы (таблица 6).
Таблица
6. Среднее значение индекса однородности
в зависимости от порядка матрицы
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
0 |
0 |
0,58 |
0,90 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
1,51 |
В
качестве допустимого используется
значение
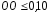 .
.
Если для матрицы парных сравнений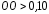 ,
,
то это свидетельствует о существенном
нарушении логики суждений, допущенном
экспертом при заполнении матрицы,
поэтому эксперту предлагается пересмотреть
данные, использованные для построения
матрицы, чтобы улучшить однородность.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Выбрать лучший вариант особенно сложно, когда все ваши варианты сильно отличаются друг от друга, критерии принятия решения субъективны или у вас нет объективных данных для принятия решения. Метод парного сравнения помогает вам определить относительную важность нескольких различных вариантов.
В этой статье мы рассмотрим, как вы можете использовать метод парного сравнения для принятия решений.
Что такое метод парного сравнения
В 1927 году специалист по психометрии Луис Леон Терстоун впервые представил метод парного сравнения, который назвал “законом сравнительного суждения”. Метод, также известный как “попарное сравнение”, заключается в правильной расстановке приоритетов.
Он поможет вам:
- определить наиболее важную проблему для решения;
- выбрать наиболее эффективное решение проблемы;
- расставить приоритеты в противоречивых требованиях к вашим ресурсам.
Этот метод особенно полезен при отсутствии объективных данных, которые можно было бы использовать для принятия решения. Он также идеален для сравнения различных субъективных вариантов. Например, вам нужно определить относительную важность квалификации, навыков, опыта и способности работать в команде при выборе кандидатов на вакантную должность.
Подобные решения принимать сложнее, чем сравнить три похожие информационные системы, где вам могут помочь матрица принятия решений или какая-либо форма финансового анализа.
Как использовать метод
Выполните следующие шесть шагов:
- Составьте список всех вариантов, которые вы хотите сравнить. Присвойте каждому варианту букву (А, Б, В, Г и так далее).
- Нарисуйте таблицу и запишите свои варианты в качестве заголовков строк и столбцов. Это необходимо для сравнения вариантов друг с другом. Заскрасьте те ячейки, в которых варианты будут сравниваться сами с собой, и те, в которых сравнение будет дублироваться. Вам нужно сравнить каждую пару только один раз.
- В каждой пустой ячейке сравнивайте попарно варианты. Решите какой из двух вариантов наиболее важен и запишите его букву в ячейку.
- Присвойте степень важности разницы между вариантами, начиная с нуля (нет разницы/одинаковая важность) до трех (большая разница/один важнее другого).
- Сложите результаты, суммируя значения для каждого из вариантов. Можно перевести баллы в проценты от общего числа.
- Используйте свой здравый смысл и при необходимости скорректируйте результаты вручную.
Пример использования метода
Филантроп выбирает между несколькими различными некоммерческими организациями, которые просят о финансировании. Чтобы добиться максимального эффекта, он хочет внести свой вклад только в две организации, и у него есть следующие варианты:
- образовательный проект за рубежом;
- местный образовательный проект;
- финансирование его университета;
- помощь в случае стихийных бедствий.
Сначала он составляет таблицу парного сравнения:
|
Финансирование |
“А” Образовательный проект за рубежом |
“Б” Местный образовательный проект |
“В” Финансирование его университета |
“Г” Помощь в случае стихийных бедствий |
|
“А” Образовательный проект за рубежом |
||||
|
“Б” Местный образовательный проект |
||||
|
“В” Финансирование его университета |
||||
|
“Г” Помощь в случае стихийных бедствий |
Таблица 1. Пример матрицы парного сравнения (не заполнена).
Затем филантроп сравнивает их, записывает букву более предпочтительного варианта и присваивает степень его важности:
|
Финансирование |
“А” Образовательный проект за рубежом |
“Б” Местный образовательный проект |
“В” Финансирование его университета |
“Г” Помощь в случае стихийных бедствий |
|
“А” Образовательный проект за рубежом |
А, 2 |
В, 1 |
А, 1 |
|
|
“Б” Местный образовательный проект |
В, 1 |
Б, 1 |
||
|
“В” Финансирование его университета |
В, 2 |
|||
|
“Г” Помощь в случае стихийных бедствий |
Таблица 2. Пример матрицы парного сравнения (заполнена).
Филантроп складывает значения А, Б, В и Г и переводит баллы в проценты:
- А = 3 (37,5%);
- Б = 1 (12,5%);
- В = 4 (50%);
- Г = 0.
В итоге он решает финансировать свой университет (В) и выделить некоторые средства на образовательный проект за рубежом (А).
Факультет экономики и управления
Кафедра математических методов и моделей в экономике
Курсовая на тему: «Принятие решений выбора оптимальной номенклатуры товаров на
основе метода парных сравнений»
Задание на курсовую работу
по дисциплине «Методы принятия управленческих решений» на
тему «Принятие решений выбора оптимальной номенклатуры товаров на
основе метода парных сравнений»
1.Рассмотреть теоретические аспекты принятия управленческих решений на основе метода парных сравнений.
2.Решить задачу выбора оптимальной номенклатуры товаров на основе метода парных сравнений.
Содержание
Введение……………………………………………………………………………3
1 Общие сведения о методе парных сравнений…………………………………6
1.1 Матрицы парных сравнений………………………………………………….6
1.2 Определение степени значимости критериев и оценка согласованности
матриц парных сравнений………………………………………………………..8
1.3 Достоинства и недостатки метода парных сравнений…………………….23
2 Решение задачи о выборе оптимальной номенклатуры товаров на основе
метода парных сравнений……………………………………………………….26
Заключение……………………………………………………………………….30
Список использованных источников……………………………………………32
Введение
Метод парных сравнений чрезвычайно мощный, общий и в принципе может использоваться для любого набора объектов или стимулов, которые можно сравнить друг с другом некоторым в психологическом отношении реальным способом. Например, в простой психофизической задаче, такой как восприятие громкости, попарно предъявляется ряд тонов вариативной интенсивности, и субъекта просят решить, который из пары громче. В более сложных областях, таких как эмоции или эстетика, можно просить субъектов сравнивать картины по красоте, запахи по приятности, лица по подобию и т.д.
Мощность этой процедуры определяется применением к данным многомерных методов и методов факторного анализа, чтобы обнаружить основные измерения, по которым производятся суждения.
Метод парных сравнений – очень общая процедура для измерения (шкалирования) объектов или стимулов и оценки определяющих их измерений. В стандартном, полном методе парных сравнений каждый объект набора представляется для оценки попарно с каждым другим объектом этого набора [ 1 ].
Его автор – американский психолог Луис Леон Терслоун. Он разработал метод еще в первой половине ХХ века. С тех пор его широко применяют и в точных естественных науках, таких как математика и физика, и в гуманитарных, например в психологии, социологии. Метод учитывает и законы логики.
Он предназначен для изучения предпочтений, при котором респондент должен из всех возможных парных сочетаний объектов, предложенных ему, выбрать самый предпочтительный в соответствии с заданным критерием. Результатом является матрица парных сравнений, в котором сумма элементов строк дает представление о ранжировке респондентом всех объектов.
||aij|1, (1)
В данном случае aij будет равно 1.
Если респондент предпочел i-тый объект j-тому, и aij = 0 во всех остальных случаях, i,j = 1,n
Степень предпочтения респондентом объекта i определяется как сумма единиц в соответствующей строке матрицы. Парные (или попарные) сравнения при небольшом числе объектов – наиболее точный и надежный метод выявления предпочтений. Он применяется обычно, чтобы выявить предпочтения экспертов «в чистом виде». Считается, что гораздо легче сделать качественное сравнение двух объектов, чем выражать свои предпочтения в балльной или ранговой шкале. Этот метод оценки считается нереактивным, он не навязывает респондентам априорных условий. Считая предпочтение некоторой случайной величиной, отражающей истинное соотношение характеристик сравниваемых объектов, можно ставить задачу определения вероятности истинного соотношения сравниваемых объектов (модели Брэдли, Терри, Льюса и др.) [ 3 ].
Анализ методом парных сравнений – очень хороший инструмент при взвешивании относительно важных, но различных направлений выбора. Это применимо в случаях, когда приоритеты не совсем ясны или, наоборот, менеджеру ясно, что «важно все».
Этот инструмент помогает обозначить наиболее важные приоритеты выбора, представить информацию наглядно и сделать наиболее удачный выбор.
Применяется при принятии решений, в условиях отсутствия точных и объективных данных. А также, при сопоставлении абсолютно различных факторов. Например, необходимо принять решение куда инвестировать: в рынок канцелярских товаров или юридических услуг. Такие сравнения гораздо сложнее, чем сравнение между собой нескольких видов бумаги.
Метод парных сравнений Тьюки – один из методов дисперсионного анализа , предназначенный для попарного сравнения средних значений зависимой переменной в отдельных группах в эксперименте факторном . F-критерий, позволяющий отклонить нулевую гипотезу об отсутствии различий между средними значениями групп , не дает ответа на вопрос, в каких именно группах средние значения различаются. Наиболее простой способ узнать это состоит в том, чтобы попарно сравнить средние значения признака во всех группах (если в эксперименте используется k групп, необходимо k(k – 1)/2 сравнений). Результаты сравнений представляются в виде таблицы, в которой отмечается, между средними значениями каких групп найдены существенные статистические различия. Для проверки нулевой гипотезы о равенстве средних значений признака в группах с номерами i и j против альтернативной гипотезы, состоящей в том, что средние значения этих групп различаются , используется критерий:
![]()
где n – число объектов в каждой группе;
yi и yj – средние значения признака в группах с номерами i и j; MSSвнгр – внутригрупповой средний квадрат.
Этот критерий имеет распределение стьюдентизованного размаха с числами степеней свободы:
[k; k (n – 1)], (3)
где n – число объектов в каждой группе; k – число групп в эксперименте.
Нулевая гипотеза отклоняется, если вычисленное значение больше, чем ql-a . М.П.С. Тьюки применяется, только если объем всех групп в эксперименте одинаков. В других случаях, а также при необходимости более сложных сравнений, используются методы множественных сравнений.
Метод парных сравнений позволяет определить значимость различий положения тех или иных объектов в иерархии и решать другие сходные задачи.
Цель работы – изучение возможности применения метода парных сравнений как инструмента для принятия управленческих решений.
Объект изучения – задача выбора оптимальной номенклатуры
товаров.
Предметом изучения является метод парных сравнений.
Для достижения поставленной цели требуются решить следующие
задачи:
1) Рассмотреть теоретические аспекты принятия управленческих решений на основе метода парных сравнений;
2) Решить задачу выбора оптимальной номенклатуры товаров на основе метода парных сравнений.
1 Общие сведения о методе парных сравнений
1.1 Матрицы парных сравнений
Для установления относительной важности элементов и составления матрицы парных сравнений используется шкала отношений . Данная шкала позволяет ЛПР ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа.
Таблица 1-Шкала отношений (степени значимости действий) [ 5 ].
|
Степень значимости |
Определение |
Объяснение |
|
1 |
2 |
3 |
|
1 |
Одинаковая значимость |
Два действия вносят одинаковый вклад в достижение цели |
|
3 |
Некоторое преобладание значимости одного действия над другим (слабая значимость) |
Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны |
|
5 |
Существенная или сильная значимость |
Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий |
|
7 |
Очевидная или очень сильная значимость |
Убедительное свидетельство в пользу одного действия перед другим |
|
9 |
Абсолютная значимость |
Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны |
|
2,4, 6,8 |
Промежуточные значения между двумя соседними суждениями |
Ситуация, когда необходимо компромиссное решение |
|
Обратные величины приведенных выше ненулевых величин |
Если действию i при сравнении с действием j приписывается одно из |
Если согласованность была постулирована при получении N числовых |
|
определенных выше |
значений для |
|
|
ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение |
образования матрицы |
Правомочность этой шкалы доказана теоретически при сравнении со многими другими шкалами. При использовании указанной шкалы ЛПР, сравнивая два объекта в смысле достижения цели, расположенной на вышележащем уровне иерархии, должен поставить в соответствие этому сравнению число в интервале от 1 до 9 или обратное значение чисел. В тех случаях, когда трудно различить столько промежуточных градаций от абсолютного до слабого предпочтения или этого не требуется в конкретной задаче, может использоваться шкала с меньшим числом градаций. В пределе шкала имеет две оценки: 1- объекты равнозначны; 2- предпочтение одного объекта над другим.
Заполнение квадратных матриц парных сравнений осуществляется по следующему правилу. Если элемент Ei доминирует над элементом Е2, то клетка матрицы, соответствующая строке Е1 и столбцу E2, заполняется целым числом, а клетка, соответствующая строке E2 и столбцу Е1, заполняется обратным к нему числом. Если элемент Е2 доминирует над Ei, то целое число ставится в клетку, соответствующую строке Е2 и столбцу Е1, а дробь проставляется в клетку, соответствующую строке Е1 и столбцу Е2. Если элементы Е1 и Е2 равнопредпочтительны, то в обе позиции матрицы ставятся единицы.
Для получения каждой матрицы эксперт или ЛПР выносит n(n – 1)/2 суждений (здесь п — порядок матрицы парных сравнений).
Рассмотрим в общем виде пример формирования матрицы парных сравнений.
Пусть Е1,Е2, …, Еп — множество из п элементов (альтернатив) и V1, V2, …, vn — соответственно их веса, или интенсивности. Сравним попарно вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели (по отношению к элементу-«родителю») [ 4 ].
Матрица парных сравнений представлена в таблице 2:
|
– |
Е1 |
Е2 |
Еп |
|
|
1 |
2 |
3 |
4 |
5 |
|
Е1 |
V1/V1 |
V1/V2 |
V1/Vn |
|
|
Е2 |
V2/V1 |
V2/V2 |
V2/V1 |
|
|
En |
Vn/V1 |
V1/V2 |
Vn/Vn |
Матрица парных сравнений обладает свойством обратной симметрии, т. е.
aij=1/aji, (1)
где aij=vi / vj.
При проведении попарных сравнений следует отвечать на следующие вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее. При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию — какая из альтернатив более предпочтительна или более вероятна.
1.2 Определение степени значимости критериев и оценка согласованности матриц парных сравнений
В настоящее время актуальной является проблема повышения эффективности управления инновационными проектами. Поскольку финансированием инновационных проектов в большинстве случаев занимаются различные инвестиционные компании, в каждой из которых есть свои особенности управления, поставленные задачи и история существования, для снижения рисков, связанных с вложением в инновационные проекты, изобретаются свои специфические средства и инструменты управления. Успешная работа по анализу инновационных проектов основана на применении многочисленных методов, применяющихся как при построении общей модели работы с проектами, так и на отдельных этапах процесса прохождения проекта внутри компании.
Одним из наиболее важных этапов работы с проектами в компании является экспертиза этих проектов. В процессе проведения экспертизы заявка, которая или будет отклонена, или станет финансируемым проектом, подвергается разносторонним исследованиям, в которых участвуют эксперты различного профиля.
Экспертиза, как правило, представляет собой процесс, в котором участвует группа высококвалифицированных и узкоспециализированных экспертов, результатом которого является набор экспертных заключений или одно сводное заключение.
Однако для получения информации от экспертов, которая достоверно отображает перспективы и недостатки анализируемого проекта, недостаточно просто найти хороших экспертов. Для получения корректных и показательных экспертных заключений необходимо определить критерии, по которым эксперты должны анализировать заявку.
Различие критериев у разных компаний может объясняться как разным финансовым положением, так и различными приоритетами и целями. По этой причине каждая организация должна самостоятельно формировать свой собственный список важных для нее критериев оценки проекта.
Однако после формирования этого списка перед всеми компаниями встает задача по определению относительной важности и значимости критериев. Для решения этой задачи можно использовать различные методы [ 2 ].
Наиболее распространенным методом является формирование балльной оценки, при котором каждому из критериев ставится определенный балл и относительную важность критериев можно оценить путем сравнения присвоенных им баллов. На сегодняшний день достаточно широкое распространение получил способ формирования весов критериев. Главная идея данного метода состоит в парном сопоставлении критериев. Все критерии, предназначенные для анализа проекта, оцениваются путем построения матрицы парных сравнений. Матрица парных сравнений представляет собой матрицу, в которой критерий, расположенный в строке, сравнивается со всеми критериями, указанными в столбцах матрицы (таблица 1). Например, если критерий №1 важнее критерия №2 в а12раз, то элемент (1, 2) матрицы равен a12 . Исходя из этого, главная диагональ матрицы всегда заполнена единицами
Таблица 1 – Матрица парных сравнений
|
– |
Критерий 1 |
Критерий 2 |
Критерий 3 |
|
1 |
2 |
3 |
4 |
|
Критерий 1 |
аи=1 |
а12 |
а1з |
|
Критерий 2 |
а21 |
а22=1 |
а2з |
|
Критерий 3 |
аз1 |
аз2 |
азз=1 |
Логично предположить, что если критерий №1 важнее критерия №2 в а12раз, а критерий №2 важнее критерия №3 в а2зраз, то критерий №1 должен быть важнее критерия №3 ровно в a12-a23 раз. Однако для матриц, заполняемых реальными людьми, это далеко не всегда так. Это связано с тем, что заполнение матрицы суждений осуществляется экспертом, который может допустить погрешность в определении относительной важности критериев по психологическим причинам. Одной из задач метода является стремление снизить влияние человеческого фактора на итоговый смысловой результат. Для определения степени корректности данных в заполненной матрице введено понятие меры согласованности матрицы. Для пояснения определения полностью согласованной матрицы приведен ее общий вид (таблица 2).
Таблица 2- Общий вид согласованной матрицы.
|
– |
Критерий 1 |
Критерий 2 |
Критерий 3 |
|
1 |
2 |
3 |
4 |
|
Критерий 1 |
1 |
а12 |
а12*а23 |
|
Критерий 2 |
1/а12 |
1 |
а23 |
|
Критерий 3 |
1/(а12*а23) |
1/а23 |
1 |
Для обработки значений полученной матрицы сравнения вводится индекс согласованности, который показывает наличие логической связи между оцененными показателями. Для нахождения индекса согласованности положительной обратно симметричной матрицы (матрица парных сравнений обладает этими свойствами), необходимо найти максимальное собственное значение матрицы и ее размерность.
Индекс согласованности рассчитывается по формуле (1):

где Лмах– максимальное собственное значение; n – размерность матрицы.
Если матрица согласована, то предположение о том, что если критерий №1 важнее критерия №2 в а12раз, а критерий №2 важнее критерия №3 в а23раз, то критерий №1 должен быть важнее критерия №3 ровно в a12 a23 раз, всегда верно. Для такой матрицы ИС равняется нулю. Однако, как правило, при анализе данных, полученных экспертным путем, матрица не является полностью согласованной.
В разработанном методе предлагается для парного сравнения критериев использовать шкалу оценки, которая содержит в себе числовые показатели от 1 до 9 и обратные им величины [4-5]. Значения шкалы 1:9 отображают девять степеней превосходства одного критерия над другим, причем, пять значений являются основными (1,3,5,7,9) и четыре -промежуточными значениями (2,4,6,8). В случае, если рассматриваемый критерий является не более, а менее важным, чем тот, с которым его сравнивают, такое соотношение описывается также посредством девяти степеней сравнения, но представленных обратными величинами значений: 1, 1/2, 1/3, …, 1/9 [ 1 0 ].
При проведении процедуры сравнения критериев происходит заполнение экспертами соответствующих матриц. От каждого эксперта требуется заполнить только верхнюю часть матрицы (выше главной диагонали), поскольку при использовании данной методики предполагается, что если критерию i при сравнении с критерием j приписывается одно из чисел в диапазоне [1; 9], то критерию j при сравнении с критерием i приписывается обратное значение.
После заполнения экспертом матрицы парных сравнений, необходимо провести проверку индекса согласованности матрицы. Для этого
по формуле (1) рассчитывается ИС матрицы и сравнивается со средним индексом согласованности случайных матриц того же порядка. Соотношение этих индексов называется отношением согласованности (ОС).
На текущий момент для шкалы [1;9] учеными рассчитаны случайные индексы согласованности (СИ) для обратно симметричных матриц размерностью от 1 до 15 (таблица 3), взятые за основу при анализе полученных матриц на предмет согласованности. В данном методе считается приемлемым значение ОС меньшее или равное 0.10.
Таблица 3- Средние случайные индексы согласованности для матриц разного порядка
|
Размернос ть обратно симметрич ных матриц |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
– |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Величина случайных индексов согласова нности |
0. 00 |
0. 00 |
0. 58 |
0. 90 |
1. 12 |
1. 24 |
1. 32 |
1. 41 |
1. 45 |
1. 49 |
1. 51 |
1. 48 |
1. 56 |
1. 57 |
1. 59 |
Безусловно, использование для анализа важности критериев шкалы от 1 до 9 имеет свои преимущества. Однако, в ряде случаев, особенно, если это касается такого сложного аспекта, как анализ инновационных проектов, данная шкала не только является избыточной по своей сути, но и может стать причиной дополнительной погрешности в процессе выставления экспертом соответствующей оценки при парных сравнениях различных критериев.
На основе анализа мнения практикующих специалистов, работающих в области инноваций, которым приходится часто сталкиваться с проведением различного рода сравнений, выявлено, что целесообразным является использование более категоричной шкалы 1:5 (таблица 4). Это связано со спецификой области, для работы в которой производится адаптация метода анализа иерархий. В данной статье речь идет о сравнении инновационных проектов, при этом метод парного сравнения объектов применяется для определения весов критериев, по которым проекты впоследствии будут сравниваться. Поскольку сформированные веса критериев могут значительно повлиять на решение, принимаемое по проекту, необходимо, чтобы шкала, с помощью которой определяются в результате веса, была однозначной и конкретной.
Таким образом, можно сделать вывод о том, что использование шкалы 1:5 является на практике более удобным, поскольку каждое численное значение имеет ярко выраженную смысловую трактовку. Кроме того,
сравнение критериев посредством такой шкалы будет характеризоваться большей степенью уверенности эксперта. Это важный факт, так как в данном случае речь идет о работе с инновациями, а значит, ситуация осложняется различными рисками. При выборе каких-либо методов для организации работы с инновационными проектами, имеющими априори большую степень неопределенности, необходимо, во избежание накопления суммарной ошибки, выбирать методы, которые сами в себе имеют как можно меньшую степень неопределенности.
Кроме того, более четкое определение признаков, которое дает шкала 1:5, позволяет конкретизировать ситуацию без значимой потери точности, с одной стороны, и со значительным повышением комфортности использования этой шкалы – с другой стороны. В связи с выявленной потребностью шкала от 1 до 9 была заменена шкалой от 1 до 5. Для данной шкалы были описаны значения каждого из выставляемых баллов (таблица 4)
Таблица 4- Модифицированная шкала относительной важности
|
Интенсивность относительной важности |
Определение |
Объяснение |
|
1 |
2 |
3 |
|
0 |
Несравнимы |
Эксперт затрудняется при сравнении |
|
1 |
Одинаковая важность |
Равная степень важности критериев i и j |
|
3 |
Не существенная степень важности |
Критерий i несущественно важнее критерия j |
|
5 |
Существенная степень важности |
Критерий i существенно важнее критерия j |
|
2,4 |
Промежуточные значения между двумя соседними значениями шкалы |
Ситуация, когда необходимо компромиссное решение, 2 – критерий i имеет слабое преимущество перед критерием j, 4 -критерий i имеет заметное преимущество перед критерием j |
|
Обратные величины приведенных выше чисел |
Если критерию i при сравнении с критерием j приписывается одно из |
Обоснованное предположение |
|
приведенных выше чисел, то критерию j при сравнении с критерием i приписывается обратное значение |
Для обеспечения более комфортных условий сравнения для экспертов был введен дополнительный пункт шкалы – нулевое значение. Эксперт имеет возможность поставить 0 при сравнении двух критериев, если считает, что критерии несравнимы или сравнение лично для него крайне затруднительно.
Большая комфортность при использовании шкалы 1:5 объясняется легкостью в различии оценок критериев (рисунок 1). Три значения шкалы: 1,
3 и 5 выступают в виде главных при оценке относительной важности, а 2 и 4
– являются компромиссными, промежуточными вариантами выбора.
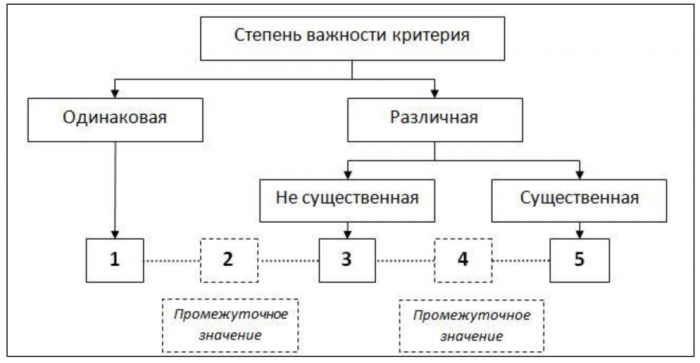
Рисунок 1- Ключевые деления шкалы 1:5
Поскольку шкала была изменена, для корректной проверки согласованности соответствующих матриц необходимо провести расчет индексов согласованности случайных матриц данного типа. Для решения этой задачи для выбранной шкалы было сгенерировано по 100 случайных матриц порядка 3, 4 и 5. Полученные в результате расчетов СИ обозначены в таблице 5.
Таблица 5- СИ по шкале оценки от 1 до 5 [1 2].
|
– |
1 |
2 |
3 |
4 |
5 |
|
Величина индексов согласованности случайных матриц |
0.000 |
0.000 |
0.211 |
0.423 |
0.464 |
В качестве примера для расчета отношения согласованности для матриц порядка 3, сформированных по шкале 1:5, был проведен анализ допустимого уровня согласованности матриц. Пороговым значением для шкалы 1:9 является уровень в 10 %. Для установления порогового значения при использовании шкалы 1:5 было проведено моделирование, заключающееся в анализе значений ОС матрицы при различных отклонениях экспертных оценок от оценок, соответствующих полностью согласованной матрице.
В рамках моделирования проводился анализ матриц со следующими отклонениями: увеличение одной величины на 1 шаг; -уменьшение одной величины на 1 шаг;-увеличение двух величин на 1 шаг; -уменьшение двух величин на 1 шаг;-увеличение трех величин на 1 шаг;-уменьшение трех величин на 1 шаг;-увеличение одной и уменьшение другой величины на 1 шаг;-увеличение двух величин и уменьшение одной величины на 1 шаг;-увеличение одной и уменьшение двух величин на 1 шаг;-увеличение 1 величины на 2 шага;-уменьшение 1 величины на 2 шага.
Для каждой размерности матрицы был проведен аналогичный анализ для пяти различных исходных согласованных матриц. В результате проведенного моделирования было получено значение 12.7 %, которое соответствует максимальному отношению согласованности при отклонении мнения эксперта на один шаг от значения полностью согласованной матрицы. Значение 12.7 % было выбрано в качестве порогового значения допустимой согласованности матрицы, составленной по шкале 1:5.
Пороговое значение 12.7 % является обоснованным для матрицы размерностью 3. Для матриц другой размерности пороговое значение ОС должно быть рассчитано не только с учетом анализа отклонений матрицы от полностью согласованной, но и с учетом того, что при сравнении большего количества критериев ошибка эксперта может возрасти.
Таким образом, с учетом особенностей, присущих повседневной практической деятельности при оценке инновационных проектов, была проведена модификация метода. Основная цель модификации – повышение эффективности метода при его применении узкопрофильными специалистами для оценки перспективности и технической реализуемости инновационных проектов. Использование данной модификации метода определения относительной важности критериев при оценке проекта может повысить эффективность и достоверность такого этапа работы с инновационными проектами, как подготовка к проведению экспертизы.
Данный момент является крайне важным, поскольку именно по установленным на этом этапе критериям происходит дальнейшая оценка проекта, а корректное соотношение критериев между собой по степени важности позволяет составить верное заключение по проекту.
Индекс согласованности – количественная оценка противоречивости результатов сравнений (для системы в целом, для узлов одного кластера или для кластеров, имеющих общую вершину) [ 8 ].Следует иметь в виду, что между достоверностью и непротиворечивостью сравнений нет явной связи. Противоречия в сравнениях возникают из-за субъективных ошибок экспертов. Индекс согласованности не зависит от шкал сравнений, но зависит от количества парных сравнений. Индекс согласованности – положительное число. Чем меньше противоречий в сравнениях, тем меньше значение индекса согласованности. При использовании способа сравнений с эталоном значение индекса согласованности равно нулю.
Относительная согласованность матрицы сравнений- отношение индекса согласованности к среднестатистическому значению индекса согласованности при случайном выборе коэффициентов матрицы сравнений. Относительная согласованность для системы в целом характеризует взвешенное среднее значение относительной согласованности по всем матрицам сравнений.
Данные можно считать практически непротиворечивыми (достаточно согласованными), если значение относительной согласованности меньше чем 0,1. Это заключение справедливо как для данных кластера, так и для данных в масштабе всей системы.
Индекс согласованности позиций двух групп (индекс согласованности)
Рассмотрим с тремя партиями А, В и С и следующим распределением голосов: A – 50 мест, В – 49 мест и С – 1 место. Предположим , что по каким-либо причинам партии А и В в коалицию не вступают. Рассчитаем для этого случая индекс Банцафа:
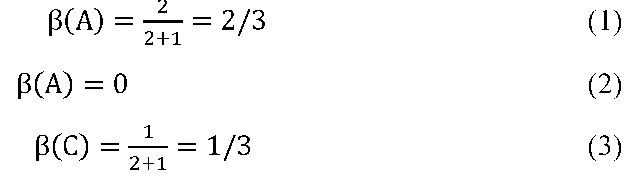
Теперь значение индекса Банцафа для партии В оказалось нулевым, а для партии С увеличилось почти в 2 раза. Естественно, возникает вопрос о том, как оценить возможность вступления партий в коалицию. В работе для этого использован индекс согласованности позиций двух групп, который описывается ниже.
Отношения между двумя группами парламентариев, естественно, отражаются на результатах голосований. Группы, придерживающиеся сходных политических позиций, имеющие общие интересы и, соответственно, находящиеся в «хороших» отношениях будут инициировать согласованные решения и будут поддерживать их при голосовании. Напротив, если парламентарии находятся в «плохих» отношениях, то в большинстве вопросов, по которым существуют различные точки зрения, они и голосовать будут по-разному, противопоставляя свое решение позиции «оппонента» 1.
Индекс согласованности был построен на основе индекса конформизма, предложенного в работе для определения того, насколько раскол в данной фракции по некоторому голосованию отличается от раскола во всем законодательном органе по тому же голосованию. В понятие конформизма не вкладывается никакого оценочного смысла, а сам индекс конформизма характеризует степень «похожести по расколу» позиции группы депутатов с позицией всего законодательного органа. Индекс определялся по следующей формуле:
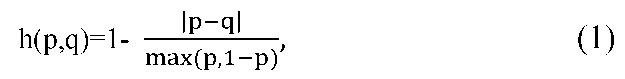
где q – доля проголосовавших «За» в группе;
p – доля проголосовавших «За» во всем парламенте 2.
Значение индекса меняются в диапазоне от 0 до 1, он учитывает и разность между p и q, и «уровень поддержки вопроса» p. При одном и том же значении |р — q| меньшее значение индекса будет достигаться при значениях
р, близких к 4.
Индекс согласованности двух групп законодателей в отдельном голосовании может быть построен с помощью двух различных подходов, приводящих к общему результату. Далее в обоих случаях q± и q2 означает долю проголосовавших «за» в 1-й и 2-й группах
В первом подходе сначала рассчитывается индекс как индекс с* конформизма для одной из групп и «общей позиции» группы:
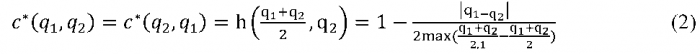
Значения индекса равно 1, если позиции групп совпадают( q1=q2), и равно 0, если позиции «противоположны» (например, q1=0 и q2=1).
Однако, использование в качестве «общей позиции» величины (q1+q2)/2 приводит к смещению (увеличению) порогового значения для . Значение индекса в «пороговой ситуации», когда позиция одной группы
равна qt =1, а другой q2 = 1/2 , равняется с* Q, 1 ) = 2 / 3 [ 1 7].
Для приведения порогового значения индекса к 1/2 может быть применено следующее преобразование с помощью функции, обратной для функции (q,1):
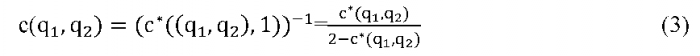
В рамках второго подхода «общей» объявляется позиция одной группы, обладающей более определенной позицией (для которой больше модуль разности (расстояние) до 1/2). Соответственно, формула расчета индекса имеет вид:
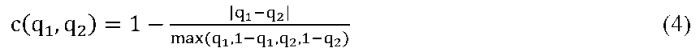
Простая проверка показывает, что формулы (3) и (4) приводят к одинаковому значению индекса.
Построенный на основе двух подходов индекс согласованности обладает следующими свойствами:
1) (значение меняется между 0 и 1) (5)
2) c ( q !, q 2 ) = с ( q 2, q t ) (коммутативность, «равноправие» групп) (6)
3) c(1,1/2)=1/2 (пороговое значение, превышение которого означает смену
плохого отношения на хорошее) (7)
4) c( (симметричность относительно порогового
значения, «равноправие» позиций «За» и «Против»).
В качестве оценки индекса согласованности в «среднем» за месяц в рамках данной работы использовалось среднее значение индекса по серии из m специально отобранных голосований.
![]()
Отбор голосований для оценки индекса согласованности «в среднем» за месяц осуществлялся по нескольким критериям, отражающим разные стороны информативности голосования для политического размежевания между фракциями, депутатскими группами и отдельными депутатами. Практика наблюдения за реальными голосованиями в Государственной Думе, в условиях, когда неучастие в голосовании в большей степени означает несогласие депутата с вопросом, чем отсутствие или нейтральную позицию, делает предпочтительными критерии, основанные на доле голосов «За» в общем списке депутатов или во фракциях.
В общем случае процедура отбора голосований производится в два этапа. В начале выделяются голосования, в которых даже при небольшом числе голосов, поданных «Против», есть существенное (по доле проголосовавших «За») расхождение позиций хотя бы для двух фракций. Для каждого голосования рассчитывается разность между максимальной и минимальной по фракциям долей голосов «За», затем отбираются голосования, для которых эта характеристика не меньше заданного уровня (для первой Думы – не меньше 0.5, для второй – не меньше 0.6 и для третьей -не меньше 0.7).
Далее из полученного списка исключаются «незначимые» голосования по заведомо проходным и заведомо непроходным «частным» вопросам (в таких голосованиях обычно число голосов «За» не менее 300-320 или не более 30). Наконец, из списка исключаются голосования, в которых расхождение обусловлено «техническими» причинами, приводящими впоследствии к переголосованию, или же пассивностью одной из фракций при голосовании по заведомо проходному вопросу и т.п.
Такая схема отбора голосований применялась в Фонде ИНДЕМ в исследованиях политического размежевания для построения политической карты и для оценки политических позиций депутатов Г осударственной Думы (Благовещенский, 2001в).
Определение однородности товаров и услуг [ 1 8 ].
«Однородный» – относящийся к тому же роду, разряду, одинаковый.
В соответствие с пунктом 6 статьи 1483 Гражданского Кодекса Российской Федерации (далее – Кодекс) не могут быть зарегистрированы в качестве товарных знаков в отношении однородных товаров обозначения, тождественные или сходные до степени смешения с товарными знаками других лиц.
Согласно пункту 3 статьи 1484 Кодекса никто не вправе использовать без разрешения правообладателя товарного знака сходные с его знаком обозначения в отношении товаров, для индивидуализации которых товарный знак зарегистрирован, или для однородных товаров, если в результате использования возникнет вероятность смешения. Таким образом, закон не допускает возможности индивидуализации однородных товаров разных производителей одинаковыми (тождественными) или сходными до степени смешения товарными знаками.
Для установления однородности товаров принимаются во внимание такие признаки как: – род (вид) товаров; – потребительские свойства товаров;
– функциональное назначение товаров (объем и цель применения); – вид материала, из которого товары изготовлены; – взаимозаменяемость и взаимодополняемость товаров; – условия реализации товаров (общее место продажи, осуществление путей продаж, – преимущественно через розницу или опт); – круг потребителей товаров; – преимущественный или традиционный уклад использования товаров; – длительность/краткосрочность пользования товарами; – стоимость товаров (дорогостоящие или не дорогие);
– другие признаки.
По результатам анализа перечисленных признаков экспертиза может прийти к выводу об однородности или неоднородности товаров. Если заявленное обозначение тождественно или сходно до степени смешения с другим (другими) товарным знаком в отношении товаров, которые экспертиза признает однородными, то в регистрации товарного знака вам будет отказано.
В отношении товаров широкого потребления, для установления однородности товаров, применяется более строгий подход, нежели чем в отношении товаров производственно-технического назначения.
При покупке товаров повседневного спроса, недорогих товаров, внимание потребителей, зачастую, снижено, следовательно, вероятность смешения товарных знаков, которыми производители маркируют товар, достаточно велика. При покупке же дорогостоящих товаров, сложной техники, покупатели, как правило, максимально внимательны и вероятность смешения гораздо ниже, чем в случаях приобретения повседневных товаров.
Существует достаточно распространенное мнение среди лиц, не являющихся специалистами в области регистрации товарных знаков, что все товары, сгруппированные в одном классе МКТУ всегда являются однородными, при этом товары, находящиеся в различных классах МКТУ всегда не однородны. Это далеко не так. Однородными могут быть признаны не только товары, находящие в разных классах МКТУ, однородными могут быть признаны даже товары и услуги. А в рамках одного и того же класса могут находиться неоднородные товары.
Рассмотрим примеры установления однородности некоторых товаров: например: – могут быть признаны однородными товары 05 класса МКТУ «воды минеральные для медицинских целей» товарам 32 класса МКТУ – «воды минеральные (напитки)» 32 класса МКТУ; – «продукты детского питания», относящиеся к 05 классу могут быть признаны однородными товарам 29 класса МКТУ – «продукты молочные» и товарам 30 класса – «каши молочные».
В качестве примеров, когда могут быть признаны однородными товары и услуги, можно привести следующие: – товар «программы для компьютеров», входящий в 09 класс МКТУ может быть признан однородным услуге, содержащейся в перечне услуг 42 класса МКТУ – «составление программ для компьютеров»; – «одежда», товар, отнесенный к 25 классу МКТУ однороден услугам 40 класса – «пошив одежды»; – однородными часто признаются товары и связанные с этими товарами услуги, например: товары 12 класса «автомобили» и услуги 37 класса – «ремонт и техническое обслуживание автомобилей».
Чем сильнее сходство рассматриваемых обозначений, тем выше вероятность того, что потребитель может их спутать, соответственно, тем больше, шире диапазон товаров, которые экспертиза расценит как однородные.
Для проведения поиска тождественных и сходных товарных знаков и установления однородности товаров Методические Рекомендации Роспатента приводят примерный перечень корреспондирующих классов.
Таблица 6 – Перечень корреспондирующих классов.
|
1 |
2,3,5, 7,19 |
|
1 |
2 |
|
2 |
1,3,17 |
|
3 |
1,2,5,21 |
|
5 |
1,3,10 |
|
6 |
7,9,11,17,20,21 |
|
7 |
6,9,11,12 |
|
8 |
7,12 |
|
9 |
6,7,10,11,12 |
|
10 |
5,9 |
|
11 |
6,7,9 |
|
12 |
7,9 |
|
17 |
1,2,6,19 |
|
19 |
1,17 |
|
20 |
6 |
|
21 |
3,6 |
|
29 |
30 |
|
30 |
29 |
|
32 |
33 |
|
33 |
32 |
В качестве примера, иллюстрирующего подход к оценке однородности товаров, казалось бы, на первый взгляд, не являющимися однородными, можно привести Постановление Высшего арбитражного суда РФ по товарному знаку «AMRO НЕВСКОЕ». Данным судебным актом был окончательно разрешен спор между ОАО «Вена», являющегося обладателем прав на товарный знак «НЕВСКОЕ» по свидетельству N 189158 с датой приоритета 07.04.1998 для товаров классов 21, 32 (в том числе пива), 33 (алкогольные напитки), 42 (обеспечение пищевыми продуктами и напитками) МКТУ и ООО «Блэк Джек-1», являющегося владельцем комбинированного товарного знака со словесным элементом «AMRO НЕВСКОЕ» по свидетельству N 241119 с более поздней датой приоритета (05.02.2001) для ряда товаров класса 29 (арахис обработанный, креветки, миндаль обработанный, орехи обработанные, чипсы, рыба, рыба соленая, рыба сушеная, кальмары обработанные, кальмары сушеные) и класса 30 МКТУ.
Общество «Вена» подало в патентную палату возражение против регистрации товарного знака “AMRO НЕВСКОЕ”, указывая: оспариваемое обозначение сходно до степени смешения с товарным знаком заявителя и вводит потребителя в заблуждение в отношении производителя товаров или лица, обеспечивающего их появление на рынке, а, следовательно, регистрация такого товарного знака противоречит требованиям пункта 3
статьи 6 и пункта 1 статьи 7 Закона о товарных знаках (на дату рассмотрения спора действовал Закон о товарных знаках).
Президиум высшего арбитражного суда РФ поставил точку в этом споре, отметив, что:
«Поскольку в данном случае имеет место столкновение двух не идентичных, а схожих товарных знаков, зарегистрированных в отношении также не идентичных товаров и услуг, для охраны первого товарного знака наличие сходства с ним более позднего знака и угроза его смешения с этим знаком должна быть установлена судом.
Следует признать, что угроза смешения имеет место, если один товарный знак воспринимается за другой или если потребитель понимает, что речь идет не об одном и том же товарном знаке, но полагает, что оба товарных знака принадлежат одному и тому же предприятию. Такая угроза зависит от нескольких обстоятельств: во-первых, от различительной способности знака с более ранним приоритетом; во-вторых, от сходства противопоставляемых знаков; в-третьих, от оценки однородности обозначенных знаком товаров и услуг.
Сравнивая обозначения «НЕВСКОЕ» и «AMRO НЕВСКОЕ», суд первой инстанции правомерно исходил из того, что первый товарный знак в отношении пива обладает существенной различительной способностью. Это один из наиболее популярных пивных брендов России с достаточно большой долей рынка и узнаваемостью среди потребителей. Поэтому не имеет решающего значения тот факт, что товарный знак «НЕВСКОЕ», образованный от слова «Нева», является производным, а не оригинальным. В результате использования на рынке в течение нескольких лет (с 1998 года) данный товарный знак приобрел достаточную различительную способность в отношении пива. На усиление различительной способности влияет наличие у общества «Вена» серии товарных знаков с указанным словесным элементом. Обозначение «НЕВСКОЕ» полностью включено в товарный знак общества и занимает в нем доминирующее положение. Как правильно отметил суд первой инстанции, признание названного элемента доминирующим связано с тем, что другой элемент «AMRO» не ассоциируется у потребителей со словом, имеющим какую-либо смысловую нагрузку.
Кроме того, согласно статьям 3 и 4 Закона о товарных знаках право на товарный знак ограничено товарами и услугами, указанными в свидетельстве, однако охрана его распространяется не только на те объекты, которые он обозначает, но и на однородные, не упомянутые в охранном документе. Однородность признается по факту, если товары по причине их природы или назначения могут быть отнесены потребителями к одному и тому же источнику происхождения.
При установлении однородности товаров должны приниматься во внимание такие обстоятельства: род (вид) товаров, их потребительские свойства и функциональное назначение (объем и цель применения), вид материала, из которого они изготовлены, взаимодополняемость либо взаимозаменяемость товаров, условия их реализации (в том числе общее место продажи, продажа через розничную либо оптовую сеть), круг потребителей, традиционный или преимущественный уклад использования товаров.
При исследовании однородности товара – пива (класс 32), услуг по обеспечению пищевыми продуктами и напитками (класс 42) и перечисленных ранее пищевых продуктов, входящих в класс 29 МКТУ, суд первой инстанции пришел к правильному выводу, что традиционность применения в качестве пивных закусок этих пищевых продуктов, условия их сбыта (совместная продажа пива и пивных закусок), общий для них круг потребителей свидетельствуют об однородности сравниваемых товаров и услуг.
Кроме того, сложившееся в обществе представление о взаимодополняемости таких товаров, как пиво и пивные закуски, при их употреблении свидетельствует об их общем (целостном) восприятии значительным кругом потребителей». Матрицы парных сравнений представлена в таблице 7.
Таблица 7 – Матрица парных сравнений
|
– |
Е1 |
Е2 |
Е3 |
|
Е1 |
1 |
е12 |
е13 |
|
Е2 |
1/е12 |
1 |
е23 |
|
Е3 |
1/е13 |
1/е23 |
1 |
Матрица парных сравнений – обратно симметричная. Диагональ состоит из единиц. Элементы матрицы a t у определяются по шкале относительной важности.
Если элемент A t превосходит элемент Ау , то в строку i столбец j заносится целое число, а в строку j, столбец i заносится обратное к нему число.
Основная проблема заполнения матрицы парных сравнений -обеспечение транзитивности суждений.
Если Е ± > Е 2 , и Е 2 > Е 3, н о Е < Е 3 то суждения не транзитивны, матрица не согласована [ 2 0 ].
Вычисление коэффициентов важности элементов по матрице парных сравнений:

Индекс согласованности:
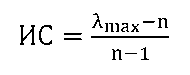
где – максимальное собственное число матрицы;
n – размер матрицы (число сравниваемых элементов).
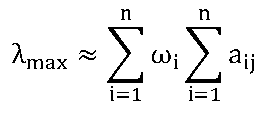
Отношение согласованности: ОС=ИС/К [ ]
Средние значения согласованности случайных матриц:
|
– |
Размер матрицы |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
– |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
К |
0,58 |
0,9 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
1,48 |
1,53 |
Критерий согласованности матрицы парных сравнений: О С <0,1 -02 Если ОС>0,1 – матрица не согласована [ 2 1 ].
1.3 Достоинства и недостатки метода парных сравнений
Основные преимущества метода заключаются в следующем
– допускается измерение неравномерно изменяющейся важности показателей, столь необходимое для решения большинства практических экономических задач;
-эксперт в процессе анализа сосредоточивает внимание не на всех показателях сразу, а только на двух, сравниваемых в каждый данный момент, что облегчает работу, а следовательно, способствует повышению ее качества; -можно получить большое число сравнений каждого показателя с другими, благодаря чему повышается точность оценки и открывается возможность изучать качество большего числа сторон объекта исследования, нежели при использовании других методов;
-можно получить не только среднюю оценку показателя, данную каждым экспертом, но и дисперсию этой оценки, что дает возможность провести в дальнейшем более глубокий экономико-математический анализ
Метод парного сравнения – наиболее простой из существующих классификационных тестов, поскольку он предусматривает сопоставление только двух образцов продукта
Преимущество метода парных сравнений перед ранжированием заключается в том, что легче вынести суждение, поскольку супервизору одновременно нужно сравнивать только двух человек. Второе преимущество
– в том, что он предоставляет возможность поставить на один уровень людей, обладающих одинаковыми способностями.
Метод парных сравнений позволяет провести строгий, статистически обоснованный анализ согласованности мнений экспертов, выявить, случайны или нет полученные оценки. Несомненно, процедура метода парных сравнений сложнее метода простой ранжировки, но проще метода последовательных сравнений.
Данный метод очень прост и он позволяет исследовать большее количество объектов (по сравнению, например, с методом рангов) и с большей точностью.
Недостаток же кроется в необходимости выполнять огромное количество парных сравнений, если приходится оценивать большие группы. Супервизор, у которого в подчинении находится 60 сотрудников, должен будет выполнить 1770 сравнений! Если же сравнение будет проводиться по пяти отдельным параметрам, то количество парных сравнений возрастет в пять раз. Обычно методом парных сравнений пользуются в двух случаях: либо при проведении оценки небольших групп, либо при проведении оценки только по одному параметру – по общей эффективности производственной деятельности
Один недостаток парных сравнений как экспериментального метода состоит в том, что сравнение п стимулов требует получения (п — 1) х (n / 2) суждений. Напр., для 10 стимулов требуется получить 45 суждений, а если бы мы захотели шкалировать набор из 50 стимулов, нам потребовалось бы 1225 суждений.
Основной минус метода парных сравнений – нет готовых программных разработок.
Чтобы воспользоваться этим методом, придется поручить компетентным работникам компании разработать специальную программу или заказывать ее у стороннего разработчика. Кроме того, пока не существует апробированных бизнес-решений в области деловой оценки, основанных исключительно на парных сравнениях, это скорее математический полуфабрикат, который служит для создания инструментов шкалирования. К тому же сама тестовая процедура выглядит довольно монотонной, что влияет на объективность исследовательских выводов. Да и качество результатов напрямую зависит от количества оценок и оцениваемых показателей, а также правильного отбора пар и их однозначного толкования.
Как правило, считается, что метод парных сравнений лучше, чем прямое ранжирование. Такая точка зрения не совсем верна, и вот почему.
Выбор метода всегда обусловлен исследовательской ситуацией, целями исследования. Естественно, если можно однозначно сформулировать основание ранжирования, то метод парных сравнений дает отличный результат и надо выбирать этот метод. Но бывают ситуации, когда невозможно и не очень нужно однозначно понимаемое основание ранжирования.
Недостатком метода является рост трудоемкости процедуры при увеличении числа объектов: уже при 12-15 объектах процедура становится трудоемкой. Кроме того, разные пары объектов иногда сопоставляются респондентами по разным критериям, что приводит к нетранзитивности предпочтений. Метод широко используется в экспертных оценках.
Тестирование — распространенный способ проверки знаний. Этот метод ценен тем, что может проводиться дистанционно (что удобно при высокой территориальной распределенности персонала), а также тем, что не занимает много времени и достаточно просто администрируется. Главное ограничение тестирований — низкая валидность при оценке по многим важным компетенциям. Оценить компетенции, напрямую не связанные со знаниями (убедительная коммуникация, управление командой и т. п.), при помощи тестирования практически невозможно. Кроме этого разработка тестов, «заточенных» под специфику деятельности Банка, — непростой и недешевый процесс. Еще один минус тестирований — высокий риск неприятия результатов оценки как самими оцениваемыми, так и руководством
2 Решение задачи о выборе оптимальной номенклатуры товаров на основе метода парных сравнений
Рассмотрим процесс приобретения стиральных порошков следующих
видов:
1)Миф;
2)Тайд;
3)Дося;
4)Ариэль.
Опишем один из способов того, как практически придать количественное наполнение сравнению объектов, действий или обстоятельств и построить соответствующую таблицу сравнений.
Для того, чтобы выбрать наиболее качественный и недорогой стиральный порошок составим матрицу парных сравнений. Для сравнения нам понадобится шкала относительной важности.
Таблица 1- Шкала относительной важности.
|
Интенсивность относительной важности |
Определение |
Объяснение |
|
1 |
2 |
3 |
|
0 |
Несравнимы |
Эксперт затрудняется в сравнении |
|
1 |
Равная важность |
Равный вклад двух видов деятельности в цель |
|
3 |
Умеренное превосходство одного над другим |
Опыт и суждения дают легкое превосходство одному виду деятельности над другим |
|
5 |
Существенное или сильное превосходство |
Опыт и суждения дают сильное превосходство одному виду деятельности над другим |
|
7 |
Значительное превосходство |
Одному из видов деятельности дается настолько сильное превосходство, что оно становится практически значительным |
|
9 |
Очень сильное превосходство |
Очевидность превосходства одного вида деятельности над другим подтверждается наиболее сильно |
|
2,4,6,8 |
Промежуточные решения между двумя соседними суждениями |
Применяются в компромиссном случае |
|
Обратные величины приведенных выше чисел |
Если при сравнении одного вида деятельности с др. получено одно из вышеуказанных чисел (3), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 1/3) |
Матрица парных сравнений строится по следующим правилам:
-если Миф и Тайд одинаково важны, заносим в позицию (Миф,Тайд) таблицы сравнений число 1,
-если Миф незначительно важнее Тайд – число 3,
-если Миф значительно важнее Тайд – число 5,
-если Миф явно важнее Тайд – число 7,
-если Миф по своей значимости абсолютно превосходит Тайд – число 9.
Числа 2, 4, 6 и 8 используются для облегчения компромиссов между оценками, слегка отличающимися от основных чисел.
Рациональные дроби используются в случае, когда желательно увеличить согласованность всей матрицы при малом числе суждений.
Предположим, что сравнивая стиральные порошки 1, 2, 3 и 4, мы получили таблицу сравнений, которая приводит к обратно-симметричной матрице.
Матрица А называется обратно-симметричной, если для любых i и k выполняется соотношение:
aki = 1 / aik (1)
Из этого, в частности, следует, что aii = 1.
Матрица А называется согласованной, если для любых i, k и l имеет место равенство:
аik* aki = ail (2)
Тем самым, идеальная матрица сравнений – обратно-симметричная и согласованная.
Справедливо следующее утверждение.
ТЕОРЕМА. Положительная обратно-симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение совпадают [ 2 9 ].
lmax = n (3)
Таблица 2- Матрица парных сравнений
|
Товар |
Миф |
Тайд |
Дося |
Ариэль |
|
Миф 1 |
1 |
5 |
6 |
7 |
|
Тайд 2 |
1/5 |
1 |
4 |
6 |
|
Дося 3 |
1/6 |
1/4 |
1 |
4 |
|
Ариэль 4 |
1/7 |
1/6 |
1/4 |
1 |
Опишем несколько способов приближенного вычисления собственного столбца
1-й способ:
1) суммируем элементы каждой строки и записываем полученные результаты в столбец,
2) складываем все элементы найденного столбца,
3) делим каждый из элементов этого столбца на полученную сумму.
2-й способ:
1) суммируем элементы каждого столбца и записываем полученные результаты в столбец,
2) заменяем каждый элемент построенного столбца на обратный ему,
3) складываем элементы столбца из обратных величин,
4) делим каждый из этих элементов на полученную сумму.
3-й способ:
1) суммируем элементы каждого столбца,
2) делим элементы каждого столбца на их сумму,
3) складываем элементы каждой строки полученной матрицы,
4) записываем результаты в столбец,
5) делим каждый из элементов последнего столбца на порядок исходной матрицы п.
4-й способ:
1) перемножаем элементы каждой строки и записываем полученные результаты в столбец,
2) извлекаем корень n-й степени из каждого элемента найденного столбца,
3) складываем элементы этого столбца,
4) делим каждый из этих элементов на полученную сумму.
Каждый из этих четырех способов, будучи примененным к идеальной матрице, приводит к одному и тому же точному результату. Пользуясь одним из способов приближенного вычисления собственных элементов этой матрицы (для определенности вторым), мы нашли и собственный столбец и собственное значение, и ИС:
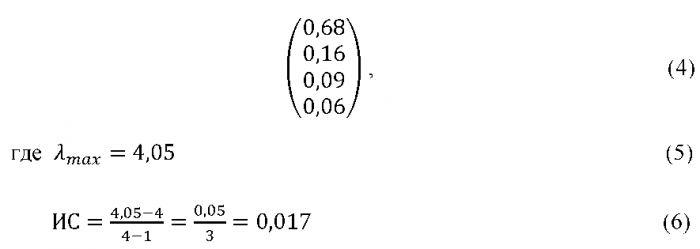
Сумма всех элементов полученного собственного столбца (его называют столбцом приоритетов) равна 1. Он позволяет подвести итог проведенному анализу таблицы сравнений: среди сравниваемых элементов 1,
2, 3 и 4 наивысший приоритет имеет Миф (68%), затем идут Тайд (16%),
Дося (9%) и Ариэль (6%) соответственно.
Заключение
Динамизм и новизна современных народнохозяйственных задач, возможность возникновения разнообразных факторов, влияющих на эффективность решений, требуют, чтобы эти решения принимались быстро и в то же время были хорошо обоснованы. Опыт, интуиция, чувство перспективы в сочетании с информацией помогают специалистам точнее выбирать наиболее важные цели и направления развития, находить наилучшие варианты решения сложных научно-технических и социально-экономических задач в условиях, когда нет информации о решении аналогичных проблем в прошлом.
Использование метода парных сравнений помогает формализовать процедуры сбора, обобщения и анализа мнений специалистов с целью преобразования их в форму, наиболее удобную для принятия обоснованного решения.
Но, следует заметить, что метод парных сравнений не может заменить ни административных, ни плановых решений, он лишь позволяет пополнить информацию, необходимую для подготовки и принятия таких решений.
Широкое использование парных сравнений правомерно только там, где для анализа будущего невозможно применить более точные методы.
Методы парных сравнений непрерывно развиваются и совершенствуются. Основные направления этого развития определяются рядом факторов, в числе которых можно указать на стремление расширить области применения, повысить степень использования математических методов и электронно-вычислительной техники, а также изыскать пути устранения выявляющихся недостатков [3 1].
Несмотря на успехи, достигнутые в последние годы в разработке и практическом использовании метода парных сравнений, имеется ряд проблем и задач, требующих дальнейших методологических исследований и практической проверки.
Необходимо совершенствовать систему отбора экспертов, повышение надежности характеристик группового мнения, разработку методов проверки обоснованности сравнений, исследование скрытых причин, снижающих достоверность парных сравнений.
Однако, уже и сегодня парные сравнения в сочетании с другими математико-статистическими методами являются важным инструментом совершенствования управления на всех уровнях.
При решении задачи о выборе оптимальной номенклатуры товаров, можно сделать следующий вывод: при приобретении стиральных порошков, для начала мы их сравнили, затем, исходя из шкалы относительной важности, выбрали самый наилучший, им оказался порошок Миф. Данный вид порошка является наиболее качественным, относительно недорогим по цене и также на рынке он пользуется спросом среди покупателей.


