Расстояния между двумя точками
На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.
Расстояние между двумя точками — это длина отрезка, которая соединяет эти точки.
Расстояния между двумя точками
Формула вычисления расстояния между двумя точками A(xa; ya) и B(xb; yb) на плоскости:
Формула вычисления расстояния между двумя точками A(xa; ya; za) и B(xb; yb; zb) в пространстве:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат x и y.
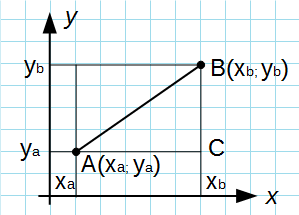
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Расстояние между отрезками
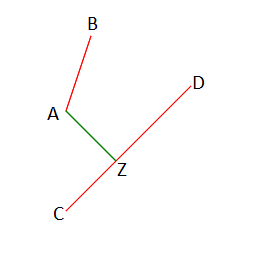
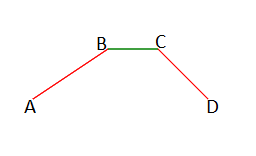
Координаты концов первого отрезка: A(xa, ya), B(xb, yb).
Координаты концов второго отрезка: C(xc, yc), D(xd, yd).
Тогда t = Δ1/Δ, s = Δ2/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).
Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(xz, yz) можно найти по формуле yz = kxz + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x2 — x1)(x3 — xz)+(y2 — y1)(y3 — yz) = 0, соответственно xz = (x3x2 — x3x1 + y2y3 — y1y3 + y1d — y2d)/(ky2 — ky1 + x2 — x1), где (x3, y3) — координаты точки, с которой была опущена высота, (x1, y1) и (x2, y2) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.
Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x3 — xz) 2 + (y3 — kxz — d) 2 ).
Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x1 — x3) 2 + (y1 — y3) 2 ), где (x1, y1) — координаты одного из концов первого отрезка, а (x3, y3) — координаты одного из концов второго отрезка.
Отрезок. Формула длины отрезка.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 — y1, а на ось х длина проекции равна х2 — х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.


Координаты концов первого отрезка: A(xa, ya), B(xb, yb).
Координаты концов второго отрезка: C(xc, yc), D(xd, yd).
Для начала проверим не пересекаются ли отрезки.
Пусть для отрезка AB: x = t(xb – xa) + xa, y = t(yb – ya) + ya, тогда для CD: x = s(xd – xc) + xc, y = s(yd – yc) + yc, где 0 ≤ t,s ≤ 1.
Если отрезки пересекаются, то выполняются равенства:
t(xb – xa) – s(xd – xc) = xc – xa и t(yb – ya) – s(yd – yc) = yc – ya.
Полученную систему уравнений решим методом Крамера:
Δ = (xb – xa)(yс – yd) – (yb – ya)(xс – xd).
Δ1 = (xb – xa)(yс – ya) – (yb – ya)(xс – xa).
Δ2 = (xc – xa)(yс – yd) – (yc – ya)(xс – xd).
Тогда t = Δ1/Δ, s = Δ2/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).
Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(xz, yz) можно найти по формуле yz = kxz + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x2 – x1)(x3 – xz)+(y2 – y1)(y3 – yz) = 0, соответственно xz = (x3x2 – x3x1 + y2y3 – y1y3 + y1d – y2d)/(ky2 – ky1 + x2 – x1), где (x3, y3) — координаты точки, с которой была опущена высота, (x1, y1) и (x2, y2) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.
Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x3 – xz)2 + (y3 – kxz – d)2).
Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x1 – x3)2 + (y1 – y3)2), где (x1, y1) — координаты одного из концов первого отрезка, а (x3, y3) — координаты одного из концов второго отрезка.
тупое решение в лоб – идем в поисковик, и просто тупо пишем: расстояние между отрезками
вторая же ссылка (ну лично у меня) – Ю2.30. Расстояние между отрезками
там и описание и решение и код, правда на Си
берем его и переписываем на Python, получаем:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import math
def ras (x1, y1, x2, y2, x3, y3):
## Если отрезок вертикальный - меняем местами координаты каждой точки.
if x1==x2:
x1, y1 = y1, x1
x2, y2 = y2, x2
x3, y3 = y3, x3
k=(y1-y2)/(x1-x2) ## Ищем коэффициенты уравнения прямой, которому принадлежит данный отрезок.
d=y1-k*x1
xz=(x3*x2-x3*x1+y2*y3-y1*y3+y1*d-y2*d)/(k*y2-k*y1+x2-x1)
dl=-1
if ( xz<=x2 and xz>=x1 ) or ( xz<=x1 and xz>=x2 ):
dl=math.sqrt((x3-xz)*(x3-xz)+(y3-xz*k-d)*(y3-xz*k-d)) ## Проверим лежит ли основание высоты на отрезке.
return dl
## Вводим параметры отрезков
# xa, ya, xb, yb = [1, 1, 2, 2]
# xc, yc, xd, yd = [2, 1, 3, 0]
xa, ya, xb, yb = [int(s) for s in input().split()]
xc, yc, xd, yd = [int(s) for s in input().split()]
min=-1
t=-2
s=-2
o=(xb-xa)*(-yd+yc)-(yb-ya)*(-xd+xc)
o1=(xb-xa)*(yc-ya)-(yb-ya)*(xc-xa)
o2=(-yd+yc)*(xc-xa)-(-xd+xc)*(yc-ya)
if o!=0:
t=o1/o
s=o2/o
if (t>=0 and s>=0) and (t<=1 and s<=1):
min=0 ## Проверим пересекаются ли отрезки.
else:
## Найдём наименьшую высоту опущенную из конца одного отрезка на другой.
dl1=ras(xa,ya,xb,yb,xc,yc)
min=dl1
dl2=ras(xa,ya,xb,yb,xd,yd)
if ( dl2<min and dl2!=-1 ) or min==-1 :
min=dl2
dl3=ras(xc,yc,xd,yd,xa,ya)
if ( dl3<min and dl3!=-1 ) or min==-1 :
min=dl3
dl4=ras(xc,yc,xd,yd,xb,yb)
if ( dl4<min and dl4!=-1) or min==-1 :
min=dl4
if min==-1 :
## В случае, если невозможно опустить высоту найдём минимальное расстояние между точками.
dl1=math.sqrt((xa-xc)*(xa-xc)+(ya-yc)*(ya-yc))
min=dl1
dl2=math.sqrt((xb-xd)*(xb-xd)+(yb-yd)*(yb-yd))
if dl2<min :
min=dl2
dl3=math.sqrt((xb-xc)*(xb-xc)+(yb-yc)*(yb-yc))
if dl3<min :
min=dl3
dl4=math.sqrt((xa-xd)*(xa-xd)+(ya-yd)*(ya-yd))
if dl4<min :
min=dl4
print (min)PS: ну, …. пробовали?? или нужно на подносе?
Длина отрезка. Расстояние между точками: онлайн-калькулятор
Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:
- Задать размерность (плоскость или пространство).
- Ввести в поля координаты точек.
- Нажать «рассчитать».
Расстояние между точками онлайн
Для нахождения длины отрезка по координатам существует формула. Для отрезка AB в трехмерном пространстве она имеет вид:
d=xb-xa2+yb-ya2+zb-za2
Даже если вы забыли данную формулу, расстояние между точками всегда можно найти по координатам онлайн. Калькулятор не только предоставляет правильный ответ, но и подробно расписывает решение.
Онлайн-калькулятор нахождения длины отрезка по координатам будет полезен школьникам и студентам в самостоятельной подготовке, а также преподавателям и всем любителям математики.
По какой формуле найти расстояние между отрезками (прямыми) в пространстве, зная координаты их концов
Профи
(678),
закрыт
11 лет назад
Игорь Елкин
Просветленный
(49544)
11 лет назад
Как ты вообще себе представляешь это расстояние? Тебе надо найти минимальный отрезок, который соединяет две точки отрезков. Эти две точки-то сразу не определить, не то, что формулу конечную.
Составь два уравнения этих прямых (на которых отрезки) посмотри, где отрезки, может есть лёгкий вариант решения. Может у одного отрезка есть один конец, который наиболее приближен. Задай функцию от этого конца до другого отрезка, и ищи минимум.
