Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.
Для чтения этой темы желательно, хоть и не обязательно, ознакомиться с темой “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи”, а также с темой “Базисные и свободные переменные. Общее и базисное решения системы линейных алгебраических уравнений”.
Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи” вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $left { begin{aligned}
& 2x_1-3x_2-x_3-x_4=0;\
& -4x_1+5x_2+3x_4=0.
end{aligned} right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.
Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:
$$
left { begin{aligned}
& 2cdot 0-3cdot 0-0-0=0;\
& -4cdot 0+5cdot 0+3cdot 0=0.
end{aligned} right.
$$
Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?
Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:
$$
left { begin{aligned}
& 2cdot 1-3cdot (-1)-2-3=0;\
& -4cdot 1+5cdot (-1)+3cdot 3=0.
end{aligned} right.
$$
Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.
Кстати сказать, чтобы не писать каждый раз выражения вроде “$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$”, пишут все значения переменных в матрицу-столбец: $left(begin{array} {c}
1 \
-1 \
2 \
3 end{array} right)$. Эту матрицу тоже называют решением СЛАУ.
Теорема Кронекера-Капелли гласит, что любая СЛАУ имеет решение (совместна) тогда и только тогда, когда ранг матрицы системы ($A$) равен рангу расширенной матрицы системы ($widetilde{A}$), т.е. $rang A=rangwidetilde{A}$. Так как мы уже выяснили, что любая однородная СЛАУ имеет решение (хотя бы одно), то для всех однородных СЛАУ $rang A=rangwidetilde{A}$. Так как ранги равны между собой, то можно обозначить их какой-то одной буквой, например, $r$. Итак, для любой однородной СЛАУ имеем: $rang A=rangwidetilde{A}=r$.
Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.
Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.
Этот случай уже был рассмотрен в теме “Базисные и свободные переменные. Общее и базисное решения СЛАУ”. По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.
Что такое базисные и свободные переменные? показатьскрыть
Фундаментальная система решений однородной СЛАУ.
С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $varphi_1$, $varphi_2$,…, $varphi_{n-r}$.
Любая совокупность $n-r$ линейно независимых решений однородной СЛАУ называется фундаментальной системой (или совокупностью) решений данной СЛАУ.
Часто вместо словосочетания “фундаментальная система решений” используют аббревиатуру “ФСР”. Если решения $varphi_1$, $varphi_2$,…, $varphi_{n-r}$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:
$$
X=C_1cdot varphi_1+C_2cdot varphi_2+ldots+C_{n-r}cdot varphi_{n-r},
$$
где $C_1$, $C_2$,…, $C_{n-r}$ – произвольные постоянные.
Что значит “линейно независимые решения”? показатьскрыть
Пример №1
Решить СЛАУ
$$left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=0\
& -x_1+2x_2+x_3+x_4=0;\
& x_1-2x_2+2x_3+3x_4=0.
end{aligned} right.$$
Если система является неопределённой, указать фундаментальную систему решений.
Решение
Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 0 \
-1 & 2 & 1 & 1 & 0 \
1 & -2 & 2 & 3 & 0 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
-1 & 2 & 1 & 1 & 0 \
3 & -6 & 9 & 13 & 0
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1end{array} rightarrow
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0 \
0 & 0 & 3 & 4 & 0
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\ r_3-r_2end{array} rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0 \
0 & 0 & 0 & 0 & 0
end{array}right).
$$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:

На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Примечание. показатьскрыть
Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:
$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0
end{array}right)
$$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$
left( begin{array} {cc|cc}
1 & 2 & 2 & -3\
0 & 3 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|cc}
1 & 2 & 2 & -3\
0 & 1 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \
rightarrow left(begin{array} {cc|cc}
1 & 0 & 2 & -1/3\
0 & 1 & 0 & -4/3
end{array}right).
$$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:
$$
left{begin{aligned}
& x_1=2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$
Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-frac{1}{3}x_4$ и $x_3=-frac{4}{3}x_4$ в левую часть первого уравнения, получим:
$$
3x_1-6x_2+9x_3+13x_4=3cdot left(2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-frac{4}{3}x_4right)+13x_4=0.
$$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $left(begin{array} {cc} 1 & 0 \0 & 1end{array}right)$. Таблица будет выглядеть так:

Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-frac{1}{3}x_4$ и $x_3=-frac{4}{3}x_4$. Если $x_2=1$, $x_4=0$, то:
$$
begin{aligned}
& x_1=2cdot 1-frac{1}{3}cdot 0=2;\
& x_3=-frac{4}{3}cdot 0=0.
end{aligned}
$$
Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:
$$
begin{array} {c|c|c|c}
x_1 & x_3 & x_2 & x_4 \
hline 2 & 0 & 1 & 0 \
hline & & 0 & 1
end{array}
$$
Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:
$$
begin{aligned}
& x_1=2cdot 0-frac{1}{3}cdot 1=-frac{1}{3};\
& x_3=-frac{4}{3}cdot 1=-frac{4}{3}.
end{aligned}
$$
Найденные значения $x_1=-frac{1}{3}$ и $x_3=-frac{4}{3}$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:
$$
begin{array} {c|c|c|c}
x_1 & x_3 & x_2 & x_4 \
hline 2 & 0 & 1 & 0 \
hline -frac{1}{3} & -frac{4}{3} & 0 & 1
end{array}
$$
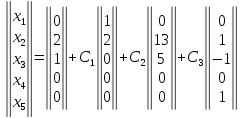
Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=left(begin{array} {c} x_1 \x_2 \x_3 \x_4 end{array}right)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:
$$
varphi_1=left(begin{array} {c} 2 \1 \0 \0 end{array}right);;
varphi_2=left(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right).
$$
Совокупность $varphi_1=left(begin{array} {c} 2 \1 \0 \0 end{array}right)$, $varphi_2=left(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$
X=C_1cdotleft(begin{array} {c} 2 \1 \0 \0 end{array}right)+C_2cdotleft(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right),
$$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Общее решение: $left{begin{aligned}
& x_1=2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$. Или так: $X=C_1cdotleft(begin{array} {c} 2 \1 \0 \0 end{array}right)+C_2cdotleft(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $varphi_1=left(begin{array} {c} 2 \1 \0 \0 end{array}right)$, $varphi_2=left(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right)$.
Пример №2
Записать ФСР однородной СЛАУ
$$
left{begin{aligned}
& x_1-5x_2-x_3-2x_4+3x_5=0;\
& 2x_1-6x_2+x_3-4x_4-2x_5=0; \
& -x_1+4x_2+5x_3-3x_4=0.
end{aligned} right.,
$$
зная общее решение. Записать общее решение с помощью ФСР.
Решение
Общее решение уже было получено в теме “метод Крамера” (пример №4). Это решение таково:
$$
left{begin{aligned}
& x_1=frac{-17x_4+144x_5}{19};\
& x_2=frac{-15x_4+41x_5}{19};\
& x_3=frac{20x_4-4x_5}{19}; \
& x_4in R; ; x_5in R.
end{aligned} right.
$$
Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.
Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.
Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.
$$
begin{array} {c|c|c|c|c}
x_1 & x_2 & x_3 & x_4 & x_5\
hline -frac{17}{19} & -frac{15}{19} & frac{20}{19} & 1 & 0 \
hline frac{144}{19} & frac{41}{19} & -frac{4}{19} & 0 & 1
end{array}
$$
Совокупность $varphi_1=left(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)$, $varphi_2=left(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$
X=C_1cdotleft(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)+C_2cdotleft(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right),
$$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Фундаментальная система решений: $varphi_1=left(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)$, $varphi_2=left(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right)$. Общее решение: $X=C_1cdotleft(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)+C_2cdotleft(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right)$, где $C_1$ и $C_2$ – произвольные константы.
Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.
Содержание:
- Однородные СЛАУ
- Фундаментальная система решений
Однородные СЛАУ
Определение
Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.
Однородная СЛАУ, записанная в
матричном виде, $A X=Theta$ всегда совместна,
так как $X=Theta$ всегда является ее решением.
Заметим, что если $x_{1}, x_{2}$ – это два решения однородной
СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:
$$Y=lambda_{1} x_{1}+lambda_{2} x_{2}$$
$$A Y=Aleft(lambda_{1} x_{1}+lambda_{2} x_{2}right)=lambda_{1} A x_{1}+lambda_{2} A x_{2}=lambda_{1} Theta+lambda_{2} Theta=Theta$$
Теорема
Если однородная квадратная СЛАУ имеет ненулевое решение, то
определитель матрицы системы равен нулю.
Пример
Задание. Выяснить, имеет ли однородная СЛАУ
$left{begin{array}{l}
3 x-2 y=-1 \
x+3 y=7
end{array}right.$ ненулевые решения.
Решение. Вычислим определитель матрицы системы:
$$Delta=left|begin{array}{rr}
3 & -2 \
1 & 3
end{array}right|=9-(-2)=9+2=11 neq 0$$
Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$
Ответ. Система имеет только нулевое решение.
Фундаментальная система решений
Рассмотрим множество всех столбцов, которые являются решениями исходной системы.
Определение
Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.
Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы.
Любое решение исходной системы есть линейная комбинация решений ФСР.
Теорема
Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и
общего решения соответствующей однородной СЛАУ.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти общее решение и ФСР однородной системы
$left{begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
end{array}right.$
Решение. Приведем систему к ступенчатому виду с помощью
метода Гаусса. Для этого записываем
матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец
свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут
получаться нули):
$$A=left(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
1 & -2 & 2 & -1 & 0 \
4 & -2 & 6 & 3 & -4 \
2 & 4 & -2 & 4 & -7
end{array}right)$$
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем
первую, от третьей – четыре первых, от четвертой – две первых:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & -6 & 6 & 15 & 0 \
0 & 2 & -2 & 10 & -5
end{array}right)$$
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три
вторых, к четвертой прибавляем вторую:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 9 & -3 \
0 & 0 & 0 & 12 & -4
end{array}right)$$
От четвертой строки отнимем $frac{4}{3}$ третьей и третью
строку умножим на $frac{1}{3}$ :
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1 \
0 & 0 & 0 & 0 & 0
end{array}right)$$
Нулевые строки можно далее не рассматривать, тогда получаем, что
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1
end{array}right)$$
Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а
ко второй строке прибавляем третью:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -6 & 0 \
0 & -2 & 2 & 5 & 0 \
0 & 0 & 0 & 3 & -1
end{array}right)$$
то есть получаем систему, соответствующую данной матрице:
$$left{begin{array}{l}
x_{1}+x_{2}-6 x_{4}=0 \
-2 x_{2}+2 x_{3}+5 x_{4}=0 \
3 x_{4}-x_{5}=0
end{array}right.$$
Или, выразив одни переменные через другие, будем иметь:
$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{2}=x_{2} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{4}=x_{4} \
x_{5}=3 x_{4}
end{array}right.$$
Здесь $x_{2}, x_{4}$ – независимые (или свободные)
переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1}, x_{3}, x_{5}$ – зависимые (связанные) переменные
(то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от
пяти переменных) и ранга матрицы $r$ (в этом
случае получили, что $r=3$ – количество
ненулевых строк после приведения матрицы к ступенчатому виду):
$n-r=5-3=2$
Так как ранг матрицы $r=3$ , а количество неизвестных
системы $n=5$ , то тогда количество решений в ФСР
$n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть
для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки).
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{5}=3 x_{4}
end{array}right.$$
Тогда придавая в первом случае, например, независимым переменным значения
$x_{2}=1$ , $x_{4}=0$ получаем, что $left{begin{array}{l}
x_{1}=-1+6 cdot 0=-1 \
x_{3}=1-frac{5}{2} cdot 0=1 \
x_{5}=3 cdot 0=0
end{array}right.$ . Полученные значения записываем в первую
строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что
{x_{1}=12, x_{3}=-5, x_{5}=6} , что и определяет второе решение ФСР.
В итоге получаем следующую таблицу:
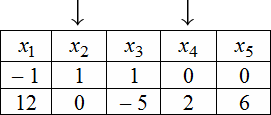
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
$$X_{1}=left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right), X_{2}=left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$
Общее решение является линейной комбинацией частных решений:
$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right)+C_{2}left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$
где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:
$left{begin{array}{l}
x_{1}=-C_{1}+12 C_{2} \
x_{2}=C_{1} \
x_{3}=C_{1}-5 C_{2} \
x_{4}=2 C_{2} \
x_{5}=6 C_{2}
end{array}right.$
$C_{1}, C_{2} neq 0$
Придавая константам $C_{1}, C_{2}$ определенные значения
и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
Читать дальше: примеры решения СЛАУ.
Фундаментальная система решений
Рассмотрим
систему однородных линейных алгебраических
уравнений.
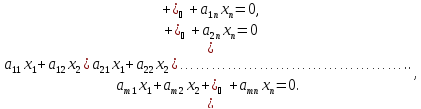 (1)
(1)
Выпишем
матрицу A

Определение
1.
Минор
матрицы называется базисным
, если
он неравен 0, и окаймляющие его миноры
либо все равны 0, либо совсем отсутствуют.
Теорема
о базисном миноре.
Столбцы
матрицы, пересекающие главный минор
линейно независимы; Всякий столбец
через них линейно выражается.
Определение
2.
Всякая
максимальная линейно независимая
система решений однородной системы
уравнений (1), называется фундаментальной
системой решений (ФСР).
Теорема:
Если
ранг r
, матрицы из коэффициентов системы
линейных однородных уравнений (1), меньше
m,
то всякая ФСР системы (1) состоит из n-r
решений.
Пример
№1.
Дана
однородная система линейных алгебраических
уравнений
 .
.
Найти
ФСР и общее решение системы.
1.Составим
матрицу системы.
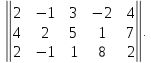
2.
Легко показать, что ранг матрицы A=2,
значит ФСР состоит из трех решений
(5-2=3).
3.
В матрице A
возьмем базисный минор (минор второго
порядка):
 .
.
4.
Отбрасываем последние уравнения системы
, а неизвестные
 ,
,
считаем
«свободными» и переносим их в правую
часть уравнений.
Получим:
 .
.
(2)
5.
Ищем первое базисное решение X
, для этого положим
 ,
,
тогда получим систему:
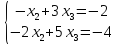 (3)
(3)
Определителем
матрицы системы является базисный
минор, он отличен от 0, значит система
(3) имеет единственное решение:
 .
.
Таким
образом
 =
=
 .
.
6.
Полагая в системе (2) ,
,
находим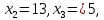 то
то
есть, вторым базисным решением является
столбец:
 .
.
7.
Полагая:
 ,
,
получаем –
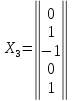 .
.
8.
Итак, ФСР получена; построенная таким
образом ФСР называется нормальной.
9.
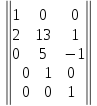
Столбцы
 образующие ФСР линейно независимы, так
образующие ФСР линейно независимы, так
как свободные неизвестные были выброшены
так, что выделенный минор третьего
порядка отличен от 0;
10.Теперь
выпишем общее решение исходной однородной
системы линейных алгебраических
уравнений.
 ,
,
 .
.
Неоднородная система линейных алгебраических уравнений
 (1)
(1)
Общее
решение неоднородной системы линейных
алгебраических уравнений (1) имеет вид:
 (2)
(2)
где
 – какое-либо решение системы (1).
– какое-либо решение системы (1).
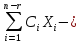
общее
решение соответствующей однородной
системы, для которой
 – ФСР.
– ФСР.
Пример
№2.
Дана
неоднородная система линейных
алгебраических уравнений:

Доказать,
что это система совместна и найти ее
общее решение.
Решение:
-
Легко
показать, что rang
Ᾱ
= rang
A -
Рассмотрим
соответствующую однородную систему
уравнений, эта система из примера №1.
Её ФСР и общее решение найдены. Выделим
в матрицу Ᾱ базисный минор, стоящий на
пересечении первых двух строк со вторым
и третьим столбцами. Тогда последовательность
уравнений системы есть следствие двух
первых уравнений системы, а неизвестные
 можно считать «свободными», поэтому
можно считать «свободными», поэтому
исходная система эквивалентна системе:



Решив
её, находим единственное решение:

Найдено
частное решение данной неоднородной
системы.
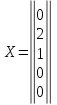 .
.
Общее
решение исходной неоднородной системы
получим с помощью формулы (2).
 =
=
или

Это
решение можно было бы получить методом
исключения неизвестных. ФСР определяется
неоднозначно,
но число элементов в ФСР всегда равно
 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Системой линейных уравнений называется система вида:
$begin{cases} a_{11} cdot x_1 +…+ a_{1n} cdot x_n = b_1 \ … \ a_{m1} cdot x_1 + a_{mn} cdot x_n = b_m end{cases}$
Замечание 1
Здесь каждая буква относится к своей группе обозначений, $x_1…x_n$ — это неизвестные числа или переменные, подлежащие поиску, $a_11…a_{mn}$ — множители, содержащиеся при неизвестных, $b_1…b_m$ — свободные члены таблицы из чисел, получаемой на основе приведённой СЛАУ.
В компактной форме СЛАУ принято записывать в виде формулы вида $A cdot X = B$. В этой формуле под большой буквой $A$ подразумевается матрица множителей при неизвестных системы, а буквами $X$ и $B$ обозначены вектор-столбец неизвестных системы и свободных членов.
Матрица $A$ называется основной матрицей системы, вот как она будет выглядеть:
$A = begin{pmatrix} a_{11} & … & a_{1n} \ vdots & … & vdots \ a_{m1} & … & a_{mn} end{pmatrix}$, $b=begin{pmatrix} b_1 \ vdots \ b_m end{pmatrix}$
Если через длинную черту после матрицы множителей при неизвестных записан столбец свободных членов, то матрицу называют расширенной матрицей системы.
Необходимая терминология
Определение 1
Решением системы называют такие $n$ значений неизвестных $x_1=c_1, x_2=c_2…x_n-c_n$, что при их использовании все её уравнения становятся верными соблюдающимися равенствами. Найденное решение системы можно записать в виде таблицы неизвестных одним столбцом:
$C= begin{pmatrix} c_1 \ c_2 \ vdots \ c_n end{pmatrix}$.
В зависимости от количеств групп переменных, подходящих для соблюдения всей системы, различают совместные и несовместные СЛАУ. Объединённая в систему группа равенств называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.
«Фундаментальная система решений СЛАУ» 👇
Среди первого типа существуют определённые СЛАУ, имеющие только одно решение и неопределённые, под такие подпадают все, которые можно решить с получением больше одного ответа.
Однородные и неоднородные системы линейных уравнений
Система линейных уравнений называется однородной, если все её свободные члены равны нулю. Если в системе хотя бы один из свободных членов ненулевой, то она называется неоднородной, другие же СЛАУ с нулевым $B$ наоборот однородны.
Однородные системы совместны, так как $x_1=x_2=…x_n=0$ будет решением для систем, имеющих особенность в виде нулевого столбца $B$. Иначе такая группа ответов называется нулевым или тривиальным способом решения.
Нетривиальными же называются ответы на СЛАУ, детерминант матрицы которой не $0$. В группе ответов таких систем хотя бы одно из неизвестных подходит под $x_i$ ≠ $0$. Для поиска детерминанта можно воспользоваться $LU$ разложениями, гаусовым методом или его модификацией в виде способа Жордана-Гаусса.
Общее, частное и фундаментальное решения
Определение 2
Частным решением системы называется индивидуальное записанное в одну строчку, тогда как общее $X_o$ записывается через свободные переменные в одну строчку, оно представляет собой некое множество чисел, подходящих под данные условия. Общее $X_o$ включает в себя все индивидуальные.
Фундаментальной же системой решений (ФСР) называется совокупность $(n-r)$ векторов, являющихся линейно независимыми векторами системы. Здесь $r$ — это ранг исследуемой матрицы, согласно теореме Капелли, он равен количеству её основных неизвестных. Найти его можно путём разрешённых преобразований над изучаемым объектом, в частности, можно использовать метод Гаусса или другие.
Фундаментальная система решений частенько представлена как сумма всех возможных решений:
$X=C_1X_1 + C_2X_2+…C_{n-r}X_{n-r}$.
Здесь $С_1, C_2,…C_{n-r}$ — некоторые постоянные.
Пример 1
Приведена пример, в котором все свободные члены ненулевые:
$begin{cases} x_1 – x_2 + x_3-x_4=4 \ x_1+x_2+2x_3+3x_4=8 \ 2x_1+4x_2+5x_3+10x_4=20 \ 2x_1-4x_2+x_3-6x_4=4\ end{cases}$.
Ранг всех матриц соответсвует двойке, рассчитаем базисный минор:
$M=begin{array}{|cc|} 1 & -1 \ 1 &1 \ end{array}=2$
Избавимся от двух нижних равенств из примера и получим:
$begin{cases} x_1 – x_2=4-c_3+c_4 \ x_1+x_2=8-2c_3-3c_4 \ end{cases}$
Общим решением системы будет строчка $(6-frac{3}{2}c_3-c_4; 2-frac{1}{2}c_3-2c_4;c_3; c_4)$.
Теперь посмотрим, что буде в случае с нулевым столбцом за чертой:
$begin{cases} x_1 – x_2 + x_3-x_4=0 \ x_1+x_2+2x_3+3x_4=0 \ 2x_1+4x_2+5x_3+10x_4=0 \ 2x_1-4x_2+x_3-6x_4=0 end{cases}$.
Ранг также соответствует двойке, а её решениями будут
$c_1=-frac{3}{2} c_3-c_4; c_2=-frac{1}{2}c_3-2c_4$. Константы же $c_3$ и $c_4$ выберем любые, например, возьмём их равными $c_3=0;c_4=1$.
Итак, используя приведённые выше значения $c_3=0;c_4=1$:
$X_1=(-frac32;-frac12;1;0)$;
$X_2=(-1;-2;0;1)$.
Фундаментальное решение системы можно записать так:
$X=C_1 (-frac{3}{2};-frac{1}{2};1;0)+C_2(-1;-2;0;1)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Warning: include_once(): Failed opening ‘/home/zarab1/matemonline.com/www/wp-content/plugins/yet-another-related-posts-plugin/includes/template_functions.php’ for inclusion (include_path=’.:/usr/local/pear/php56′) in /home/zarab1/matemonline.com/www/wp-content/plugins/yet-another-related-posts-plugin/yarpp.php on line 52
Фундаментальная система решений (конкретный пример)
Вы можете заказать подробное решение вашей задачи здесь!!!
Чтобы понять, что такое фундаментальная система решений вы можете посмотреть видео-урок для этого же примера кликнув здесь. Теперь перейдем собственно к описанию всей необходимой работы. Это поможет вам более детально разобраться в сути данного вопроса.
Как найти фундаментальную систему решений линейного уравнения?
Возьмём для примера такую систему линейных уравнений:

Найдём решение этой линейной системы уравнений методом Гаусса. Для начала нам надо выписать матрицу коэффициентов системы.

Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под $a_{11}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.

Первую и вторую строку переписываем без изменений. И все элементы, что стоят под $a_{22}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{32}$, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{42}$, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{52}$, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.

Видим, что последние три строки – одинаковые, поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.

По этой матрице записываем новую систему уравнений.

Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов. Значит, нам надо перенести две последние неизвестные вправо.

Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим $x_3$, потом полученный результат подставим во второе уравнение и выразим $x_2$, а потом в первое уравнение и тут выразим $x_1$. Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.

После чего вы вместо $x_4$ и $x_5$, можем подставлять любые числа и находить $x_1$, $x_2$ и $x_3$. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.
Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

Для лучшего понимания хода роботы можете посмотреть видео-урок по данном задании.
Материалы по теме:
- Метод Гаусса (конкретный пример)
- Матрицы и определители
- Три метода решения определителя (детерминанта) матрицы!
- Сложение и вычитание матриц
![]() Загрузка…
Загрузка…
