Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
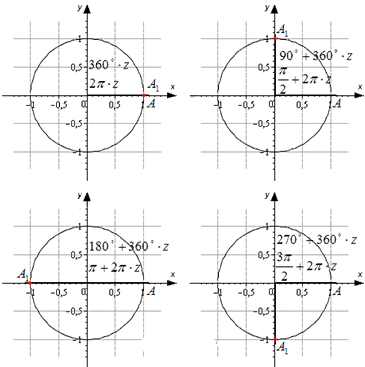
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
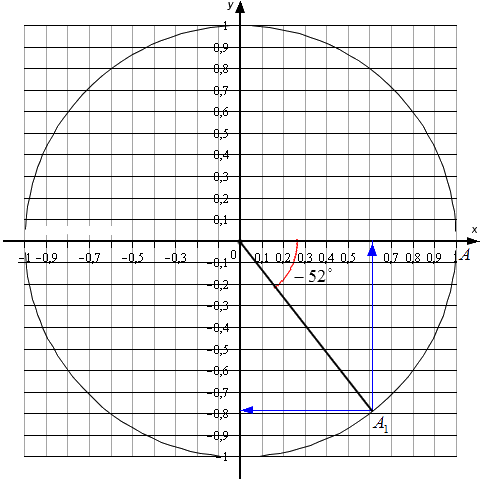
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
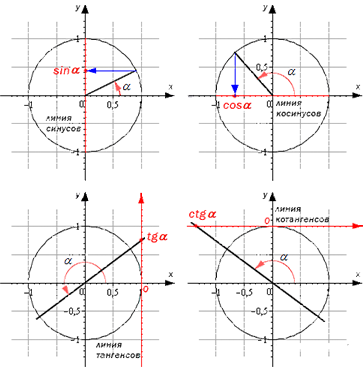
Как найти sin α, cos α, tg α, ctg α
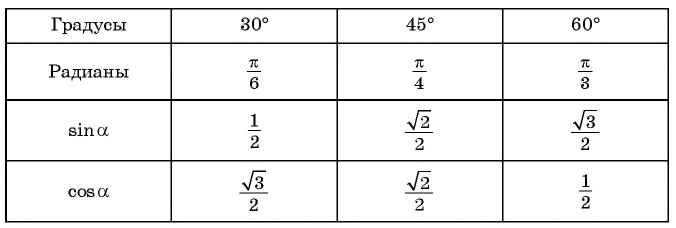
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
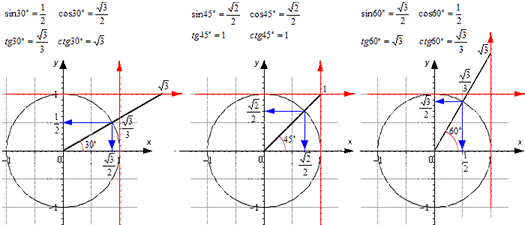
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Тангенс по известному косинусу tg2α+1=1cos2α .
Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Как найти приближенное значение синуса и косинуса на единичной окружности?
Кристофер Донн
Ученик
(67),
закрыт
1 год назад
Вот есть задание, найдите cos 36° на единичной окружности. И как это сделать? В решебнике написано ≈0.8, но откуда они взяли? Как это понять? Помогите, пожалуйста.
Маша Малинина
Просветленный
(29208)
1 год назад
Можно, например, косинус разложить по степеням малого параметра:
36° = 30° + 6° = π/6 + π/30,
cos(x0+ε) =
cos(x0)-sin(x0)·ε-cos(x0)·ε²/2+sin(x0)·ε³/6+O(ε⁴)
Если x0=30°, то соs(x0)=½·√3, a sin(x0)=½.
cos(36°)≈½·[√3·(1-π²/1800)-π/30·(1-π²/5400)]
Так получается 0,809012708978, что довольно близко к cos36°=0,809016994374…
Содержание:
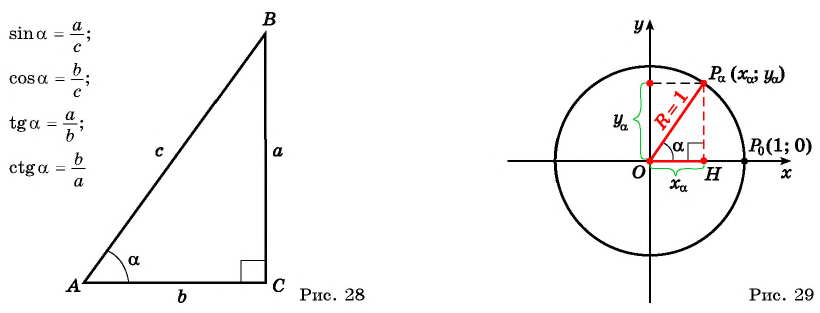
При изучении геометрии вы рассматривали отношения сторон в прямоугольном треугольнике и познакомились с понятиями синуса, косинуса, тангенса и котангенса острого угла (рис. 28).
Построение синуса и косинуса произвольного угла
Построим точку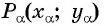 
Рассмотрим прямоугольный треугольник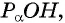 
в котором гипотенуза 
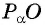равна 1 (радиусу единичной окружности). По определению синуса и косинуса острого угла получим: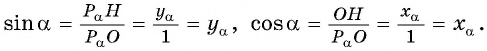 
Таким образом, синус угла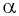 
равен ординате точки 
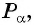а косинус угла 
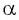равен абсциссе точки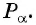 
Поскольку в тригонометрии рассматриваются углы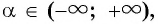 
то определим синус и косинус для любого угла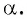 
Определение синуса произвольного угла
Определение:
Синусом угла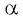 
называется ордината точки 
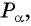полученной поворотом точки 
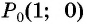единичной окружности вокруг начала координат на угол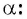 
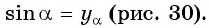
Определение косинуса произвольного угла
Определение:
Косинусом угла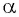 
называется абсцисса точки 
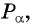полученной поворотом точки 
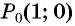единичной окружности вокруг начала координат на угол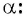 
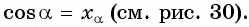
Для того чтобы найти синус и косинус произвольного угла 
нужно:
- Построить точку
единичной окружности. - Найти ординату точки
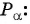
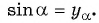
- Найти абсциссу точки
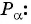
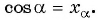
Найдите синус и косинус угла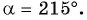 
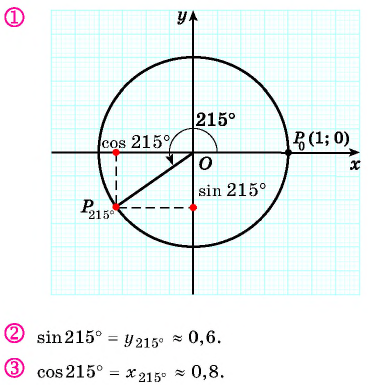
Значения синуса и косинуса произвольного угла с помощью единичной окружности в основном можно указать только приближенно.
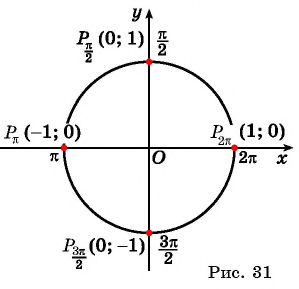
Однако для некоторых углов значения синуса и косинуса можно указать точно. Определим значения синуса и косинуса для углов, которые соответствуют точкам пересечения окружности с осями координат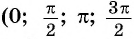 
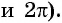Найдем 
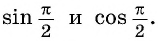Углу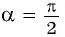 
соответствует точка 
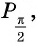имеющая координаты 
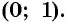По определению синус угла 
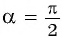равен ординате точки 
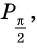значит, 
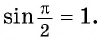Косинус угла 
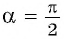равен абсциссе точки 
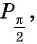т.е.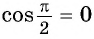 
(рис. 31).
Пользуясь определением синуса и косинуса угла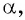 
получим, что: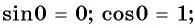 
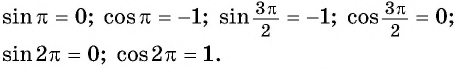
Так как ординаты и абсциссы точек единичной окружности изменяются от -1 до 1, то значения синуса и косинуса произвольного угла принадлежат промежутку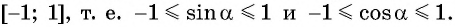 
Например, выясним, может ли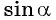 
принимать значения, равные:
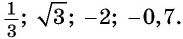
Значения синуса произвольного угла принадлежат отрезку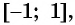 
значит, 
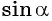может принимать значения, равные 
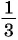и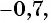 
так как 
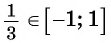и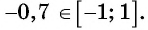 
Поскольку 
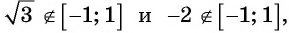то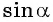 
не может принимать значения, равные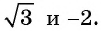 
По определению синуса и косинуса угла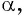 
синус угла 
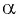равен ординате точки 
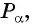а косинус угла 
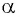равен абсциссе этой точки. Значит, знак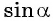и 
и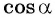 
совпадают со знаками ординаты и абсциссы точки 
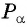соответственно.
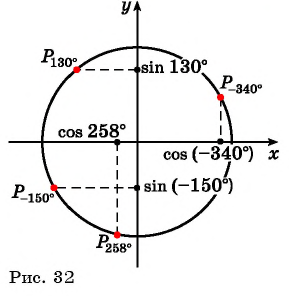
Пример №1
Определите знак выражения:
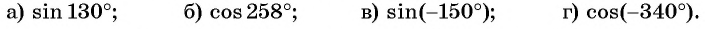
Решение:
а) Так как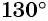 
— угол второй четверти (рис. 32), а ординаты точек единичной окружности, находящихся во второй четверти, положительны, то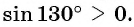 
б) Так как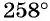 
— угол третьей четверти (см. рис. 32), а абсциссы точек единичной окружности, находящихся в третьей четверти, отрицательны, то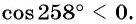 
в) Так как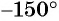 
— угол третьей четверти (см. рис. 32), а ординаты точек единичной окружности, находящихся в третьей четверти, отрицательны, то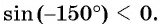 
г) Так как 
— угол первой четверти (см. рис. 32), а абсциссы точек единичной окружности, находящихся в первой четверти, положительны, то 
Из геометрии нам известны значения синусов и косинусов острых углов (см. табл.).
С помощью этих значений можно находить значения синусов и косинусов некоторых других углов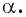 
Пример №2
Вычислите:
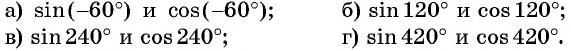
Решение:
а) Отметим на единичной окружности точку 
Поскольку известно, что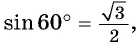 
а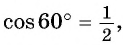 
то ордината точки 
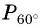равна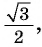 
а абсцисса этой точки равна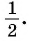 
Точки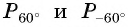 
единичной окружности симметричны относительно оси абсцисс (рис. 33), значит, их ординаты (синусы углов 
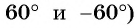противоположны, а абсциссы (косинусы углов 
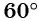и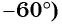 
равны. Таким образом, 
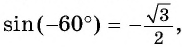а 
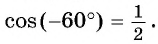
б) Так как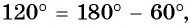 
то точки 
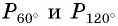единичной окружности симметричны относительно оси ординат (рис. 34). Тогда их ординаты (синусы углов 
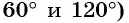равны, а абсциссы (косинусы углов 
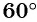и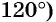 
противоположны. Значит,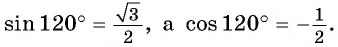 
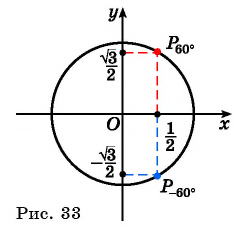
в) Точки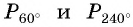 
единичной окружности симметричны относительно начала координат (рис. 35), поскольку 
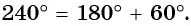Тогда и их ординаты противоположны, и их абсциссы противоположны, т. е.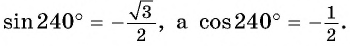
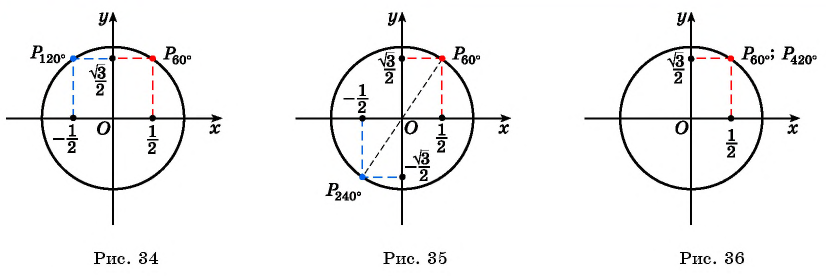
г) Поскольку 
то точки 
и 
единичной окружности совпадают (рис. 36), а значит, их координаты равны. Тогда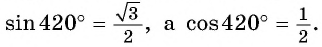 
Пример №3
Вычислите:
Решение:
а) Так как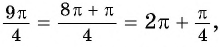 
то точка 
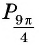единичной окружности совпадает с точкой 
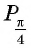(рис. 37).
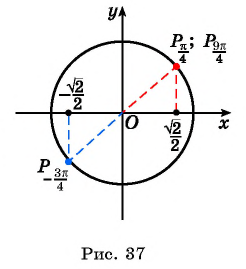
Поскольку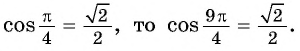 
б) Точки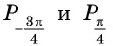 
единичной окружности симметричны относительно начала координат (см. рис. 37), а значит, их абсциссы (косинусы углов 
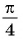и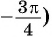 
отличаются только знаком. Так как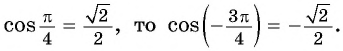 
Пример №4
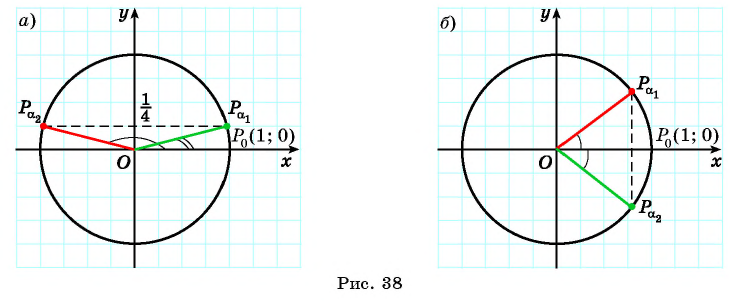
Постройте один из углов, если:
Решение:
а) Так как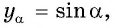 
то на оси ординат отметим 
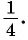Проведем прямую, параллельную оси абсцисс, и найдем на единичной окружности точки 
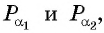ордината каждой из которых равна 
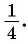Отметим один из углов, соответствующих точкам 
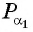или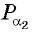 
(рис. 38, а).
б) Так как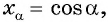 
то на оси абсцисс отметим 0,8. Проведем прямую, параллельную оси ординат, и найдем на единичной окружности точк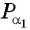и 
и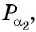 
абсцисса каждой из которых равна 0,8. Отметим один из углов,соответствующих точкам 
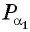или 
(рис. 38, б).
- Заказать решение задач по высшей математике
Примеры заданий и их решения:
Пример №5
Точка 
единичной окружности имеет координаты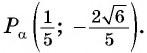 
Используя определение синуса и косинуса произвольного угла, найдите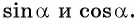 
Решение:
Синусом угла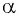 
называется ордината точки 
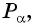полученной поворотом точки 
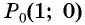единичной окружности вокруг начала координат на угол 
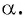По условию ордината точки 
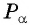равна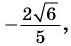 
значит,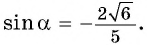 
Косинусом угла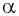 
называется абсцисса точки 
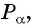полученной поворотом точки 
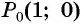единичной окружности вокруг начала координат на угол 
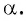По условию абсцисса точки 
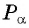равна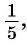 
значит,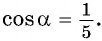 
Пример №6
Если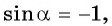 
то угол 
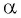может быть равен:
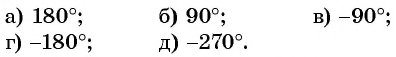
Выберите правильный ответ.
Решение:
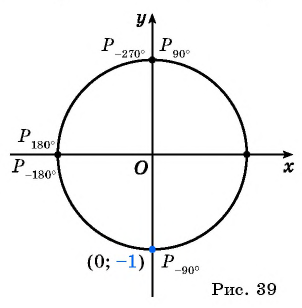
Так как синусом угла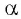 
называется ордината точки 
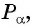полученной поворотом точки 
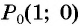единичной окружности вокруг начала координат на угол 
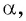то нужно найти точку единичной окружности, ордината которой равна -1. Эта точка лежит на оси ординат, и из данных углов ей соответствует угол 
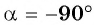(рис. 39). Правильный ответ в).
Пример №7
Если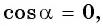 
то угол 
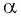может быть равен:
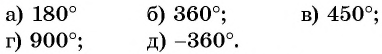
Выберите правильный ответ.
Решение:
Так как косинусом угла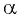 
называется абсцисса точки 
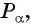полученной поворотом точки 
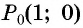единичной окружности вокруг начала координат на угол 
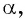то нужно найти точку единичной окружности, абсцисса которой равна 0. Эта точка лежит на оси ординат, и из данных углов ей соответствует угол 
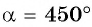(рис. 40). Правильный ответ в).
Пример №8
Найдите значение выражения:
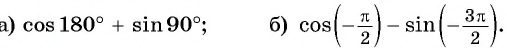
Решение:
а) Абсцисса точки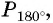 
соответствующей углу 
равна -1 (рис. 41), значит, 
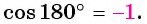Ордината точки 
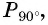соответствующей углу 
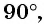равна 1 (см. рис. 41), т. е. 
Значит,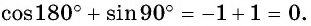 
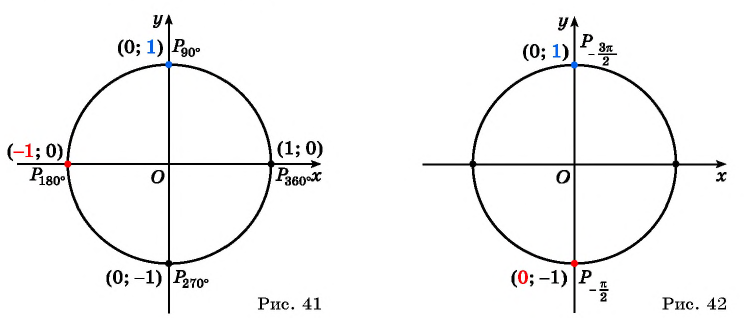
б)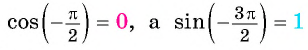 
( рис. 42) тогда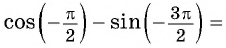 
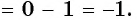
Может ли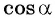 
быть равным:
Решение:
Поскольку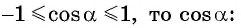 
а) не может быть равным 1,2, так как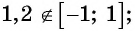 
б) может быть равным 0,89, так как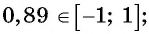 
в) не может быть равным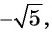 
так как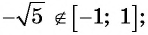 
г) может быть равным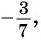 
так как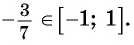 
Пример №9
Определите знак выражения:
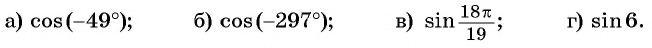
Решение:
а)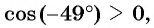 
так как 
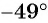— угол четвертой четверти, а косинус в четвертой четверти положителен;
б)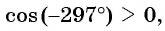 
так как 
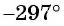— угол первой четверти, а косинус в первой четверти положителен;
в)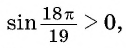 
так как 
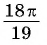угол второй четверти, а синус во второй четверти положителен;
г)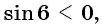 
так как 6 радиан — угол четвертой четверти, а синус в четвертой четверти отрицателен.
Пример №10
Сравните: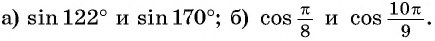 
Решение:
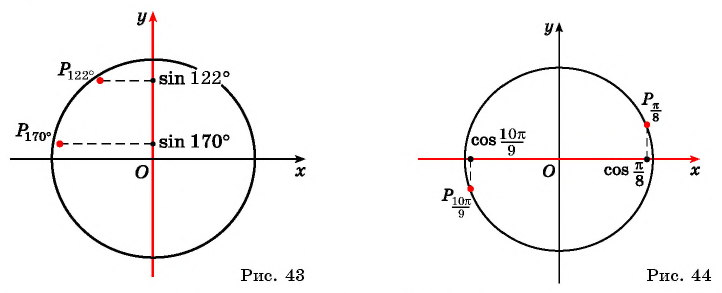
а) Отметим на единичной окружности точки, соответствующие углам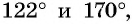 
и сравним ординаты этих точек. Ордината точки 
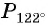больше ординаты точки 
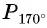(рис. 43), значит,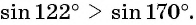 
б) Сравним абсциссы точек единичной окружности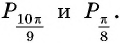 
Так как абсцисса точки 
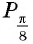больше абсциссы точки 
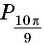(рис. 44), то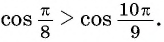 
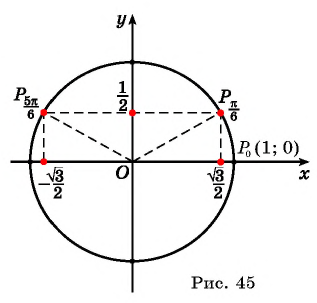
Пример №11
С помощью единичной окружности найдите значение:
Решение:
а) Ордината точки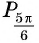 
равна ординате точки 
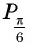(рис. 45), поэтому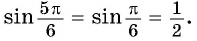 
б) Абсцисса точки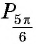 
противоположна абсциссе точки 
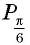(см. рис. 45), поэтому
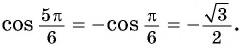
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Единичная окружность – в тригонометрии
Тригонометрия. Единичная окружность
В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).
Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:
- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:
Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)
Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)
Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.
Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)
(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).
(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).
Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)
Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)
(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
