- Подробности
- Обновлено 30.05.2018 20:11
- Просмотров: 706

Задачи по физике – это просто!
Вспомним
Формулы, по которым можно вычислить работу силы:



Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Типовые задачи из курса школьной физики по динамике на расчет работы, совершаемой силой тяжести.
Задача 1
Автомобиль массой 500 кг движется вверх по наклонной плоскости, расположенной под угломм 30o к горизонту. Найти работу силы тяжести на пути в 200 метров.

Задача 2
Какую работу совершит сила тяжести при падении мяча массой 0,5 кг на землю из состояния покоя с высоты 5 метров?

Задача 3
Какую работу совершает сила тяжести при отскоке мяча от земли, если он поднимается на высоту 2-х метров? Масса мяча составляет 0,4 кг.

Задача 4
Скорость падающего кирпича массой 2 кг на некотором отрезке пути изменилась от 3 м/с до 6 м/с. Определить работу, совершенную силой тяжести.

Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
Полезно ознакомиться в отдельности с работой каждой из механических сил, с которыми мы ознакомились в пятой главе: силы тяжести, силы упругости и силы трения. Начнем с силы тяжести. Сила тяжести равна $vec{F} = m vec{g}$ и направлена по вертикали вниз. Вблизи поверхности Земли ее можно считать постоянной.

рис. 1
При движении тела по вертикали вниз сила тяжести совпадает по направлению с перемещением. При переходе с высоты $h_{1}$ над каким-то уровнем, от которого мы начинаем отсчет высоты, до высоты $h_{2}$ над тем же уровнем (рис. 1), тело совершает перемещение, по абсолютной величине равное $h_{1} – h_{2}$. Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
$A = mg (h_{1} – h_{2})$.
Высоты $h_{1}$ и $h_{2}$ не обязательно отсчитывать от поверхности Земли. Для начала отсчета высот можно выбрать любой уровень. Это может быть пол комнаты, стол или стул, это может быть и дно ямы, вырытой в земле, и т. д. Ведь в формулу для работы входит разность высот, а она не зависит от того, откуда начинать их отсчет. Мы могли бы, например, условиться начинать отсчет высоты с уровня $B$ (см. рис. 1). Тогда высота этого уровня была бы равна нулю, а работа выражалась бы равенством
$A = mgh$,
где $h$ – высота точки $A$ над уровнем $B$.
Если тело движется вертикально вверх, то сила тяжести направлена против движения тела и ее работа отрицательна. При подъеме тела на высоту $h$ над тем уровнем, с которого оно брошено, сила тяжести совершает работу, равную
$A = – mgh$.
Если после подъема вверх тело возвращается в исходную течку, то работа на таком пути, начинающемся и кончающемся в одной и той же точке (на замкнутом пути), на пути «туда и обратно», равна нулю. Это одна из особенностей силы тяжести: работа силы тяжести на замкнутом пути равна нулю.
Теперь выясним, какую работу совершает сила тяжести в случае, когда тело движется не по вертикали.

рис. 2
В качестве примера рассмотрим движение тела по наклонной плоскости (рис. 2). Допустим, что тело массой $m$ по наклонной плоскости высотой $h$ совершает перемещение $vec{s}$, по абсолютной величине равное длине наклонной плоскости. Работу силы тяжести $m vec{g}$ в этом случае надо вычислять по формуле $A = mgs cos alpha$. Но из рисунка видно, что
$cos alpha = frac{h}{s}$.
Поэтому
$A = mgs frac{h}{s} = mgh$.
Мы получили для работы то же самое значение.

рис. 3
Выходит, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. При одной и той же «потере высоты» работа силы тяжести одинакова (рис. 3).

рис. 4
Это справедливо не только при движении по наклонной плоскости, но и по любому другому пути. В самом деле, допустим, что тело движется по какому-то произвольному пути, например по такому, какой изображен на рисунке 4. Весь этот путь мы можем мысленно разбить на ряд малых участков: $AA_{1}, A_{1}A_{2}, A_{2}A_{3}$ и т. д. Каждый из них может считаться маленькой наклонной плоскостью, а все движение тела на пути $AB$ можно представить как движение по множеству наклонных плоскостей, переходящих одна в другую. Работа силы тяжести на каждой такой наклонной плоскости равна произведению $mg$ на изменение высоты тела на ней. Если изменения высот на отдельных участках равны $h_{1}, h_{2}, h_{3}$ и т. д., то работы силы тяжести на них равны $mgh_{1}, mgh_{2}, mgh_{3}$ и т. д. Тогда полную работу на всем пути можно найти, сложив все эти работы:
$A = mgh_{1} + mgh_{2} + mgh_{3} + cdots = mg (h_{1} + h_{2} + h_{3} + cdots)$.
Но
$h_{1} + h_{2} + h_{3} + cdots = h$.
Следовательно,
$A = mgh$.
Таким образом, работа силы тяжести не зависит от траектории движения тела и всегда равна произведению силы тяжести на разность высот в исходном и конечном положениях. При движении вниз работа положительна, при движении вверх – отрицательна.
Почему же в технике и быту при подъеме грузов часто пользуются наклонной плоскостью? Ведь работа перемещения груза по наклонной плоскости такая же, как и при движении по вертикали!
Это объясняется тем, что при равномерном движении груза по наклонной плоскости сила, которая должна быть приложена к грузу в направлении перемещения, меньше силы тяжести. Правда, груз при этом проходит больший путь. Больший путь – это плата »а то, что по наклонной плоскости груз можно поднимать с помощью меньшей силы.
Задача. Шарик массой $m$ скатывается по рельсам, образующим круговую петлю радиусом $r$ (рис. 196). Какую работу совершает сила тяжести к моменту, когда шарик достигает высшей точки петли $C$, если в начальный момент он находится на высоте $H$ над нижней точкой петли?

рис. 5
Решение. Работа силы тяжести равна произведению ее значения на разность высот начального и конечного положений шарика. Начальная высота равна $H$, а конечная, как это видно из рисунка, равна $2r$. Следовательно,
$A = mg (H – 2r) = mgh$.
С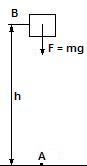
ила
тяжести-сила
действующая на тела вследствие его
притяжения к планете
Сила тяжести,
действующая на тело, является суммой сил,
действующей на
его отдельные части. Если
считать силу тяжести однородной,
то суммарная сила тяжести,
действующая на тело равна произведению
массы всего
тела на ускорение свободного падения.
Работа
силы тяжести равна изменению потенциальной
энергии тела,взятому со знаком минус.
Работу
силы тяжести рассмотрим на примере.
Пусть тело падает под действием силы
тяжести F = mg с высоты h из точки B в точку
A. Формула работы силы:
A
= |F||S|cosα
Подставим
значения для нашего примера:
A
= mgh
косинус
альфа здесь равен единице.
Работа
силы тяжести не зависит от траектории.
То есть, если тело скатывается под
действием силы тяжести с какой-то
наклонной поверхности, то работа силы
тяжести всё равно будет равна mgh.
На
замкнутой траектории работа силы тяжести
равна нулю. Значит сила тяжести является
консервативной силой.
21 Консервативные силы, поле центральных сил
В
физике консервати́вные
си́лы (потенциальные
силы) — силы, работа которых
не зависит от формы траектории (зависит
только от начальной и конечной точки
приложения сил). Отсюда следует следующее
определение: консервативные силы —
такие силы, работа по любой замкнутой
траектории которых
равна 0.Если в системе действуют только
консервативные силы, то механическая
энергия системы сохраняется. Для
консервативных сил выполняются следующие
тождества:
-
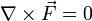
— ротор консервативных
сил равен 0; -
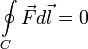
— работа консервативных
сил по произвольному замкнутому контуру
равна 0; -

—
консервативная
сила является градиентом некой скалярной
функции U,
называемой силовой. Эта функция
равна потенциальной
энергии взятой
с обратным знаком.
Примерами
консервативных сил являются: сила
тяжести, сила
упругости
Модель
поля центральных сил
поле,
характерной особенностью которого
является то, что силы, действующие на
него при любом его положении в поле,
всегда проходят через некоторую
определенную
точку
называемую центром сил или центром
поля. Поле центральных сил может иметь
различную
физическую
природу, но напряженность его всегда
обратно пропорциональна квадрату
расстояния до
центра поля.
Примерами
центральных сил служат силы тяготения,
направленные к центру Солнца или
планеты,
кулоновские
силы электростатического притяжения
и отталкивания и др. Рассмотрим
важный случай поля центральных сил.
Всякое силовое поле вызывается действием
определенных тел. Сила, действующая на
частицу А в таком поле, обусловлена
взаимодействием этой частицы с данными
телами. Если силы, зависят только от
расстояния между взаимодействующими
частицами и направлены по прямой,
соединяющей эти частицы, от их
называют центральными. Такими
примерами служат силы гравитационные,
кулоновские и упругие.
Центральную
силу, действующую на частицу А со
стороны частицы В, можно представить
в общем виде:
|
|
(5.8) |
где ![]()
-функция,
зависящая при данном характере
взаимодействия только от r – расстояния
между частицами; ![]()
единичный
вектор, задающий направление радиус-вектора
частицы А относительно частицы В
(рис.5.6).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Совсем недавно, мы
изучили работу силы. Напомним, что работа силы равна произведению модуля силы,
модуля перемещения и косинуса угла между направлениями силы и перемещения:
Рассмотрим теперь частный
случай — работу силы тяжести при перемещении тела с высоты h1
на высоту h2.
Первый случай — это
падение тела вертикально вниз.
В этом случае,
перемещение, конечно же, будет равно
Сила тяжести, как мы
знаем, равна
.
Поскольку сила тяжести
направлена вертикально вниз, как и перемещение, косинус угла между
направлениями этих векторов равен единице. Таким образом, мы получим, что
работа силы тяжести равна:
Второй случай — это когда
тело, наоборот, подбрасывают вертикально вверх с высоты h1
на высоту h2.
В этом случае, угол между
направлением силы тяжести и направлением перемещения составит 180о.
Это приводит нас к тому, что работа силы тяжести опять-таки равна:
Наконец, рассмотрим
случай, когда между направлением силы тяжести и перемещением существует
произвольный угол α.
Обозначим модуль
перемещения за s. В этом случае,
работа силы тяжести равна:
Но, исходя из определения
косинуса:
Таким образом, мы в
третий раз получили одинаковый результат.
Более того, если даже мы
рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.
Любую кривую мы можем
представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и
вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет
равна нулю, поскольку в этом случае направление перемещения перпендикулярно
направлению силы тяжести. На вертикальных участках работа будет равна: A
= mg(s1
+ … + sn).
Очевидно, что эта сумма будет равна (h1
– h2):
Таким образом, мы
убедились, что работа силы тяжести не зависит от траектории движения тела.
Имеет значение лишь то, насколько начальное положение тела отличается от
конечного. Это плавно подводит нас к понятию потенциальной энергии, которое
мы рассмотрим немного позже.
Из приведенных примеров
вытекает еще один важный вывод: при движении тела по замкнутой траектории
работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму
прямоугольника. Как мы уже убедились, при движении тела в горизонтальном
направлении, работа силы тяжести равна нулю. Вектор перемещения направлен
перпендикулярно вектору силы тяжести. При перемещении же по противолежащим
вертикальным сторонам контура, сила тяжести совершает работу, равную по
абсолютной величине, но противоположную по знаку.
В одном случае вектор
перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в
противоположную сторону. Это довольно логично, поскольку при движении тела
вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.
Мы можем сколь угодно
усложнить эту траекторию, получив совершенно произвольный замкнутый контур.
Но опять же, разбив все
кривые на ломаные линии с горизонтальными и вертикальными участками, мы
убедимся, что суммарная работа будет равна нулю.
Силы, обладающие такими
свойствами, называются консервативными. То есть, консервативная сила — это
такая сила, работа которой в замкнутом контуре равна нулю.
Примеры решения задач.
Задача 1. Охотник
стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы
тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы,
то какова её масса?
Задача 2. Находясь
на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом
перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна
5 кг, то каково ускорение свободного падения на Нептуне?
