Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
32 743

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.

Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
( 32 оценки, среднее 4.44 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.
Что такое треугольник
Треугольник – это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.
Сумма трех углов треугольника должна быть равна 180°.
Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту. Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).

Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.

Равнобедренный треугольник
Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.

Прямоугольный треугольник
Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.

Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.
Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.
Равносторонний треугольник
Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.

Площадь треугольника
Площадь разностороннего треугольника
Вычисляем площадь треугольника без особенностей – все его стороны разные и все углы разные.

Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле “площадь треугольника через две стороны и угол между ними”:
Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:

Формула Герона определения площади треугольника
Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.

, где
Площадь равнобедренного треугольника
Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.

К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:

Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:
Площадь прямоугольного треугольника
Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:

Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе

Площадь прямоугольного треугольника, если в него вписана окружность:

Площадь равностороннего треугольника
Площадь равностороннего треугольника можно найти через радиус описанной окружности.

Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:

Площадь равностороннего треугольника, если известна сторона треугольника:
Площадь равностороннего треугольника, если известна высота треугольника:

Как найти площадь разностороннего треугольника
Разносторонним треугольником называется такой треугольник, длины сторон которого не равны между собой. При этом подразумевается, что не равны также никакие две стороны (иначе треугольник получился бы равнобедренным). Для вычисления площади разностороннего треугольника используется несколько разных формул. Рассмотрены все основные варианты, которые могут встретиться на практике и при решении геометрических задач.
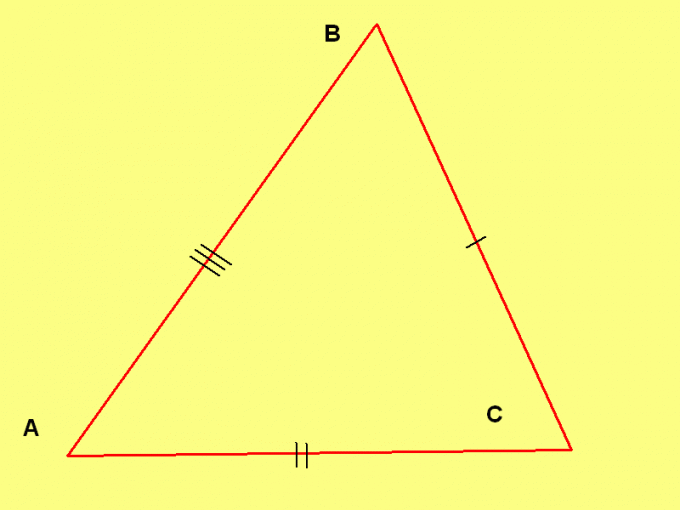
Вам понадобится
- – калькулятор;
- – транспортир;
- – линейка.
Инструкция
Чтобы найти площадь треугольника, умножьте длину его стороны на высоту (перпендикуляр, опущенный на эту сторону из противоположной вершины) и разделите полученное произведение на два. В виде формулы данное правило выглядит следующим образом:
S = ½ * а * h,
где:
S – площадь треугольника,
а – длина его стороны,
h – высота, опущенной на эту сторону.
Длина стороны и высота должны быть представлены в одинаковых единицах измерения. При этом площадь треугольника получится в соответствующих «квадратных» единицах.
Пример.
На одну из сторон разностороннего треугольника длиной 20 см, опущен перпендикуляр из противоположной вершины длиной 10 см.
Требуется определить площадь треугольника.
Решение.
S = ½ * 20 * 10 = 100 (см²).
Если известны длины двух любых сторон разностороннего треугольника и угол между ними, то воспользуйтесь формулой:
S = ½ * а * b * sinγ,
где: а, b – длины двух произвольных сторон, а γ – величина угла между ними.
На практике, например, при измерении площади земельных участков, использование вышеприведенных формул иногда бывает затруднительно, так как требует дополнительных построений и измерения углов.
Если вам известны длины всех трех сторон разностороннего треугольника, то воспользуйтесь формулой Герона:
S = √(p(p-a)(p-b)(p-c)),
где:
a, b, c – длины сторон треугольника,
р – полупериметр: p = (a+b+c)/2.
Если кроме длин всех сторон известен радиус вписанной в треугольник окружности, то воспользуйтесь следующей компактной формулой:
S = p * r,
где: r – радиус вписанной окружности (р – полупериметр).
Для вычисления площади разностороннего треугольника через радиус описанной окружности и длины его сторон, используйте формулу:
S = abc/4R,
где: R – радиус описанной окружности.
Если известна длина одной из сторон треугольника и величины трех углов (в принципе, достаточно двух – величина третьего вычисляется из равенства суммы трех углов треугольника – 180º), то воспользуйтесь формулой:
S = (a² * sinβ * sinγ)/2sinα,
где α – величина противолежащего стороне а угла;
β, γ – величины остальных двух углов треугольника.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прежде, чем говорить всяко-разные, не обязательно печатные, выражения и оскорблять представителей вида Capra aegagrus hircus сравнением авторов учебника с этими животными – желательно бы видеть фото этой страницы учебника…
Четвёртый класс… Только вводятся основные понятия геометрии, абсолютно нет никаких сведений по тригонометрии, даже и намёка нет об основных аксиомах и теоремах геометрии, ноль понятия об иррациональных числах (и, соответственно, квадратных корнях) – и посчитай площадь разностороннего треугольника!
Единственный способ, который не использует ни тригонометрии, ни корней – через радиус вписаной окружности: площадь треугольника равна произведению радиуса вписаной окружности на полупериметр.
Если “четвертачкам” уже объяснили смысл биссектрисы и способы её построения, объяснили, что точка пересечения биссектрис равноудалена от сторон треугольника, объяснили понятие вписаной окружности (в чём я капитально сомневаюсь) – построят и найдут. Но – “плюс-минус убежало”: радиус вписаной окружности можно будет только измерить линейкой.
А это – “не наш метод”: в геометрии построение считается правильным только тогда, когда оно выполнено линейкой без делений и циркулем без шкалы углов. Но зато – математически обосновано.
А математический аппарат таких обоснований излагают школярам далеко не в четвёртом классе…
Кому интересна методика построения вписаной окружности – пожалуйста:
1) Из вершины А любым (в разумных пределах…) раскрывом циркуля делаем засечки на прилегающих сторонах треугольника;
2) Из этих точек тем же раскрывом циркуля рисуем вспомогательные сегменты окружностей внутри угла между сторонами треугольника;
3) Через точку пересечения этих вспомогательных сегментов рисуем луч из точки А – это и будет биссектриса угла а;
4) Повторяем 1), 2) и 3) для остальных двух вершин. Точка пересечения трёх биссектрис и будет центром вписаной окружности;
5) Строим перпендикуляр к стороне треугольника, проходящий через центр вписаной окружности: из точки пересечения биссектрис делаем (подобрав подходящий раскрыв циркуля) две засечки на любой стороне треугольника. Из этих точек тем же раскрывом циркуля строим симметричную относительно стороны треугольника точку и проводим линию, соединяющую полученную точку и центр вписаной окружности. Точка пересечения этой линии со стороной треугольника будет точкой касания вписаной окружности к стороне треугольника. Расстояние от точки касания до центра вписаной окружности – и есть необходимый нам радиус вписаной окружности.
Можно повторить 5) для каждой из сторон треугольника – это ничего не изменит, поскольку вписаная окружность может быть только одна, и радиус её, естественно, тоже один. Единственный плюс: мы получим все три точки касания вписаной окружности к сторонам треугольника…
А теперь измеряйте длину этого радиуса милиметровой линейкой, микрометром, нанометром, … Всё это филькина грамота – до тех пор, пока мы математически не обоснуем формулу нахождения этого самого радиуса.
А это – не по “четвертачку” панамка!
Я могу поизголяться и через ещё тыщонку знаков результат по Герону (три корня из пятнадцати) подтвердить через “Пифагоровы штаны”. Но – снова упираемся в корни…

