Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»

где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Что такое внутреннее сопротивление источника питания
Содержание
- 1 Что такое внутреннее сопротивление
- 2 Как измеряется внутреннее сопротивление
- 3 Зачем нужно знать внутреннее сопротивление
- 4 Видео по теме
Любой источник тока, будь то генератор или гальванический элемент, обладает внутренним сопротивлением. Его величина характеризирует количество энергетических потерь, появляющихся при протекании тока через источник питания. Для генератора внутреннее сопротивление определяется сопротивлением обмоток статора, для аккумулятора — электродов и электролита. Для него используется та же единица измерения, что и для общего сопротивления цепи — Ом.

Что такое внутреннее сопротивление
В электрической цепи обязательно присутствует источник питания. Обычно, оценивая его параметры, указывают, какую разность потенциалов между клеммами он обеспечивает. Если говорить об идеальной модели источника питания, то можно предположить, что он способен обеспечить в электрической цепи любую мощность с учётом имеющейся разности потенциалов.
Реальные устройства в этом аспекте сильно отличаются друг от друга. Чтобы определить работоспособность аккумулятора важно знать, что такое внутреннее сопротивление. Обычно с течением времени и вследствие износа оно постепенно возрастает. Анализируя уровень и скорость того, как изменяется внутреннее сопротивление источника тока, можно принять решение о продолжении использования батареи или о необходимости её замены.

Сказанное следует пояснить на примере. Для запуска мотора автомобиля используется аккумулятор на 12 Вольт. Известно, что при этом сила тока может достигать 250 Ампер. Однако, если взять другой элемент питания с такой же разницей потенциалов, то вполне возможна ситуация, когда от него запуск мотора осуществить не получится.
В качестве примера такого источника можно рассмотреть несколько гальванических элементов, соединённых последовательно. Разница в двух рассматриваемых ситуациях определяется наличием различного внутреннего сопротивления.
Этот параметр для аккумулятора представляет собой сумму нескольких слагаемых: сопротивление каждого вывода, корпуса и используемого электролита. В некоторых источниках тока при этом могут учитываться дополнительные элементы, включённые в данную цепь.
Важно учитывать, что понятие омического сопротивления в этой ситуации неприменимо, поскольку требуется наличие в цепи только пассивных элементов. Когда создана замкнутая цепь, ток протекает не только по ней, но и внутри источника тока. Внутреннее сопротивление определяет величину потерь энергии в нём.
Его наличие в цепи можно проиллюстрировать ещё одним примером. Если на клеммах аккумулятора имеется 12 вольт, то на первый взгляд можно легко предсказать, какая сила тока будет при нагрузке 1 Ом. Очевидно, что нужно ожидать, что по цепи пройдёт ток, равный 12 Ампер.
На самом деле это утверждение не соответствует действительности: ток будет немного меньше — примерно 11.2 Ампера. Здесь нет никакого несоответствия физике. Ведь при расчёте дополнительно требуется учитывать сопротивление источника тока, из-за которого происходит расход энергии. Оно называется внутренним. Его можно мысленно представить как резистор, соединённый последовательно с источником тока.

Как измеряется внутреннее сопротивление
Для определения значения рассматриваемой характеристики применяются измерения во время прямого замыкания клемм, которое называют коротким замыканием. Как известно, если закоротить клеммы источника, между ними протечёт значительный ток. Часто это является следствием неосторожности и приводит к обгоранию изоляции и расплавлению провода.
При коротком замыкании сопротивление цепи становится минимальным. Точно измерив силу тока в этой ситуации и зная величину напряжения на клеммах при отсутствии нагрузки, можно определить внутреннее сопротивление источника питания. Для этого понадобится следующая формула:
r = U / I(зам), где
- буквой r обозначено внутреннее сопротивление источника тока;
- U — разность потенциалов на клеммах батареи без подсоединения к электрической цепи;
- I(зам) — ток, который проходит при непосредственном замыкании клемм друг на друга.

Находить значение нагрузки таким образом не всегда возможно или целесообразно, поскольку короткое замыкание может стать причиной серьезной аварии.
Поэтому используются другие решения вопроса, как найти внутреннее сопротивление источника. Например, с помощью специальных измерительных приборов. Функцией измерения данного параметра снабжены оригинальные зарядные устройства iMax B6, ToolkinRC M8, M6, M600.
Зачем нужно знать внутреннее сопротивление
На первый взгляд может показаться, что наличие внутреннего сопротивления интересно только с теоретической точки зрения. На самом деле в некоторых ситуациях знать чему оно равно бывает жизненно важным.
Одна из таких ситуаций — определение работоспособности автомобильного аккумулятора. Его внутреннее сопротивление не является постоянным. Оно изменяется под воздействием различных факторов и влияет на напряжение на клеммах. Чтобы быть уверенным в работоспособности оборудования, нужно не только уметь найти его внутреннее сопротивление, но и знать, какая его величина соответствует норме.

На внутреннее сопротивление источника питания могут оказывать влияние такие факторы:
- Температурные условия. Чем холоднее, тем с меньшей скоростью в аккумуляторе протекают химические процессы. Это приводит к увеличению внутреннего сопротивления и постепенному уменьшению напряжения на клеммах.
- Срок службы аккумулятора. У новых устройств внутреннее сопротивление имеет минимальную величину. Постепенно оно начинает расти. Это связано с тем, что в аккумуляторе происходит необратимый химический процесс. В некоторых случаях он относительно медленный, а в других может быть довольно заметным. Последнее, например, относится к свинцово-кислотным аккумуляторам.
- Емкость аккумулятора.
- Иногда на устройство может оказываться механическое воздействие, из-за которого появляются внутренние обрывы.
- Количество используемого электролита.
- Ток, который создаётся батареей, зависит от нагрузки цепи. В зависимости от него меняется сопротивление.

Влияние большого количества факторов приводит к тому, что в качестве нормального можно рассматривать различные значения внутреннего сопротивления. Однако его стандартным увеличением за год принято считать 5%. Если эта норма превышена, значит, на исправность аккумулятора нужно обратить особое внимание.
При анализе стоит принимать во внимание не только те значения, которые указаны в технической документации. Необходимо учитывать и то, насколько интенсивно происходят изменения сопротивления со временем. Это даст более точную информацию об исправности батареи и поможет понять, чего нужно добиваться, чтобы обеспечить работоспособность оборудования.

Один из наиболее простых способов измерения внутреннего сопротивления можно продемонстрировать на следующем примере. Его применение возможно при условии, что ЭДС аккумулятора известна.
ЭДС (ℰ, единица измерения — вольты, В) — это электродвижущая сила источника питания, равная отношению работы сторонних сил по перемещению заряда от отрицательного полюса источника к положительному к величине этого заряда: ℰ=A/q. Если к источнику питания не подключена нагрузка, то ЭДС по своему значению равно напряжению на его клеммах.
Будет рассмотрена ситуация, когда ЭДС равна 1.5 В. Составляется электрическая цепь, в которой выходы аккумулятора присоединяются к электрической лампочке. Измеряется падение напряжения на ней и ток, проходящий через цепь. Они, соответственно, равны 1.2 В и 0.3 А.
Цифры, которые здесь приводятся, являются условными. При измерении мастер может выбрать другой тип электрической нагрузки, если сочтёт это необходимым.

По закону Ома можно определить сопротивление лампочки:
R = U / I = 1.2 / 0.3 = 4 Ом.
В этой формуле буквой R обозначается полное сопротивление цепи. Его можно выразить, как сумму r + R, где r — внутреннее и R — обычное сопротивление.
Тогда: R + r = ℰ / I
Из этой формулы определяется r = ℰ / I − R = 1.5 / 0.3 − 4 = 1 Ом.
Важным условием нахождения значения r является знание величины электродвижущей силы. Эта характеристика имеет максимальное значение у новых и хорошо заряженных батарей. Те, что уже долго были в использовании, могут иметь значительно меньшую ЭДС вследствие разряда, износа, который часто связан с необратимыми химическими процессами в аккумуляторе.
Для определения ℰ необходимо отключить любую нагрузку от клемм источника питания и подключить вольтметр или мультиметр в режиме измерения напряжения. Прибор покажет значение ЭДС. Почему — это легко понять. По закону Ома для полной цепи:
I = ℰ / (R + r),
так как вольтметр имеет сопротивление R→∞, то ток I≈0. Следовательно напряжение на клеммах равно ЭДС:
U = I·R = ℰ – I·r = ℰ.
Также следует упомянуть, что нулевым внутренним сопротивлением «r» обладает только идеальный генератор напряжения. Также существуют элементы с большим внутренним сопротивлением — это разные датчики, источники сигналов, а r=∞ обладает только идеальный источник тока. Помимо этого, существуют двухполюсники с отрицательным значением r, его можно получить в схемах с обратной связью и в элементах с отрицательным дифференциальным сопротивлением. Расчеты применимы не только для аккумулятора, но и для любого другого источника тока, например, гальванической батареи, двухполюсника, петли фаза-нуль. Использовать эти знания можно для согласования источника и нагрузки, понижения высоких напряжений и минимизации шума.
Видео по теме
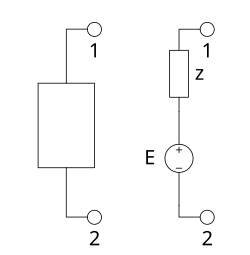
Двухполюсник и его эквивалентная схема
Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.
Введение[править | править код]
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
- Автомобильный свинцово-кислотный аккумулятор с напряжением 12 вольт и ёмкостью 55 А·ч.
- Батарея из 8 гальванических элементов, например, типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч.
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток порядка 250 А), а от батареи элементов стартер вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартера упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 А).
В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.
Эквивалентная схема активного двухполюсника[править | править код]
Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Идеальный генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это эквивалентное сопротивление и называется внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть физического «резистора» как электронного компонента внутри двухполюсников обычно нет.
Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.
В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.
Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.
Сопротивление и внутреннее сопротивление[править | править код]
Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс[1]). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=I·r не выполняется[2].
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины[править | править код]
Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:
- Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход системы [4]
- Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.
Физические принципы[править | править код]
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
- Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
- В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
- Внутреннее сопротивление невозможно убрать из двухполюсника[5]
- Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.
Влияние внутреннего сопротивления на свойства двухполюсника[править | править код]
Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Если к источнику с ЭДС[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:

|
Нахождение внутреннего сопротивления[править | править код]
Расчёт[править | править код]
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).
Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме.
Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».
Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

|
(Напряжения) |
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:

|
(ОбщийСлучай) |
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:

|
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

|
(ВнутрСопр) |
Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:
- Рассчитать выходное напряжение двухполюсника в режиме холостого хода
- Рассчитать выходной ток двухполюсника в режиме короткого замыкания
- На основании полученных значений найти r и U по формуле (ВнутрСопр).
Измерение[править | править код]
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Иногда применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление[править | править код]
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
- Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Измерение сопротивления петли фаза-нуль[править | править код]
Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросети
Частным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:
- активная составляющая: 0,49 Ом
- реактивная составляющая: 0,09 Ом
- модуль полного сопротивления: 0,5 Ом
- ожидаемый ток короткого замыкания: 440 А
Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I1=0.
Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.
Применение[править | править код]
В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.
Упрощение эквивалентных схем[править | править код]
Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.
Согласование источника и нагрузки[править | править код]
Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:
- Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
- Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен Imax=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
- Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной Pmax=E²/(4r)[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
- Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений[править | править код]
Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.
Минимизация шума[править | править код]
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Ограничения[править | править код]
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.
Примеры[править | править код]
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление[править | править код]
- Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
- Автомобильная свинцово-кислотная стартерная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
- Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
- Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).
Большое внутреннее сопротивление[править | править код]
Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).
- Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
- Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
- Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.
Отрицательное внутреннее сопротивление[править | править код]
Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:
- обратной связи
- элементов с отрицательным дифференциальным сопротивлением, например, туннельных диодов
Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.
См. также[править | править код]
- Входной импеданс антенны
Ссылки[править | править код]
- [www.batteryuniversity.com/partone-22.htm How does the internal battery resistance affect performance?] (англ.) Как внутреннее сопротивление батареи влияет на её эксплуатационные качества.
- Что такое внутреннее сопротивление аккумулятора?
Литература[править | править код]
- Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
- Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
- Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.
Примечания[править | править код]
- ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
- ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣUint, где ΣUint — алгебраическая сумма ЭДС внутренних источников.
- ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
- ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
- ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
- ↑ То же самое, что и напряжение
- ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА. Дата обращения: 6 апреля 2014. Архивировано 12 апреля 2013 года.
- ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
- ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
- ↑ В рабочем диапазоне частот
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
ЭДС. Закон Ома для полной цепи
-
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
-
Сторонняя сила
-
Закон Ома для полной цепи
-
КПД электрической цепи
-
Закон Ома для неоднородного участка
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила
, направленная против движения заряда (т.е. против направления тока).
к оглавлению ▴
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы
называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом,
— это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду
. Поэтому отношение
уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается
:
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
к оглавлению ▴
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением
подключён к резистору
(который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение
на резисторе
.
За время по цепи проходит заряд
. Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и
. Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и
(рис. 2). Потенциал точки
равен потенциалу положительной клеммы источника; потенциал точки
равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь
умножается на дробь, меньшую единицы. Но есть два случая, когда
.
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт
.
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина
неотличима от
, и формула (5) снова даёт нам
.
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
к оглавлению ▴
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время
, обозначим
.
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
к оглавлению ▴
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна
, его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно
, можно просто заменить резистор
на резистор
).

Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки
к точке
. Этот ток не обязательно вызван одним лишь источником
. Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток
является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и
равны соответственно
и
. Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время
через участок проходит заряд
, при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло:
.
Подставляем сюда выражения для ,
и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд
от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки
к точке
.
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем
— закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене
на
:
Теперь замкнём наш участок, соединив точки и
. Получим рассмотренную выше полную цепь. При этом окажется, что
и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от
к
, направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке
. Если направление тока совпадает с направлением сторонних сил, то перед
ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Повторим основные понятия и определения по теме «Закон Ома».
Напомним, что напряжение измеряется в вольтах.
Сила тока измеряется в амперах.
Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.
Основные определения, которые мы используем в решении задач:
Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.
Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.
Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.
По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).
Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.
Сопротивление измеряют в омах (Ом).
Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).
Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:
- Сопротивление проводника тем больше, чем больше его длина.
- Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.
Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:![]()
Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.
Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм2 от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм2/м.

Решение:
Из закона Ома для проводника или участка цепи без источника следует:
По графику: при
Из формулы сопротивления выражаем и находим длину проводника:
![]()
Ответ: 10.
Задача 2. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике? Ответ дайте в амперах.
Решение:
По определению силы тока:
Заряд всех электронов: где е — модуль заряда электрона,
Кл.
Тогда
Ответ: 2.
Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)
Решение:
По закону Ома для полной цепи:

Тогда
Ответ: 0,07.
Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.
Решение:
Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.
Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:
Выражаем время в секундах: t = 10 минут = 600 с.
Определяем силу тока по закону Ома для полной цепи:


Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.
По определению силы тока:
Отсюда Кл.
Ответ: 1500.
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание
- 1 Как найти внутреннее сопротивление формула?
- 2 Как определить внутреннее сопротивление источника энергии?
- 3 Что называется внутреннее сопротивление?
- 4 Чему равно внутреннее сопротивление источника тока?
- 5 Как найти эдс формула?
- 6 Как определить силу тока при коротком замыкании?
- 7 Что такое внутреннее сопротивление аккумулятора?
- 8 Что такое внутреннее и внешнее сопротивление цепи?
- 9 Как рассчитать мощность зная ток и напряжение?
- 10 Что такое сопротивление?
- 11 Какая буква обозначает сопротивление?
Как найти внутреннее сопротивление формула?
Нужно определить внутреннее сопротивление аккумулятора. По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом; Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.
Как определить внутреннее сопротивление источника энергии?
Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами. Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи: I = ε / (r + R).
Что называется внутреннее сопротивление?
В электрической цепи, состоящей из источника тока и проводников с электрическим сопротивлением R, ток совершает работу не только на внешнем, но и на внутреннем участке цепи. Электрическое сопротивление источника тока называется внутренним сопротивлением.
Чему равно внутреннее сопротивление источника тока?
Внутреннее сопротивление источника тока r будет определяться формулой: r = ЭДС / I — R. Подставим данные из условия задачи: r = 10 В / 2 А — 4 Ом = 1 Ом. Ответ: источник тока имеет внутреннее сопротивление r = 1 Ом.10 мая 2020 г.
Как найти эдс формула?
На внутреннем участке цепи: Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q. ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи. 4. Если R растет, то I уменьшается.
Как определить силу тока при коротком замыкании?
Формула для измерения силы тока короткого замыкания: Iкз = E/r.
…
Сила тока при коротком замыкании участка цепи
- -I – величина тока (его сила);
- U – разность потенциалов (напряжение сети);
- R – электрическое сопротивление.
Что такое внутреннее сопротивление аккумулятора?
Внутренее сопротивление аккумуляторов — параметр, позволяющий оценить «здоровье» аккумулятора … Омическое сопротивление является суммой сопротивлений сепараторов аккумулятора, электродов, положительного и отрицательного выводов, мостовых сварных соединений между элементами и электролита.
Что такое внутреннее и внешнее сопротивление цепи?
Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а сопротивление самого источника тока — внутренним сопротивлением. Внутреннее сопротивление обозначается буквой r.
Как рассчитать мощность зная ток и напряжение?
Формула расчета мощности электрического тока
Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.
Что такое сопротивление?
Сопротивление — это величина, которая отражает противодействие движению тока в электрической цепи. Сопротивление измеряется в омах, для обозначения которых используется греческая буква омега (Ω).
Какая буква обозначает сопротивление?
Электрическое сопротивление характеризует способность электрического проводника препятствовать прохождению электрического тока. Электрическое сопротивление обозначается буквой R. Единицей сопротивления является ом (Ом). Сила тока I прямо пропорциональна напряжению U.

