Задания
Версия для печати и копирования в MS Word
Тип 2 № 541050 

i
Из единичного куба вырезана правильная четырёхугольная призма со стороной основания 0,8 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба
Спрятать решение
Решение.
Площадь поверхности получившегося многогранника равна сумме площадей поверхностей куба с ребром 1 и четырех граней параллелепипеда с ребрами 1, 0,8, 0,8, уменьшенной на две площади основания вырезанной призмы:
Ответ: 7,92.
Аналоги к заданию № 27075: 541050 73329 73331 … Все
Кодификатор ФИПИ/Решу ЕГЭ:
5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность;
5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде;
5.7.2* Комбинации стереометрических тел.
Классификатор стереометрии: Площадь поверхности куба, Площадь поверхности призмы
Спрятать решение
·
Прототип задания
·
Видеокурс
·
Помощь
В данной задаче нам нужно найти площадь поверхности оставшейся части куба после того, как из него вырезали правильную четырехугольную призму.
Для начала вспомним формулу площади поверхности куба: S = 6a^2, где a – длина стороны куба.
Так как из куба вырезана призма, которая имеет основания со стороной 0,5, значит ее длина будет равна 0,5. Боковое ребро призмы равно 1. Значит, нам нужно вырезать из куба шесть таких призм: по одной с каждой стороны куба.
Следовательно, мы вырезаем из куба 6 призм, каждая из которых имеет площадь b^2 + 4l^2 (b – длина стороны основания, l – длина бокового ребра).
В нашем случае:
– b = 0.5
– l = 1
Подставляем значения в формулу и получаем:
S призмы = 0.25 + 4 = 4.25.
Соответственно, общая площадь всех вырезанных призм будет равна 6*S призмы = 25.5.
Таким образом, площадь поверхности оставшейся части куба будет равна S куба – площадь всех вырезанных призм:
S = 6a^2 – 25.5.
Для нахождения площади поверхности оставшейся части куба, нам нужно знать длину стороны куба, но в задаче ее не указано. Поэтому дать конкретный ответ на этот вопрос без дополнительных данных невозможно.
Из единичного куба вырезана правильная четырёхугольная
призма со стороной основания 0,5 и боковым ребром 1.
Найдите площадь поверхности оставшейся части куба.
Площадь поверхности куба с вырезанной четырёхугольной правильной призмой (вар. 50)
Сначала посчитаем площадь поверхности внешней боковой части многогранника.
B10. Площадь поверхности куба с вырезанной правильной призмой (вар. 50)
Она состоит из четырёх одинаковых квадратов со стороной 1. S1 = 4·(1·1) = 4.
Теперь посчитаем боковую поверхность многогранника с внутренней стороны.
B10. Площадь поверхности куба с вырезанной правильной призмой (вар. 50)
Она состоит из четырёх прямоугольников со сторонами 1 и 0,5.S2 = 4·(1·0,5) = 2.
И наконец, посчитаем площади оснований дырявого куба. Оснований тут два,
они представляют из себя квадраты с вырезанными из них квадратами.
B10. Площадь поверхности куба с вырезанной правильной призмой (вар. 50)
У большого квадрата сторона 1, у маленького 0,5. S3 = 2·(1·1 – 0,5·0,5) = 1,5.
Сложим все получившиеся площади поверхностей S = 4 + 2 + 1,5 = 7,5.
Ответ: 7,5
Решение:
Площадь поверхности оставшейся части куба – это сумма площадей всех его граней:
1) 4 боковых квадратных граней (спереди, сзади, слева, справа) со сторонами 1 (куб единичный), найдём иx площадь:
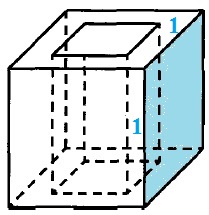
S◻ = 1·1 = 1
S1 = 4·S◻ = 4·1 = 4
2) 2 квадратных 1х1 грани (вверх и низ) с вырезанным квадратом 0,4х0,4, найдём их площадь:
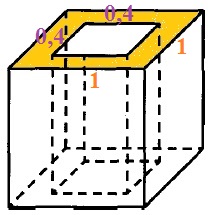
S▣ = 1·1 – 0,4·0,4 = 1 – 0,16 = 0,84
S2 = 2·S▣ = 2·0,84 = 1,68
3) 4 образовавшихся внутри куба прямоугольных грани 1х0,4, найдём их площадь:
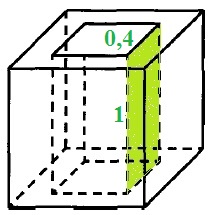
S▭ = 1·0,4 = 0,4
S3 = 4·S▭ = 4·0,4 = 1,6
Найдём сумму площадей всех граней куба:
S = S1 + S2 + S3 = 4 + 1,68 + 1,6 = 7,28
Ответ: 7,28.
Из единичного куба вырезана правильная четырёхугольная призма со стороной основания $0{,}7$ и боковым ребром $1$. Найдите площадь поверхности получившейся фигуры (cм. рис.).
Поверхность оставшейся части куба состоит из боковой поверхности куба, площадь которой равна 4·1·1=4, боковой поверхности призмы, площадь которой равна 4·0,7·1=2.8, и двух равных фигур (см. заштрихованную фигуру на рисунке), площадь каждой из которых равна 1·1 — 0,7·0,7 = 0.51. Таким образом, площадь поверхности оставшейся части куба равна 4 + 2.8 + 2 · 0.51 = 7.82.
Ответ: 7.82
