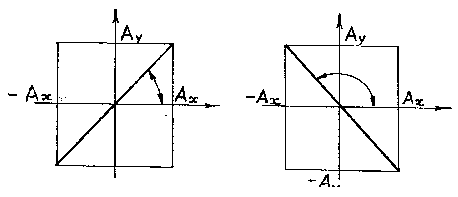Сложение гармонических колебаний
Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача – найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний – нахождение траектории результирующего колебания.
Метод векторных диаграмм
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j0 где j0 – начальный угол.
Проекции вектора А на оси координат запишутся:
Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу – начальную фазу.
Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:
Сопоставим этим колебаниям два вектора А1 и А2, вращающихся с соответствующими угловыми скоростями.
Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).
Из очевидных геометрических соображений находим:
Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
получим уравнение суммарного колебания:
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.
Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот – частотой биений (циклической).
При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).
например, сложим два колебания с одинаковыми частотами:
исключив время, получим:
В общем случае это – уравнение эллипса. При A1=A2 – окружность, при (m – целое) – отрезок прямой.
Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.
Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.
Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид
1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.
2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.
3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .
За период система совершает одно полное колебание.
4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле
5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением
6) Фаза колебаний ωt + φ0 − фаза указывает местоположение колеблющейся точки в данный момент времени.
7) Начальная фаза φ0 − указывает местоположение колеблющейся точки в момент времени t = 0 .
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ0 , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ0)
1. Сложение одинаково направленных гармонических колебаний.
Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x1 и x2 , которые запишутся следующим образом:
Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x2+x2 , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов
Так как угол между векторами А 1 и А 2 равен φ=π-(φ2-φ1) , то cos[π-(φ2-φ1)]=-cos(φ2-φ1) , следовательно, результирующая амплитуда колебания будет равна
Определим начальную фазу результирующего колебания.
Из рисунка видно, что начальная фаза результирующего колебания
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.
2. Сложение взаимно перпендикулярных гармонических колебаний.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид
где φ − разность фаз обоих колебаний.
Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$xover A_1$$ , а sinωt= $$sqrt<1-cos^2 ωt>=sqrt<1-x^2over A_1^2>$$ Разложим косинус во втором из уравнений (5.2.6)
Перепишем это уравнение в следующем виде
После преобразования, получим
Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим
Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.
Рассмотрим несколько частных случаев и определим форму траектории для них:
a) разность фаз равна нулю [φ=0]
В этом случае $$( < xover A_1 >- < yover A_2 >)^2=0$$ , откуда получается уравнение прямой
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= sqrt+A_2<^2>>$$ .
2) разность фаз равна ±π[φ=±π] .
В этом случае $$( < xover A_1 >- < yover A_2 >)^2=0$$ , откуда получается уравнение прямой
3) Разность фаз равна ± $$πover 2$$ [φ=± $$π over2$$ ] . Тогда
Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$πover 2$$ и φ=- $$πover 2$$ отличаются направлением движения. Если φ=+ $$πover 2$$ , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=-A2sinωt и движение совершается по часовой стрелке. Если φ=- $$πover 2$$ , , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=A2sinωt и движение совершается против часовой стрелке.
Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис
4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.
На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.
По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
Продифференцируем по времени уравнение гармонических колебаний
и получим выражение для скорости
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .
Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).
Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний
Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы
Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,
где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .
Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением
ω0 − собственная частота осциллятора.
Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ0) .
5.4. Энергия гармонических колебаний.
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
Потенциальная энергия тела, совершающего гармонические колебания равна
Кинетическая энергия тела, совершающего гармонические колебания равна
Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом
Следовательно, полная энергия гармонического колебания
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период колебания
Аналогично получается для среднего значение кинетической энергии
Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2
5.5. Пружинный, математический и физический маятники.
Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox Fупр=ma . Упругая сила Fупр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим
Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой
Так как период колебаний определяется по формуле T= $$2πover ω_0$$ , то период колебаний пружинного маятника
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.
При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения
где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φover dt^2$$ , получим
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .
Согласно основному уравнению динамики вращательного движения получаем
где I − момент инерции маятника относительно оси, проходящей через точку подвеса.
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$sqrt$$ и T=2π $$sqrt$$ получается, что математический маятник с длиной
будет иметь такой же период колебаний, что и данный физический маятник.
Величина lпр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
Сложение перпендикулярных колебаний. Фигуры Лиссажу.
|
Сложение взаимно перпендикулярных колебаний |
|
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде (1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как и заменяя во втором уравнении на и на , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: (2) Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2, . ). В этом случае эллипс становится отрезком прямой (3) где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2. ). В этом случае уравнение станет иметь вид (4) Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу. Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ). Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний. |
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или вырождаются в отрезки прямых, а при разности фаз и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
Математическое выражение для кривой Лиссажу[править | править вики-текст]
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности(A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
являются полиномами Чебышёва первого рода степени N.
| | | следующая лекция ==> | |
| Метод векторных диаграмм. Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А | | | Неинерциальные системы отсчета. Описание движения в неинерциальных системах. Силы инерции. Центробежная сила. Сила Кориолиса. |
Дата добавления: 2016-01-29 ; просмотров: 9562 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
[spoiler title=”источники:”]
http://physics.belstu.by/mechanics_lk/mechanics_lk7.html
http://helpiks.org/6-64688.html
[/spoiler]
Рассмотрим
результат сложения двух гармонических
колебаний одинаковой частоты ,
происходящих во взаимно перпендикулярных
направлениях вдоль осей х
и
у.
Для
простоты начало отсчета выберем так,
чтобы начальная фаза первого колебания
была равна нулю:

Разность
фаз обоих колебаний равна ,
А
и
В
— амплитуды
складываемых колебаний.
Уравнение
траектории результирующего колебания
находится исключением из выражений
(145.1) параметра t.
Записывая складываемые колебания в
виде

и
заменяя во втором уравнении cost
на х/А
и
sint
на
(1-(х/A)2),
получим после несложных преобразований
уравнение
эллипса, оси
которого ориентированы относительно
координатных осей произвольно:

Так
как траектория результирующего колебания
имеет форму эллипса, то такие колебания
называются эллиптически
поляризованными.
Ориентация
осей эллипса и его размеры зависят
от амплитуд складываемых колебаний и
разности фаз .
Рассмотрим некоторые частные случаи,
представляющие физический интерес:
1)
=m(m=0,
±1, ±2,…). В данном случае эллипс
вырождается в
отрезок
228

прямой
у=±(В/А)х,
(145.3)
где знак плюс соответствует нулю и
четным значениям т
(рис.
205, a),
a знак
минус — нечетным значениям т
(рис.
205, б). Результирующее колебание
является гармоническим колебанием
с
частотой
и амплитудой (A2+В2),
совершающимся вдоль прямой (145.3),
составляющей с осью х
угол
=

В данном случае
имеем
дело с линейно
поляризованными колебаниями.
![]()
В данном случае
уравнение примет вид


229
Это
уравнение эллипса, оси которого совпадают
с осями координат, а его полуоси равны
соответствующим амплитудам (рис.206).
Кроме того, если А=В,
то
эллипс (145.4) вырождается в
окружность. Такие
колебания называются циркулярно
поляризованными колебаниями или
колебаниями, поляризованными по кругу.
Если
частоты складываемых взаимно
перпендикулярных колебаний различны,
то замкнутая траектория результирующего
колебания довольно сложна. Замкнутые
траектории, прочерчиваемые точкой,
совершающей одновременно два взаимно
перпендикулярных колебания, называются
фигурами
Лиссажу.
Форма
этих кривых зависит от соотношения
амплитуд, частот и разности фаз
складываемых колебаний. На рис. 207
представлены фигуры Лиссажу для
различных соотношений частот (указаны
слева) и разностей фаз (указаны
вверху).
Отношение частот
складываемых колебаний равно отношению
числа пересечений фигур Лиссажу с
прямыми, параллельными осям координат.
По виду фигур можно определить неизвестную
частоту по известной или определить
отношение частот складываемых колебаний.
Поэтому анализ фигур Лиссажу — широко
используемый метод исследования
соотношений частот и разности фаз
складываемых колебаний, а также формы
колебаний.
§ 146. Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания
Рассмотрим
свободные затухающие
колебания —
колебания, амплитуда которых из-за
потерь энергии реальной колебательной
системой с течением времени уменьшается.
Простейшим механизмом уменьшения
энергии колебаний является ее превращение
в теплоту вследствие трения в механических
колебательных системах,
а также омических
потерь и излучения электромагнитной
энергии в электрических колебательных
системах.
Закон
затухающих колебаний определяется
свойствами колебательных систем. Обычно
рассматривают линейные
системы —
идеализированные реальные системы,
в которых параметры, определяющие
физические свойства системы, в ходе
процесса не изменяются. Линейными
системами являются, например, пружинный
маятник при малых растяжениях пружины
(когда справедлив закон Гука), колебательный
контур, индуктивность, емкость и
сопротивление которого не зависят ни
от тока в контуре, ни от напряжения.
Различные по своей природе линейные
системы описываются идентичными
линейными дифференциальными уравнениями,
что позволяет подходить к изучению
колебаний различной физической природы
с единой точки зрения, а также проводить
их моделирование, в том числе и на
ЭВМ.
Дифференциальное
уравнение свободных затухающих
колебаний линейной
системы задается
в виде

где s
—
колеблющаяся величина, описывающая
тот или иной физический процесс,
=const
—
коэффициент
затухания, 0
— циклическая частота свободных
незатухающих
колебаний
той же колебательной системы, т. е.
при =0
(при отсутствии потерь энергии) называется
собственной
частотой колебательной
системы.
Решение уравнения
(146.1) рассмотрим в виде
s=e–u
(146.2)
где
u=u(t).
После
нахождения первой и второй производных
выражения (146.2) и подстановки их в (146.1)
получим
![]()
Решение уравнения
(146.3) зависит от знака коэффициента перед
искомой величиной. Рассмотрим случай,
когда этот коэффициент положителен:
2=20-2
(146.4)
230
(если
(2-2)>0,
то такое обозначение мы вправе сделать).
Тогда получим уравнение типа (142.1)
![]()
решением
которого является функция и=А0cos(t+)
(см. (140.1)).
Таким
образом, решение уравнения (146.1) в случае
малых затуханий (2<<20)
s=A0е–tсоs(t+),
(146.5) где А=А0е–t
(146.6)
— амплитуда
затухающих колебаний,
а
a0
—
начальная амплитуда. Зависимость (146.5)
показана на рис.208 сплошной линией, а
зависимость (146.6) — штриховыми линиями.
Промежуток времени =1/,
в течение которого амплитуда затухающих
колебаний уменьшается в е раз, называется
временем
релаксации.
Затухание нарушает
периодичность колебаний, поэтому
затухающие колебания не являются
периодическими и, строго говоря, к ним
неприменимо понятие периода или
частоты. Однако если затухание мало, то
можно условно пользоваться понятием
периода как промежутка времени между
двумя последующими максимумами (или
минимумами) колеблющейся физической
величины (рис. 208). Тогда период
затухающих колебаний с учетом формулы

(146.4) равен
![]()
Если
A(t)
и
A(t+T)—
амплитуды двух последовательных
колебаний, соответствующих моментам
времени, отличающимся на период, то
отношение

называется
декрементом
затухания, а его
логарифм
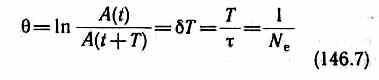
— логарифмическим
декрементом затухания; Ne
—
число колебаний, совершаемых за время
уменьшения амплитуды в е раз. Логарифмический
декремент затухания — постоянная для
данной колебательной системы величина.
Для
характеристики колебательной системы
пользуются понятием добротности
Q,
которая
при малых значениях логарифмического
декремента равна

(так
как затухание невелико (2<<20),
то
Т
принято
равным Т0).
Из
формулы (146.8) следует, что добротность
пропорциональна числу колебаний Ne,
совершаемых
системой за время релаксации.
Применим выводы,
полученные для свободных затухающих
колебаний линейных систем, для
колебаний различной физической
природы — механических (в качестве
примера рассмотрим пружинный маятник)
и электромагнитных (в качестве примера
рассмотрим электрический колебательный
контур).
1.
Свободные затухающие колебания пружинного
маятника. Для
пружинного маятника (см. § 142) массой т,
совершающего
малые колебания под действием упругой
силы F=-kx,
сила
трения пропорциональна скорости, т.
е.
![]()
231
где r
—
коэффициент сопротивления; знак
минус указывает на противоположные
направления силы трения и скорости.
При данных условиях
закон движения маятника будет иметь
вид
![]()
Используя
формулу 0=k/m
(см.
(142.2)) и принимая, что коэффициент
затухания
=r/(2m),
(146.10)
получим идентичное
уравнению (146.1) дифференциальное уравнение
затухающих колебаний, маятника:
![]()
Из выражений
(146.1) и (146.5) вытекает, что маятник колеблется
по закону
х=A0е–tcos(t+)
с частотой =(20-r2/4m2)
(см.
(146.4)).
Добротность
пружинного маятника,
согласно
(146.8) и (146.10), Q=1/rkm.
Соседние файлы в папке Трофимова Курс физики
- #
16.03.2016181.76 Кб16713.doc
- #
16.03.2016336.38 Кб13614.doc
- #
16.03.2016206.34 Кб14015.doc
- #
16.03.2016169.98 Кб9616.doc
- #
16.03.2016123.39 Кб9417.doc
- #
16.03.2016629.25 Кб22318.doc
- #
16.03.2016194.05 Кб9419.doc
- #
16.03.2016170.5 Кб1032.doc
- #
16.03.2016137.73 Кб9820.doc
- #
16.03.2016324.61 Кб13721.doc
- #
16.03.2016242.69 Кб10922.doc
2.1. Сложение гармонических колебаний одного направления
2.2. Сложение взаимно перпендикулярных колебаний
Одно и то же тело может одновременно участвовать в двух и более движениях. Простым примером является движение шарика, брошенного под углом к горизонту. Можно считать, что шарик участвует в двух независимых взаимно перпендикулярных движениях: равномерном по горизонтали и равнопеременном по вертикали. Одно и то же тело (материальная точка) может участвовать в двух (и более) движениях колебательного типа.
Под сложением колебаний понимают определение закона результирующего колебания, если колебательная система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.
2.1. Сложение гармонических колебаний одного направления
1. Сложение двух колебаний одного направления (сонаправленных колебаний)
![]()
![]()
можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.
На Рисунке 2.1 показаны векторы амплитуд А1(t) и А2(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны ![]() и
и ![]() . Сложение колебаний сводится к определению
. Сложение колебаний сводится к определению ![]() . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.
. Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.
Результирующему колебанию ![]() соответствует на векторной диаграмме вектор амплитуды
соответствует на векторной диаграмме вектор амплитуды ![]() и фаза
и фаза ![]() .
.
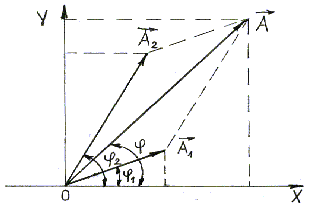
Рисунок 2.1 – Сложение сонаправленных колебаний.
Величина вектора А(t) может быть найдена по теореме косинусов:
![]() .
.
Фаза результирующего колебания задается формулой:
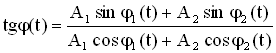 .
.
Если частоты складываемых колебаний ω1 и ω2 не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.
2. Два гармонических колебания x1 и x2 называются когерентными, если разность их фаз не зависит от времени:
![]() .
.
Но так как ![]() , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты
, то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты ![]() .
.
Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:
![]() .
.
Начальную фазу результирующего колебания легко найти, если спроектировать векторы А1 и А2 на координатные оси ОХ и ОУ (см. Рисунок 9):
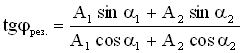 .
.
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием ![]() .
.
3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.
Если ![]() , где n – любое целое неотрицательное число
, где n – любое целое неотрицательное число
(n = 0, 1, 2…), то ![]() , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При
, т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При ![]() результирующая амплитуда равна нулю
результирующая амплитуда равна нулю ![]() .
.
Если ![]() , то
, то ![]() , т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы
, т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы ![]() , то
, то ![]() .
.
4. Сложение сонаправленных колебаний с неравными, но близкими частотами.
Частоты складываемых колебаний не равны ![]() , но разность частот
, но разность частот ![]() много меньше и ω1, и ω2. Условие близости складываемых частот записывается соотношениями
много меньше и ω1, и ω2. Условие близости складываемых частот записывается соотношениями ![]()
![]() .
.
Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k1 и k2.
Пусть амплитуды складываемых колебаний одинаковы![]() , а начальные фазы равны нулю
, а начальные фазы равны нулю ![]() . Тогда уравнения складываемых колебаний имеют вид:
. Тогда уравнения складываемых колебаний имеют вид: ![]() ,
, ![]() .
.
Результирующее колебание описывается уравнением:
![]() .
.
Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой ![]() , другая – с частотой
, другая – с частотой ![]() , где ω близка к частотам складываемых колебаний (ω1 или ω2). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.
, где ω близка к частотам складываемых колебаний (ω1 или ω2). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.
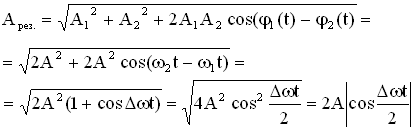 Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости хрез.при биениях показан на Рисунке 2.2.
Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости хрез.при биениях показан на Рисунке 2.2.
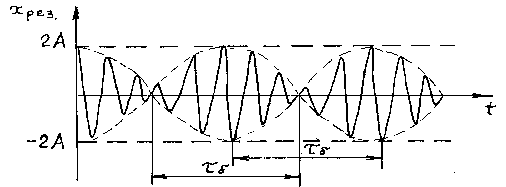
Рисунок 2.2 – Зависимость смещения от времени при биениях.
Амплитуда биений медленно меняется с частотой ![]() . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τб, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:
. Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τб, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:
![]() .
.
Величина ![]() – период биений.
– период биений.
Величина 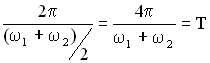 есть период результирующего колебания (Рисунок 2.4).
есть период результирующего колебания (Рисунок 2.4).
1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.
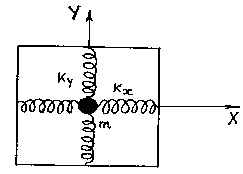
Рисунок 2.3
Складываемые колебания имеют вид:
![]()
![]() .
.
Частоты колебаний определяются как 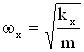 ,
, 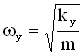 , где
, где ![]() ,
, ![]() -коэффициенты жесткости пружин.
-коэффициенты жесткости пружин.
2. Рассмотрим случай сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами ![]() , что соответствует условию
, что соответствует условию![]() (одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:
(одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:
![]()
![]()
Когда точка участвует одновременно в двух движениях, ее траектория может быть различной и достаточно сложной. Уравнение траектории результирующего колебаний на плоскости ОХУ при сложении двух взаимно перпендикулярных с равными частотами можно определить, исключив из исходных уравнений для х и y время t:
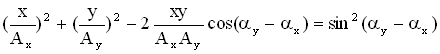 .
.
Вид траектории определяется разностью начальных фаз складываемых колебаний, которые зависят от начальных условий (см. § 1.1.2). Рассмотрим возможные варианты.
а) Если ![]() , где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:
, где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:
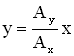 (Рисунок 2.3 а).
(Рисунок 2.3 а).
|
|
|
|
Рисунок 2.3.а |
Рисунок 2.3 б |
б) Если ![]() (n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:
(n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:
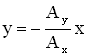 (Рисунок 2.3б).
(Рисунок 2.3б).
В обоих случаях ( а, б) результирующее движение точки будет колебание по прямой, проходящей через точку О. Частота результирующего колебания равна частоте складываемых колебаний ω0, амплитуда определяется соотношением:
![]() .
.
Угол, который прямая (траектория) составляет с осью ОХ, можно найти из уравнения:
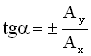 (знак “плюс” – случай а, знак “минус” – случай б).
(знак “плюс” – случай а, знак “минус” – случай б).
Результатом сложения взаимно перпендикулярных колебаний (случай а и б) является колебание, которое называется линейно поляризованным.
в) Если ![]() (n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:
(n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:
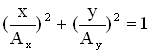 .
.
Это уравнение эллипса, его оси совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны ![]() и
и ![]() (Рисунок 2.4 ).
(Рисунок 2.4 ).
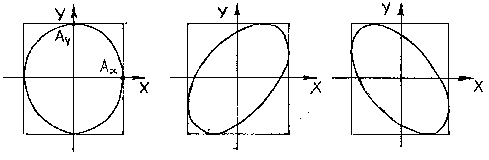
Рисунок 2.4
Точка в результате участия в двух взаимно перпендикулярных колебаниях описывает эллипс за время, равное периоду складываемых колебаний ![]() .
.
3. Сложение взаимно перпендикулярных колебаний с кратными частотами.
Складываются взаимно перпендикулярные колебания, частоты которых не равны ![]() , но
, но ![]() ,
, ![]() , где a и b – целые числа.
, где a и b – целые числа.
![]()
![]()
Периоды колебаний вдоль осей ОХ и ОУ соответственно равны ![]() и
и ![]() . Отношение периодов
. Отношение периодов 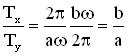 .
.
Траектория точки, участвующей во взаимно перпендикулярных колебаниях с кратными частотами, – замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории называются фигурами Лиссажу.