В данной статье репетитор по физике и математике рассказывает о том, как рассчитать перегрузку, которую испытывает тело в момент разгона или торможения. Данный материал очень плохо рассматривается в школе, поэтому школьники очень часто не знают, как осуществлять расчёт перегрузки, а ведь соответствующие задания встречаются на ЕГЭ и ОГЭ по физике. Так что дочитайте эту статью до конца или посмотрите прилагающийся видеоурок. Знания, которые вы получите, пригодятся вам на экзамене.
Начнём с определений. Перегрузкой называется отношение веса тела к величине силы тяжести, действующей на это тело у поверхности земли. Вес тела — это сила, которая действует со стороны тела на опору или подвес. Обратите внимание, вес — это именно сила! Поэтому измеряется вес в ньютонах, а не в килограммах, как некоторые считают.
Таком образом, перегрузка — это безразмерная величина (ньютоны делятся на ньютоны, в результате ничего не остаётся). Однако, иногда эту величину выражают в ускорениях свободного падения. Говорят, к примеру, что перегрузка равна ![]() , имея ввиду, что вес тела вдвое больше силы тяжести.
, имея ввиду, что вес тела вдвое больше силы тяжести.
Примеры расчёта перегрузки
Покажем, как осуществлять расчёт перегрузки на конкретных примерах. Начнём с самых простых примеров и перейдём далее к более сложным.
Пример 1. Чему равна перегрузка человека, стоящего на земле? Чему равна перегрузка человека, свободно падающего с некоторой высоты?
Очевидно, что человек, стоящий на земле, не испытывает никаких перегрузок. Поэтому хочется сказать, что его перегрузка равна нулю. Но не будем делать поспешных выводов. Нарисуем силы, действующие на этого человека:
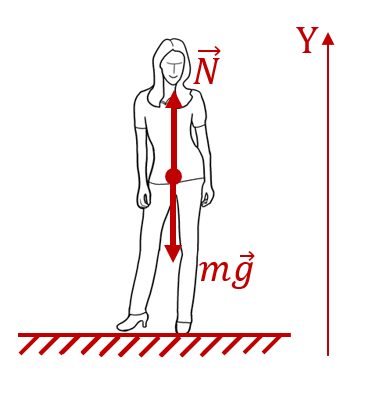
К человеку приложены две силы: сила тяжести ![]() , притягивающая тело к земле, и противодействующая ей со стороны земной поверхности сила реакции
, притягивающая тело к земле, и противодействующая ей со стороны земной поверхности сила реакции ![]() , направленная вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.
, направленная вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.
Вес человека ![]() приложен к опоре (к поверхности земли), в ответ в соответствии с 3-м законом Ньютона со стороны опоры на человека действует равная по величине и противоположно направленная сила
приложен к опоре (к поверхности земли), в ответ в соответствии с 3-м законом Ньютона со стороны опоры на человека действует равная по величине и противоположно направленная сила ![]() . Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.
. Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.
Поскольку человек стоит на месте и не проваливается сквозь землю, то силы, которые на него действуют скомпенсированы. То есть ![]() , и, соответственно,
, и, соответственно, ![]() . То есть расчёт перегрузки в этом случае даёт следующий результат:
. То есть расчёт перегрузки в этом случае даёт следующий результат:
![]()
Запомните это! При отсутствии перегрузок перегрузка равна 1, а не 0. Как бы странно это не звучало.
Определим теперь, чему равна перегрузка человека, который находится в свободном падении.

Если человек пребывает в состоянии свободного падения, то на него действует только сила тяжести, которая ничем не уравновешивается. Силы реакции опоры нет, как нет и веса тела. Человек находится в так называемом состоянии невесомости. В этом случае перегрузка равна 0.
Пример 2. Определите перегрузку космонавтов, находящихся в ракете, движущейся на небольшой высоте вверх с ускорением 40 м/с2.
Космонавты находятся в горизонтальном положении в ракете во время её старта. Только так они могут выдержать перегрузки, которые они испытывают, не потеряв при этом сознания. Изобразим это на рисунке:
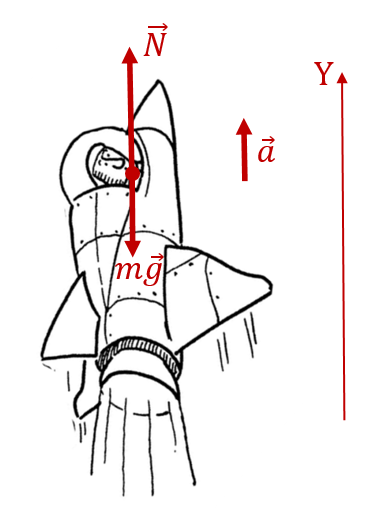
В этом состоянии на них действует две силы: сила реакции опоры ![]() и сила тяжести
и сила тяжести ![]() . Как и в прошлом примере, модуль веса космонавтов равен величине силы реакции опоры:
. Как и в прошлом примере, модуль веса космонавтов равен величине силы реакции опоры: ![]() . Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением
. Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением ![]() . С этим же ускорением синхронно с ракетой ускоряются и космонавты.
. С этим же ускорением синхронно с ракетой ускоряются и космонавты.
Тогда в соответствии со 2-м законом Ньютона в проекции на ось Y (см. рисунок), получаем следующее выражение: ![]() , откуда
, откуда ![]() . То есть искомая перегрузка равна:
. То есть искомая перегрузка равна:
![]()
Надо сказать, что это не самая большая перегрузка, которую приходится испытывать космонавтам во время старта ракеты. Перегрузка может доходить до 7. Длительное воздействие таких перегрузок на тело человека неминуемо приводит к летальному исходу.
Пример 3. Рассчитайте перегрузку, которую испытывает пилот самолёта, выполняющего «мёртвую петлю» в нижней точке траектории. Скорость самолёта в этой точке составляет 360 км/ч. Радиус «мёртвой петли» составляет 200 м.
В нижней точке «мёртвой петли» на пилота будут действовать две силы: вниз — сила ![]() , вверх, к центру «мёртвой петли», — сила
, вверх, к центру «мёртвой петли», — сила ![]() (со стороны кресла, в котором сидит пилот):
(со стороны кресла, в котором сидит пилот):
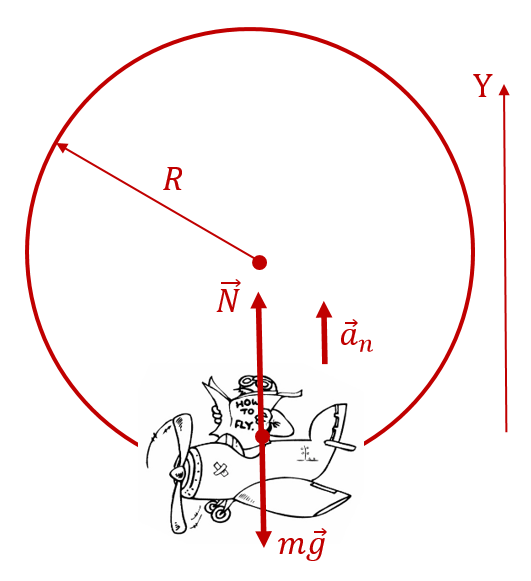
Туда же будет направлено центростремительное ускорение пилота ![]() , где
, где ![]() км/ч
км/ч ![]() м/с — скорость самолёта,
м/с — скорость самолёта, ![]() — радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:
— радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:
![]()
Тогда вес равен ![]() . Итак, расчёт перегрузки даёт следующий результат:
. Итак, расчёт перегрузки даёт следующий результат:
![Rendered by QuickLaTeX.com [ frac{mleft(g+frac{upsilon^2}{R}right)}{mg} = 1+frac{upsilon^2}{gR} = 1+frac{100^2}{10cdot 200} = 6. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bd0d66979d42352b265faec5a2a13b2e_l3.png)
Весьма существенная перегрузка. Спасает жизнь пилота только то, что действует она не очень длительно.
Ну и напоследок, рассчитаем перегрузку, которую испытывает водитель автомобиля при разгоне.
Пример 4. Рассчитайте перегрузку, которую испытывает водитель автомобиля, разгоняющегося с места до скорости 180 км/ч за 10 с.
Итак, конечная скорость автомобиля равна ![]() км/ч
км/ч ![]() м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за
м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за ![]() c, то его ускорение равно
c, то его ускорение равно ![]() м/с2.
м/с2.
На водителя в процессе ускорения действуют две составляющие силы реакции опоры: со стороны седушки кресла (вертикальная составляющая) ![]() и со стороны спинки кресла (горизонатльная составляющая)
и со стороны спинки кресла (горизонатльная составляющая) ![]() :
:
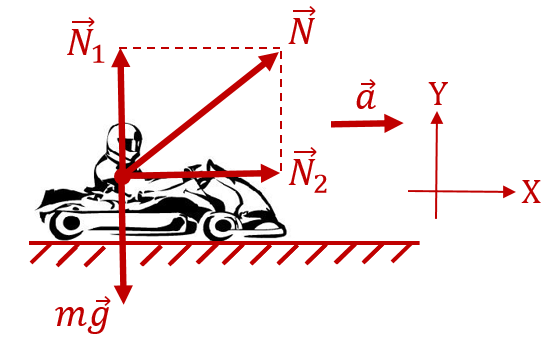
Автомобиль движется горизонтально, следовательно, вертикальная составляющая силы реакции опоры уравновешена силой тяжести, то есть ![]() . В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна
. В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна ![]() .
.
Величину общей силы реакции опоры найдём по теореме Пифагора: ![]() . Она будет равна модулю веса. То есть искомая перегрузка будет равна:
. Она будет равна модулю веса. То есть искомая перегрузка будет равна:
![Rendered by QuickLaTeX.com [ frac{P}{mg} = frac{N}{mg} = frac{msqrt{g^2+a^2}}{mg} = sqrt{1+frac{a^2}{g^2}} approx 1.12. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-57f6de2348b1dde4ac2ab7c3c900e407_l3.png)
Сегодня мы научились рассчитывать перегрузку. Запомните этот материал, он может пригодиться при решении заданий из ЕГЭ или ОГЭ по физике, а также на различных вступительных экзаменах и олимпиадах.
Материал подготовил репетитор по физике в Москве, Сергей Валерьевич
Смотрите также:
- Как рассчитать скорость спутника, вращающегося вокруг земли
- Как легко решить сложную задачу на относительность движения
Давайте разберёмся, что называют перегрузкой в физике, в каких единицах она измеряется и научимся рассчитывать её.
Итак, Перегрузка – отношение веса тела к силе тяжести, действующей на это тело (1*).
Как известно (см. статью блога «Консультация онлайн репетитора по физике. Сила тяжести. Вес тела. Невесомость.» от 22 декабря 2011), сила тяжести (F = mg) – сила, с которой планета действует на тело, а вес тела (/P/ = /N/) – сила с которой тело, под действием силы тяжести, действует на опору (или подвес), удерживающие это тело от свободного падения.
И исходя из определения (1*), перегрузка рассчитывается по формуле N/mg (2*).
Задача 1.
Тело массой m = 100 г. падает с высоты h1 = 1,25 м и после упругого удара о пол подскакивает на высоту h2 = 0,8 м. Рассчитать перегрузку, которую испытывает тело во время удара, если удар длится Δt = 0,1 с.
Решение.
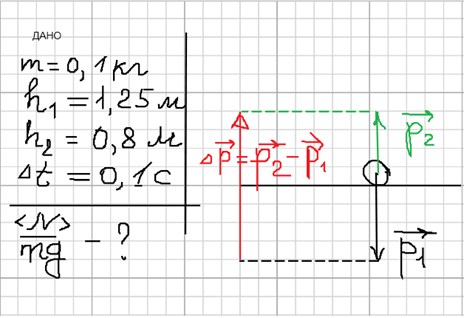
Найдём <N> при ударе тела о пол, написав предварительно формулу для изменения импульса тела:
/Δp–/ = /p2-> – p1->/ = mϑ2 + mϑ1 = m(√(2gh2) + √(2gh1)) (3*)
Во время удара на тело со стороны Земли действует сила тяжести F = mg и со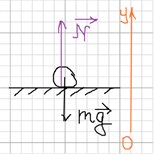 стороны пола сила реакции опоры <N>.
стороны пола сила реакции опоры <N>.
Учитывая это, запишем II закон Ньютона в векторном виде: ma-> = N-> + mg->
В проекции на ось ОУ это уравнение будет иметь вид:
<F> = <N> – mg.
Умножим левую и правую часть уравнения на Δt, получаем:
<F> Δt = <N>Δt – mg · Δt.
Так как импульс силы равен импульсу тела
<F->> · Δt = Δp->, то Δp = <N> · Δt – mg · Δt.
Выразим <N>: <N> = (Δp/Δt) + mg.
Используя выражения (2*) и (3*), запишем решение нашей задачи в общем виде:
N/mg = ((Δp/Δt) + mg)/mg = (Δp/Δt · mg) + 1 = (m[√(2gh2) + √(2gh1)] / Δtmg) + 1 =
= (√(2gh2) + √(2gh1) / Δt · g) + 1 (4*).
Обратите внимание, что в конечном виде формулы (4*) не присутствует масса тела. И поэтому можем сделать вывод о том, что при расчёте перегрузки, которую может испытывать тело, масса тела значения не имеет.
Подставим в выражение (4*) числовые значения и рассчитаем его, приняв g = 10 м/с2
N/mg = ([√(2 · 10 м/с2 · 0,8м) + √(2 · 10 м/с2 · 1,25 м)] / 0,1 с · 10 м/с2) + 1 = ([√16 м2/с2 + √25 м2/с2)] / 1с · м/с2) + 1 =
=([4 м/с + 5 м/с] / 1м/с) + 1 = 10.
Говорят так: «Перегрузка равна 10 g (десять жэ)». Это и есть единицы измерения перегрузки.
Ответ: 10 g.
Зная выражение (2*), можно легко рассчитать перегрузку, которую испытывает космонавт при старте корабля. Попробуйте и у Вас всё получится 🙂
Остались вопросы? Не знаете, как рассчитать перегрузку, которую испытывает тело?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
§ 69. Вес,
перегрузка и невесомость
1. Вес тела.
В земных
условиях большинство тел движутся без
ускорения относительно Земли. В
практике взвешивания обычно тело и
весы находятся в покое относительно
Земли. В таких случаях под весом тела
понимают силу, с которой тело давит на
горизонтальную неподвижную опору или
растягивает пружину или нить, на
которой оно подвешено неподвижно. Итак,
вес тела приложен к опоре.
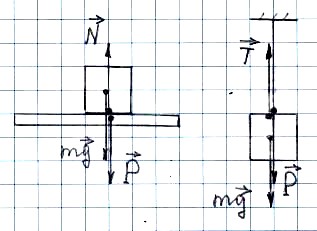
![]()
– вес
Если
система, в которой находятся тела,
движется с ускорением, то весом тела
также называют силу, с которой тело
действует на опору или растягивает
подвес.
2. Перегрузка.
Рассмотрим вес тела в лифте, когда лифт
имеет ускорение, направленное вверх.
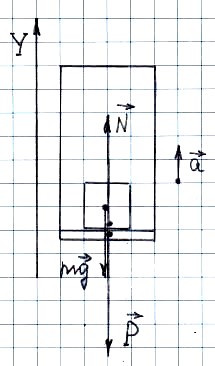
Запишем
II закон Ньютона для тела: ![]() .
.
В
проекциях на ось OY: ![]()
;
![]()
;
![]() .
.
По III
закону Ньютона: ![]()
или ![]() .
.
![]()
Мы видим,
что вес тела в системе, которая
относительно Земли имеет ускорение,
направленное вверх, больше силы
тяжести.
В таких случаях говорят, что
тело испытывает перегрузку.
Определение.
Перегрузкой
называется число, показывающее, во
сколько раз вес больше силы тяжести.
![]()
– перегрузка
![]() ;
;
![]()
Однако часто перегрузка указывается в единицах ускорения свободного падения.
Например, перегрузка, испытываемая телом, покоящимся на поверхности Земли на уровне моря, равна 1g.
Перегрузка в 0g (ноль-жэ) испытывается телом, находящемся в состоянии свободного падения, то есть в состоянии невесомости.
Одно из основных требований к военным летчикам и космонавтам — способность организма переносить перегрузки. Тренированные пилоты в
специальных противоперегрузочных костюмах могут переносить перегрузки
до 12g.
3. Невесомость.
Пусть
лифт движется с ускорением,
направленным вниз.
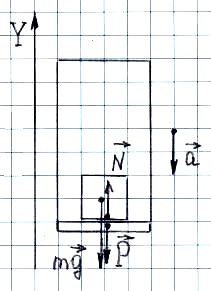
По II
закону Ньютона для тела в лифте: ![]() .
.
В
проекциях на ось OY: ![]()
;
![]()
.
По III
закону Ньютона: ![]()
или ![]() .
.
![]()
Видим,
что, когда ускорение лифта направлено
вниз, то вес тела уменьшается.
Если ![]() ,
,
то ![]() .
.
Если ![]() ,
,
то ![]() ,
,
то есть вес тела становится равным нулю.
Это состояние и называется невесомостью.
При этом на тело в лифте будет
действовать только одна сила тяжести.
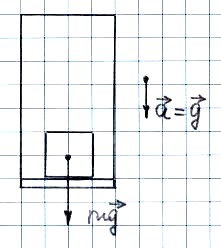
Невесомость можно объяснить так.
При свободном падении и на лифт,
и на груз в лифте действует лишь одна
сила – сила тяжести.
Известно, что эта сила всем
телам независимо от масс сообщает одно
и то же ускорение g.
Лифт и груз имеют одно и то же
ускорение g. То есть быстрота
изменения их скорости одинакова, они не
могут опережать один другого в
движении. Из-за этого отсутствует
взаимодействие груза и дна лифта, груз
не давит на дно лифта.
Если
тело бросить под углом к горизонту,
вертикально вверх или горизонтально,
то при отсутствии сопротивления
воздуха на него действует лишь одна
сила тяжести, и тело находится в
состоянии невесомости.
Для
осуществления состояния невесомости
для человека самолёты запускают по
параболам так, как если бы они летели
подобно телу, брошенному под углом к
горизонту.
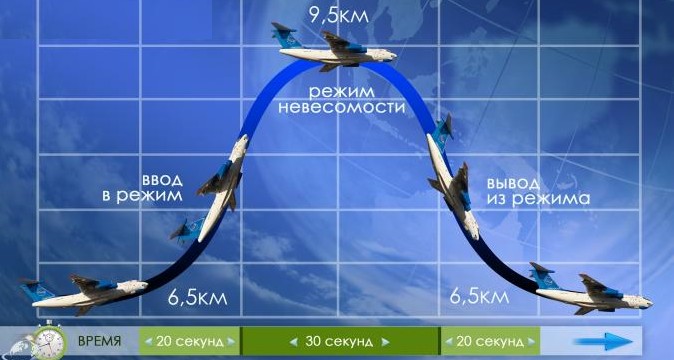
При этом
внутри самолёта наблюдается
невесомость.
Спутники летают вокруг Земли лишь под
действием силы тяжести, поэтому внутри
них наблюдается невесомость
длительное время.
4.
Относительность понятий “верх” и
“низ”.
Пусть
ускорение лифта направлено вниз и
равно 2g.
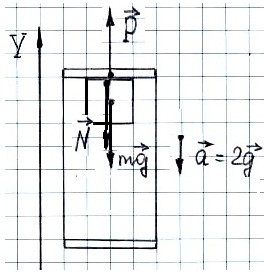
По II
закону Ньютона для груза в лифте: ![]() .
.
В
проекциях на ось OY: ![]()
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
По III
закону Ньютона: ![]()
или ![]() .
.
![]()
Если
ускорение=2g, то лифт будет
опережать груз в своём движении, и
через некоторое время груз коснётся
потолка; верх и низ поменяются местами.
5. Вес,
направленный под углом к вертикали.
Пусть
автомобиль разгоняется от нуля до
скорости ![]()
за время t секунд. Считая, что
процесс разгона происходит по
горизонтали и является
равноускоренным, вычислим вес водителя
во время разгона.
Из
кинематики знаем: ![]() .
.
Найдём
ускорение.
В проекциях на горизонтальную
ось: ![]()
=> ![]()
(1), где ![]()
– по условию задачи.
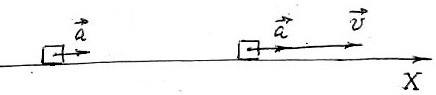
Изобразим силы, действующие на
водителя во время разгона, и вес
водителя.
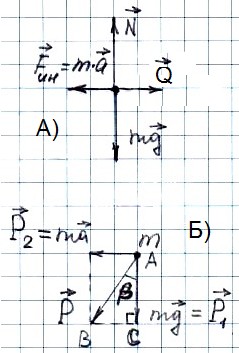
А) Силы,
действующие на водителя в
неинерциальной системе отсчёта,
связанной с автомобилем (
– сила реакции, действующая на
водителя во время разгона со
стороны спинки сиденья).
Б) Вес
водителя во время разгона.
По
теореме Пифагора из прямоугольного ![]()
АВС (см. рис. Б):
![]()
;
![]()
;
![]()
(2).
(1) в (2): ![]()
– вес водителя во время разгона
автомобиля.
Угол,
который составляет вектор ![]()
с вертикалью:
![]()
;
![]()
;
![]()
;
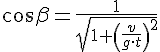 .
.
Итак,
вес – это сила, с которой
покоящееся тело давит на
горизонтальную неподвижную опору или
растягивает подвес, на котором оно
неподвижно. Во всех остальных случаях – это
результирующая сила, с которой тело в
данных условиях воздействует на связь.
6. Вычисление
перегрузки.

Большинство болидов Формулы 1 способны разогнаться до 100 км/час за
1,9 с. Это самый быстрый показатель для автомобилей на механической тяге.
Вычислим перегрузку, которую
испытывает пилот болида во время
разгона.
1) Знаем: 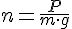 .
.
2) Также
из вычислений, представленных выше,
знаем формулу для вычисления веса
водителя при разгоне автомобиля: 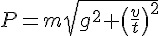 .
.
3) Имеем:
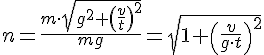 .
.
4)
Учитывая, что 100 км/ч=250/9 м/с, получаем: 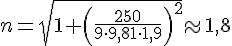 .
.
Таким образом, перегрузка
пилота болида Формулы 1 при разгоне
автомобиля составляет почти 2g.
Преподаватель который помогает студентам и школьникам в учёбе.
Зависимость веса тела от вида движения в физике – формулы и определение с примерами
Зависимость веса тела от вида движения:
В настоящее время большинство административных и жилых зданий являются многоэтажными. Для подъема на верхние этажи и спуска вниз пользуются лифтами. Рассмотрим движение человека, поднимающегося и опускающегося в лифте.
1. Человек с массой 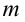
Иначе говоря, при движении лифта с постоянной скоростью вес тела будет таким же, каким он был, когда лифт находился в покое (рис. 2.5а).
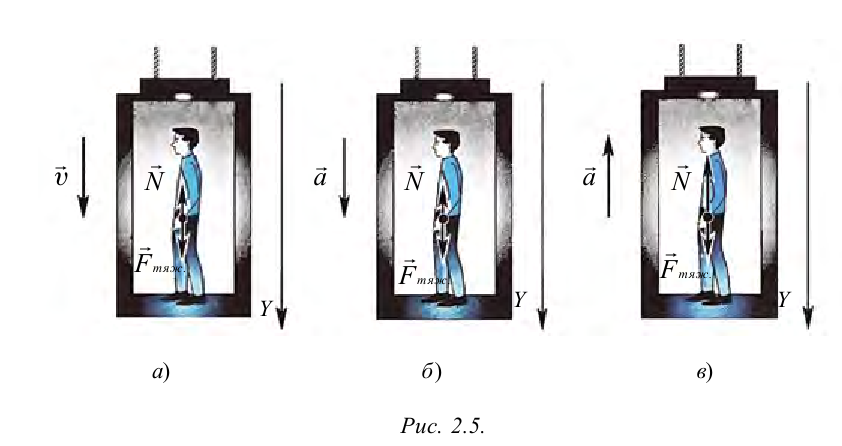
2. Лифт двигается вниз с ускорением 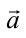 (рис. 2.5 б). Согласно второму закону Ньютона:
(рис. 2.5 б). Согласно второму закону Ньютона:

Здесь 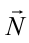 – сила реакции пола лифта,
– сила реакции пола лифта, 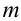 – масса тела.
– масса тела.
По третьему закону Ньютона, вес тела 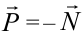 . С учетом формулы (2.7) получаем
. С учетом формулы (2.7) получаем
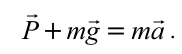
Итоговый вес тела во время движения будет:

Отсюда видно, что когда лифт двигается вниз с ускорением 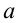 , вес человека уменьшается на величину
, вес человека уменьшается на величину 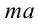 . Если резко освободить трос, который держит лифт, то лифт будет двигаться вниз с ускорением
. Если резко освободить трос, который держит лифт, то лифт будет двигаться вниз с ускорением 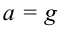 , а вес человека будет:
, а вес человека будет:
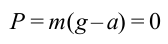
Состояние, при котором сила взаимодействия тела с опорой или подвесом равна нулю, называется невесомостью.
Значит, чтобы тело перешло в невесомое состояние, оно должно двигаться вниз с ускорением 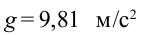 . Отсюда вытекает, что во время свободного падения тела находятся в невесомом состоянии. Частичное состояние невесомости наблюдается при раскачивании на качелях в момент спуска и во время прыжка. Это продолжается очень короткое время. Космонавты, проживающие в искусственных спутниках Земли и на орбитальных станциях, находятся долгое время в состоянии невесомости. В этот период нарушается система кровообращения и питания организма. Для профилактики отрицательных последствий состояния невесомости на орбитальных станциях предпринимаются специальные меры.
. Отсюда вытекает, что во время свободного падения тела находятся в невесомом состоянии. Частичное состояние невесомости наблюдается при раскачивании на качелях в момент спуска и во время прыжка. Это продолжается очень короткое время. Космонавты, проживающие в искусственных спутниках Земли и на орбитальных станциях, находятся долгое время в состоянии невесомости. В этот период нарушается система кровообращения и питания организма. Для профилактики отрицательных последствий состояния невесомости на орбитальных станциях предпринимаются специальные меры.
3. Лифт поднимается вверх с ускорением 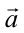 (рис. 2.5в). Воздействие, оказываемое человеком на пол (опору) лифта, равняется:
(рис. 2.5в). Воздействие, оказываемое человеком на пол (опору) лифта, равняется:

Отсюда видно, что при подъеме лифта вверх с ускорением, вес человека увеличивается на величину 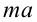 . Это называется дополнительная нагрузка (перегрузка).
. Это называется дополнительная нагрузка (перегрузка).
Перегрузка определяется отношением веса тела при движении с ускорением к весу тела в состоянии покоя:

В этом состоянии полная нагрузка приходится на опору. Однако появляются частичные нагрузки на тело человека. Например, вес головы человека давит на шею, вес головы, шеи, плеч и рук давит на корпус и т.д., к ногам. Если ускорение лифта будет в пределе 0,3 – 1 м/с2 , то человек этого не почувствует. Но в сверхзвуковых самолетах, при взлете ракеты ускорение доходит до 100 м/с2. По рассказам летчиков и космонавтов, которые находились в этом состоянии, перегрузка прижимала их к креслам, поднять руки было очень трудно, даже открыть глаза удавалось с
трудом.
Образец решения задачи:
Лифт опускается вниз с ускорением 4,5 м/с2. Во сколько раз уменьшается вес тела, находящегося в лифте?
Дано:
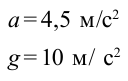
Найти:
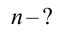
Формула:
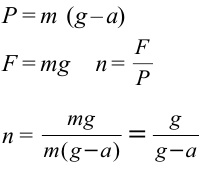
Решение:
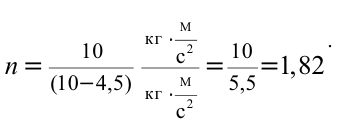
Ответ: 1,82 раза.
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Движение горизонтально брошенного тела
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
Вес тела


4.2
Средняя оценка: 4.2
Всего получено оценок: 101.
Обновлено 16 Июля, 2021
4.2
Средняя оценка: 4.2
Всего получено оценок: 101.
Обновлено 16 Июля, 2021
Понятие «вес тела» очень часто используется в повседневной жизни. Многие продукты и материалы покупаются, исходя из измеренного веса. Как правило, в быту понятие веса отождествляется с понятием массы тела. Однако в физике это не одно и то же. Более того, эти величины не равны. Рассмотрим эту тему подробнее, приведём определение и формулу веса тела.
Вес тела
Чтобы понять физическую природу веса тела, достаточно вспомнить, как происходит взвешивание на пружинных весах. На чашку весов укладывается тело, под действием силы тяжести оно сжимает пружину, и по степени этого сжатия можно судить о том, сколько весит тело.
То есть сила, с которой тело воздействует на опору, называется весом.
Найдём величину этой силы. На тело, имеющее опору, действует сила тяжести $m overrightarrow {mathrm{g}}$ и сила реакции опоры $ overrightarrow {N}$.
По третьему закону Ньютона, тело также действует на опору с равной силой $ overrightarrow {P}= – overrightarrow {N}$ (противоположной по направлению). Эта сила и есть вес тела.
Если опора (и тело вместе с ней) движется вверх с ускорением $ overrightarrow {a}$, то по второму закону Ньютона имеем:
$$overrightarrow {N}+ m overrightarrow {mathrm{g}} = m overrightarrow {a}$$
Учитывая равенство веса и его противоположную направленность относительно реакции опоры, после проецирования на ось координат, направленную вниз, можно записать:
$$P = m (mathrm{g} – a)$$
Это и есть формула веса тела массой $m$, существующего в условиях гравитации (ускорение свободного падения $mathrm{g}$), имеющего опору, которая двигается вверх с ускорением $a$.

Свойства веса тела
Из вышесказанного можно сделать важные выводы.
- Во-первых, как физическая величина, вес является силой. Поэтому единица измерения веса в физике — ньютон.
- Во-вторых, вес — фактически, это проявление сил упругости. Вес появляется в результате взаимодействия тела с опорой.
- В-третьих, вес зависит от ускорения, с которым движется опора. Если опора неподвижна (или движется равномерно и прямолинейно), то вес равен силе тяжести.
Последнее свойство показывает, что вес — это величина непостоянная, и может быть как меньше, так и больше силы тяжести, в зависимости от движения опоры.
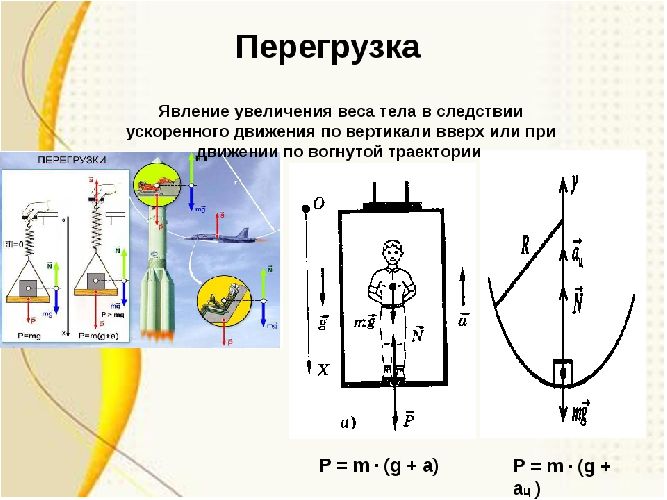
Невесомость и перегрузки
Таким образом, вес без опоры не существует. Говорят, что тело, у которого нет опоры, находится в состоянии невесомости.

Обратите внимание, состояние невесомости не зависит от того, действует ли на тело гравитационная сила или нет. Предмет во время свободного падения, кабина лифта в момент начала спуска, когда натяжение троса исчезло, человек во время прыжка — всё это примеры состояния невесомости, которое появляется, несмотря на действие силы тяжести.
Из формулы веса тела следует, что если опора движется с ускорением, у тела появляется вес, который может быть даже больше, чем сила тяжести. В этом случае говорят о возникновении перегрузок.
Поскольку в формулу веса входит масса и сумма ускорения, перегрузку можно измерять в единицах $mathrm{g}$. Для нахождения перегрузки используется формула:
$$k= {m(mathrm{g} + a) over mmathrm{g}}=1+{aover mathrm{g}}$$
Фактически перегрузка показывает, во сколько раз вес тела больше силы тяжести, действующей на тело на Земле. Перегрузка $k=1$ означает обычный вес тела, перегрузка $k=2$ означает, что вес тела вдвое больше, чем сила тяжести и так далее.

Что мы узнали?
Вес тела — это сила, с которой тело действует на опору. Фактически это проявление силы упругости. Тело, у которого нет опоры, находится в состоянии невесомости. Если опора тела двигается с ускорением, тело испытывает перегрузки.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 101.
А какая ваша оценка?

