Как найти заряд в вершине треугольника

Напряженность и закон Кулона

Закон сохранения электрического заряда

Потенциал электростатического поля

Теория

Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.

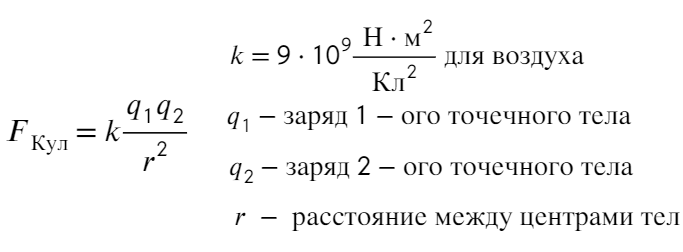
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:

Наглядно рассказывается об этом в видео.
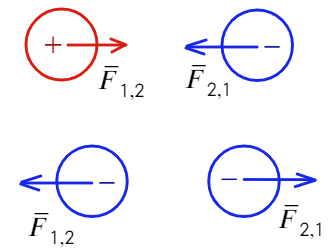
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.

Напряженность НЕ зависит от величины заряда, помещенного в поле!

Задачи

Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F ₁ . Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F ₂ . Определите отношение F ₂ к F ₁ .

Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:

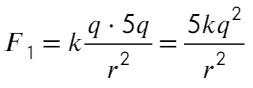
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:

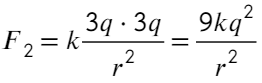
Отношение получится таким:

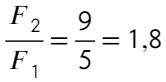
Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F ₁ . Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F ₂ . Определите отношение F ₁ к F ₂ .

Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).

А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:

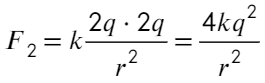
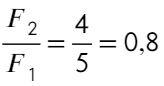
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?

В начальный момент времени на шарик действуют две силы:

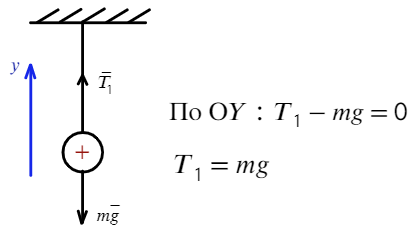а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:

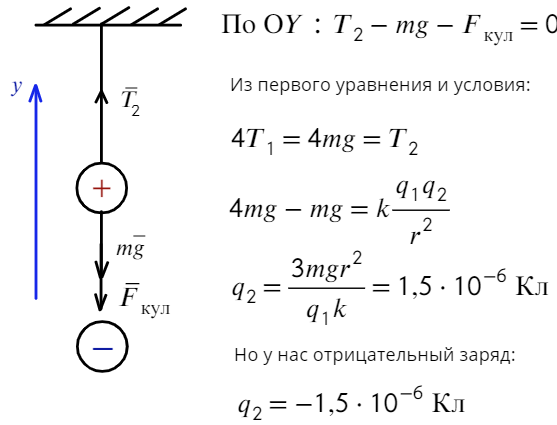б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:

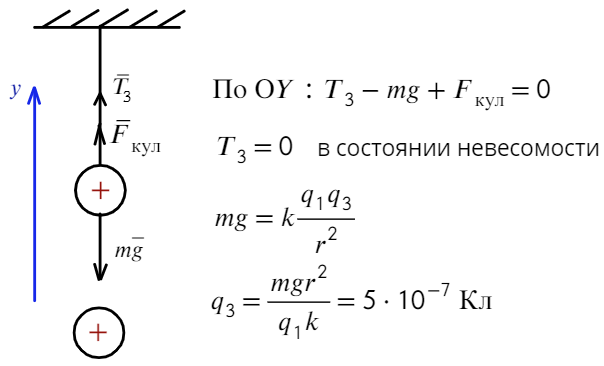Ответ: −1,5 мкКл, 500 нКл.

Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.

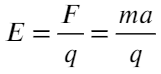
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.

Найдем ускорение электрона в электрическом поле:

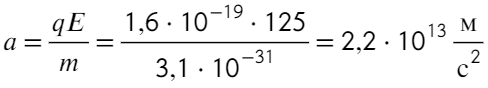
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:

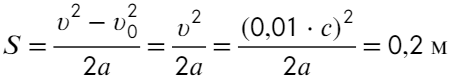
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?

Для начала разберемся, какие силы действуют на заряд:

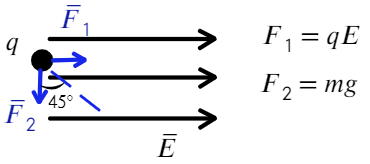
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:

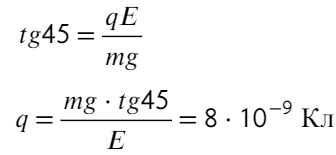
Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10 ⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)

Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:

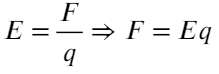
Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:

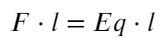
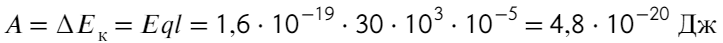
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹

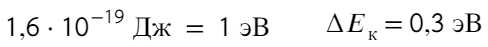
Задача 6 В вершинах равностороннего треугольника со стороной « а » находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.

Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).

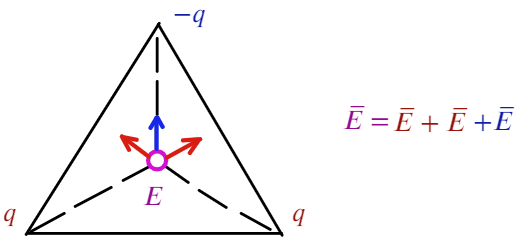
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:

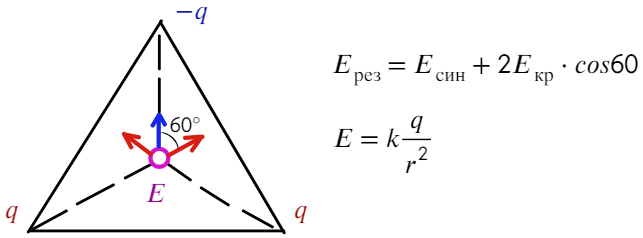
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:

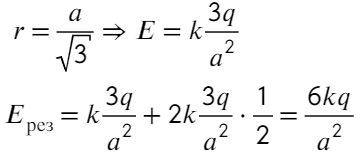
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)

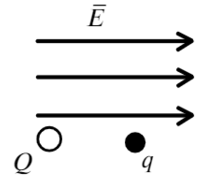
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.

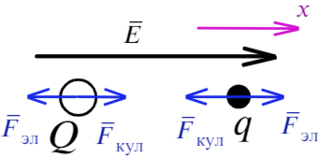
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:

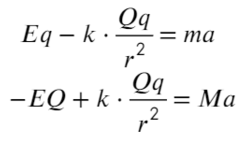
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.

Разделим одно уравнение на другое и выразим массу:

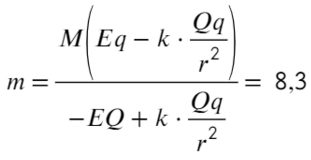
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)

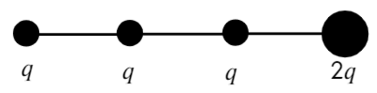
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:

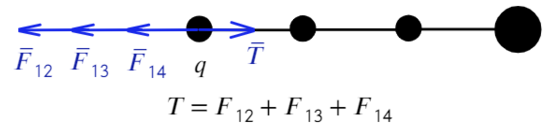
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.

Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:

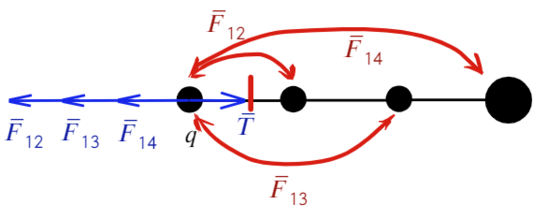
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:

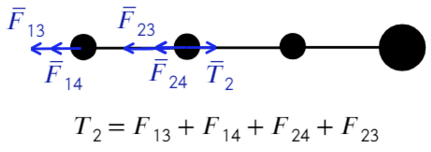
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:

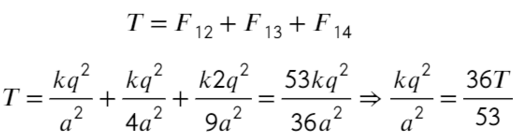
Второе уравнение с подстановкой выражения из первого:

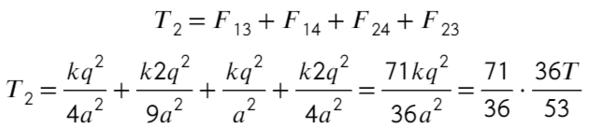
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)

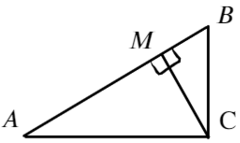
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:

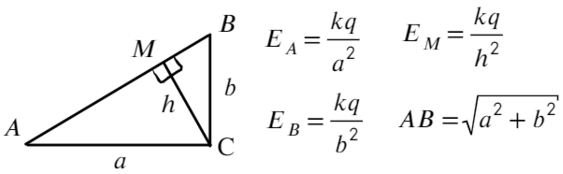
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:

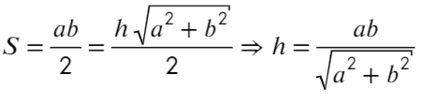
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:

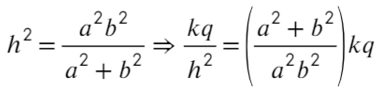
Выразим a² и b² через напряженность:

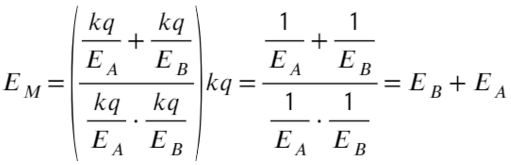
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)

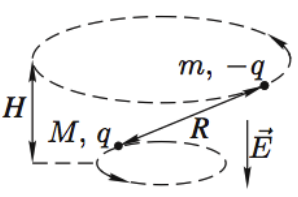Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:

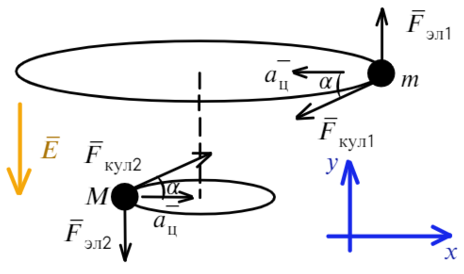
Запишем уравнения по осям на верхнюю частицу:

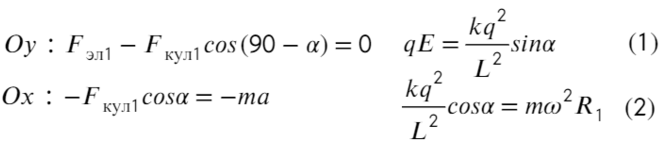
На нижнюю частицу:

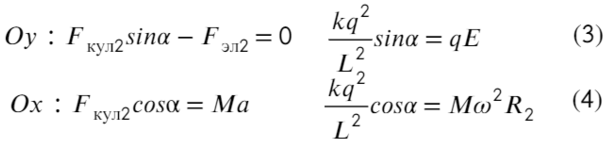
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.

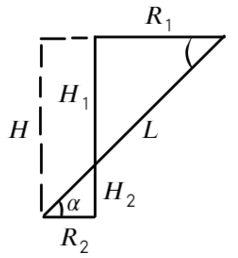
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:

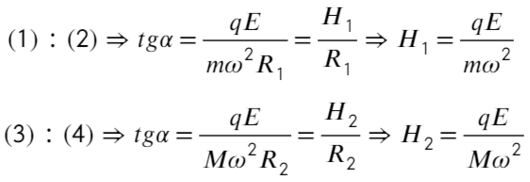
Сложим два уравнения, чтобы найти расстояние между плоскостями:

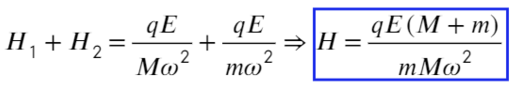
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:

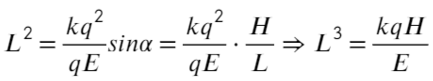
Вместо Н подставим то, что мы нашли:

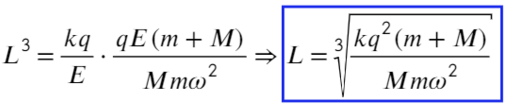
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q ₂ и измеряемый заряд Q ₁ установлены на расстояниях L ₂ и L ₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q ₁ , если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q ₂ и Q ₁ . (Всеросс. 2018)

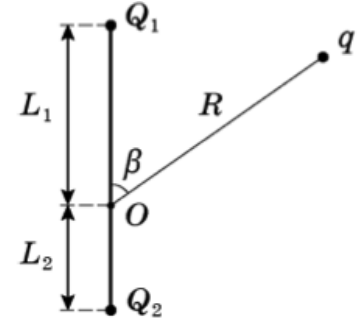
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:

Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:

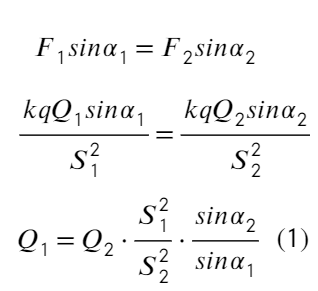
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:

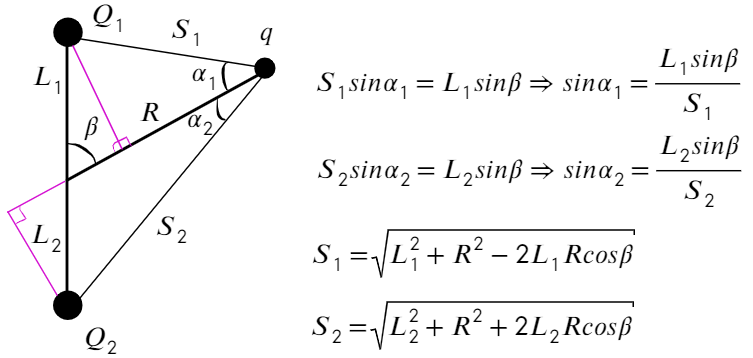
Подставим в ур-ие (1):

В качестве закрепления материала решите несколько похожих задач с ответами.

В вершинах равностороннего треугольника со стороной а находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,084
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Электрическое поле. Напряженность. Линии напряженности

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема данного урока – это изучение вопросов, связанных с понятием электрического поля. Мы познакомимся с очень важной характеристикой электрического поля – напряженностью – и рассмотрим изображение различных электрических полей с помощью силовых линий.

[spoiler title=”источники:”]

http://www.soloby.ru/310113/%D1%80%D0%B0%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D0%BE%D1%80%D0%BE%D0%BD%D0%BD%D0%B5%D0%B3%D0%BE-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0-%D0%BD%D0%B0%D0%BF%D1%80%D1%8F%D0%B6%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0

http://interneturok.ru/lesson/physics/10-klass/osnovy-elektrodinamiki-2/elektricheskoe-pole-napryazhennost-linii-napryazhennosti

[/spoiler]

Спрятать решение

Источник: Гельф­гат И. М. Сбор­ник задач по фи­зи­ке для 10 клас­са, Х.: «Гим­на­зия», 2001 (№ 7.26)

Условие задачи:

Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах равностороннего треугольника. Найти величину точечного заряда, который надо поместить в центре треугольника, чтобы вся система находилась в равновесии?

Задача №6.1.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(q=-1,7) нКл, (Q-?)

Решение задачи:

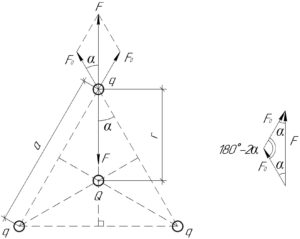Каждый заряд (q) действует на другой такой же заряд с силой отталкивания (F_0), которую можно определить из закона Кулона:

[{F_0} = frac{{k{{left| q right|}^2}}}{{{a^2}}};;;;(1)]

Коэффициент пропорциональности (k) равен 9·10⁹ Н·м²/Кл².

Теперь найдём равнодействующую двух сил (F), с которой два заряда действуют на третий. Для этого воспользуемся принципом независимости действия сил (принципом суперпозиции) и теоремой косинусов (смотри схему к решению).

[{F^2} = F_0^2 + F_0^2 – 2F_0^2 cdot cos left( {180^circ – 2alpha } right)]

Из тригонометрии известно, что:

[cos left( {180^circ – 2alpha } right) = – cos 2alpha ]

Тогда:

[{F^2} = F_0^2 + F_0^2 + 2F_0^2 cdot cos 2alpha ]

Также в равностороннем треугольнике угол (alpha) равен 30°, поэтому:

[{F^2} = F_0^2 + F_0^2 + 2F_0^2 cdot cos 60^circ = 3F_0^2]

[F = sqrt 3 {F_0}]

Учитывая (1), имеем:

[F = frac{{sqrt 3 k{{left| q right|}^2}}}{{{a^2}}};;;;(2)]

Помещенный в центр равностороннего треугольника заряд должен быть положительным, чтобы уравновесить силу (F), при этом силу притяжения можно также найти из закона Кулона:

[F = frac{{kQleft| q right|}}{{{r^2}}}]

Здесь (r) – расстояние от вершины равностороннего треугольника до его центра (центр – это точка пересечения медиан треугольника), его можно найти по такой формуле (за выводом формулы обратитесь к учебнику по математике):

[r = frac{{sqrt 3 a}}{3}]

В таком случае:

[F = frac{{3kQleft| q right|}}{{{a^2}}};;;;(3)]

Осталось только приравнять (2) и (3):

[Q = frac{{left| q right|}}{{sqrt 3 }}]

Посчитаем ответ к задаче:

[Q = frac{{1,7 cdot {{10}^{ – 9}}}}{{sqrt 3 }} = 9,8 cdot {10^{ – 10}};Кл approx 1;нКл]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.1.21 На нити подвешен маленький шарик массой 10 г, которому сообщили заряд 1 мкКл
6.1.23 Две частицы массой 10 г и зарядом 2 мкКл находятся в вершинах равностороннего
6.1.24 В вертикальной трубке, заполненной воздухом, закреплен точечный заряд 5 мкКл

Решение. 
Определим энергию взаимодействия зарядов.

[ begin{align}
  & W={{W}_{12}}+{{W}_{23}}+{{W}_{13}}, {{W}_{12}}=frac{kcdot {{q}_{1}}cdot {{q}_{2}}}{a}, {{W}_{23}}=frac{kcdot {{q}_{2}}cdot {{q}_{3}}}{a}, {{W}_{13}}=frac{kcdot {{q}_{1}}cdot {{q}_{3}}}{a}, \
 & {{q}_{1}}={{q}_{2}}={{q}_{3}},{{W}_{12}}={{W}_{23}}={{W}_{13}} , W=frac{3cdot kcdot {{q}^{2}}}{a}. \
end{align} ]

W = 6,75∙10^-4 Дж.
Найдем потенциал поля φ в центре треугольника. Радиус описанной окружности около равностороннего треугольника определяется по формуле:

[  begin{align}
  & r=frac{a}{sqrt{3}} (1). \
 & varphi ={{varphi }_{1}}+{{varphi }_{2}}+{{varphi }_{3}}, {{varphi }_{1}}={{varphi }_{2}}={{varphi }_{3}}, varphi =3cdot {{varphi }_{1}} \
 & {{varphi }_{1}}=frac{kcdot q}{r}, {{varphi }_{1}}=frac{kcdot qcdot sqrt{3}}{a}, varphi =frac{3cdot kcdot qcdot sqrt{3}}{a}. \
end{align} ]

φ = 2,33∙10⁵ В.
Определим какой заряд q₀ необходимо поместить в точку О, чтобы система зарядов находилась в равновесии. Система будет находится в равновесии когда равнодействующая сила которая действует на заряд который находится в вершине треугольника равна нулю. Покажем рисунок.

[ begin{align}
  & {{{vec{F}}}_{12}}+{{{vec{F}}}_{13}}+{{{vec{F}}}_{10}}=0 (1). \
 & {{{vec{F}}}_{12}}+{{{vec{F}}}_{13}}={{{vec{F}}}_{23}}. \
end{align} ]

Для нахождения равнодействующей силы F₂₃ используем теорему косинусов:

[ begin{align}
  & {{F}_{23}}^{2}=F_{12}^{2}+F_{13}^{2}+2cdot {{F}_{12}}cdot {{F}_{13}}cdot cos alpha , alpha =60{}^circ , \
 & {{F}_{23}}=sqrt{F_{12}^{2}+F_{13}^{2}+2cdot {{F}_{12}}cdot {{F}_{13}}cdot frac{1}{2}} , \
 & {{F}_{12}}=frac{kcdot left| {{q}_{1}} right|cdot left| {{q}_{2}} right|}{{{a}^{2}}}=frac{kcdot {{q}^{2}}}{{{a}^{2}}}, {{F}_{13}}=frac{kcdot left| {{q}_{1}} right|cdot left| {{q}_{3}} right|}{{{a}^{2}}}=frac{kcdot {{q}^{2}}}{{{a}^{2}}}, \
 & {{F}_{23}}=frac{sqrt{3}cdot kcdot {{q}^{2}}}{{{a}^{2}}} (2). \
end{align} ]

[ {{F}_{23}}={{F}_{10}}, frac{sqrt{3}cdot kcdot {{q}^{2}}}{{{a}^{2}}}=frac{kcdot left| {{q}_{0}} right|cdot qcdot 3}{{{a}^{2}}}, {{q}_{0}}=-frac{q}{sqrt{3}}. ]

k = 9∙10⁹ Н∙м² / Кл².
 q₀ = -2,89∙10^-9 Кл.

 

Три шарика, заряженные
равными одноименными зарядами q₀ каждый, расположены в вершинах равностороннего треугольника со
стороной a. Определите напряженность и потенциал электростатического поля
в центре треугольника.

Решение.

Предположим, что шарики
покоятся относительно инерциальной системы отсчета, связанной с лабораторией.

В качестве физической
системы будем рассматривать три заряженных шарика. Если пренебречь
перераспределением зарядов шариков вследствие электростатической индукции, то
их заряды можно считать точечными. Для определения напряженности и потенциала
поля, созданного этими зарядами в центре треугольника, воспользуемся принципом
суперпозиции.

Укажем на схематическом
рисунке направления векторов E₁ , E₂ и E₃ (считая заряды шариков
положительными). Начало координат выберем в центре треугольника, ось OY направим вертикально вниз, ось OX – горизонтально.
Проецируя векторы, изображающие напряженности на оси координат, получим систему
уравнений.

По условию задачи q₁ = q₂ = q₃ = q₀ . Расстояние
между центром треугольника и его вершинами равно r₀ .

Следовательно, E_x =
0.

Так как α = p/6, то sinα = 1/2, т.е. E_y = 0. С учетом этого найдем модуль напряженности
электростатического поля в центре треугольника.

Если нулевой уровень
потенциала выбрать в бесконечности, то найдем потенциалы полей каждого заряда в
центре треугольника.

По принципу
суперпозиции потенциал поля в центре треугольника j.

Ответ: .

Источник: Физика. Полный курс подготовки к ЦТ.  Под общей редакцией проф. В.А. Яковенко.