Скорость, время и высота свободного падения
- Главная
- /
- Физика
- /
- Скорость, время и высота свободного падения
Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Скорость свободного падения
Если известно время падения
Ускорение свободного падения g =
Время падения
t =
Расстояние h =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Если известно расстояние (высота падения)
Ускорение свободного падения g =
Расстояние h =
Время падения
t =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Расстояние и время свободного падения
Ускорение свободного падения g =
Скорость свободного падения
V =/
Расстояние h =
0
Время падения
t =
0
Округление ответа:
Просто введите данные, и получите ответ.
Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.
Теория
Ускорение свободного падения
Ускорение свободного падения (g) – ускорение, которое придаёт падающему телу сила тяжести. У каждого небесного тела своё значение ускорения свободного падения, например, у планеты Земля оно составляет g = 9,80665 м/с².
Для небесных тел солнечной системы ускорение свободного падения имеет следующие значения:
- Земля – 9,80665 м/с²
- Луна – 1,62 м/с²
- Меркурий – 3,7 м/с²
- Венера – 8,87 м/с²
- Марс – 3,711 м/с²
- Сатурн – 10,44 м/с²
- Юпитер – 24,79 м/с²
- Нептун – 11,15 м/с²
- Уран – 8,87 м/с²
- Плутон – 0,617 м/с²
- Ио – 1,796 м/с²
- Европа – 1,315 м/с²
- Ганимед – 1,428 м/с²
- Каллисто – 1,235 м/с²
- Солнце – 274,0 м/с²
Как найти скорость свободного падения
Скорость свободного падения V можно рассчитать, зная расстояние (высоту) падения h или время падения t.
Зная время падения:
Формула
V = g⋅t
Пример
Для примера, рассчитаем с какой скоростью врежется в землю монета, брошенная из окна небоскрёба, если известно, что она упала за 5 секунд:
V = 9.8 ⋅ 5 = 49 м/с
Монетка ударилась об землю на скорости 49 м/с
Зная высоту падения:
Формула
V = √2⋅h⋅g
Пример
Для примера, определим скорость при ударе об землю ядра скинутого с 100 метровой вышки:
V = √2 ⋅ 100 ⋅ 9.8 = √1960 ≈ 44 м/с
Ядро ударится об землю на скорости 44 м/с
Время свободного падения
Время свободного падения – время, которое потребуется телу для того чтоб упасть на землю под действием силы тяжести. Чтобы рассчитать время свободного падения t необходимо знать высоту падения h или скорость в конце падения V.
Зная высоту падения:
Формула
t = √2h⁄g
Пример
Посчитаем чему будет равно время свободного падения t тела упавшего с высоты h = 100 метров:
t = √2⋅100⁄9.8 = √20.4 ≈ 4.5 с
Время свободного падения данного тела составит 4.5 секунды.
Зная скорость в конце падения:
Формула
t = V⁄g
Пример
Если тело после падения ударилось об землю со скоростью V = 50 м/с, то сколько секунд оно падало?
t = 50 ÷ 9.8 = 5.1 с
Время падения данного тела составило 5.1 секунды.
Высота свободного падения
Высота падения – высота с которой сбросили тело, численно равная расстоянию, которое пролетает тело за время падения. Чтобы рассчитать высоту падения h необходимо знать время падения t или скорость в конце падения V.
Зная время падения:
Формула
h = gt²⁄2
Пример
Для примера определим с какой высоты сбросили тело, если известно, что время его падения составило t = 5с:
h = 9.8 ⋅ 5² ÷ 2 = 122.5 м
Тело сбросили с высоты в 122.5 метров.
Зная скорость в конце падения:
Формула
h = V²⁄2g
Пример
Если тело после падения ударилось об землю со скоростью V = 60 м/с, то с какой высоты оно упало?
h = 60² ÷ 2⋅9.8 = 3600 ÷ 19.6 = 183.67 м
Тело упало с высоты в 183.67 метра.
См. также
Как определить скорость тела в момент удара о землю?
Ученик
(231),
на голосовании
8 лет назад
Голосование за лучший ответ
Александра Левина
Профи
(990)
8 лет назад
по закону сохранения энергии Е1=Е2
Е1-мех. энергия тела, когда оно начало падать
Е2-мех. энергия тело в момент удара о землю
Е1=К1+П1 ( в этот момент К1=0, т. к. когда тело начало падать, его скорость равна 0)
П1=mgh
E1=mgh
Е2=К2+П2 (в этот момент П2=0, т. к. высота равна 0)
К2=mv^2/2
E2=mv^2/2
т. к. Е1=Е2 то mgh=mv^2/2
сократим на m: gh=v^2/2
h=v^2/2g= 100^2/2*10=500 м
Unit Converter
Enter the height at which an object is being dropped into the calculator to determine the impact velocity. This calculator can also calculate the height when given the impact velocity.
- Final Velocity Calculator
- Free Fall Velocity Calculator
- Initial Velocity Calculator
- Maximum Height of a Projectile Calculator
- Angle of Impact Calculator
- Falling Force Calculator
- Impact G Force Calculator
- Average Impact Force Calculator
- Force From Height Calculator
Impact Velocity Formula
The following formula is used to calculate an impact velocity.
- Where v is the impact velocity (m/s)
- g is the acceleration due to gravity (9.8 m/s^2)
- h is the height of the object (m)
To calculate impact velocity, multiply the height by 2 times the acceleration due to gravity, then take the square root of the result.
Impact Velocity Definition
An impact velocity is the total speed of an object when it makes an impact with the ground or another object after falling from a certain distance.
Impact Velocity Example
How to calculate impact velocity?
The following example goes over the necessary steps to calculate the impact velocity of a falling object given the height of the object and assuming that there is no air resistance and no other forces acting on the object.
The first step is to determine or measure the height that the object is going to be dropped from.
For this example, the height of the object is 10 meters (m).
The next and last step is to use the formula above to calculate the impact velocity:
v = Sqrt ( 2 * g * h )
v = Sqrt ( 2 * 9.81 * 10 )
v = 14.007 m/s.
FAQ
What is an impact velocity?
An impact velocity is a measure of the speed of an object when it impacts another surface. It’s most often used when analyzing objects that are dropped from a certain height.

Определение скорости свободного падения
Свободное падение тела — это его равнопеременное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист прыгает из самолета, первые несколько секунд после прыжка он падает в свободном состоянии. Этот короткий отрезок времени характеризуется ощущением невесомости, сходным с тедж.м, что испытывают космонавты на борту космического корабля.
История открытия явления
О свободном падении тела ученые узнали еще в Средневековье: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Например, они утверждали, что скорость падающего тяжелого предмета возрастает прямо пропорционально пройденному расстоянию. В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.

В 1590 г. итальянский физик Галилео Галилей сформулировал закон, который устанавливает четкую зависимость пройденного падающим предметом пути от времени. Также ученым было доказано, что при отсутствии воздушного сопротивления все предметы на Земле падают с одинаковым ускорением, хотя до его открытия было принято считать, что тяжелые предметы падают быстрее.
Была открыта новая величина — ускорение свободного падения, которое состоит из двух составляющих: гравитационного и центробежного ускорений. Обозначается ускорение свободного падения буквой g и имеет различное значение для разных точек земного шара: от 9,78 м/с 2 (показатель для экватора) до 9,83 м/с 2 (значение ускорения на полюсах). На точность показателей влияют долгота, широта, время суток и некоторые другие факторы.
Стандартное значение g принято считать равным 9,80665 м/с 2 . В физических расчетах, которые не требуют соблюдения высокой точности, значение ускорения принимают за 9,81 м/с 2 . Для облегчения расчетов допускается принимать значение g равным 10 м/с 2 .
Для того чтобы продемонстрировать, как предмет падает в соответствии с открытием Галилея, ученые устраивают такой опыт: в длинную стеклянную трубку помещают предметы с различной массой, из трубки выкачивают воздух. После этого трубку переворачивают, все предметы под действием силы тяжести падают одновременно на дно трубки, независимо от их массы.
Когда эти же предметы помещены в какую-либо среду, одновременно с силой тяжести на них действует сила сопротивления, поэтому предметы в зависимости от своей массы, формы и плотности будут падать в разное время.
Формулы для расчетов
Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с 2 ).
Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.
Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2 /2.
Формула для определения скорости падающего предмета в конце падения при известном времени падения: u = gt .
Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.

Интересные факты
Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.
В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.
В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.
В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.
Видео
Посмотрите интересное и познавательное видео, которое расскажет вам о скорости падения тел.
Задачи на свободное падение тел: примеры решения задач по кинематике

Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:

Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
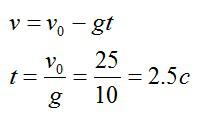
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
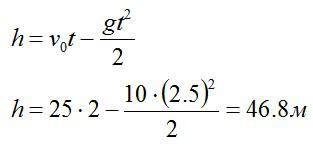
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
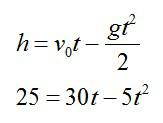
Мы получили квадратное уравнение. Упростим его и найдем корни:
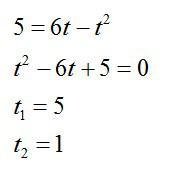
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
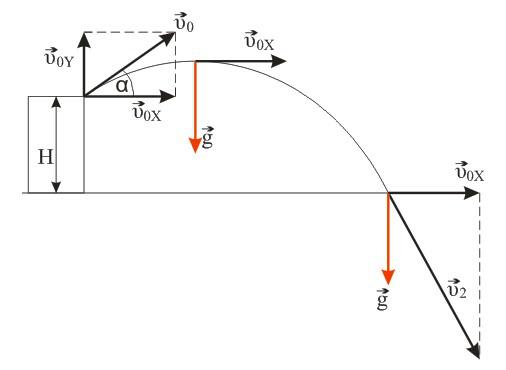
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
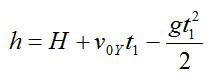
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
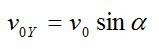
Подставив выражение для скорости в первое уравнение, получим:
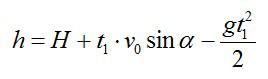
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
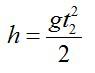
Для высоты дома можно записать:
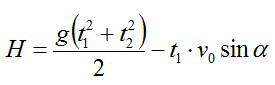
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
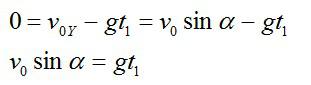
Подставляем в формулу для высоты H и вычисляем:
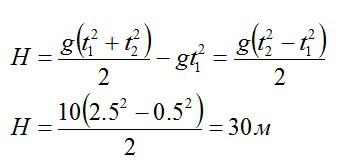
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
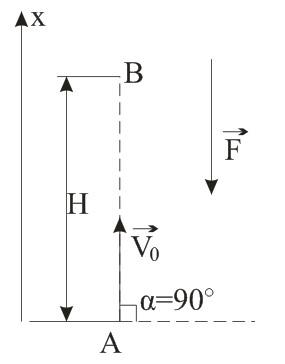
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
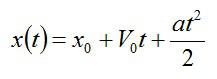
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
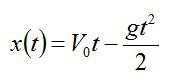
Далее будем использовать еще одно общее кинематическое соотношение:

где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
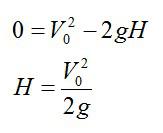
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
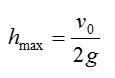
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:

Скорость тела в момент падения с высоты h:
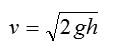
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
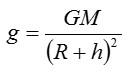
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Конвертер величин
Калькулятор скорости, времени и расстояния при свободном падении

Этот калькулятор определяет скорость и время свободного вертикального падения тела на поверхность Земли или другой планеты, если известна высота, с которой сброшено тело. Сопротивление воздуха не учитывается. Калькулятор может также рассчитать высоту и время падения, если известна скорость, или скорость и высоту, если известно время.
Пример: Рассчитать скорость при ударе об землю тела, сброшенного с высоты 1000 м.
Для расчета введите ускорение свободного падения g или выберите планету и введите одну из трех величин h, t or v в соответствующие поля, выберите британские или метрические единицы и нажмите на кнопку Рассчитать. Будут рассчитаны две другие единицы.

Определения и формулы
В классической механике состояние объекта, который свободно движется в гравитационном поле, называется свободным падением. Если объект падает в атмосфере, на него действует дополнительная сила сопротивления и его движение зависит не только от гравитационного ускорения, но и от его массы, поперечного сечения и других факторов. Однако на тело, падающее в вакууме, действует только одна сила, а именно сила тяжести.
Примерами свободного падения являются космические корабли и спутники на околоземной орбите, потому что на них действует единственная сила — земное притяжение. Планеты, вращающиеся вокруг Солнца, также находятся в свободном падении. Предметы, падающие на землю с небольшой скоростью, также могут считаться свободно падающими, так как в этом случае сопротивление воздуха незначительно и им можно пренебречь. Если единственной силой, действующей на предметы, является сила тяжести, а сопротивление воздуха отсутствует, ускорение одинаково для всех предметов и равно ускорению свободного падения на поверхности Земли 9,8 метров в секунду за секунду second (м/с²) или 32,2 фута в секунду за секунду (фут/ с²). На поверхности других астрономических тел ускорение свободного падения будет другим.

Парашютисты, конечно, говорят, что перед раскрытием парашюта они в свободном падении, но на самом деле в свободном падении парашютист не может быть никогда, даже если парашют еще не раскрыт. Да, на парашютиста в «свободном падении» действует сила притяжения, но на него также действует противоположная сила — сопротивление воздуха, причем сила сопротивления воздуха лишь слегка меньше силы земного притяжения.
Если бы не было сопротивления воздуха, скорость тела, находящегося в свободном падении, каждую секунду увеличивалась бы на 9,8 м/с.
Скорость и расстояние свободно падающего тела вычисляется так:
v₀ — начальная скорость (м/с).
v — конечная вертикальная скорость (м/с).
h₀ — начальная высота (м).
h — высота падения (м).
t — время падения (с).
g — ускорение свободного падения (9,81 м/с² у поверхности Земли).
Если v₀=0 и h₀=0, имеем:

если известно время свободного падения:
если известно расстояние свободного падения:
если известна конечная скорость свободного падения:
Эти формулы и используются в данном калькуляторе свободного падения.
В свободном падении, когда нет силы для поддержания тела, возникает невесомость. Невесомость — это отсутствие внешних сил, действующих на тело со стороны пола, стула, стола и других окружающих предметов. Иными словами — сил реакции опоры. Обычно эти силы действуют в направлении, перпендикулярном поверхности соприкосновения с опорой, и чаще всего вертикально вверх. Невесомость можно сравнить с плаванием в воде, но так, что кожа воду не ощущает. Все знают это ощущение собственного веса, кода выходишь на берег после долгого купания в море. Именно поэтому для имитации невесомости при тренировках космонавтов и астронавтов используются бассейны с водой.
Само по себе гравитационное поле не может создать давление на ваше тело. Поэтому если вы находитесь в состоянии свободного падения в большом объекте (например, в самолете), который также находится в этом состоянии, на ваше тело не действуют никакие внешние силы взаимодействия тела с опорой и возникает ощущение невесомости, почти такое же, как и в воде.

Самолет для тренировок в условиях невесомости предназначен для создания кратковременной невесомости с целью тренировки космонавтов и астронавтов, а также для выполнения различных экспериментов. Такие самолеты использовались и в настоящее время эксплуатируются в нескольких странах. В течение коротких периодов времени, которые длятся около 25 секунд в течение каждой минуты полета самолет находится в состоянии невесомости, то есть для находящихся в нем людей отсутствует реакция опоры.
Для имитации невесомости использовались различные самолеты: в СССР и в Росси для этого с 1961 года использовались модифицированные серийные самолеты Ту-104АК, Ту-134ЛК, Ту-154МЛК и Ил-76МДК. В США астронавты тренировались с 1959 г. на модифицированных AJ-2, C-131, KC-135 и Boeing 727-200. В Европе Национальным центром космических исследований (CNES, Франция) для тренировок в невесомости используют самолет Airbus A310. Модификация заключается в доработке топливной, гидравлической и некоторых других систем с целью обеспечения их нормальной работы в условиях кратковременной невесомости, а также усиления крыльев для того чтобы самолет мог выдерживать повышенные ускорения (до 2G).
Несмотря на то, что иногда при описании условий свободного падения во время космического полета на орбите вокруг Земли говорят об отсутствии гравитации, конечно сила тяжести присутствует в любом космическом аппарате. Что отсутствует, так это вес, то есть сила реакции опоры на объекты, находящиеся в космическом корабле, которые движутся в пространстве с одинаковым ускорением свободного падения, которое только немного меньше, чем на Земле. Например, на околоземной орбите высотой 350 км, на которой Международная космическая станция (МКС) летает вокруг Земли, гравитационное ускорение составляет 8,8 м/с², что всего на 10% меньше, чем на поверхности Земли.
.jpg)
Для описания реального ускорения объекта (обычно летательного аппарата) относительно ускорения свободного падения на поверхности Земли обычно используют особый термин — перегрузка. Если вы лежите, сидите или стоите на земле, на ваше тело действует перегрузка в 1 g (то есть ее нет). Если же вы находитесь в самолете на взлете, вы испытываете перегрузку примерно в 1,5 g. Если тот же самолет выполняет координированный поворот с малым радиусом, то пассажиры, возможно, испытают перегрузку до 2 g, означающую, что их вес удвоился.

Люди привыкли жить в условиях отсутствия перегрузок (1 g), поэтому любая перегрузка сильно влияет на человеческий организм. Как и в самолетах-лабораториях для создания невесомости, в которых все системы, работающие с жидкостями, должны быть модифицированы для того, чтобы они правильно работали в условиях нулевой (невесомость) и даже отрицательной перегрузки, люди также нуждаются в помощи и аналогичной «модификации», чтобы выжить в таких условиях. Нетренированный человек может потерять сознание при перегрузке 3–5 g (в зависимости от направления действия перегрузки), так как такая перегрузка достаточна для того, чтоб лишить мозг кислорода, потому что сердце не может подать в него достаточно крови. В связи с этим военные пилоты и космонавты тренируются на центрифугах в условиях высоких перегрузок, чтобы предотвратить потерю сознания при них. Для предотвращения кратковременной потери зрения и сознания, которые, по условиям работы, могут оказаться фатальными, пилоты, космонавты и астронавты надевают высотно-компенсирующие костюмы, который ограничивает отток крови от мозга во время перегрузок путем обеспечения равномерного давления на всю поверхность тела человека.
|
Какова будет скорость тела при ударе об землю? Сопротивлением воздуха пренебрегать нельзя! Поясню, в чем проблема, для тех кто не понимает. Обычно в школе мы решаем такие задачи через ускорение свободного падения g при условии отсутствия сопротивления воздуха. А что произойдёт, если его учесть? И главное, как учесть? Есть экспертное мнение, что пролетев определённое расстояние, скорость тела станет постоянной. Весь вопрос – чему она будет равна? Я знаю, что такие задачи решают артиллеристы, это реальная задача на полет снаряда. Но это военная область, и формулы секретные для штатских лиц. Во всяком случае, ни в школе, ни в институте такое не проходят. Может быть, кто-нибудь откроет тайну? бонус за лучший ответ (выдан): 20 кредитов
Если посмотреть, какими задачами по теме свободного падения тела наполнен интернет, то окажется, что все они относятся к школьному курсу. Потому что в их условиях пишется “сопротивлением воздуха следует пренебречь” и они, прекрасно решаются согласно закону сохранения энергии. Кинетическая энергия Ек равна потенциальной Еп.
И получается, что, падая с высоты 1000 м, тело любой массы достигает Земли со скоростью 140 м/c. Чтобы было бы, если с высоты 3000 м падали капли дождя и градины со скоростью 242 м/c, всем понятно. Ну, а метеоритный дождь, если бы он не тормозился и не сгорал от трения в атмосфере, просто оставлял выжженными огромные участки поверхности на Земле. Однако, сопротивление воздуха ограничивает скорость падения тел при достижении ими определённой скорости. Так мелкие капли моросящего дождя, перемещаясь в ламинарный потоке, достигают своей предельной скорости, равной всего около 1 м/c. Крупные тела, не являющиеся сферическими, площадь поперечного сечения S которых зависит от ориентации тела относительно набегающего потока воздуха, испытывают такое же сопротивление, как снаряды и пули:
Откуда скорость равна:
где Схо – аэродинамический коэффициент лобового сопротивления тела. Например, парашютисты могут изменять в свободном падении S и Схо своего тела. Ныряя “солдатиком”, они развивают максимальную скорость 67 м/с (240 км/ч), а раскинув руки, падая плашмя, – 53 м/с (190 км/ч). Что же касается “секретных формул”, то они остались в секретных тетрадях лекций по баллистике, в стенах учреждения, где её преподавали наряду с высшей математикой, поэтому можно привести то, что находится в общем доступе. Нахождение предельной скорости сводилось к решению дифференциальных уравнений. Сила сопротивления воздуха от скорости v была представлена формулой:
И, насколько помнится, секретность заключалась в точном значении величины (0,0096). Далее по закону Ньютона F = ma составляется уравнение:
Откуда следует:
Зависимость dv/dt=f(v) представляет собой решение задачи Коши c начальным условием v(0)=0. Когда сопротивление воздуха уравновесит силу тяжести, то f(v) станет равна 0, тогда и будет достигнута предельная скорость падения:
Пример решения аналогичной задачи (парашютист прыгает с вертолёта) методом Рунге-Кутты есть в книге “Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB” (стр. 208). Конечно, в годы учёбы ни о каких программах, как “компьютерная процедура Solve” речи не шло, всё “лопатили” в ручную. автор вопроса выбрал этот ответ лучшим
Чтобы ответ был более конкретным и корректным, неплохо бы задать в условиях форму и размеры тела (или форму и его объемную плотность). В общем случае, тело массы m движется с переменным (уменьшающимся) ускорением под действием двух сил: постоянной силы тяжести Р=mg, направленной вниз, и силы сопротивления воздуха F, увеличивающейся c нарастанием скорости, и направленной вверх. По мере роста скорости падения, сила F быстро растет (по квадратичному закону), становится равной по модулю силе Р, скорость стабилизируется, и дальше тело падает равномерно. Такая скорость называется установшейся, или предельной. Опять-же, в общем случае предельная скорость равна:
где Р=mg – сила тяжести cx – аэродинамический безразмерный коэффициент, зависящий от формы падающего тела ρ – плотность среды (т.е. воздуха в тропосфере) S – площадь проекции падающего тела на плоскость, перпендикулярную линии падения vvastro 5 лет назад Чтобы учесть сопротивление воздуха надо знать:
Например, 1 кг плоского листа и авиабомба в 1 кг ударяться о землю с большой вероятностью с на порядки разной скоростью, тем более лист у земли может спланировать, так что вертикальная составляющая скорости будет на удивление малой, но зато в направлении удара может приблизится к скорости авиабомбы. Заостренный штырь с небольшим оперением на “хвосте” намного обгонит авиабомбу. Артиллерийские формулы вам не подойдут – там на порядки большее начальное ускорение, а кроме того снаряды разрабатываются такой формы, чтоб воздух оказывал минимальное сопротивление, которым можно максимально пренебречь. А на излете скорость снаряда нет смысла считать: пробивная способность будет, ясно, незначительной, а для фугаса вообще не важной – там главное мощность заряда. Grisha2018 5 лет назад Зависит от формы тела. Сила сопротивления воздуха F=c*p*v^2*S/2, где с- коэффициент сопротивления формы, который зависит от формы тела (например для сферы с=0.47, а для парашюта с круглым куполом с=0,9), р – плотность среды (в данном случае воздуха р= 1,225 кг/м^3), v – скорость тела, S – площадь тела перпендикулярно потоку воздуха. Таким образом на тело действует две силы, сила тяжести и сила сопротивление воздуха. Применяем второй закон Ньютона (сила есть масса на ускорение, F=ma). Ускорение производная от скорости. Получаем дифференциальное уравнение m*v’=-mg+c*p*v^2*S/2 (m – масса тела, g=9,8 – ускорение свободного падения), v(0)=0 (начальная скорость равна нулю, если я правильно понял задачу). Решаем v=-sqrt{2gm/cpS}th(2sqrt{cpSg/2m}t), где sqrt – квадратный корень, th – гиперболический тангенс, t – время (скорость отрицательная, поскольку ось координат направлена вверх). При стремлении t к бесконечности (т.е. при затяжном падении) скорость равна sqrt{2gm/cpS}. Это и есть та “постоянная” скорость. Теперь нужно знать время падения. Либо эмпирически проверяем. Либо интегрируем правую часть по t, учитываем Ваши начальные условия x(0)=1000. Находим t.
Alfred Teplov 5 лет назад “Опять-же, в общем случае предельная скорость равна:…” (формула Juga [15.2K] почему-то не скопировалась). Думаю, что эта формула чисто эмпирическая. Предназначена только для тела определенной формы и с определенной плотностью. И вообще,задача, поставленная в той форме вопроса, который мы имеем, не может иметь определенного решения. Даже, зная S, вы все равно ничего не определите, т.к. на хвосте тело может иметь или небольшой парашютик, или иметь какие-либо, неровности, выпуклости, шероховатости и даже какие-то лопасти, которые не оказывают никакого влияния на величину S, но скорость тела в воздушной среде могут изменять очень даже существенно. Знаете ответ? |








