1. Расположите листья (или другие объекты) в порядке нарастания их длины, измерьте длину листовой пластинки;
На основании вариационного ряда строится вариационная кривая — графическое отображение частоты встречаемости каждой варианты Частота встречаемости отдельных вариант обозначается буквой p. Например, если взять 100 колосьев пшеницы (n) и подсчитать число колосков в колосе, то это количество будет от 14 до 20 — это численное значение вариант (v).
Вариационный ряд:
v = 14 15 16 17 18 19 20
Частота встречаемости каждой варианты
p = 2 7 22 32 24 8 5
Среднее значение признака встречается чаще, а вариации, значительно отличающиеся от него, — значительно реже. Это называется нормальным распределением.
Кривая на графике бывает, как правило, симметричной. Вариации, как большие, чем средние, так и меньшие, встречаются одинаково часто
ВЫВОД: Среднее значение признака встречается чаще, а вариации, значительно отличающиеся от него, — значительно реже. Это называется нормальным распределением. Кривая на графике бывает, как правило, симметричной. Вариации, как большие, чем средние, так и меньшие, встречаются одинаково часто
Вычисление частоты генотипов в популяции с использованием формул первого и второго закона Харди-Вайнберга
Задача 81.
У озимой ржи антоциановая (красно-фиолетовая) окраска всходов определяется доминантной аллелью (А), 3еленая – рецессивной (а).Н а участке площадью
1000 м2 произрастает 322000 растений, из них 78890 имеют зеленую окраску всходов. Какова частота встречаемости аллеля (а) в данной популяции? Каково количество гомозиготных и гетерозиготных растений?
Решение:
(А) – алель гена красно-фиолетовой окраски растения;
(а) – алель гена зеленой окраски растения;
(АА) – гомозигота – красно-фиолетовая окраска растения;
(Аа) – гетерозигота – красно-фиолетовая окраска растения;
(аа) – рецессивная гомозигота – зеленая окраска растения;
p2 – доля растений с генотипом (АА);
2pq – доля растений с генотипом (Аа);
q2 – доля растений с генотипом (аа);
р – частота встречаемости аллеля (А);
q – частота встречаемости аллеля (а).
1. Нам нужно рассчитать долю растений с генотипом (аа) от общего количества всех растений ржи, получим:
q2 = 78890/322000 = 0,245.
2. Находим частоту встречаемости аллеля (а). Согласно формуле Харди-Вайнберга:
р2 + 2рq + q2 = 1
Отсюда
q2 = 0,245
Тогда
q = 0,495
3. Находим частоту встречаемости аллеля (а). Согласно формуле Харди-Вайнберга:
р + q = 1
р = 1 – 0,495 = 0,505.
4. Рассчитаем долю генотипов среди растений ржи, получим:
р2 + 2рq + q2 = 1;
(0,505)2 + (2 . 0,505 . 0,495) + (0,495)2 = 1;
0,255(АА) + 0,5(Аа) + 0,245(аа) = 1.
5. Рассчитаем количество гомозиготных растений, получим:
N(AA) = 0,255 . 322000 = 82110 гомозиготных растений ржи.
6. Рассчитаем количество гетерозиготных растений, получим:
N(Aа) = 0,5 . 322000 = 161000 гетерозиготных растений ржи.
Ответ: q = 0,495; N(AA) = 82110 гомозиготных растений; N(Aа) = 161000 гетерозиготных растений.
Задача 82.
У подсолнечника наличие панцирного слоя в семянке доминирует над отсутствием его и наследуется моногенно. При апробации установлено, что из 10000 семянок 384 не имеют панцирного слоя. Каков процентный состав генотипов растений в популяции подсолнечника?
Решение:
(А) – алель гена панцирного слоя в семянке подсолнечника;
(а) – алель гена отсутствия панцирного слоя в семянке подсолнечника;
(АА) – гомозигота – наличие панцирного слоя в семянке;
(Аа) – гетерозигота – наличие панцирного слоя в семянке;
(аа) – рецессивная гомозигота – отсутствие панцирного слоя в семянке;
p2 – доля растений с генотипом (АА);
2pq – доля растений с генотипом (Аа);
q2 – доля растений с генотипом (аа);
р – частота встречаемости аллеля (А);
q – частота встречаемости аллеля (а).
Формулы Харди-Вайнберга имеют вид:
1) Сумма частот аллелей одного гена в популяции:
p + q = 1, где
p – частота доминантного аллеля А, q – частота рецессивного аллеля а. Обе величины обычно принято выражать в долях единицы, реже – в процентах (тогда p + q = 100 %).
2) Формула для вычисления частот генотипов в популяции:
p2 + 2pq + q2 = 1, где
p2 – частота гомозиготных особей по доминантному аллелю (генотип АА), 2pq – частота гетерозигот (генотип Аa), q2 – частота гомозиготных особей по рецессивному аллелю (генотип аа).
Общаяя численность всех семянок нам известна 10000, а в частях это будет равно 1, то доля гомозиготных рецессивных семянок (аа) равная q2, которых всего 384 семянок, составит q2 = (384 : 10000) = 0,0384 или 3,84%, тогда q = 0,196; p = 1 – q = 1 – 0,196 = 0,804,
тогда 2pq(Аа) = 2 . 0,804 . 0,196 = 0,3152 или 31,52% и р2(АА) = (0,804)2 = 0,6464 или 64,64%.
Ответ: р2(АА) = 64,64%; 2pq(Аа) = 31,52%; q2 = 3,84%.
Задача 83.
У дикорастущей земляники красная окраска ягод доминирует над розовой. В популяции земляники 3% растений земляники из 9860 имеют розовую окраску ягод. Каково процентное содержание доминантных гомозигот и гетерозигот в данной панмиктической популяции?
Решение:
(А) – алель гена красной окраски ягод земляники;
(а) – алель гена розовой окраски ягод земляники;
(АА) – гомозигота – красная окраска ягод;
(Аа) – гетерозигота – красная окраска ягод;
(аа) – рецессивная гомозигота – розовая окраска ягод;
p2 – доля растений с генотипом (АА);
2pq – доля растений с генотипом (Аа);
q2 – доля растений с генотипом (аа);
р – частота встречаемости аллеля (А);
q – частота встречаемости аллеля (а).
Формулы Харди-Вайнберга имеют вид:
1) Сумма частот аллелей одного гена в популяции:
p + q = 1, где
p – частота доминантного аллеля А, q – частота рецессивного аллеля а. Обе величины обычно принято выражать в долях единицы, реже – в процентах (тогда p + q = 100 %).
2) Формула для вычисления частот генотипов в популяции:
p2 + 2pq + q2 = 1, где
p2 – частота гомозиготных особей по доминантному аллелю (генотип АА), 2pq – частота гетерозигот (генотип Аa), q2 – частота гомозиготных особей по рецессивному аллелю (генотип аа).
1. Выражаем частоту встречаемости рецессивной гомозиготы в процентах:
аа – 3%, или 0,03
2. Согласно закону Харди-Вайнберга вычислим частоты встречаемости аллелей (а) и (А), получим:
q2 = 0,03, q = 0,17;
р + q = 1, р = 1 – q = 1 – 0,17 = 0,83.
3. По формуле Харди-Вайнберга рассчитаем процентное содержание генотипов, получим:
p2(АА) + 2pq(Аа) + q2(аа) = 1;
(0,83)2 + (2 . 0,83 . 0,17) + ( 0,17)2 = 1;
[0,6889 или 69%(АА)] + [0,2822 или 28%(Аа)] + [0,03 или 3%(аа)] = 1.
Ответ: p2(АА) = 69%, 2pq(Аа) = 28%.
Introduction
The population of plant species in any geographical region can be determined by understanding the plant population frequency. Frequency is the degree of uniformity for plant species’ individual occurrences. It is a bit hard to determine the plant population in large areas. The quadrat method is used to know the frequency of plant population.
What is the Quadrat Method?
Quadrat means a sample plot sized specifically to study a community or population. Quadrats have heavy usage in botanical purposes like plant density, plant biomass, and plant frequency determination. Quadrats’ shapes and sizes control the frequency. Metre-square quadrats are generally used for herbaceous vegetation. The quadrat method is a popular technique to determine frequency variations in plant populations.
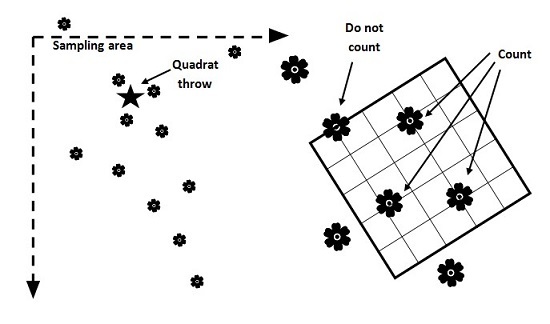
Figure 1: Quadrat Method
Plant Population Frequency in Quadrat Method
Plant population varies in different geographical locations and in different ecosystems. The frequency is the percentage ratio of plant species count in quadrats and number of sample quadrats. In the experiment results, the frequency value denotes how many times the plant species is present for a given count of sample quadrats.
Experiment Objectives
The objective of this experiment is to study the frequency of plant population with the help of the quadrat method.
Required Materials
Three materials are mandatory for this experiment. The materials required for this observation are
-
Nails
-
Hammer
-
Thread
Required Procedure
In biology, the frequency of plant population is studied with the help of the quadrat method. There are two types of procedures applicable to this method. The experiment is done both online and offline. The offline procedure is called real lab procedure and the online procedure is called simulator procedure. Both of them are discussed below.
Real Lab Procedure
-
In this process, the nails should be firmly hammered in the soil so that no damage could occur to vegetation.
-
Two pairs of nails need to be fixed to make a square shape.
-
The square-shaped quadrats’ dimension is 1 m x 1 m and to do this a thread needs to be used to tie each nail end.
-
In the same process 9 more quadrats needs to be prepared.
-
Then the plant species needs to be selected for the population frequency study.
-
Species A’s presence in this experiment needs to be observed in the first quadrat and it needs to be marked in the observation table.
-
In the same way, the other nine quadrats need to be checked carefully whether species A is present there or not. The output data needs to be entered in respective fields.
-
Then all the quadrats again need to be observed for the presence of species B and the results should be noted on the observation table in the same way.
-
This process should be repeated for species C and also the responses need to be marked on the table.
-
The following formula needs to be applied to determine plant population frequency Percentage Frequency=(Number of sampling units in which the species occurs)/(Total number of sampling units employed for the study)*100.
Simulator Procedure
Online labs are used to virtually perform this quadrat method. The steps required for the simulator procedure are mentioned below.
-
Each quadrat has its corresponding pop-up. The view can be enlarged by clicking on them.
-
The preferred study environment can be chosen from the select the environment dropdown menu.
-
Then the observations of plant species’ presence need to be noted down.
-
In the worksheet, the results need to be marked either with Y or N for the presence or absence of particular plants respectively.
-
Revert to the normal view by clicking the back button.
-
The population frequency for each plant species is determined by the entered values.
-
The reset option helps to perform this experiment again.
Observation
The following results can be observed from the above experiment. The plant species A, B and C are taken in the experiment and their presence in quadrats is taken as a sample here. Species A is observed in five random quadrats out of ten quadrats, therefore the quadrat count will be written as 5 and the frequency percentage will be 5/10*100=50. Similarly, for species B and C, if the number of quadrat count is 1 and 4, the frequency will be 10% AND 40% respectively.
Experiment Outcomes
The experiment gives a clear understanding of the term quadrat method. Students can get a clear knowledge of plant population frequency calculation. Better experiments can be done in real labs with simulation and animation.
Conclusion
The plant population is an important factor in ecosystems. Plant population frequency knowledge is necessary to know the status of the environment. The quadrat method is known to be the easiest method to know the frequency. The experiment is done through several steps using some materials. The above experiment shows the highest frequency in species A and the lowest frequency in species B. This way, the frequency differences of various plant populations can be determined.
FAQs
Q1. What is meant by plant population frequency?
Ans. Frequency is the count of times a specified aspect can occur per unit time. The plant population frequency means the presence of particular plant species found out of the total number of plants taken for sampling.
Q2. How plant population frequency is calculated?
Ans. Plant population frequency is calculated by using the following formula.
Percentage Frequency = (Number of Sampling Units in which species occur) / (Total Number of Sampling Units Employed for the Study) * 100.
Q3. How frequency variation occurs in plants?
Ans. The frequency means the count of differences of plant species in a particular region at a certain time in comparison to the total number of plants in that region. Various controlling factors cause variation in frequency. They are soil conditions, soil quality, vegetation propagation, diseases, grazing, biotic activities, topography, area habitat, atmospheric conditions, and environmental conditions.
Интерактив: Модификационная
изменчивость. Построение модели вариационной кривой любого признака (на примере
листьев лавра, 100 шт.).
Изучить методику построения вариационной
кривой на примере размеров семян тыквы, и выполнить свое задание.
1.
Расположите листья (или другие объекты) в порядке нарастания их
длины, измерьте длину листовой пластинки;

2.
Определим частоту встречаемости разных вариант. Мы измерили длину
каждого листа. Занесём в таблицу наши измерения. Итак, 1 лист имел длину 43 мм;
1- 45 мм; 2 листа 48 мм; 6 листов имели длину 53 мм; 3 – 56 мм и 1 лист 58 мм.

3.
Обнаружили, что чаще всего встречаются варианты со
среднимзначением длинны, реже с большей или меньшей длинной. Также
модификационную изменчивость данного признака можно представить в виде графика.

ВЫВОД: Причина такого
распределения вариант в вариационном ряду опять же внешняя среда и реакция на
неё, организма. Чем однообразнее условия развития, тем меньше выражена
модификационная изменчивость, тем короче будет вариационный ряд. А чем
разнообразнее условия среды, тем шире модификационная изменчивость. Также
изменчивость вариаций зависит и от генотипа.
В качестве примера определим среднюю величину семян тыквы
одного сорта. Измерим длину (в мм) 50 взятых произвольно семян.
|
12 |
11 |
10 |
9 |
14 |
16 |
9 |
11 |
14 |
13 |
|
13 |
14 |
8 |
15 |
16 |
15 |
10 |
15 |
16 |
17 |
|
12 |
11 |
9 |
13 |
14 |
17 |
13 |
16 |
12 |
16 |
|
10 |
15 |
12 |
17 |
15 |
14 |
10 |
15 |
13 |
17 |
|
14 |
15 |
13 |
18 |
14 |
12 |
16 |
19 |
18 |
11 |
Расположим числа, отображающие последовательное изменение
признака, в порядке его увеличения: от самого малого до самого большого. Каждая
величина семени в ряду представляет собой варианту. Если расположить все
значения величины семян в порядке их возрастания, то получится вариационный
ряд.
Для определения предела
изменчивости признака определим частоту встречаемости каждой варианты.
Подсчитаем количество семян, имеющих одинаковую величину. Составим на основе
данных первый ряд чисел, отображающий величину изменения признака, и второй ряд
чисел, соответствующий частоте встречаемости этих изменений (количество семян
каждой величины).
|
Величинв семян (мм) |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
Частота встречаемости признаков |
I |
III |
IV |
IV |
V |
VI |
VII |
VII |
VI |
IV |
II |
I |
Таблица отражает распределение частоты встречаемости признака в
зависимости от величины. Представим полученные результаты в виде графика. Для
этого на оси абсцисс отложим значение отдельных вариант (величину семян), по
оси ординат – числа, соответствующие частотам встречаемости каждой варианты
(признака). Соединив точки на графике, получим кривую, которая является
графическим выражением изменчивости признака. Вариационная кривая – это
графическое выражение характера изменчивости признака, которая отражает размах
вариаций и частоту встречаемости вариант (рис. 1).

Из графика видно, что варианты со средним значением встречаются наиболее
часто. Варианты с двумя крайними значениями встречаются наиболее редко.
Они являются отклонениями от средней величины нормы. Чем сильнее
отклонение, тем меньше частота встречаемости варианты.
Для объективной
характеристики изменчивости признака определяется среднее значение по формуле:
M = ∑ ( • ) / n,
где M – средняя величина; ∑ – знак
суммирования; – варианта; – частота
встречаемости вариант; n – общее число вариант
вариационного ряда.
Определим среднее значение величины семян тыквы, исходя из данных,
приведенных в таблице.
|
|
|
( • ) |
|
8 |
1 |
8 |
|
9 |
2 |
27 |
|
10 |
4 |
40 |
|
11 |
5 |
44 |
|
12 |
6 |
60 |
|
13 |
7 |
78 |
|
14 |
7 |
98 |
|
15 |
6 |
105 |
|
16 |
4 |
96 |
|
17 |
2 |
68 |
|
18 |
1 |
36 |
|
19 |
19 |
|
|
n= 50 |
∑ = 679 |
M =.679 : 50 = 13,58
Средней величине признака на графике соответствует
самая высокая точка.
Комбинативная изменчивость
– это изменчивость потомства, обусловленная возникновением новых сочетаний
(комбинаций) генов родителей.
Источниками комбинативной
изменчивости являются: кроссинговер, независимое расхождение хромосом в анафазе
I мейоза, случайное сочетание гамет при оплодотворении. Первые два процесса
обеспечивают образование гамет с разными комбинациями генов. Случайное слияние
гамет приводит к образованию зигот с различными сочетаниями генов обоих
родителей. В результате у гибридов появляются новые комбинации родительских
признаков, а также новые признаки, которых не было у родителей. Структура генов
при этом не изменяется.
Примером комбинативной
изменчивости может служить рождение детей с I или IV группой крови у
гетерозиготных родителей, имеющих II и III группы крови (у потомков появились
новые признаки, отличные от родительских). Другим примером может быть появление
мух с серым телом, зачаточными крыльями и с черным телом, нормальными крыльями
при скрещивании дигетерозиготной дрозофилы (серое тело, нормальные крылья) с
черным самцом, имеющим зачаточные крылья. В данном случае у потомства
вследствие кроссинговера возникли новые сочетания признаков родителей.
Рекомбинантная структура
(англ. Recombinant structure) — гибридная (англ. recombination — рекомбинация)
нуклеиновая кислота (ДНК или РНК) или белок, полученные в результате
объединения in vitro чужеродных фрагментов и содержащие новые сочетания
последовательностей нуклеотидов или аминокислот соответственно.
Мутационная изменчивость
связана с возникновением мутаций. Мутации (лат. mutatio – изменение) –
внезапные, возникающие спонтанно или вызванные мутагенами наследуемые изменения
генетического материала, приводящие к изменению тех или иных признаков
организма.
В основе возникновения
мутационной изменчивости лежат изменения генетического материала: меняется
структура генов, строение или количество хромосом. Комбинативная изменчивость
обусловлена возникновением у потомства новых сочетаний родительских генов, при
этом структура генов, строение и количество хромосом остаются неизменными.
Мутации, в
отличие от модификаций:
•
наследуются;
•
не развиваются постепенно, а возникают внезапно;
•
не образуют непрерывных рядов изменчивости и не имеют нормы
реакции;
•
являются ненаправленными (неопределенными);
•
проявляются индивидуально, а не носят массовый характер.
Общее: оба вида изменчивости
обусловлены изменениями в генетическом материале.
Отличия: комбинативная
изменчивость возникает из-за рекомбинации генов во время слияния гамет, а
мутационная вызвана действием на организм мутагенов.
Модификационная (фенотипическая)
изменчивость — изменения в организме, связанные с изменение фенотипа
вследствие влияния окружающей среды и носящие, в большинстве случаев,
адаптивный характер. Генотип при этом не изменяется. В целом современное
понятие «адаптивные модификации» соответствует понятию «определенной
изменчивости», которое ввел в науку Чарльз Дарвин.
Вариационный ряд —
ряд модификационной изменчивости свойства организма, который состоит из
отдельных свойств видоизменений, размещенных в порядке увеличения или
уменьшения количественного выражения свойства (размеры листка, изменение
интенсивности роста и т.д.
Алгоритм построения вариационного ряда и установления предела изменчивости на примере размера семян тыквы:
- Измеряем длину семян от вершины до основания. Все данные записываем в ряд.
2. Располагаем данные числа в порядке увеличения.
3. Определяем частоту встречаемости каждой варианты. Для этого подсчитываем количество семян, имеющих одинаковую длину, и записываем данные в таблицу.
4. На основании данных таблицы строим вариационную кривую: по оси абцисс отмечаем длину семян, по оси ординат – частоту встречаемости. Соединяем точки на графике.
5. Анализируем график. Максимальная возможная величина семян тыквы равна 19 мм, минимальная — 8 мм, средняя — 13-14 мм. Варианты со средним значением встречаются чаще, а с крайними – реже. Они являются отклонениями от нормы – от среднего значения. Чем сильнее отклонение, тем меньше частота встречаемости.
Чтобы точно определить среднее значение изменчивости признака, нужно высчитать его по формуле:
M=Ʃ(ʋ х p)/n,
где M – среднее значение, Ʃ – знак суммирования, ʋ — значение варианты, p – частота встречаемости этой варианты, n – общее число вариант ряда. Это формула нахождения среднего значения вам знакома из математики.
