Как найти тепловой поток через коэффициент теплоотдачи

12.2. Теплопередача через цилиндрическую стенку

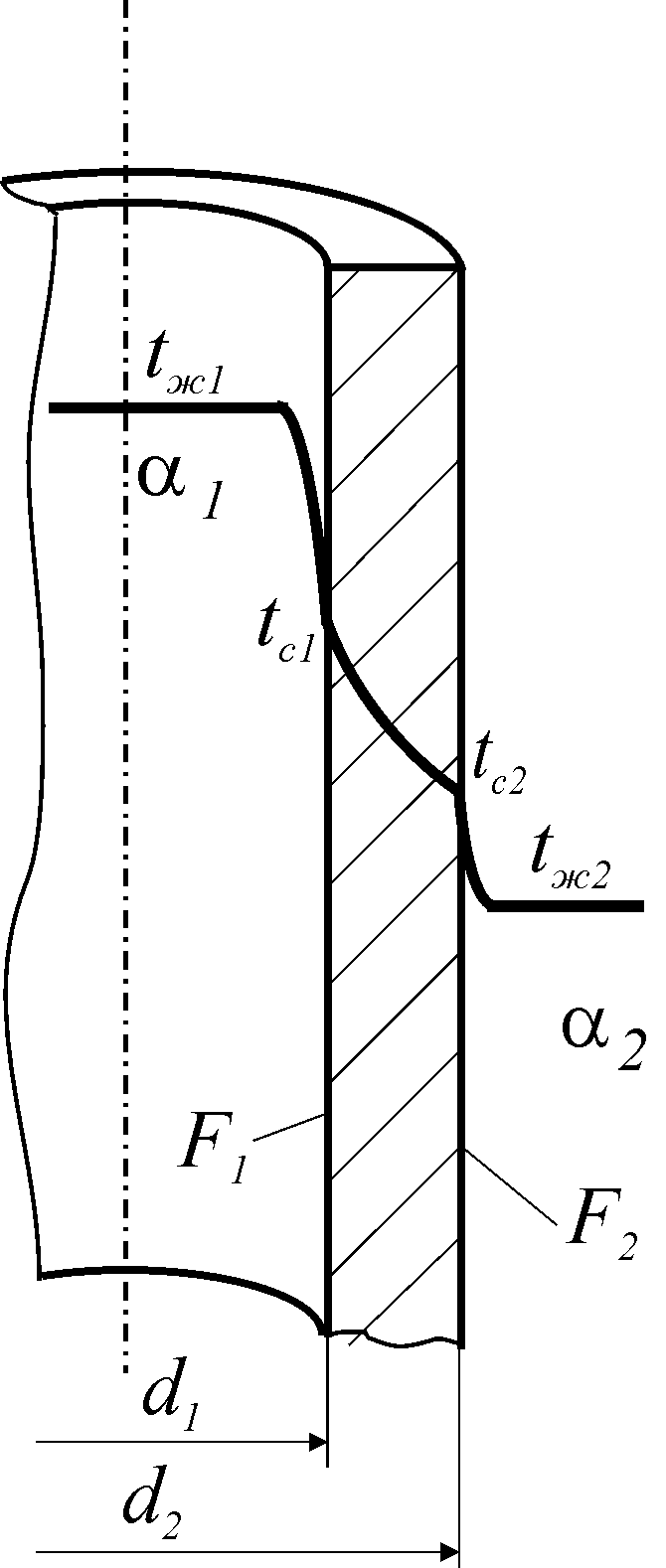
Принцип расчета теплового потока через цилиндрическую
стенку аналогична как и для плоской стенки. Рассмотрим однородную трубу (рис.12.2)
с теплопроводностью l,
внутренний диаметр d₁, наружный диаметр d₂, длина l.
Внутри трубы находится горячая среда с температурой t^‘_ж,
а снаружи холодная среда с температурой t^”_ж.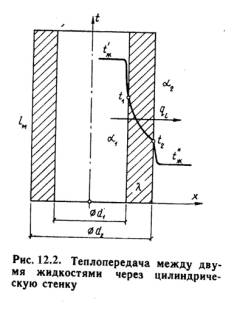

Количество
теплоты, переданной от горячей среды к внутренней стенке трубы по закону
Ньютона-Рихмана имеет вид:

Q
= p·d₁·a₁·l·(t^‘_ж
– t₁) , (12.9)

Q = 2·p·l·l·(t₁ – t₂) / ln (d₂/d₁). (12.10)

Тепловой поток от второй поверхности стенки трубы к холодной среде
определяется по формуле:

Q
= p·d₂·a₂·l·(t₁
– t^”_ж) , (12.11)

Q
= p
l·(t^‘_ж – t^”_ж) • К, (12.12)

• полное
  линейное термическое сопротивление

Р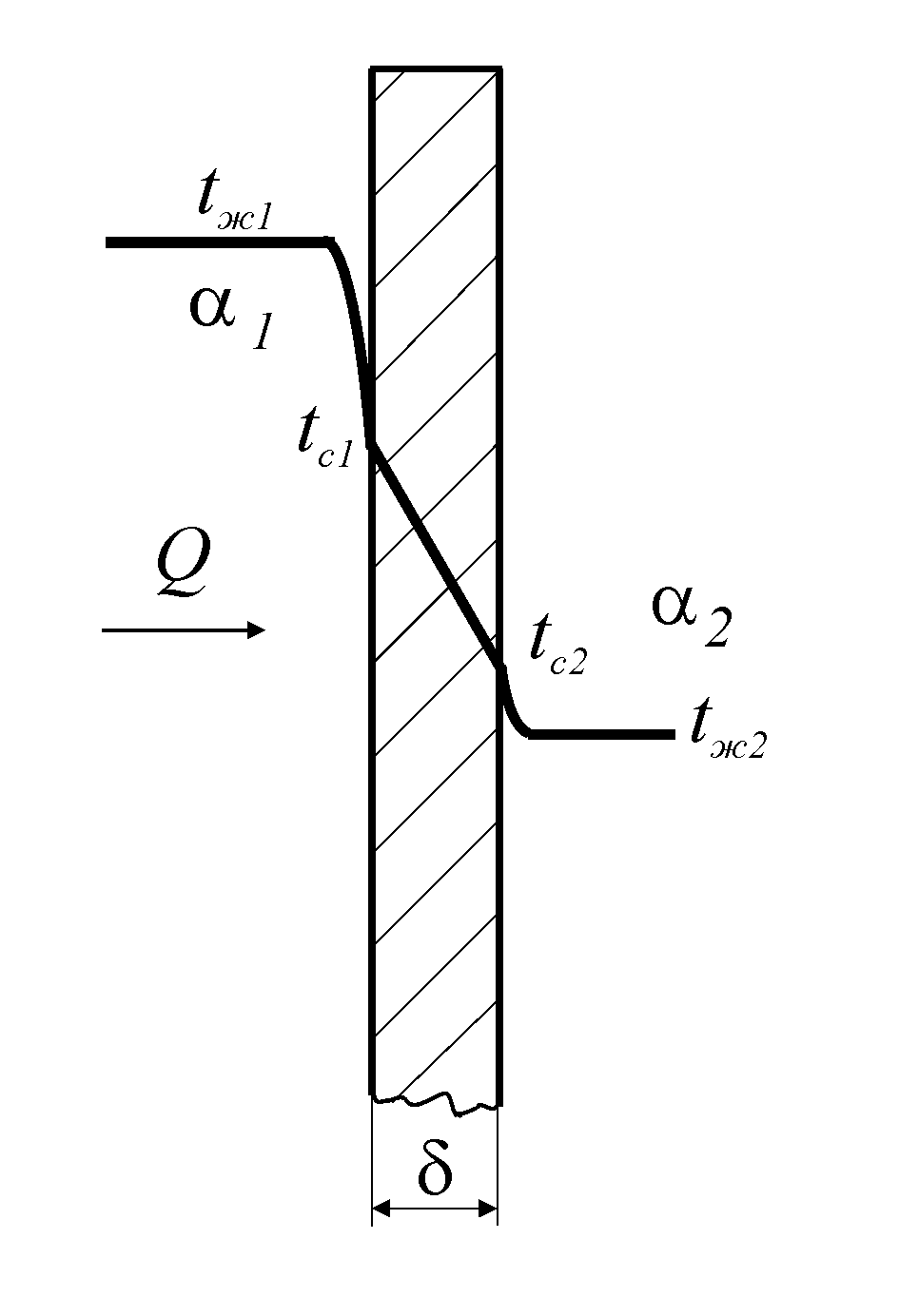ассмотрим
процесс передачи теплоты через плоскую
стенку поверхностьюF,
толщиной
и
коэффициентом теплопроводности.
При известных температурах горячегои холодного теплоносителя,
а также коэффициентов теплоотдачи от
горячегои холодноготеплоносителей решение сводится к
определению теплового потока, плотности
теплового и температур внутренней и
наружной поверхности стенки (граничные
условия третьего рода). Принимая во
внимание условие постоянства теплового
потока можно записать ряд равенств

;

;(1.204)

В этом ряду равенств
первое уравнение определяет количество
теплоты, передаваемой конвекцией (и
излучением) от горячего теплоносителя
к стенке; второе уравнение – то же
количество теплоты, передаваемой
теплопроводностью через стенку; третье
уравнение – передачу того же самого
количества теплоты, передаваемого
конвекцией (и излучением) от стенки к
холодному теплоносителю.

Выделим из этого
ряда равенств разности температур

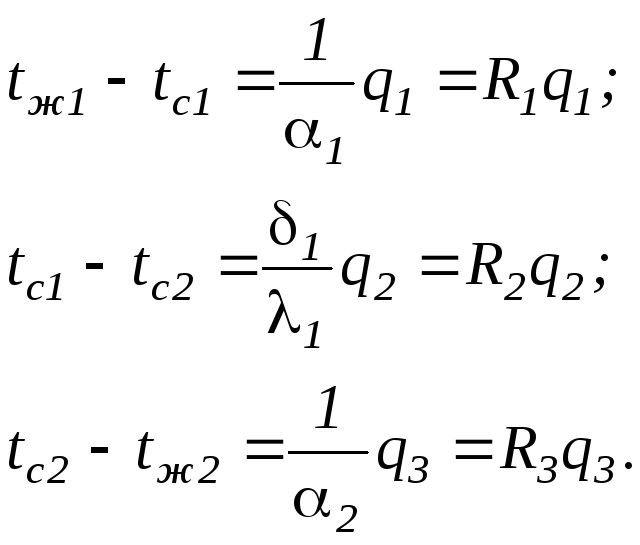(1.205)

Складывая левые
и правые части уравнений характеризующих
разности температур и учитывая, что
получим выражение для итоговой разности
температур

(1.206)

где
–термическое
сопротивление плоской стенки
(м^2
0СBm)

Отсюда, следует
выражение для плотности теплового
потока и теплового потока (уравнение
теплопередачи плоской стенки)

,
(1.207)

где q
– плотность теплового потока (Вт/м²
);
Q
– тепловой поток (Вт);

k=1/R
– коэффициентом теплопередачи плоской
стенки (Вт/м²
ºС)

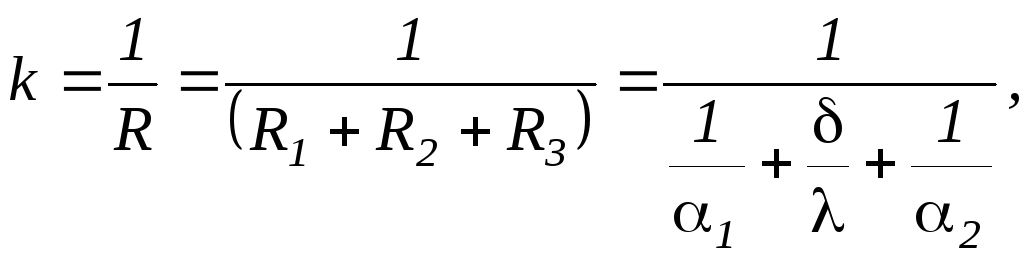(1.208
)

где

—термическое сопротивление теплопередачи
плоской стенки (м²
ºС/Вт);
;– термические сопротивления теплоотдачи
со стороны горячего теплоносителя,
теплопроводности плоской стенки и
термические сопротивления теплоотдачи
со стороны холодного теплоносителя
соответственно.

Температура
внутренней и наружной поверхности
стенки определяется из следующих
соображений:

,
(1.209)

отсюда имеем

,

(1.210)

В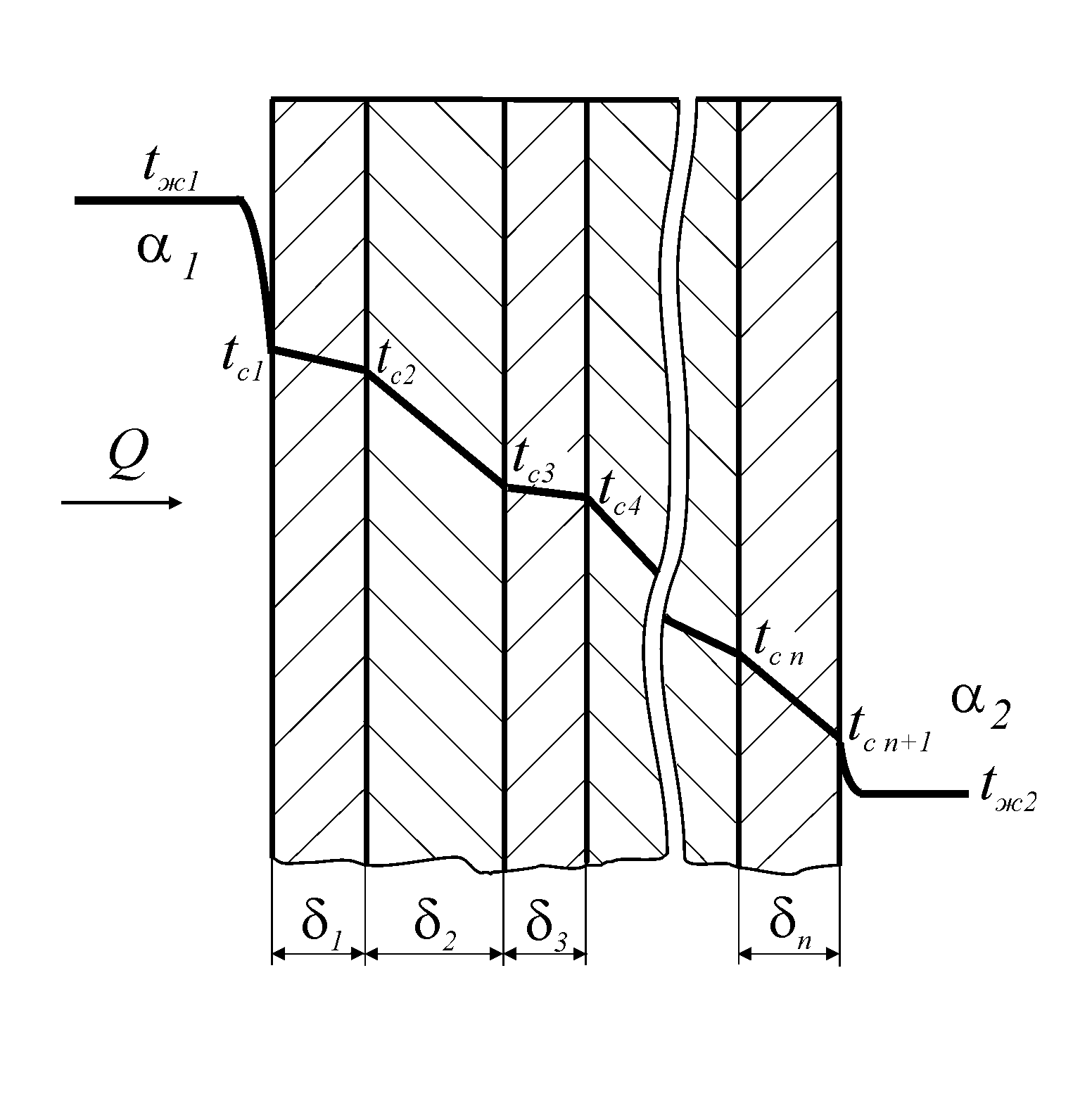случае многослойной стенки состоящей
из п слоев тепловой поток и плотность
теплового потока определяются по
уравнениям аналогичным однослойной
(1.207) за исключением того, что термическое
сопротивление и следовательно коэффициент
теплопередачи определяются с учетом
термических сопротивлений каждого
слоя.

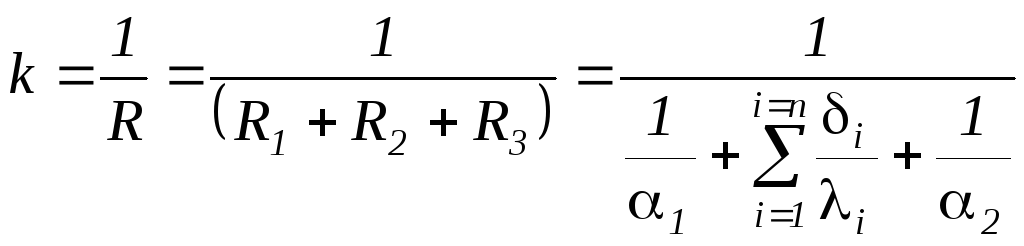(1.211)

Температура
поверхности и на стыке слоев определяется
из тех же соображений, что и для однослойной
стенки

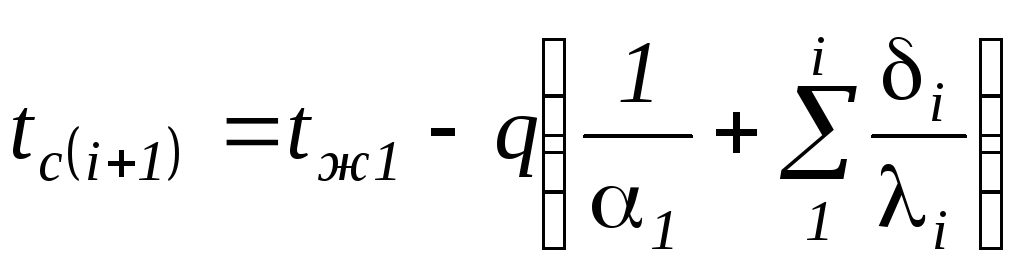(1.212)

38. Теплопередача через криволинейные однослойные и многослойные стенки.

Для криволинейных
стенок произведение kF
неразделимо
и только для плоской стенки вследствие
равенства F₁
= F_m,i
= F₂
= F
это
произведение распадается на k
и F. Тогда
для плоской стенки выражение коэффициента
теплопередачи запишется следующим
образом;

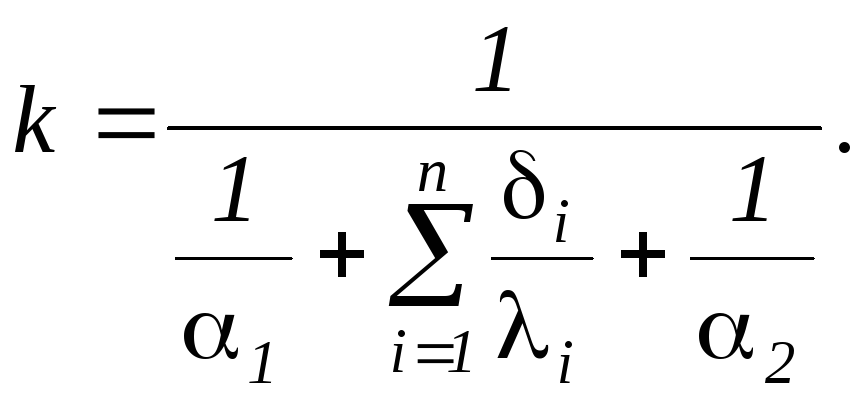(1.213)

Для криволинейных
стенок коэффициент теплопередачи
принято определять по тому же уравнению,
что и для плоской стенки. В этом случае
для криволинейных стенок расчетная
поверхность теплопередачи определяется
из выражения

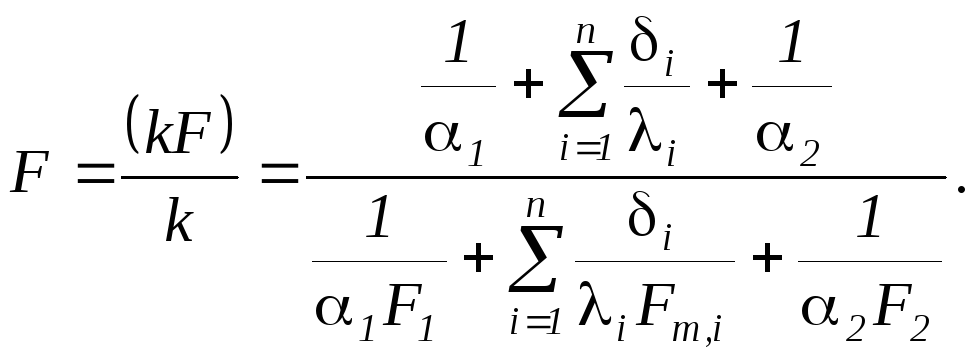( 2.69 )

Удельная линейная
плотность теплового потока q_l
для цилиндрической стенки в условиях
теплопередачи является частным выражением
основного уравнения

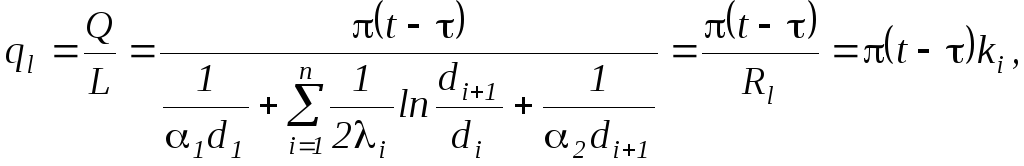( 2.70 )

где
—
линейное термическое сопротивление;

( 2.71 )

В технических
расчетах чаще всего приходится решать
проблему двух видов: уменьшение тепловых
потерь (изоляция поверхности теплообмена)
и увеличение количества передаваемого
тепла (интенсификация теплопередачи).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Коэффициент теплоотдачи поверхность — воздух

Опубликовано 06 Апр 2020
Рубрика: Теплотехника | 29 комментариев

В статье рассмотрен расчет мощности теплового потока от горизонтальных и вертикальных плоских поверхностей тела, помещенного в «безразмерное» воздушное пространство при принудительной и естественной конвекции с учетом радиационной составляющей теплоотдачи.

Зная коэффициент теплоотдачи на поверхности (α), разделяющей твердое тело и окружающее это тело воздушное пространство, очень просто определить мощность теплового потока (Q) по известной разности температур (Δt).

Q=α*A*Δt, Вт – мощность теплового потока от или к поверхности тела.

• α=α_к+α_р, Вт/(м²*К) – суммарный коэффициент теплоотдачи на границе воздух – поверхность тела
  • α_к=?, Вт/(м²*К) – коэффициент конвективной теплоотдачи
  • α_р=ε*5,67*10^-8*((t_п+273,15)⁴— (t_в+273,15)⁴)/(t_п-t_в)), Вт/(м²*К) – коэффициент радиационной теплоотдачи (теплоотдачи излучением), ε – степень черноты поверхности
• А, м² – площадь поверхности
• Δt=|t_п-t_в|, К – разность температур поверхности и воздушной среды
  • t_п, °C – температура поверхности
  • t_в, °C – температура воздуха

Основная сложность расчета заключается в определении коэффициента конвективной теплоотдачи (α_к)! Автоматизировать в первую очередь решение этой трудоемкой задачи поможет Excel.

Нестабильность процесса естественной конвекции у поверхностей различной формы и расположения в пространстве породила большое разнообразие эмпирических формул для вычисления коэффициента конвективной теплоотдачи (α_к). Неизбежные погрешности экспериментальных данных привели к тому, что результаты вычислений для одних и тех же поверхностей и условий по формулам разных авторов отличаются друг от друга на 20% и более.

После тщательного детального ознакомления с материалами современных западных изданий по теплообмену (список литературы – в конце статьи) были выбраны формулы, рекомендованные к применению большинством авторов, для использования в представленной далее программе в Excel.

Схемы теплообмена:

На представленных ниже рисунках показаны 8 вариантов схем, для которых программа может выполнить вычисления.

Розовый цвет пластин свидетельствует о том, что они горячее окружающего воздуха. Голубой цвет – пластины холоднее воздуха.

На схемах 1а и 1б воздух принудительно движется (вентилятор, ветер) вдоль поверхности пластины независимо от её ориентации в пространстве. На всех остальных схемах окружающий воздух находится в спокойном состоянии (помещение, полный штиль), а положение пластин сориентировано в пространстве.

Расчет в Excel:

Формулы алгоритма программы:

t₀=(t_в+t_п)/2

l₀=L – для схем 1а и 1б

l₀=(B*L)/(2*(B+L)) – для схем 2а, 2б, 3а, 3б, 4а, 4б

Для определения теплофизических параметров воздуха при определяющей температуре (t₀) в диапазоне -70°C … +1200°C использованы формулы из предыдущей статьи на сайте.

Re=w*l₀/ν

Gr=g*β*|t_п— t_в|*l₀³/ν²

Ra=Gr*Pr

α_к=Nu*λ/l₀

α_р=ε*0,00000005670367*((t_п+273,15)⁴— (t_в+273,15)⁴)/(t_п-t_в)) – при t_в<t_п

^*)α_р=0 – при t_в>t_п

α=α_к+α_р

q=α*(t_п-t_в)

Q=q*B*L

^*)Нагрев поверхностей Солнцем или иными источниками теплового излучения программой игнорируется.

Вычисление теплофизических параметров воздуха и числа Нуссельта, как видно из вышеприведенных формул, являются ключевыми и самыми трудоемкими при определении конвективного коэффициента теплоотдачи.

Тестирование программы проводилось на примерах из книг, представленных в  конце статьи. Отклонения результатов в основном не выходили за пределы ±5%.

Замечание:

В отечественной теплотехнической литературе для решения рассмотренных задач широко используются формулы второй половины прошлого века М.А. Михеева и В.П. Исаченко, которые в современной западной литературе не упоминаются. Беглый сравнительный анализ результатов расчетов по формулам разных авторов дал противоречивые и неоднозначные ответы. Если при принудительной конвекции результаты фактически идентичны, то при естественной конвекции отличаются порой на 30% и более, но иногда почти совпадают…

Литература:

1. John H. Lienhard IV, John H. Lienhard V, A Heat Transfer Textbook (Fifth Edition), 2019.
2. Frank Kreith, Raj M. Manglik, Mark S. Bohn, Principles of heat transfer (Seventh Edition), 2011.
3. Adrian Bejan, Convection Heat Transfer (Fourth Edition), 2013.
4. Michel Favre-Marinet, Sedat Tardu, Convective Heat Transfer, 2009.
5. Harlan H. Bengtson, Convection Heat Transfer Coefficient Estimation, 2010.
6. Rajendra Karwa, Heat and Mass Transfer, 2017.
7. Stuart W. Churchill, Humbert H. S. Chu, Correlating equations for laminar and turbulent free convection from a vertical plate, International Journal of Heat and Mass Transfer, Volume 18, Issue 11, November 1975.
8. http://people.csail.mit.edu/jaffer/SimRoof/Convection/
9. И. И. Кирвель, М. М. Бражников, Е. Н. Зацепин ЭНЕРГОСБЕРЕЖЕНИЕ В ПРОЦЕССАХ ТЕПЛООБМЕНА, 2007.

Ссылка на скачивание файла: koehfficient-teplootdachi-poverhnost-vozduh (xlsx 225KB).

P. S. (01.11.2020)

Дополнение по естественной конвекции у вертикальной поверхности:

Если построить графики по вышеприведенным формулам Черчилля и Чу для числа Нуссельта при естественной конвекции у вертикальной изотермической поверхности (схемы 2а и 2б), то можно увидеть, что при Ra=10⁹ кривые не совпадают!

По этому поводу авторы формул Черчилль и Чу дают примерно следующее пояснение: «уравнение, основанное на исследованиях Черчилля и Усаги Nu=(0,825+0,387*Ra^1/6/(1+(0,492/Pr)^9/16)^8/27)² дает хорошие результаты для средней теплопередачи при свободной конвекции у изотермической вертикальной пластины во всем диапазоне значений Ra и Pr от 0 до ∞, даже если оно не работает для обозначения дискретного перехода от ламинарного к турбулентному потоку». Линхарды в [1] отмечают, что рассматриваемое уравнение чуть менее точно для ламинарных условий при Ra<10⁹ и рекомендуют в этом диапазоне использовать первое уравнение тех же авторов Nu=0,68+0,67*Ra^¼/(1+(0,492/Pr)^9/16)^4/9. Хотя, судя по графикам, в диапазоне Ra<10⁷ для воздуха обе функции чрезвычайно близки друг к другу.

Еще один нюанс, который встретился только у Линхардов в [1]: «свойства флюида следует оценивать при t₀=(t_в+t_п)/2 за одним исключением, если флюид – газ, то коэффициент объемного расширения β следует определять при t₀=t_в». Но сами авторы зависимостей Черчилль и Чу о таком условии ничего не пишут. По этому поводу в их статье [7], говорится, что «для больших температурных перепадов, когда физические свойства существенно различаются, Ид рекомендует оценивать физические свойства как средние значения температуры поверхности и объема, а Уайли дает более подробные теоретические указания для режима ламинарного пограничного слоя».

Максимальная относительная ошибка для Nu=(0,825+0,387*Ra^1/6/(1+(0,492/Pr)^9/16)^8/27)², если β=1/t_в вместо β=2/( t_в+t_п), составляет в процентах:

ε=(((t_в+t_п)/(2*t_в))^1/3-1)*100%, или

ε=((|(t_п— t_в)|/(2*t_в)+1)^1/3-1)*100%

Как видно из графика при температуре среды – воздуха t_в=20°C=293,15K и при перепаде температур поверхности и воздуха Δt=|t_п— t_в|<90 °C максимальная погрешность ε не превышает 5%.

При Δt>90 °C расхождение результатов быстро нарастает.

Правы Линхарды или множество других авторов, рассчитывающих все свойства флюидов при одном значении определяющей температуры t₀=(t_в+t_п)/2? Однозначного ответа у меня нет.

(По материалам Обри Джаффера [8].)

Эмпирические уравнения для суммарного коэффициента теплоотдачи:

В инженерных расчетах для быстрого приближенного определения суммарного коэффициента теплоотдачи, учитывающего и конвекцию, и излучение на границе поверхность тела – среда, можно использовать более простые зависимости, приведенные в [9].

При расчете тепловых потерь через наружные поверхности тел, которые находятся в спокойном воздухе закрытых помещений, можно применить нижеприведенные формулы. Результаты вычислений по этим формулам достаточно близки к результатам более точных расчетов.

α=9,74+0,07*(t_п-t_в), Вт/(м2*°C)  при t_п<150 °C

α=9,3+0,058*t_п, Вт/(м2*°C)  при t_п=50…350 °C

On-line калькуляторы для расчетов коэффициентов конвективной теплоотдачи от плоских, цилиндрических и сферических поверхностей:

Инструменты представлены Группой исследований теплопередачи (HTRG). Группа была создана в 2014 году преподавателями Лаборатории теплотехники и жидкостей факультета машиностроения инженерной школы Сан-Карлоса (EESC) Университета Сан-Паулу (USP) для проведения передовых, качественных фундаментальных и прикладных исследований по вопросам теплопередачи для многофазных и однофазных систем.

www.heatgroup.eesc.usp.br/tools/

Точность результатов вычислений по on-line калькуляторам детально не проверял.

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

КРАТКИЕ СВЕДЕНИЯ О ТЕПЛОПЕРЕДАЧЕ

Вопросы передачи теплоты, или теплового обмена, являются основными вопросами отопительной техники. Необходимым условием теплообмена между телами или веществами является наличие разности температур. Чем больше эта разность, тем интенсивнее происходит теплообмен.

Различают три вида передачи теплоты: а) теплопроводностью, или кондукцией; б) конвекцией, или переносом теплоты движущимися частицами вещества; в) лучеиспусканием, или радиацией.

В большинстве случаев в различных тепловых процессах имеют место одновременно все три вида теплопередачи с преобладанием какого-либо из них.

Передача теплоты теплопроводностью. Такая передача осуществляется при непосредственном соприкосновении каких-либо двух тел или веществ. Теплопередача происходит внутри самого тела или вещества, которое проводит теплоту. В отопительной технике теплопередача теплопроводностью играет большую роль.

Теплопроводность обусловлена различием температур отдельных частей тела, поэтому можно считать, что распространение теплоты неразрывно связано с распределением температуры. Температурное поле, изменяющееся с течением времени, называют неустановившимся, или нестационарным. Если же температурное поле не меняется, его называют установившимся, или стационарным.

Для характеристики процесса распространения теплоты вводят понятие о тепловом потоке. Тепловой поток Q – это количество теплоты W, Дж, проходящей за время т, с, через данную поверхность в направлении нормали к ней:

(1)

Тепловой поток измеряют в ваттах (Вт).

Если количество переданной теплоты W отнести к площади поверхности F и времени т, то получим величину

(2)

которую называют плотностью теплового потока, или удельным тепловым потоком, и измеряют в Вт/м².

Рассмотрим стационарный процесс распространения теплоты через однородную плоскую однослойную стенку (рис. 1, а).

Рисунок 1. Передача теплоты через плоскую стенку: а – однослойную; б – многослойную

Из закона распространения теплоты путем теплопроводности (закона Фурье) следует:

(3)

где W – количество переданной теплоты, Дж; λ – коэффициент пропорциональности, называемый коэффициентом теплопроводности, Вт/(м·К); t_с^l – температура одной поверхности стенки, К; t_с^ll – температура другой поверхности стенки, К; δ – толщина стенки, м; F – площадь поверхности стенки, м²; τ – время, с.

Отсюда

(4)

т.е. коэффициент теплопроводности численно равен количеству теплоты, которое проходит в единицу времени (1с) в теле через единицу поверхности (1 м²) при падении температуры на 1 К на 1 м пути теплового потока.

Если обе части уравнения (3) разделить на Ft, to получим

(5)

или

(6)

где δ/λ – термическое сопротивление теплопроводности.

Таким образом, плотность теплового потока q прямо пропорциональна разности температур на поверхностях стенки и обратно пропорциональна термическому сопротивлению теплопроводности.

Коэффициент теплопроводности λ у различных материалов неодинаков и зависит от их свойств, а у газообразных и жидких веществ – от плотности, влажности, давления и температуры этих веществ. При технических расчетах значения λ выбирают по соответствующим справочным таблицам.

Рассмотрим теперь процесс передачи теплоты через многослойную стенку.

На рис. 1, б изображена плоская стенка, состоящая из трех слоев, указаны промежуточные температуры на границах этих слоев, а также толщина слоев и значения коэффициентов теплопроводности для каждого слоя. При стационарном режиме тепловой поток, проходящий через каждый отдельный слой, будет один и тот же. Тогда для каждого слоя в соответствии с формулой (6) можно записать:

Отсюда

Сложив правые и левые части этих уравнений, получим:

Следовательно, плотность теплового потока многослойной стенки

(7)

Из записанных уравнений для трех разностей температур можно получить формулы для вычисления промежуточных температур. Например:

и

ПЕРЕДАЧА ТЕПЛОТЫ КОНВЕКЦИЕЙ.

Конвекция – это перенос теплоты движущейся массой жидкости или газа из области с одной температурой в область с другой температурой. Конвекция всегда сопровождается теплопроводностью, этот процесс называют конвективным теплообменом.

Теплоотдача конвекцией зависит от большого числа различных факторов:

характера конвекции – конвекции свободной, происходящей под действием внутренних сил, возникающих вследствие разности плотностей нагретых и холодных частиц, или вынужденной, происходящей под действием внешних сил – ветра, насоса, вентилятора;

режима течения жидкости – течения при малых скоростях параллельно-струйчатого характера без перемешивания (ламинарный режим) или течения при больших скоростях (течение неупорядоченное, вихревое), когда в теплоносителе наблюдаются вихри, перемещающие жидкость не только в направлении движения, но и в поперечном направлении (турбулентный режим);

скорости движения теплоносителя;

направления теплового потока (нагревание или охлаждение);

физических свойств теплоносителя – коэффициента теплопроводности, теплоемкости, плотности, вязкости, температурного напора, зависящего от разности температур теплоносителя и поверхности стенок;

площади поверхности стенки F, омываемой теплоносителем;

формы стенки, ее размеров и других факторов.

Расчет процесса конвективного теплообмена производят на основе закона Ньютона, который выражается формулой

(8)

где W – количество переданной теплоты, Дж; α – коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К); F – площадь поверхности теплообмена, м²; t и t_c^l – температуры соответственно жидкости и стенки, К; т – время, с.

Коэффициент теплоотдачи а показывает, какое количество теплоты передается от жидкости (греющего тела) к стенке или наоборот в единицу времени через единицу поверхности при разности температур между поверхностью стенки и жидкостью в 1 К.

Разделив обе части уравнения (8) на Ft, получим выражение для плотности теплового потока при теплоотдаче:

(9)

или

(10)

где 1/α – термическое сопротивление теплоотдачи.

Коэффициент теплоотдачи а определяют опытным или аналитическим методом. Аналитический метод весьма сложен и не обеспечивает нужной точности.

ПЕРЕДАЧА ТЕПЛОТЫ ИЗЛУЧЕНИЕМ.

Все тела излучают электромагнитные волны. Излучение, причиной которого является возбуждение атомов и молекул вещества вследствие их теплового движения, называют тепловым. Лучистый поток – это энергия излучения, Дж, проходящая в единицу времени (1 с) через поверхность площадью F, м², во всех направлениях пространства.

Излучение зависит от температуры тела: чем выше температура тела, тем интенсивнее испускание тепловых лучей.

Тела, полностью поглощающие падающую на них лучистую энергию, называют абсолютно черными. Тела, обладающие свойством полного и правильного отражения всей падающей лучистой энергии, называют зеркальными, а тела, обладающие свойством полного диффузного отражения этой энергии, называют абсолютно белыми. Тела, полностью пропускающие сквозь себя падающую лучистую энергию, называют абсолютно прозрачными, или проницаемыми.

Согласно закону Стефана-Больцмана полное количество энергии, излучаемой единицей поверхности абсолютно черного тела в единицу времени,

(11)

где С₀ – коэффициент излучения абсолютно черного тела, равный 5,67 Вт/(м² ·К⁴); Т – абсолютная температура поверхности тела, К.

Из этого уравнения следует, что энергия излучения пропорциональна абсолютной температуре в четвертой степени.

Поток излучения ?Q, проходящий через единицу поверхности, называют плотностью потока излучения, Вт/м²,

(12)

Энергия излучения, падающего на тело Е_пад, частично поглощается (Е_А), частично отражается (Е_R) и частично проникает сквозь него (E_D):

Отношение А = Е_А/Е_пад называют коэффициентом поглощения, R = E_R/ Е_пад – коэффициентом отражения, D = Е_D/Е_пад – коэффициентом пропускания. Для абсолютно черного тела А = 1. Тела, для которых А < 1, называют серыми. Для абсолютно белого тела R = 1, для абсолютно прозрачного тела D = 1.

Согласно закону Кирхгофа, учитывающему способность различных тел к лучеиспусканию и лучепоглощению, коэффициент лучеиспускания любого тела при определенной температуре и определенной длине волны излучения пропорционален поглощательной способности данного тела при той же температуре и той же длине волны. При данной температуре тело излучает тем больше теплоты, чем больше оно поглощает лучей, т.е. чем оно чернее. Идеальное абсолютно черное тело поглощает все падающие на него лучи, поэтому абсолютно черное тело и излучает наибольшее количество тепловых лучей.

При термодинамическом равновесии отношение излучательной способности тела к его поглощательной способности не зависит от природы тела, а является одинаковой для всех тел функцией температуры и равно излучательной способности абсолютно черного тела Е₀ при той же температуре:

(13)

Отношение излучательной способности данного тела к излучательной способности абсолютно черного тела при той же температуре называют степенью черноты тела

(14)

Следовательно, излучательную способность тела можно представить как степень его черноты, умноженную на излучательную способность абсолютно черного тела: Е = εЕ₀

Степень черноты различных тел меняется от нуля до единицы и зависит от состояния поверхности, материала, температуры и других факторов.

СЛОЖНЫЙ ТЕПЛООБМЕН.

Рассмотренные выше явления передачи теплоты протекают обычно одновременно. Например, когда тело (поверхность нагрева) омывается газом, то наряду с конвективным теплообменом имеется теплообмен излучением (радиацией). В системах отопления, вентиляции и кондиционирования наиболее часто встречающийся случай теплообмена – это передача теплоты от греющей жидкости, нагреваемой среде (воздух, жидкость) через разделительную стенку (рис. 2, а). В этом случае вначале происходит теплоотдача от греющей жидкости со средней температурой t₁ стенке с температурой t_c^l. Далее теплота передается в результате теплопроводности стенки ее противоположной поверхности с температурой t_c^ll и, наконец, эта поверхность стенки отдает теплоту нагреваемой среде со средней температурой t₂. Тогда плотность теплового потока для однослойной стенки с учетом формул (6) и (10) будет

(15)

где α₁ – коэффициент теплоотдачи от греющей жидкости левой (см. рис. 2, а) поверхности стенки; δ – толщина стенки; λ – коэффициент теплопроводности разделительной стенки; α₂ – коэффициент теплоотдачи от правой поверхности стенки, нагреваемой среде.

Рисунок 2. Передача теплоты от греющей жидкости, нагреваемой среде через разделительную стенку: а – однослойную; б – многослойную

Если дробь

обозначить буквой k, то формула для подсчета количества теплоты, передаваемой через площадь F за время τ, примет следующий вид:

(16)

Величину k называют коэффициентом теплопередачи [измеряется в Вт/(м²·К)], а обратную ему величину – полным термическим сопротивлением теплопередачи R₀ = 1/k = 1/α₁ + δ/λ + 1/α₂.

Если разделительная стенка состоит из нескольких слоев, например из трех (рис. 2, б), то плотность теплового потока с учетом формул (7) и (10) будет

(17)

а коэффициент теплопередачи

(18)

В многочисленных теплообменных устройствах, применяемых в любой области промышленности, в том числе в системах отопления, вентиляции и кондиционирования, основным рабочим процессом является теплообмен между теплоносителями. Такой теплообмен называют теплопередачей.