Как найти коэффициент сжатия в информатике

У этого термина существуют и другие значения, см. Сжатие.

Запрос «Коэффициент сжатия» перенаправляется сюда; о коэффициенте сжимаемости (в физике) см. Сжимаемость.

Сжа́тие да́нных (англ. data compression) — алгоритмическое (обычно обратимое) преобразование данных, производимое с целью уменьшения занимаемого ими объёма. Применяется для более рационального использования устройств хранения и передачи данных. Синонимы — упаковка данных, компрессия, сжимающее кодирование, кодирование источника. Обратная процедура называется восстановлением данных (распаковкой, декомпрессией).

Сжатие основано на устранении избыточности, содержащейся в исходных данных. Простейшим примером избыточности является повторение в тексте фрагментов (например, слов естественного или машинного языка). Подобная избыточность обычно устраняется заменой повторяющейся последовательности ссылкой на уже закодированный фрагмент с указанием его длины. Другой вид избыточности связан с тем, что некоторые значения в сжимаемых данных встречаются чаще других. Сокращение объёма данных достигается за счёт замены часто встречающихся данных короткими кодовыми словами, а редких — длинными (энтропийное кодирование). Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или белый шум, зашифрованные сообщения), принципиально невозможно без потерь.

Сжатие без потерь позволяет полностью восстановить исходное сообщение, так как не уменьшает в нем количество информации, несмотря на уменьшение длины. Такая возможность возникает только если распределение вероятностей на множестве сообщений не равномерное, например часть теоретически возможных в прежней кодировке сообщений на практике не встречается.

Принципы сжатия данных[править | править код]

В основе любого способа сжатия лежит модель источника данных, или, точнее, модель избыточности. Иными словами, для сжатия данных используются некоторые априорные сведения о том, какого рода данные сжимаются. Не обладая такими сведениями об источнике, невозможно сделать никаких предположений о преобразовании, которое позволило бы уменьшить объём сообщения. Модель избыточности может быть статической, неизменной для всего сжимаемого сообщения, либо строиться или параметризоваться на этапе сжатия (и восстановления). Методы, позволяющие на основе входных данных изменять модель избыточности информации, называются адаптивными. Неадаптивными являются обычно узкоспециализированные алгоритмы, применяемые для работы с данными, обладающими хорошо определёнными и неизменными характеристиками. Подавляющая часть достаточно универсальных алгоритмов является в той или иной мере адаптивной.

Все методы сжатия данных делятся на два основных класса:

• Сжатие без потерь
• Сжатие с потерями

При использовании сжатия без потерь возможно полное восстановление исходных данных, сжатие с потерями позволяет восстановить данные с искажениями, обычно несущественными с точки зрения дальнейшего использования восстановленных данных. Сжатие без потерь обычно используется для передачи и хранения текстовых данных, компьютерных программ, реже — для сокращения объёма аудио- и видеоданных, цифровых фотографий и т. п., в случаях, когда искажения недопустимы или нежелательны. Сжатие с потерями, обладающее значительно большей, чем сжатие без потерь, эффективностью, обычно применяется для сокращения объёма аудио- и видеоданных и цифровых фотографий в тех случаях, когда такое сокращение является приоритетным, а полное соответствие исходных и восстановленных данных не требуется.

Характеристики алгоритмов сжатия и их применимость[править | править код]

Коэффициент сжатия[править | править код]

Коэффициент сжатия — основная характеристика алгоритма сжатия. Она определяется как отношение объёма исходных несжатых данных к объёму сжатых данных, то есть:
,
где k — коэффициент сжатия, S_o — объём исходных данных, а S_c — объём сжатых.
Таким образом, чем выше коэффициент сжатия, тем алгоритм эффективнее. Следует отметить:

• если k = 1, то алгоритм не производит сжатия, то есть выходное сообщение оказывается по объёму равным входному;
• если k < 1, то алгоритм порождает сообщение большего размера, нежели несжатое, то есть, совершает «вредную» работу.

Ситуация с k < 1 вполне возможна при сжатии. Принципиально невозможно получить алгоритм сжатия без потерь, который при любых данных образовывал бы на выходе данные меньшей или равной длины. Обоснование этого факта заключается в том, что поскольку число различных сообщений длиной n бит составляет ровно 2ⁿ, число различных сообщений с длиной меньшей или равной n (при наличии хотя бы одного сообщения меньшей длины) будет не больше 2ⁿ. Это значит, что невозможно однозначно сопоставить все исходные сообщения сжатым: либо некоторые исходные сообщения не будут иметь сжатого представления, либо нескольким исходным сообщениям будет соответствовать одно и то же сжатое, а значит их нельзя различить.
Однако даже когда алгоритм сжатия увеличивает размер исходных данных, легко добиться того, чтобы их объём гарантировано не мог увеличиться более, чем на 1 бит. Тогда даже в самом худшем случае будет иметь место неравенство:

Делается это следующим образом: если объём сжатых данных меньше объёма исходных, возвращаем сжатые данные, добавив к ним «1», иначе возвращаем исходные данные, добавив к ним «0»).

Коэффициент сжатия может быть как постоянным (некоторые алгоритмы сжатия звука, изображения и т. п., например А-закон, μ-закон, ADPCM, усечённое блочное кодирование), так и переменным. Во втором случае он может быть определён либо для каждого конкретного сообщения, либо оценён по некоторым критериям:

• средний (обычно по некоторому тестовому набору данных);
• максимальный (случай наилучшего сжатия);
• минимальный (случай наихудшего сжатия);

или каким-либо другим. Коэффициент сжатия с потерями при этом сильно зависит от допустимой погрешности сжатия или качества, которое обычно выступает как параметр алгоритма. В общем случае постоянный коэффициент сжатия способны обеспечить только методы сжатия данных с потерями.

Допустимость потерь[править | править код]

Основным критерием различия между алгоритмами сжатия является описанное выше наличие или отсутствие потерь. В общем случае алгоритмы сжатия без потерь универсальны в том смысле, что их применение безусловно возможно для данных любого типа, в то время как возможность применения сжатия с потерями должна быть обоснована. Для некоторых типов данных искажения не допустимы в принципе. В их числе

• символические данные, изменение которых неминуемо приводит к изменению их семантики: программы и их исходные тексты, двоичные массивы и т. п.;
• жизненно важные данные, изменения в которых могут привести к критическим ошибкам: например, получаемые с медицинской измерительной аппаратуры или контрольных приборов летательных, космических аппаратов и т. п.;
• многократно подвергаемые сжатию и восстановлению промежуточные данные при многоэтапной обработке графических, звуковых и видеоданных.

Системные требования алгоритмов[править | править код]

Различные алгоритмы могут требовать различного количества ресурсов вычислительной системы, на которых они реализованы:

• оперативной памяти (под промежуточные данные);
• постоянной памяти (под код программы и константы);
• процессорного времени.

В целом, эти требования зависят от сложности и «интеллектуальности» алгоритма. Общая тенденция такова: чем эффективнее и универсальнее алгоритм, тем большие требования к вычислительным ресурсам он предъявляет. Тем не менее, в специфических случаях простые и компактные алгоритмы могут работать не хуже сложных и универсальных. Системные требования определяют их потребительские качества: чем менее требователен алгоритм, тем на более простой, а следовательно, компактной, надёжной и дешёвой системе он может быть реализован.

Так как алгоритмы сжатия и восстановления работают в паре, имеет значение соотношение системных требований к ним. Нередко можно, усложнив один алгоритм, значительно упростить другой. Таким образом, возможны три варианта:

Алгоритм сжатия требует больших вычислительных ресурсов, нежели алгоритм восстановления.

Это наиболее распространённое соотношение, характерное для случаев, когда однократно сжатые данные будут использоваться многократно. В качестве примера можно привести цифровые аудио- и видеопроигрыватели.

Алгоритмы сжатия и восстановления требуют приблизительно равных вычислительных ресурсов.

Наиболее приемлемый вариант для линий связи, когда сжатие и восстановление происходит однократно на двух её концах (например, в цифровой телефонии).

Алгоритм сжатия существенно менее требователен, чем алгоритм восстановления.

Такая ситуация характерна для случаев, когда процедура сжатия реализуется простым, часто портативным, устройством, для которого объём доступных ресурсов весьма критичен, например, космический аппарат или большая распределённая сеть датчиков. Это могут быть также данные, распаковка которых требуется в очень малом проценте случаев, например запись камер видеонаблюдения.

Алгоритмы сжатия данных неизвестного формата[править | править код]

Имеется два основных подхода к сжатию данных неизвестного формата:

• На каждом шаге алгоритма сжатия очередной сжимаемый символ либо помещается в выходной буфер сжимающего кодера как есть (со специальным флагом, помечающим, что он не был сжат), либо группа из нескольких сжимаемых символов заменяется ссылкой на совпадающую с ней группу из уже закодированных символов. Поскольку восстановление сжатых таким образом данных выполняется очень быстро, такой подход часто используется для создания самораспаковывающихся программ.
• Для каждой сжимаемой последовательности символов однократно либо в каждый момент времени собирается статистика её встречаемости в кодируемых данных. На основе этой статистики вычисляется вероятность значения очередного кодируемого символа (либо последовательности символов). После этого применяется та или иная разновидность энтропийного кодирования, например, арифметическое кодирование или кодирование Хаффмана, для представления часто встречающихся последовательностей короткими кодовыми словами, а редко встречающихся — более длинными.

См. также[править | править код]

• Архив (информатика)
• Список алгоритмов
• Энтропийное кодирование
• Теория информации
• Теория вероятностей
• Статистика

Литература[править | править код]

• Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. — Диалог-МИФИ, 2002. — С. 384. — ISBN 5-86404-170-X. 3000 экз.
• Д. Сэломон. Сжатие данных, изображения и звука. — М.: Техносфера, 2004. — С. 368. — ISBN 5-94836-027-X. 3000 экз.

Ссылки[править | править код]

• compression.ru — ресурс, посвященный сжатию данных

From Wikipedia, the free encyclopedia

Data compression ratio, also known as compression power, is a measurement of the relative reduction in size of data representation produced by a data compression algorithm. It is typically expressed as the division of uncompressed size by compressed size.

Definition[edit]

Data compression ratio is defined as the ratio between the uncompressed size and compressed size:^{[1][2][3][4][5]}

Thus, a representation that compresses a file’s storage size from 10 MB to 2 MB has a compression ratio of 10/2 = 5, often notated as an explicit ratio, 5:1 (read “five” to “one”), or as an implicit ratio, 5/1. This formulation applies equally for compression, where the uncompressed size is that of the original; and for decompression, where the uncompressed size is that of the reproduction.

Sometimes the space saving is given instead, which is defined as the reduction in size relative to the uncompressed size:

Thus, a representation that compresses the storage size of a file from 10MB to 2MB yields a space saving of 1 – 2/10 = 0.8, often notated as a percentage, 80%.

For signals of indefinite size, such as streaming audio and video, the compression ratio is defined in terms of uncompressed and compressed data rates instead of data sizes:

and instead of space saving, one speaks of data-rate saving, which is defined as the data-rate reduction relative to the uncompressed data rate:

For example, uncompressed songs in CD format have a data rate of 16 bits/channel x 2 channels x 44.1 kHz ≅ 1.4 Mbit/s, whereas AAC files on an iPod are typically compressed to 128 kbit/s, yielding a compression ratio of 10.9, for a data-rate saving of 0.91, or 91%.

When the uncompressed data rate is known, the compression ratio can be inferred from the compressed data rate.

Lossless vs. Lossy[edit]

Lossless compression of digitized data such as video, digitized film, and audio preserves all the information, but it does not generally achieve compression ratio much better than 2:1 because of the intrinsic entropy of the data. Compression algorithms which provide higher ratios either incur very large overheads or work only for specific data sequences (e.g. compressing a file with mostly zeros). In contrast, lossy compression (e.g. JPEG for images, or MP3 and Opus for audio) can achieve much higher compression ratios at the cost of a decrease in quality, such as Bluetooth audio streaming, as visual or audio compression artifacts from loss of important information are introduced. A compression ratio of at least 50:1 is needed to get 1080i video into a 20 Mbit/s MPEG transport stream.^[1]

Uses[edit]

The data compression ratio can serve as a measure of the complexity of a data set or signal. In particular it is used to approximate the algorithmic complexity. It is also used to see how much of a file is able to be compressed without increasing its original size.

References[edit]

External links[edit]

• Nondegrading lossy compression

Коэффициент сжатия

Коэффициент
сжатия — основная характеристика
алгоритма сжатия. Она определяется как
отношение объёма исходных несжатых
данных к объёму сжатых, то есть:
,
гдеk— коэффициент сжатия,S_o—
объём исходных данных, аS_c—
объём сжатых. Таким образом, чем выше
коэффициент сжатия, тем алгоритм
эффективнее. Следует отметить:

• если k= 1, то алгоритм не
  производит сжатия, то есть выходное
  сообщение оказывается по объёму равным
  входному;

• если k< 1, то алгоритм порождает
  сообщение большего размера, нежели
  несжатое, то есть, совершает «вредную»
  работу.

Ситуация
с k< 1 вполне возможна при
сжатии. Принципиально невозможно
получить алгоритм сжатия без потерь,
который при любых данных образовывал
бы на выходе данные меньшей или равной
длины. Обоснование этого факта заключается
в том, что поскольку число различных
сообщений длинойnбит составляет
ровно 2ⁿ, число различных
сообщений с длиной меньшей или равнойn(при наличии хотя бы одного сообщения
меньшей длины) будет меньше 2ⁿ.
Это значит, что невозможно однозначно
сопоставить все исходные сообщения
сжатым: либо некоторые исходные сообщения
не будут иметь сжатого представления,
либо нескольким исходным сообщениям
будет соответствовать одно и то же
сжатое, а значит их нельзя отличить.
Однако даже когда алгоритм сжатия
увеличивает размер исходных данных,
легко добиться того, чтобы их объём
гарантировано не мог увеличиться более,
чем на 1 бит. Тогда даже в самом худшем
случае будет иметь место
неравенство:Делается
это следующим образом: если объём сжатых
данных меньше объёма исходных, возвращаем
сжатые данные, добавив к ним «1», иначе
возвращаем исходные данные, добавив к
ним «0»). Пример того, как это реализуется
на псевдо-C++,
показан ниже:

bin_data_t
__compess(bin_data_t input) // bin_data_t – тип данных,
означающий произвольную последовательность
бит переменной длины

{

bin_data_t
output = arch(input); // функция bin_data_t arch(bin_data_t
input) реализует некий алгоритм сжатия
данных

if
(output.size()<input.size()) // если объём сжатых
данных меньше объёма исходных, функция
bin_data_t::size() возвращает размер данных

{

output.add_begin(1);
// функция bin_data_t::add_begin(bool __bit__) добавляет
бит, равный __bit__ в начало последовательности

return
output; // возвращаем сжатую последовательность
с добавленной «1»

}

else
// иначе (если объём сжатых данных больше
или равен объёму исходных)

{

input.add_begin(0);
// добавляем «0» к исходной последовательности

return
input; // возвращаем исходный файл с
добавленным «0»

}

}

Коэффициент
сжатия может быть как постоянным
(некоторые алгоритмы сжатия звука,
изображения и т. п., например
А-закон,μ-закон,ADPCM,усечённое
блочное кодирование), так и
переменным. Во втором случае он может
быть определён либо для каждого
конкретного сообщения, либо оценён по
некоторым критериям:

• средний (обычно по некоторому тестовому
  набору данных);

• максимальный (случай наилучшего сжатия);

• минимальный (случай наихудшего сжатия);

или
каким-либо другим. Коэффициент сжатия
с потерями при этом сильно зависит от
допустимой погрешности сжатия или
качества, которое обычно выступает
как параметр алгоритма. В общем случае
постоянный коэффициент сжатия способны
обеспечить только методы сжатия данных
с потерями.

Основным
критерием различия между алгоритмами
сжатия является описанное выше наличие
или отсутствие потерь. В общем случае
алгоритмы сжатия без потерь универсальны
в том смысле, что их применение безусловно
возможно для данных любого типа, в то
время как возможность применения сжатия
с потерями должна быть обоснована. Для
некоторых типов данных искажения не
допустимы в принципе. В их числе

• символические данные, изменение которых
  неминуемо приводит к изменению их
  семантики: программы и их исходные
  тексты, двоичные массивы и т. п.;

• жизненно важные данные, изменения в
  которых могут привести к критическим
  ошибкам: например, получаемые с
  медицинской измерительной аппаратуры
  или контрольных приборов летательных,
  космических аппаратов и т. п.;

• многократно подвергаемые сжатию и
  восстановлению промежуточные данные
  при многоэтапной обработке графических,
  звуковых и видеоданных.

Соседние файлы в папке курсач docx283

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Министерство образования и науки Российской Федерации

федеральное государственное бюджетное образовательное учреждение

высшего образования

«название вуза»

Реферат по дисциплине

« название»

на тему:

Способы сжатия файлов

Выполнила:

студентка № курса группы №

название факультета полностью

Фамилия И.О.

Проверил(а):

Фамилия И.О.

Город 2017

Оглавление

Введение 3

Глава I. Основные понятия и методы сжатия данных. 4

1.1. Основные способы сжатия. 4

1.2. Характеристики алгоритмов сжатия и их применимость. 6

1.2.1. Коэффициент сжатия. 6

1.2.2. Системные требования алгоритмов 7

Глава II. Программы-архиваторы. 9

2.1. Программа-архиватор WinRAR. 10

2.1.1. Работа с программой-архиватором WinRAR 11

2.1.2. Архивация файлов. 12

2.2. Программа-архиватор WinZip. 14

Заключение 15

Литература 16

Введение

Методы сжатия данных имеют достаточно длинную историю развития, которая началась задолго до появления первого компьютера.

Сжатие информации – проблема, имеющая достаточно давнюю историю, гораздо более давнюю, нежели история развития вычислительной техники, которая (история) обычно шла параллельно с историей развития проблемы кодирования и шифровки информации. Все алгоритмы сжатия оперируют входным потоком информации, минимальной единицей которой является бит, а максимальной – несколько бит, байт или несколько байт. Целью процесса сжатия, как правило, есть получение более компактного выходного потока информационных единиц из некоторого изначально некомпактного входного потока при помощи некоторого их преобразования. Основными техническими характеристиками процессов сжатия и результатов их работы являются:

– степень сжатия (compress rating) или отношение (ratio) объемов исходного и результирующего потоков;

– скорость сжатия – время, затрачиваемое на сжатие некоторого объема информации входного потока, до получения из него эквивалентного выходного потока;

– качество сжатия – величина, показывающая на сколько сильно упакован выходной поток, при помощи применения к нему повторного сжатия по этому же или иному алгоритму.

Существует несколько различных подходов к проблеме сжатия информации. Одни имеют весьма сложную теоретическую математическую базу, другие основаны на свойствах информационного потока и алгоритмически достаточно просты. Любой способ, подход и алгоритм, реализующий сжатие или компрессию данных, предназначен для снижения объема выходного потока информации в битах при помощи ее обратимого или необратимого преобразования.

Глава I. Основные понятия и методы сжатия данных. 1.1. Основные способы сжатия.

Во многих стадиях информация, содержащаяся в файлах, избыточна. Для устранения избыточности используются специальные методы сжатия данных, основанные на поиске в файле избыточной информации и последующем ее кодировании с целью получения минимального объема.

Сжатие информации – это процесс преобразования информации, хранящейся в файле, к виду, при котором уменьшается избыточность в ее представлении и соответственно требуется меньший объем памяти для хранения; процесс сокращения количества битов, необходимых для хранения и передачи некоторого объема информации.

Существует сжатие без потерь, когда информация, восстановленная из сжатого сообщения, в точности соответствует исходной (применяется при обработке текстов, записанных на естественном или искусственном языках), и сжатие с потерями (необратимое), когда восстановленная информация только частично соответствует исходной (применяется при обработке изображений и звука, для цифровой записи аналоговых сигналов).

Основные способы сжатия: статистический и словарный.

При первом каждому символу присваивается код, основанный на вероятности его появления в тексте. Высоко вероятные символы получают короткие коды и наоборот. Одним из самых ранних и широко известных статистических методов является алгоритм Хаффмана , при котором символы заменяются кодом, состоящим из целого количества битов. Позднее он был вытеснен арифметическим кодированием,  имеющим схожую с кодом Хаффмана функцию и основанным на идее кодирования символов дробным числом битов. Арифметическое сжатие может быть использовано в тех случаях, когда степень сжатия важнее, чем временные затраты на сжатие информации.

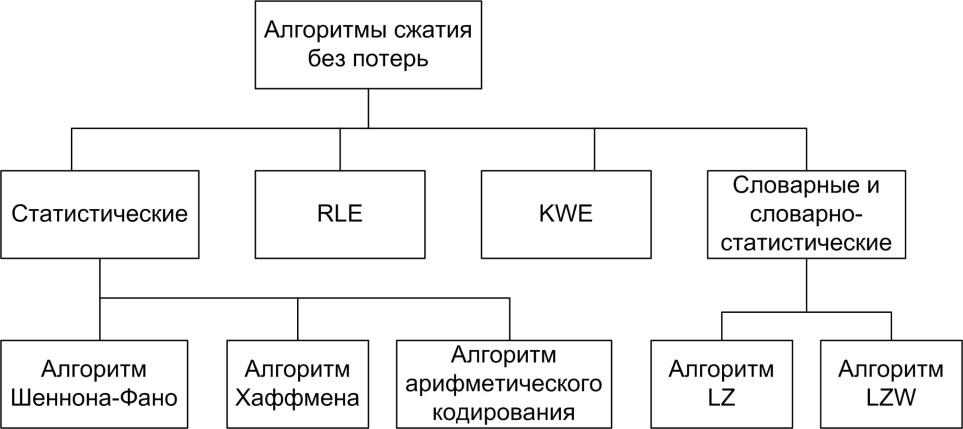
Рис. 1. Классификация алгоритмов сжатия файлов без потерь.

При словарном способе группы последовательных символов или “фраз” заменяются кодом. Замененная фраза может быть найдена в некотором словаре. В 1977 году Лемпель и Зив предложили свою модификацию словарного метода, отличающуюся от Хаффмановского и арифметического методов в которой сжатие основано на свойстве “потока символов” иметь повторяющиеся участки. Поток символов – это исходные данные для сжатия (например текстовый файл, массив). Основная идея алгоритма Лемпеля и Зива состоит в том, что второе и последующие вхождения некоторой строки символов в сообщении заменяются ссылкой на ее первое появление в сообщении.

В последнее время было показано, что любая практическая схема словарного сжатия может быть сведена к соответствующей статистической схеме сжатия, и найден общий алгоритм преобразования словарного метода в статистический. По этому при поиске лучшего сжатия статистическое кодирование обещает быть наиболее плодотворным, хотя словарные методы отличаются быстротой.

Одним из наиболее простых и наглядных является метод сжатия последовательностей одинаковых символов , не относящийся к названным основным методам.

Метод основан на представлении последовательности одинаковых символов в виде двух величин K и S, где K – количество повторяющихся символов, S – код этого символа. Основным недостатком данного метода является то, что он обеспечивает сжатие лишь в случае, когда в исходном файле основную часть составляют повторяющиеся символы. В противном случае сжатый файл может занимать больше места, чем исходный неуплотненный файл. Наиболее эффективно метод сжатия последовательностей одинаковых символов работает в случае двоичных файлов.

Рассмотренные выше алгоритмы в «чистом виде» на практике не применяются из-за того, что эффективность каждого из них сильно зависит от начальных условий. В связи с этим, современные средства архивации, используют более сложные алгоритмы, основанные на комбинации нескольких теоретических методов. Общим принципом в работе таких «синтетических» алгоритмов является предварительный просмотр и анализ исходных данных для индивидуальной настройки алгоритма на особенности обрабатываемого материала.

1.2. Характеристики алгоритмов сжатия и их применимость. 1.2.1. Коэффициент сжатия.

Коэффициент сжатия — основная характеристика алгоритма сжатия. Она определяется как отношение объёма исходных несжатых данных к объёму сжатых, то есть:

k = So/Sc,

где k — коэффициент сжатия, So — объём исходных данных, а Sc — объём сжатых. Таким образом, чем выше коэффициент сжатия, тем алгоритм эффективнее. Следует отметить:

• если k = 1, то алгоритм не производит сжатия, то есть выходное сообщение оказывается по объёму равным входному;

• если k 

Ситуация с k 

Коэффициент сжатия может быть как постоянным (некоторые алгоритмы сжатия звука, изображения и т. п., например А-закон, μ-закон, ADPCM, усечённое блочное кодирование), так и переменным. Во втором случае он может быть определён либо для каждого конкретного сообщения, либо оценён по некоторым критериям:

• средний (обычно по некоторому тестовому набору данных);

• максимальный (случай наилучшего сжатия);

• минимальный (случай наихудшего сжатия);

• или каким-либо другим.

Коэффициент сжатия с потерями при этом сильно зависит от допустимой погрешности сжатия или качества, которое обычно выступает как параметр алгоритма. В общем случае постоянный коэффициент сжатия способны обеспечить только методы сжатия данных с потерями.

1.2.2. Системные требования алгоритмов

Различные алгоритмы могут требовать различного количества ресурсов вычислительной системы, на которых они реализованы:

• оперативной памяти (под промежуточные данные);

• постоянной памяти (под код программы и константы);

• процессорного времени.

В целом, эти требования зависят от сложности и «интеллектуальности» алгоритма. Общая тенденция такова: чем эффективнее и универсальнее алгоритм, тем большие требования к вычислительным ресурсам он предъявляет. Тем не менее, в специфических случаях простые и компактные алгоритмы могут работать не хуже сложных и универсальных. Системные требования определяют их потребительские качества: чем менее требователен алгоритм, тем на более простой, а следовательно, компактной, надёжной и дешёвой системе он может быть реализован.

Так как алгоритмы сжатия и восстановления работают в паре, имеет значение соотношение системных требований к ним. Нередко можно усложнив один алгоритм значительно упростить другой. Таким образом, возможны три варианта:

1. Алгоритм сжатия требует больших вычислительных ресурсов, нежели алгоритм восстановления.

Это наиболее распространённое соотношение, характерное для случаев, когда однократно сжатые данные будут использоваться многократно. В качестве примера можно привести цифровые аудио- и видеопроигрыватели.

1. Алгоритмы сжатия и восстановления требуют приблизительно равных вычислительных ресурсов.

Наиболее приемлемый вариант для линий связи, когда сжатие и восстановление происходит однократно на двух её концах (например, в цифровой телефонии).

1. Алгоритм сжатия существенно менее требователен, чем алгоритм восстановления.

Такая ситуация характерна для случаев, когда процедура сжатия реализуется простым, часто портативным устройством, для которого объём доступных ресурсов весьма критичен, например, космический аппарат или большая распределённая сеть датчиков. Это могут быть также данные, распаковка которых требуется в очень малом проценте случаев, например запись камер видеонаблюдения.

Глава II. Программы-архиваторы.

На основе методов сжатия данных созданы различные программы, называемые архиваторами или упаковщиками . Существует много программ-архиваторов, имеющих различные показатели по степени и времени сжатия. Среди самых известных и часто используемых программ выделяются следующие: ARJ, PKZIP, RAR, НА и т. д. для DOS, WinARJ, WinZip, WinRAR, ZipMagic для Windows. Обычно упаковщики осуществляют сжатие сразу несколькими способами.

Как правило, программы для архивации файлов позволяют помещать копии файлов на диске в сжатом виде в архивный файл, извлекать файлы из архива, просматривать оглавление архива и др. В настоящее время архиваторы, работающие под Windows, вытесняют конкурентов в основном за счет использования 32-х битной шины данных, более удобного и интеллектуального интерфейса, расширенных возможностей и более совершенных алгоритмов сжатия. А также эти программы поддерживают не один, как раньше, а сразу несколько различных форматов архивных файлов.

Программы-архиваторы позволяют создавать и такие архивы, для извлечения из которых содержащихся в них файлов не требуются какие-либо программы, так как сами архивные файлы

Могут содержать программу распаковки. Такие архивные файлы называются самораспаковывающимися.

Самораспаковывающийся архивный файл – это загрузочный, исполняемый модуль, который способен к самостоятельной разархивации находящихся в нем файлов без использования программы-архиватора.

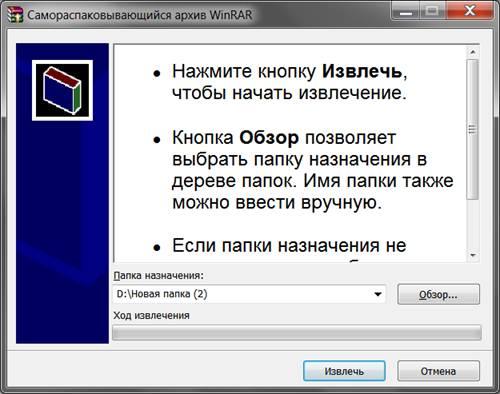
Рис. 2. Пример самораспаковывающегося архивного файла.

К базовым функциям , которые выполняют большинство современных архиваторов, относятся:

– извлечение файлов из архивов;

– создание новых архивов;

– добавление файлов в имеющийся архив;

– создание самораспаковывающихся архивов;

– создание распределенных архивов на носителях малой емкости;

– тестирование целостности структуры архивов;

– полное или частичное восстановление поврежденных архивов;

– защита архивов от просмотра или несанкционированной модификации.

Далее будут рассмотрены две программы-архиваторы WinRAR и WinZip.

2.1. Программа-архиватор WinRAR.

WinRAR – 32-битовая версия Windows архиватора RAR – мощное средство, которое позволяет создавать и управлять архивными файлами.

Достоинства WinRAR :

– интеллектуальный алгоритм сжатия (глубокий анализ данных, подлежащих сжатию, и др.);

– специальный алгоритм сжатия для мультимедиа-файлов;

– не архивное управление RAR;

– плотная архивация, которая может поднять коэффициент сжатия на 10 % -50 % по сравнению с общими методами, особенно при упаковке большого количества небольших аналогичных файлов (при этом файлы представляются как непрерывный поток данных).

Возможности WinRAR :

– создание архивов с различной степенью уплотнения;

– просмотр как архивных, так и обычных файлов;

– создание многотомных архивов;

-создание самораспаковывающихся архивов (в том числе и многотомных);

– восстановление физически поврежденных архивов;

– возможность работы в двух режимах: полноэкранного интерактивного интерфейса и интерфейса командной строки;

– поддержка других типов архивов, просмотра их содержимого, изменения и преобразования;

– защита архивов паролем.

Кроме того, WinRAR обладает рядом других возможностей, таких, например, как шифрование, архивные комментарии, регистрация ошибок и т. п.

2.1.1. Работа с программой-архиватором WinRAR

Для запуска программы WinRAR необходимо выполнить одно из следующих действий:

– открыть меню Пуск;

– выбрать Программы / WinRAR.

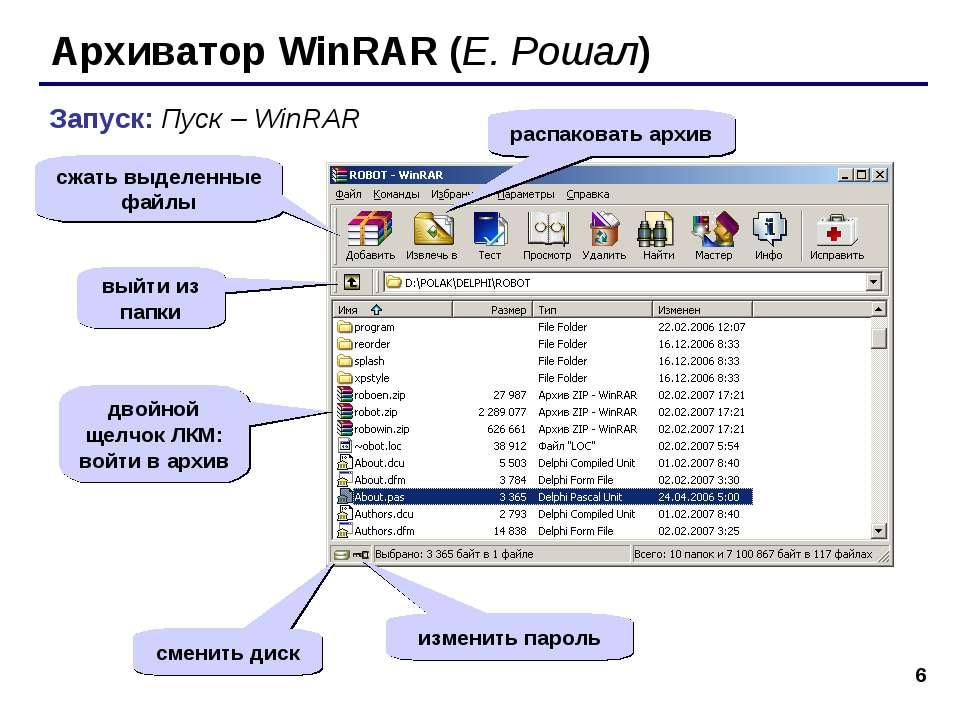
Рис. 3. Вид запущенной программы WinRAR.

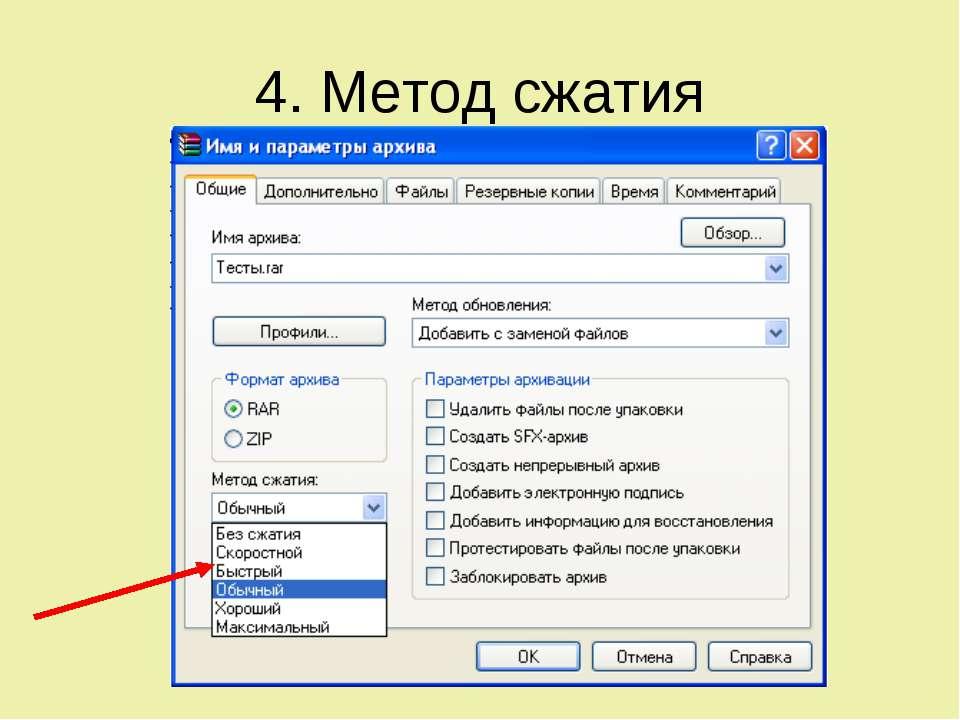
Рис. 4. Метод сжатия файлов в WinRAR.

2.1.2. Архивация файлов.

Для создания архива необходимо сначала выбрать необходимые файлы и/или директории из списка файлов в основном окне WinRAR, что можно сделать, используя клавишу Пробел, Shift + клавиши позиционирования или щелкнув левой кнопкой мыши. Затем, выбрав один или более файлов, нажать Alt – A . После этого появится диалоговое окно, в верхнем поле Archive которого надо ввести имя и расположение архивного файла или просто принять предложенное имя. В поле Compression можно выбрать степень уплотнения, что будет влиять на скорость архивации и размер архивного файла. Следующая строка Dictionary size дает возможность изменить размер внутреннего словаря архиватора. Этот параметр также будет влиять на размер конечного файла. С помощью диалогового поля Volume size можно разбить архивный файл на тома разного размера. Диалоговый блок Archiving options также предоставляет возможность изменять некоторые опции архивации, такие как:

– Solid archive / Плотный архив – при этом все файлы в архиве будут представляться как непрерывный поток данных что позволит увеличить степень сжатия, но замедлит обращение к файлам внутри архива;

– SFX archive / Самораспаковывающийся архив – создается ЕХЕ модуль архива;

– Multimedia compression / Мультимедиа-уплотнение – в этом режиме RAR выполняет интеллектуальный анализ данных, направленный на улучшение архивации звука, видео и т. п.;

– Put recovery record / Добавление записи восстановления данных – облегчение восстановления данных при их порче или потере;

– Pat authenticity verification / Добавлять проверку достоверности -WinRAR будет помещать в каждом новом и скорректированном архиве информацию относительно создателя, последнего времени коррекции и архивного имени;

– Delete files after archiving / Удалять файлы после их архивации – после перемещения в архив файлы будут удалены.

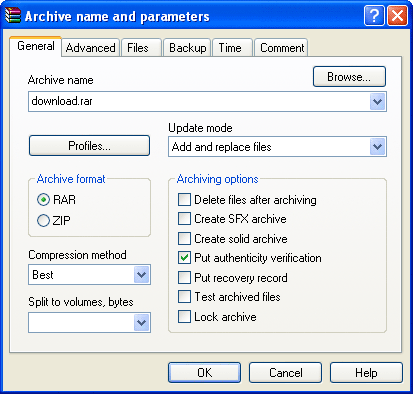
Рис. 5. Опции архивации в Win-RAR.

2.2. Программа-архиватор WinZip.

Программа-архиватор WinZip – один из старейших (представлен на рынке с 1991 года) архиваторов для Windows, имеющих собственный графический интерфейс. Столь солидный возраст, по всей видимости, и обеспечивает данному архиватору столь внушительную аудиторию пользователей.

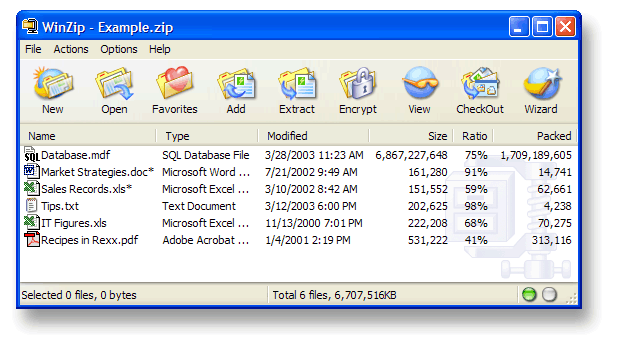
Рис. 6. Интерфейс программы-архиватора WinZip.

Архиватор WinZip сжимает файлы, преобразуя их в такие форматы, как: .zip, LHA (.lzh и .lha). Кроме того, WinZip имеет и собственный формат сжатия .zipx, использование которого позволяет добиться максимальной компрессии данных.

WinZip имеет поддержку практически всех известных на сегодня форматов, используемых для сжатия файлов, это: .rar, .7z, .bz2, .cab, .gzip, .tar, .cab и многие другие, кроме того WinZip располагает функционалом, позволяющим преобразовывать сжатые файлы этих форматов в Zip.

С помощью WinZip очень удобно сжимать цифровые фото без потери качества изображения, что может понадобиться, к примеру, для отправки большого количества файлов по электронной почте или FTP, а также и для хранения на всевозможных съемных носителях. В WinZip имеется возможность просмотра и редактирования файлов содержащихся в архивах других типовых форматов, например таких как: 7z или RAR.

Заключение

Сжатие файлов основано на устранении избыточности, содержащейся в исходных данных. Простейшим примером избыточности является повторение в тексте фрагментов (например, слов естественного или машинного языка). Подобная избыточность обычно устраняется заменой повторяющейся последовательности ссылкой на уже закодированный фрагмент с указанием его длины. Другой вид избыточности связан с тем, что некоторые значения в сжимаемых данных встречаются чаще других. Сокращение объёма данных достигается за счёт замены часто встречающихся данных короткими кодовыми словами, а редких — длинными (энтропийное кодирование). Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или шум, зашифрованные сообщения), принципиально невозможно без потерь.

Таким образом, было рассмотрено понятие сжатия данных, способы и методы их архивации. Существует множество алгоритмов архивации данных, основанных на различных подходах, с разными вариантами полученных сжатых файлов. Также , на основе этих способов, были разработаны многообразные программы-архиваторы, представляющие собой более простой метод сжатия данных. В данной работе были подробно рассмотрены два архиватора WinRAR и WinZip.

Литература

1. Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. — Диалог-МИФИ, 2002.

2. Информатика, ч. I: Методические указания к лабораторным работам / Сост. Н. И. Иопа – Рязань: РГРТА 2002.

3. Информатика. Базовый курс / С. В. Симонович и др. СПб.: Питер 2001

4. Информатика: Учебник/ Под ред. проф. Макаровой. 3-е изд. М.: Финансы и статистика, 2001

5. Д. Сэломон. Сжатие данных, изображения и звука. — М.: Техносфера, 2004.

Сжатие информации

Сжатие информации, компрессия, Шаблон:Англ. data compression — алгоритмическое преобразование данных (кодирование), при котором за счет уменьшения их избыточности уменьшается их обьём.

Принципы сжатия информации

В основе любого способа сжатия информации лежит модель источника информации, или, более конкретно, модель избыточности. Иными словами для сжатия информации используются некоторые сведения о том, какого рода информация сжимается — не обладая никакми сведениями об информации нельзя сделать ровным счётом никаких предположений, какое преобразование позволит уменьшить объём сообщения. Эта информация используется в процессе сжатия и разжатия. Модель избыточности может также строиться или параметризоваться на этапе сжатия. Методы, позволяющие на основе входных данных изменять модель избыточности информации, называются адаптивными. Неадаптивными являются обычно узкоспецифичные алгоритмы, применяемые для работы с хорошо определёнными и неизменными характеристиками. Подавляющая часть же достаточно универсальных алгоритмов являются в той или иной мере адаптивными.

Любой метод сжатия информации включает в себя два преобразования обратных друг другу:

• преобразование сжатия;
• преобразование расжатия.

Преобразование сжатия обеспечивает получение сжатого сообщения из исходного. Разжатие же обеспечивает получение исходного сообщения (или его приближения) из сжатого.

Все методы сжатия делятся на два основных класса

• без потерь,
• с потерями.

Кардинальное различие между ними в том, что сжатие без потерь обеспечивает возможность точного восстановления исходного сообщения. Сжатие с потерями же позволяет получить только некоторое приближение исходного сообщения, то есть отличающееся от исходного, но в пределах некоторых заранее определённых погрешностей. Эти погрешности должны определяться другой моделью — моделью приёмника, определяющей, какие данные и с какой точностью представленные важны для получателя, а какие допустимо выбросить.

Характеристики алгоритмов сжатия и применимость

Коэффициент сжатия

Коэффициент сжатия — основная характеристика алгоритма сжатия, выражающая основное прикладное качество. Она определяется как отношение размера несжатых данных к сжатым, то есть:

k = S_o/S_c,

где k — коэффициент сжатия, S_o — размер несжатых данных, а S_c — размер сжатых. Таким образом, чем выше коэффициент сжатия, тем алгоритм лучше. Следует отметить:

• если k = 1, то алгоритм не производит сжатия, то есть получает выходное сообщение размером, равным входному;
• если k < 1, то алгоритм порождает при сжатии сообщение большего размера, нежели несжатое, то есть, совершает «вредную» работу.

Ситуация с k < 1 вполне возможна при сжатии. Невозможно получить алгоритм сжатия без потерь, который при любых данных образовывал бы на выходе данные меньшей или равной длины. Обоснование этого факта заключается в том, что количество различных сообщений длиной n Шаблон:Е:бит составляет ровно 2ⁿ. Тогда количество различных сообщений с длиной меньшей или равной n (при наличии хотя бы одного сообщения меньшей длины) будет меньше 2ⁿ. Это значит, что невозможно однозначно сопоставить все исходные сообщения сжатым: либо некоторые исходные сообщения не будут иметь сжатого представления, либо нескольким исходным сообщениям будет соответствовать одно и то же сжатое, а значит их нельзя отличить.

Коэффициент сжатия может быть как постоянным коэффициентом (некоторые алгоритмы сжатия звука, изображения и т. п., например А-закон, μ-закон, ADPCM), так и переменным. Во втором случае он может быть определён либо для какого либо конкретного сообщения, либо оценён по некоторым критериям:

• среднее (обычно по некоторому тестовому набора данных);
• максимальное (случай наилучшего сжатия);
• минимальное (случай наихудшего сжатия);

или каким либо другим. Коэффициент сжатия с потерями при этом сильно зависит от допустимой погрешности сжатия или его качества, которое обычно выступает как параметр алгоритма.

Допустимость потерь

Основным критерием различия между алгоритмами сжатия является описанное выше наличие или отсутствие потерь. В общем случае алгоритмы сжатия без потерь универсальны в том смысле, что их можно применять на данных любого типа, в то время как применение сжатия потерь должно быть обосновано. Некоторые виды данных не приемлят каких бы то ни было потерь:

• символические данные, изменение которых неминуемо приводит к изменению их семантики: программы и их исходные тексты, двоичные массивы и т. п.;
• жизненно важные данные, изменения в которых могут привести к критическим ошибкам: например, получаемые с медицинской измерительной техники или контрольных приборов летательных, космических аппаратов и т. п.
• данные, многократно подвергаемые сжатию и расжатию: рабочие графические, звуковые, видеофайлы.

Однако сжатие с потерями позволяет добиться гораздо больших коэффициентов сжатия за счёт отбрасывания незначащей информации, которая плохо сжимается. Так, например алгоритм сжатия звука без потерь FLAC, позволяет в большинстве случаев сжать звук в 1,5—2,5 раза, в то время как алгоритм с потерями Vorbis, в зависимости от установленного параметра качетсва может сжать до 15 раз с сохранением приемлемого качества звучания.

Системные требования алгоритмов

Различные алгоритмы могут требовать различного количества ресурсов вычислительной системы, на которых исполняются:

• оперативной памяти (под промежуточные данные);
• постоянной памяти (под код программы и константы);
• процессорного времени.

В целом, эти требования зависят от сложности и «интеллектуальности» алгоритма. По общей тенденции, чем лучше и универсальнее алгоритм, тем большие требования с машине он предъявляет. Однако в специфических случаях простые и компактные алгоритмы могут работать лучше. Системные требования определяют их потребительские качества: чем менее требователен алгоритм, тем на более простой, а следовательно, компактной, надёжной и дешёвой системе он может работать.

Так как алгоритмы сжатия и разжатия работают в паре, то имеет значение также соотношение системных требований к ним. Нередко можно усложнив один алгоритм можно значительно упростить другой. Таким образом мы можем иметь три варианта:

Алгоритм сжатия гораздо требовательнее к ресурсам, нежели алгоритм расжатия.

Это наиболее распространённое соотношение, и оно применимо в основном в случаях, когда однократно сжатые данные будут использоваться многократно. В качетсве примера можно привести цифровые аудио и видеопроигрыватели.

Алгоритмы сжатия и расжатия имеют примерно равные требования.

Наиболее приемлемый вариант для линии связи, когда сжатие и расжатие происходит однократно на двух её концах. Например, это могут быть телефония.

Алгоритм сжатия существенно менее требователен, чем алгоритм разжатия.

Довольно экзотический случай. Может применяться в случаях, когда передатчиком является ультрапортативное устройство, где объём доступных ресурсов весьма критичен, например, космический аппарат или большая распределённая сеть датчиков, или это могут быть данные распаковка которых требуется в очень малом проценте случаев, например запись камер видеонаблюдения.

---

См. также

• Теория информации
• Теория вероятностей
• Статистика