Напряженность поля: шарики на нитках и работа поля
В этой статье собраны задачи, где необходимо применить закон сохранения энергии для того, чтобы найти требуемую силу. Кроме того, нужно вспомнить, что такое центростремительное ускорение, и правильно записать второй закон Ньютона в проекциях на оси. Если все это сделать внимательно – успех гарантирован.
Задача 1.
Тело массой г, имеющее заряд
мкКл, подвешено на нити. Тело отклоняют на
и отпускают. Чему равна сила натяжения нити в тот момент, когда нить составляет угол
с вертикалью? Тело находится в однородном электрическом поле с напряженностью
кВ/м, направленном вертикально вниз.
Решение.

К задаче 1
Когда шарик находился вверху, он обладал потенциальной энергией, во-первых, гравитационного взаимодействия, во-вторых, электрического. Определим, на какое расстояние по высоте переместился шарик, когда перешел из начальной точки в конечную:
Энергия шарика переходит из потенциальной в кинетическую:
Таким образом, скорость шарика в конечном положении равна
В конечном положении на шарик действуют силы: тяжести, кулонова, центробежная, сила натяжения нити. Составим уравнения по второму закону для каждой координатной оси, причем систему координат введем, направив ось ординат вдоль нити вверх. Тогда:
Подставим скорость, найденную ранее:
Задача решена, считаем:
Ответ: Н.
Задача 2.
В однородном электрическом поле с напряженностью кВ/м на нити прикреплен шарик массой
г и зарядом
мкКл. Шарик отклоняют от положения равновесия на угол
и отпускают. Найти натяжение нити в тот момент, когда шарик проходит положение равновесия. Силовые линии поля вертикальны.

К задаче 2
В верхнем положении равновесия на шарик действует сила тяжести, кулонова сила воздействия электрического поля, сила натяжения нити и центробежная сила. Уравнение по второму закону Ньютона будет записано так:
Скорость найдем из уравнения для энергий: шарик приобретает потенциальную энергию гравитационного взаимодействия и кинетическую, но теряет потенциальную энергию взаимодействия с электрическим полем, так как двигается вдоль его линий:
Тогда:
Определим теперь силу натяжения нити:
Задача решена, подставляем числа:
Ответ: Н
Задача 3.
В однородном электрическом поле с напряженностью , направление силовых линий которого совпадает с направлением силы тяжести, на нити длиной
висит шарик массой
, имеющий заряд
. Какую минимальную горизонтальную скорость надо сообщить шарику, чтобы он смог вращаться в вертикальной плоскости?

К задаче 3
Решение.
Так как шарик подвешен на нити, а не на стержне, то ему обязательно обладать скоростью в верхней точке траектории, чтобы не упасть. Эта скорость может быть определена из условия равенства нулю равнодействующей всех сил: на шарик действует сила тяжести и кулонова сила, а также центробежная сила. Силу натяжения нити считаем равной нулю.
С другой стороны, чтобы шарик мог забраться наверх, да еще преодолев силу, с которой поле на него воздействует, ему надо сообщить достаточную энергию: потенциальную, чтобы он поднялся на высоту
Кинетическую:
Да еще потенциальную энергию на преодоление воздействия поля:
Тогда ему нужно сообщить суммарную энергию:
Упростим:
Извлечем корень:
Ответ:
Задача 4.
В однородном электрическом поле с напряженностью на нити длиной
вращается вокруг вертикальной оси шарик массой
, имеющий заряд
. Направление силовых линий электрического поля совпадает с направлением силы тяжести. Определить минимальную работу
, которую нужно произвести для разгона шарика из состояния покоя до угловой скорости
.
Решение.
Поскольку шарик разогнали, следовательно, ему сообщили кинетическую энергию:
Пока шарик не вращался, а просто висел, он находился на расстоянии от точки крепления нити.

К задаче 4
Можно считать, что его потенциальная энергия гравитационного взаимодействия на данной высоте – нулевая. Когда угловая скорость шарика достигла , то очевидно, что, вращаясь по окружности радиуса
, он приподнялся, и его потенциальная энергия перестала быть нулевой – ведь теперь он поднялся на высоту
, где
. Тогда потенциальная энергия шарика, связанная с гравитацией, равна:
Также, приподнявшись, шарик приобрел потенциальную энергию, связанную с перемещением его в поле против силовых линий этого поля. Работа поля при этом отрицательна, но энергия, приобретенная шариком – положительна: при движении по линиям поля потенциальная энергия уменьшается, зато растет кинетическая, и наоборот.
Тогда потенциальная энергия электростатического взаимодействия заряда и поля равна:
В итоге минимальная работа, которую потребуется выполнить, – это сумма всех трех видов энергии, которые приобрел шарик:
Осталось совсем немного: определить радиус окружности, по которой вращается шарик.
Разделим второе уравнение на первое:
С другой стороны,
Тогда:
Или
Возведем в квадрат:
Теперь по теореме Пифагора определим радиус:
Теперь можем записывать окончательное выражение для работы:
Ответ:
Поле бесконечно заряженной нити
Рассмотрим бесконечную нить, несущую заряд, равномерно распределённый по её длине. Заряд, сосредоточенный на бесконечно нити, конечно, тоже бесконечен, и поэтому он не может служить количественной характеристикой степени заряженности нити. В качестве такой характеристики принимается «линейная плотность заряда». Эта величина равна заряду, распределённому на отрезке нити единичной длины:
 .
.
Выясним, какова напряженность поля, создаваемого заряженной нитью на расстоянии а от неё (рис. 1.12).

Для вычисления напряжённости вновь воспользуемся принципом суперпозиции электрических полей и законом Кулона. Выберем на нити элементарный участок dl.На этом участке сосредоточен заряд dq = tdl, который можно считать точечным. В точке А такой заряд создаёт поле (см. 1.3)
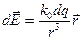
Исходя из симметрии задачи, можно заключить, что искомый вектор напряжённости поля 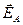 будет направлен по линии, перпендикулярной нити, то есть вдоль оси х. Поэтому сложение векторов напряжённости, можно заменить сложением их проекцией на это направление.
будет направлен по линии, перпендикулярной нити, то есть вдоль оси х. Поэтому сложение векторов напряжённости, можно заменить сложением их проекцией на это направление.
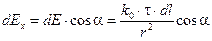 (1.7)
(1.7)
Рис. (1.12 b) позволяет сделать следующие заключения:
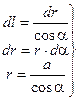 (1.8)
(1.8)
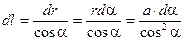 . (1.9)
. (1.9)
Используя (1.8) и (1.9) в уравнении (1.7), получим
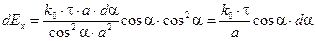 (1.10)
(1.10)
Теперь для решения задачи осталось проинтегрировать (1.10) по всей длине нити. Это означает, что угол a будет меняться от 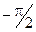 до
до 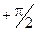 .
.
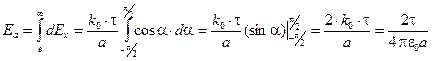 (1.11)
(1.11)
В этой задаче поле обладает цилиндрической симметрией. Напряжённость поля прямо пропорциональна линейной плотности заряда на нити t и обратно пропорциональна расстоянию а от нити до той точки, где измеряется напряжённость.
Лекция 2 «Теорема Гаусса для электрического поля»
Поток вектора напряженности электрического поля.
Теорема Гаусса для электрического поля.
Применение теоремы Гаусса для расчёта электрических полей.
Поле бесконечной заряженной нити.
Поле бесконечной заряженной плоскости. Поле плоского конденсатора.
Поле сферического конденсатора.
Первую лекцию мы закончили расчётом напряжённости полей электрического диполя и бесконечно заряженной нити. В обоих случаях использовался принцип суперпозиции электрических полей. Теперь обратимся ещё к одному методу вычисления напряжённости, основанному на теореме Гаусса для электрического поля. В этой теореме речь идёт о потоке вектора напряжённости через произвольную замкнутую поверхность. Поэтому прежде чем преступить к формулировке и доказательству теоремы, обсудим понятие «поток вектора».
Поток вектора напряжённости электрического поля
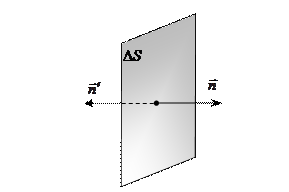
Выделим в однородном электрическом поле плоскую поверхность 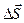 (рис. 2.1.). Эта поверхность — вектор, численно равный площади поверхности DS и направленный перпендикулярно поверхности
(рис. 2.1.). Эта поверхность — вектор, численно равный площади поверхности DS и направленный перпендикулярно поверхности
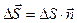 (2.1)
(2.1)
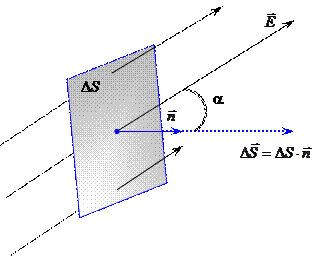
Но единичный нормальный вектор 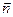 может быть направлен как в одну, так и в другую сторону от поверхности (рис. 2.2.). Произвольно выберем положительное направление нормали так, как это показано на рис. 2.1. По определению потоком вектора напряжённости электрического поля
может быть направлен как в одну, так и в другую сторону от поверхности (рис. 2.2.). Произвольно выберем положительное направление нормали так, как это показано на рис. 2.1. По определению потоком вектора напряжённости электрического поля 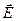 через выделенную поверхность
через выделенную поверхность 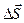 называется скалярное произведение этих двух векторов:
называется скалярное произведение этих двух векторов:
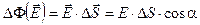 (2.2)
(2.2)
Если поле в общем случае неоднородно, а поверхность S, через которую следует вычислить поток, не плоская, то эту поверхность делят на элементарные участки 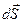 , в пределах которых напряжённость можно считать неизменённой, а сами участки — плоскими (рис. 2.3.) Поток вектора напряжённости через такой элементарный участок
, в пределах которых напряжённость можно считать неизменённой, а сами участки — плоскими (рис. 2.3.) Поток вектора напряжённости через такой элементарный участок 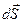 вычисляется по определению потока
вычисляется по определению потока
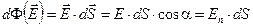 (2.3)
(2.3)
Здесь En = E ∙ cosa — проекция вектора напряжённости на направление нормали 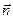 . Полный поток через всю поверхность S найдём, проинтегрировав (2.3) по всей поверхности
. Полный поток через всю поверхность S найдём, проинтегрировав (2.3) по всей поверхности
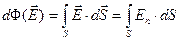 (2.4)
(2.4)
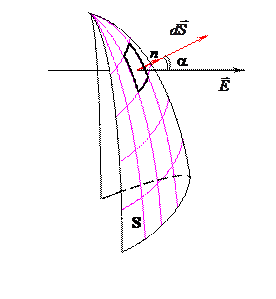
Теперь представим себе замкнутую поверхность в электрическом поле. Для отыскания потока вектора напряжённости через подобную поверхность проделаем следующие операции (рис. 2.4.):
Разделим поверхность на участки 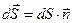 . Важно отметить при этом, что в случае замкнутой поверхности положительной считается только «внешняя» нормаль
. Важно отметить при этом, что в случае замкнутой поверхности положительной считается только «внешняя» нормаль 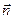 .
.
Вычислим поток на каждом элементарном участке 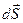 :
:
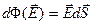
Обратите внимание на то, что вектор 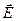 «вытекающий» из замкнутой поверхности создаёт положительный поток, а «втекающий» — отрицательный.
«вытекающий» из замкнутой поверхности создаёт положительный поток, а «втекающий» — отрицательный.
Для вычисления полного потока вектора напряжённости через всю замкнутую поверхность, все эти потоки нужно алгебраически сложить, то есть уравнение (2.3) проинтегрировать по замкнутой поверхности S
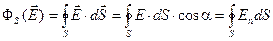 (2.5)
(2.5)
Кружок на знаке интеграл 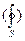 означает, что интегрирование производится по замкнутой поверхности.
означает, что интегрирование производится по замкнутой поверхности.

Напомним, что при графическом изображении полей, густота силовых линий в произвольной точке поля числено равна значению напряжённости поля в этой точке. Это означает, что
 .
.
Тогда число силовых линий, пронизывающих поверхность dS, можно записать так
Но ведь это определение потока вектора напряжённости через поверхность dS.
Таким образом, поток вектора напряжённости через поверхность dS численно равен числу силовых линий, пронизывающих эту поверхность (!).
Этот вывод справедлив и для потока электрического поля через замкнутую поверхность: этот поток будет равен алгебраической сумме силовых линий втекающих (–) и вытекающих (+) из замкнутой поверхности.
Теперь обратимся к теореме Гаусса.
Дата добавления: 2015-08-08 ; просмотров: 8885 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Напряженность поля заряженной нити
Модуль напряженности поля, создаваемого бесконечно длинной прямой однородно заряженной нитью (или цилиндром) на расстоянии r от ее оси
,
где t – линейная плотность заряда (см. п. 3).
Если заряженная нить имеет конечную длину, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из середины нити, на расстоянии r от нее
,
где q – угол между направлением нормали к нити и радиус-вектором, проведенным из рассматриваемой точки к концу нити.
Поверхностная плотность заряда
Заряд, распределенный на поверхности S, характеризуется поверхностной плотностью s
,
где Q – заряд, однородно распределенный на площадке S.
Напряженность заряженной плоскости
Напряженность поля, создаваемая бесконечной равномерно заряженной плоскостью,
.
Напряженность поля плоского конденсатора
Напряженность поля, создаваемая внутри заряженного плоского конденсатора для случая, если расстояние между пластинами много меньше линейных размеров пластин конденсатора
.
СПРАВОЧНЫЙ МАТЕРИАЛ
Электрическая постоянная e0=8,85×10 -12 Ф/м.
Элементарный заряд q=1,6×10 -19 Кл.
Масса электрона m=9,1×10 -31 кг.
Постоянная м/Ф.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какие фундаментальные свойства присущи электрическому заряду? Сформулируйте закон сохранения заряда.
2. В каких единицах измеряется электрический заряд? Чему равен элементарный заряд?
3. Какому закону подчиняется сила взаимодействия точечных зарядов? Какие утверждения содержит закон Кулона?
4. Получите численное значение и единицу электрической постоянной e0.
5. Как рассчитывается сила взаимодействия точечного заряда и зарядов, распределенных на телах конечных размеров?
6. Можно ли воспользоваться законом Кулона при расчете силы взаимодействия двух заряженных тел сферической формы?
7. Что является источником электрического поля? Как обнаруживается и исследуется электрическое поле?
8. Дайте определение напряженности электрического поля. В каких единицах измеряется напряженность?
9. Напишите формулу для напряженности E точечного заряда q. Изобразите график зависимости E(r), где r – расстояние от точечного заряда до точки поля, в которой определяется напряженность.
10. Каково содержание принципа суперпозиции электрических полей?
11. Как рассчитать напряженность поля заданного распределения точечных электрических зарядов?
12. Как вычисляется поток вектора напряженности электрического поля через любую поверхность?
13. Сформулируйте и запишите теорему Гаусса в интегральной форме.
14. Получите выражение для напряженности Е однородно заряженной бесконечной плоскости с поверхностной плотностью заряда s.
15. Получите выражение для напряженности E однородно заряженной сферы, цилиндра.
16. Напишите теорему Остроградского-Гаусса в дифференциальной форме.
ЗАДАЧИ ГРУППЫ А
1.(9.13) Два точечных заряда q1=7,5 нКл и q2=–14,7 нКл расположены на расстоянии r=5 см друг от друга. Найти напряженность E электрического поля в точке, находящейся на расстоянии a=3 см от положительного заряда и b=4 см от отрицательного заряда.
Ответ: E=112 кВ/м.
2.(9.15) Два металлических шарика одинакового радиуса и массы подвешены в одной точке на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд Q нужно сообщить шарикам, чтобы сила натяжения нитей стала равной T=98 мН? Расстояние от центра шарика до точки подвеса равно l=10 см, масса каждого шарика m=5 г.
Ответ: Q=1,1 мкКл.
3.(9.19) К вертикально расположенной бесконечной однородно заряженной плоскости прикреплена нить, на другом конце которой расположен одноименно заряженный шарик массой m=40 мг и зарядом q=31,8 нКл. Сила натяжения нити, на которой висит шарик, T=0,5 мН. Найти поверхностную плотность заряда s на плоскости. Диэлектрическая проницаемость среды, в которой находится заряд e=6. Ускорение свободного падения g=10 м/с 2 .
Ответ: s=1×10 -6 Кл/м 2 .
4.(9.20) Найти силу F, действующую на заряд q=0,66 нКл, если заряд помещен: а) на расстоянии r1=2 см от длинной однородно заряженной нити с линейной плотностью заряда t=0,2 мкКл/м; б) в поле однородно заряженной плоскости с поверхностной плотностью заряда s=20 мкКл/м 2 ; в) на расстоянии r2=2 см от поверхности однородно заряженного шара радиусом R=2 см и поверхностной плотностью заряда s=20 мкКл/м 2 . Диэлектрическая проницаемость среды e=6.
Ответ: а) F1=20мкН; б) F2=126мкН; в) F3=62,8 мкН.
5.(9.23) С какой силой Fl электрическое поле бесконечной однородно заряженной плоскости действует на единицу длины однородно заряженной бесконечно длинной нити, помещенной в это поле? Линейная плотность заряда на нити t=3 мкКл/м и поверхностная плотность заряда на плоскости s=20 мкКл/м 2 .
6.(9.26) С какой силой Fs на единицу площади отталкиваются две одноименные однородно заряженные бесконечно протяженные плоскости. Поверхностная плотность заряда на плоскостях s=0,3 мкКл/м 2 .
7.(9.29) Показать, что электрическое поле, образованное однородно заряженной нитью конечной длины, в предельных случаях переходит в электрическое поле: а) бесконечно длинной заряженной нити; б) точечного заряда.
8.(9.30) Длина однородно заряженной нити l=25 см. При каком предельном расстоянии a от нити по нормали к ее середине возбуждаемое ею электрическое поле можно рассматривать как поле бесконечно длинной заряженной нити? Ошибка d при таком допущении не должна превышать 0,05. Указание: допускаемая ошибка d равна (E2–E1)/E2, где E2 – напряженность электрического поля бесконечно длинной нити, E1 – напряженность поля нити конечной длины.
Ответ: a=4,18 см.
9.(9.33) Напряженность электрического поля на оси однородно заряженного кольца имеет максимальное значение на некотором расстоянии от центра кольца. Во сколько раз напряженность электрического поля в точке, расположенной на половине этого расстояния, будет меньше максимального значения напряженности?
Ответ: в 1,3 раза.
10. По четверти кольца радиусом r=6,1 см однородно распределен положительный заряд с линейной плотностью t=64 нКл/м. Найти силу F, действующую на заряд q=12 нКл, расположенный в центре кольца.
Ответ: F=160 мкН.
11. Получите соотношения п.12 раздела “Основные формулы для решения задач”.
ЗАДАЧИ ГРУППЫ Б
1.(3.2) Два одинаковых заряженных алюминиевых шарика, подвешенных в воздухе на нитях одинаковой длины, закрепленных в одной точке, опускают в жидкий диэлектрик. При этом оказалось, что угол расхождения нитей не изменился. Какова плотность r жидкого диэлектрика, если его относительная диэлектрическая проницаемость e=2? Плотность алюминия ra=2700 кг/м 3 .
Ответ: r=1350 кг/м 3 .
2.(3.6) В вершинах квадрата находятся одинаковые заряды по q=300 пКл каждый. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания зарядов была уравновешена силой притяжения к отрицательному заряду?
Ответ: Q=–0,287 нКл.
3.(3.7) В вершинах правильного шестиугольника со стороной b=10 см находятся одинаковые заряды по q=1 нКл каждый. Чему равна сила F, действующая на каждый заряд со стороны пяти остальных?
Ответ: F=1,64×10 -6 Н.
4.(3.8) Два положительных точечных заряда q1=1 нКл и q2=2 нКл находятся на расстоянии r=5 см друг от друга. Какой величины и в каком месте нужно расположить отрицательный заряд Q, чтобы вся система находилась в равновесии?
Какое будет равновесие?
Ответ: Q=–0,34 нКл нужно расположить на расстоянии 2,07 см от заряда q1 на линии, соединяющей заряды. Равновесие неустойчивое.
5.(3.13) Электрическое поле создается двумя длинными параллельными равномерно и одинаково заряженными нитями, расположенными на расстоянии l=5 см друг от друга. Напряженность электрического поля в точке, равноотстоящей от каждой нити на расстояние b=5 см, равна E=1 мВ/м. Определить линейную плотность заряда t на каждой нити.
Ответ: t=1,6·10 -15 Кл/м.
6. Плоский горизонтально расположенный конденсатор с расстоянием между обкладками d=1 см заполнен касторовым маслом с плотностью r0=900 кг/м 3 . В масле взвешен заряженный медный шарик радиусом R=1 мм, несущий заряд Q=1 мкКл. Определить напряжение U, подаваемое на обкладки конденсатора, если плотность меди r=8,6×10 3 кг/м 3 , а ускорение свободного падения g=10 м/с 2 .
Ответ: U=3,2 В.
7.(3.17) Электрическое поле создается тонким проволочным однородно заряженным кольцом. Определить радиус R кольца, если точка, в которой напряженность электрического поля максимальна, расположена на оси кольца на расстоянии x=1 см от его центра.
Ответ: R=1,41 см.
8.(3.21) Поверхностная плотность заряда бесконечно протяженной вертикальной плоскости равна s=200 мкКл/м 2 . К плоскости на нити подвешен заряженный шарик массой m=10 г. Определить заряд q шарика, если нить образует с плоскостью угол a=30 0 .
Ответ: q=5 нКл.
9.(3.24) На отрезке тонкого прямого стержня длиной l=10 см однородно распределен заряд с линейной плотностью t=3 мкКл/см. Вычислить напряженность E, создаваемую этим зарядом, в точке, расположенной на оси стержня и удаленной от ближайшего его конца на расстояние a=10 см.
Ответ: E=13,5 МВ/м.
10.(3.28) Отрицательно заряженная пылинка находится в равновесии между двумя пластинами плоского конденсатора, расположенными горизонтально. Расстояние между пластинами d=2 см, разность потенциалов на пластинах U=612 В. Масса пылинки m=10 пг. Сколько электронов несет на себе пылинка? Ускорение свободного падения g=10 м/с 2 .
Ответ: 20.
11.(3.33) Капля массой m=10 -10 г и зарядом q, равным 10 зарядам электрона, поднимается вертикально вверх с ускорением a=2,2 м/с 2 между горизонтально расположенными пластинами плоского конденсатора. Определить поверхностную плотность заряда s на пластинах конденсатора. Силой сопротивления воздуха пренебречь. Ускорение свободного падения g=10 м/с 2 .
Ответ: s=6,75 мкКл/м 2 .
ЗАДАЧИ ГРУППЫ С
1. Получите соотношения п.14 раздела “Основные формулы для решения задач”.
2. Рассчитайте поле однородно заряженного по объему шара на расстоянии r от его центра, если радиус шара R, а объемная плотность заряда r.
Ответ: r R, .
3. Найти напряженность электрического поля в заштрихованной плоскости, образованной пересечением двух однородно заряженных по объему шаров, с плотностями заряда r и –r. Расстояние между центрами шаров а 2 . Найти напряженность поля Е в центре полусферы.
Ответ: E=s/(4e0)=1,9 кВ/м.
6. Прямая бесконечная тонкая нить несет заряд с линейной плотностью t1. Перпендикулярно нити расположен тонкий стержень длиной l (см. рис. 3.2). Ближайший к нити конец стержня находится на расстоянии а от нее. Определить силу F, действующую на стержень со стороны нити, если он заряжен с линейной плотностью t2.
Ответ: .
7. По тонкой нити, изогнутой по дуге окружности, однородно распределен заряд с линейной плотностью t=10 нКл/м. Определить напряженность электрического поля Е, создаваемую распределенным зарядом, в точке, совпадающей с центром кривизны дуги. Длина нити l=15 см составляет одну треть длины окружности.
Ответ: =2,17 кВ/м.
8. Длинный цилиндр радиусом R однородно заряжен с объемной плотностью заряда r. Найти зависимость напряженности электростатического поля, создаваемой этим цилиндром от расстояния r до его оси.
Ответ: 0 R, .
9. Напряженность электрического поля в точке, находящейся на перпендикуляре, восстановленном из центра однородно заряженного диска, на расстоянии x от него, имеет вид: , где s – поверхностная плотность заряда диска, R – его радиус. Получите это соотношение. Как изменится ответ задачи, если однородно заряженный диск радиусом R2 имеет концентрическое отверстие радиусом R1 (R2>R1)?
Ответ: .
10. Горизонтально расположенный диск, радиус которого R=0,5 м, заряжен однородно с поверхностной плотностью s=3,33×10 -4 Кл/м 2 . Маленький шарик массой m=3,14 г, имеющий заряд q=3,27×10 -7 Кл, находится над центром диска в состоянии равновесия. Определить его расстояние от центра диска. Ускорение свободного падения g=10 м/c 2 .
Ответ: =1,5 м.
11. Напряженность электрического поля зависит только от координат по закону где а – постоянная, , , – орты осей х, у и z. Найти величину заряда q, находящегося внутри сферы радиусом R с центром в начале координат.
Ответ: q=4pe0aR.
12. Пользуясь теоремой Остроградского-Гаусса в дифференциальной форме, найти напряженность E электрического поля внутри и вне бесконечной пластинки толщиной 2a, однородно заряженной с объемной плотностью заряда r.
Ответ: если –a£x£a;
если
Электростатика: элементы учебной физики
Лекция 5. Напряжённость электрического поля
Понятие электрического поля оказалось плодотворным потому, что удалось ввести количественные характеристики, которые позволяют решать конкретные физические задачи. К ним в первую очередь относятся напряжённость и потенциал электрического поля.
Экспериментальные исследования учащихся должны показать, что напряжённость реально может быть измерена и что эта величина действительно характеризует электрическое поле. Относительно новое для школьников – один и тот же прибор, электростатический динамометр, при соответствующей градуировке может быть использован в качестве измерителя и силы, и напряжённости. Однако это вовсе не значит, что этим прибором можно измерить любую электростатическую величину: ни при какой градуировке электростатического динамометра не удастся получить прибор, измеряющий, скажем, потенциал электрического поля.
Принципиально важно экспериментальное обоснование принципа суперпозиции электрических полей. Такое обоснование можно было бы осуществить уже при введении понятия электрического поля, но предпочтительнее сделать это, когда учащиеся будут ознакомлены с понятием напряжённости.
5.1. Напряжённость электрического поля. Силовой характеристикой электрического поля является вектор напряжённости электрического поля E, равный отношению вектора силы, действующей в данной точке поля на пробный положительный заряд, к величине этого заряда:
( 5.1)
Напряжённость в системе единиц СИ выражается в ньютонах на кулон (Н/Кл).
5.2. Напряжённость электрического поля точечного заряда. Во многих задачах электростатики размерами заряженных тел по сравнению с расстояниями до точек наблюдения можно пренебречь. В таких случаях говорят о точечных зарядах. Понятно, что на самом деле никаких точечных зарядов или заряженных точек в природе не существует, — это просто удобная абстракция.
Закон Кулона, как вы знаете, справедлив именно для точечных зарядов. Непосредственно из закона Кулона следует, что модуль вектора напряжённости электрического поля точечного заряда Q:
(5.2)
где R – расстояние до точки наблюдения, q – пробный положительный заряд.
5.3. Силовые линии электростатического поля. Фарадей, который ввёл понятие электрического поля, внутренним взором видел заряды, окружённые полями. Изображать их он стал линиями, вдоль которых на пробный заряд со стороны поля действуют силы. Силовые линии электростатического поля часто называют линиями напряжённости, т.к. вектор напряжённости электрического поля в любой точке такой линии касателен к ней. Вместо пробного заряда для построения силовых линий удобнее использовать электрический диполь.
Введя в электрическое поле положительный пробный заряд на нити, по его отклонению от положения равновесия определим направление напряжённости поля. Уберём заряд и вместо него в ту же точку внесём диполь. При этом обнаружим, что он повернулся своим положительным полюсом в направлении вектора напряжённости электрического поля. Используя диполь, нетрудно экспериментально доказать, что электрическое поле можно характеризовать силовыми линиями, т.е. такими линиями, в каждой точке которых напряжённость поля является касательной к ним.
Для этого создадим произвольное электрическое поле, введём в него диполь и отметим положение его положительного и отрицательного полюсов. Переместим диполь так, чтобы его, например, отрицательный полюс совпал с точкой, в которой находился положительный. Многократно повторяя эту операцию, получим совокупность точек. Соединив эти точки плавной линией, получим силовую линию исследуемого электростатического поля.
Опыт показывает, что через каждую точку поля проходит только одна силовая линия. Если бы было не так, то в точке пересечения двух силовых линий одного поля на заряд действовали бы разные силы.
Повторяя описанные выше действия, построим семейство силовых линий так, чтобы их начальные точки находились на поверхности заряженного тела на равных расстояниях друг от друга. Обнаружим, что силовые линии располагаются с различной густотой. Внесём в поле пробный заряд на нити в области с максимальной и минимальной густотой силовых линий и обнаружим, что в этих областях напряжённость электрического поля соответственно максимальна и минимальна.
Силовые линии сгущаются возле зарядов, т.е. там, где модуль вектора напряжённости электрического поля больше. Значит, густота силовых линий определяется напряжённостью поля. Семейство силовых линий в принципе может полностью охарактеризовать электрическое поле.
Проделанные опыты показывают, что силовые линии начинаются или заканчиваются на зарядах, идут в бесконечность или выходят из неё. В электростатическом поле замкнутых силовых линий нет.
5.4. Принцип суперпозиции напряжённостей электростатических полей. Из принципа суперпозиции полей следует, что сила, действующая на пробный заряд со стороны других зарядов, равна геометрической сумме всех действующих на заряд сил по отдельности. Но если это так, то напряжённости электрических полей, равные отношениям сил к величине пробного заряда, складываются подобно силам.
Таким образом, для электрических полей справедлив принцип суперпозиции в следующей формулировке: напряжённость результирующего электрического поля есть геометрическая (векторная) сумма напряжённостей полей, создаваемых отдельными зарядами:
E = E1 + E2 + E3 + … (5.3)
Применение принципа суперпозиции для напряжённостей позволяет существенно облегчить решение многих задач электростатики.
5.5. Поток вектора напряжённости электрического поля. Представим себе точечный положительный заряд Q, находящийся в центре сферической поверхности 1 радиусом r. В точках этой поверхности напряжённость электрического поля Так как площадь
поверхности сферы S = 4r 2 , то её произведение на напряжённость электрического поля не зависит ни от чего, кроме заряда:
(5.4)
поэтому характеризует электрическое поле в целом. Эта величина получила название потока вектора напряжённости электрического поля.
Поток напряжённости через концентрические сферические поверхности 1 и 2 одинаков. Так как он характеризует поле заряда в целом, нужно, чтобы он оставался тем же и для произвольной замкнутой поверхности 3. Но для неё вектор напряжённости уже не является нормалью к элементу поверхности. Поэтому для определения потока вектора E через элемент поверхности вместо площади этого элемента следует брать площадь его проекции на плоскость, перпендикулярную вектору E. Условимся поток считать положительным, если вектор напряжённости выходит из замкнутой поверхности, и отрицательным, если он входит в неё. Если заряд находится вне замкнутой поверхности 4, то поток напряжённости через неё равен нулю. Дело в том, что входящий внутрь области поток по модулю равен выходящему.
5.6. Теорема Гаусса. Мысленно переместим заряд из центра сферической поверхности в любую точку внутри неё. Очевидно, поток вектора напряжённости электрического поля от этого не изменится, т.к., по самому определению, он один и тот же для любой замкнутой поверхности, окружающей заряд. Разместим внутри этой поверхности не один, а несколько в общем случае различных зарядов. По принципу суперпозиции электрические поля этих зарядов не влияют друг на друга, значит, потоки, созданные каждым зарядом по отдельности, остаются неизменными. Результирующий поток, очевидно, равен сумме потоков от всех зарядов.
Это и есть теорема Гаусса: поток вектора напряжённости через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, делённой на электрическую постоянную:
(5.5)
Если алгебраическая сумма зарядов внутри замкнутой поверхности равна нулю, то поток напряжённости электрического поля через эту поверхность также равен нулю. Это понятно, поскольку положительные заряды внутри поверхности создают положительный поток, а отрицательные – равный ему по модулю отрицательный.
5.7. Поверхностная плотность заряда. Если проводящему телу сообщить заряд, то он будет распределён по его поверхности. В общем случае на участках поверхности одинаковой площади окажутся разные заряды. Отношение заряда Q к площади поверхности S, на которой он распределён, называется поверхностной плотностью заряда
(5.6)
Поверхностная плотность заряда выражается в кулонах на квадратный метр (Кл/м 2 ).
5.8. Напряжённость электрического поля заряженного шара. Используя теорему Гаусса, нетрудно определить напряжённость электрического поля, созданного заряженным проводящим шаром. Действительно, если на поверхности сферы радиусом r > R, центр которой совпадает с центром шара, равномерно распределён заряд Q, то поток вектора E через сферическую поверхность радиусом r, согласно теореме Гаусса, равен:
Отсюда напряжённость электрического поля на расстоянии r от центра заряженной сферы равна
(5.7)
Сравнивая (5.7) с (5.2), приходим к выводу, что напряжённость электрического поля заряженного шара равна напряжённости такого же точечного заряда, расположенного в центре шара.
5.9. Напряжённость электрического поля заряженной плоскости. Рассмотрим бесконечную плоскость, заряженную равномерно с поверхностной плотностью заряда . Электрическое поле такой поверхности однородно, причём силовые линии перпендикулярны поверхности. Чтобы найти напряжённость поля, воспользуемся теоремой Гаусса. Для этого построим замкнутую цилиндрическую поверхность, ось которой параллельна силовым линиям поля, а основания площадью S находятся по разные стороны от поверхности. Поток напряжённости через боковую поверхность цилиндра равен нулю, т.к. силовые линии её не пересекают. Поэтому полный поток напряжённости через выбранную поверхность равен сумме потоков через основания цилиндра: N = 2 • ЕS. Полный заряд внутри цилиндра равен Q = S. Согласно теореме Гаусса, Отсюда напряжённость электрического поля
(5.8)
Итак, напряжённость электрического поля заряженной плоскости равна поверхностной плотности заряда, делённой на удвоенное значение электрической постоянной.
5.10. Напряжённость электрического поля разноимённо заряженных параллельных плоскостей. Пусть некоторая плоскость заряжена равномерно с плотностью заряда . Параллельно этой плоскости расположим вторую, с такой же плотностью заряда противоположного знака. Найдём напряжённость электрического поля в этом случае.
Каждая плоскость создаёт поле напряжённостью E’ = /(20). Согласно принципу суперпозиции, напряжённость результирующего электрического поля равна сумме напряжённостей этих полей. Так как между плоскостями напряжённости полей имеют одинаковое направление, то результирующая напряжённость Е = 2E’:
(5.9)
Следовательно, напряжённость электрического поля между параллельными плоскостями, несущими равные по модулю разноимённые заряды, равна поверхностной плотности заряда одной из плоскостей, делённой на электрическую постоянную. Вне плоскостей векторы напряжённостей направлены противоположно и, поскольку их модули равны, поле вообще отсутствует. Обратите внимание, что не важно, проводят плоскости электричество или нет.
Исследование 5.1. Напряжённость электрического поля
Проблема. Возможна ли в доступном учебном эксперименте количественная оценка напряжённости электрического поля, создаваемого зарядами на наэлектризованных телах?
Задание. Используя электростатический динамометр, разработайте методику введения понятия напряжённости электрического поля и предложите прибор для измерения напряжённостей.
Вариант выполнения. Проводящему шару сообщите заряд, для определённости положительный. На пробный шарик электростатического динамометра (см. исследование 3.4) также нанесите некоторый заряд. Введите динамометр в электрическое поле заряженного шара и разверните так, чтобы его показания стали максимальны. Это означает, что пробный шарик электростатического динамометра отклоняется в ту же сторону, куда направлена сила, действующая на него со стороны электрического поля.
Прикоснитесь к пробному шарику таким же незаряженным шариком и уберите его: пробный заряд уменьшится в два раза, показания динамометра для того же расстояния до точки наблюдения тоже уменьшаются в два раза.
Повторяя опыт с разными зарядами, убедитесь, что отношение силы f, действующей на пробный заряд q, к величине этого заряда в данной точке поля остаётся постоянным, а при переходе от одной точки к другой, вообще говоря, меняется. Значит, это отношение может характеризовать электрическое поле. Оно и получило название напряжённости электрического поля. Шкалу электростатического динамометра, которым вы пользовались для измерения силы электростатического взаимодействия, можно отградуировать в единицах напряжённости. Тогда допустимо считать этот прибор измерителем напряжённости электрического поля. Градуировку нетрудно осуществить в единицах Н/Кл, если предварительно измерить величину пробного заряда (см. исследование 3.6).
Учащиеся должны понять, каким образом один и тот же прибор превратился из измерителя силы в измеритель напряжённости.
Исследование 5.2. Зависимость напряжённости электрического поля от радиуса заряженного шара
Задание. Разработайте демонстрационный эксперимент, который может служить обоснованием справедливости теоремы Гаусса для электростатических полей.
Зарядите стоящий на диэлектрической подставке небольшой проводящий шар. К нему подведите измеритель напряжённости электрического поля, пробный шарик которого несёт такой же по знаку заряд, как заряд, создающий исследуемое поле. Запомните отклонение стрелки измерителя.
Первый шар с зарядом опустите в полость второго проводящего шара значительно большего диаметра, установленного на диэлектрической подставке. Приближайте этот второй шар к пробному шарику измерителя напряжённости. Оказывается, когда центр второго шара совпадает с точкой, в которой находился центр первого шара, стрелка измерителя отклоняется на первоначальное число делений.
Отсюда следует, что независимо от радиуса заряженного шара на одном и том же расстоянии от его центра напряжённость электрического поля одна и та же. Тем самым теорема Гаусса получила подтверждение в демонстрационном эксперименте.
Понятно, что теорема Гаусса носит общий характер и, строго говоря, не нуждается в обоснованиях, подобных здесь рассмотренному. Но в дидактических целях такое обоснование совершенно необходимо, поскольку оно способствует укреплению в сознании учащихся неразрывной связи физической теории с объективной реальностью.
Исследование 5.3. Суперпозиция электрических полей
Информация. Чтобы убедиться в справедливости принципа суперпозиции электрических полей, нужно уметь определять не только модули сил, действующих на заряды, но и их направления. Делать это с помощью электростатического динамометра неудобно. Кроме того, он не позволяет графически изображать векторы сил. Если на нити подвесить лёгкое заряженное тело, то силу, действующую на него в электрическом поле, можно оценить по отклонению тела из положения равновесия. Но для измерения этого отклонения воспользоваться линейкой не удастся: приближение её к заряженному телу вызывает изменение его положения. Чтобы устранить эту трудность, можно спроецировать заряженное тело на горизонтальную плоскость.
Задание. Разработайте и выполните эксперимент, доказывающий справедливость принципа суперпозиции электрических полей.
Вариант выполнения. К стеклянному баллону маленькой лампочки приклейте тонкую нить с лёгким проводящим шариком небольшого радиуса на конце. Нанесите на шарик пробный заряд. Лампочку закрепите над листом бумаги и включите её. На листе бумаги цифрой 0 отметьте положение тени от шарика, находящегося в положении равновесия. Приблизьте к пробному заряду заряд Q1 и цифрой 1 отметьте на листе положение тени отклонившегося шарика. Уберите заряд Q1 и вместо него вблизи пробного шарика расположите заряд Q2. При этом тень от шарика займёт новое положение 2.
Верните заряд Q1 в первоначальное положение. Теперь пробный шарик находится в поле сразу двух зарядов и отклоняется от положения равновесия так, что его тень занимает положение 3. Проанализируйте результат эксперимента. Очевидно, при смещении шарика из положения равновесия его тень смещается на величину, пропорциональную силе, действующей на шарик в новом положении равновесия (см. исследование 3.5). При малых отклонениях пробного шарика эту силу приближённо можно считать равной силе, действующей на шарик в исходном положении. Длины отрезков, соединяющих точку 0 с точками 1, 2 и 3, пропорциональны модулям соответствующих сил. Соединив указанные точки векторами, вы обнаружите, что вектор результирующей силы, действующей на пробный заряд, примерно равен сумме векторов сил, действующих на него со стороны каждого заряда по отдельности. Понятно, что точные измерения, выполненные с более совершенными приборами, вместо приближённого дадут точное равенство.
Поразительно единство природы: силы, созданные электрическими полями, складываются так же, как механические! Но если это так, то напряжённости электрических полей, равные отношениям сил к величине пробного заряда, складываются подобно силам. Оставив шары неподвижными, изменяйте их заряды в одинаковое число раз (см. п. 2.6). При этом вы обнаружите, что направление напряжённости результирующего поля остаётся неизменным.
Таким образом, принцип суперпозиции электростатических полей экспериментально обоснован.
Исследование 5.4. Демонстрация принципа суперпозиции напряжённостей
Проблема. Индивидуальный опыт, выполненный в результате предыдущего исследования, не позволяет убедиться в справедливости принципа суперпозиции напряжённостей электростатических полей всему классу непосредственно на уроке. Как решить эту проблему?
Задание. Учитывая возможности кодоскопа, разработайте демонстрационный вариант эксперимента, обосновывающего справедливость принципа суперпозиции, и методику проведения его на уроке.
Вариант выполнения. Из толстой алюминиевой проволоки в изоляции выгните специальный штатив высотой примерно 30 см и поставьте его на конденсор кодоскопа. К верхнему концу штатива привяжите конец тонкой нейлоновой нити длиной примерно 20 см. На нижнем конце нити закрепите шарик диаметром около 3 мм из тонкой алюминиевой фольги. На конденсор кодоскопа на стойках высотой 10 см, изготовленных из полиэтиленовых трубок, поставьте пенопластовые шары диаметром 15–20 мм, обёрнутые тонкой фольгой. Основания стоек лучше сделать из прозрачного оргстекла.
Уберите с конденсора стойки с шарами, включите осветитель кодоскопа и на классной доске получите изображение висящего на нити пробного шарика. Одноимёнными зарядами зарядите пробный шарик и два шара на стойках. На доске мелом отметьте положение пробного шарика. Поставьте на конденсор один из заряженных шаров, отметьте его положение и положение пробного шарика. Уберите первый заряженный шар и в произвольное место поставьте второй, отметив на доске новое положение пробного шарика. Верните в первоначальное положение первый шар, обозначьте результирующее положение пробного шарика, мелом на доске нарисуйте соответствующие векторы сил и предложите учащимся сделать вывод из продемонстрированного опыта.
Исследование 5.5. Плотность заряда на поверхности проводника
Задание. Докажите, что плотность заряда на поверхности проводника, вообще говоря, различна.
Вариант выполнения. Зарядите расположенный на изолирующей подставке проводник цилиндрической формы с остриём и коническим углублением. Пробным шариком на изолирующей ручке, предварительно заземлённым, коснитесь цилиндрической поверхности проводника и поместите его внутрь полого шара, соединённого с электрометром. Если угол отклонения стрелки мал, повторите перенос заряда несколько раз. Запомните показания электрометра, разрядите его и пробный шарик. Попробуйте снять заряд из конического углубления в поверхности проводника, и вы убедитесь, что там он практически отсутствует. Повторите опыт, касаясь пробным шариком теперь уже точки поверхности, расположенной на острие проводника. В этом случае угол отклонения стрелки электрометра будет значительно больше, чем в первом опыте. Так как вблизи острия пробный шарик заряжается до большей величины, то в этой области плотность распределения заряда по поверхности проводника больше.
Зарядите металлический диск, закреплённый за изолирующую ручку в штативе. Проведя опыты, аналогичные описанным, покажите, что плотность заряда во всех точках плоской поверхности диска вдали от его края одинакова, а на краю возрастает.
Исследование 5.6. Напряжённость электрического поля вблизи заряженного проводника
Задание. Поставьте опыт, показывающий, что напряжённость электрического поля вблизи заряженного проводника определяется поверхностной плотностью заряда.
Вариант выполнения. Вблизи проводника сложной формы расположите электростатический динамометр и перемещайте его так, чтобы расстояние до поверхности проводника оставалось постоянным, а сила действовала на шарик динамометра по нормали к поверхности. Опыт должен показать, что там, где на поверхности проводника плотность заряда больше, вблизи этой поверхности больше и напряжённость электрического поля (см. исследование 5.5). Проанализируйте полученные результаты и сделайте соответствующие выводы.
Исследование 5.7. Электрическое поле вблизи заряженных плоскостей
Задание. Прямым экспериментом подтвердите, что равномерно заряженная плоскость даёт электрическое поле по обе стороны от неё, а две параллельно установленные плоскости, несущие равные заряды противоположных знаков, создают электрическое поле только в области между ними.
Вариант выполнения. На нитях подвесьте два одинаковых обёрнутых алюминиевой фольгой пенопластовых шарика так, чтобы они касались металлического диска с противоположных сторон. Зарядите диск от пьезоэлектрического или иного источника. При этом шарики отойдут от диска на равные расстояния, свидетельствуя о том, что электрическое поле существует по обе стороны от заряженного диска.
Точно такой же диск зарядите равным по модулю и противоположным по знаку зарядом. Постепенно приближайте второй диск к первому так, чтобы они оставались параллельными. Вы заметите, что отклонение шарика, находящегося вне дисков, уменьшается, а находящегося между дисками – увеличивается. Наконец, первый шарик касается диска, показывая, что поле вне дисков практически исчезло, а второй шарик отклоняется на угол, примерно в два раза превышающий первоначальный.
Исследование 5.8. Точное подтверждение закона Кулона
На диэлектрической стойке закрепите металлический шар и заключите его между двумя проводящими полусферами, одна из которых имеет отверстие. Через отверстие проводником на изолированной нити соедините шар с полусферами. Зарядите полусферы. За нить удалите проводник. Разомкнув шар и полусферы, разведите полусферы в стороны, разрядите их, а к шару подсоедините чувствительный электрометр: никакого заряда на шаре вы не обнаружите. Значит, эксперимент ещё раз показывает, что на проводнике, находящемся внутри другого проводника, заряда нет.
Это справедливо потому, что справедлив закон Кулона. Действительно, внутри проводящей равномерно заряженной сферы выберем произвольную точку А и вертикальными конусами вырежем на сфере площадки S1 и S2. Из геометрии известно, что Но эти площадки имеют заряды, пропорциональные их величинам: Небольшие площадки создают в точке А поля напряжённостями и отношение которых
Значит, поскольку напряжённости полей, созданных любыми подобными парами площадок на сфере, равны по модулю и противоположно направлены, результирующая напряжённость поля, созданного в точке А всей заряженной сферой, должна быть равна нулю.
Это и показывает эксперимент. Если бы на опыте был обнаружен хотя бы слабый заряд на внутреннем шаре, то оказалась бы неверной формула для напряжённости поля точечного заряда (5.2) и, следовательно, в законе Кулона (3.1) сила взаимодействия между зарядами не была бы обратно пропорциональна квадрату расстояния между ними. Так как заряд можно измерить с гораздо более высокой точностью, чем силу взаимодействия между зарядами, а из закона Кулона следует, что поле внутри тела отсутствует независимо от его формы, то рассмотренный эксперимент корректнее доказывает справедливость закона Кулона, чем ранее описанные опыты.
Задание. Разработайте и поставьте доступный вариант рассмотренного эксперимента, с максимальной убедительностью показывающий, что внутри заряженного полого проводника электрическое поле отсутствует.
Вариант выполнения. Чтобы обнаружить электрическое поле, можно воспользоваться явлением электростатической индукции. Внесём в поле два соприкасающихся проводящих тела на изолированных ручках. В них произойдёт перераспределение зарядов. Не удаляя из поля, разъединим эти тела – на них останутся заряды противоположных знаков. Эти заряды можно измерить электрометром, находящимся вне исследуемого поля.
Эксперимент можно поставить так. На подставке из диэлектрика закрепите полый металлический шар. Проводником в хорошей изоляции соедините его с одним из кондукторов электрофорной машины. К шару приблизьте второй кондуктор и приведите машину в действие. При этом возникнут мощные искровые разряды длиной до 10 см. Аккуратно введите внутрь шара одинаковые металлические пластинки на ручках из оргстекла. Приведите пластинки в соприкосновение, затем разъедините, аккуратно достаньте из полости шара и по очереди введите в шар электрометра. Вы обнаружите, что никакого заряда на пластинках нет! Значит, внутри проводящего шара электрическое поле отсутствует, несмотря на то, что шар в целом несёт значительный заряд, сообщаемый ему работающей электрофорной машиной. Повторите опыт, прикоснувшись пробным шариком изнутри к металлу заряженного шара, – вы вновь не обнаружите никакого заряда. Таким образом, весь электрический заряд сосредоточен на поверхности проводящего тела. Объясняется этот результат тем, что справедлив закон Кулона. В свою очередь, этот экспериментальный факт с высокой точностью подтверждает справедливость закона Кулона.
Вопросы для самоконтроля
1. В чём суть методики введения и формирования понятия напряжённости электрического поля?
2. Сравните метод построения силовых линий посредством диполя с методом визуализации электростатического поля мелким порошком, взвешенным в жидком диэлектрике.
3. Изложите методику демонстрации на уроке принципа суперпозиции электростатических полей.
4. Каким экспериментом можно подтвердить справедливость теоремы Гаусса?
5. Как зависят плотность заряда и напряжённость электрического поля от формы проводника?
6. Предложите демонстрационный опыт, прямо показывающий зависимость плотности заряда от площади проводника.
7. В чём дидактическая ценность опыта с обнаружением электрического поля вблизи одной и двух параллельных заряженных проводящих пластин?
8. Нужно ли в школе рассматривать метод точного подтверждения закона Кулона?
Бутиков Е.И., Кондратьев А.С. Физика: Учеб. пособие: В 3-х кн. Кн. 2. Электродинамика. Оптика. – М.: Физматлит, 2004.
Демонстрационный эксперимент по физике в старших классах средней школы: Т. 2. Электричество. Оптика. Физика атома: Под ред. А.А.Покровского. – М.: Просвещение, 1972.
Кабардин О.Ф., Орлов В.А., Эвенчик Э.Е. Физика: Учеб. для 10 кл. шк. и кл. с углубл. изуч. физики: Под ред. А.А.Пинского. – М.: Просвещение, 1997.
Учебное оборудование для кабинетов физики общеобразовательных учреждений: Под ред. Г.Г.Никифорова. — М.: Дрофа, 2005. (Cм. также «Физика» («ПС») № 10/2005; № 4/2007.)
Продолжение см. в № 22/07
[spoiler title=”источники:”]
http://zdamsam.ru/b51085.html
http://fiz.1sept.ru/article.php?ID=200702110
[/spoiler]
Для
расчёта полей, созданных зарядами,
которые равномерно распределены по
сферическим, цилиндрическим или плоским
поверхностям, применяют теорему
Остроградского – Гаусса (раздел 2.2).
Методика
расчёта полей с помощью теоремы
Остроградского
– Гаусса.
1) Выбираем
произвольную замкнутую поверхность,
охватывающую заряженное тело.
2) Вычисляем поток
вектора напряжённости сквозь эту
поверхность.
3) Вычисляем
суммарный заряд, охваченный этой
поверхностью.
4) Подставляем в
теорему Гаусса вычисленные величины и
выражаем напряжённость электростатического
поля.
Примеры расчёта некоторых полей
-
Поле
равномерно заряженного бесконечного
цилиндра (нити).

Пусть
бесконечный цилиндр радиусом R
равномерно заряжен с линейной плотностью
заряда +
τ (рис.
16).
Из
соображений симметрии следует, что
линии напряжённости поля в любой точке
будут направлены вдоль радиальных
прямых, перпендикулярных оси цилиндра.
В
качестве замкнутой поверхности выберем
коаксиальный с данным (с общей осью
симметрии) цилиндр радиусом
r
и высотой
ℓ.
Рассчитаем
поток вектора
![]() через
через
данную поверхность:
![]() ,
,
где
Sосн,
Sбок
– площади оснований и боковой поверхности.
Поток
вектора напряжённости сквозь площади
оснований равен нулю, поэтому
![]()
Суммарный заряд,
охватываемый выбранной поверхностью:
![]() .
.
Подставив
всё в теорему Гаусса, с учетом того, что
ε
= 1, получим:
![]() .
.
Напряжённость
электростатического поля, созданного
бесконечно длинным равномерно заряженным
цилиндром или бесконечно длинной
равномерно заряженной нитью в точках,
расположенных вне её:
![]() , (2.5)
, (2.5)
где
r
– расстояние
от оси
цилиндра до заданной точки (r
≥ R);
τ
– линейная плотностью заряда.
Если
r
< R,
то рассматриваемая замкнутая поверхность
зарядов внутри не содержит, поэтому в
этой области Е
= 0, т. е. внутри
цилиндра, поля нет.
-
Поле
равномерно заряженной бесконечной
плоскости
П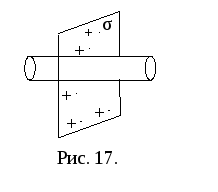 усть
усть
бесконечная плоскость заряжена с
постоянной поверхностной плотностью+σ.
В качестве
замкнутой поверхности выберем цилиндр,
основания которого параллельны заряженной
плоскости, а ось перпендикулярна ей
(рис. 17). Так как линии, образующие боковую
поверхность цилиндра, параллельны
линиям напряжённости, то поток вектора
напряжённости сквозь боковую поверхность
равен нулю. Поток вектора напряженности
сквозь две площади основания
![]() .
.
Суммарный
заряд, охватываемый выбранной поверхностью:
![]() .
.
Подставив
всё в теорему Гаусса, получим:
![]()
Напряженность
электростатического поля бесконечной
равномерно заряженной плоскости
![]() . (2.6)
. (2.6)
Из данной формулы
вытекает, что Е
не зависит от длины цилиндра, то есть
напряжённость поля одинакова во всех
точках. Иными словами, поле равномерно
заряженной плоскости однородно.
-
Поле
двух бесконечных параллельных
разноимённо
заряженных плоскостей
П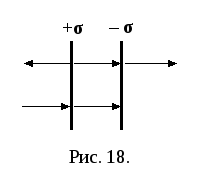 усть
усть
плоскости равномерно заряжены с
одинаковыми по величине поверхностными
плотностями +σ
и –σ
(рис. 18).
Согласно
принципу суперпозиции,
![]() .
.
Из
рисунка видно, что в области между
плоскостями силовые линии сонаправлены,
поэтому результирующая напряжённость
![]() . (2.7)
. (2.7)
Вне
объёма, ограниченного плоскостями,
складываемые поля имеют противоположные
направления, так что результирующая
напряженность равна нулю.
Таким
образом, поле оказывается сосредоточенным
между плоскостями. Полученный результат
приближённо справедлив и для плоскостей
конечных размеров, если расстояние
между плоскостями много меньше их
площади (плоский конденсатор).
Если
на плоскостях распределены заряды
одного знака с одинаковой поверхностной
плотностью, то поле отсутствует между
пластинами, а вне пластин вычисляется
по формуле (2.7).
-
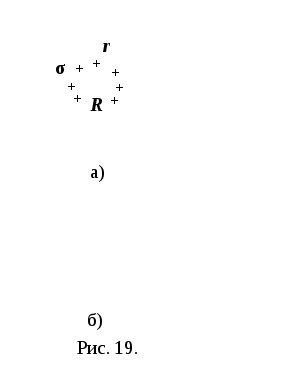
Напряжённость
поля
равномерно
заряженной сферы
Поле,
создаваемое сферической поверхностью
радиуса R,
заряженной с поверхностной плотностью
заряда σ,
будет центрально симметричным, поэтому
линии напряжённости направлены вдоль
радиусов сферы (рис. 19, а).
В качестве замкнутой
поверхности выберем сферу радиуса r,
имеющую общий центр с заряженной сферой.
Если r
> R,
то внутрь поверхности попадает весь
заряд Q.
Поток вектора
напряжённости сквозь поверхность сферы
![]()
Подставив это
выражение в теорему Гаусса, получим:
![]() .
.
Напряжённость
электростатического поля вне равномерно
заряженной сферы:
![]() , (2.8)
, (2.8)
где r
– расстояние от
центра
сферы.
Отсюда
видно, что поле тождественно с полем
точечного заряда той же величины,
помещённого в центр сферы.
Если
r
< R,
то замкнутая поверхность не содержит
внутри зарядов, поэтому внутри
заряженной сферы поле отсутствует
(рис.19, б).
-
Напряженность
поля объёмно
заряженного
шара
П усть
усть
шар радиусаR
заряжен с постоянной объёмной плотностью
заряда ρ.
Поле
в этом случае обладает центральной
симметрией. Для напряжённости поля вне
шара получается тот же результат, что
и в случае поверхностно заряженной
сферы
(2.8).
Для
точек внутри шара напряжённость будет
другая (рис. 20). Сферическая поверхность
охватывает заряд
![]()
Поэтому,
согласно теореме Гаусса
![]()
Учитывая,
что
![]() ,
,
получим:
Напряжённость
электростатического поля, внутри объемно
заряженного шара
![]() (r
(r
≤ R). (2.9)
 .
.
Задача
2.3. В поле
бесконечно длинной плоскости с
поверхностной плотностью заряда σ
подвешен на нити маленький шарик массой
m,
имеющий заряд того же знака, что и
плоскость. Найти заряд шарика, если нить
образует с вертикалью угол α
Решение.
Вернемся к разбору решения задачи 1.4.
Разница заключается в том, что в задаче
1.4 сила
![]() вычисляется по закону Кулона (1.2), а в
вычисляется по закону Кулона (1.2), а в
задаче 2.3 – из определения напряженности
электростатического поля (2.1)![]() .
.
Напряженность электростатического
поля бесконечной равномерно заряженной
плоскости выведена с использованием
теоремы Остроградского-Гаусса (2.4).
П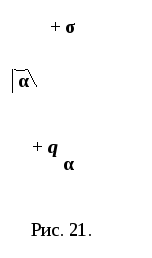 оле
оле
плоскости однородно и не зависит от
расстояния до плоскости. Из рис. 21:
![]() .
.
Обратите
внимание,
что для нахождения силы, действующей
на заряд, помещенный в поле распределенного
заряда, необходимо использовать формулу
![]() ,
,
а
напряженность поля, созданного несколькими
распределенными зарядами, находить по
принципу суперпозиции. Поэтому последующие
задачи посвящены нахождению напряженности
электростатического поля распределенных
зарядов с использованием теоремы
Остроградского-Гаусса.
Задача
2.4. Опередить
напряженность поля внутри и вне равномерно
заряженной пластинки толщиной d,
объемная плотность заряда внутри
пластинки ρ.
Построить график зависимости Е(х).
Решение.
Начало
координат поместим в средней плоскости
пластинки, а ось ОХ
направим перпендикулярно к ней (рис.
22, а). Применим теорему Остроградского-Гаусса
для расчета напряженности электростатического
поля заряженной бесконечной плоскости,
тогда
![]()
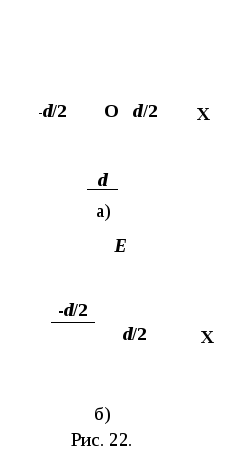 .
.
Из
определения объемной плотности заряда
![]() ,
,
тогда
для напряженности получим
![]() .
.
Отсюда
видно, что поле внутри пластинки зависит
от х.
Поле вне пластинки рассчитывается
аналогично:
![]()
Отсюда
видно, что поле вне пластинки однородно.
График зависимости напряженности Е
от х
на рис. 22, б.
Задача
2.5. Поле
создано двумя бесконечно длинными
нитями, заряженными с линейными
плотностями зарядов –
τ1
и + τ2.
Нити расположены перпендикулярно друг
другу (рис. 23). Найти напряженность поля
в точке, находящейся на расстоянии r1
и r2
от нитей.
Р ешение.
ешение.
Покажем на рисунке напряжённость поля,
созданного каждой нитью отдельно. Вектор
![]() направленк
направленк
первой
нити, так как она заряжена отрицательно.
Вектор
![]() направленот
направленот
второй нити, так как она заряжена
положительно. Векторы
![]() и
и![]() взаимно перпендикулярны, поэтому
взаимно перпендикулярны, поэтому
результирующий вектор![]() будет являться гипотенузой прямоугольного
будет являться гипотенузой прямоугольного
треугольника. Модули векторов![]() и
и![]() определяются по формуле (2.5).
определяются по формуле (2.5).
По принципу
суперпозиции
![]() .
.
По теореме Пифагора
 .
.
Задача
2.6. Поле
создано двумя заряженными бесконечно
длинными полыми коаксиальными цилиндрами
радиусами
R1
и R2 > R1.
Поверхностные плотности зарядов равны
–σ1
и +σ2.
Найти напряжённость электростатического
поля в следующих точках:
а)
точка А
расположена на расстоянии d1<
R1;
б)
точка В
расположена
на расстоянии R1
< d2
< R2;
в)
точка С
расположена на расстоянии d3
> R1>
R2.
Расстояния
отсчитываются от оси цилиндров.
Решение.
Коаксиальные цилиндры – это цилиндры,
имеющие общую ось симметрии. Сделаем
рисунок и покажем на нем точки (рис. 24).
-
т
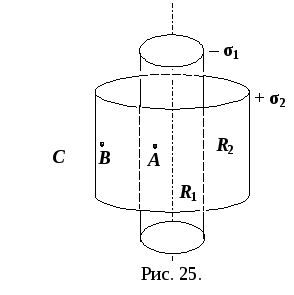 очкаА
очкаА
расположена внутри обоих цилиндров.
Так как внутри цилиндров поля нет, то
напряжённость в этой точке равна нулю:
ЕА
= 0.
-
точка
В
расположена внутри бóльшего цилиндра,
поэтому в этой точке поле создаётся
только меньшим цилиндром:
![]() .
.
Выразим
линейную плотность заряда через
поверхностную плотность заряда. Для
этого воспользуемся формулами (1.4) и
(1.5), из которых выразим заряд:
![]()
Приравняем правые
части и получим:
![]() ,
,
где
S1
– площадь поверхности первого цилиндра.
С
учётом того, что
![]() ,
,
окончательно получим:
![]()
-
точка
С
расположена снаружи обоих цилиндров,
поэтому поле создаётся обоими цилиндрами.
По принципу суперпозиции:
![]() .
.
С учётом направлений
и расчётов, полученных выше, получим:
![]() .
.
Задача
2.7. Поле
создано двумя заряженными бесконечно
длинными параллельными плоскостями.
Поверхностные плотности зарядов равны
σ1
и σ2
> σ1.
Найти напряжённость электростатического
поля в точках, находящихся между
пластинами и вне пластин. Решить задачу
для двух случаев:
а)
пластины одноимённо заряжены;
б)
пластины разноимённо заряжены.
Решение.
В векторном виде напряжённость
результирующего поля в любом случае
записывается одинаково. Согласно
принципу суперпозиции:
![]() .
.
Модули
векторов
![]() и
и![]() вычисляются по формуле (2.6).
вычисляются по формуле (2.6).
а)
Если плоскости заряжены одноимённо, то
между плоскостями напряжённости
направлены в разные стороны (рис. 26, а).
Модуль результирующей напряжённости
![]()
Вне
плоскостей напряжённости
![]() и
и![]() направлены
направлены
в одну сторону. Так как поле бесконечных
заряженных плоскостей однородно, то
есть не зависит от расстояния до
плоскостей, то в любой точке и слева и
справа от плоскостей поле будет одинаково:
.
![]()
б)
Если плоскости заряжены разноимённо,
то, наоборот, между плоскостями
напряжённости направлены в одну сторону
(рис. 26, б), а вне плоскостей – в разные.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электростатика: элементы учебной физики
Лекция 5. Напряжённость электрического поля
Продолжение. См. № 17,
18, 19, 20/07
В.В.МАЙЕР,
ГОУ ВПО ГГПИ им. В.Г.Короленко, г. Глазов,
Республика Удмуртия
varaksina_ei@list.ru
Электростатика: элементы учебной
физики
Понятие электрического поля оказалось
плодотворным потому, что удалось ввести
количественные характеристики, которые
позволяют решать конкретные физические задачи. К
ним в первую очередь относятся напряжённость и
потенциал электрического поля.
Экспериментальные исследования
учащихся должны показать, что напряжённость
реально может быть измерена и что эта величина
действительно характеризует электрическое поле.
Относительно новое для школьников – один и тот
же прибор, электростатический динамометр, при
соответствующей градуировке может быть
использован в качестве измерителя и силы, и
напряжённости. Однако это вовсе не значит, что
этим прибором можно измерить любую
электростатическую величину: ни при какой
градуировке электростатического динамометра не
удастся получить прибор, измеряющий, скажем,
потенциал электрического поля.
Принципиально важно
экспериментальное обоснование принципа
суперпозиции электрических полей. Такое
обоснование можно было бы осуществить уже при
введении понятия электрического поля, но
предпочтительнее сделать это, когда учащиеся
будут ознакомлены с понятием напряжённости.
5.1. Напряжённость электрического
поля. Силовой характеристикой
электрического поля является вектор
напряжённости электрического поля E,
равный отношению вектора силы, действующей в
данной точке поля на пробный положительный
заряд, к величине этого заряда:
( 5.1)
Напряжённость в системе единиц СИ
выражается в ньютонах на кулон (Н/Кл).
5.2. Напряжённость электрического
поля точечного заряда. Во многих задачах
электростатики размерами заряженных тел по
сравнению с расстояниями до точек наблюдения
можно пренебречь. В таких случаях говорят о
точечных зарядах. Понятно, что на самом деле
никаких точечных зарядов или заряженных точек в
природе не существует, — это просто удобная
абстракция.
Закон Кулона, как вы знаете, справедлив
именно для точечных зарядов. Непосредственно из
закона Кулона следует, что модуль вектора
напряжённости электрического поля точечного
заряда Q:
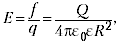
(5.2)
где R – расстояние до точки
наблюдения, q – пробный положительный заряд.
5.3. Силовые линии
электростатического поля. Фарадей, который
ввёл понятие электрического поля, внутренним
взором видел заряды, окружённые полями.
Изображать их он стал линиями, вдоль которых на
пробный заряд со стороны поля действуют силы. Силовые
линии электростатического поля часто
называют линиями напряжённости, т.к. вектор
напряжённости электрического поля в любой точке
такой линии касателен к ней. Вместо пробного
заряда для построения силовых линий удобнее
использовать электрический диполь.
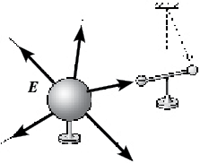
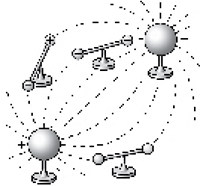
Введя в электрическое поле
положительный пробный заряд на нити, по его
отклонению от положения равновесия определим
направление напряжённости поля. Уберём заряд и
вместо него в ту же точку внесём диполь. При
этом обнаружим, что он повернулся своим
положительным полюсом в направлении вектора
напряжённости электрического поля. Используя
диполь, нетрудно экспериментально доказать, что
электрическое поле можно характеризовать
силовыми линиями, т.е. такими линиями, в каждой
точке которых напряжённость поля является
касательной к ним.
Для этого создадим произвольное
электрическое поле, введём в него диполь и
отметим положение его положительного и
отрицательного полюсов. Переместим диполь так,
чтобы его, например, отрицательный полюс совпал с
точкой, в которой находился положительный.
Многократно повторяя эту операцию, получим
совокупность точек. Соединив эти точки плавной
линией, получим силовую линию исследуемого
электростатического поля.
Опыт показывает, что через каждую
точку поля проходит только одна силовая линия.
Если бы было не так, то в точке пересечения двух
силовых линий одного поля на заряд действовали
бы разные силы.
Повторяя описанные выше действия,
построим семейство силовых линий так, чтобы их
начальные точки находились на поверхности
заряженного тела на равных расстояниях друг от
друга. Обнаружим, что силовые линии
располагаются с различной густотой. Внесём в
поле пробный заряд на нити в области с
максимальной и минимальной густотой силовых
линий и обнаружим, что в этих областях
напряжённость электрического поля
соответственно максимальна и минимальна.
Силовые линии сгущаются возле зарядов,
т.е. там, где модуль вектора напряжённости
электрического поля больше. Значит, густота
силовых линий определяется напряжённостью поля.
Семейство силовых линий в принципе может
полностью охарактеризовать электрическое поле.
Проделанные опыты показывают, что
силовые линии начинаются или заканчиваются на
зарядах, идут в бесконечность или выходят из неё.
В электростатическом поле замкнутых силовых
линий нет.
5.4. Принцип суперпозиции
напряжённостей электростатических полей.
Из принципа суперпозиции полей следует, что сила,
действующая на пробный заряд со стороны других
зарядов, равна геометрической сумме всех
действующих на заряд сил по отдельности. Но если
это так, то напряжённости электрических полей,
равные отношениям сил к величине пробного
заряда, складываются подобно силам.
Таким образом, для электрических полей
справедлив принцип суперпозиции в
следующей формулировке: напряжённость
результирующего электрического поля есть
геометрическая (векторная) сумма напряжённостей
полей, создаваемых отдельными зарядами:
E = E1 + E2 + E3 + …
(5.3)
Применение принципа суперпозиции для
напряжённостей позволяет существенно облегчить
решение многих задач электростатики.
5.5. Поток вектора напряжённости
электрического поля. Представим себе
точечный положительный заряд Q, находящийся
в центре сферической поверхности 1 радиусом r.
В точках этой поверхности напряжённость
электрического поля 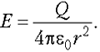 Так как площадь
Так как площадь
поверхности сферы S = 4![]() r2, то её
r2, то её
произведение на напряжённость электрического
поля не зависит ни от чего, кроме заряда:
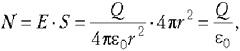
(5.4)
поэтому характеризует электрическое
поле в целом. Эта величина получила название потока
вектора напряжённости электрического поля.
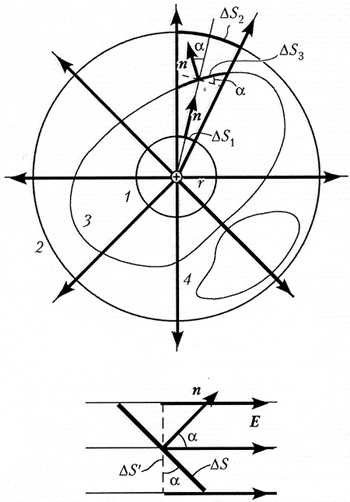
Поток напряжённости через
концентрические сферические поверхности 1 и
2 одинаков. Так как он характеризует поле
заряда в целом, нужно, чтобы он оставался тем же и
для произвольной замкнутой поверхности 3. Но
для неё вектор напряжённости уже не является
нормалью к элементу поверхности. Поэтому для
определения потока вектора E через
элемент поверхности вместо площади этого
элемента следует брать площадь его проекции на
плоскость, перпендикулярную вектору E.
Условимся поток считать положительным, если
вектор напряжённости выходит из замкнутой
поверхности, и отрицательным, если он входит в
неё. Если заряд находится вне замкнутой
поверхности 4, то поток напряжённости через
неё равен нулю. Дело в том, что входящий внутрь
области поток по модулю равен выходящему.
5.6. Теорема Гаусса. Мысленно
переместим заряд из центра сферической
поверхности в любую точку внутри неё. Очевидно,
поток вектора напряжённости электрического поля
от этого не изменится, т.к., по самому определению,
он один и тот же для любой замкнутой поверхности,
окружающей заряд. Разместим внутри этой
поверхности не один, а несколько в общем случае
различных зарядов. По принципу суперпозиции
электрические поля этих зарядов не влияют друг
на друга, значит, потоки, созданные каждым
зарядом по отдельности, остаются неизменными.
Результирующий поток, очевидно, равен сумме
потоков от всех зарядов.
Это и есть теорема Гаусса: поток
вектора напряжённости через произвольную
замкнутую поверхность равен алгебраической
сумме зарядов, расположенных внутри этой
поверхности, делённой на электрическую
постоянную:
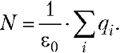
(5.5)
Если алгебраическая сумма зарядов
внутри замкнутой поверхности равна нулю, то
поток напряжённости электрического поля через
эту поверхность также равен нулю. Это понятно,
поскольку положительные заряды внутри
поверхности создают положительный поток, а
отрицательные – равный ему по модулю
отрицательный.
5.7. Поверхностная плотность
заряда. Если проводящему телу сообщить
заряд, то он будет распределён по его
поверхности. В общем случае на участках
поверхности одинаковой площади окажутся разные
заряды. Отношение заряда ![]() Q к площади поверхности
Q к площади поверхности ![]() S, на которой
S, на которой
он распределён, называется поверхностной
плотностью заряда
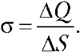
(5.6)
Поверхностная плотность заряда
выражается в кулонах на квадратный метр (Кл/м2).
5.8. Напряжённость электрического
поля заряженного шара. Используя теорему
Гаусса, нетрудно определить напряжённость
электрического поля, созданного заряженным
проводящим шаром. Действительно, если на
поверхности сферы радиусом r > R, центр
которой совпадает с центром шара, равномерно
распределён заряд Q, то поток вектора E
через сферическую поверхность радиусом r,
согласно теореме Гаусса, равен:
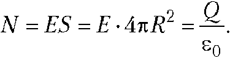
Отсюда напряжённость электрического
поля на расстоянии r от центра заряженной сферы
равна
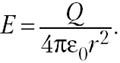
(5.7)
Сравнивая (5.7) с (5.2), приходим к выводу,
что напряжённость электрического поля
заряженного шара равна напряжённости такого же
точечного заряда, расположенного в центре шара.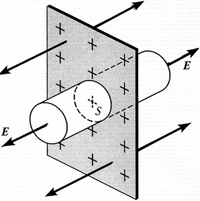
5.9. Напряжённость электрического поля
заряженной плоскости. Рассмотрим
бесконечную плоскость, заряженную равномерно с
поверхностной плотностью заряда ![]() . Электрическое поле такой
. Электрическое поле такой
поверхности однородно, причём силовые линии
перпендикулярны поверхности. Чтобы найти
напряжённость поля, воспользуемся теоремой
Гаусса. Для этого построим замкнутую
цилиндрическую поверхность, ось которой
параллельна силовым линиям поля, а основания
площадью S находятся по разные стороны от
поверхности. Поток напряжённости через боковую
поверхность цилиндра равен нулю, т.к. силовые
линии её не пересекают. Поэтому полный поток
напряжённости через выбранную поверхность равен
сумме потоков через основания цилиндра: N = 2 • ЕS.
Полный заряд внутри цилиндра равен Q = ![]() S. Согласно
S. Согласно
теореме Гаусса, 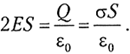
Отсюда напряжённость электрического поля
![]()
(5.8)
Итак, напряжённость электрического
поля заряженной плоскости равна поверхностной
плотности заряда, делённой на удвоенное значение
электрической постоянной.
5.10. Напряжённость электрического
поля разноимённо заряженных параллельных
плоскостей. Пусть некоторая плоскость
заряжена равномерно с плотностью заряда ![]() . Параллельно этой
. Параллельно этой
плоскости расположим вторую, с такой же
плотностью заряда противоположного знака.
Найдём напряжённость электрического поля в этом
случае.
Каждая плоскость создаёт поле
напряжённостью E’ = ![]() /(2
/(2![]() 0).
0).
Согласно принципу суперпозиции, напряжённость
результирующего электрического поля равна сумме
напряжённостей этих полей. Так как между
плоскостями напряжённости полей имеют
одинаковое направление, то результирующая
напряжённость Е = 2E’:
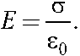 (5.9)
(5.9)
Следовательно, напряжённость
электрического поля между параллельными
плоскостями, несущими равные по модулю
разноимённые заряды, равна поверхностной
плотности заряда одной из плоскостей, делённой
на электрическую постоянную. Вне плоскостей
векторы напряжённостей направлены
противоположно и, поскольку их модули равны, поле
вообще отсутствует. Обратите внимание, что не
важно, проводят плоскости электричество или нет.
Исследование 5.1. Напряжённость
электрического поля
Проблема. Возможна ли в доступном
учебном эксперименте количественная оценка
напряжённости электрического поля, создаваемого
зарядами на наэлектризованных телах? 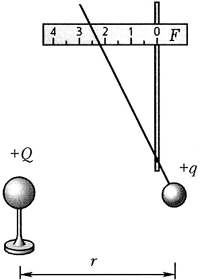
Задание. Используя
электростатический динамометр, разработайте
методику введения понятия напряжённости
электрического поля и предложите прибор для
измерения напряжённостей.
Вариант выполнения. Проводящему
шару сообщите заряд, для определённости
положительный. На пробный шарик
электростатического динамометра (см.
исследование 3.4) также нанесите некоторый заряд.
Введите динамометр в электрическое поле
заряженного шара и разверните так, чтобы его
показания стали максимальны. Это означает, что
пробный шарик электростатического динамометра
отклоняется в ту же сторону, куда направлена
сила, действующая на него со стороны
электрического поля.
Прикоснитесь к пробному шарику таким
же незаряженным шариком и уберите его: пробный
заряд уменьшится в два раза, показания
динамометра для того же расстояния до точки
наблюдения тоже уменьшаются в два раза.
Повторяя опыт с разными зарядами,
убедитесь, что отношение силы f, действующей
на пробный заряд q, к величине этого заряда в
данной точке поля остаётся постоянным, а при
переходе от одной точки к другой, вообще говоря,
меняется. Значит, это отношение может
характеризовать электрическое поле. Оно и
получило название напряжённости
электрического поля. Шкалу
электростатического динамометра, которым вы
пользовались для измерения силы
электростатического взаимодействия, можно
отградуировать в единицах напряжённости. Тогда
допустимо считать этот прибор измерителем
напряжённости электрического поля.
Градуировку нетрудно осуществить в единицах
Н/Кл, если предварительно измерить величину
пробного заряда (см. исследование 3.6).
Учащиеся должны понять, каким образом
один и тот же прибор превратился из измерителя
силы в измеритель напряжённости.
Исследование 5.2. Зависимость
напряжённости электрического поля от радиуса
заряженного шара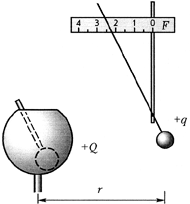
Задание. Разработайте
демонстрационный эксперимент, который может
служить обоснованием справедливости теоремы
Гаусса для электростатических полей.
Вариант выполнения.
Зарядите стоящий на диэлектрической
подставке небольшой проводящий шар. К нему
подведите измеритель напряжённости
электрического поля, пробный шарик которого
несёт такой же по знаку заряд, как заряд,
создающий исследуемое поле. Запомните
отклонение стрелки измерителя.
Первый шар с зарядом опустите в
полость второго проводящего шара значительно
большего диаметра, установленного на
диэлектрической подставке. Приближайте этот
второй шар к пробному шарику измерителя
напряжённости. Оказывается, когда центр второго
шара совпадает с точкой, в которой находился
центр первого шара, стрелка измерителя
отклоняется на первоначальное число делений.
Отсюда следует, что независимо от
радиуса заряженного шара на одном и том же
расстоянии от его центра напряжённость
электрического поля одна и та же. Тем самым
теорема Гаусса получила подтверждение в
демонстрационном эксперименте.
Понятно, что теорема Гаусса носит
общий характер и, строго говоря, не нуждается в
обоснованиях, подобных здесь рассмотренному. Но
в дидактических целях такое обоснование
совершенно необходимо, поскольку оно
способствует укреплению в сознании учащихся
неразрывной связи физической теории с
объективной реальностью.
Исследование 5.3. Суперпозиция
электрических полей
Информация. Чтобы убедиться в
справедливости принципа суперпозиции
электрических полей, нужно уметь определять не
только модули сил, действующих на заряды, но и их
направления. Делать это с помощью
электростатического динамометра неудобно. Кроме
того, он не позволяет графически изображать
векторы сил. Если на нити подвесить лёгкое
заряженное тело, то силу, действующую на него в
электрическом поле, можно оценить по отклонению
тела из положения равновесия. Но для измерения
этого отклонения воспользоваться линейкой не
удастся: приближение её к заряженному телу
вызывает изменение его положения. Чтобы
устранить эту трудность, можно спроецировать
заряженное тело на горизонтальную плоскость.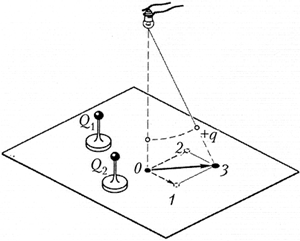
Задание. Разработайте и выполните
эксперимент, доказывающий справедливость
принципа суперпозиции электрических полей.
Вариант выполнения. К стеклянному
баллону маленькой лампочки приклейте тонкую
нить с лёгким проводящим шариком небольшого
радиуса на конце. Нанесите на шарик пробный
заряд. Лампочку закрепите над листом бумаги и
включите её. На листе бумаги цифрой 0
отметьте положение тени от шарика, находящегося
в положении равновесия. Приблизьте к пробному
заряду заряд Q1 и цифрой 1 отметьте
на листе положение тени отклонившегося шарика.
Уберите заряд Q1 и вместо него вблизи
пробного шарика расположите заряд Q2.
При этом тень от шарика займёт новое положение 2.
Верните заряд Q1 в
первоначальное положение. Теперь пробный шарик
находится в поле сразу двух зарядов и
отклоняется от положения равновесия так, что его
тень занимает положение 3. Проанализируйте
результат эксперимента. Очевидно, при смещении
шарика из положения равновесия его тень
смещается на величину, пропорциональную силе,
действующей на шарик в новом положении
равновесия (см. исследование 3.5). При малых
отклонениях пробного шарика эту силу
приближённо можно считать равной силе,
действующей на шарик в исходном положении. Длины
отрезков, соединяющих точку 0 с точками 1,
2 и 3, пропорциональны модулям
соответствующих сил. Соединив указанные точки
векторами, вы обнаружите, что вектор
результирующей силы, действующей на пробный
заряд, примерно равен сумме векторов сил,
действующих на него со стороны каждого заряда по
отдельности. Понятно, что точные измерения,
выполненные с более совершенными приборами,
вместо приближённого дадут точное равенство.
Поразительно единство природы: силы,
созданные электрическими полями, складываются
так же, как механические! Но если это так, то
напряжённости электрических полей, равные
отношениям сил к величине пробного заряда,
складываются подобно силам. Оставив шары
неподвижными, изменяйте их заряды в одинаковое
число раз (см. п. 2.6). При этом вы обнаружите, что
направление напряжённости результирующего поля
остаётся неизменным.
Таким образом, принцип суперпозиции
электростатических полей экспериментально
обоснован.
Исследование 5.4. Демонстрация
принципа суперпозиции напряжённостей
Проблема. Индивидуальный опыт,
выполненный в результате предыдущего
исследования, не позволяет убедиться в
справедливости принципа суперпозиции
напряжённостей электростатических полей всему
классу непосредственно на уроке. Как решить эту
проблему?
Задание. Учитывая возможности
кодоскопа, разработайте демонстрационный
вариант эксперимента, обосновывающего
справедливость принципа суперпозиции, и
методику проведения его на уроке.
Вариант выполнения. Из толстой
алюминиевой проволоки в изоляции выгните
специальный штатив высотой примерно 30 см и
поставьте его на конденсор кодоскопа. К верхнему
концу штатива привяжите конец тонкой нейлоновой
нити длиной примерно 20 см. На нижнем конце нити
закрепите шарик диаметром около 3 мм из тонкой
алюминиевой фольги. На конденсор кодоскопа на
стойках высотой 10 см, изготовленных из
полиэтиленовых трубок, поставьте пенопластовые
шары диаметром 15–20 мм, обёрнутые тонкой фольгой.
Основания стоек лучше сделать из прозрачного
оргстекла.
Уберите с конденсора стойки с шарами,
включите осветитель кодоскопа и на классной
доске получите изображение висящего на нити
пробного шарика. Одноимёнными зарядами зарядите
пробный шарик и два шара на стойках. На доске
мелом отметьте положение пробного шарика.
Поставьте на конденсор один из заряженных шаров,
отметьте его положение и положение пробного
шарика. Уберите первый заряженный шар и в
произвольное место поставьте второй, отметив на
доске новое положение пробного шарика. Верните в
первоначальное положение первый шар, обозначьте
результирующее положение пробного шарика, мелом
на доске нарисуйте соответствующие векторы сил и
предложите учащимся сделать вывод из
продемонстрированного опыта.
Исследование 5.5. Плотность заряда
на поверхности проводника 
Задание. Докажите, что плотность
заряда на поверхности проводника, вообще говоря,
различна.
Вариант выполнения. Зарядите
расположенный на изолирующей подставке
проводник цилиндрической формы с остриём и
коническим углублением. Пробным шариком на
изолирующей ручке, предварительно заземлённым,
коснитесь цилиндрической поверхности
проводника и поместите его внутрь полого шара,
соединённого с электрометром. Если угол
отклонения стрелки мал, повторите перенос заряда
несколько раз. Запомните показания электрометра,
разрядите его и пробный шарик. Попробуйте снять
заряд из конического углубления в поверхности
проводника, и вы убедитесь, что там он
практически отсутствует. Повторите опыт, касаясь
пробным шариком теперь уже точки поверхности,
расположенной на острие проводника. В этом
случае угол отклонения стрелки электрометра
будет значительно больше, чем в первом опыте. Так
как вблизи острия пробный шарик заряжается до
большей величины, то в этой области плотность
распределения заряда по поверхности проводника
больше.
Зарядите металлический диск,
закреплённый за изолирующую ручку в штативе.
Проведя опыты, аналогичные описанным, покажите,
что плотность заряда во всех точках плоской
поверхности диска вдали от его края одинакова, а
на краю возрастает.
Исследование 5.6. Напряжённость
электрического поля вблизи заряженного
проводника
Задание. Поставьте опыт,
показывающий, что напряжённость электрического
поля вблизи заряженного проводника определяется
поверхностной плотностью заряда.
Вариант выполнения. Вблизи
проводника сложной формы расположите
электростатический динамометр и перемещайте его
так, чтобы расстояние до поверхности проводника
оставалось постоянным, а сила действовала на
шарик динамометра по нормали к поверхности. Опыт
должен показать, что там, где на поверхности
проводника плотность заряда больше, вблизи этой
поверхности больше и напряжённость
электрического поля (см. исследование 5.5).
Проанализируйте полученные результаты и
сделайте соответствующие выводы.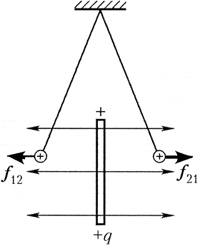
Исследование 5.7. Электрическое
поле вблизи заряженных плоскостей
Задание. Прямым экспериментом
подтвердите, что равномерно заряженная
плоскость даёт электрическое поле по обе стороны
от неё, а две параллельно установленные
плоскости, несущие равные заряды
противоположных знаков, создают электрическое
поле только в области между ними.
Вариант выполнения. На нитях
подвесьте два одинаковых обёрнутых алюминиевой
фольгой пенопластовых шарика так, чтобы они
касались металлического диска с противоположных
сторон. Зарядите диск от пьезоэлектрического или
иного источника. При этом шарики отойдут от диска
на равные расстояния, свидетельствуя о том, что
электрическое поле существует по обе стороны от
заряженного диска.
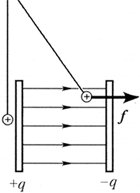 Точно такой же диск зарядите равным по
Точно такой же диск зарядите равным по
модулю и противоположным по знаку зарядом.
Постепенно приближайте второй диск к первому
так, чтобы они оставались параллельными. Вы
заметите, что отклонение шарика, находящегося
вне дисков, уменьшается, а находящегося между
дисками – увеличивается. Наконец, первый шарик
касается диска, показывая, что поле вне дисков
практически исчезло, а второй шарик отклоняется
на угол, примерно в два раза превышающий
первоначальный.
Исследование 5.8. Точное
подтверждение закона Кулона
Информация.
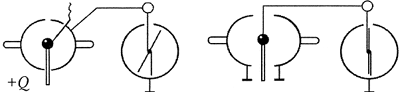
На диэлектрической стойке закрепите
металлический шар и заключите его между двумя
проводящими полусферами, одна из которых имеет
отверстие. Через отверстие проводником на
изолированной нити соедините шар с полусферами.
Зарядите полусферы. За нить удалите проводник.
Разомкнув шар и полусферы, разведите полусферы в
стороны, разрядите их, а к шару подсоедините
чувствительный электрометр: никакого заряда на
шаре вы не обнаружите. Значит, эксперимент ещё
раз показывает, что на проводнике, находящемся
внутри другого проводника, заряда нет.
Это справедливо потому, что справедлив
закон Кулона. Действительно, внутри проводящей
равномерно заряженной сферы выберем
произвольную точку А и вертикальными
конусами вырежем на сфере площадки ![]() S1 и
S1 и ![]() S2. Из геометрии
S2. Из геометрии
известно, что ![]() Но
Но
эти площадки имеют заряды, пропорциональные их
величинам: ![]()
Небольшие площадки создают в точке А поля
напряжённостями ![]()
и ![]() отношение
отношение
которых
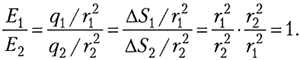
Значит, поскольку напряжённости полей,
созданных любыми подобными парами площадок на
сфере, равны по модулю и противоположно
направлены, результирующая напряжённость поля,
созданного в точке А всей заряженной сферой,
должна быть равна нулю.
Это и показывает эксперимент. Если бы
на опыте был обнаружен хотя бы слабый заряд на
внутреннем шаре, то оказалась бы неверной
формула для напряжённости поля точечного заряда
(5.2) и, следовательно, в законе Кулона (3.1) сила
взаимодействия между зарядами не была бы обратно
пропорциональна квадрату расстояния между ними.
Так как заряд можно измерить с гораздо более
высокой точностью, чем силу взаимодействия между
зарядами, а из закона Кулона следует, что поле
внутри тела отсутствует независимо от его формы,
то рассмотренный эксперимент корректнее
доказывает справедливость закона Кулона, чем
ранее описанные опыты. 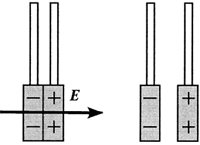
Задание. Разработайте и поставьте
доступный вариант рассмотренного эксперимента,
с максимальной убедительностью показывающий,
что внутри заряженного полого проводника
электрическое поле отсутствует.
Вариант выполнения. Чтобы
обнаружить электрическое поле, можно
воспользоваться явлением электростатической
индукции. Внесём в поле два соприкасающихся
проводящих тела на изолированных ручках. В них
произойдёт перераспределение зарядов. Не удаляя
из поля, разъединим эти тела – на них останутся
заряды противоположных знаков. Эти заряды можно
измерить электрометром, находящимся вне
исследуемого поля.
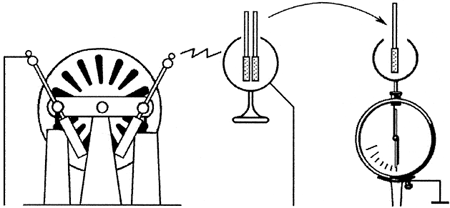
Эксперимент можно поставить так. На
подставке из диэлектрика закрепите полый
металлический шар. Проводником в хорошей
изоляции соедините его с одним из кондукторов
электрофорной машины. К шару приблизьте второй
кондуктор и приведите машину в действие. При этом
возникнут мощные искровые разряды длиной до 10 см.
Аккуратно введите внутрь шара одинаковые
металлические пластинки на ручках из оргстекла.
Приведите пластинки в соприкосновение, затем
разъедините, аккуратно достаньте из полости шара
и по очереди введите в шар электрометра. Вы
обнаружите, что никакого заряда на пластинках
нет! Значит, внутри проводящего шара
электрическое поле отсутствует, несмотря на то,
что шар в целом несёт значительный заряд,
сообщаемый ему работающей электрофорной
машиной. Повторите опыт, прикоснувшись пробным
шариком изнутри к металлу заряженного шара, – вы
вновь не обнаружите никакого заряда. Таким
образом, весь электрический заряд сосредоточен
на поверхности проводящего тела. Объясняется
этот результат тем, что справедлив закон Кулона.
В свою очередь, этот экспериментальный факт с
высокой точностью подтверждает справедливость
закона Кулона.
Вопросы для самоконтроля
1. В чём суть методики введения и
формирования понятия напряжённости
электрического поля?
2. Сравните метод построения силовых
линий посредством диполя с методом визуализации
электростатического поля мелким порошком,
взвешенным в жидком диэлектрике.
3. Изложите методику демонстрации на
уроке принципа суперпозиции электростатических
полей.
4. Каким экспериментом можно
подтвердить справедливость теоремы Гаусса?
5. Как зависят плотность заряда и
напряжённость электрического поля от формы
проводника?
6. Предложите демонстрационный опыт,
прямо показывающий зависимость плотности заряда
от площади проводника.
7. В чём дидактическая ценность
опыта с обнаружением электрического поля вблизи
одной и двух параллельных заряженных проводящих
пластин?
8. Нужно ли в школе рассматривать
метод точного подтверждения закона Кулона?
Литература
Бутиков Е.И., Кондратьев А.С.
Физика: Учеб. пособие: В 3-х кн. Кн. 2.
Электродинамика. Оптика. – М.: Физматлит, 2004.
Демонстрационный эксперимент по
физике в старших классах средней школы: Т. 2.
Электричество. Оптика. Физика атома: Под ред.
А.А.Покровского. – М.: Просвещение, 1972.
Кабардин О.Ф., Орлов В.А., Эвенчик
Э.Е. Физика: Учеб. для 10 кл. шк. и кл. с углубл.
изуч. физики: Под ред. А.А.Пинского. – М.:
Просвещение, 1997.
Учебное оборудование для кабинетов физики
общеобразовательных учреждений: Под ред.
Г.Г.Никифорова. — М.: Дрофа, 2005. (Cм. также «Физика»
(«ПС») № 10/2005; № 4/2007.)
Продолжение см. в № 22/07

Закон Кулона
Закон сохранения электрического заряда
Напряженность
Принцип суперпозиции
Электрическое поле
Потенциал электростатического поля
Разность потенциалов
Теория
Совсем чуть−чуть.
Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.
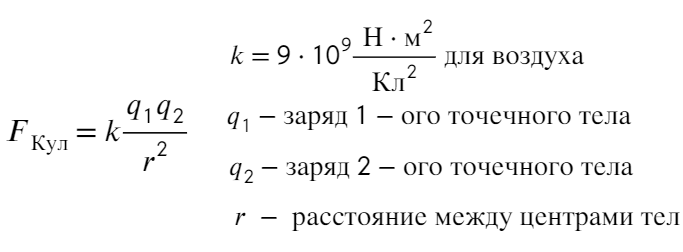
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:
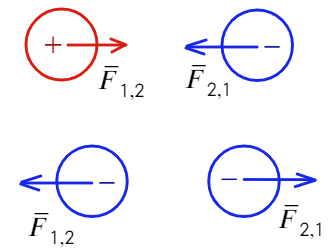
Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.
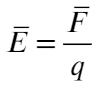
Напряженность НЕ зависит от величины заряда, помещенного в поле!
Задачи
Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.
Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:
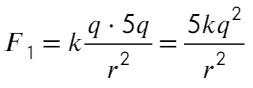
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:
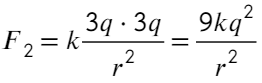
Отношение получится таким:
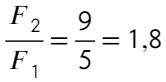
Ответ: 1,8
Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.
Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).
А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:
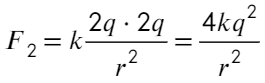
Отношение:
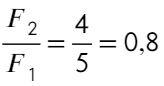
Ответ: 0,8
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?
В начальный момент времени на шарик действуют две силы:
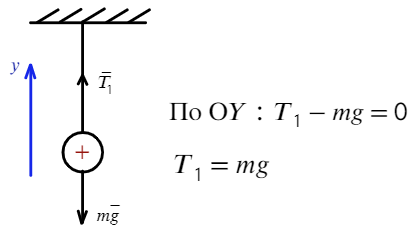 а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
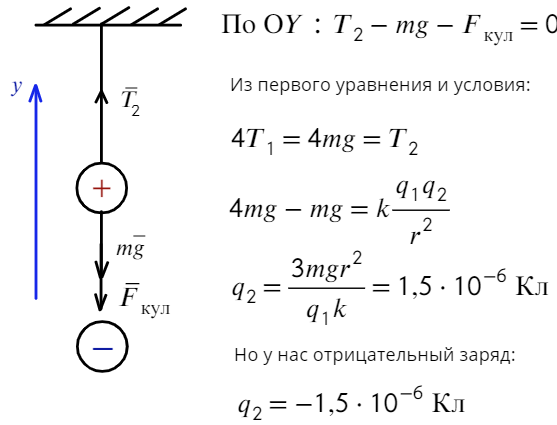 б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
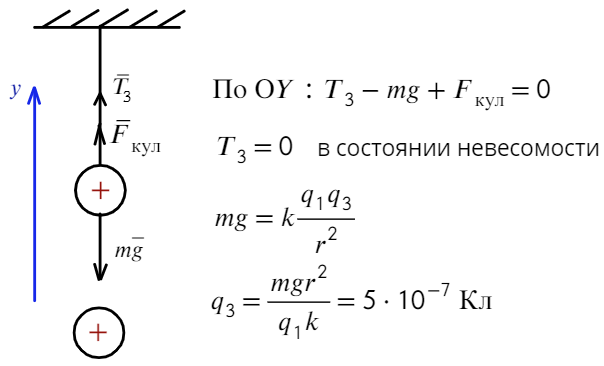 Ответ: −1,5 мкКл, 500 нКл.
Ответ: −1,5 мкКл, 500 нКл.
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.
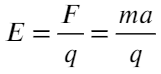
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.
Найдем ускорение электрона в электрическом поле:
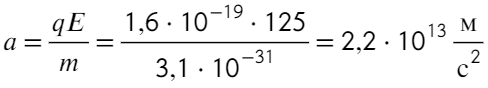
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:
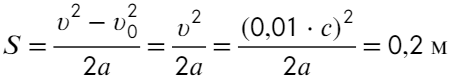
Ответ: 0,2 м
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?
Для начала разберемся, какие силы действуют на заряд:
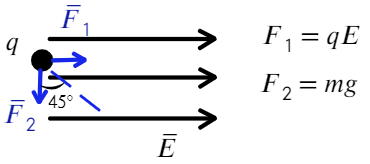
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:
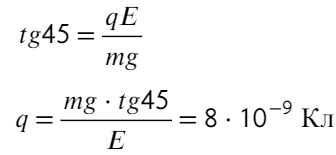
Ответ: 8×10⁻⁹ Кл
Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)
Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:
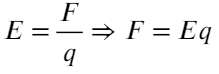
Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:
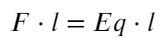
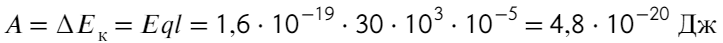
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹
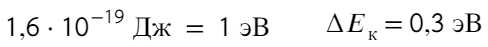
Ответ: 0,3 эВ
Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.
Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).
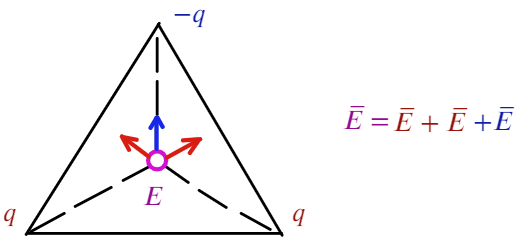
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:
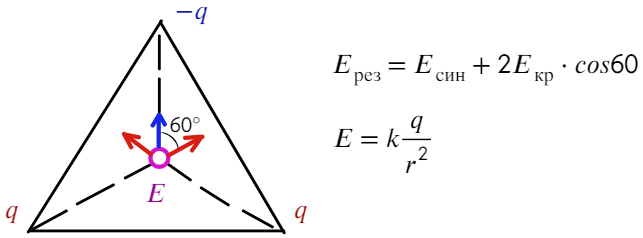
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:
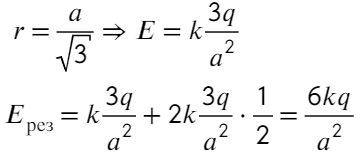
Ответ: 6kq/a²
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)
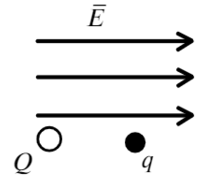
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.
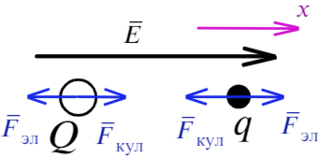
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:
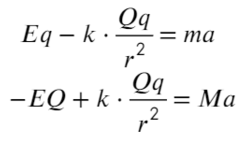
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.
Разделим одно уравнение на другое и выразим массу:
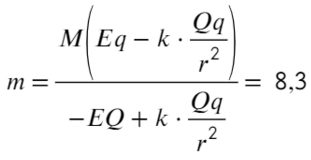
Ответ: 8,3 гр.
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)
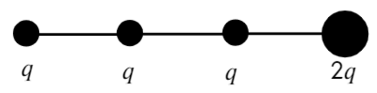
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:
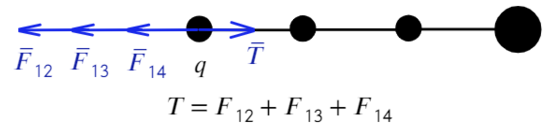
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:
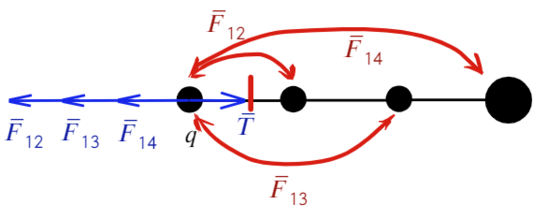
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:
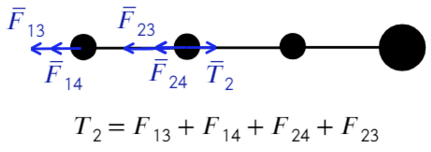
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:
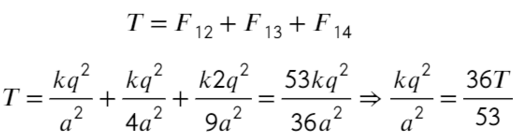
Второе уравнение с подстановкой выражения из первого:
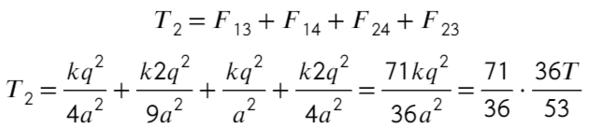
Ответ: 71T/53
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)
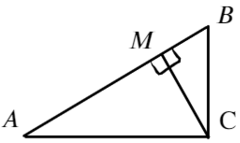
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:
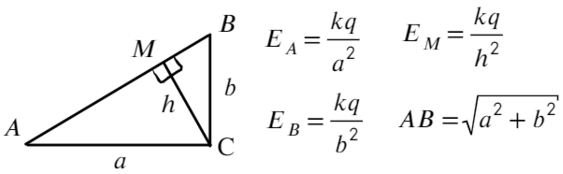
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:
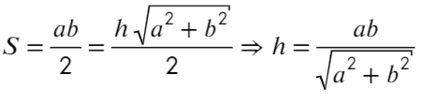
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:
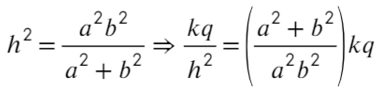
Выразим a² и b² через напряженность:
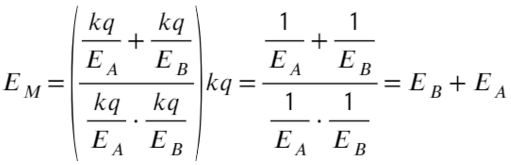
Ответ: Ea+Eb
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)
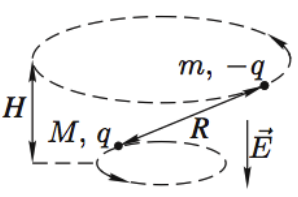 Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
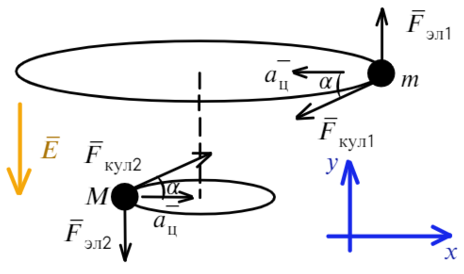
Запишем уравнения по осям на верхнюю частицу:
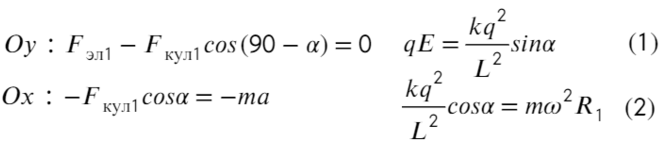
На нижнюю частицу:
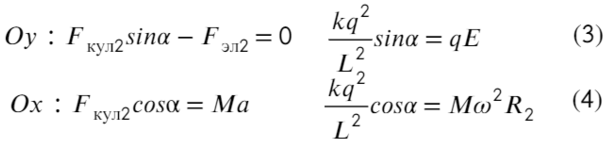
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.
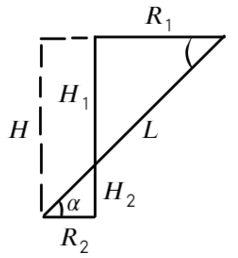
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:
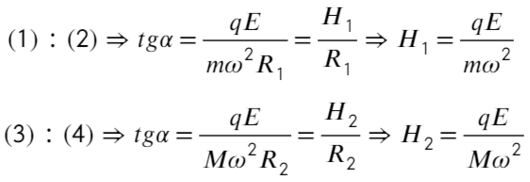
Сложим два уравнения, чтобы найти расстояние между плоскостями:
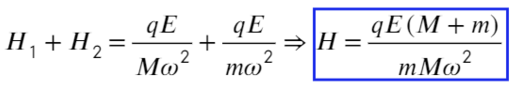
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:
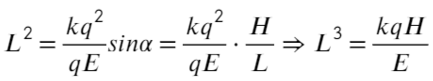
Вместо Н подставим то, что мы нашли:
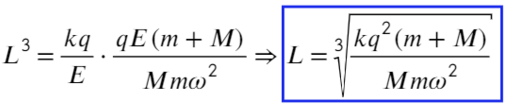
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)
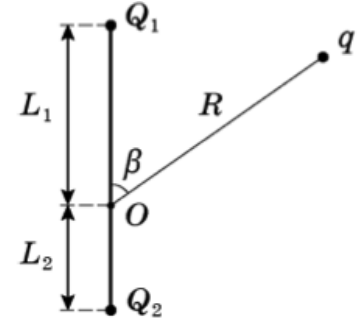
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:
 Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
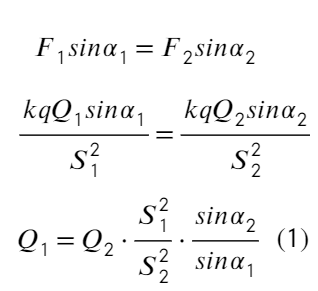
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:
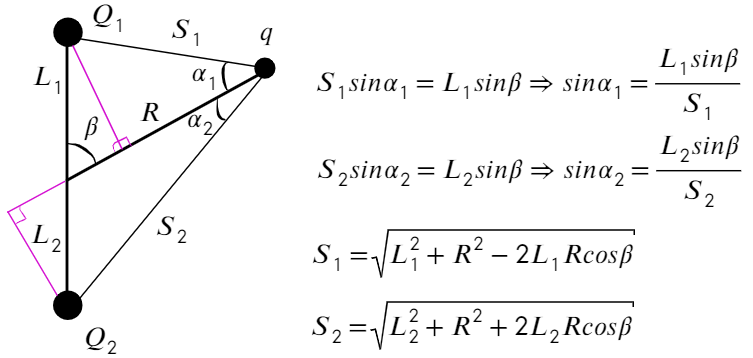
Подставим в ур-ие (1):
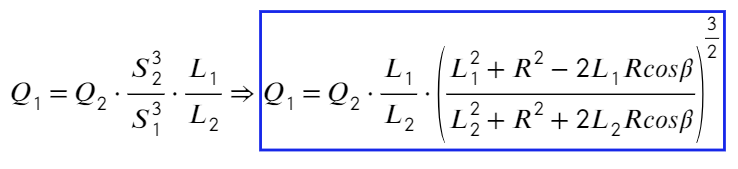
В качестве закрепления материала решите несколько похожих задач с ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
