Алгоритм вычисления собственных значений — алгоритм, позволяющий определить собственные значения и собственные векторы заданной матрицы. Создание эффективных и устойчивых алгоритмов для этой задачи является одной из ключевых задач вычислительной математики.
Собственные значения и собственные векторы[править | править код]
Если задана n × n квадратная матрица A над вещественными или комплексными числами, то собственное значение λ и соответствующий ему корневой вектор v — это пара, удовлетворяющая равенству[1]
где v ненулевой n × 1 вектор-столбец, E является n × n единичной матрицей, k — положительным целым, а λ и v могут быть комплексными, даже если A вещественна. Если k = 1, вектор просто называется собственным вектором. В этом случае Av = λv. Любое собственное значение λ матрицы A имеет простой[note 1] собственный вектор, соответствующий ему так, что если k — наименьшее целое, при котором (A – λE)k v = 0 для корневого вектора v, то (A – λE)k-1 v будет простым собственным вектором. Значение k всегда можно взять меньше либо равным n. В частности, (A – λE)n v = 0 для всех корневых векторов v, соответствующих λ.
Для любого собственного значения λ матрицы A ядро ker(A – λE) состоит из всех собственных векторов, соответствующих λ, (вместе с 0) и называется собственным подпространством числа λ, а векторное подпространство ker((A – λE)n) состоит из всех корневых векторов (дополненное нулевым вектором) и называется корневым подпространством. Геометрическая кратность значения λ является размерностью его собственного подпространства. Алгебраическая кратность значения λ является размерностью его корневого подпространства. Дальнейшие термины связаны с равенством
Здесь det — определитель, λi — все различные собственные значения матрицы A, а αi — соответствующие алгебраические кратности. Функция pA(z) — это характеристический многочлен матрицы A. Таким образом, алгебраическая кратность является кратностью собственных значений как корней характеристического многочлена. Поскольку любой собственный вектор является корневым вектором, геометрическая кратность меньше либо равна алгебраической кратности. Сумма алгебраических кратностей равна n степени характеристического многочлена. Уравнение pA(z) = 0 называется характеристическим уравнением, поскольку его корни являются в точности собственными значениями матрицы A. По теореме Гамильтона — Кэли сама матрица A удовлетворяет тому же самому уравнению: pA(A) = 0[note 2]. Как следствие, столбцы матрицы 

Любой набор корневых векторов различных собственных значений линейно независим, так что базис для всего C n можно выбрать из набора корневых векторов. Точнее этот базис {vi}n
i=1 можно выбрать и выстроить так, что
-
- если vi и vj имеют одно и то же собственное значение, то тоже будет верно для любого vk при k между i и j;
- если vi не является простым собственным вектором и если λi его собственное значение, то (A – λiE )vi = vi-1 (в частности v1 должен быть простым собственным вектором).
Если эти базисные вектора расположить как столбцы матрицы V = [ v1 v2 … vn ], то V можно использовать для преобразования матрицы A в её нормальную жорданову форму:
где λi — собственные значения, βi = 1 если (A – λi+1)vi+1 = vi и βi = 0 в других случаях.
Если W является обратимой матрицей и λ — собственное значение матрицы A с соответствующим корневым вектором v, то (W -1AW – λE )k W –kv = 0. Таким образом, λ является собственным значением матрицы W -1AW с соответствующим корневым вектором W –kv. Таким образом, подобные матрицы имеют те же самые собственные значения.
Нормальные, эрмитовы и вещественные симметричные матрицы[править | править код]
Эрмитово-сопряжённая матрица M* к комплексной матрице M — это траспонированная матрица с заменой всех элементов на сопряжённые значения: M * = M T. Квадратная матрица A называется нормальной, если она коммутирует с эрмитово-сопряжённой: A*A = AA*. Матрица называется эрмитовой, если она равна своей сопряжённой: A* = A. Все эрмитовы матрицы нормальны. Если A имеет только вещественные элементы, то сопряжённая к ней — это просто транспонированная матрица, и она будет эрмитовой в том и только в том случае, когда она симметрична. Если применить это к столбцам, сопряжённость можно использовать для определения канонического скалярного произведения в C n: w • v = w* v[note 3]. Нормальные, эрмитовы и вещественные симметричные матрицы имеют ряд полезных свойств:
-
- Каждый корневой собственный вектор нормальной матрицы является простым собственным вектором.
- Любая нормальная матрица подобна диагональной, поскольку её нормальная жорданова форма является диагональной матрицей.
- Собственные вектора, соответствующие различным собственным значениям нормальной матрицы, ортогональны.
- Для любой нормальной матрицы A C n имеет ортонормальный базис, состоящий из собственных векторов матрицы A. Соответствующая матрица собственных векторов является унитарной.
- Собственные значения эрмитовой матрицы являются вещественными числами, поскольку (λ – λ)v = (A* – A)v = (A – A)v = 0 для ненулевого собственного вектора v.
- Если матрица A вещественна, существует ортонормальный базис для R n, состоящий из собственных векторов матрицы A, в том и только в том случае, когда A симметрична.
Возможно как для вещественных, так и для комплексных матриц иметь все собственные значения вещественными, не будучи при этом эрмитовой матрицей. Например, вещественная треугольная матрица имеет все свои собственные значения на диагонали, но, в общем случае, не симметрична.
Число обусловленности[править | править код]
Любую задачу вычислительной математики можно рассматривать как вычисление некоторой функции ƒ от некоторого аргумента x. Число обусловленности κ(ƒ, x) задачи — это отношение относительной ошибки результата вычисления к относительной ошибке параметра функции и зависит как от функции, так и от параметра. Число обусловленности описывает насколько возрастает ошибка во время вычислений. Десятичный логарифм этого числа говорит о количестве знаков, которые мы теряем по отношению к исходным данным. Число обусловленности относится к наилучшему сценарию, отражая нестабильность самой задачи, независимо от способа решения. Никакой алгоритм не может дать результат лучше, чем определённый числом обусловленности, разве что случайно. Однако плохо разработанный алгоритм может дать существенно более плохие результаты. Например, как будет упомянуто ниже, задача нахождения собственных значений нормальной матрицы всегда хорошо обусловлена, однако задача нахождения корней многочлена может быть очень плохо обусловлена[en]. Такие алгоритмы вычисления собственных значений, которые работают путём нахождения корней характеристического многочлена, могут оказаться плохо обусловленными, даже если сама задача хорошо обусловлена.
Для задачи решения системы линейных уравнений Av = b, где A является обратимой, число обусловленности κ(A-1, b) определяется выражением ||A||op||A-1||op, где || ||op — операторная норма, подчинённая обычной евклидовой норме на C n. Поскольку это число не зависит от b и является тем же самым как для A, так и для A-1, оно обычно называется числом обусловленности κ(A) матрицы A. Это значение κ(A) является также абсолютным значением отношения наибольшего собственного значения матрицы A к её наименьшему собственному значению. Если A является унитарной, то ||A||op = ||A-1||op = 1, так что κ(A) = 1. В общем случае для матриц часто сложно вычислить операторную норму. По этой причине обычно используют другие нормы матрицы для оценки числа обусловленности.
Для задачи вычисления собственных значений Бауэр и Файк доказали[en], что если λ является собственным значением диагонализируемой n × n матрицы A с матрицей собственных векторов V, то абсолютная ошибка вычисления λ ограничена произведением κ(V) и абсолютной ошибкой в A:
[2]. Как следствие, число обусловленности для вычисления λ равно
κ(λ, A) = κ(V) = ||V ||op ||V -1||op. Если матрица A нормальна, то V является унитарной и κ(λ, A) = 1. Таким образом, задача вычисления собственных значений нормальных матриц хорошо обусловлена.
Было показано, что число обусловленности задачи вычисления собственного подпространства нормальной матрицы A, соответствующего собственному значению λ, обратно пропорционально минимальному расстоянию между λ и другими, отличными от λ, собственными значениями матрицы A[3]. В частности, задача определения собственного подпространства для нормальных матриц хорошо обусловлена для изолированных собственных значений. Если собственные значения не изолированы, лучшее, на что мы можем рассчитывать, это определение подпространства всех собственных векторов близлежащих собственных значений.
Алгоритмы[править | править код]
Любой нормированный многочлен является характеристическим многочленом сопровождающей матрицы, поэтому алгоритм для вычисления собственных значений можно использовать для нахождения корней многочленов. Теорема Абеля — Руффини показывает, что любой такой алгоритм для размерности большей 4 должен либо быть бесконечным, либо вовлекать функции более сложные, чем элементарные арифметические операции или дробные степени. По этой причине алгоритмы, вычисляющие точно собственные значения за конечное число шагов, существуют только для специальных классов матриц. В общем случае алгоритмы являются итеративными, дающими на каждой итерации очередное приближение к решению.
Некоторые алгоритмы дают все собственные значения, другие дают несколько значений или даже всего одно, однако и эти алгоритмы можно использовать для вычисления всех собственных значений. Как только собственное значение λ матрицы A определено, его можно использовать либо для приведения алгоритма к получению другого собственного значения, либо для сведения задачи к такой, которая не имеет λ в качестве решения.
Приведение обычно осуществляется сдвигом: A заменяется на A – μE для некоторой константы μ. Собственное значение, найденное для A – μE, должно быть добавлено к μ, чтобы получить собственное значение матрицы A. Например, в степенном методе μ = λ. Итерация степенного метода находит самое большое по абсолютной величине значение, так что даже если λ является приближением к собственному значению, итерация степенного метода вряд ли найдёт его во второй раз. И наоборот, методы, основанные на обратных итерациях находят наименьшее собственное значение, так что μ выбирается подальше от λ в надежде оказаться ближе к какому-нибудь другому собственному значению.
Приведение можно совершить путём сужения матрицы A к пространству столбцов матрицы A – λE. Поскольку A – λE вырождена, пространство столбцов имеет меньшую размерность. Алгоритм вычисления собственных значений можно тогда применить к этой суженой матрице. Процесс можно продолжать, пока не будут найдены все собственные значения.
Если алгоритм не даёт к собственные значения, общей практикой является применение алгоритма, основанного на обратной итерации, с приравниванием μ к ближайшей аппроксимации собственного значения. Это быстро приводит к собственному вектору ближайшего к μ собственного значения. Для небольших матриц альтернативой служит использование столбцового подпространства произведения A – λ́E для каждого из остальных собственных значений λ́.
Матрицы Хессенберга и трёхдиагональные матрицы[править | править код]
Поскольку собственными значениями треугольной матрицы являются диагональные элементы, в общем случае не существует конечного метода, подобного исключениям Гаусса, для приведения матрицы к треугольной форме, сохраняя при этом собственные значения, однако можно получить нечто близкое к треугольной матрице. Верхняя матрица Хессенберга — это квадратная матрица, у которой все элементы ниже первой поддиагонали равны нулю. Нижняя матрица Хессенберга — это квадратная матрица, у которой все члены выше первой наддиагонали равны нулю. Матрицы, которые являются как нижними, так и верхними матрицами Хессенберга — это трёхдиагональные матрицы. Матрицы Хессенберга и трёхдиагональные матрицы являются исходными точками многих алгоритмов вычисления собственных значений, поскольку нулевые значения уменьшают сложность задачи. Существует несколько методов сведения матриц к матрицам Хессенберга с теми же собственными значениями. Если исходная матрица симметрична или эрмитова, то результирующая матрица будет трёхдиагональной.
Если нужны только собственные значения, нет необходимости вычислять матрицу подобия, поскольку преобразованная матрица имеет те же собственные значения. Если также нужны и собственные векторы, матрица подобия необходима для преобразования собственных векторов матрицы Хессенберга к собственным векторам исходной матрицы.
| Метод | Применим к матрицам | Результат | Цена без матрицы подобия | Цена с матрицей подобия | Описание |
|---|---|---|---|---|---|
| Преобразования Хаусхолдера | общего вида | матрица Хессенберга | 2n3⁄3 + O(n2)[4] | 4n3⁄3 + O(n2)[4] | Отражение каждого столбца относительно подпространства для обнуления нижних элементов столбца. |
| Повороты Гивенса | общего вида | матрица Хессенберга | 4n3⁄3 + O(n2)[4] | Осуществляется плоское вращении для обнуления отдельных элементов. Вращения упорядочены так, что следующие вращения не затрагивают нулевые элементы. | |
| Итерации Арнольди | общего вида | матрица Хессенберга | Осуществляется ортогонализация Грама ― Шмидта на подпространствах Крылова. | ||
| Алгоритм Ланцоша[en][5] | эрмитова | трёхдиагональная матрица | Итерации Арнольди для эрмитовых матриц. |
Итеративные алгоритмы[править | править код]
Итеративные алгоритмы решают задачу вычисления собственных значений путём построения последовательностей, сходящихся к собственным значениям. Некоторые алгоритмы дают также последовательности векторов, сходящихся к собственным векторам. Чаще всего последовательности собственных значений выражаются через последовательности подобных матриц, которые сходятся к треугольной или диагональной форме, что позволяет затем просто получить собственные значения. Последовательности собственных векторов выражаются через соответствующие матрицы подобия.
| Метод | Применим к матрицам | Результат | Цена за один шаг | Сходимость | Описание |
|---|---|---|---|---|---|
| Степенной метод | общего вида | наибольшее собственное значение и соответствующий вектор | O(n2) | Линейная | Многократное умножение матрицы на произвольно выбранный начальный вектор с последующей нормализацией. |
| Обратный степенной метод | общего вида | ближайшее к μ собственное значение и соответствующий вектор | Линейная | Степенная итерация с матрицей (A – μE )-1 | |
| Метод итераций Рэлея | общего вида | ближайшее к μ собственное значение и соответствующий вектор | Кубическая | Степенная итерация с матрицей (A – μiE )-1, где μi является отношением Рэлея от предыдущей итерации. | |
| Предобусловленная обратная итерация[6] или LOBPCG[en] | положительно определённая вещественная симметричная | ближайшее к μ собственное значение и соответствующий вектор | Обратная итерация с предобуславливанием (приближённое обращение матрицы A). | ||
| Метод деления пополам[7] | вещественная симметричная трёхдиагональная | любое собственное значение | Линейная | Использует метод бисекции для поиска корней характеристического многочлена и свойства последовательности Штурма. | |
| Итерации Лагерра | вещественная симметричная трёхдиагональная | любое собственное значение | Кубическая[8] | Использует метод Лагерра[en] вычисления корней характеристического многочлена и свойства последовательности Штурма. | |
| QR-алгоритм[9] | хессенберга | все собственные значения | O(n2) | Кубическая | Разложение A = QR, где Q ортогональная, R ― треугольная, затем используется итерация к RQ. |
| все собственные значения | 6n3 + O(n2) | ||||
| Метод Якоби | вещественная симметричная | все собственные значения | O(n3) | квадратичная | Использует поворот Гивенса в попытке избавиться от недиагональных элементов. Попытка не удаётся, но усиливает диагональ. |
| Разделяй и властвуй[en] | эрмитова трёхдиагональная | все собственные значения | O(n2) | Матрица разбивается на подматрицы, которые диагонализируются, затем воссоединяются. | |
| все собственные значения | (4⁄3)n3 + O(n2) | ||||
| Метод гомотопии | вещественная симметричная трёхдиагональная | все собственные значения | O(n2)[10] | Строится вычисляемая гомотопия. | |
| Метод спектральной свёртки[en] | вещественная симметричная | ближайшее к μ собственное значение и соответствующий собственный вектор | Предобусловленная обратная итерация, применённая к (A – μE )2 | ||
| Алгоритм MRRR[11] | вещественная симметричная трёхдиагональная | некоторые или все собственные значения и соответствующие собственные вектора | O(n2) | «Multiple Relatively Robust Representations» — Осуществляется обратная итерация с разложением LDLT смещённой матрицы. |
Прямое вычисление[править | править код]
Не существует простых алгоритмов прямого вычисления собственных значений для матриц в общем случае, но для многих специальных классов матриц собственные значения можно вычислить прямо. Это:
Треугольные матрицы[править | править код]
Поскольку определитель треугольной матрицы является произведением её диагональных элементов, то для треугольной матрицы T 
Разложимые полиномиальные уравнения[править | править код]
Если p ― любой многочлен и p(A) = 0, то собственные значения матрицы A удовлетворяют тому же уравнению. Если удаётся разложить многочлен p на множители, то собственные значения A находятся среди его корней.
Например, проектор ― это квадратная матрица P, удовлетворяющая уравнению P2 = P. Корнями соответствующего скалярного полиномиального уравнения λ2 = λ будут 0 и 1. Таким образом, проектор имеет 0 и 1 в качестве собственных значений. Кратность собственного значения 0 ― это дефект P, в то время как кратность 1 ― это ранг P.
Другой пример ― матрица A, удовлетворяющая уравнению A2 = α2E для некоторого скаляра α. Собственные значения должны быть равны ±α. Операторы проектирования
удовлетворяют равенствам
и
Пространства столбцов матриц P+ и P– являются подпространствами собственных векторов матрицы A, соответствующими +α и -α, соответственно.
Матрицы 2×2[править | править код]
Для размерностей от 2 до 4 существуют использующие радикалы формулы, которые можно использовать для вычисления собственных значений. Для матриц 2×2 и 3×3 это обычная практика, но для матриц 4×4 растущая сложность формул корней[en] делает этот подход менее привлекательным.
Для матриц 2×2
характеристический многочлен равен
Собственные значения можно найти как корни квадратного уравнения:
Если определить 
с подобными формулами для c и d. Отсюда следует, что вычисление хорошо обусловлено, если собственные значения изолированы.
Собственные векторы можно получить, используя теорему Гамильтона — Кэли. Если λ1, λ2 — собственные значения, то (A – λ1E )(A – λ2E ) = (A – λ2E )(A – λ1E ) = 0, так что столбцы (A – λ2E ) обнуляются матрицей (A – λ1E ) и наоборот. Предполагая, что ни одна из матриц не равна нулю, столбцы каждой матрицы должны содержать собственные векторы для другого собственного значения (если же матрица нулевая, то A является произведением единичной матрицы на константу и любой ненулевой вектор является собственным).
Например, пусть
тогда tr(A) = 4 – 3 = 1 и det(A) = 4(-3) – 3(-2) = -6, так что характеристическое уравнение равно
а собственные значения равны 3 и −2. Теперь
,
В обеих матрицах столбцы отличаются скалярными коэффициентами, так что можно выбирать любой столбец. Так, (1, -2) можно использовать в качестве собственного вектора, соответствующего собственному значению −2, а (3, -1) в качестве собственного вектора для собственного числа 3, что легко можно проверить умножением на матрицу A.
Матрицы 3×3[править | править код]
Если A является матрицей 3×3, то характеристическим уравнением будет:
Это уравнение можно решить с помощью методов Кардано или Лагранжа, но аффинное преобразование матрицы A существенно упрощает выражение и ведёт прямо к тригонометрическому решению. Если A = pB + qE, то A и B имеют одни и те же собственные векторы и β является собственным значением матрицы B тогда и только тогда, когда α = pβ + q является собственным значением матрицы A. Если положить 

Подстановка β = 2cos θ и некоторое упрощение с использованием тождества cos 3θ = 4cos3 θ – 3cos θ сводит уравнение к cos 3θ = det(B) / 2. Таким образом,
Если det(B) является комплексным числом или больше 2 по абсолютной величине, арккосинус для всех трёх величин k следует брать из одной и той же ветви. Проблема не возникает, если A вещественна и симметрична, приводя к простому алгоритму:[12]
% Given a real symmetric 3x3 matrix A, compute the eigenvalues p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2 if (p1 == 0) % A is diagonal. eig1 = A(1,1) eig2 = A(2,2) eig3 = A(3,3) else q = trace(A)/3 p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1 p = sqrt(p2 / 6) B = (1 / p) * (A - q * E) % E is the identity matrix r = det(B) / 2 % In exact arithmetic for a symmetric matrix -1 <= r <= 1 % but computation error can leave it slightly outside this range. if (r <= -1) phi = pi / 3 elseif (r >= 1) phi = 0 else phi = acos(r) / 3 end % the eigenvalues satisfy eig3 <= eig2 <= eig1 eig1 = q + 2 * p * cos(phi) eig3 = q + 2 * p * cos(phi + (2*pi/3)) eig2 = 3 * q - eig1 - eig3 % since trace(A) = eig1 + eig2 + eig3 end
Снова, собственные векторы A можно получить путём использования теоремы Гамильтона — Кэли. Если α1, α2, α3 — различные собственные значения матрицы A, то (A – α1E)(A – α2E)(A – α3E) = 0. Тогда столбцы произведения любых двух из этих матриц содержат собственные векторы третьего собственного значения. Однако если a3 = a1, то (A – α1E)2(A – α2E) = 0 и (A – α2E)(A – α1E)2 = 0. Таким образом, корневое собственное подпространство α1 натянуто на столбцы A – α2E, в то время как обычное собственное подпространство натянуто на столбцы (A – α1E)(A – α2E). Обычное собственное подпространство α2 натянуто на столбцы (A – α1E)2.
Например, пусть
Характеристическое уравнение равно
с собственными значениями 1 (кратности 2) и −1. Вычисляем
,
а затем
.
Тогда (-4, -4, 4) является собственным вектором для −1, а (4, 2, -2) является собственным вектором для 1. Векторы (2, 3, -1) и (6, 5, -3) являются корневыми векторами, соответствующими значению 1, любой из которых можно скомбинировать с (-4, -4, 4) и (4, 2, -2), образуя базис корневых векторов матрицы A.
См. также[править | править код]
- Список алгоритмов вычисления собственных значений[en]
Комментарии[править | править код]
- ↑ Термин «простой» здесь употребляется лишь для подчёркивания различия между «собственным вектором» и «корневым вектором».
- ↑ где постоянный член умножается на единичную матрицу E.
- ↑ Такой порядок в скалярном произведении (с сопряжённым элементом слева) предпочитают физики. Алгебраисты часто предпочитают запись w • v = v* w.
Примечания[править | править код]
- ↑ Sheldon Axler. Down with Determinants! // American Mathematical Monthly. — 1995. — Вып. 102. — С. 139—154.
- ↑ F. L. Bauer, C. T. Fike. Norms and exclusion theorems // Numer. Math. — 1960. — Вып. 2. — С. 137—141.
- ↑ S. C. Eisenstat, I. C. F. Ipsen. Relative Perturbation Results for Eigenvalues and Eigenvectors of Diagonalisable Matrices // BIT. — 1998. — Т. 38, вып. 3. — С. 502—9. — doi:10.1007/bf02510256.
- ↑ 1 2 3 William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C. — 2nd. — Cambridge University Press, 1992. — ISBN 0-521-43108-5.
- ↑ Х. Д. Икрамов. Разреженные матрицы. — 1982. — Т. 20. — (Итоги науки и техники. Сер. Мат. анал).
- ↑ K. Neymeyr. A geometric theory for preconditioned inverse iteration IV: On the fastest convergence cases. // Linear Algebra Appl. — 2006. — Т. 415, вып. 1. — С. 114—139. — doi:10.1016/j.laa.2005.06.022.
- ↑ Уилкинсон, 1970, стр. 274, Метод деления пополам
- ↑ T. Y Li, Zhonggang Zeng. Laguerre’s Iteration In Solving The Symmetric Tridiagonal Eigenproblem – Revisited // SIAM Journal on Scientific Computing. — 1992.
- ↑ Парлетт, 1983, стр. 156, глава 8, Алгоритмы QR и QL
- ↑ Moody T. Chu. A Note on the Homotopy Method for Linear Algebraic Eigenvalue Problems // Linear Algebra Appl. — 1988. — Т. 105. — С. 225—236. — doi:10.1016/0024-3795(88)90015-8.
- ↑ Inderjit S. Dhillon, Beresford N. Parlett, Christof Vömel. The Design and Implementation of the MRRR Algorithm // ACM Transactions on Mathematical Software. — 2006. — Т. 32, вып. 4. — С. 533—560. — doi:10.1145/1186785.1186788.
- ↑ Oliver K. Smith. Eigenvalues of a symmetric 3 × 3 matrix // Communications of the ACM. — Т. 4, вып. 4. — С. 168. — doi:10.1145/355578.366316.
Литература[править | править код]
- Дж. Голуб, Ч. Ван Лоун. Матричные вычисления. — Москва: «Мир», 1999. — ISBN 5-03-002406-9.
- Б. Парлетт. Симметричная проблема собственных значений. — Москва: «Мир», 1983.
- Дж. Х. Уилкинсон. Алгебраическая проблема собственных значений. — Москва: «Наука» Главная редакция физико-математической литературы, 1970.
Дополнительная литература[править | править код]
- Adam W. Bojanczyk, Adam Lutoborski. Computation of the Euler angles of a symmetric 3X3 matrix // SIAM Journal on Matrix Analysis and Applications. — Jan 1991. — Т. 12, вып. 1. — С. 41—48. — doi:10.1137/0612005.
Собственные векторы и собственные значения матрицы
Пусть — числовая квадратная матрица n-го порядка. Матрица
называется характеристической для
, а ее определитель
характеристическим многочленом матрицы
(7.12)
Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.
Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец
, удовлетворяющий условию
(7.13)
называется собственным вектором матрицы . Число
в равенстве (7.13) называется собственным значением матрицы
. Говорят, что собственный вектор
соответствует {принадлежит) собственному значению
.
Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде , где
— единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему
линейных алгебраических уравнений с
неизвестными
(7.14)
Поскольку нас интересуют только нетривиальные решения однородной системы, то определитель матрицы системы должен быть равен нулю:
(7.15)
В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена матрицы
. Уравнение
называется характеристическим уравнением матрицы
. Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде
где — корни многочлена кратности
соответственно, причем
. Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.
Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.
Действительно, если число — собственное значение матрицы
, которому соответствует собственный вектор
, то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число
удовлетворяет характеристическому уравнению (7.15). Наоборот, если
— корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е.
.В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец
, удовлетворяющий условию (7.14). Значит,
— собственное значение матрицы
.
Свойства собственных векторов
Пусть — квадратная матрица n-го порядка.
1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.
В самом деле, пусть и
— собственные векторы, соответствующие собственным значениям
и
, причем
. Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:
(7.16)
Надо показать, что это равенство возможно только в тривиальном случае, когда . Действительно, умножая обе части на матрицу
и подставляя
и
имеем
Прибавляя к последнему равенству равенство (7.16), умноженное на , получаем
Так как и
, делаем вывод, что
. Тогда из (7.16) следует, что и
(поскольку
). Таким образом, собственные векторы
и
линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.
2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.
Действительно, если собственному значению соответствуют собственные векторы
, то из равенств
, следует, что вектор
также собственный, поскольку:
3. Пусть — присоединенная матрица для характеристической матрицы
. Если
— собственное значение матрицы
, то любой ненулевой столбец матрицы
является собственным вектором, соответствующим собственному значению
.
В самом деле, применяя формулу (7.7) имеем . Подставляя корень
, получаем
. Если
— ненулевой столбец матрицы
, то
. Значит,
— собственный вектор матрицы
.
Замечания 7.5
1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.
2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем
Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.
3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.
4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).
5. Для простого корня характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы
по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы
, является собственным вектором.
Нахождение собственных векторов и собственных значений матрицы
Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.
1. Составить характеристический многочлен матрицы .
2. Найти все различные корни характеристического уравнения
(кратности
корней определять не нужно).
3. Для корня найти фундаментальную систему
решений однородной системы уравнений
, где
Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).
4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению
(7.17)
где — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению
, образуют ненулевые столбцы вида
. Здесь и далее собственные векторы матрицы будем обозначать буквой
.
Повторить пункты 3,4 для остальных собственных значений .
Пример 7.8. Найти собственные значения и собственные векторы матриц:
Решение. Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Поделив его на (- 3), получим
.
Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Умножив его на (-1), получим
.
Матрица 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):
Ранг матрицы системы равен 2 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисные переменные
через свободную
и, полагая
, получаем решение
.
4(1). Все собственные векторы, соответствующие собственному значению , вычисляются по формуле
, где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
, так как
Разделив его на 3, получим .
3(2). Для собственного значения имеем однородную систему
. Решаем ее методом Гаусса:
Ранг матрицы системы равен единице , следовательно, фундаментальная система решений состоит из двух решений
. Базисную переменную
, выражаем через свободные:
. Задавая стандартные наборы свободных переменных
и
, получаем два решения
4(2). Записываем множество собственных векторов, соответствующих собственному значению , где
— произвольные постоянные, не равные нулю одновременно. В частности, при
получаем
; при
. Присоединяя к этим собственным векторам собственный вектор
, соответствующий собственному значению
(см. пункт 4(1) при
), находим три линейно независимых собственных вектора матрицы
Заметим, что для корня собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы
равно нулю.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
В этой главе
рассматриваются вопросы о собственных
векторах и собственных значениях
произвольной квадратной матрицы,
симметрической матрицы и подобных
матриц.
1. Основные понятия.
Определение.
Вектор
![]() ,
,
называетсясобственным
вектором
квадратной матрицы
![]() ,
,
если существует такое число![]() ,
,
что
![]() .
.
При
этом число![]() называетсясобственным
называетсясобственным
значением
матрицы
![]() ,
,
соответствующим собственному вектору![]() .
.
Уравнение
![]() может быть записано в виде
может быть записано в виде
![]() .
.
Определение.
Если
![]() – собственное значение матрицы
– собственное значение матрицы![]() ,
,
а![]() соответствующий ему собственный вектор,
соответствующий ему собственный вектор,
то![]() называютсобственной
называютсобственной
парой матрицы
![]() .
.
● Пример 1.
Показать,
что вектор
![]() является собственным вектором матрицы
является собственным вектором матрицы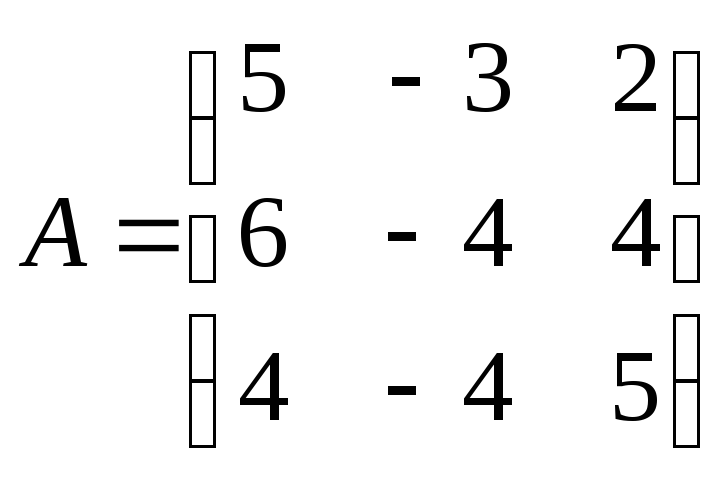 .
.
Найти
соответствующее ему собственное
значение.
Решение.
Так как
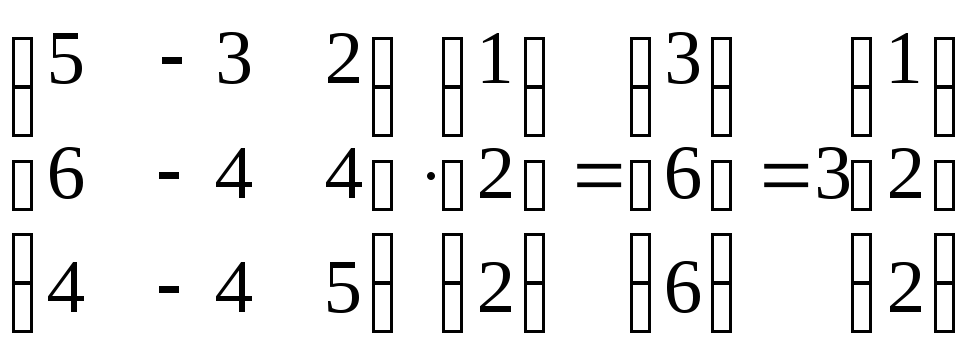 (
(![]() ),
),
то![]() –
–
собственный вектор матрицы![]() ,
,
соответствующий собственному значению![]() .●
.●
● Пример 2.
Показать,
что если
![]() – собственная пара матрицы
– собственная пара матрицы![]() ,
,
то![]() – собственная пара матрицы
– собственная пара матрицы![]() .
.
Решение.
Действительно,
![]()
![]() ,
,
т.е.
![]() .
.
Из последнего следует, что![]() – собственная пара матрицы
– собственная пара матрицы![]() .●
.●
● Пример 3.
При каких
![]() и
и![]() вектор
вектор![]() является собственным вектором матрицы
является собственным вектором матрицы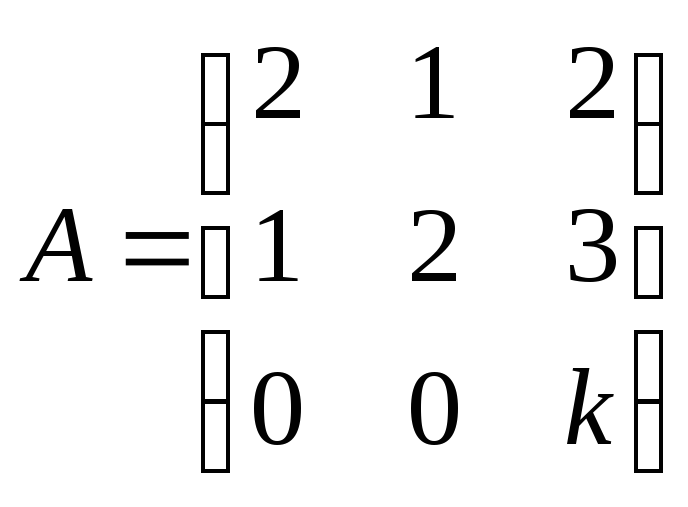 ?
?
Решение.
Найдем вектор
![]() .
.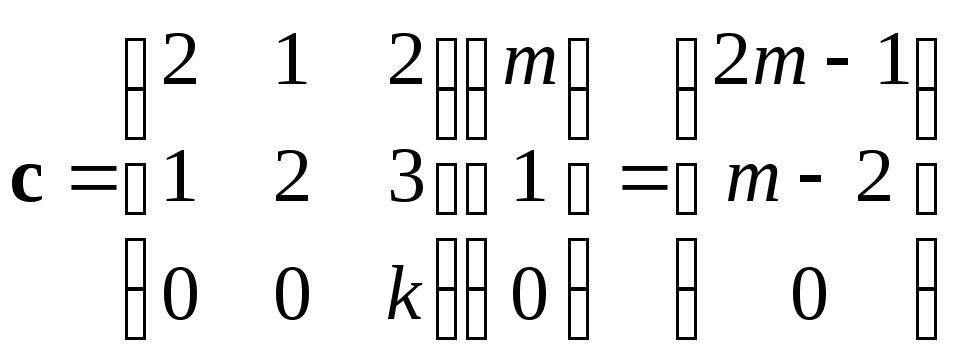 .
.
Если ![]() –
–
собственный вектор матрицы
![]() ,
,
то![]() ,
,
откуда![]() .
.
Из последнего имеем![]() и
и![]() и
и![]() .
.
Ответ:
при
![]() и произвольном
и произвольном![]() вектор
вектор![]() собственный вектор матрицы
собственный вектор матрицы![]() .
.
● Пример 4.
Существует
ли
![]() ,
,
при котором![]() –
–
собственный вектор матрицы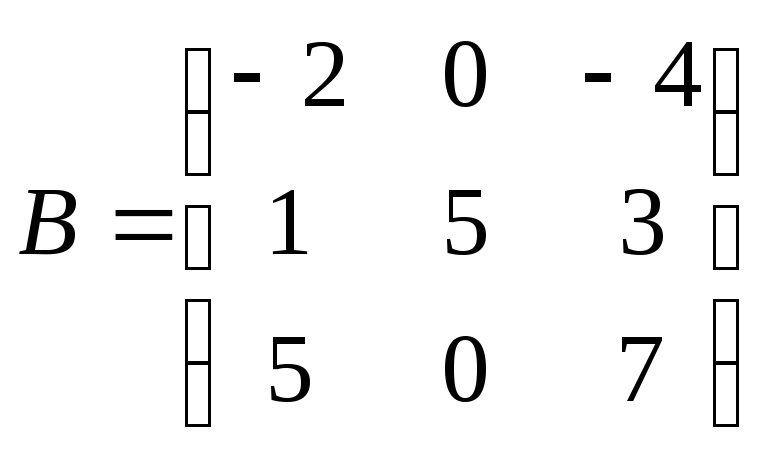 ?
?
Если существует, указать соответствующую
собственную пару.
Решение.
Вычислим произведение
![]()
Если
![]() –
–
собственная пара матрицы![]() ,
,
то
![]() .
.
Из последнего
равенства имеем
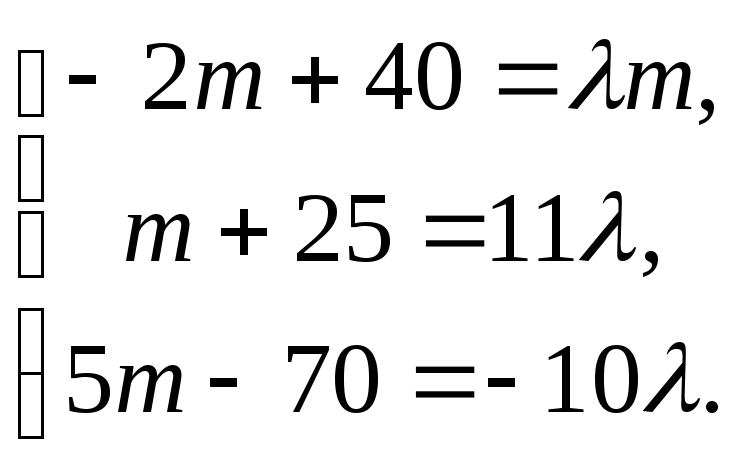 Откуда,
Откуда,![]() ,
,![]() .
.
![]() –
–
собственная пара матрицы![]() .●
.●
2. Свойства собственных векторов.
1)
Если ![]() –
–
собственный вектор матрицы
![]() ,
,
а![]() –
–
соответствующее ему собственное
значение, то при любом![]() вектор
вектор![]() также является собственным вектором
также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.
►Действительно,
![]() .◄
.◄
Замечание. Любой
собственный вектор матрицы определяет
целое направление
собственных векторов этой матрицы с
одним и тем же собственным значением.
2)
Собственные векторы матрицы, соответствующие
различным
её собственным значениям, линейно
независимы.
►Доказательство.
Пусть
![]() и
и![]() –
–
собственные пары матрицы![]() ,
,
где![]() .
.
Предположим, что
![]() и
и![]() линейно зависимые векторы.
линейно зависимые векторы.
Если
![]() и
и![]() линейно зависимы, то хотя бы один из
линейно зависимы, то хотя бы один из
этих векторов можно представить в виде
линейной комбинации другого (пусть![]() ).
).
Тогда
![]() ,
,
откуда следует, что![]() .
.
Так как![]() ,
,
то![]() .
.
Полученное
противоречие доказывает утверждение.◄
3)
Если
![]() и
и![]() линейно независимые собственные векторы
линейно независимые собственные векторы
матрицы![]() ,
,
соответствующие одному и тому же
собственному значению![]() ,
,
то любая нетривиальная линейная
комбинация этих векторов![]() (
(![]() )
)
также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению![]() .
.
►Действительно,
![]()
![]() ,
,
что и требовалось доказать.◄
4)
Если матрица
![]() диагональная
диагональная
![]() ,
,
то ее собственные значения совпадают
с диагональными элементами этой матрицы
(![]()
![]() ),
),
а единичный вектор![]() является собственным вектором,
является собственным вектором,
соответствующим собственному значению![]() .
.
►Действительно,
![]()
![]() ◄
◄
3 Нахождение собственных значений и собственных векторов.
Собственные
значения и собственные векторы матрицы
![]() удовлетворяют матричному уравнению
удовлетворяют матричному уравнению![]() .
.
Если ![]()
собственный вектор матрицы
![]() ,
,
то однородная система![]() имеет нетривиальное решение, поэтому
имеет нетривиальное решение, поэтому![]() (
(![]() порядок
порядок
матрицы![]() и
и![]() .
.
Последнее
уравнение позволяет найти собственные
значения матрицы![]() .
.
Определение.
Многочлен
![]() называютхарактеристическим многочленомматрицы
называютхарактеристическим многочленомматрицы![]() .
.
Определение.
Уравнение
![]()
называется
характеристическим
уравнением
матрицы
![]() .
.
Корни характеристического
уравнения
матрицы
![]() являются собственными значениями
являются собственными значениями
матрицы![]() .
.
Характеристическое
уравнение матрицы
![]() может быть записано в виде
может быть записано в виде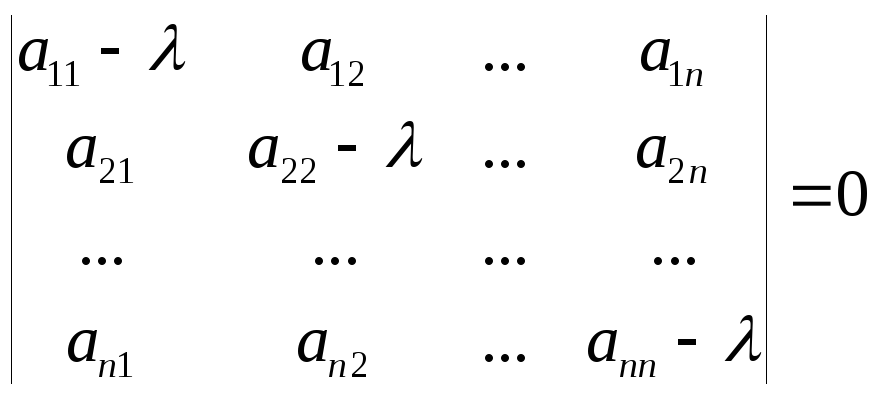 .
.
Определение.
Множество всех собственных значений
квадратной матрицы называется спектром
этой
матрицы.
Спектр матрицы
![]() -го
-го
порядка содержит![]() собственных значений матрицы, которые
собственных значений матрицы, которые
могут быть как действительными, так и
комплексными, простыми так и кратными.
Для матрицы
 характеристическое уравнение
характеристическое уравнение![]() может быть может быть преобразовано к
может быть может быть преобразовано к
виду
![]() .
.
![]() ,
,
поэтому характеристическое уравнение
матрицы
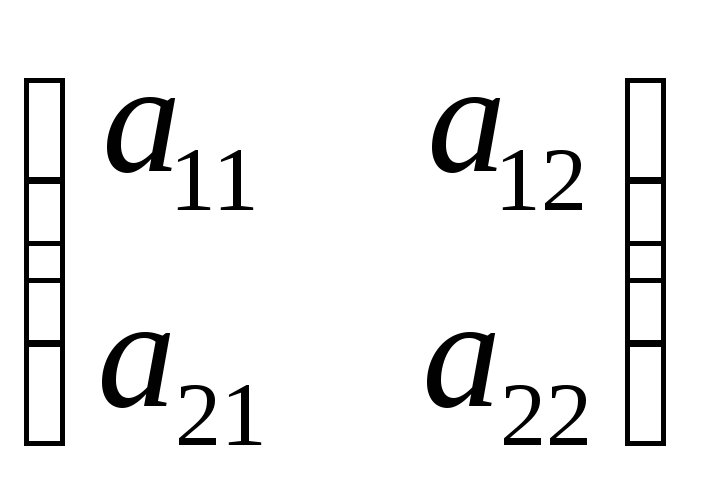 имеет вид
имеет вид
![]() . (8.1)
. (8.1)
При этом
![]() ,(8.2)
,(8.2)
![]() .(8.3)
.(8.3)
Уравнение
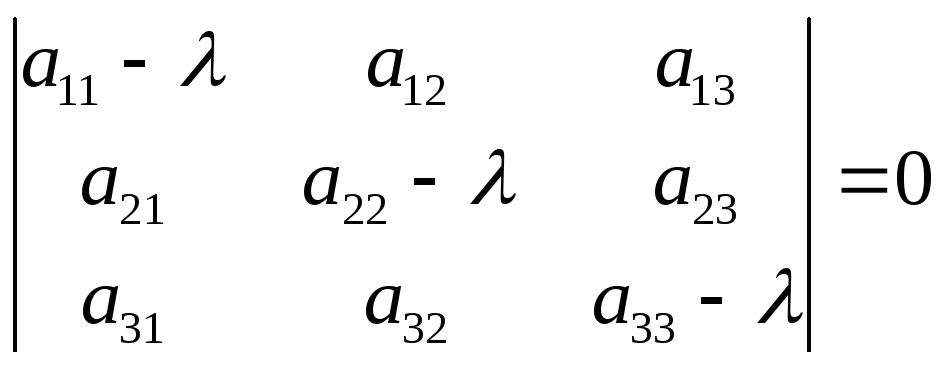 является характеристическим уравнением
является характеристическим уравнением
матрицы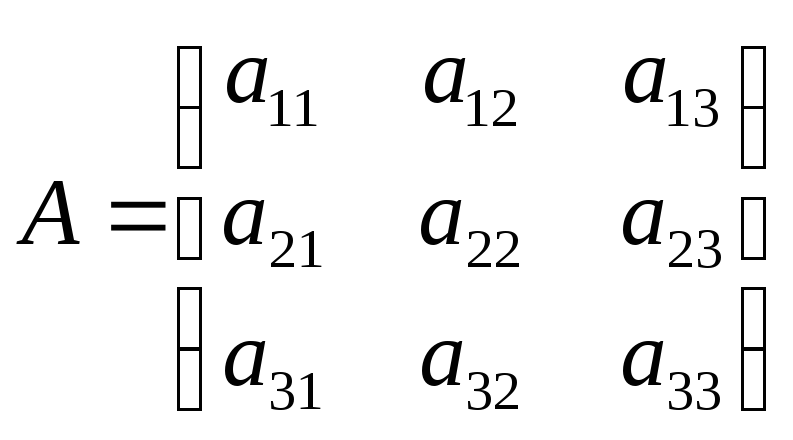 .Это
.Это
уравнение может быть представлено в
виде
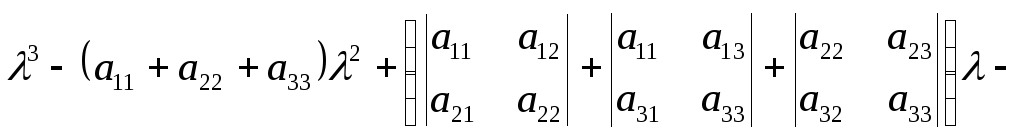
![]() или
или
![]() ,
,
(8.4)
где
![]() ,
,
а![]() миноры определителя
миноры определителя![]() .
.
Если
![]() ,
,![]() и
и![]() корни характеристического уравнения
корни характеристического уравнения
(8.4), то это уравнение может быть записано
в виде
![]() . (8.5)
. (8.5)
Сравнивая уравнения
(8.4) и (8.5), можно записать следующее:
![]() ,(8.6)
,(8.6)
![]() ,(8.7)
,(8.7)
![]() .(8.8)
.(8.8)
Собственные векторы
матрицы
![]() ,
,
соответствующие собственному значению![]() ,
,
удовлетворяют матричному уравнению![]() ,
,
которое может быть записана в форме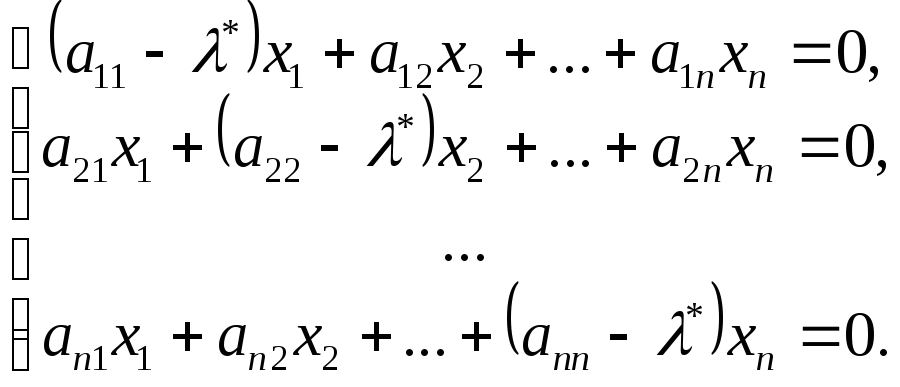 Так
Так
как ранг матрицы этой системы меньше
числа неизвестных (![]() =0),
=0),
то система имеет бесконечное множество
решений, каждое
ненулевое
из которых является собственным вектором,
соответствующим собственному значению
![]() .
.
● Пример 5.
Найти собственные значения и собственные
векторы матрицы
![]() .
.
Решение.
![]() – характеристическое уравнение для
– характеристическое уравнение для
данной матрицы, откуда![]() ,
,![]() и
и![]() .
.
Для нахождения
собственных векторов, соответствующих
собственному
значению
![]() ,
,
имеем систему![]() эквивалентную уравнению
эквивалентную уравнению![]() .
.
Вектор![]() является решением этого уравнения, а
является решением этого уравнения, а
при![]() вектор
вектор![]() – искомый собственный вектор.
– искомый собственный вектор.
Для
нахождения собственных векторов,
соответствующих собственному значению
![]() ,
,
имеем систему![]() из которой следует, что вектор
из которой следует, что вектор![]() при
при![]() является собственным вектором,
является собственным вектором,
соответствующим собственному значению![]() .
.
Ответ.
![]() ,
,![]() при
при![]() ;
;![]() ,
,![]() при
при![]() .
.
● Пример 6.
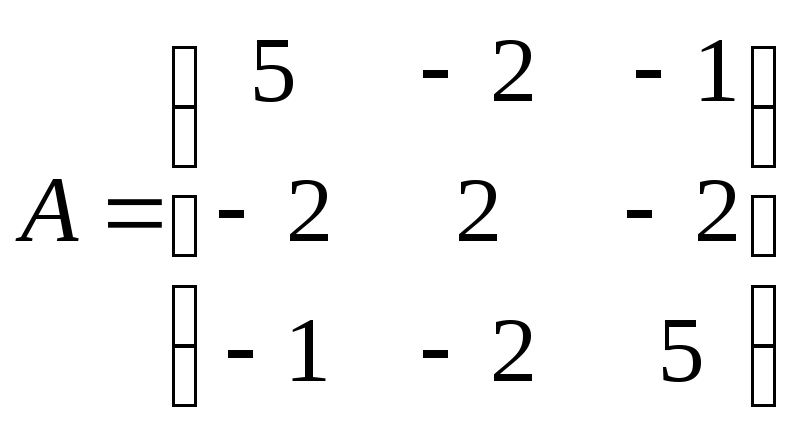
Найти собственные
пары матрицы
 .
.
Решение.
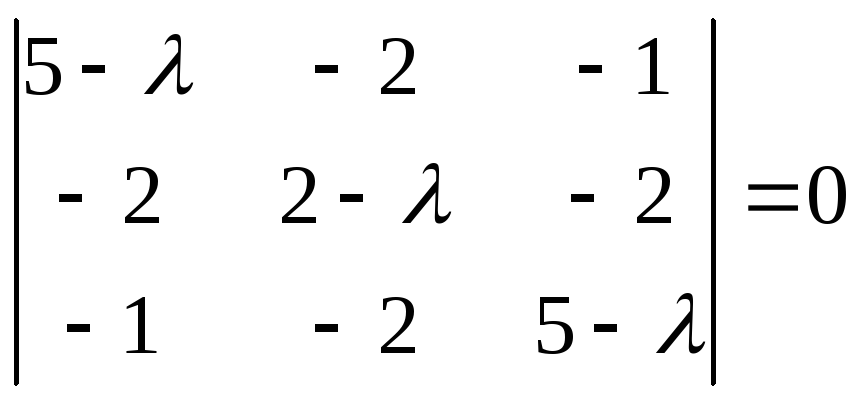 – характеристическоеуравнение
– характеристическоеуравнение
матрицы
![]() ,
,
которое может быть записано в виде![]() ,
,
где![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (проверьте).
(проверьте).
![]() –
–
характеристическое уравнение матрицы
![]() ,
,
корни которого![]() .
.
Собственные
векторы, соответствующие собственному
значению
![]() ,
,
находим из системы![]() .
.
При![]() имеем систему
имеем систему
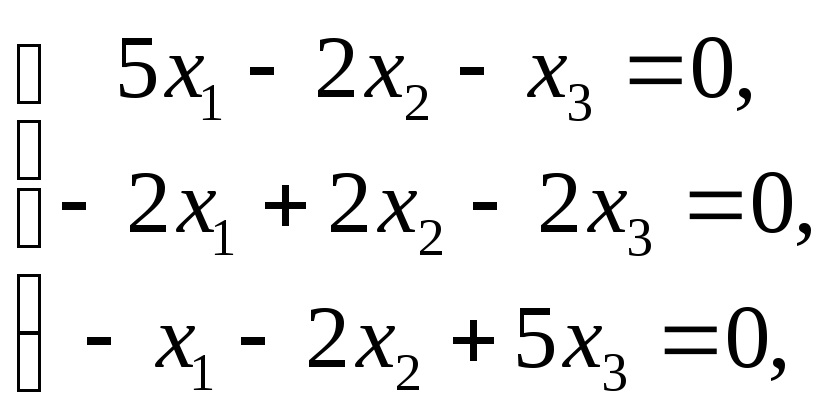 которая
которая
равносильна системе
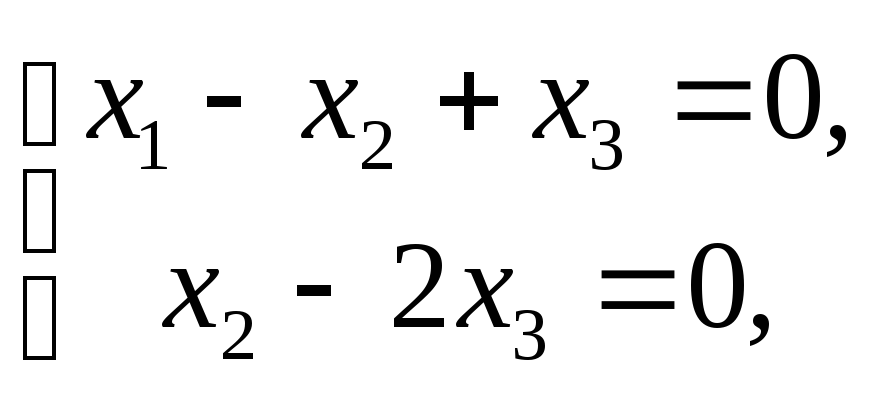 решение
решение
которой
![]() .
.
При
![]() вектор
вектор![]() является собственным вектором матрицы
является собственным вектором матрицы![]() ,
,
соответствующим собственному значению![]() .
.
При
![]() для нахождения собственных векторов
для нахождения собственных векторов
имеем систему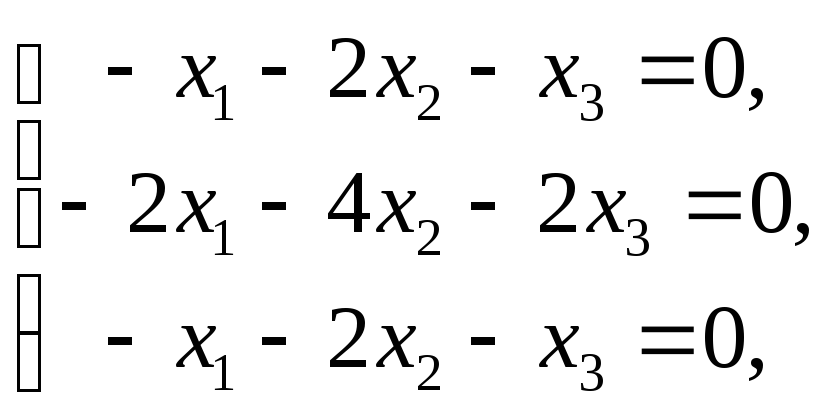 которая равносильна одному уравнению
которая равносильна одному уравнению![]() .
.
При любых
![]() и
и![]() вектор
вектор![]() есть решение уравнения
есть решение уравнения![]() ,
,
а при![]()
![]() является собственным
является собственным
вектором, который соответствует
собственному значению
![]() .
.
Ответ:
![]() при
при![]() ;
;![]() при
при![]() .
.
● Пример 7.
Найти собственные значения и собственные
векторы матрицы
![]() .
.
Решение.
Характеристическое уравнение для
указанной матрицы имеет вид
![]() ,
,
откуда![]() и
и![]() .
.
Для нахождения
собственных векторов, соответствующих
собственному значению
![]() ,
,
имеем систему![]() из которой следует
из которой следует![]() при
при![]() .
.
Для нахождения
собственных векторов, соответствующих
собственному значению
![]() ,
,
имеем систему![]() из которой следует
из которой следует![]() при
при![]() .
.
Ответ.
![]() ,
,![]() при
при![]() ;
;![]() ,
,![]() при
при![]() .
.
● Пример 8.
Доказать, что если
![]() собственная
собственная
пара невырожденной матрицы
![]() ,
,
то
![]() –собственная
–собственная
пара матрицы
![]() .
.
►Так матрица
![]() невырожденная (
невырожденная (![]() ),
),
то существует![]() .
.
Произведение собственных значений
матрицы![]() равно
равно![]() ,
,
а так как![]() ,
,
то собственное значение![]() .
.
![]() – собственная
– собственная
пара матрицы
![]() ,
,
поэтому![]() .Умножив
.Умножив
последнее равенство слева на
![]() ,
,
имеем![]() ,
,
откуда![]() ,
,![]() и
и![]() .
.
Последнее равенство означает, что
![]() –
–
собственная
пара матрицы
![]() .◄
.◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Download Article
Download Article
The matrix equation 


Eigenvalues and eigenvectors have immense applications in the physical sciences, especially quantum mechanics, among other fields.
Steps
-

1
Understand determinants. The determinant of a matrix
when
is non-invertible. When this occurs, the null space of
becomes non-trivial – in other words, there are non-zero vectors that satisfy the homogeneous equation
[1]
-

2
Advertisement
-

3
-

4
-

5
Solve the characteristic polynomial for the eigenvalues. This is, in general, a difficult step for finding eigenvalues, as there exists no general solution for quintic functions or higher polynomials. However, we are dealing with a matrix of dimension 2, so the quadratic is easily solved.
-

6
Substitute the eigenvalues into the eigenvalue equation, one by one. Let’s substitute
first.[3]
- The resulting matrix is obviously linearly dependent. We are on the right track here.
-

7
Row-reduce the resulting matrix. With larger matrices, it may not be so obvious that the matrix is linearly dependent, and so we must row-reduce. Here, however, we can immediately perform the row operation
to obtain a row of 0’s.[4]
-

8
Advertisement
Add New Question
-
Question
Why do we replace y with 1 and not any other number while finding eigenvectors?

For simplicity. Eigenvectors are only defined up to a multiplicative constant, so the choice to set the constant equal to 1 is often the simplest.
-
Question
How do you find the eigenvectors of a 3×3 matrix?

Alphabet
Community Answer
First, find the solutions x for det(A – xI) = 0, where I is the identity matrix and x is a variable. The solutions x are your eigenvalues. Let’s say that a, b, c are your eignevalues. Now solve the systems [A – aI | 0], [A – bI | 0], [A – cI | 0]. The basis of the solution sets of these systems are the eigenvectors.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
The determinant of a triangular matrix is easy to find – it is simply the product of the diagonal elements. The eigenvalues are immediately found, and finding eigenvectors for these matrices then becomes much easier.[5]
- Beware, however, that row-reducing to row-echelon form and obtaining a triangular matrix does not give you the eigenvalues, as row-reduction changes the eigenvalues of the matrix in general.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 109,185 times.






















