В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.
-
Формулы расчета радиуса сферы (шара)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
-
Правильная шестиугольная пирамида
Формулы расчета радиуса сферы (шара)
Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.
Правильная треугольная пирамида

На этом рисунке и чертежах далее:
- a – ребро основания пирамиды;
- h – высота фигуры.
Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:
![]()
Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:
![]()
Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:
![]()
Нахождение радиуса сферы (шара), описанной около правильной пирамиды
В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.
Формулы расчета радиуса сферы (шара)
Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.
Правильная треугольная пирамида

На этом рисунке и чертежах далее:
- a – ребро основания пирамиды;
- h – высота фигуры.
Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:
Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу
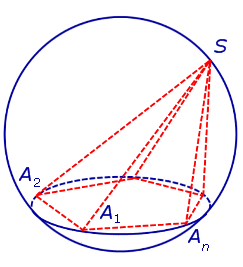
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).
Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.



Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.
Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

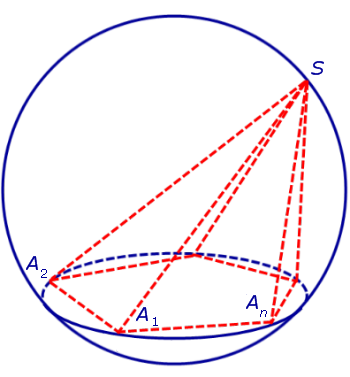
На рисунке 2 изображена пирамида SA1A2 . An , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A1A2 . An – основание пирамиды. Доказано.
Теперь предположим, что около основания A1A2 . An пирамиды SA1A2 . An можно описать окружность. Докажем, что в этом случае около пирамиды SA1A2 . An можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A1A2 . An , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A1A2 . An (рис. 3).
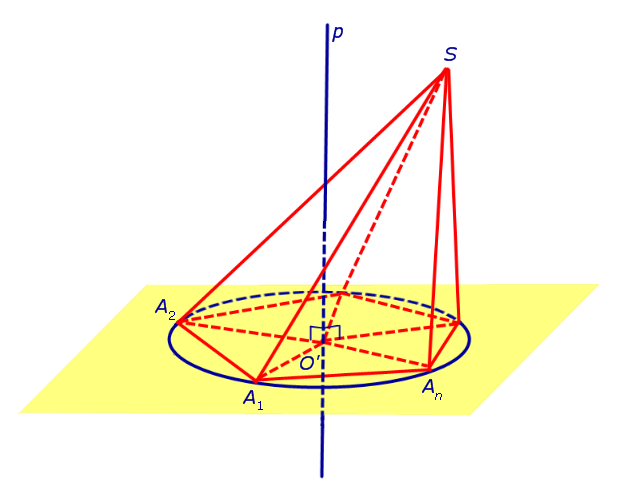
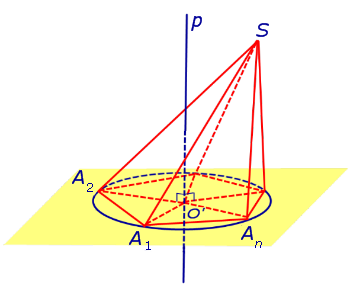
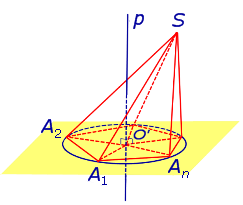
Рассмотрим плоскость β, проходящую через середину отрезка SAn и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA1A2 . An . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.
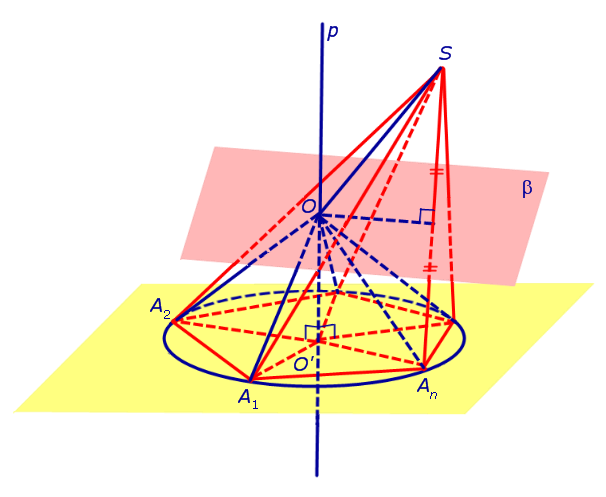
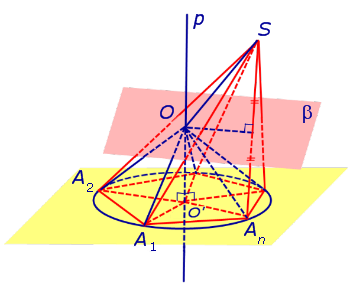
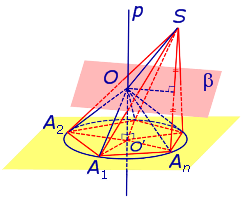
Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA1A2 . An . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA1A2 . An .
Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A1A2 . An , что противоречит определению пирамиды.
Следствие 1. Около любой правильной пирамиды можно описать сферу.
Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.
Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.
Радиус сферы, описанной около правильной n – угольной пирамиды
Задача 1. Высота правильной n – угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.
Решение. Рассмотрим правильную n – угольную пирамиду SA1A2 . An и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’An (рис. 5).
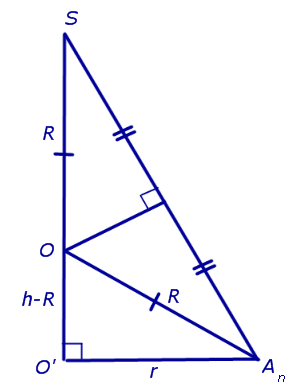
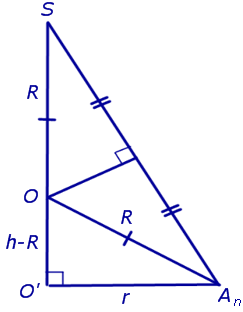
Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OAn получаем
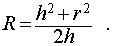 |
(1) |
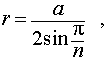
из формулы (1) получаем соотношение
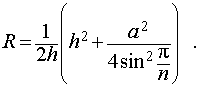 |
(2) |
Ответ. 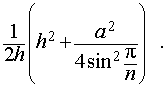
Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен
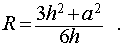
Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен
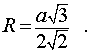
Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен
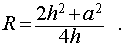
Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен
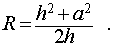
Отношение объемов правильной n – угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды
Задача 2. Около правильной n – угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.
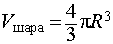
Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:
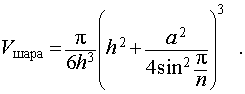
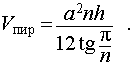
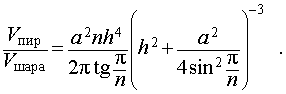
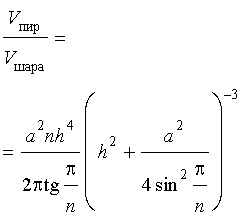
Ответ. 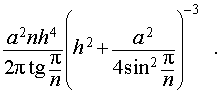
Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно
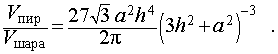
Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно
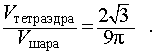
Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
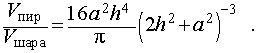
Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
Формула для описанной окружности пирамиды
14.1. Определение пирамиды и её элементов
Определение. Пирамидой называется многогранник, у которого одна грань — многоугольник, а остальные грани — треугольники с общей вершиной (рис. 95, 96).
Многоугольник называется основанием пирамиды, остальные грани — боковыми гранями пирамиды, их общая вершина — вершиной пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами её основания, называются боковыми рёбрами пирамиды .
Пирамиду с основанием АВСDЕ и вершиной Р обозначают PABCDE .
Перпендикуляр, опущенный из вершины пирамиды на плоскость её основания, называется высотой пирамиды . Длину этого перпендикуляра также называют высотой пирамиды.
Пирамида называется n-угольной, если её основанием является n-угольник .
На рисунке 96 изображена четырёхугольная пирамида PABCD, у которой: четырёхугольник ABCD — основание пирамиды; точка Р — вершина пирамиды; отрезки РA, РВ, PC, PD — боковые рёбра пирамиды; отрезки АВ, ВС, CD, DA — стороны (рёбра) основания пирамиды; отрезок РО — высота пирамиды; треугольники РАВ, РВС, PCD, PDA — боковые грани пирамиды.
У n- угольной пирамиды имеется ( n + 1) вершин, 2 n рёбер и ( n + 1) граней. Диагоналей пирамида не имеет. В пирамиде различают плоские углы при её вершине и двугранные углы при её рёбрах. Двугранным углом при ребре пирамиды называют содержащий пирамиду двугранный угол, образованный плоскостями граней, проходящими через данное ребро.
Треугольную пирамиду (рис. 97) называют также тетраэдром ( « тетраэдр» по-гречески означает «четырёхгранник» ) . Тетраэдр — это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.
Любую пирамиду можно разбить на некоторое число тетраэдров, а любой выпуклый многогранник — на некоторое число пирамид. Для этого достаточно, например, взять любую точку внутри данного многогранника и соединить её отрезками со всеми его вершинами. Такое разбиение часто используется при нахождении объёмов многогранников.
14.2. Некоторые виды пирамид
Если все боковые рёбра пирамиды составляют с плоскостью основания равные углы, то : а ) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды ; б ) все боковые рёбра пирамиды равны между собой.
Доказательств о. а) Пусть отрезок РО — высота пирамиды PABCDEF, все рёбра которой составляют с плоскостью основания угол ϕ (рис. 98). Тогда прямоугольные треугольники РОА, POB, POC, POD, РОЕ и POF, имея общий катет РО, равны между собой (по катету и острому углу ϕ ) . Из равенства этих треугольников следует: ОА = OВ = ОС = OD = OE = OF, т. е. вершины основания пирамиды равноудалены от основания О её высоты РО. Это означает, что точка О — центр окружности, описанной около основания ABCDEF данной пирамиды.
б) Из ОА = OВ = ОС = OD = ОЕ = OF следует, что боковые рёбра РА, РВ, PC, PD, РЕ, PF пирамиды равны, как наклонные, имеющие равные проекции, т. е. РА = РВ = PC = PD = РЕ = PF. Что и требовалось доказать. ▼
Вы самостоятельно можете доказать обратные утверждения.
1. Если основание высоты пирамиды совпадает с центром окружности, описанной около её основания, то: а) все боковые рёбра пирамиды образуют с плоскостью основания равные углы; б) все боковые рёбра пирамиды равны между собой.
2. Если все боковые рёбра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды составляют с плоскостью её основания равные между собой углы.
Также имеет место следующее утверждение.
Если высота пирамиды пересекает её основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в её основание.
Доказательств о. Пусть РО — высота пирамиды PABCDE, боковые грани которой образуют с плоскостью основания пирамиды двугранные углы, равные ϕ (рис. 99).
Проведём высоты РН 1 , РH 2 , РН 3 , PH 4 , РH 5 боковых граней.
Тогда по теореме о трёх перпендикулярах получаем OH 1 ⟂ AB, OH 2 ⟂ BC, OH 3 ⟂ CD, OH 4 ⟂ DE, OH 5 ⟂ EA, следовательно, ∠ OH 1 P = ∠ OH 2 P = ∠ OH 3 P = ∠ OH 4 P = ∠ OH 5 P = ϕ . Поэтому △ OH 1 P = △ OH 2 P = △ OH 3 P = △ OH 4 P = △ OH 5 P (как прямоугольные с общим катетом OP и острым углом ϕ ) . Из равенства этих треугольников следует ОН 1 = OH 2 = OH 3 = ОН 4 = ОН 5 , т. е. точка О — основание высоты РО пирамиды — равноудалена от всех сторон многоугольника ABCDE. Это означает, что точка O является центром окружности, вписанной в основание ABCDE данной пирамиды. Теорема доказана. ▼
Самостоятельно докажите обратное утверждение.
Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
Перечислим ещё несколько часто встречающихся в задачах видов пирамид.
• Пирамида, ровно одна боковая грань которой перпендикулярна плоскости основания. Высота такой пирамиды лежит в этой, перпендикулярной основанию, грани (рис. 100).
• Пирамида, две соседние боковые грани которой перпендикулярны плоскости основания. Высотой такой пирамиды служит боковое ребро, общее для этих граней (рис. 101).
• Пирамида, две не соседние боковые грани которой перпендикулярны плоскости основания. Высота такой пирамиды лежит на прямой пересечения плоскостей этих граней (рис. 102).
14.3. Правильная пирамида
Определение. Пирамида называется правильной, если её основание — правильный многоугольник и вершина пирамиды проектируется в центр этого основания.
Из определения следует алгоритм построения изображения правильных пирамид, что, в свою очередь, доказывает существование таких пирамид.
Для построения изображения правильной пирамиды достаточно построить изображение соответствующего правильного многоугольника (основания пирамиды) и его центра. Затем из построенного центра провести перпендикуляр к плоскости многоугольника и выбрать на этом перпендикуляре (в качестве вершины пирамиды) любую точку, отличную от центра многоугольника. Соединив отрезками прямых эту точку со всеми вершинами многоугольника, получим изображение правильной пирамиды.
На рисунке 103, а, б, в построены изображения правильных пирамид: а) треугольной; б) четырёхугольной; в) шестиугольной.
Правильные пирамиды обладают замечательным свойством.
В правильной пирамиде все боковые рёбра равны, а все боковые грани — равные равнобедренные треугольники.
Доказательств о. Рассмотрим правильную n- угольную пирамиду РА 1 А 2 . A n . Пусть точка O — центр n- угольника A 1 A 2 A 3 . A n ; отрезок РО — перпендикуляр к плоскости основания пирамиды (рис. 104).
Так как центр правильного многоугольника является центром окружности, описанной около этого многоугольника, то ОА 1 = OA 2 = OA 3 = . = OA n (как радиусы описанной окружности). Тогда равны боковые рёбра пирамиды, как наклонные к плоскости её основания, имеющие равные проекции, т. е. PA 1 = PA 2 = PA 3 = . = PA n .
Таким образом, имеем:
РА 1 = РA 2 = . = PA n (как боковые рёбра);
A 1 A 2 = A 2 A 3 = . = A n A 1 (как стороны правильного n- угольника).
Следовательно, треугольники PA 1 A 2 , РA 2 A 3 , . PA n A 1 являются равнобедренными и по третьему признаку равенства треугольников равны между собой.
Это свойство правильной пирамиды можно доказать при помощи поворота пирамиды вокруг оси, содержащей её высоту.
Так как точка О — центр правильного n- угольника A 1 A 2 A 3 . A n , лежащего в основании правильной пирамиды PA 1 A 2 . A n , РО — перпендикуляр к плоскости её основания, то при вращении данной пирамиды вокруг оси ОР на угол, равный (где k = 1, 2, 3, . n ), происходит самосовмещение этой пирамиды: вершины основания пирамиды отображаются на его же вершины (основание совмещается с самим собой); вершина Р (как точка оси вращения) отображается на себя. Следовательно, боковые рёбра пирамиды отображаются на боковые рёбра, а боковые грани пирамиды — на её боковые грани. А так как вращение вокруг прямой — движение, то все боковые рёбра правильной пирамиды равны между собой, а грани являются равными равнобедренными (почему?) треугольниками. Утверждение доказано. ▼
Следствием доказанного выше является утверждение.
Все боковые рёбра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани — равные двугранные углы.
Докажите это предложение самостоятельно.
Высота боковой грани правильной пирамиды, проведённая к ребру её основания, называется апофемой пирамиды. На рисунке 104 отрезок РН — одна из апофем пирамиды.
Все апофемы правильной пирамиды равны вследствие равенства всех её боковых граней.
Имеют место признаки правильной пирамиды:
Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все её боковые рёбра равны; б) все её боковые рёбра образуют с плоскостью основания равные углы; в) все её боковые грани — равные равнобедренные треугольники.
Докажите это самостоятельно.
ЗАДАЧА (2.245). Высота правильной четырёхугольной пирамиды равна h и образует с боковой гранью угол α . Через сторону основания пирамиды проведена плоскость, перпендикулярная противоположной грани и пересекающая её. Найти площадь сечения.
Дан о: PABCD — правильная пирамида (рис. 105); РО — высота пирамиды, РО = h ; ∠ OPF = α .
Решени е. Первый спосо б . Пусть отрезок EF — средняя линия основания пирамиды. Тогда AD ⟂ EF, AD ⟂ PF ⇒ АD ⟂ ( РEF ) ⇒ ( PEF ) ⟂ ( ADP ) (по признаку перпендикулярности двух плоскостей). Поэтому прямая PF является ортогональной проекцией прямой РO на плоскость ADP. Значит, ∠ OPF — угол между высотой PO и боковой гранью ADP пирамиды: ∠ OPF = α .
Далее имеем: AD ⟂ ( PEF ), ВС || AD ⇒ ВC ⟂ ( PEF ) ⇒ прямая ВС перпендикулярна любой прямой плоскости PEF. Поэтому если FL ⟂ РЕ (в плоскости PEF ) , то BС ⟂ FL. Тогда FL ⟂ ВС, FL ⟂ PE ⇒ FL ⟂ ( BCP ) ⇒ ( ADL ) ⟂ ( ВCР ) (по признаку перпендикулярности двух плоскостей); при этом ( ADL ) ∩ ( ВСР ) = МK , МK || AD, так как плоскости ВСР и АDL проходят через параллельные прямые ВС и AD. Значит, сечение ADKM — трапеция, у которой FL — высота (почему?), откуда
S сеч = • FL.
Найдём AD, МK и FL.
В △ OPF ( ∠ POF = 90 ° ):
OF = OP • tg α = h • tg α ; PF = = = PE.
EF = 2 FO = 2 h • tg α = ВС.
В плоскости PEF получаем:
FL ⟂ РЕ, РО ⟂ EF ⇒ ∠ EFL = ∠ OPE = α .
Тогда в △ ЕFL : FL = ЕF • cos α = 2 h • tg α • cos α = 2 h sin α ;
в △ PLF ( ∠ PLF = 90 ° , ∠ PFL = 90 ° – 2 α ):
PL = PF • sin (90 ° – 2 α ) = PF • cos 2 α = .
Так как MK | | BC, то △ МKР ∾ △ ВСР, откуда
= ⇒ MK = = =
= 2 h tg α • cos 2 α .
AD = EF = 2 h • tg α , FL = 2 h • sin α , MK = 2 h • tg α • cos 2 α .
S сеч = • FL = • 2 h • sin α =
= = 4 h 2 • sin 2 α • cos α .
Замечание. Отрезок MK можно найти следующим образом. Сечением данной пирамиды плоскостью, проходящей через прямую MK параллельно основанию пирамиды, является квадрат MKD 1 A 1 (см. рис. 105). F 1 = A 1 D 1 ∩ PF. У этого квадрата LF 1 = MK. Найдём F 1 L .
В треугольнике LFF 1 имеем ∠ FLF 1 = α ( LF 1 || EF ) ,
∠ F 1 FL = ∠ OFP – ∠ OFL = (90 ° – α ) – α = 90 ° – 2 α ;
∠ FF 1 L = 180 ° – ∠ OFF 1 = 90 ° + α . Тогда по теореме синусов
= ⇒
⇒ LF 1 = = .
Значит, MK = LF 1 = 2 h • tg α • cos 2 α .
Второй спосо б . Пусть точки M 1 , K 1 , L 1 — ортогональные проекции на плоскость основания соответственно точек М, K, L (рис. 105, 106). Так как плоскости АСР, BDP и EFP перпендикулярны плоскости основания пирамиды, то ортогональными проекциями прямых PC, РВ и РЕ на эту плоскость являются соответственно прямые АС, BD и EF. Следовательно, M 1 ∈ BD, K 1 ∈ AC, L 1 ∈ EF, причём четырёхугольник ADK 1 M 1 — равнобедренная трапеция.
Таким образом, трапеция ADK 1 M 1 — ортогональная проекция сечения ADKM. Это означает, что S ADKM = . Найдём . Так как диагонали квадрата взаимно перпендикулярны и M 1 K 1 || AD, то OL 1 = L 1 K 1 , OF = FD. Значит,
= • L 1 F = • FL 1 = .
S ADKM = = = 4 h 2 • sin 2 α • cos α .
Ответ: 4 h 2 • sin 2 α • cos α .
1 4.4. Площади боковой и полной поверхностей пирамиды
Поверхность пирамиды состоит из основания и боковых граней. В этой связи различают боковую и полную поверхности пирамиды, а также их площади.
Площадью боковой поверхности пирамиды (обозначают S бок ) называется сумма площадей всех её боковых граней: S бок = S 1 + S 2 + . + S n , где S 1 , S 2 , . S n — площади боковых граней пирамиды.
Площадью полной поверхности пирамиды (обозначают S полн ) называется сумма площадей всех её граней, т. е. сумма площади основания пирамиды и площади её боковой поверхности.
Из определения следует: S полн = S бок + S осн .
О площади боковой поверхности правильной пирамиды имеет место следующая теорема.
Теорема 18. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.
Доказательств о. PA 1 A 2 . A n — правильная пирамида, a — длина её апофемы (рис. 107).
Боковые грани правильной пирамиды — равные равнобедренные треугольники, у которых основаниями являются стороны правильного n- угольника A 1 A 2 . A n , а высоты равны апофеме пирамиды, т. е.
РE 1 = РE 2 = PE 3 = . = PE n = a.
S бок = S △ PA 1 A 2 + S △ PA 2 A 3 + . + S △ PA n A 1 =
= A 1 A 2 • PE 1 + A 2 A 3 • PE 2 + . + A n A 1 • PE n =
= a • ( A 1 A 2 + A 2 A 3 + . + A n A 1 ) = P • a,
где Р — периметр основания пирамиды. Теорема доказана. ▼
Теорема 19. Если все боковые грани пирамиды наклонены к плоскости основания под углом ϕ и высота пересекает основание, то S бок = .
Доказательств о. Пусть отрезок PO — высота пирамиды РA 1 A 2 A 3 . A n , все боковые грани которой образуют с плоскостью основания углы, равные ϕ (рис. 108); отрезки PH 1 , PH 2 , . PH n — высоты боковых граней. Тогда (по теореме о трёх перпендикулярах) OH 1 ⟂ A 1 A 2 , OH 2 ⟂ A 2 A 3 , . OH n ⟂ A n A 1 . Значит,
∠ OH 1 P = ∠ OH 2 P = ∠ OH 3 P = .
. = ∠ OH n P = ϕ .
Так как точка О является центром круга, вписанного в основание пирамиды (почему?), то эта точка лежит внутри n- угольника A 1 A 2 A 3 . A n . Поэтому n- угольник A 1 A 2 . A n является объединением непересекающихся треугольников A 1 OA 2 , A 2 OA 3 , . A n OA 1 . Эти треугольники являются ортогональными проекциями на плоскость основания пирамиды её соответствующих боковых граней. По теореме о площади ортогональной проекции многоугольника имеем:
S △ A 1 OA 2 = S △ A 1 PA 2 • cos ϕ ,
S △ A 2 OA 3 = S △ A 2 PA 3 • cos ϕ ,
.
S △ A n OA 1 = S △ A n PA 1 • cos ϕ .
Сложив почленно эти равенства, получим S осн = S бок • cos ϕ , откуда S бок = . Теорема доказана. ▼
Так как все боковые грани правильной пирамиды образуют с плоскостью основания равные двугранные углы (пусть величина этих углов равна ϕ , см. рис. 107), то для площади боковой поверхности и площади основания правильной пирамиды также справедлива формула
S бок = .
14 . 5 . Свойства параллельных сечений пирамиды
Если плоскость α параллельна основанию пирамиды и пересекает её, то в сечении пирамиды получается некоторый многоугольник (рис. 109).
Теорема 20. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательств о. 1) Пусть сечением пирамиды PABCD плоскостью α , параллельной плоскости β её основания, является четырёхугольник A 1 B 1 C 1 D 1 (см. рис. 109).
Проведём высоту РО данной пирамиды и обозначим O 1 = РО ∩ α .
Рассмотрим гомотетию с центром Р , при которой плоскость основания данной пирамиды отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание ABCD пирамиды на её параллельное сечение — многоугольник А 1 В 1 С 1 D 1 , при этом вершины А, В, С, D основания пирамиды — на вершины соответственно A 1 , B 1 , C 1 , D 1 , а точку O — на точку O 1 (почему?).
Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
= = = = = k, (*)
где k — коэффициент гомотетии . Это означает, что параллельное сечение пирамиды делит её рёбра и высоту на пропорциональные части. А поскольку гомотетия является подобием, то многоугольник A 1 B 1 C 1 D 1 , являющийся параллельным сечением пирамиды, подобен её основанию ABCD .
Вследствие того, что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии, а k = РO 1 : РО , где РO 1 и РО — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
S A 1 B 1 C 1 D 1 : S ABCD = k 2 = : PO 2 .
Следствие. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.
14.6. Усечённая пирамида
Плоскость α , параллельная основанию пирамиды PABCD и пересекающая её, делит эту пирамиду на два многогранника: пирамиду РA 1 B 1 C 1 D 1 и многогранник ABCDA 1 B 1 C 1 D 1 (см. рис. 109).
Многогранник ABCDA 1 B 1 C 1 D 1 (рис. 110) называют усечённой пирамидой. Грани ABCD и A 1 B 1 C 1 D 1 , лежащие в параллельных плоскостях, называются соответственно нижним и верхним основаниями усечённой пирамиды , остальные грани — её боковыми гранями . Так как нижнее и верхнее основания усечённой пирамиды гомотетичны (т. 20), то все её боковые грани — трапеции.
Таким образом, усечённой пирамидой называется часть полной пирамиды, заключённая между её основанием и параллельным ему сечением.
У n- угольной усечённой пирамиды 2 n вершин, 3 n рёбер, ( n + 2) грани и n ( n – 3) диагоналей.
Высотой усечённой пирамиды называется перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённой пирамиды. На рисунке 110 отрезки О 1 О, B 1 K — высоты усечённой пирамиды.
Усечённая пирамида называется правильной, если она получена из правильной пирамиды (рис. 111).
Из теоремы 20 следует, что основания правильной усечённой пирамиды — подобные правильные многоугольники, а боковые грани — равные равнобедренные трапеции.
Высоты этих трапеций, соединяющие середины их оснований, называются апофемами усечённой пирамиды . Все её апофемы равны между собой.
Отрезок OO 1 , соединяющий центры оснований правильной усечённой пирамиды, является её высотой .
Площадью боковой поверхности усечённой пирамиды называется сумма площадей всех её боковых граней.
Для правильной усечённой пирамиды имеет место
Теорема 21. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему .
Для доказательства теоремы достаточно площадь одной из боковых граней пирамиды умножить на их число. В результате получим формулу S бок = • h , где Р 1 , P 2 — периметры нижнего и верхнего оснований усечённой пирамиды, h — её апофема.
Проведите доказательство теоремы самостоятельно.
Полная поверхность усечённой пирамиды — это объединение её оснований и боковой поверхности, поэтому для усечённой пирамиды
S полн = S бок + S 1 + S 2 ,
где S 1 и S 2 — площади большего и меньшего оснований этой пирамиды.
Для усечённой пирамиды, у которой все двугранные углы при рёбрах большего основания равны ϕ , справедливо: S бок = . (Для вывода этой формулы достаточно учесть следующий факт: если R и r — радиусы окружностей, вписанных соответственно в большее и меньшее основания данной пирамиды, то S 1 = 0,5 • P 1 • R , S 2 = 0,5 • P 2 • r, cos ϕ = , где h — высота боковой грани этой пирамиды.)
14 . 7 . Объём пирамиды
Лемма. Две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики .
Доказательств о. Пусть пирамиды РАВС и P 1 A 1 B 1 C 1 имеют высоты, равные H , и равновеликие основания с площадью S ; их объёмы — соответственно V 1 и V 2 . Докажем, что V 1 = V 2 .
Расположим пирамиды РАВС и P 1 A 1 B 1 C 1 так, чтобы их основания лежали в одной плоскости, а сами пирамиды были расположены по одну сторону от этой плоскости (рис. 112). Тогда любая плоскость, параллельная плоскости оснований и пересекающая первую пирамиду, пересекает и вторую, причём по теореме о параллельных сечениях пирамиды площади этих сечений равны. Следовательно, на основании принципа Кавальери равны и объёмы этих пирамид. Лемма доказана. ▼
Теорема 22. Объём любой треугольной пирамиды равен одной трети произведения площади основания на высоту.
Доказательств о. Пусть А 1 AВC — данная треугольная пирамида с вершиной A 1 и основанием ABC (рис. 113). Дополним эту пирамиду до треугольной призмы ABCA 1 B 1 C 1 с тем же основанием, одним из боковых рёбер которой является боковое ребро АA 1 данной пирамиды. Это означает, что высота призмы равна высоте данной пирамиды.
Призма АВCA 1 B 1 C 1 является объединением трёх треугольных пирамид с общей вершиной A 1 : A 1 ABC, A 1 BB 1 C 1 и A 1 BCC 1 . Основания BB 1 C 1 и BCC 1 пирамид A 1 BB 1 C 1 и A 1 BCC 1 равны, а высота у них общая. Значит, по лемме эти пирамиды имеют равные объёмы.
Будем считать точку В вершиной пирамиды A 1 BB 1 C 1 , a △ A 1 B 1 C 1 — её основанием. Тогда эта пирамида равновелика пирамиде А 1 AВС, так как у них общая высота, а основания АВС и A 1 B 1 C 1 равновелики (как основания призмы). Таким образом, призма ABCA 1 B 1 C 1 является объединением трёх равновеликих пирамид, одной из которых является данная пирамида A 1 ABC. Это означает, что объём V пирамиды A 1 АВС составляет одну треть объёма призмы ABCA 1 B 1 C 1 , т. е. V = S ocн • Н, где Н — длина высоты призмы. Но построенная призма и данная пирамида имеют общую высоту, длина которой равна Н, следовательно, объём треугольной пирамиды вычисляется по формуле
V = S осн • H ,
где Н — длина высоты данной пирамиды. Теорема доказана. ▼
На рисунке 114 изображены треугольная призма ABCDEF и составляющие её три равновеликие треугольные пирамиды ABDF, ABCF и BDEF .
Для вычисления объёма n- угольной пирамиды PA 1 A 2 . A n (рис. 115) разобьём её основание A 1 A 2 . A n диагоналями A 1 A 3 , A 1 A 4 , . A 1 A n – 1 на треугольники с общей вершиной A 1 . Тогда данная пирамида разбивается в объединение пирамид PA 1 A 2 A 3 , PA 1 A 3 A 4 , . PA 1 A n – 1 A n с общей вершиной Р и общей высотой, которая равна высоте данной пирамиды. Основаниями этих пирамид являются треугольники разбиения основания данной пирамиды. Это означает (свойство 2 объёмов), что объём V пирамиды PA 1 A 2 . A n равен сумме объёмов V 1 , V 2 , . V n – 2 треугольных пирамид соответственно PA 1 A 2 A 3 , PA 1 A 3 A 4 , . PA 1 A n – 1 A n .
Пусть длина высоты пирамиды равна Н, площадь её основания — S, а площади треугольников разбиения этого основания равны S 1 , S 2 , . S n – 2 . Это означает, что S 1 + S 2 + . + S n – 2 = S. Тогда получаем:
V = V 1 + V 2 + . + V n – 2 = H ( S 1 + S 2 + . + S n – 2 ) = S • H.
Таким образом, объём любой пирамиды вычисляется по формуле
V = S осн • H ,
где S осн — площадь основания, Н — длина высоты пирамиды.
Итак, доказана теорема.
Теорема 23. Объём любой пирамиды равен одной трети произведения площади основания на высоту. ▼
14.8. Об объёме тетраэдра
У тетраэдра за основание можно принять любую его грань, на каждую из которых можно провести высоту тетраэдра из вершины, противоположной этой грани. Поэтому для объёма V одного и того же тетраэдра имеют место соотношения
V = S 1 • h 1 = S 2 • h 2 = S 3 • h 3 = S 4 • h 4 ,
где S k и h k ( k = 1, 2, 3, 4) — площадь грани и длина опущенной на неё высоты. Эти соотношения часто используют при решении задач.
Заметим, что не в любом тетраэдре все четыре высоты пересекаются в одной точке (для сравнения — все три высоты любого треугольника пересекаются в одной точке). Тетраэдр, все высоты которого пересекаются в одной точке, называется ортоцентрическим.
Интересен также тетраэдр (рис. 116, а ), все грани которого равны. Такой тетраэдр называется равногранным. Его развёрткой является остроугольный треугольник (рис. 116, б ).
Докажите самостоятельно, что в равногранном тетраэдре:
— скрещивающиеся рёбра попарно равны;
— все высоты равны;
— сумма плоских углов трёхгранного угла при каждой вершине тетраэдра равна 180 ° ;
— двугранные углы при скрещивающихся рёбрах тетраэдра равны.
Не менее интересен следующий факт. Пусть дан тетраэдр A 1 C 1 BD . Проведём через каждое его ребро плоскость, параллельную скрещивающемуся с ним ребру. Проведённые шесть плоскостей при пересечении образуют некоторый параллелепипед АВСDA 1 В 1 C 1 D 1 (рис. 117), параллельные грани ABCD и A 1 B 1 C 1 D 1 которого содержат скрещивающиеся рёбра А 1 C 1 и BD данного тетраэдра. Тогда расстояние между основаниями АВСD и А 1 В 1 С 1 D 1 полученного параллелепипеда равно длине его высоты и равно расстоянию между скрещивающимися рёбрами А 1 C 1 и BD данного тетраэдра.
Этот параллелепипед можно разбить на пять тетраэдров — данный тетраэдр A 1 С 1 ВD и ещё четыре тетраэдра: A 1 ABD ; ВВ 1 A 1 C 1 ; C 1 CBD ; DD 1 A 1 C 1 . Объём каждого из четырёх последних тетраэдров равен одной трети высоты h параллелепипеда, умноженной на половину площади его основания ABCD , т. е. шестой части объёма V полученного параллелепипеда.
V A 1 C 1 BD = V – 4 • V = V = h • S ABCD = h • AC • BD • sin ϕ =
= h • A 1 C 1 • BD • sin ϕ ,
где ϕ — угол между диагоналями АС и BD параллелограмма ABCD . А так как AC || A 1 C 1 , то величина угла между скрещивающимися диагоналями A 1 С 1 и BD тетраэдра А 1 С 1 BD также равна ϕ .
Мы получили: объём тетраэдра равен одной шестой произведения длин любых двух его скрещивающихся рёбер, расстояния между ними и синуса угла между скрещивающимися прямыми, содержащими эти рёбра.
Отметим ещё несколько очевидных и менее очевидных свойств тетраэдров, связанных с их объёмами.
1. Объёмы тетраэдров с равными основаниями относятся как их высоты, опущенные на эти основания.
2. Объёмы тетраэдров с равными высотами относятся как площади их оснований.
3. Объёмы тетраэдров, имеющих равные трёхгранные углы, относятся, как произведения длин рёбер, образующих эти углы.
Используя рисунок 118, вы сможете легко доказать третье утверждение.
14.9. Объём усечённой пирамиды
Теорема 24. Объём усечённой пирамиды, у которой площади оснований равны S 1 и S 2 , а высота — Н , вычисляется по формуле
V = H ( S 1 + + S 2 ) .
Доказательств о. Пусть дана усечённая пирамида (рис. 119), у которой S 1 > S 2 , а высота OO 1 = H. Дополним эту пирамиду до полной пирамиды с вершиной Р. Объём V данной усечённой пирамиды равен разности объёмов полной и дополнительной пирамид.
Если длина высоты PO 1 дополнительной пирамиды равна x , то высота PO полной пирамиды равна H + x .
Выразим х через S 1 , S 2 и Н. По теореме 20 (o площадях параллельных сечений пирамиды) имеем
S 1 : S 2 = ( H + x ) 2 : x 2 ⇒ : = ( H + x ) : x ⇒
⇒ x = .
Поэтому для объёма V усечённой пирамиды находим
V = S 1 ( H + x ) – S 2 • x = ( S 1 • H + ( S 1 – S 2 ) • x ) =
= = ( S 1 H + ( + ) H ) =
= H ( S 1 + + S 2 ) ,
[spoiler title=”источники:”]
http://www.resolventa.ru/spr/stereometry/piramide_sphere.htm
http://reader.lecta.rosuchebnik.ru/demo/8285/data/chapter15.xhtml
[/spoiler]
 Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.
Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.
Обозначения
- $SABCDEF$ — правильная шестиугольная пирамида
- $O$ — центр основания пирамиды
- $a$ — длина стороны основания пирамиды
- $h$ — длина бокового ребра пирамиды
- $S_{text{осн.}}$ — площадь основания пирамиды
- $V_{text{пирамиды}}$ — объем пирамиды
Площадь основания пирамиды
В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$
Правильный шестиугольник в основании пирамиды
 По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.
По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.
Находим $SO$
Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$
Объем пирамиды
Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$
Находим $ST$ и $TO$
 Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=frac{sqrt{3}}{2}cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=sqrt{SO^2+TO^2}=sqrt{h^2-frac{1}{4}cdot a^2} $$
Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=frac{sqrt{3}}{2}cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=sqrt{SO^2+TO^2}=sqrt{h^2-frac{1}{4}cdot a^2} $$
Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.
Площадь основания правильной пирамиды
Правильная пирамида может быть трех видов:
- треугольная,
- четырехугольная,
- шестиугольная.
Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:
Площадь основания правильной треугольной пирамиды
В основании равносторонний треугольник – находим его площадь:
, где
– сторона треугольника.

Площадь основания правильной четырехугольной пирамиды
В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:
, где
– сторона квадрата.

Площадь основания правильной шестиугольной пирамиды
Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

Площадь основания любой пирамиды
Площадь основания любой пирамиды – это площадь ее основания.
Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.
В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.
Теперь давайте решим несколько задач для нахождения площади основания пирамиды
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона
, тогда
![]()
Ответ:
Задача 2
Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны
. Получим:
![]() м2.
м2.
Теперь подсчитаем, сколько нам понадобится досок: ![]() .
.
Ответ: 108 досок.
Задача 3
Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:
.
Ответ: 8
Зная сторону основания правильной пирамиды, то есть пирамиды, в основании которой лежит правильный многоугольник, можно найти периметр основания, его площадь, радиус окружностей, которые можно вписать или описать около него, а также угол между сторонами многоугольника.
Периметр правильного многоугольника равен произведению длины его стороны на их удвоенное количество, а площадь представляет собой отношение количества сторон, умноженного на квадрат длины одной стороны, к четырем тангенсам 180 градусов, деленных на количество сторон.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла.(рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Параметры самой пирамиды, как объемного тела, такие как боковое ребро и апофема пирамиды вычисляются через теорему Пифагора в прямоугольном треугольнике с высотой во внутреннем пространстве пирамиды. Вторым катетом прямоугольного треугольника с апофемой является радиус вписанной окружности, а катетом треугольника с боковым ребром – радиус описанной окружности основания. (рис.34.4,34.5)
l=√(h^2+r^2 )=√(h^2+(a/(2 tan〖(180°)/n〗 ))^2 )
b=√(h^2+R^2 )=√(h^2+(a/(2 sin〖(180°)/n〗 ))^2 )
Угол между апофемой и основанием рассчитывается как отношение синуса – высоты к радиусу вписанной окружности, а угол между боковым ребром и основанием аналогично – высоты к радиусу описанной окружности, из тех же прямоугольных треугольников.
sinα=h/r=(2h tan〖(180°)/n〗)/a
sinβ=h/R=(2h sin〖(180°)/n〗)/a
Зная апофему и сторону основания пирамиды, можно найти площадь боковой поверхности, а затем площадь полной поверхности пирамиды.
S_(б.п.)=lan/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))
Объем пирамиды равен трети произведения площади основания на высоту, таким образом, зная высоту и сторону основания пирамиды, вычислить ее объем можно, подставив соответствующее выражение вместо площади основания.
V=1/3 S_(осн.) h=(na^2 h)/(12 tan〖(180°)/n〗 )
В любую правильную пирамиду (в основании которой лежит правильный многоугольник) можно вписать сферу, а также описать сферу около нее. Радиусы вписанной и описанной сфер зависят не только от высоты и стороны основания, но и от объема пирамиды, площади полной поверхности и бокового ребра пирамиды, поэтому для их вычисления необходимо произвести алгебраические преобразования формул. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =ah/(tan〖(180°)/n〗 (2l+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=(h^2+(a/(2 sin〖(180°)/n〗 ))^2)/2h
