-
Подготовка исходной информации для разработки числовой эмм задачи
Исходной информацией
для составления экономико-математической
модели служат, как правило, годовые
отчеты, производственно-финансовые
планы, технологические карты, текущая
отчетность сельскохозяйственных
предприятий, а также различного рода
нормативы. Основные требования,
предъявляемые к исходной информации,
— высокое качество, достаточное
количество и соответствующая размерность
(единицы измерения).
При подготовке
исходной информации необходимо тщательно
проверять ее достоверность. Количество
и содержание исходной информации зависят
от постановки экономико-математической
задачи и будут рассмотрены ниже. Для
любой задачи исходная информация,
необходимая для составления
экономико-математической модели, должна
быть представлена в виде технико-экономических
коэффициентов (аij
), оценок целевой функции (сj
) и свободных членов уравнений и неравенств
(Bi
).
Технико-экономические
коэффициенты в зависимости от
ограничений, к которым они относятся,
могут характеризовать затраты
ресурсов, выход продукции, выработку
в расчете на принятую единицу измерения
переменной. Так, если единицей
измерения переменной избран 1 га площади
посева, то все технико-экономические
коэффициенты, находящиеся в соответствующем
столбце, должны выражать затраты ресурсов
или выпуск продукции в расчете на 1 га
посева.
Технико-экономические
коэффициенты, относящиеся к одному
ограничению, должны иметь ту единицу
измерения, в которой вводится свободный
член соответствующего уравнения или
неравенства. Так, если нужно ввести в
модель условие, гарантирующее, что
использование трудовых ресурсов по
оптимальному плану не должно превышать,
например, 20000 человеко-дней, тогда
соответствующее ограничение примет
вид:
2,1х1+ 3,5х2 +…+ 20х20 <
20 000,
где х1 – х20 —
переменные задачи, а технико-экономические
коэффициенты при них выражают затраты
труда в человеко-днях в расчете на
принятую единицу измерения переменной.
Оценки целевой
функции определяются в соответствии с
избранным критерием оптимальности и
могут быть натуральными или стоимостными.
Так, если в качестве критерия оптимальности
принят показатель валовой продукции в
денежном выражении, то коэффициенты
с, будут характеризовать стоимость
валовой продукции в расчете на принятую
единицу измерения соответствующих
переменных.
-
Числовая эмм задачи
Следующий этап
моделирования — составление числовой
экономико-математической модели. Она
может быть представлена в виде системы
линейных неравенств или в матричной
форме.
Матричная форма
экономико-математической модели
наглядна, удобна для визуального контроля
информации и ее кодирования при
решении на ЭВМ. Однако требуется
определенный опыт и навык в моделировании,
чтобы экономико-математическую модель
сразу оформить в виде матрицы коэффициентов.
Поэтому целесообразно сначала условия
задачи выразить с помощью линейных
соотношений, а затем составить матричную
форму модели.
Задача:
Рассчитать на
весеннее-летний период оптимальный
кормовой рацион для коровы с живым весом
500 кг, суточным удоем 20 кг, жирностью
молока 3,8%. Кормовой рацион должен
содержать не менее 14,2 кормовых единиц
и переваримого протеина 1650 г.. Общий вес
рациона не должен превышать 60 кг.
Концентрированных кормов в рационе
должно быть не более 3,6 кг. Остальная
исходная информация приведена в таблице.
Корма, их питательная
ценность
|
Показатели |
Комбикорм |
Зел.корм оз. |
Зел.корм бобовых |
|
Содержание |
1 |
0,2 |
0,2 |
|
Содержание |
80 |
18 |
35 |
|
Себестоимость |
6 |
0,25 |
0,28 |
Критерий оптимизации
– минимальная себестоимость кормового
рациона.
Постановка
задачи.
Необходимо составить
такой рацион кормления коров на
весенне-летний период, который обеспечивал
бы животных питательными веществами в
необходимом объеме и имел бы минимальную
себестоимость.
Формализуем
задачу:
Переменные величины:
х1 – колич. комбикорма
в рационе;
х2 – кол-во зел.
корма озимых культур;
х3 – кол-во зел.
корма бобовых культур;
Числовая модель
задачи:
-
По балансу кормовых
единиц, кг. корм. ед.
1х1 + 0,2х2 + 0,2х3 >=
14.2
2. По балансу
переваримого протеина, г.
80х1 + 18х2 + 35х3 >=
1650
3. По общему весу
рациона, кг.
х1 +х2 + х3 <= 60
4. По содержанию
комбикорма в рационе, кг.
х1 <= 3,6
5. По неотрицательности
переменных.
xj
>= 0
Критерий оптимальности
С = 6х1 + 0,25х2 +
0,28х3
min
Матричная модель
задачи.
|
№ |
Ограничения |
Един. измер. |
Переменные |
Тип огран. |
Объем огран. |
||
|
Х1-комбикорм |
Х2–зел. корм озимых |
Х3–зел. корм бобовых |
|||||
|
1 |
По балансу кормовых единиц |
Кг.к.ед. |
1 |
0,2 |
0,2 |
≥ |
14,2 |
|
2 |
По балансу переваримого протеина |
г |
80 |
18 |
35 |
≥ |
1650 |
|
3 |
По общему весу рациона |
кг |
1 |
1 |
1 |
≤ |
60 |
|
4 |
По содержанию комбикорма в рационе |
кг |
1 |
≤ |
3,6 |
||
|
Критерий оптимальности |
ДЕ |
6 |
0,25 |
0,28 |
|
min |
6. Решение задачи
на ПК с использованием программы LPSAR.
Программа разработана
под операционную систему DOS.
Поэтому необходимо войти в режим NC,
перейти на диск R,
выбрать каталог STAT,
войти в него, затем создать файл данных
с помощью текстового редактора NC
и т.д.
(дать инструкцию
по работе с программой LPSAR)
Решение получают
в виде нового файла с тем же именем,
которое было задано при создании файла
данных, но с новым расширением .res
В результате
решения задачи может быть получено
несколько вариантов:
1) Получен оптимальный
план, тогда просмотрев содержимое файла
при помощи клавиши F3,
необходимо удостовериться, удовлетворяет
ли решение поставленной задаче. Если
удовлетворяет, то решение выводят на
печать.
2) Может быть
получено промежуточное решение, это
значит, что система ограничений задачи
не совместна. В этом случае необходимо
провести корректировку модели задачи,
т.е. найти исходный файл данных и
отредактировать его (F4),
выполнить исправления, сохранить
изменения и повторно решить задачу.
3) Файл с расширением
.res
не образуется. В этом случае необходимо
закрыть панели NC
и прочитать сообщение системы о возможной
ошибке в файле. Затем найти ее и исправить.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Введение.
Умение решать текстовые задачи является одним из основных показателей уровня математического развития ребёнка, глубины усвоения им учебного материала. К сожалению, не
все учащиеся умеют и любят решать задачи. Это происходит потому, что дети не научены анализировать данные, видеть взаимосвязь между искомым и данным, структурировать ход решения. А при отсутствии потребности в глубоком осмыслении описанных в задаче связей у ребёнка формируется прочная привычка сводить решение к простому вычислению. Организация работы, заключающаяся в многократном прочитывании, устном анализе, составлении только краткой записи оказалась неинтересной и малоэффективной. Фронтальный анализ и решение задачи ограничивается правильными ответами двух-трёх человек, а остальные просто записывают готовые решения без глубокого понимания.
Так передо мной встала серьёзная проблема: как, используя традиционный УМК по математике ( программа М.И.Моро, М.А.Бантовой, Т.В.Бельтюковой ), анализировать задачу более продуктивно, чтобы она из просто арифметической превратилась в развивающую? Можно ли научить самостоятельно решать задачи каждого ученика?
Изучив теоретические подходы к обучению решать задачи, а также разнообразные практические приёмы, я пришла к выводу, что можно. Главное для каждого ученика на этом этапе – понять задачу, т.е. уяснить о чём эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами и т.т. Для этого надо применять моделирование задачи и учить этому детей.
Цель моей работы: показать, что приём моделирования задачи позволяет сделать каждую задачу учебника развивающей, нестандартной, многогранной.
Задачи: – разработать методические рекомендации по использованию разных моделей при решении задач;
– накопление дидактического материала, используемого как для всего класса,
так и для индивидуальной работы учащихся;
Я предлагаю пособие, которое рекомендую использовать при изучении важной темы программы по математике: «Решение текстовых задач». Оно может оказать практическую помощь учителям, как в организации работы на уроке, так и в индивидуальной работе в классе и дома.
Методическое пособие содержит следующие разделы:
1. Справочный материал. Виды моделей задач. В нём я кратко рассказываю о видах моделей, которые применимы к задачам , и когда целесообразно с ними знакомить учащихся.
2.Методика работы с каждой моделью.
В пособии показана работа над задачей, используя приём моделирования. Приведены конкретные примеры и предложен фрагмент урока по теме. « Решение задач алгебраическим и арифметическим способом », используя приём моделирования.
3.Приложение. Дидактический материал.
Дидактический материал, который использую на уроке со всем классом, а также в индивидуальной работе.
Так что же такое моделирование? Моделирование-это процесс построения моделей
для каких-либо познавательных целей. Для простоты восприятия учеником какого-либо предмета или ситуации, описанной в задаче, я применяю модель. Постепенно моделирование стало неотъемлемой частью каждого урока математики в моём классе.
Систему работы по усвоению детьми моделирования задачи я разбиваю на три этапа:
1.Обучение детей преобразованию предметных действий в работающую модель.
2.Обучение детей составлению обратных задач к данной на основе работы с моделью.
3.Творческая работа детей над задачей на основе использования модели.
После систематической работы учащиеся добились следующих результатов: изучили
шесть видов моделей; научились применять в одной и той же задаче несколько видов моделей ( с целью выбора каждым учеником наиболее понятной ему модели );
сравнивать несколько моделей между собой ( с целью выбора наиболее рациональной );
выбирать наиболее подходящую к предложенной задаче. На основе моих наблюдений за детьми в процессе этой деятельности я пришла к выводу. Мои ученики не боятся самостоятельно начать анализ задачи; в случае неудачи они, используя другую модель, анализируют задачу вновь.
Следовательно, моделирование помогает вооружить ребёнка такими приёмами, которые позволяют ему при самостоятельной работе над задачей быть активным, успешным, не бояться трудностей. Каждый, не сравнивая себя с другими, выбирает собственный путь рассуждения, моделирования и, следовательно, решения задач.
Справочный материал. Виды моделей.
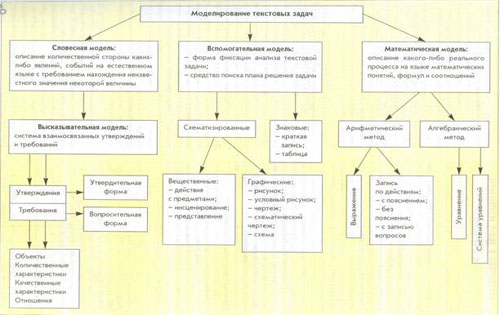
Вспомогательная модель.
1. Рисунок. Знакомство с этой моделью начинаю в 1 классе Во-первых, рисование- любимый вид деятельности малышей, во-вторых, приём хорош для развития моторики рук, в-третьих, рисование является развивающим упражнением.
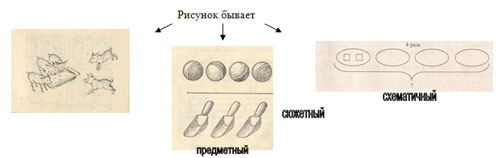
2.Краткая запись. С этой моделью начинаю работать в конце 1-го класса. Удачное введение краткой записи параллельно с рисунком.
3.Таблица. Знакомлю с этой моделью в конце 1-го, начале 2-го класса.
| Было | Вынесли | Осталось | Цена | Количество | Стоимость | v | t | s | ||
4.Чертёж. Применяю тогда, когда числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины.

5.Схема. Знакомлю в начале 2-го класса. Подбор задач в этом классе позволяет применять эту модель на материале обратных задач, при решении задач разными способами.

6.Блок-схема (разбор задачи аналитическим способом, то есть с вопроса). Изучение этой модели возможно уже в конце 2-го класса, когда все предыдущие модели изучены хорошо, широко и системно используются на уроке
Методика работы с моделями.
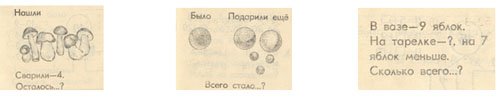
1.Рисунок. Он должен изображать реальные предметы (кубики, платки, яблоки и т. д.), о которых говорится в задаче, или условные предметы в виде геометрических фигур.
Пример. Когда с полки сняли 2 книги, там осталось 4. Сколько книг лежало на полке сначала?
У. Сколько книг осталось на полке? 4
Изобразим.
![]()
У. Раньше книг было больше или меньше? Почему?
Д. Больше. Здесь нет книг, которые сняли с полки.
У. Знаем ли мы, сколько книг было сначала? Нет.
Покажем это скобкой или дугой и вопросительным знаком.

У. Почему книг стало меньше?
Д. С полки сняли две книги.
У. Изобразим две книги внизу, под скобкой.

У. Как узнать, сколько всего книг было на полке?
Д. Нужно сложить книги, которые остались на полке, и те, которые сняли.
1.1. Следующим шагом в работе над этой задачей будет составление новой модели –
это краткая запись и таблица. Краткая запись – представление в лаконичной форме содержание задачи, выполненное с помощью опорных слов.
|
Было |
Подарила |
Осталось |
|
? |
2к. |
5к. |
Было – ?
Подарила – 2к.
Осталось – 5к.
Слово «подарила» говорит младшему школьнику о том, что количество книг уменьшилось, значит, нужно производить вычитание. Так в сравнении дети видят какая из моделей позволяет проследить за количественными изменениями в задаче.
2.Таблица. Наиболее удачно применение таблицы при решении задач на тройку пропорциональных величин: цена – количество – стоимость; расход на 1 шт.- количество штук – общий расход; масса – количество – общая масса; скорость – время – расстояние; и т. д.
Пример. «Из двух городов, расстояние между которыми равно 1200 км, одновременно вышли навстречу друг другу два поезда. Один из них проходит это расстояние за 20ч., а другой – за 30 ч. Через сколько часов поезда встретятся?»
При решении задач на движение, учителя часто используют схематический чертёж.

2.1.Однако, такой чертёж может направить ученика по неверному пути, так как два времени могут подтолкнуть ребёнка к сложению соответствующих чисел, а затем к делению расстояния на полученный результат. Поэтому целесообразнее использовать таблицу.
|
скорость |
время |
расстояние |
|
|
1 поезд |
? |
20 ч. |
1200 км |
|
2 поезд |
? |
30 ч. |
1200 км |
2.2.После того как найдены скорости поездов, нужно выполнить схематический чертёж с целью осознания учащимися сути второй части задачи.
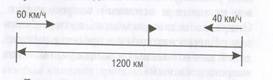
2.3.Данный чертёж даёт возможность учащимся представить и осознать задачную ситуацию, что, в свою очередь, помогает понять и закончить решение:60+40=100км/ч; 1200:100=12ч
Вот теперь дети сами могут составить модель задачи , используя таблицу, и выявить все ситуации, все данные и искомые.
|
скорость |
время |
расстояние |
|
|
1 поезд |
? |
20 ч. |
1200 км |
|
2 поезд |
? |
30 ч. |
1200 км |
|
1 и 2 поезда |
? |
? |
1200 км |
Опираясь на данную модель, путь решения задачи легко находится в процессе рассуждений как «от данных к вопросу», так и «от вопроса к данным».
3.Рассуждая «от данных к вопросу», получим схему (рис.1), которую называют моделью поиска решений данной задачи. Рассуждая «от вопроса к данным (блок-схема) модель будет иметь другой вид (рис.2.)
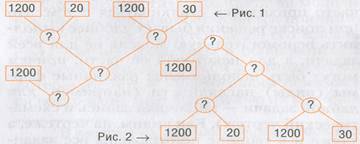
4. Схема –это чертёж, на котором все взаимосвязи и взаимоотношения величин передаются приблизительно, без соблюдения масштаба,
Пример. « Из двух кусков ткани сшили 18 одинаковых занавесок. В первом куске было 30 м , во втором – 24 м. Сколько занавесок сшили из каждого куска?»
Обычно условие записывают в таблицу.
|
Расход на одно платье |
Количество изделий |
Общий расход |
|
одинаковый |
? |
30 м |
Однако по этой модели рассуждение у детей вызывает затруднение. Детям трудно увидеть ,что нужно знать для определения расхода ткани на одну занавеску. Я рекомендую использовать такую схему.
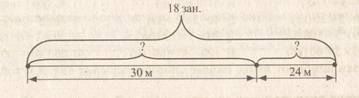
Понимание облегчается тем, что на схеме один и тот же отрезок изображает и (30+24)м ткани, и 18 занавесок.
5.Чертёж. Применяют эту модель, если числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины. Ученики должны усвоить поэтапное выполнение чертежа.
Пример. « Когда шланг длинной 5 метров удлинили на несколько метров, то получился шланг длиной 8 метров. На сколько метров удлинили шланг?
Этапы работы.
Какой длины был сначала шланг? (5 м)
Какой длины вычерчиваем первый отрезок? (5см)
Что произошло со шлангом? (Увеличился на несколько метров.)
Как изменится отрезок?( Увеличится на несколько сантиметров.)
Какой длины стал шланг?(8м)
Какой длины станет наш отрезок?(8см)
Отметим на чертеже , насколько увеличился наш отрезок.
Что нужно узнать в задаче?
Как на нашей модели отмечено искомое?

Далее выбирается арифметическое действие.
Пример. « У Васи 2 машинки, а у Коли в 3 раза больше, чем у Васи. Сколько машинок к Коли? » Чертёж имеет такой вид.
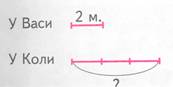
Далее выбирается арифметическое действие.
Фрагмент урока
Тема. Алгебраический и арифметический способ решения задач ( 2 класс )
Цель. – учить решать задачи разными способами;
– развивать умения сравнивать, анализировать, делать вывод;
– воспитание самостоятельности, творческой активности;
Ход урока.
1.Актуализация опорных знаний
– Составь разные задачи по выражению
28 – 16
– Выбери модели к этим задачам
Дети выходят к доске и из предложенных моделей выбирают следующие:

2. Освоение новых знаний
– Какая из ваших моделей подойдёт к этому уравнению?
28 – Х = 16
После сравнения и обсуждения дети выбирают
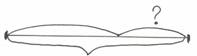
– Проговорите текст задачи. ( В магазине было 28 ящиков груш, когда несколько продали , осталось 16. Сколько ящиков груш продали?)
– Решим это уравнение. Какой компонент неизвестен? Как его найти?
Мы использовали уравнение для решения задачи . Это алгебраический способ решения задачи. ( Вывешиваю аншлаг слова алгебра. Поясняю, что алгебра – это раздел математики, который изучает буквенные выражения ,)
–А теперь решите эту задачу арифметическим способом ( Вывешиваю аншлаг слова
арифметика и поясняю, что это раздел математики, который изучает свойства чисел и действия над ними,)
На доске появляется такая запись
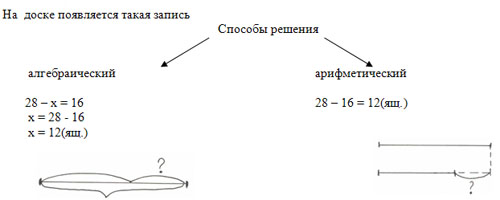
Делаем с ребятами вывод о том, что одну и ту же задачу можно решить разными способами .
-А как помогают модели в решении задачи? ( Помогают выбрать способ её решения )
Наряду с выше изложенным, педагог должен помнить, что одного составления модели к задаче недостаточно. Следует включать и обратные задания, а именно: составление текстов задач по модели. Учащиеся могут работать за партой и у доски, используя набор цифр.
Смотри приложение 1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ТЕКСТОВЫХ ЗАДАЧАХ.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Суслова Д.А. 1
1МОУ “Темповская средняя общеобразовательная школа Ртищевского района Саратовской области”
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение.
Текстовые задачи – одни из самых сложных задач в школьном курсе математики. Алгебраический метод решения не всегда бывает удобным для решения задач подобного типа – нередко бывает сложным выбрать нужную неизвестную величину так, чтобы решение было максимально простым и понятным.
С каждым годом текстовые задачи в школьном курсе математики усложняются, причем времени на совершенствование решений этих задач практически не выделяется. И если раньше их решение не вызывало особых затруднений, то теперь с этим могут возникнуть некоторые трудности. Поэтому решить задачу стандартным способом вряд ли получится. Решая одну из текстовых задач, я решила обратиться к математическому моделированию.
Для того чтобы устранить эти трудности, я решила рассмотреть другие возможные методы решения этих задач, а в частности задач на движение по окружности. Предметом моего исследования является математическое моделирование, как процесс, без которого, на мой взгляд, решение подобных задач будет наиболее трудоемким или даже невозможным.
Цель моей работы – рассмотреть основные виды математических моделей, применяемых к решению математических задач, и выбрать наиболее оптимальные к конкретной из них. К постановке этой цели меня привела следующая проблема: в современном мире, насыщенном информацией, необходимо умение представлять информацию в доступном (упрощенном) виде с целью достижения результата (решения задачи).
Исходя из цели, были поставлены следующие задачи:
-
Проанализировать научно-учебную литературу по теме работы.
-
Рассмотреть процесс математического моделирования и этапы создания модели для конкретной задачи.
-
Рассмотреть этапы создания математической модели.
-
Научиться составлять математические модели различного типа.
-
Выявить оптимальный метод математического моделирования для решения конкретной задачи (подобрать оптимальные модели для решения определённого типа задач).
Гипотеза: Существует универсальная математическая модель, с помощью которой можно решить любую текстовую задачу.
Объект исследования: текстовые задачи различного типа.
Методы исследования: анализ, аналогия, обобщение, прогнозирование, эксперимент.
Основная часть.
Глава I. Что такое математическая модель?
1.1 Краткая теоретическая справка.
Заинтересовавшись математическим моделированием, я проанализировала литературу, подробно описывающую данный метод. Существуют различные трактовки и классификации этого понятия. Я остановилась на учебном пособии [1] И.А. Печерских и А.Г. Семенова, которые дают следующее определение математической модели:
Математическая модель представляет собой формализованное описание системы на некотором абстрактном языке, например, в виде совокупности математических соотношений, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению. Любая математическая модель описывает реальный объект, явление или процесс с некоторой степенью приближения к действительности. Целью математического моделирования является анализ реальных процессов математическими методами.
1.2 Этапы математического моделирования.
-
Постановка задачи.
На этом этапе требуется четкое понимание поставленной задачи.
-
Изучение теоретических основ и сбор информации об объекте оригинала.
На этом этапе подбирается или разрабатывается подходящая теория
-
Формализация.
Заключается в выборе системы условных обозначений.
-
Выбор метода решения.
На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта.
-
Реализация модели.
Выполнятся построение математической модели (строится график, таблица, рисунок или эскиз, граф) и решается задача исходя из новых условий.
-
Анализ полученной информации.
Сопоставляется полученное и предполагаемое решение.
7. Проверка адекватности реальному объекту.
Результаты, полученные по модели, сопоставляются с условиями исходной задачи.
Глава II. Применение моделирования к решению задачи.
Для достижения поставленной цели я составила несколько математических моделей, и постаралась к решению одной задачи (на движение по окружности) применить этот метод.
Задача.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 18 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?
Данную задачу решим с помощью математических моделей:
1. Таблица.
2. «Математический маятник».
3. Графическая модель.
2.1 Таблица – математическая модель, которая помогает упорядочить все данные в задаче для более удобного восприятия.
(Приложение 1. Таблица. Стр. 14.)
Решение.
Пусть x кмч – скорость первого мотоциклиста, тогда скорость 2-го мотоциклиста (x + 25) км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый (то есть второй ) должен преодолеть изначально разделяющее их расстояние, равное половине длины всей трассы ( т.к. мотоциклисты расположены в диаметрально противоположных точках )
( x + 25 )t – xt = 9
tx + 25t – tx = 9
25t = 9
t = 21,6 (минут)
Ответ: 21,6 минут.
2.2 «Математический маятник».
Математическим маятником [2] называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Математический маятник имеет следующие характеристики: период, частота колебаний, количество колебаний и длина нити, но для решения этой задачи я остановилась на двух из них: период частота. Если связать эти величины со скоростью, временем и расстоянием, то задачу на движение по окружности можно будет решать с помощью формул, которые свойственны математическому маятнику.
T – период – это время, затраченное на один круг.
ʋ – частота колебаний – это величина обратная периоду.
Составим математическую модель.
(Приложение 2. «Математический маятник». Стр.14).
Пусть х км/ч – скорость первого мотоциклиста, тогда скорость второго мотоциклиста (х+25) км/ч. Длина всей трассы 18 км.
Т1 = время, затраченное 1-ым мотоциклистом на прохождение полного круга (период).
Т2 = время, затраченное 2-ым мотоциклистом на прохождение полного круга (период).
Для того чтобы мотоциклисты поравнялись в первый раз их частоты должны совпасть, значит:
– частота первого мотоциклиста.
– частота второго мотоциклиста.
Тогда разность – частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
Тогда (ч) = 21,6 (мин.)
Ответ: 21,6 мин.
2.3 Графическая модель.
Графики законов, которые описывают зависимость S от t, строятся в системе координат SOt. Поскольку t > 0 и S > О, то построения выполняются в первой координатной четверти.
График движения тела по окружности можно заменить графиком движения по прямой. Обход телом окружности и возвращение в исходную точку равносильны достижению телом на прямой точки, удаленной от начальной на расстояние S0, равное длине окружности.
Изобразим схематически в системе SOt движение мотоциклистов.
Так как все величины положительны, то достаточно рассмотреть графики в первой четверти.
Пусть x ч – время, за которое первый мотоциклист догнал второго, y км – путь, пройденный вторым мотоциклистом до момента встречи с первым. Решение сводится к решению геометрической задачи.
(Приложение 3. Графическая модель. Стр. 15)
Ответ: 21, 6 минуты.
На примере решения данной задачи были выявлены следующие преимущества решения задач с помощью геометрической модели: наглядность, оперативность, простота решения.
Глава 3. Выявление оптимальных моделей для решения конкретных
задач.
3.1 Задачи на совместную работу.
Задачи подобного типа удобнее всего решать с помощью таблицы, потому что производительность, объем работы и время на выполнение всей работы можно легко связать со скоростью, временем и расстоянием. Роль скорости выполняет производительность труда, роль расстояния – вся работа, время выполняет свою роль.
Задача.
Двое рабочих, работая вместе, могут выполнить производственное задание за 40 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 18 дней больше, чем другому?
Решение:
Примем весь объем работы за единицу. Пусть 2-ой рабочий, работая самостоятельно, может выполнить все задание за x дней, тогда 1-ый — за (x+18) дней.
(Приложение 4. Таблица. Стр. 15)
Вместе за 1 день рабочие выполняют задания. За 40 дней рабочие выполнят всю работу. Составим уравнение:
40× ( ) = 1
→
→
Второй корень не подходит по смыслу задачи (так как время не может быть отрицательным числом). Значит, 2-ой рабочий, работая самостоятельно, может выполнить всю работу за 10 дней, а 1-ый — за 10+9=19 дней.
Ответ: 10 дней, 19 дней.
3.2 Задачи на движение.
Задачи на движение по прямой удобнее всего решать с помощью графической модели.
Задача: Два пешехода вышли одновременно из своих сел W и C навстречу друг другу. После встречи первый шел 25 минут до села C, а второй шел 16 минут до села W. Сколько минут они шли до встречи?
(Приложение 5. Графическая модель. Стр. 16)
Решение:
Пусть ОЕ расстояние между сёлами W и C. OD – график движения первого пешехода ( который шёл медленнее), а EF – график движения второго. М – место встречи.
1) ∆ MND~∆MPO,
2) ∆MNE~∆MPF,
3)
4) => что t = 20 (мин.)
Ответ: 20 мин.
3.3 Задачи на движение по окружности.
Два велосипедиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение:
Используя модель «математического маятника», описанного выше, задача решается практически устно.- частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
Тогда (ч) = (ч) = 20 (мин.)
Ответ: через 20 минут.
С помощью этой модели можно также быстро решать задачи, в которых отставание составляет не половину трассы, а конкретное расстояние. Решим эту же задачу, изменив в ней условие.
Два велосипедиста стартуют одновременно в одном направлении из двух точек круговой трассы, расстояние между которыми равно 3 км. Длина трассы равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение: Задача будет иметь 2 решения в зависимости от направления
движения по круговой трассе.
Составим математическую модель (для данной задачи их будет две).
(Приложение 6. «Математический маятник». Стр. 16)
В первом случае решение будет таким:
– частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда
∙ = 7; тогда Т = (ч).
Во втором случае
– частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда
=∙ = ; тогда Т = (ч).
Ответ: через часа; или через часа.
Таким образом, модель «Математический маятник» подходит для решения задач на движение по окружности. Применение такого способа решения значительно сокращает время на решение задачи, что позволит при выполнении контрольных работ и на экзамене увеличить время на решение более трудных задач.
Заключение.
В результате исследования были получены следующие результаты:
-
Был изучен процесс математического моделирования и этапы создания модели для конкретной задачи.
-
В ходе исследования была опровергнута гипотеза, о существовании универсальной математической модели для решения всех типов задач.
-
Я научилась составлять математические модели различного типа.
-
Были выявлены оптимальные математические модели для решения конкретной задачи.
Я думаю, что за моделированием – будущее. Умение составлять математические модели сможет помочь в решении задач из различных отраслей науки, а также жизненных задач. Хочется отметить, что решение задач с применением моделирования активизирует мыслительную деятельность, помогает лучше понять задачу, самостоятельно найти рациональный путь ее решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет яснее увидеть зависимости между данными и искомыми величинами, оценить задачу в целом, продемонстрировать разные варианты решения.
Библиографический список.
1. Рецензенты Черкасов В.С., кандидат физ.-мат. наук, доцент;
Чуешев А.В., кандидат физ.-мат. наук, доцент; Печерских, И.А. П 31 Математические модели в экономике: учебное пособие / И.А. Печерских, А.Г. Семенов; Кемеровский технологический институт пищевой промышленности. – Кемерово, 2011. – 191 с.
2. Перышкин, А. В.
П27 Физика. 9 кл. : учебник для общеобразоват. учреждений / А. В.
Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М. : Дрофа, 2009, – 300,
с, : ил, ; 1 л, цв. Вкл.
3. http://www.pedsovet.info/info/pages/referats/inf_00002.htm
Приложения
Приложение 1. Таблица
|
V (км/ч) |
t (ч) |
S (км) |
|
|
1-ый мотоциклист |
X |
t |
xt |
|
2-ой мотоциклист |
(х+25) |
t |
( x + 25 )t |
Приложение 2. «Математический маятник».
Приложение 3. Графическая модель.
18
A
O
y
D
9
C
t
x
Приложение 4. Таблица.
|
Производительность труда |
Время работы |
Работа |
|
|
1-ый рабочий |
ч/день |
(x+18) дней |
1часть |
|
2-ой рабочий |
ч/день |
1часть |
Приложение 5. Графическая модель.
25 минут
Приложение 6. «Математический маятник».
1) 2)
х
х
х+21
х+21
25
Просмотров работы: 9076
На прошлом уроке нами была установлена взаимозависимость между математическим языком и математической моделью. Теоретический базис заложен, так что теперь самое время переходить к практике. Далее мы подробнее рассмотрим составление математической модели и простые задачи, решаемые с помощью математической модели.
На первых порах тема может даваться с трудом. Но есть хорошая новость. Составление математической модели — это во многом навык.
Чем больше типовых задач вы нарешаете, тем проще вам будет ориентироваться в моделировании.
Этапы составления математической модели
Ранее мы описывали, что этапы составления математической модели включают в себя:
| 1. Наблюдение | 2. Моделирование | 3. Предсказание |
|---|---|---|
| Анализ задачи; на основе анализа подготовка частей будущей математической модели. | Логическое объединение частей и составление математической модели. | Использование составленной математической модели для заключений по вопросу задачи. |
С практической точки зрения наибольшую сложность представляют два первых этапа — наблюдение и моделирование. Чтобы их успешно завершать, необходимо умение правильно переводить текстовые утверждения на язык математики.
Что нужно хорошо понимать. На этапе наблюдения обычно переводятся части будущего алгебраического выражения. В процессе этапа моделирования эти части объединяются.
«Типовая задача»?
Еще раз подчеркнем, что задачи для седьмого класса, решаемые с помощью математической модели, являются типовыми. Что это означает? Они отличаются одинаковостью алгоритма решения.
Логика вычислений в них зациклена. А составление математической модели от задачи к задаче также следует одной схеме.
Например, пусть дана части задачи:
«Стоимость яблочного сока $x$ рублей, а томатного — $y$ рублей. Известно, что $5$ стаканов яблочного сока стоят столько же, сколько $6$ стаканов томатного…»
То, как составлена задача, подводит нас к двум концепциям — приравниванию и умножению. Опорным для решения будет следующее алгебраическое выражение:
$$5x=6y$$
Раз задача типовая, то выражения наподобие «$ax=by$» непременно встретятся еще раз, просто уже, так скажем, не в контексте сока. Вот почему мы выше говорили про то, что составление математической модели — это навык. Оно же умение отбросить текст и увидеть алгебру за ним.
Задачи на наблюдение и моделирование
Рассмотрим далее некоторые задачи, решаемые с помощью математической модели, в которых опущен этап наблюдения — где нет вывода ответа. Это поможет освоиться в основных типах учебных задач и научит выражать важные части текста алгебраически.
Операции сложения и вычитания
Задача. Первый рабочий выполняет порученное задание за $x$ часов, второй то же задание — за $y$ часов, при этом первый работает на три часа больше, чем второй.
Решение
Между производительностью двух рабочих можно установить отношение равенства, но с учетом условия «на три часа больше». Для начала составим каркасное тождество, которое дополним далее:
$$x=y$$
«Полноправно» приравнять данные переменные мы можем, только дополнив, что первый рабочий ($x$) работает на три часа больше. Интуитивно так и хочется переписать тождество следующим образом:
$$x+3=y$$
Однако это неверное составление математической модели для данной задачи. Мало того, что по условию очевидно неравенство $x>y$, так еще и тождество с частью «$x+3$» увеличивает разрыв между значениями $x$ и $y$ на лишние три раза.
Чтобы производительность рабочих все-таки приравнять, у первого, наоборот, нужно «отобрать» три часа и «отдать» их тому, кто работает быстрее:
$$x=y+3$$
Операции умножения и деления
Задача. На двух стройках трудится одинаковое количество рабочих. На первой стройке работает 5 бригад по $x$ человек в каждой, на второй стройке — 3 бригады по $y$ человек в каждой.
РЕШЕНИЕ
Первая стройка. В одной бригаде трудится $x$ человек. По условию таких бригад пять. Откуда получаем количество человек всего, трудящихся на первой стройке: $5x$.
Вторая стройка. Здесь же в одной бригаде трудится $y$ человек. По условию имеем три бригады. Следовательно количество работников, трудящихся на второй стройке: $3y$.
Также нам известно, что на двух стройках работает одно и то же количество рабочих. Остается данные части приравнять, чтобы получить тождество:
$$5x=3y$$
Вот, буквально мгновение — и мы вновь увидели составление математической модели коэффициентного типа «$ax=bx$».
Задачи, решаемые с помощью математической модели, со смешанной арифметикой
Задача. У Кати $x$ марок, а у Димы $y$ марок. Если Катя отдаст Диме 5 марок, то у Димы станет марок вдвое больше, чем останется у Кати.
РЕШЕНИЕ
Внимание на следующие части текста задачи:
| «Отдаст пять марок…» | «Вдвое больше» |
| Сложение/вычитание | Умножение/деление |
В зависимости от того, какая часть тождества отражает данные положения, операция может быть как прямой («Катя отдаст, $x-5$»), так и обратной («Дима возьмет, $y+5$).
Разделим составление математической модели задачи на два шага.
1. Катя отдает Диме 5 марок и у нее остается $x-5$ марок. Теперь у Димы $y+5$ марок.
2. В результате у Димы марок в два раза больше.
Однако нам нужно количество марок ребят приравнять. Раз у Димы их по условию задачи больше, то для равенства с количеством марок Кати у него их должно быть меньше. Значит, мы можем либо умножить количество марок Кати на 2, либо разделить количество марок Димы на 2:
| $$2(x-5)=y+5$$ | $$x-5=frac{y+5}{2}$$ |
Составление математической модели — полные задачи
Самое время усложнить содержание задач и ввести все этапы составления математической модели, включая этап планирования. Далее мы решим ряд показательных задач, где требуется дать ответ.
Задача. В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нем в 3 раза больше мест, чем в малом?
РЕШЕНИЕ
Заметим, что в данном случае составление математической модели задачи будет вестись в двух направлениях. С одной стороны, устанавливается алгебраическое равенство между количеством мест в залах. С другой стороны, нам известна их сумма. Составим эти выражения.
Приравнивание. Пусть количество мест в большом зале равняется $x$. Вместо того, чтобы вводить лишнюю переменную $y$ для количества мест в малом зале, выразим места малого зала через уже введенную переменную $x$ — как $frac{x}{3}$. Это краткая модель записи:
$$y=frac{x}{3}$$
Сложение. Всего в залах 460 мест. Количество мест в большом зале $x$, в малом — $frac{x}{3}$, одна треть от мест в большом. Вместе:
$$x+frac{x}{3}=460$$
Задаче требуется ответ; этапы составления математической модели должны завершаться в полном объеме. С этой целью мы и взяли за «главную» переменную количество мест в большом зале. Остается решить уравнение выше.
$$frac{4}{3}x=460\x=345$$
Ответ: 345.
Составление математической модели — задачи на движение
Задача. От пристани отошел теплоход со скоростью 22 км/ч, а от другой пристани навстречу ему через три часа отошел теплоход со скоростью 26 км/ч. Расстояние между пристанями составляет 306 км. Сколько времени в пути был каждый из теплоходов до встречи?
Для решения нам понадобится формула пути:
$$S=vt$$
Этап наблюдения
Время в пути — искомый параметр, введем его в качестве переменной $t$.
Пусть $t_1$ — это количество времени, затраченное первым теплоходом на преодоление всего своего пути. Сколько при этом затратил времени второй теплоход? На три часа меньше, ведь по условию от пристани он отошел в сравнении с первым с задержкой:
$$t_1-3$$
Этап моделирования
Каркасная модель выглядит так:
$$v_{1}t_1+ v_{2}t_2=S,$$
где $S$ — расстояние между пристанями, $v_1$ — скорость первого теплохода, $v_2$ — скорость второго, $t_1$ и $t_2$ — соответствующее время в пути.
Откуда взялась модель? Зарисуем перемещение теплоходов, что бывает иногда очень полезно при решении задач на движение. Теплоходы двигаются навстречу друг другу. Значит, в сумме они проходят расстояние между пристанями.
Доработаем модель и добавим в нее имеющиеся у нас данные:
$$22t_1+26(t_{1}-3)=306$$
Этап предсказания
Остается решить уравнение, найти значение $t_1$ и вычесть из него 3, чтобы получить $t_2$.
$$22t_1+26t_1=306+78\t_1=8$$
Первый теплоход затратил 8 часов. Второй, соответственно, 5 часов.
Ответ: 8 и 5.
Решите сами!
Показать решение
Спрятать решение
🔵 РЕШЕНИЕ
Не очевидно, но за переменную $x$ удобно взять количество учащихся в старших классах. Почему — увидите далее.
Выразим количество учащихся в начальных и средних классах также через $x$. Для этого проанализируем утверждения, заданные условием задачи.
Утверждение первое: «В начальных классах учащихся в три раза больше, чем в старших». Раз их в три раза больше, то количество учеников в начальных классах через $x$ — это $3x$.
Утверждение второе: «В начальных классах учащихся в два раза меньше, чем в средних». Количество учащихся в начальных классах мы выразили ранее как $3x$. Сколько тогда учеников в средних классах? В два раза больше, то есть $2cdot{3x}=6x$.
Остается составить модель:
$$x+3x+6x=900$$
Решаем и находим количество учеников в старших классах ($x$):
$$10x=900\x=90$$
Откуда получаем, что в начальных классах учится 270 учеников ($3x$), а в средних классах — 540 учеников ($6x$).
Ответ: 270, 540, 90.
