Арккосинус(y = arccos(x)) – это обратная тригонометрическая функция к косинусу x = cos(y). Область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
| arccos(1) = 0° | arccos(-0.5) = 120° | arccos(-0.5) = 240° |
| arccos(0.9998476952) = 1° | arccos(-0.5150380749) = 121° | arccos(-0.4848096202) = 241° |
| arccos(0.999390827) = 2° | arccos(-0.5299192642) = 122° | arccos(-0.4694715628) = 242° |
| arccos(0.9986295348) = 3° | arccos(-0.544639035) = 123° | arccos(-0.4539904997) = 243° |
| arccos(0.9975640503) = 4° | arccos(-0.5591929035) = 124° | arccos(-0.4383711468) = 244° |
| arccos(0.9961946981) = 5° | arccos(-0.5735764364) = 125° | arccos(-0.4226182617) = 245° |
| arccos(0.9945218954) = 6° | arccos(-0.5877852523) = 126° | arccos(-0.4067366431) = 246° |
| arccos(0.9925461516) = 7° | arccos(-0.6018150232) = 127° | arccos(-0.3907311285) = 247° |
| arccos(0.9902680687) = 8° | arccos(-0.6156614753) = 128° | arccos(-0.3746065934) = 248° |
| arccos(0.9876883406) = 9° | arccos(-0.629320391) = 129° | arccos(-0.3583679495) = 249° |
| arccos(0.984807753) = 10° | arccos(-0.6427876097) = 130° | arccos(-0.3420201433) = 250° |
| arccos(0.9816271834) = 11° | arccos(-0.656059029) = 131° | arccos(-0.3255681545) = 251° |
| arccos(0.9781476007) = 12° | arccos(-0.6691306064) = 132° | arccos(-0.3090169944) = 252° |
| arccos(0.9743700648) = 13° | arccos(-0.6819983601) = 133° | arccos(-0.2923717047) = 253° |
| arccos(0.9702957263) = 14° | arccos(-0.6946583705) = 134° | arccos(-0.2756373558) = 254° |
| arccos(0.9659258263) = 15° | arccos(-0.7071067812) = 135° | arccos(-0.2588190451) = 255° |
| arccos(0.9612616959) = 16° | arccos(-0.7193398003) = 136° | arccos(-0.2419218956) = 256° |
| arccos(0.956304756) = 17° | arccos(-0.7313537016) = 137° | arccos(-0.2249510543) = 257° |
| arccos(0.9510565163) = 18° | arccos(-0.7431448255) = 138° | arccos(-0.2079116908) = 258° |
| arccos(0.9455185756) = 19° | arccos(-0.7547095802) = 139° | arccos(-0.1908089954) = 259° |
| arccos(0.9396926208) = 20° | arccos(-0.7660444431) = 140° | arccos(-0.1736481777) = 260° |
| arccos(0.9335804265) = 21° | arccos(-0.7771459615) = 141° | arccos(-0.156434465) = 261° |
| arccos(0.9271838546) = 22° | arccos(-0.7880107536) = 142° | arccos(-0.139173101) = 262° |
| arccos(0.9205048535) = 23° | arccos(-0.79863551) = 143° | arccos(-0.1218693434) = 263° |
| arccos(0.9135454576) = 24° | arccos(-0.8090169944) = 144° | arccos(-0.1045284633) = 264° |
| arccos(0.906307787) = 25° | arccos(-0.8191520443) = 145° | arccos(-0.08715574275) = 265° |
| arccos(0.8987940463) = 26° | arccos(-0.8290375726) = 146° | arccos(-0.06975647374) = 266° |
| arccos(0.8910065242) = 27° | arccos(-0.8386705679) = 147° | arccos(-0.05233595624) = 267° |
| arccos(0.8829475929) = 28° | arccos(-0.8480480962) = 148° | arccos(-0.0348994967) = 268° |
| arccos(0.8746197071) = 29° | arccos(-0.8571673007) = 149° | arccos(-0.01745240644) = 269° |
| arccos(0.8660254038) = 30° | arccos(-0.8660254038) = 150° | arccos(0) = 270° |
| arccos(0.8571673007) = 31° | arccos(-0.8746197071) = 151° | arccos(0.01745240644) = 271° |
| arccos(0.8480480962) = 32° | arccos(-0.8829475929) = 152° | arccos(0.0348994967) = 272° |
| arccos(0.8386705679) = 33° | arccos(-0.8910065242) = 153° | arccos(0.05233595624) = 273° |
| arccos(0.8290375726) = 34° | arccos(-0.8987940463) = 154° | arccos(0.06975647374) = 274° |
| arccos(0.8191520443) = 35° | arccos(-0.906307787) = 155° | arccos(0.08715574275) = 275° |
| arccos(0.8090169944) = 36° | arccos(-0.9135454576) = 156° | arccos(0.1045284633) = 276° |
| arccos(0.79863551) = 37° | arccos(-0.9205048535) = 157° | arccos(0.1218693434) = 277° |
| arccos(0.7880107536) = 38° | arccos(-0.9271838546) = 158° | arccos(0.139173101) = 278° |
| arccos(0.7771459615) = 39° | arccos(-0.9335804265) = 159° | arccos(0.156434465) = 279° |
| arccos(0.7660444431) = 40° | arccos(-0.9396926208) = 160° | arccos(0.1736481777) = 280° |
| arccos(0.7547095802) = 41° | arccos(-0.9455185756) = 161° | arccos(0.1908089954) = 281° |
| arccos(0.7431448255) = 42° | arccos(-0.9510565163) = 162° | arccos(0.2079116908) = 282° |
| arccos(0.7313537016) = 43° | arccos(-0.956304756) = 163° | arccos(0.2249510543) = 283° |
| arccos(0.7193398003) = 44° | arccos(-0.9612616959) = 164° | arccos(0.2419218956) = 284° |
| arccos(0.7071067812) = 45° | arccos(-0.9659258263) = 165° | arccos(0.2588190451) = 285° |
| arccos(0.6946583705) = 46° | arccos(-0.9702957263) = 166° | arccos(0.2756373558) = 286° |
| arccos(0.6819983601) = 47° | arccos(-0.9743700648) = 167° | arccos(0.2923717047) = 287° |
| arccos(0.6691306064) = 48° | arccos(-0.9781476007) = 168° | arccos(0.3090169944) = 288° |
| arccos(0.656059029) = 49° | arccos(-0.9816271834) = 169° | arccos(0.3255681545) = 289° |
| arccos(0.6427876097) = 50° | arccos(-0.984807753) = 170° | arccos(0.3420201433) = 290° |
| arccos(0.629320391) = 51° | arccos(-0.9876883406) = 171° | arccos(0.3583679495) = 291° |
| arccos(0.6156614753) = 52° | arccos(-0.9902680687) = 172° | arccos(0.3746065934) = 292° |
| arccos(0.6018150232) = 53° | arccos(-0.9925461516) = 173° | arccos(0.3907311285) = 293° |
| arccos(0.5877852523) = 54° | arccos(-0.9945218954) = 174° | arccos(0.4067366431) = 294° |
| arccos(0.5735764364) = 55° | arccos(-0.9961946981) = 175° | arccos(0.4226182617) = 295° |
| arccos(0.5591929035) = 56° | arccos(-0.9975640503) = 176° | arccos(0.4383711468) = 296° |
| arccos(0.544639035) = 57° | arccos(-0.9986295348) = 177° | arccos(0.4539904997) = 297° |
| arccos(0.5299192642) = 58° | arccos(-0.999390827) = 178° | arccos(0.4694715628) = 298° |
| arccos(0.5150380749) = 59° | arccos(-0.9998476952) = 179° | arccos(0.4848096202) = 299° |
| arccos(0.5) = 60° | arccos(-1) = 180° | arccos(0.5) = 300° |
| arccos(0.4848096202) = 61° | arccos(-0.9998476952) = 181° | arccos(0.5150380749) = 301° |
| arccos(0.4694715628) = 62° | arccos(-0.999390827) = 182° | arccos(0.5299192642) = 302° |
| arccos(0.4539904997) = 63° | arccos(-0.9986295348) = 183° | arccos(0.544639035) = 303° |
| arccos(0.4383711468) = 64° | arccos(-0.9975640503) = 184° | arccos(0.5591929035) = 304° |
| arccos(0.4226182617) = 65° | arccos(-0.9961946981) = 185° | arccos(0.5735764364) = 305° |
| arccos(0.4067366431) = 66° | arccos(-0.9945218954) = 186° | arccos(0.5877852523) = 306° |
| arccos(0.3907311285) = 67° | arccos(-0.9925461516) = 187° | arccos(0.6018150232) = 307° |
| arccos(0.3746065934) = 68° | arccos(-0.9902680687) = 188° | arccos(0.6156614753) = 308° |
| arccos(0.3583679495) = 69° | arccos(-0.9876883406) = 189° | arccos(0.629320391) = 309° |
| arccos(0.3420201433) = 70° | arccos(-0.984807753) = 190° | arccos(0.6427876097) = 310° |
| arccos(0.3255681545) = 71° | arccos(-0.9816271834) = 191° | arccos(0.656059029) = 311° |
| arccos(0.3090169944) = 72° | arccos(-0.9781476007) = 192° | arccos(0.6691306064) = 312° |
| arccos(0.2923717047) = 73° | arccos(-0.9743700648) = 193° | arccos(0.6819983601) = 313° |
| arccos(0.2756373558) = 74° | arccos(-0.9702957263) = 194° | arccos(0.6946583705) = 314° |
| arccos(0.2588190451) = 75° | arccos(-0.9659258263) = 195° | arccos(0.7071067812) = 315° |
| arccos(0.2419218956) = 76° | arccos(-0.9612616959) = 196° | arccos(0.7193398003) = 316° |
| arccos(0.2249510543) = 77° | arccos(-0.956304756) = 197° | arccos(0.7313537016) = 317° |
| arccos(0.2079116908) = 78° | arccos(-0.9510565163) = 198° | arccos(0.7431448255) = 318° |
| arccos(0.1908089954) = 79° | arccos(-0.9455185756) = 199° | arccos(0.7547095802) = 319° |
| arccos(0.1736481777) = 80° | arccos(-0.9396926208) = 200° | arccos(0.7660444431) = 320° |
| arccos(0.156434465) = 81° | arccos(-0.9335804265) = 201° | arccos(0.7771459615) = 321° |
| arccos(0.139173101) = 82° | arccos(-0.9271838546) = 202° | arccos(0.7880107536) = 322° |
| arccos(0.1218693434) = 83° | arccos(-0.9205048535) = 203° | arccos(0.79863551) = 323° |
| arccos(0.1045284633) = 84° | arccos(-0.9135454576) = 204° | arccos(0.8090169944) = 324° |
| arccos(0.08715574275) = 85° | arccos(-0.906307787) = 205° | arccos(0.8191520443) = 325° |
| arccos(0.06975647374) = 86° | arccos(-0.8987940463) = 206° | arccos(0.8290375726) = 326° |
| arccos(0.05233595624) = 87° | arccos(-0.8910065242) = 207° | arccos(0.8386705679) = 327° |
| arccos(0.0348994967) = 88° | arccos(-0.8829475929) = 208° | arccos(0.8480480962) = 328° |
| arccos(0.01745240644) = 89° | arccos(-0.8746197071) = 209° | arccos(0.8571673007) = 329° |
| arccos(0) = 90° | arccos(-0.8660254038) = 210° | arccos(0.8660254038) = 330° |
| arccos(-0.01745240644) = 91° | arccos(-0.8571673007) = 211° | arccos(0.8746197071) = 331° |
| arccos(-0.0348994967) = 92° | arccos(-0.8480480962) = 212° | arccos(0.8829475929) = 332° |
| arccos(-0.05233595624) = 93° | arccos(-0.8386705679) = 213° | arccos(0.8910065242) = 333° |
| arccos(-0.06975647374) = 94° | arccos(-0.8290375726) = 214° | arccos(0.8987940463) = 334° |
| arccos(-0.08715574275) = 95° | arccos(-0.8191520443) = 215° | arccos(0.906307787) = 335° |
| arccos(-0.1045284633) = 96° | arccos(-0.8090169944) = 216° | arccos(0.9135454576) = 336° |
| arccos(-0.1218693434) = 97° | arccos(-0.79863551) = 217° | arccos(0.9205048535) = 337° |
| arccos(-0.139173101) = 98° | arccos(-0.7880107536) = 218° | arccos(0.9271838546) = 338° |
| arccos(-0.156434465) = 99° | arccos(-0.7771459615) = 219° | arccos(0.9335804265) = 339° |
| arccos(-0.1736481777) = 100° | arccos(-0.7660444431) = 220° | arccos(0.9396926208) = 340° |
| arccos(-0.1908089954) = 101° | arccos(-0.7547095802) = 221° | arccos(0.9455185756) = 341° |
| arccos(-0.2079116908) = 102° | arccos(-0.7431448255) = 222° | arccos(0.9510565163) = 342° |
| arccos(-0.2249510543) = 103° | arccos(-0.7313537016) = 223° | arccos(0.956304756) = 343° |
| arccos(-0.2419218956) = 104° | arccos(-0.7193398003) = 224° | arccos(0.9612616959) = 344° |
| arccos(-0.2588190451) = 105° | arccos(-0.7071067812) = 225° | arccos(0.9659258263) = 345° |
| arccos(-0.2756373558) = 106° | arccos(-0.6946583705) = 226° | arccos(0.9702957263) = 346° |
| arccos(-0.2923717047) = 107° | arccos(-0.6819983601) = 227° | arccos(0.9743700648) = 347° |
| arccos(-0.3090169944) = 108° | arccos(-0.6691306064) = 228° | arccos(0.9781476007) = 348° |
| arccos(-0.3255681545) = 109° | arccos(-0.656059029) = 229° | arccos(0.9816271834) = 349° |
| arccos(-0.3420201433) = 110° | arccos(-0.6427876097) = 230° | arccos(0.984807753) = 350° |
| arccos(-0.3583679495) = 111° | arccos(-0.629320391) = 231° | arccos(0.9876883406) = 351° |
| arccos(-0.3746065934) = 112° | arccos(-0.6156614753) = 232° | arccos(0.9902680687) = 352° |
| arccos(-0.3907311285) = 113° | arccos(-0.6018150232) = 233° | arccos(0.9925461516) = 353° |
| arccos(-0.4067366431) = 114° | arccos(-0.5877852523) = 234° | arccos(0.9945218954) = 354° |
| arccos(-0.4226182617) = 115° | arccos(-0.5735764364) = 235° | arccos(0.9961946981) = 355° |
| arccos(-0.4383711468) = 116° | arccos(-0.5591929035) = 236° | arccos(0.9975640503) = 356° |
| arccos(-0.4539904997) = 117° | arccos(-0.544639035) = 237° | arccos(0.9986295348) = 357° |
| arccos(-0.4694715628) = 118° | arccos(-0.5299192642) = 238° | arccos(0.999390827) = 358° |
| arccos(-0.4848096202) = 119° | arccos(-0.5150380749) = 239° | arccos(0.9998476952) = 359° |
Найти угол, зная косинус угла: примеры решения
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.
Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).
Замечание 1
Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.
Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:
Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.
В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.
Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите, чему равен $arccos 0,456$.
Решение:
Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:
Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ
После нажатия кнопки мы получили значение $α = 27,129°$.
Пример 2
Определите, чему равен угол, если известен его косинус, и он равен $0,95$.
Решение:
Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
Определение арккосинуса(arccos)
Арккосинус(y = arccos(x)) – это обратная тригонометрическая функция к косинусу x = cos(y). Область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
Функция арккосинус не является четной или нечетной
Видео
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.
Теорема косинусов
Для любого треугольника справедливо равенство:
a2 = b2 + c2 — 2b × c × cosA,
где угол A — это угол, противолежащий стороне a.
Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:
a2 = b2 + c2,
где a — гипотенуза.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6. Из треугольника АВС найдем cos B:

- Из треугольника СМВ по теореме косинусов найдём СМ:



Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:

- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.

- Если c2 < a2 + b2, то ∠C — острый.

Теги
Как найти угол зная косинус
Кроме прямых тригонометрических функций синус и косинус, существуют и обратные им арксинус и арккосинус. С их помощью можно вычислять величины углов по известным значениям прямых функций. Есть несколько вариантов практической реализации таких расчетов.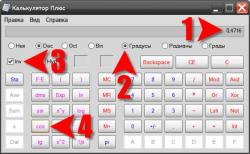
Используйте функцию, обратную косинусу (арккосинус) для нахождения угла по известному значению косинуса. Нужное значение арктангенса, а по нему и величину угла, можно найти, например, в «таблицах Брадиса». Бумажные экземпляры этого справочника есть в библиотеках и книжных магазинах, а электронные можно найти в интернете.
Найдите в сети он-лайн калькуляторы для вычисления обратных тригонометрических функций и определите с их помощью нужное значение. Пользоваться такими сервисами намного удобнее, чем искать значения в таблицах. К тому же они могут упростить расчеты, так как многие такие калькуляторы позволяют вычислять не только отдельные значения, но и получать результаты на основе введенных формул, составленных из нескольких операций с тригонометрическими функциями.
Воспользуйтесь стандартным калькулятором ОС Windows, если хотите обойтись без выхода в интернет. Команда запуска калькулятора помещена в главное меню на кнопке «Пуск». Открыв его, перейдите в раздел «Все программы», затем в подраздел «Стандартные» и щелкните пункт «Калькулятор». По умолчанию он запустится с простейшим интерфейсом, не имеющим инструментов для тригонометрических вычислений. Раскройте в его меню раздел «Вид» и выберите пункт с надписью «Инженерный».
Введите значение косинуса с клавиатуры, или щелкая соответствующие кнопки интерфейса калькулятора. Можно использовать для ввода операции копирования (CTRL + C) и вставки (CTRL + V). Затем выберите единицы измерения, в которых должен быть представлен результат (градусы, радианы или грады) – соответствующий селектор находится строчкой ниже поля ввода числа. После этого надо выставить отметку инвертирования функций в чекбоксе Inv. Этим все приготовления заканчиваются, щелкните кнопку cos и калькулятор рассчитает значение обратной косинусу функции (арккосинус) заданного значения и представит вам результат в выбранных единицах.
План урока:
Арккосинус
Арксинус
Арктангенс
Решение уравнения cosx = a
Решение уравнения sinx = a
Решение уравнений tgx = a и ctgx = a
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:

Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1<а < 1, то должно получиться две точки, которым соответствуют два противоположных угла:

Получается, что каждому значению числа а соответствует некоторый угол α. А если есть соответствие, то есть и функция:
α = f (a)
В математике ее называют арккосинусом. Записывается она так:

Вертикальная прямая может пересекать единичную окружность в двух разных точках. Им соответствуют разные углы. Принято считать, что арккосинус – это значение того угла, который лежит в первой или второй четверти, то есть ему соответствует точка, лежащая выше оси Ох. Тогда другая точка пересечения будет соответствовать углу (– arccosa):

Выходит, что арккосинус может принимать только значения из отрезка [0; π]. Дадим определение арккосинуса:

Задание. Вычислите арккосинус числа 1/2.
Решение. Мы помним, что косинус угла π/3 равен 1/2:

Следовательно, arccos 1/2 – это и есть угол π/3:

Ответ: π/3.
Обратим внимание, что если число а равно 1 или (– 1), то его арккосинус равен нулю в первом случае и π во втором:

В тех случаях, когда а > 1 либо а <– 1, то соответствующая прямая не пересечет единичную окружность. Это значит, что эти значения не входят в область определения арккосинуса:

Получается, что область определения арккосинуса – это промежуток [– 1; 1].
Для вычисления арккосинусов от отрицательных величин удобно пользоваться формулой

Действительно, если отложить на координатной прямой числа а и (– а), то вертикальные прямые, проходящие через них, пересекут окружность в некоторых точках А и С:

Дополнительно обозначим буквой В точку с координатами (1; 0) и буквой D точку с координатами (– 1; 0). Эти точки располагаются на пересечении оси Ох и единичной окружности. Тогда можно записать, что

ведь эти два угла образуют вместе развернутый угол ВОD, равный π. С другой стороны, из симметрии очевидно, что углы ∠COD и ∠АОВ равны друг другу, значит, ∠COD = ∠АОВ = arccosa. Тогда

Но ∠СОВ – это арккосинус от (– а), поэтому


Задание. Вычислите arccos (– 1/2).
Решение. Используем только что полученную формулу:


Ответ: 2π/3.
Арксинус
Арккосинус – это ф-ция, обратная косинусу. Аналогично можно вести и другие обратные тригонометрические ф-ции. Пусть нам требуется узнать, синус какого угла равен числу а. Так как синус – это координата у точки на единичной окружности, то достаточно провести горизонтальную линию у = а:

Прямая может пересечь окружность сразу в двух точках. За арксинус принимают угол, соответствующей точке, расположенной правее оси Оу. Вторая же точка соответствует углу π – arcsin α:

Арксинус может быть вычислен и для отрицательного значения а. В этом случае точка пересечения прямой и окружности будет располагаться в IV четверти, а соответствующий ему угол окажется отрицательным:

При значениях а, равных (– 1) и 1, точка пересечения будет только одна. В этих случаях арксинус окажется равным либо углу π/2, либо углу (– π/2):

Таким образом, арксинус может принимать значения из отрезка [– π/2; π/2], а вычислить его можно для чисел а, принадлежащих отрезку [– 1; 1]. Если же число а выходит за пределы этого промежутка, то горизонтальная прямая не пересекает единичную окружность, а потому ф-ция арксинуса становится неопределенной:

Получается, что областью определения арксинуса является промежуток [– 1; 1], а областью значений – промежуток [– π/2; π/2].
Дадим определение арксинусу:

Задание. Чему равен arcsin0,5?
Решение. Мы знаем, что sinπ/6 = 1/2 = 0,5. Следовательно, арксинус 0,5 равен π/6.

Для вычисления арксинусов отрицательных углов используется формула

Справедливость этой формулы очевидна из картинки:


Задание. Вычислите arcsin (– 0,5).
Решение. Используем формулу для арксинуса отрицательного числа:

Арктангенс
Введем ф-цию, обратную тангенсу. Она называется арктангенс.
Напомним, что величину тангенса на координатной плоскости можно получить, если продолжить угол до его пересечения с вертикальной прямой х = 1. Аналогично, чтобы определить арктангенс некоторого числа а, надо отметить на этой прямой точку с координатами (1; а) и соединить её с началом координат:

Несложно видеть, что, какое бы число а нами не было выбрано, мы с помощью построения всегда сможем соединить точку А с началом координат и получить некоторый угол arctga. Это значит, что область определения арктангенса – это вся числовая прямая, то есть промежуток (– ∞; + ∞).
Ещё раз уточним, что вводимые нами функции arcos, arcsin, arctg называются ОБРАТНЫМИ тригонометрическими функциями. C их помощью можно определить угол, если известно значение его синуса, косинуса или тангенса.Образно говоря, обратные триг-кие функции играют в тригонометрии ту же роль, что и квадратные корни при исследовании квадратных ур-ний. Как без квадратных корней невозможно решать квадратные ур-ния, так и без знания об обратных триг-ких функций нельзя решать уже тригом-кие уравнения.
Теперь вернемся к понятию арктангенса. При положительном значении числа а угол arctga будет принадлежать I четверти. Если же а – отрицательное число, то угол arctga окажется также отрицательным и будет принадлежать IV четверти:

Получается, что величина arctgа может принадлежать промежутку (– π/2; π/2). Обратите внимание, что в данном случае у промежутка круглые скобки. Действительно для углов (– π/2) и π/2 тангенс не определен, а потому арктангенс не может принимать эти два значения.

Задание. Чему равен arctg 1?
Решение. Из таблицы тангенсов мы знаем, что tgπ/4 = 1. Это значит, что

Для вычисления арктангенсов отрицательных чисел используют формулу

В ее справедливости можно убедиться, взглянув на рисунок:


Задание. Вычислите arctg (– 1).
Решение.

Ответ: – 1
В принципе можно ввести ещё ф-цию, обратную котангенсу – арккотангенс. Однако для решения тригонометрических уравнений, как мы убедимся далее, она не требуется, а поэтому в рамках школьного курса математики ее можно не изучать.
В заключение приведем таблицы, которые помогают вычислять значение обратных тригон-ких функций:

Решение уравнения cosx = a
Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:

По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь

Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:

Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:

Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:

Здесь мы использовали тот факт, косинус – четная функция, то есть

Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:

Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть

Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:

Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение

При n = 5 получим корень

При n = – 10 у нас получится решение

Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:

Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень

Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:

Объединить же обе серии можно одной записью:

Напомним, что мы решали ур-ние

и получили для него решение

Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид

где а – некоторое число, его решением будут все такие х, что


Для краткости запись «n– целое число» заменяют эквивалентной записью
«n ∈ Z»
Напомним, что буквой Z обозначают множество целых чисел.
Задание. Решите ур-ние

Решение. Вспомним, что

Задание. Решите ур-ние

Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:

Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.
Задание. Укажите три наименьших положительных корня ур-ния

Решение. Так как

то все решения образуют две серии:

Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.
Для первой серии:

Для второй серии:

Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):

Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4
Ответ: π/4, 7π/4 и 9π/4.
Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния

На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния

являются точки, в которых график пересекает ось Ох:

Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок [– 1; 1].
Решение уравнения sinx = a
Ур-ние cosx = a называют простейшим тригонометрическим уравнением, ведь, ведь для его решения не требуется проводить никаких преобразований. Аналогично простейшими являются ур-ния sinx = a, tgx = a и ctgx = a.
Ситуация с ур-нием sinx = a аналогична ситуации с косинусом. Если число а не принадлежит промежутку [– 1; 1], то корней у ур-ния не будет. Если же число а будет принадлежать этому промежутку, то у ур-ния окажется бесконечное число решений.
Рассмотрим случай, когда 0<а< 1. Тогда решениями ур-ния окажутся числа arcsina и π – arcsina:

В свою очередь каждое из этих двух решений порождает свою собственную бесконечную серию решений

Однако, как и в случае с косинусом, существует способ записать одной формулой сразу оба этих решения. Для этого перепишем первую серию таким образом:

Действительно, если n окажется четным, то, то выражение (– 1)n,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1)n окажется равным (– 1), и мы получим вторую серию.

Задание. Решите ур-ние

Задание. Запишите корни ур-ния

Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.

Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:

Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние

Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:

Решениями ур-ния


Наконец, решениями ур-ния

Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):

Таким образом, у ур-ния tgx = a существует очевидное решение
x = arctg a
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:



Задание. Решите ур-ние

Задание. Запишите формулу корней ур-ния

Далее рассмотрим ур-ние вида

Задание. Решите ур-ние

Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии

Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.



