Как составить функцию по схеме информатика

Как составить функцию по схеме информатика

Содержание

  1. Лабораторный практикум по основам языка C/С++
  2. Справочник
  3. Правила оформления блок-схем
  4. Назначение блоков
  5. Построение логических схем
  6. Построение таблиц истинности
  7. Алгоритм построения таблицы истинности логической функции
  8. Готовые работы на аналогичную тему
  9. Алгоритм построения логической функции по ее таблице истинности

Лабораторный практикум по основам языка C/С++

Справочник

Правила оформления блок-схем

Блок-схема является графическим представлением алгоритма решения задачи. Блок-схема никак не связана с каким-либо языком программирования. Таким образом все выражения в блоках блок-схемы записываются по правилам обычной математики.

В блок-схемах нельзя использовать элементы языка программирования.

  • в качестве оператора присваивания в блок-схемах используется двухсимвольный знак «:=»
  • в качестве оператора логического сравнения на равенство в блок-схемах используется одинарный символ знак «=»
  • в качестве оператора логического сравнения «больше или равно» («меньше или равно») в блок-схемах используется одинарный символ » ≥ » ( » ≤ » )
  • в качестве логических операторов используются слова AND , OR
  • индексы у элементов массива указываются также, как в математических выражениях: aij .
  • математические выражения записываются согласно всем правилам математики. Особенно это касается выражений с дробями, то есть формула должна записываться следующим образом 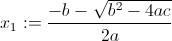, а не x1=(-b-sqrt(b*b-4*a*c))/(2*a).

Назначение блоков

Наименование Обозначение Функция
Терминатор Элемент отображает выход во внешнюю среду и вход из внешней среды (наиболее частое применение − начало и конец программы). Внутри фигуры записывается соответствующее действие.
Процесс Выполнение одной или нескольких операций, обработка данных любого вида (изменение значения данных, формы представления, расположения). Внутри фигуры записывают непосредственно сами операции, например, операцию: a := 10 b + c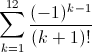

Для вычисления суммы ряда в программе необходимо выполнить следующие действия:

  1. Описать переменные, которые будут использоваться для хранения текущего значения суммы, текущего значения счетчика элементов цикла, а также общего количества суммируемых элементов.
    Примечание: это действие необходимо только для определения количества переменных, которые потребуются алгоритму и потому в блок-схеме эти действия никак не учитываются.
  2. Получить у пользователя число элементов ряда, которые следует просуммировать, то есть ввести данные в программу.
  3. Обнулить переменную, которая будет хранить сумму ряда.
  4. Инициализировать счетчик цикла начальным значением.
  5. Рассчитать значение элемента ряда с номером, равным текущему значению счетчика и прибавить получившееся значение к значению переменной-суммы.
  6. увеличить значение счетчика на единицу.
  7. Если значение счетчика меньше количества суммируемых элементов, которое задано пользователем, то перейти к выполнению пункта 5.
  8. Вывести значение суммы.

Это текстовая запись алгоритма. Теперь реализуем ее в виде графической схемы (блок-схемы).

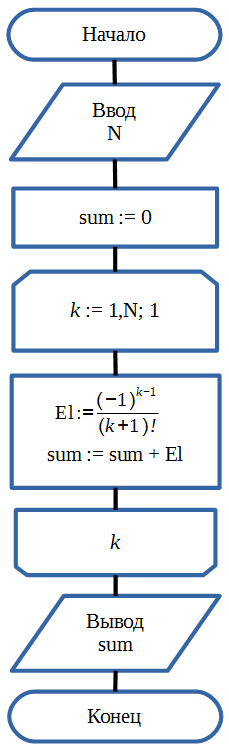
Если вы не занете при помощи чего создавать блок-схемы, то рекомендуем ознакомиться со следующей статьей:
6 сервисов для работы с блок-схемами

Источник

Построение логических схем

Образовательные:

  • закрепить у учащихся представление об устройствах элементной базы компьютера;
  • закрепить навыки построения логических схем.

Развивающие:

  • формировать развитие алгоритмического мышления;
  • развить конструкторские умения;
  • продолжать способствовать развитию ИКТ — компетентности;

Воспитательные:

  • продолжить формирование познавательного интереса к предмету информатика;
  • воспитывать личностные качества:
  • активность,
  • самостоятельность,
  • аккуратность в работе;

Требования к знаниям и умениям:

Учащиеся должны знать:

  • основные базовые элементы логических схем;
  • правила составления логических схем.

Учащиеся должны уметь:

  • составлять логические схемы.

Тип урока: урок закрепления изученного материала

Вид урока: комбинированный

Методы организации учебной деятельности:

  • фронтальная;
  • индивидуальная;

Программно-дидактическое обеспечение:

  • ПК, SMART Board, карточки с индивидуальным домашним заданием.

Урок разработан с помощью программы Macromedia Flash.

I. Постановка целей урока.

Сегодня мы продолжаем изучение темы «Построение логических схем».

Приготовьте раздаточный материал «Логические основы ЭВМ. Построение логических схем» Приложение 1

Вопрос учителя. Назовите основные логические элементы. Какой логический элемент соответствует логической операции И, ИЛИ, НЕ?

Ответ учащихся. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Основные логические элементы конъюнктор (соответствует логическому умножению), дизъюнктор (соответствует логическому сложению), инвертор (соответствует логическому отрицанию).

Вопрос учителя. По каким правилам логические элементы преобразуют входные сигналы. Рассмотрим элемент И. В каком случае на выходе будет ток (сигнал равный 1).

Ответ учащихся. На первом входе есть ток (1, истина), на втором есть (1, истина), на выходе ток идет (1, истина).

Вопрос учителя. На первом входе есть ток, на втором нет, однако на выходе ток идет. На входах тока нет и на выходе нет. Какую логическую операцию реализует данный элемент?

Ответ учащихся. Элемент ИЛИ — дизъюнктор.

Вопрос учителя. Рассмотрим логический элемент НЕ. В каком случае на выходе не будет тока (сигнал равный 0)?

Ответ учащихся. На входе есть ток, сигнал равен 1.

Вопрос учителя. В чем отличие логической схемы от логического элемента?

Ответ учащихся. Логические схемы состоят из логических элементов, осуществляющих логические операции.

Проанализируем схему и определим сигнал на выходе.

II. Закрепление изученного материала.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Дома вам необходимо было построить логические схемы, соответствующие логическим выражениям.

Вопрос учителя. Каков алгоритм построение логических схем?

Ответ учащихся. Алгоритм построение логических схем:

Определить число логических переменных.

Определить количество базовых логических операций и их порядок.

Изобразить для каждой логической операции соответствующий ей элемент (вентиль).

Соединить вентили в порядке выполнения логических операций.

Проверка домашнего задания Приложение 1. Домашнее задание. Часть 1

Построить логическую схему для логического выражения: .

  1. Две переменные — А и В.
  2. Две логические операции: &,
  3. Строим схему.

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Вычислить значение данного выражения для А=1, В=0.

III. Пропедевтика (законы логики)

Выполним задачу обратную данной. Составим логическое выражение по заданной логической схеме:

Данное логическое выражение можно упростить.

Операция И — логическое умножение, ИЛИ — сложение. Запишем выражение, заменяя знаки & и U на * и + соответственно.

F= (A*B+B*С) Упростим F= (B*(А+С)), затем запишем и тогда логическая схема примет вид:

Вывод: Логические схемы, содержащие минимальное количество элементов, обеспечивают большую скорость работы и увеличивают надёжность устройства.

Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических схем. Проще, и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.

Таким образом, цель нашего следующего урока — изучить законы алгебры логики.

IV. Домашнее задание. Часть 2

V. Практическая работа.

Программа — тренажер «Построение логических схем»

Источник

Построение таблиц истинности

Вы будете перенаправлены на Автор24

Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.

Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.

Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.

Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.

При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:

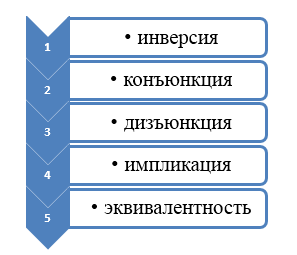
Приоритетом в выполнении порядка выполнения операций пользуются скобки.

Алгоритм построения таблицы истинности логической функции

Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.

Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.

Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.

Готовые работы на аналогичную тему

Составить таблицу истинности логического выражения $D=bar vee (B vee C)$.

Определим количество строк:

Количество простых выражений – $n=3$, значит

Определим количество столбцов:

Количество логических операций и их последовательность:

Заполним таблицу, учитывая таблицы истинности логических операций.

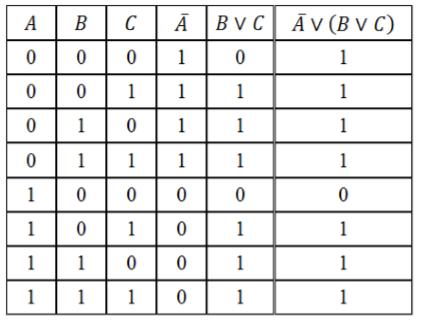
По данному логическому выражению построить таблицу истинности:

Определим количество строк:

Количество простых выражений – $n=3$, значит

Определим количество столбцов:

Количество логических операций и их последовательность:

  1. отрицание ($bar$);
  2. дизъюнкция, т.к. она находится в скобках ($A vee B$);
  3. конъюнкция ($(Avee B)bigwedge overline$);
  4. отрицание, которое обозначим $F_1$ ($overline<(Avee B)bigwedge overline>$);
  5. дизъюнкция ($A vee C$);
  6. конъюнкция ($(Avee C)bigwedge B$);
  7. отрицание, которое обозначим $F_2$ ($overline<(Avee C)bigwedge B>$);

Заполним таблицу, учитывая таблицу истинности логических операций.

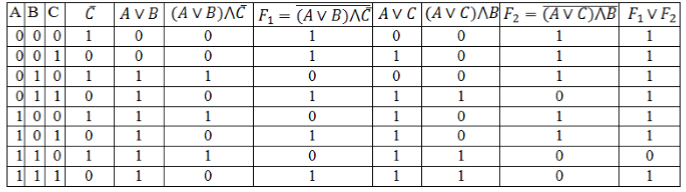
Алгоритм построения логической функции по ее таблице истинности

  1. Выделяют в таблице истинности строки со значением функции, равным $1$.
  2. Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
  3. Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
  4. В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.

По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.

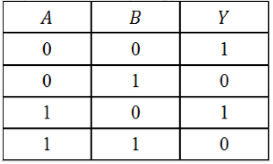
  1. Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
  2. Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:

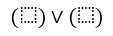
  • Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
  • В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overlinewedge overlineright)vee left(Awedge overlineright).]

    • Получи деньги за свои студенческие работы

    Курсовые, рефераты или другие работы

    Автор этой статьи Дата написания статьи: 12 04 2016

    Источник

    Источник

    Редактор схемы логических элементов

    Сервис представляет собой ряд калькуляторов: создание схемы из логических элементов, построение таблицы истинности по булевой функции (с помощью него можно будет также упростить эту функцию) и редактор карт Карно.

    С помощью первой программы можно онлайн создать схему логических элементов. По построенной схеме находятся СКНФ, СДНФ, полином Жегалкина. Имеется возможность минимизировать булеву функцию.

    Если схему необходимо построить по заданной таблице истинности, то используйте этот калькулятор (иногда задается просто строка, например, f=10001011).

    • Ввод данных
    • Параметры схемы
    • Решение
    • Видеоинструкция
    • Оформление Word

    Количество переменных
    Стандарт изображений элементов
    Инверсные входы

    INV

    AND

    NAND

    OR

    NOR

    XOR

    MOD

    IF

    Размеры графического полотна

    Ширина
    Высота

    Созданную логическую схему можно сохранить в форматах docx и png (меню Действия).

    По логической схеме можно построить СКНФ, СДНФ, полином Жегалкина, карты Вейча-Карно, а также минимизировать булеву функцию.

    Здесь будет показано решение

    Инструкция к сервису

    Для добавления логического элемента необходимо выделить его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле.

    Чтобы соединить элементы, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить. Для соединения с переменной xi нажмите на соответствующее ей название.

    Построенную схему можно сохранить в формате docx или png.

    Булевы функции

    С помощью этого калькулятора по булевой функции строится таблица истинности, определяются свойства функции и другие параметры (см. вкладку Параметры решения). При этом вводится только само логическое выражение без префикса. Например, при f(x,y,z) = x → y!z, ввести необходимо только x → y!z.

    Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение).

    (...) – ввод скобок, x -отрицание (NOT, !, ¬), & – логическое И, AND, ∧, *, v – логическое ИЛИ, OR, ∨, = – эквивалентность, ˜, ≡, ↔, ⊕ – сумма по модулю 2, | – штрих Шеффера, И-НЕ, AND-NOT, ↓ – стрелка Пирса, ИЛИ-НЕ, OR-NOT, ← – обратная импликация.

    Для вложенного отрицания необходимо использовать знак !. Например, x v y = !(x v y) или x v y = x v !y

    По найденной таблице истинности можно определить логические значения высказываний, например, при x=0, y=0, z=1

    Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно (=). Например, A+B→A&B=1, необходимо ввести A+B→A&B. Если в результате преобразований получится, что f=1, то высказывание истинно, если f=0 – ложно.

    Логические (функциональные) элементы {v,&, ¬} являются наиболее распространенными: в силу полноты системы любую булеву функцию (БФ) можно представить в виде суперпозиции дизъюнкции, конъюнкции и отрицания. В качестве функциональных элементов (ФЭ) можно рассматривать любые булевы функции, при этом их можно соединять друг с другом, подавая выходы одних элементов на входы других (суперпозиция БФ).

    Область определения БФ E – конечное множество, поэтому БФ можно задать с помощью таблицы истинности, содержащей |E|=2n строк. Столбец значений БФ при этом представляет собой двоичное слово длиной 2n. Поэтому количество различных БФ n переменных равно 22n.

    • Отрицание, ¬

      x f

      0 1

      1 0

    • Конъюнкция, &

      x y f

      0 0 0

      0 1 0

      1 0 0

      1 1 1

    • Дизъюнкция, v

      x y f

      0 0 0

      0 1 1

      1 0 1

      1 1 1

    • Сумма по модулю 2, x⊕y

      x y f

      0 0 0

      0 1 1

      1 0 1

      1 1 0

    • Стрелка Пирса, x↓y

      x y f

      0 0 1

      0 1 0

      1 0 0

      1 1 0

    • Эквивалентность, x↔y

      x y f

      0 0 1

      0 1 0

      1 0 0

      1 1 1

    • Импликация, x→y

      x y f

      0 0 1

      0 1 1

      1 0 0

      1 1 1

    • Штрих Шеффера, x|y

      x y f

      0 0 1

      0 1 1

      1 0 1

      1 1 0

    Другие БФ строятся из элементарных с помощью суперпозиций функций.

    Основные равносильности логики высказываний

    Название Формула
    Закон исключенного третьего X v !X ≡ И
    Закон противоречия X & !X ≡ Л
    Закон коммутативности X & Y ≡ Y & X
    X v Y ≡ Y v X
    Закон ассоциативности (X & Y)&Z ≡ X&(Y&Z)
    (X v Y) v Z ≡ X v (Y v Z)
    Закон дистрибутивности X&(Y v Z) ≡ X&Y v X&Z
    X v Y&Z ≡ (X v Y)&(X v Z)
    Закон двойного отрицания !!X ≡ X
    Закон идемпотентности X&X ≡ X, X v X ≡ X
    Законы де Моргана !(X v Y) ≡ !X & !Y
    !(X & Y) ≡ !X v !Y
    Закон поглощения X v X&Y ≡ X
    X&(X v Y) ≡ X
    Законы склеивания (X & Y)v(X & !Y) ≡ X
    (X v Y)&(X v !Y) ≡ X
    Замена импликации X → Y ≡ !X v Y
    Замена эквиваленции X = Y ≡ X&Y v !X&!Y

    Пример. Упростите выражение: (x˅y˅z)→(x˅y)*(x˅z)

    Упростим функцию, используя основные законы логики высказываний.

    Замена импликации: A → B = !A v B

    Для нашей функции:

    (x v y v z)→((x v y) (x v z)) = x v y v z v (x v y) (x v z)

    Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B

    Для нашей функции:

    x v y v z = x y z

    По закону дистрибутивности:

    (x v y) (x v z) = x v x z v y x v y z

    получаем:

    f = x y z v x v x z v y x v y z

    После элементарных преобразований получаем:

    f = x y z v x v x z v y x v y z = x y z v x v y z

    f = y z v y z v x

    Минимизация булевых функций

    В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

    Сократить БФ можно, применяя некоторые равносильности логики высказываний:

    1. Kx v K ≡ K – тождество поглощения;
    2. Kx v Kx ≡ K – тождество склеивания;
    3. Kx v Ky ≡ K(xvy) – дистрибутивный закон,

    где K– элементарная конъюнкция. Большинство методов минимизации БФ основываются на первых двух тождествах. А третье – дистрибутивный закон – уменьшает количество букв в формуле, но выводит формулу из класса ДНФ.
    При минимизации БФ используют различные термины (и обозначения) для полных элементарных конъюнкций (ПЭК). Наиболее часто используются термины «минтерм» и «конституента единицы». (Для полных элементарных дизъюнкций (ПЭД) используются термины «макстерм» и «конституента нуля»). Слово «конституента» означает «составляющая», а название «минтерм» исходит из определения конъюнкции, как минимального значения ее операндов. При этом используются обозначения mi – для минтерма и Mi – для макстерма. Номер i соответствует двоичной записи той оценки переменных, для которой mi=1.

    Метод карт Карно

    Склеить можно как целиком всю карту, либо только выделенные единицы (меню Операции).




    Количество переменных
    Сетка

    После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)

    Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K – две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название – диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой кнопкой мышки на соответствующую ячейку.

    Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.

    Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.

    Минимизая функции через равносильные преобразования

    см. таблицу равносильных преобразований

    Алгоритм минимизии логической функции

    1. Замена импликации и эквиваленции.
    2. Упрощение функции через законы де Моргана.
    3. Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
    4. Минимизация через закон дистрибутивности.

    Алгоритм Куайна построения сокращенной ДНФ

    1. Получить СДНФ функции.
    2. Провести все операции неполного склеивания.
    3. Провести все операции поглощения.

    Построение логической схемы по таблице истинности

    По заданной СДНФ (по таблице истинности) определяются существенные и фиктивные переменные, полином Жегалкина и принадлежность классам T0,T1, S, M, L. Также можно создать новую логическую схему (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

    Название переменных можно изменить. Для этого их необходимо выбрать (первая строка таблицы).

    Количество переменных
    Ввести как вектор значений (в виде строки)

    a b c f
    0 0 0
    0 0 1
    0 1 0
    0 1 1
    1 0 0
    1 0 1
    1 1 0
    1 1 1

    Для установки параметров решения, необходимо нажать Далее.

    Пример. Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = xvyv(x→y)&x

    Таблица истинности

    x y x y xvy xvy x→y (x→y)&x xvyv(x→y)&x
    0 0 1 1 1 0 1 0 0
    0 1 1 0 1 0 1 0 0
    1 0 0 1 1 0 0 0 0
    1 1 0 0 0 1 1 1 1

    Упростим функцию, используя основные законы логики высказываний.

    Замена импликации

    A → B = !A v B

    Для нашей функции:

    x→y = x v y

    f = x v y v (x v y) x

    Упростим функцию, используя законы де Моргана онлайн.

    !(A v B) = !A & !B

    !(A & B) = !A v !B

    Для нашей функции:

    x v y = x y

    f = x y v (x v y) x

    По закону дистрибутивности:

    x x = 0

    (x v y) x = y x

    x y v (x v y) x = x y v y x

    f = x y

    Используя равносильные преобразования, найдем СДНФ(А).

    СДНФ(А) = x y

    Используя равносильные преобразования, найдем СДНФ(А).

    1. Для получения элементарных дизъюнкций используем закон дистрибутивности XvYZ=(XvY)(XvZ).

    2. Закон исключенного третьего Xv!X=1. При этом элементарную дизъюнкцию можно отбросить (в силу равносильности C & 1 = C).

    3. По закону поглощения XvXYZ = X

    A = x y

    Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ А.

    1. Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную xi, тогда заменяем В на Bv(xi & !xi) = (B v xi)(B v !xi)

    2. Если в некоторую элементарную дизъюнкцию В переменная xi входит дважды, то лишнюю переменную нужно отбросить, так как xi v xi = xi.

    3. Если КНФ А содержит две одинаковых элементарных дизъюнкций, то одну можно отбросить, так как B & B = B

    4. Если в элементарную дизъюнкцию входит пара xi v !xi, то ее можно отбросить так как xi v !xi=1, а истинное высказывание из конъюнкции можно выбросить (в силу равносильности C & 1 = C).

    A = (x v y y) (y v x x) = (x v y) (x v y) (y v x) (y v x)

    A = (x v y) (x v y) (y v x) (y v x)

    СКНФ(А) = (x v y) (x v y) (x v y)

    Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:

    1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,…xn).

    2. Все логические слагаемые формулы различны.

    3. Ни одно логическое слагаемое не содержит переменную и её отрицание.

    4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

    F = x y

    Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:

    1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,…xn).

    2. Все элементарные дизъюнкции различны.

    3. Каждая элементарная дизъюнкция содержит переменную один раз.

    4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание

    F = (x v y) (x v y) (x v y)

    Список литературы

    1. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
    2. Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
    3. Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.

    Количество входов

    Текст

    РазмерЦвет

    Линия

    ТолщинаЦвет

    пунктирная – – – –

    Размеры в px и фон

    wh

    Номер входа

    Текст

    РазмерЦвет

    Линия

    ТолщинаЦвет

    пунктирная – – –

    Введите название переменных

    Введите название переменных

    Количество входов у элемента

    Источник

    Практическое занятие

    Работа с таблицами истинности и функциональными схемами

    Цель занятия:

    • учить составлять таблицы истинности для логических функций;

    • учить строить функциональной схемы по логической формуле;

    • учить составлять логическую формулу по функциональной схеме.

    Пояснение к работе.

    Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Буль первым показал, что существует аналогия между алгебраическими и логическими действиями, так как и те, и другие предполагают лишь два варианта ответов – истина или ложь, нуль или единица.

    На основе анализа логической связи между высказываниями делается логический вывод. Для получения логического вывода составляется  таблица истинности, в которой записывают все возможные комбинации каждого простого высказывания.

    Работа ЭВМ как автоматических устройств основана исключи­тельно на математически строгих правилах выполнения команд, программ и интерпретации данных. Тем самым работа компьютеров допускает строгую однозначную проверку правильности своей работы в плане заложенных в них процедур и алгоритмов обработки информации. Это позволяет использовать математический аппарат для анализа и разработки логических устройств вычислительной техники.

    Функцией логических переменных называют взаимосвязь логических переменных по законам логики. Значения входных переменных и выходных функций связаны некоторым преобразованием, которое реализует логическую функцию.

    Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

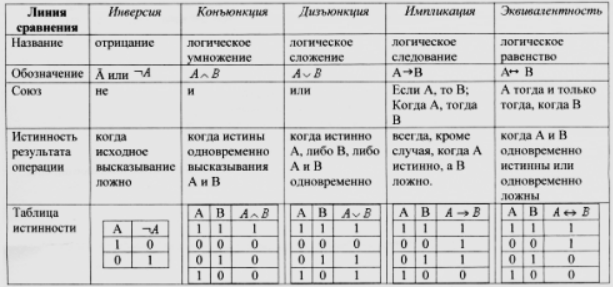
    Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность (таблица №1).

    В алгебре логики любую логическую функцию можно выразить через основные логические операции, записать ее в виде логического выражения и упростить ее, применяя законы логики и свойства логических операций. По формуле логической функции легко рассчитать ее таблицу истинности. Необходимо только учитывать порядок выполнения логических операций (приоритет) и скобки. Операции в логическом выражении выполняются слева направо с учетом скобок. 

    Приоритет выполнения логических операций:

    1. Действие в скобках; 2. Действие под отрицанием; 3. Инверсия; 4. Конъюнкция; 5. дизъюнкция.

    1. Таблица №1

      1. Логическая операция

      1. Название

      1. Соответствует союзу

      1. Обозначение знаками

      1. Таблица истинности

      1. Логическая операция

      1. Инверсия

      2. (от лат. inversion – переворачиваю)

      1. отрицание

      1. не А

      1. А

      1. 1

      1. 0

      1. 0

      1. 1

      1. Опр. 8 Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

      1. Конъюнкция

      2. (от лат. conjunction – связываю)

      1. Логическое умножение

      1. А и В

      1. А

      1. В

      1. 1

      1. 1

      1. 1

      1. 1

      1. 0

      1. 0

      1. 0

      1. 1

      1. 0

      1. 0

      1. 0

      1. 0

      1. Опр.9Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны.

      1. Дизъюнкция

      2. (от лат. disjunction – различаю)

      1. Логическое сложение

      1. А или В

      1. А

      1. В

      1. 1

      1. 1

      1. 1

      1. 1

      1. 0

      1. 1

      1. 0

      1. 1

      1. 1

      1. 0

      1. 0

      1. 0

      1. Опр. 10 Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.

      1. Импликация

      2. (от лат. implication – тесно связывать)

      1. Логическое следование

      1. Если А,

      2. то В;

      3. Когда А, тогда В

      1.  

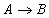
      2. А–условие

      3. В-следствие

      1. А

      1. В

      1. 1

      1. 1

      1. 1

      1. 1

      1. 0

      1. 0

      1. 0

      1. 1

      1. 0

      1. 0

      1. 0

      1. 1

      1. Опр. 11 Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие.

      1. Эквивалентность (от лат. equivalents – равноценность)

      1. Логическое равенство

      1. А тогда и только тогда, когда В

      1. А

      1. В

      1. 1

      1. 1

      1. 1

      1. 1

      1. 0

      1. 0

      1. 0

      1. 1

      1. 0

      1. 0

      1. 0

      1. 1

      1. Опр. 12 Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны

    2. Пример1.

    3. Построить таблицу истинности для логической функции

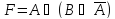
    4. Решение:

    1. Определить количество строк в таблице истинности, которое равно  количеству возможных комбинаций значений логических переменных, входящих в логическое выражение: количество строк равно 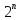, где n – количество переменных

    1. Количество логических переменных – 2 (A, B) поэтому количество строк – 2n = 4

    1. A

    1. B

    1. 0

    1. 0

    1. 0

    1. 1

    1. 1

    1. 0

    1. 1

    1. 1

    1. Определить количество столбцов:

    1. количество столбцов=количество переменных + количество операций, используя приоритет операций.

    2. Количество логических операций -3 (умножение – 1, сложение – 1, отрицание – 1), поэтому количество столбцов 2+3=5

    1. Построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных и заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности:

    1. A

    1. B

    1. 0

    1. 0

    1. 1

    1. 1

    1. 0

    1. 0

    1. 1

    1. 1

    1. 1

    1. 0

    1. 1

    1. 0

    1. 0

    1. 0

    1. 0

    1. 1

    1. 1

    1. 0

    1. 1

    1. 1

    2. Арифметико-логические основы работы компьютера

    3. Все логические схемы ЭВМ строятся на логических элементах, реализующих логические функции. Под логическим элементом понимают техническое устройство, реализующее одну элементарную булеву функцию.

    4. Обычно для построения схем используются логические элементы, реализующие основные логические функции И, ИЛИ, НЕ: конъюнктор (схема И); дизъюнктор (схема ИЛИ), инвертор (схема НЕ). Стандартные обозначения этих элементов выглядят следующим образом:

    5. элементы

    6. х1 х1

      1

      &

    7. у=х1х2 у=х1х2 х у=

    8. х2 х2

    9. конъюнктор дизъюнктор инвертор

    11. Конструктивно логические объединяются в единые корпуса – интегральные микросхемы (ИМС). В одном корпусе ИМС могут быть один, две и более логических элементов.

    12. Схемы И, ИЛИ, НЕ образуют базис, то есть с их помощью можно реализовать любую булеву функцию на основе суперпозиции. Применяемые на практике комплексы ИМС имеют в своём составе такие логические элементы, как И-НЕ, ИЛИ-НЕ, которые образуют универсальный базис. Стандартные схемы этих элементов имеют следующий вид:

    15. Схема, показывающая связи между различными логическими элементами, называется функциональной схемой. Рассмотрим на рисунке функциональную схему.

    16. t3

      t2

      t1

      1

      &

      &

      &

      у

      Х2

      Х1

    28. Существуют разные задачи работы с функциональными схемами.

    29. Задача1. Найти по функциональной схеме логическую функцию, описывающую работу этой схемы с помощью аппарата алгебры логики. В качестве примера построим логическую функцию, представленной на рисунке выше.

    30. Для этого каждому логическому элементу схемы поставим в соответствие логический оператор:

    31. ; ; ;

    32. Этим установлено однозначное соответствие между элементами схемы и её математическим описанием. Затем выполним последовательно операции подстановки и преобразования до тех пор, пока не получится функция, выраженная через входные переменные:

    33. ==

    34. Задача 2. Построить функциональную схему по логической функции . Затем построить схему, используя как базисные, так и дополнительные вентили, следуя по приоритету операций.

    35. Построим схему:

    37. 1

      f

      z

      y

      х

      1

    42. &

    46. Вопросы для размышления

    47. 1. Для чего нужно изучать функциональные схемы в информатике?

    48. 2. Как правильно написать логическую функцию по функциональной схеме?

    49. 3. Как правильно составить функциональную схему?

    50. 4. В чем процесс составления таблицы истинности по функциональной схеме?

    52. Задания

    1. Построить таблицу истинности для логической функции;

    2. Проверить справедливость равенств;

    3. Построить по логической функции функциональную схему;

    4. Построить по логической функции функциональную схему;

    5. По логической схеме записать логическую функцию.

      1. Вариант 1

      1. Вариант 2

      1. Вариант 3

      5. .

      1. Вариант 4

      5. .

      1. Вариант 5

      1. Вариант 6

      1. Вариант 7

      1. Вариант 8

      1. Вариант 9

      1. Вариант 10

      1. Вариант 11

      1. Вариант 12

      1. Вариант 13

      1. Вариант 14
    Источник

    Знания из области
    математической логики можно использовать
    для конструирования электронных
    устройств. Нам известно, что 0 и 1 в логике
    не просто цифры, а обозначение состояний
    какого-то предмета нашего мира, условно
    называемых “ложь” и “истина”.
    Таким предметом, имеющим два фиксированных
    состояния, может быть электрический
    ток. Устройства, фиксирующие два
    устойчивых состояния, называются
    бистабильными (например, выключатель,
    реле). Если вы помните, первые вычислительные
    машины были релейными. Позднее были
    созданы новые устройства управления
    электричеством ― электронные схемы,
    состоящие из набора полупроводниковых
    элементов. Такие электронные схемы,
    которые преобразовывают сигналы только
    двух фиксированных напряжений
    электрического тока (бистабильные),
    стали называть логическими
    элементами    .

    На элементарном
    уровне конъюнкцию можно представить
    себе в виде последовательно соединенных
    выключателей, а дизъюнкцию ― в виде
    параллельно соединенных выключателей:

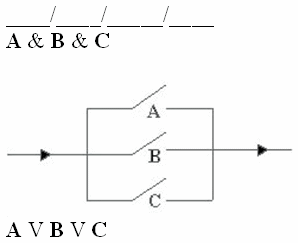
    Логические элементы
    имеют один или несколько входов и один
    выход, через которые проходят электрические
    сигналы, обозначаемые условно 0, если
    “отсутствует” электрический сигнал,
    и 1, если “имеется” электрический
    сигнал. Простейшим логическим элементом
    является инвертор,
    выполняющий функцию отрицания. Если на
    вход поступает сигнал, соответствующий
    1, то на выходе будет 0. И наоборот. У этого
    элемента один вход и один выход. На
    функциональных схемах он обозначается:

    Логический элемент,
    выполняющий логическое сложение,
    называется дизъюнктор.
    Он имеет, как минимум, два входа. На
    функциональных схемах он обозначается:

    Логический элемент,
    выполняющий логическое умножение,
    называется конъюнктор. Он имеет, как
    минимум, два входа. На функциональных
    схемах он обозначается:

    Специальных
    логических элементов для импликации и
    эквивалентности нет, т.к. А => В можно
    заменить на ¬А V В ; А <=> В можно заменить
    на (A & B)V(¬A & ¬B).

    Другие логические
    элементы построены из этих трех простейших
    и выполняют более сложные логические
    преобразования информации. Сигнал,
    выработанный одним логическим элементом,
    можно подавать на вход другого элемента,
    это дает возможность образовывать
    цепочки из отдельных логических
    элементов. Например:

    Эта схема
    соответствует сложной логической
    функции F(A,B)= ¬ (А V В).

    Попробуйте
    проследить изменения электрического
    сигнала в этой схеме. Например, какое
    значение электрического сигнала (0 или
    1) будет на выходе, если на входе: А=1 и
    В=0.

    Такие цепи из
    логических элементов называются
    логическими
    устройствами    .
    Логические устройства же, соединяясь,
    в свою очередь образуют функциональные
    схемы     (их
    еще называют структурными или логическими
    схемами    ). По
    заданной функциональной схеме можно
    определить логическую формулу, по
    которой эта схема работает, и наоборот.

    Пример 1.
    Логическая схема для функции
    будет
    выглядеть следующим образом:

    Правила составления
    электронных логических схем по заданным
    таблицам истинности остаются такими
    же, как для контактных схем.
         Пример
    2.     Составить
    логическую схему для тайного голосования
    трех персон A, B, C, условия которого
    определяются следующей таблицей
    истинности:

    A

    0

    0

    0

    0

    1

    1

    1

    1

    B

    0

    0

    1

    1

    0

    0

    1

    1

    C

    0

    1

    0

    1

    0

    1

    0

    1

    F

    0

    0

    0

    1

    0

    1

    1

    1

    Решение
         По
    таблице построим СДНФ логической функции
    и упростим ее:

    Правильность
    полученной формулы можно проверить,
    составив для нее таблицу истинности:

    Значение полученной
    функции совпадает с исходным, что можно
    заметить, сравнивая таблицы.
         Логическая
    схема полученной функции имеет вид:

    Рассмотрим еще
    два логических элемента, которые играют
    роль базовых при создании более сложных
    элементов и схем.

    Логический элемент
    И―НЕ состоит из конъюнктора и
    инвертора:
         Выходная
    функция выражается формулой
    .
         Логический
    элемент ИЛИ―НЕ состоит из дизъюнктора
    и инвертора:

    Выходная функция
    выражается формулой
    .

    Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    Источник

    Цели урока:

    Образовательные:

    • закрепить у учащихся представление об
      устройствах элементной базы компьютера;
    • закрепить навыки построения логических схем.

    Развивающие:

    • формировать развитие алгоритмического
      мышления;
    • развить конструкторские умения;
    • продолжать способствовать развитию ИКТ –
      компетентности;

    Воспитательные:

    • продолжить формирование познавательного
      интереса к предмету информатика;
    • воспитывать личностные качества:
    • активность,
    • самостоятельность,
    • аккуратность в работе;

    Требования к знаниям и умениям:

    Учащиеся должны знать:

    • основные базовые элементы логических схем;
    • правила составления логических схем.

    Учащиеся должны уметь:

    • составлять логические схемы.

    Тип урока: урок закрепления
    изученного материала

    Вид урока: комбинированный

    Методы организации учебной деятельности:

    • фронтальная;
    • индивидуальная;

    Программно-дидактическое обеспечение:

    • ПК, SMART Board, карточки с индивидуальным домашним
      заданием.

    Урок разработан с помощью программы Macromedia Flash.

    Ход урока

    I. Постановка целей урока.

    Добрый день!

    Сегодня мы продолжаем изучение темы
    “Построение логических схем”.

    Приготовьте раздаточный материал “Логические
    основы ЭВМ. Построение логических схем”     Приложение 1

    Вопрос учителя. Назовите основные
    логические элементы. Какой логический элемент
    соответствует логической операции И, ИЛИ, НЕ?

    Ответ учащихся. Логический элемент
    компьютера – это часть электронной логической
    схемы, которая реализует элементарную
    логическую функцию. Основные логические
    элементы конъюнктор (соответствует логическому
    умножению), дизъюнктор (соответствует
    логическому сложению), инвертор (соответствует
    логическому отрицанию).

    Вопрос учителя. По каким правилам
    логические элементы преобразуют входные
    сигналы. Рассмотрим элемент И. В каком случае на
    выходе будет ток (сигнал равный 1).

    Ответ учащихся. На первом входе есть
    ток (1, истина), на втором есть (1, истина), на выходе
    ток идет (1, истина).

    Вопрос учителя. На первом входе есть
    ток, на втором нет, однако на выходе ток идет. На
    входах тока нет и на выходе нет. Какую логическую
    операцию реализует данный элемент?

    Ответ учащихся. Элемент ИЛИ –
    дизъюнктор.

    Вопрос учителя. Рассмотрим логический
    элемент НЕ. В каком случае на выходе не будет тока
    (сигнал равный 0)?

    Ответ учащихся. На входе есть ток,
    сигнал равен 1.

    Вопрос учителя. В чем отличие
    логической схемы от логического элемента?

    Ответ учащихся. Логические схемы
    состоят из логических элементов, осуществляющих
    логические операции.

    Проанализируем схему и определим сигнал на
    выходе.

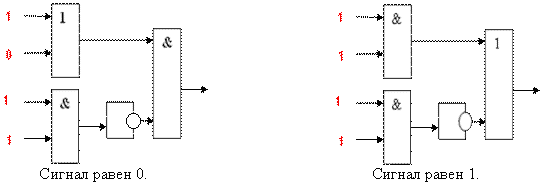
    II. Закрепление изученного материала.

    Почему необходимо уметь строить логические
    схемы?

    Дело в том, что из вентилей составляют более
    сложные схемы, которые позволяют выполнять
    арифметические операции и хранить информацию.
    Причем схему, выполняющую определенные функции,
    можно построить из различных по сочетанию и
    количеству вентилей. Поэтому значение
    формального представления логической схемы
    чрезвычайно велико. Оно необходимо для того,
    чтобы разработчик имел возможность выбрать
    наиболее подходящий ему вариант построения
    схемы из вентилей. Процесс разработки общей
    логической схемы устройства (в том числе и
    компьютера в целом), становится иерархическим,
    причем на каждом следующем уровне в качестве
    “кирпичиков” используются логические схемы,
    созданные на предыдущем этапе.

    Дома вам необходимо было построить логические
    схемы, соответствующие логическим выражениям.

    Вопрос учителя. Каков алгоритм
    построение логических схем?

    Ответ учащихся. Алгоритм построение
    логических схем:

    Определить число логических переменных.

    Определить количество базовых логических
    операций и их порядок.

    Изобразить для каждой логической операции
    соответствующий ей элемент (вентиль).

    Соединить вентили в порядке выполнения
    логических операций.

    Работа со SMART Board Приложение 2

    Проверка домашнего задания Приложение
    1    . Домашнее задание. Часть 1

    Построить логическую схему для логического
    выражения: .

    1. Две переменные – А и В.
    2. Две логические операции: &,
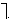
    3. Строим схему.

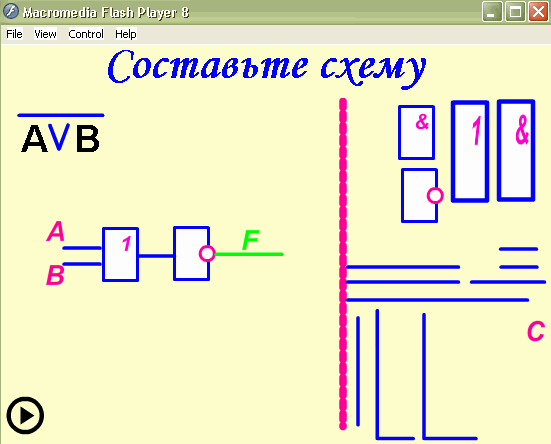
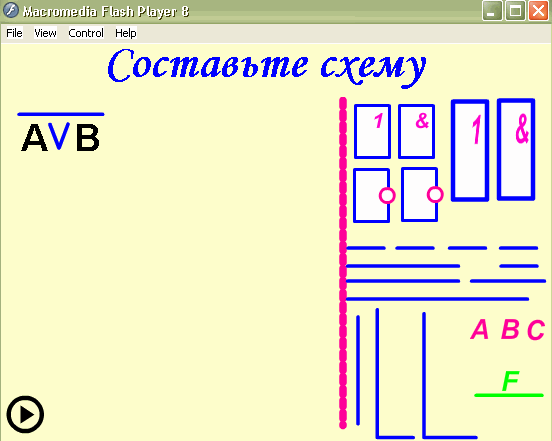
    Построить логическую схему для логического
    выражения:

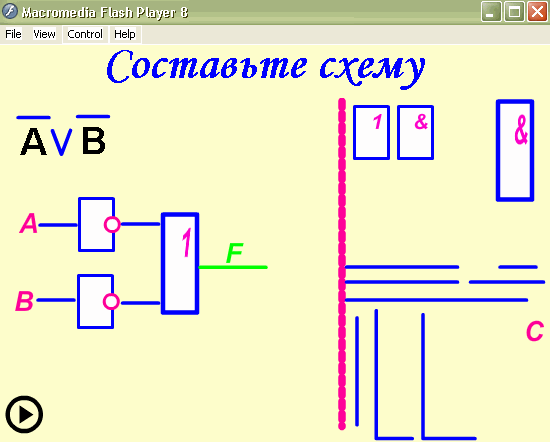
    Построить логическую схему для логического
    выражения:

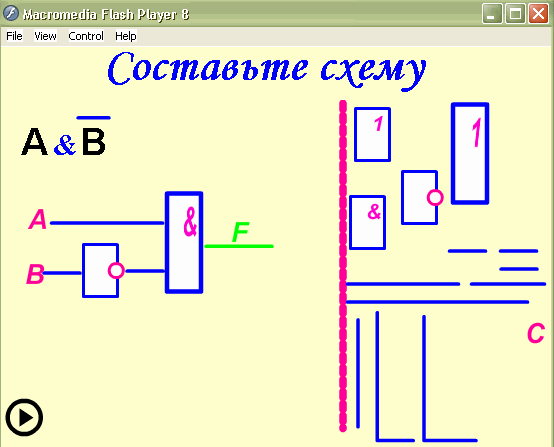
    Построить логическую схему для логического
    выражения:

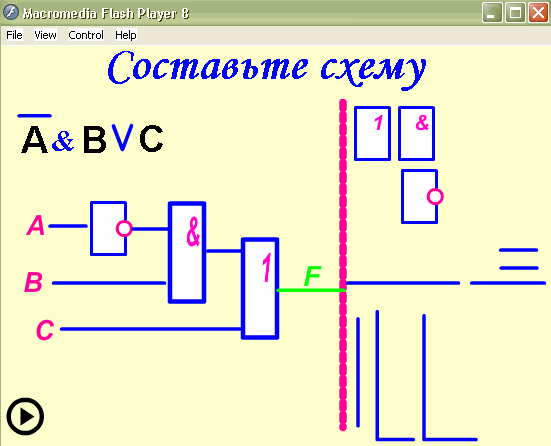
    Построить логическую схему для логического
    выражения:

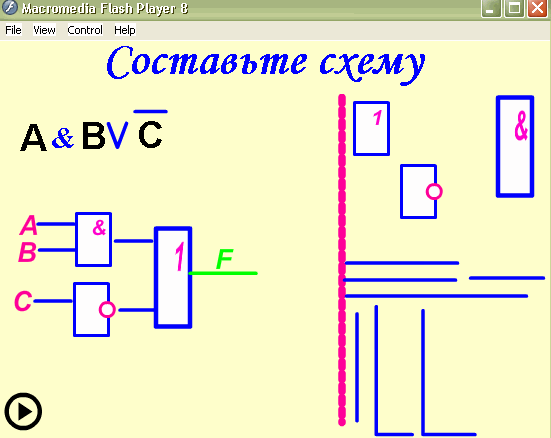
    Построить логическую схему для логического
    выражения:

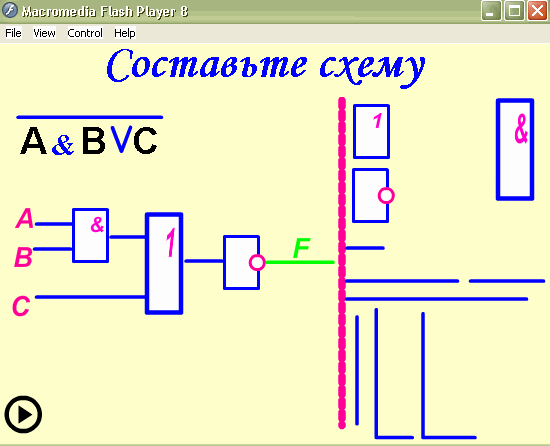
    Построить логическую схему для логического
    выражения:

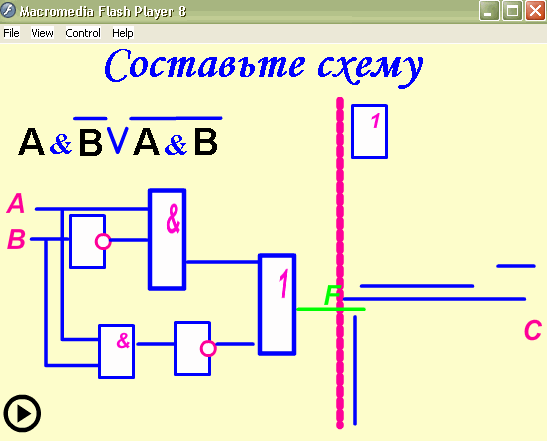
    Вычислить значение данного выражения для А=1,
    В=0.

    Ответ F=1

    III. Пропедевтика (законы логики)

    Выполним задачу обратную данной. Составим
    логическое выражение по заданной логической
    схеме:

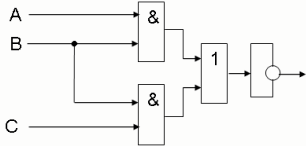
    Данное логическое выражение можно упростить.

    Операция И – логическое умножение, ИЛИ –
    сложение. Запишем выражение, заменяя знаки & и U
    на * и + соответственно.

    F= (A*B+B*С) Упростим F= (B*(А+С)), затем запишем и тогда
    логическая схема примет вид:

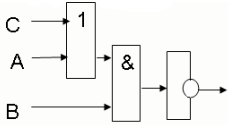
    Вывод: Логические схемы, содержащие
    минимальное количество элементов, обеспечивают
    большую скорость работы и увеличивают
    надёжность устройства.

    Алгебра логики дала конструкторам мощное
    средство разработки, анализа и
    совершенствования логических схем. Проще, и
    быстрее изучать свойства и доказывать
    правильность работы схемы с помощью выражающей
    её формулы, чем создавать реальное техническое
    устройство.

    Таким образом, цель нашего следующего урока –
    изучить законы алгебры логики.

    IV. Домашнее задание. Часть 2

    V. Практическая работа.

    Программа – тренажер “Построение логических
    схем”

    www.Kpolyakov.narod.ru Программа “Logic”,

    Спасибо за урок!

    Источник

    Добавить комментарий