Абсолютная и относительная частота
Абсолютная частота
Абсолютная частота определяет как часто определенное событие происходит в ходе эксперимента. Это всегда натуральное число между нулем и общим числом попыток.
i
Подсказка
Абсолютная частота относится только к количеству частоты определенного события.
Относительная частота
Относительная частота описывает насколько велика пропорция абсолютной частоты в общем количестве экспериментов. Она вычисляется следующим образом:
$text{Относительная частота} n_i$ $=frac{text{Абсолютная частота} f_i}{text{Количество попыток} N}$
Пример
Монету подбрасывают 10 раз. 6 раз выпадает орел и 4 раза решка. Определите абсолютную и относительную частоту.
Aбсолютная частота:
$f_{10}(орел)=6$
$f_{10}(решка)=4$
Относительная частота:
$N=10$
$n_{10}(орел)=frac{6}{10}=frac{3}{5}$
$n_{10}(решка)=frac{4}{10}=frac{2}{5}$
Абсолютная частота – всего одна статистическая мера используется в области изучение, – это количество раз, когда данные повторяются в наборе из них, значение, которое наблюдается в случайный эксперимент для каждой характеристики, время, в течение которого фазы или явления, которые наблюдая.
Его использование очень распространено в Описательная статистика, поскольку с помощью этой меры можно узнать, как наблюдения одной и той же характеристики распределены в выборке.
Следовательно, его расчет очень прост, так как он требует только подсчета того, сколько раз наблюдается характеристика или сколько раз она появляется в группе данных.
Его представление можно выразить через следующие номенклатуры: Fя, Иксяили же пя, где буквы f, x, n соответствуют частоте, а буква i обозначает i-ю итерацию проводимого эксперимента.
В этой статье вы найдете:
Расчет абсолютной частоты
Существует очень простой способ проверить точность ваших вычислений, то есть всех абсолютных частот выборочной совокупности, и это получить сумму всех из них.
Это означает, что сумма каждой из абсолютных частот выборки точно соответствует общему количеству данных того же самого, эти данные представлены как N.
В этом случае формула для расчета абсолютной частоты:
я = п
Ʃ fя = f1+ f2+ f3 +… + Fп = N
я = п
Полезность абсолютной частоты
Абсолютная частота позволяет:
- Графически изобразить частота появления каждого из выборочных данных с помощью частотных гистограмм, гистограмм, круговых диаграмм и других элементов, специально разработанных для каждого исследования.
- Узнайте больше о характеристиках выборки, совокупности и вселенной.
- Создай таблица частот как для количественных, так и для качественных переменных, которые можно расположить по порядку.
- Создавайте частотные таблицы с дискретными переменными, те, которые упорядочены от наивысшего к наименьшему, и таблицы частоты с непрерывными переменными, которые позволяют упорядочить их от низшего к высшему и сгруппировать в классы или интервалы.
- Рассчитать Накопленная абсолютная частота и Относительная частота, все важно заполнить таблицу частот, расчет других измерений статистика и разработка соответствующей графики
Примеры абсолютной частоты
Чтобы проиллюстрировать абсолютную частоту, будут рассмотрены две формы, рассматривая значения в дискретных переменных и непрерывных переменных.
Пример абсолютной частоты для дискретных переменных
Компания хочет развлечь детей своих 20 сотрудников (таким образом, N = 20) и сделать им подарок, после консультации были получены следующие данные:
2, 1, 0, 2, 4, 3, 4, 3, 2, 0, 1, 3, 2, 1, 1, 3, 0, 2, 2, 0
Табулирование данных дает следующую таблицу:
| Количество детей | Fя |
| 0 | 4 |
| 1 | 4 |
| 2 | 6 |
| 3 | 4 |
| 4 | 2 |
| Общее | 20 |
Затем можно проверить, что все данные были подсчитаны, поскольку сумма всех абсолютных частот полностью совпадает с размером выборки: Всего = 20 равно N = 20.
Таким же образом можно определить частоту количества детей каждого работника: 4 работника не имеют детей, 4 имеют только 1 ребенка, 6 рабочих имеют 2 детей, 4 имеют 3 детей и, наконец, 2 из них имеют 4 дети.
Пример абсолютной частоты для непрерывных переменных
Та же компания из предыдущего примера также должна знать рост каждого из своих сотрудников (N по-прежнему = 20), в этом случае данные будут десятичными числами, учитывая эту характеристику, удобнее работать с интервалами данных, так как иначе работа табулирование.
После выполнения соответствующих измерений были получены следующие 20 измерений:
1.67, 1.72, 1.90, 1.76, 1.72, 1.96, 1.78, 1.68, 1.87, 1.84, 1.92, 1.72, 1.71, 1.88, 1.77, 1.66, 1.73, 1.82, 1.90, 1.79
Табулирование данных дает следующую таблицу:
| Рост сотрудника | фи |
| [1.60 – 1.70) | 3 |
| [1.70 – 1.80) | 9 |
| [1.80 – 1.90) | 4 |
| [1.90 – 2.00) | 4 |
| Общее | 20 |
Символ «[» указывает, что номер, следующий за ним, включен в категорию, а символ «)» указывает, что номер, предшествующий ему, не включен в категорию.
Тогда можно проверить, что все данные, поскольку сумма всех абсолютных частот полностью совпадает с размером выборки: Total = 20 равно N = 20.
Таким же образом можно определить частоту роста рабочих: 3 сотрудника имеют рост от 1,60 до 1,70, Рост 9 сотрудников от 1,70 до 1,80, рост 4 сотрудников от 1,80 до 1,90 и, наконец, 4 сотрудника ростом от 1,90 до 2.00.
Графическое представление абсолютной частоты
Есть разные способы построить абсолютную частоту, некоторые из них:
- Диаграммы секторов: Этот график состоит из круга, разделенного на секторы, пропорциональные относительной частоте, которую он представляет.
- Гистограмма абсолютной частоты: представляет каждый Переменная в виде столбиков, его основание пропорционально соответствующей абсолютной частоте.
- Диаграммы многоугольника или прямоугольника: выполняется путем рисования линий, соединяющих самые высокие точки столбцов гистограммы абсолютной частоты.
Содержание
- Формулы
- Другие частоты
- Как получить абсолютную частоту?
- Табулирование
- Расширенная частотная таблица
- Распределение частоты
- Распределение частот для сгруппированных данных
- пример
- Упражнение решено
- Решение
- Ссылки
В Абсолютная частота Он определяется как количество раз, когда одни и те же данные повторяются в наборе наблюдений числовой переменной. Сумма всех абсолютных частот эквивалентна суммированию данных.
Когда у вас есть много значений статистической переменной, их удобно организовать соответствующим образом, чтобы извлечь информацию о ее поведении. Такую информацию дают меры центральной тенденции и меры рассеивания.
В расчетах этих показателей данные представлены через частоту, с которой они появляются во всех наблюдениях.
В следующем примере показано, насколько раскрывается абсолютная частота каждой части данных. В первой половине мая это были самые продаваемые размеры коктейльных платьев из известного магазина женской одежды:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Сколько платьев продается определенного размера, например размера 10? Владельцам интересно знать его на заказ.
Сортировка данных упрощает подсчет, всего имеется ровно 30 наблюдений, которые отсортированы от наименьшего размера к наибольшему следующим образом:
4;4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12;14; 14; 14;16;16; 18; 18
И теперь видно, что размер 10 повторяется 6 раз, поэтому его абсолютная частота равна 6. Такая же процедура проводится для определения абсолютной частоты остальных размеров.
Формулы
Абсолютная частота, обозначаемая как fя, равно тому, сколько раз определенное значение Xя находится в группе наблюдений.
Предполагая, что общее количество наблюдений равно N значениям, сумма всех абсолютных частот должна быть равна этому числу:
∑fя = f1 + f2 + f3 +… Fп = N
Другие частоты
Если каждое значение fя деленное на общее количество данных N, мы имеем относительная частота Fр значения Xя:
Fр = fя / N
Относительные частоты – это значения от 0 до 1, потому что N всегда больше любого fя, но сумма должна быть равна 1.
Умножение каждого значения f на 100р у тебя есть относительная частота в процентах, сумма которых составляет 100%:
Относительная частота в процентах = (fя / N) x 100%
Также важно накопленная частота Fя с точностью до определенного наблюдения, это сумма всех абсолютных частот до этого наблюдения включительно:
Fя = f1 + f2 + f3 +… Fя
Если накопленную частоту разделить на общее количество данных N, мы получим совокупная относительная частота, который умножается на 100 дает кумулятивная относительная частота в процентах.
Как получить абсолютную частоту?
Чтобы найти абсолютную частоту определенного значения, которое принадлежит набору данных, все они упорядочены от наименьшего к наибольшему, и подсчитывается, сколько раз появляется это значение.
В примере с размерами платьев абсолютная частота размера 4 составляет 3 платья, то есть f.1 = 3. Для размера 6 было продано 4 платья: f2 = 4. В размере 8 также было продано 4 платья, f3 = 4 и так далее.
Табулирование
Общие результаты могут быть представлены в таблице, в которой указаны абсолютные частоты каждого из них:
Очевидно, что лучше упорядочить информацию и иметь возможность получить к ней быстрый доступ, вместо того, чтобы работать с отдельными данными.
Важный: обратите внимание, что при сложении всех значений столбца fявы всегда получаете общее количество данных. Если нет, вам необходимо проверить бухгалтерию, так как есть ошибка.
Расширенная частотная таблица
Приведенную выше таблицу можно расширить, добавив другие типы частот в последовательные столбцы справа:
Распределение частоты
Частотное распределение является результатом организации данных с точки зрения их частот. При работе с большим количеством данных их удобно сгруппировать по категориям, интервалам или классам, каждая со своей соответствующей частотой: абсолютная, относительная, накопленная и процентная.
Их цель – облегчить доступ к информации, содержащейся в данных, а также правильно ее интерпретировать, что невозможно, если она представлена в произвольном порядке.
В примере с размерами данные не сгруппированы, так как это не слишком много размеров, и ими можно легко управлять и учитывать. Таким же образом можно обрабатывать и качественные переменные, но когда данных очень много, лучше всего сгруппировать их по классам.
Распределение частот для сгруппированных данных
Чтобы сгруппировать данные в классы равного размера, примите во внимание следующее:
-Размер, ширина или широта класса: разница между самым высоким значением в классе и самым низким.
Размер класса определяется путем деления ранга R на количество рассматриваемых классов. Диапазон – это разница между максимальным значением данных и самым маленьким, например:
Размер класса = Ранг / Количество классов.
-Предел класса: диапазон от нижней границы до верхней границы класса.
-Классовый знак: это середина интервала, который считается представителем класса. Он рассчитывается на основе полусуммы верхнего и нижнего пределов класса.
–Кол-во классов: Формула Стерджеса может быть использована:
Количество классов = 1 + 3,322 log N
Где N – количество классов. Поскольку это обычно десятичное число, оно округляется до следующего целого числа.
пример
Машина на большом заводе вышла из строя из-за повторяющихся сбоев. Последовательные периоды простоя в минутах указанной машины записаны ниже, всего 100 данных:
Сначала определяется количество классов:
Количество классов = 1 + 3,322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8
Размер класса = Диапазон / Количество классов = (88-21) / 8 = 8,375
Это также десятичное число, поэтому за размер класса принимается 9.
Оценка класса – это среднее значение между верхней и нижней границей класса, например, для класса [20-29) есть оценка:
Оценка класса = (29 + 20) / 2 = 24,5
Таким же образом мы ищем метки классов оставшихся интервалов.
Упражнение решено
40 молодых людей указали, что время в минутах, которое они провели в Интернете в прошлое воскресенье, было следующим, в порядке возрастания:
0; 12; 20; 35; 35; 38; 40; 45; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Предлагается построить частотное распределение этих данных.
Решение
Диапазон R набора N = 40 данных:
R = 220 – 0 = 220
Применение формулы Стерджеса для определения количества классов дает следующий результат:
Количество классов = 1 + 3 322 журнала N = 1 + 3,32 журнала 40 = 6,3
Поскольку это десятичное число, непосредственное целое число равно 7, поэтому данные сгруппированы в 7 классов. Каждый класс имеет ширину:
Размер класса = Ранг / Количество классов = 220/7 = 31,4
Близкое и округленное значение – 35, поэтому выбрана ширина класса 35.
Оценки за класс рассчитываются путем усреднения верхнего и нижнего пределов каждого интервала, например, для интервала [0,35):
Оценка класса = (0 + 35) / 2 = 17,5
Таким же образом поступаем и с другими классами.
Наконец, частоты вычисляются в соответствии с процедурой, описанной выше, в результате получается следующее распределение:
Ссылки
- Беренсон, М. 1985. Статистика для управления и экономики. Interamericana S.A.
- Деворе, Дж. 2012. Вероятность и статистика для техники и науки. 8-е. Издание. Cengage.
- Левин, Р. 1988. Статистика для администраторов. 2-й. Издание. Прентис Холл.
- Шпигель, М. 2009. Статистика. Серия Шаум. 4-й Издание. Макгроу Хилл.
- Уолпол, Р. 2007. Вероятность и статистика для инженерии и науки. Пирсон.
Загрузить PDF
Загрузить PDF
В статистике абсолютная частота показывает, какое количество раз конкретное значение появляется в наборе данных. В отличие от нее, накопительная частота показывает сумму (или нарастающий итог) всех частот вплоть до текущей точки в наборе данных. Не беспокойтесь, если поначалу это кажется не совсем понятным: возьмите ручку и лист бумаги, и вы быстро во всем разберетесь!
-
1
Отсортируйте набор данных. «Набор данных» — это просто изучаемый вами список числовых значений. Отсортируйте его так, чтобы числа располагались по возрастанию.[1]
- Пример: предположим, список чисел представляет собой количество книг, которые каждый студент прочитал за последний месяц. После сортировки у вас получился следующий набор чисел: 3, 3, 5, 6, 6, 6, 8.
-
2
Посчитайте абсолютную частоту каждой величины. Частота значения показывает, сколько раз данное значение появляется в наборе данных. Это число можно называть абсолютной частотой, чтобы не путать его с накопительной частотой. Наиболее простой способ заключается в том, чтобы составить таблицу. Вверху левой колонки напишите «Значение» (или укажите, что измеряется данными числами). Вверху второй колонки напишите «Частота». Заполните таблицу для всех значений из списка.[2]
- Пример: вверху левой колонки напишите «Количество книг», а вверху правой колонки — «Частота».
- Во второй строке напишите первое количество прочитанных книг, то есть число 3.
- Посчитайте, сколько раз число 3 встречается в списке данных. В списке есть два числа 3, поэтому во второй строке колонки «Частота» запишите цифру 2.
- Повторите данную процедуру для всех значений списка, пока не заполните таблицу:
- 3 | Ч = 2
- 5 | Ч = 1
- 6 | Ч = 3
- 8 | Ч = 1
-
3
Найдите накопительную частоту для первого значения. Накопительная частота отвечает на вопрос «сколько раз встречается в списке данное значение или меньшая величина?». Всегда начинайте с наименьшего значения в наборе данных. Поскольку в нашем примере нет меньших значений, для данной величины накопительная частота равна абсолютной.[3]
-
Пример: наименьшее значение равно 3. Количество прочитавших 3 книги студентов составляет 2. Никто из студентов не прочитал меньшее число книг, поэтому накопительная частота равна 3. Впишите это значение в третью колонку таблицы:
- 3 | F = 2 | НЧ=2
-
Пример: наименьшее значение равно 3. Количество прочитавших 3 книги студентов составляет 2. Никто из студентов не прочитал меньшее число книг, поэтому накопительная частота равна 3. Впишите это значение в третью колонку таблицы:
-
4
Найдите накопительную частоту для следующей величины. Перейдите к следующему значению списка. Выше мы определили, сколько раз встречается в списке наименьшая величина. Чтобы определить накопительную частоту для второго значения списка, необходимо прибавить его абсолютную частоту к накопительной частоте предыдущего значения. Иными словами, следует взять последнюю накопительную частоту и прибавить к ней абсолютную частоту данной величины.[4]
-
Пример:
- 3 | Ч = 2 | НЧ = 2
- 5 | Ч = 1 | НЧ = 2+1 = 3
-
Пример:
-
5
Повторите процедуру для остальных значений. Постепенно продвигайтесь к более высоким числам. При этом каждый раз прибавляйте текущую абсолютную частоту к последней накопительной частоте.
-
Пример:
- 3 | Ч = 2 | НЧ = 2
- 5 | Ч = 1 | НЧ = 2 + 1 = 3
- 6 | Ч = 3 | НЧ = 3 + 3 = 6
- 8 | Ч = 1 | НЧ = 6 + 1 = 7
-
Пример:
-
6
Проверьте полученные результаты. В итоге вы сложите абсолютные частоты всех значений списка. Конечная накопительная частота должна соответствовать числу значений в списке. Есть два способа проверить, так ли это:
- Сложите абсолютные частоты всех значений: 2 + 1 + 3 + 1 = 7, в результате у вас получится накопительная частота.
- Посчитайте число значений в наборе данных. В нашем примере список имел следующий вид: 3, 3, 5, 6, 6, 6, 8. В этом списке семь величин, и итоговая накопительная частота также равна 7.
Реклама
-
1
Поймите разницу между дискретными и непрерывными данными. Дискретные данные можно посчитать, они не дробятся на более мелкие составляющие. Непрерывные данные часто не поддаются конечному счету, между двумя произвольными величинами обязательно найдутся другие возможные значения. Ниже приведена пара примеров:[5]
- Количество собак является дискретным множеством. Нет такого понятия, как половина собаки.
- Глубина снега представляет собой непрерывное множество. Она возрастает постепенно и непрерывно, а не на дискретные величины. Если вы измерите глубину снега в сантиметрах, то точное значение может оказаться, например, 20,6 сантиметра.
-
2
Разбейте непрерывные данные на интервалы. Наборы непрерывных данных часто имеют большое количество значений. Если попробовать представить такой набор описанным выше методом, таблица получится слишком длинной и малопонятной. В этом случае удобно разбить данные на отдельные интервалы. Эти интервалы должны быть одинаковой длины (например, 0—10, 11–20, 21–30 и так далее) независимо от того, сколько значений попадает в каждый интервал. Ниже приведена возможная таблица для непрерывного набора данных:[6]
- Набор данных: 233, 259, 277, 278, 289, 301, 303
- Таблица (в первой колонке интервал значений, во второй частота, в третьей накопительная частота):
- 200–250 | 1 | 1
- 251–300 | 4 | 1 + 4 = 5
- 301–350 | 2 | 5 + 2 = 7
-
3
Постройте линейный график. После того как вы рассчитаете накопительную частоту, возьмите лист миллиметровой бумаги. Отложите по горизонтальной оси (ось x) значения из набора данных, а по вертикальной (ось y) — накопительную частоту, и постройте график. Это значительно облегчит последующие вычисления.[7]
- Например, если набор данных включает числа от 1 до 8, отложите по горизонтальной оси 8 делений. Над каждым делением отметьте точкой соответствующее ему значение накопительной частоты. Соедините получившиеся точки линией.
- Если какое-либо значение не встречается, его абсолютная частота составляет 0. В этом случае прибавьте 0 к последней величине накопительной частоты и поставьте точку на том же уровне, что и в предыдущий раз.
- Поскольку накопительная частота всегда растет с продвижением к большим значениям, с перемещением вправо линия будет оставаться на той же самой высоте или подниматься. Если в какой-то точке линия опустилась вниз, значит, вы допустили ошибку (например, вместо накопительной частоты взяли абсолютную).
-
4
Найдите по графику медиану. Медиана — это значение, расположенное точно посередине набора данных. Половина значений находится выше медианы, а вторая половина расположена ниже нее. Медиану можно найти по графику следующим образом:
- Посмотрите на последнее значение в самом правом конце графика. Для него величина y соответствует суммарной накопительной частоте, которая равна общему числу точек в наборе данных. Предположим, эта величина равна 16.
- Умножьте эту величину на ½ и найдите соответствующее значение на оси y. В нашем примере получится 8. Найдите число 8 на оси y.
- Найдите точку на линии графика, значение y которой соответствует найденной величине. Проведите от цифры 8 на оси y горизонтальную прямую и определите точку ее пересечения с линией графика. Именно эта точка делит набор данных точно пополам.
- Найдите значение x в данной точке. Проведите из точки вертикальную прямую до пересечения с осью x. Точка пересечения определит медиану для изучаемого набора данных. Например, если получилось 65, значит половина данных расположена ниже 65, а вторая половина лежит выше этого значения.
-
5
Найдите по графику квартили. Квартили делят набор данных на четыре части. Эта процедура очень похожа на определение медианы. Единственное различие заключается в нахождении значений y:
- Чтобы определить величину y для нижнего квартиля, умножьте максимальное значение накопительной частоты на ¼. В результате вы получите значение x, ниже которого будет лежать ровно ¼ всех данных.
- Чтобы найти величину y для верхнего квартиля, умножьте максимальное значение накопительной частоты на ¾. В результате вы получите значение x, ниже которого будет лежать ¾, а выше — ¼ всех данных.
Реклама
Советы
- С помощью интервалов можно представлять любые большие, в том числе и дискретные наборы данных.
Реклама
Об этой статье
Эту страницу просматривали 72 860 раз.
Была ли эта статья полезной?
From Wikipedia, the free encyclopedia
In statistics, the frequency (or absolute frequency) of an event 

Types[edit]
The cumulative frequency is the total of the absolute frequencies of all events at or below a certain point in an ordered list of events.[1]: 17–19
The relative frequency (or empirical probability) of an event is the absolute frequency normalized by the total number of events:
The values of 

In the case when 

Depicting frequency distributions[edit]
A frequency distribution shows us a summarized grouping of data divided into mutually exclusive classes and the number of occurrences in a class. It is a way of showing unorganized data notably to show results of an election, income of people for a certain region, sales of a product within a certain period, student loan amounts of graduates, etc. Some of the graphs that can be used with frequency distributions are histograms, line charts, bar charts and pie charts. Frequency distributions are used for both qualitative and quantitative data.
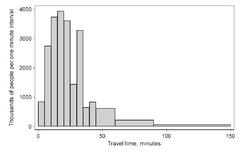
Histogram of travel time (to work), US 2000 census.
Horizontal 3D bar chart
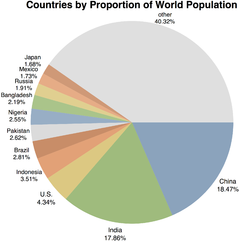
Pie chart of world population by country
Different ways of depicting frequency distributions
Construction[edit]
- Decide the number of classes. Too many classes or too few classes might not reveal the basic shape of the data set, also it will be difficult to interpret such frequency distribution. The ideal number of classes may be determined or estimated by formula:
(log base 10), or by the square-root choice formula
where n is the total number of observations in the data. (The latter will be much too large for large data sets such as population statistics.) However, these formulas are not a hard rule and the resulting number of classes determined by formula may not always be exactly suitable with the data being dealt with.
- Calculate the range of the data (Range = Max – Min) by finding the minimum and maximum data values. Range will be used to determine the class interval or class width.
- Decide the width of the classes, denoted by h and obtained by
(assuming the class intervals are the same for all classes).
Generally the class interval or class width is the same for all classes. The classes all taken together must cover at least the distance from the lowest value (minimum) in the data to the highest (maximum) value. Equal class intervals are preferred in frequency distribution, while unequal class intervals (for example logarithmic intervals) may be necessary in certain situations to produce a good spread of observations between the classes and avoid a large number of empty, or almost empty classes.[2]
- Decide the individual class limits and select a suitable starting point of the first class which is arbitrary; it may be less than or equal to the minimum value. Usually it is started before the minimum value in such a way that the midpoint (the average of lower and upper class limits of the first class) is properly[clarification needed] placed.
- Take an observation and mark a vertical bar (|) for a class it belongs. A running tally is kept till the last observation.
- Find the frequencies, relative frequency, cumulative frequency etc. as required.
The following are some commonly used methods of depicting frequency:[3]
Histograms[edit]
A histogram is a representation of tabulated frequencies, shown as adjacent rectangles or squares (in some of situations), erected over discrete intervals (bins), with an area proportional to the frequency of the observations in the interval. The height of a rectangle is also equal to the frequency density of the interval, i.e., the frequency divided by the width of the interval. The total area of the histogram is equal to the number of data. A histogram may also be normalized displaying relative frequencies. It then shows the proportion of cases that fall into each of several categories, with the total area equaling 1. The categories are usually specified as consecutive, non-overlapping intervals of a variable. The categories (intervals) must be adjacent, and often are chosen to be of the same size.[4] The rectangles of a histogram are drawn so that they touch each other to indicate that the original variable is continuous.[5]
Bar graphs[edit]
A bar chart or bar graph is a chart with rectangular bars with lengths proportional to the values that they represent. The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column bar chart.
Frequency distribution table[edit]
A frequency distribution table is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of values in the sample.
This is an example of a univariate (=single variable) frequency table. The frequency of each response to a survey question is depicted.
| Rank | Degree of agreement | Number |
|---|---|---|
| 1 | Strongly agree | 22 |
| 2 | Agree somewhat | 30 |
| 3 | Not sure | 20 |
| 4 | Disagree somewhat | 15 |
| 5 | Strongly disagree | 15 |
A different tabulation scheme aggregates values into bins such that each bin encompasses a range of values. For example, the heights of the students in a class could be organized into the following frequency table.
| Height range | Number of students | Cumulative number |
|---|---|---|
| less than 5.0 feet | 25 | 25 |
| 5.0–5.5 feet | 35 | 60 |
| 5.5–6.0 feet | 20 | 80 |
| 6.0–6.5 feet | 20 | 100 |
Joint frequency distributions[edit]
Bivariate joint frequency distributions are often presented as (two-way) contingency tables:
| Dance | Sports | TV | Total | |
|---|---|---|---|---|
| Men | 2 | 10 | 8 | 20 |
| Women | 16 | 6 | 8 | 30 |
| Total | 18 | 16 | 16 | 50 |
The total row and total column report the marginal frequencies or marginal distribution, while the body of the table reports the joint frequencies.[6]
Interpretation[edit]
Under the frequency interpretation of probability, it is assumed that as the length of a series of trials increases without bound, the fraction of experiments in which a given event occurs will approach a fixed value, known as the limiting relative frequency.[7][8]
This interpretation is often contrasted with Bayesian probability. In fact, the term ‘frequentist’ was first used by M. G. Kendall in 1949, to contrast with Bayesians, whom he called “non-frequentists”.[9][10] He observed
- 3….we may broadly distinguish two main attitudes. One takes probability as ‘a degree of rational belief’, or some similar idea…the second defines probability in terms of frequencies of occurrence of events, or by relative proportions in ‘populations’ or ‘collectives’; (p. 101)
- …
- 12. It might be thought that the differences between the frequentists and the non-frequentists (if I may call them such) are largely due to the differences of the domains which they purport to cover. (p. 104)
- …
- I assert that this is not so … The essential distinction between the frequentists and the non-frequentists is, I think, that the former, in an effort to avoid anything savouring of matters of opinion, seek to define probability in terms of the objective properties of a population, real or hypothetical, whereas the latter do not. [emphasis in original]
Applications[edit]
Managing and operating on frequency tabulated data is much simpler than operation on raw data. There are simple algorithms to calculate median, mean, standard deviation etc. from these tables.
Statistical hypothesis testing is founded on the assessment of differences and similarities between frequency distributions. This assessment involves measures of central tendency or averages, such as the mean and median, and measures of variability or statistical dispersion, such as the standard deviation or variance.
A frequency distribution is said to be skewed when its mean and median are significantly different, or more generally when it is asymmetric. The kurtosis of a frequency distribution is a measure of the proportion of extreme values (outliers), which appear at either end of the histogram. If the distribution is more outlier-prone than the normal distribution it is said to be leptokurtic; if less outlier-prone it is said to be platykurtic.
Letter frequency distributions are also used in frequency analysis to crack ciphers, and are used to compare the relative frequencies of letters in different languages and other languages are often used like Greek, Latin, etc.
See also[edit]
- Aperiodic frequency
- Count data
- Cross tabulation
- Cumulative distribution function
- Cumulative frequency analysis
- Empirical distribution function
- Law of large numbers
- Multiset multiplicity as frequency analog
- Probability density function
- Probability interpretations
- Statistical regularity
- Word frequency
References[edit]
- ^ a b Kenney, J. F.; Keeping, E. S. (1962). Mathematics of Statistics, Part 1 (3rd ed.). Princeton, NJ: Van Nostrand Reinhold.
- ^ Manikandan, S (1 January 2011). “Frequency distribution”. Journal of Pharmacology & Pharmacotherapeutics. 2 (1): 54–55. doi:10.4103/0976-500X.77120. ISSN 0976-500X. PMC 3117575. PMID 21701652.
- ^ Carlson, K. and Winquist, J. (2014) An Introduction to Statistics. SAGE Publications, Inc. Chapter 1: Introduction to Statistics and Frequency Distributions
- ^ Howitt, D. and Cramer, D. (2008) Statistics in Psychology. Prentice Hall
- ^ Charles Stangor (2011) “Research Methods For The Behavioral Sciences”. Wadsworth, Cengage Learning. ISBN 9780840031976.
- ^ Stat Trek, Statistics and Probability Glossary, s.v. Joint frequency
- ^ von Mises, Richard (1939) Probability, Statistics, and Truth (in German) (English translation, 1981: Dover Publications; 2 Revised edition. ISBN 0486242145) (p.14)
- ^ The Frequency theory Chapter 5; discussed in Donald Gilles, Philosophical theories of probability (2000), Psychology Press. ISBN 9780415182751 , p. 88.
- ^ Earliest Known Uses of Some of the Words of Probability & Statistics
- ^ Kendall, Maurice George (1949). “On the Reconciliation of Theories of Probability”. Biometrika. Biometrika Trust. 36 (1/2): 101–116. doi:10.1093/biomet/36.1-2.101. JSTOR 2332534.