Абсолютная погрешность мощности как найти

Лабораторная работа № 1.

Расчет погрешностей емкости с помощью коэффициента Стьюдента.

Расчет погрешности измерения мощности и сопротивления

Цели занятия:

1. Общеобразовательная – Умение решать задачи по теме погрешности.

2. Развивающая – Углубление знаний .

3. Воспитательная – Проверить сформированность качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А (1)

Действительная относительная погрешность представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:

(2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,

т .е. к показанию прибора

(3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора

(4)

Для приборов с двухсторонней шкалой А_макс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального значения, то А_макс равно разности между конечным и начальным значениями шкалы.

Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как

,

где а₁, а₂, …, а_n – результаты отдельных измерений;

n – число измерений.

Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:

где Р₁ = а₁ – А_ср; Р₂ = а₂ – А_ср; Р_n = а_n – А_ср.

Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента t_n, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:

А = Аср t_n

Контрольное задание

Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):

• Действительное значение измеряемой емкости;

• Среднюю квадратическую и максимальную погрешности однократного измерения;

• Доверительный интервал для результата измерения при доверительной вероятности Р_д (табл.3).

• Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения С_ср (таб.1, таб.2).

Таблица 1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица 2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание. Количество и номера наблюдений значений емкости для каждого варианта определяются данными таблицы 1 и 2, например для варианта 1 следует взять результаты измерений 1-3 табл.2.

Указания к решению

1. Для удобства выполнения и проверки расчетов по заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица 3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

1. Далее определить среднеквадратическую погрешность :

1. По таблице (4) определить коэффициент Стьюдента.

2. В конце решения следует записать окончательный (с учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание 2._. Используя формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей измерения мощности и сопротивления. Расчет выполняется в соответствии с вариантами указанными в задании.

Задача 1. Для определения сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены напряжение и ток. Зная основные параметры измерительных приборов (амперметра и вольтметра), определить ошибку косвенных измерений мощности и сопротивления.

Пример. Определить абсолютную и относительную погрешности измерения мощности, выделяемой на резисторе, если известны показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А = 1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем мощность Р = U * I ( Вт)

2. Абсолютная ошибка измерения напряжения, В

1. Абсолютная ошибка измерения тока, _М А

1. В соответствии с таблицей абсолютная ошибка измерения мощности, Вт

Относительная ошибка

1. Формула для сопротивления R = U / I

2. 

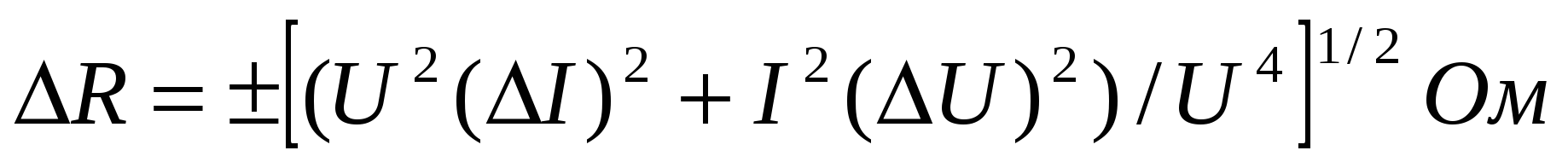
3. Относительная погрешность

Примечание:

1. Для вычисления погрешностей измерения мощности используются формулы 1,2,3,4,

2. Для вычисления погрешностей измерения сопротивления используются формулы 2,3,5,6,7.

Формулы для выполнения контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

3 Номинальная относительная погрешность

4.Приведенная относительная погрешность

1. Сопротивление шунта

R_Ш = R_А / Р-1 (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1) (Ом)

1. Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

1. Напряжение сети:

U_C = K_U* U (В)

1. Активная мощность сети:

P_C = K_i * K_U *P (Вт)

1. Реактивная мощность сети :

Q = U*I* sinφ (Вар)

1. Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление сети :

Z_C = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C / S_C

1. Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

1. Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

1. Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%

Лекция №3

Основные понятия
теории погрешностей.

Классификация погрешностей.

Качество средств и результатов измерений
принято характеризовать, указывая их
погрешности. Введение понятия “погрешность”
требует определения и четкого разграничения
трех понятий: истинного и действительного
значений измеряемой физической величины
и результата измерения. Истинное
значение физической величины – это
значение, идеальным образом отражающее
свойство данного объекта как в
количественном, так и в качественном
отношении. Оно не зависит от средств
нашего познания и является той абсолютной
истиной, к которой мы стремимся, пытаясь
выразить ее в виде числовых значений.
На практике это абстрактное понятие
приходится заменять понятием
“действительное значение”.
Действительное значение физической
величины – значение, найденное
экспериментально и настолько приближающееся
к истинному, что для данной цели оно
может быть использовано вместо него.
Результат измерения представляет
собой приближенную оценку истинного
значения величины, найденную путем
измерения.

Понятие
“погрешность” – одно из центральных
в метрологии, где используются понятия
“погрешность результата измерения”
и “погрешность средства измерения”.
Погрешность результата измерения
– это разница между результатом измерения
X и истинным (или действительным) значением
Q измеряемой величины:

Она
указывает границы неопределенности
значения измеряемой величины. Погрешность
средства измерения – разность между
показанием СИ и истинным (действительным)
значением измеряемой ФВ. Она характеризует
точность результатов измерений,
проводимых данным средством.

Эти
два понятия во многом близки друг к
другу и классифицируются по одинаковым
признакам.

По
характеру проявления погрешности
делятся на случайные, систематические,
прогрессирующие и грубые (промахи).

Заметим,
что из приведенного выше определения
погрешности никак не следует, что она
должна состоять из каких-либо составляющих.
Деление погрешности на составляющие
было введено для удобства обработки
результатов измерений исходя из характера
их проявления. В процессе формирования
метрологии было обнаружено, что
погрешность не является постоянной
величиной. Путем элементарного анализа
установлено, что одна ее часть проявляется
как постоянная величина, а другая –
изменяется непредсказуемо. Эти части
назвали систематической и случайной
погрешностями.

Случайная
погрешность – составляющая погрешности
измерения, изменяющаяся случайным
образом (по знаку и значению) в серии
повторных измерений одного и того же
размера ФВ, проведенных с одинаковой
тщательностью в одних и тех же условиях.
В появлении таких погрешностей (рис. 1)
не наблюдается какой-либо закономерности,
они обнаруживаются при повторных
измерениях одной и той же величины в
виде некоторого разброса получаемых
результатов. Случайные погрешности
неизбежны, неустранимы и всегда
присутствуют в результате измерения.
Описание случайных погрешностей возможно
только на основе теории случайных
процессов и математической статистики.

Рис. 1 Изменение случайной погрешности
от изменения к измерению

В
отличие от систематических случайные
погрешности нельзя исключить из
результатов измерений путем введения
поправки, однако их можно существенно
уменьшить путем увеличения числа
наблюдений. Поэтому для получения
результата, минимально отличающегося
от истинного значения измеряемой
величины, проводят многократные измерения
требуемой величины с последующей
математической обработкой экспериментальных
данных.

Большое
значение имеет изучение случайной
погрешности как функции номера наблюдения
i или соответствующего ему момента
времени t_i проведения
измерений, т.е.
_i=(t_i)
Отдельные значения погрешности являются
значениями функции
(t),
следовательно, погрешность измерения
есть случайная функция времени. При
проведении многократных измерений
получается одна реализация такой
функции. Именно такая реализация показана
на рис. 1. Повтор серии измерений даст
нам другую реализацию этой функции,
отличающуюся от первой, и т. д. Погрешность,
соответствующая каждому i-му измерению,
является сечением случайной функции
(t).
В каждом сечении данной функции можно
найти среднее значение, вокруг которого
группируются погрешности в различных
реализациях. Если через полученные
таким образом средние значения провести
плавную кривую, то она будет характеризовать
общую тенденцию изменения погрешности
во времени.

Систематическая
погрешность – составляющая погрешности
измерения, остающаяся постоянной или
закономерно меняющаяся при повторных
измерениях одной и той же ФВ. Постоянная
и переменная систематические погрешности
показаны на рис. 2. Их отличительный
признак заключается в том, что они могут
быть предсказаны, обнаружены и благодаря
этому почти полностью устранены введением
соответствующей поправки.

Следует
отметить, что в последнее время,
приведенное выше определение
систематической погрешности, подвергается
обоснованной критике, особенно в связи
с техническими измерениями. Весьма
аргументировано предлагается считать
систематическую погрешность специфической,
“вырожденной” случайной величиной,
обладающей некоторыми, но не всеми
свойствами случайной величины, изучаемой
в теории вероятностей и математической
статистике. Ее свойства, которые
необходимо учитывать при объединении
составляющих погрешности, отражаются
теми же характеристиками, что и свойства
“настоящих” случайных величин:
дисперсией (средним квадратическим
отклонением) и коэффициентом взаимной
корреляции.

Рис. 2 Постоянная и переменная
систематические погрешности

Грубая погрешность (промах) – это
случайная погрешность результата
отдельного наблюдения, входящего в ряд
измерений, которая для данных условий
резко отличается от остальных результатов
этого ряда. Они, как правило, возникают
из-за ошибок или неправильных действий
оператора. Возможной причиной возникновения
промахов также могут быть резкие
кратковременные изменения условий
проведения измерений. Если промахи
обнаруживаются в процессе измерений,
то результаты, их содержащие, отбрасывают.
Однако чаще всего промахи выявляют
только при окончательной обработке
результатов измерений с помощью
специальных критериев.

По способу выражения различают
абсолютную, относительную и приведенную
погрешности.

Абсолютная погрешность описывается
формулой (1) и выражается в единицах
измеряемой величины.

(1)

Относительная погрешность – это
отношение абсолютной погрешности
измерения к истинному значению измеряемой
величины:

(2)

Приведенная погрешность – это
относительная погрешность, в которой
абсолютная погрешность СИ отнесена к
условно принятому значению X_N,
постоянному во всем диапазоне измерений
или его части:

(3)

Условно принятое значение X_N
называют нормирующим. Чаще всего
за него принимают верхний предел
измерений данного СИ.

В зависимости от места возникновения
различают инструментальные, методические
и субъективные погрешности.

Инструментальная погрешность
обусловлена погрешностью применяемого
СИ. Иногда эту погрешность называют
аппаратурной.

Методическая погрешность измерения
обусловлена:

• отличием принятой модели объекта
  измерения от модели, адекватно описывающей
  его свойство, которое определяется
  путем измерения;

• влиянием способов применения СИ;

• влиянием алгоритмов (формул), по которым
  производятся вычисления результатов
  измерений;

• влиянием других факторов, не связанных
  со свойствами используемых средств
  измерения.

Отличительной особенностью методических
погрешностей является то, что они не
могут быть указаны в нормативно-технической
документации на используемое СИ,
поскольку от него не зависят, а должны
определяться оператором в каждом
конкретном случае. В связи с этим оператор
должен четко различать фактически
измеряемую им величину и величину,
подлежащую измерению.

Пример. Определить в общем виде
методическую погрешность измерения
мощности постоянного тока косвенным
методом по показаниям амперметра и
вольтметра при двух схемах их включения,
показанных на рис. 3. Внутренние
сопротивления амперметра и вольтметра
соответственно равны R_A
и R_V.

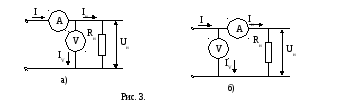
При использовании схемы на рис. 3, а
измеренное значение мощности постоянного
тока:

,

где I – ток, измеряемый
амперметром; I_н –
ток, протекающий через сопротивление
нагрузки R_н; I_V
– ток, протекающий через вольтметр; P_н
– действительное значение измеряемой
мощности.

Абсолютная методическая погрешность
измерения мощности по схеме на рис 3, а
составляет

.

Относительная методическая погрешность
в этом случае рассчитывается по формуле:

.

Аналогично для схемы на рис. 3, б измеряемое
значение мощности:

,

где U – напряжение,
измеряемое вольтметром; U_А
– падение напряжения на амперметре.
При этом абсолютная методическая
погрешность измерения мощности:

.

Относительная методическая погрешность
в данном случае рассчитывается по
формуле:

.

Анализ формул, описывающих относительные
погрешности, показывает, что первую
схему (рис. 3, а) целесообразно использовать
для измерения низкоомных нагрузок, так
как при

погрешность также стремится к нулю. По
аналогичным причинам вторую схему (рис.
3, б) выгоднее применять для измерения
мощности на высоомных нагрузках. Граница
между высоомными и низкоомными нагрузками
определяется в рассматриваемом случае
параметрами используемых средств
измерений. Действительно, из равенства
методических погрешностей для каждой
из схем получаем:

.

Пусть R_А=0,002 Ом, а
R_V=1000
Ом, тогда R_н=1,41 Ом.
В этом случае методическая погрешность
измерения мощности составит 0,14%.

Субъективная (личная) погрешность
измерения обусловлена погрешностью
отсчета оператором показаний по шкалам
СИ. Характеристики личной погрешности
определяют на основе нормированной
номинальной цены деления шкалы
измерительного прибора с учетом
способности “среднего оператора” к
интерполяции в пределах деления шкалы.

Пример. Пусть цена деления равномерной
шкалы равна X_д единиц
измеряемой физической величины, длина
деления равна L_д
мм. Определить наибольшее значение
личной погрешности.

При условии, что средний оператор может
интерполировать в пределах деления
шагами по 0,2 деления, т. е. по 0,2L_д,
наибольшее значение личной погрешности:

.

По зависимости абсолютной погрешности
от значений измеряемой величины
различают погрешности (рис. 4):

• аддитивные
  ,
  не зависящие от измеряемой величины
  (рис. 4, а);

• мультипликативные
  ,
  которые прямо пропорциональны измеряемой
  величине (рис. 4, б);

• нелинейные
  ,
  имеющие нелинейную зависимость от
  измеряемой величины (рис 4, в).

Эти погрешности применяют в основном
для описания метрологических характеристик
СИ.

Примеры аддитивных погрешностей – от
постоянного груза на чашке весов, от
неточной установки на нуль стрелки
прибора перед измерением, от термо-ЭДС
в цепях постоянного тока.

Причинами возникновения мультипликативных
погрешностей могут быть: изменение
коэффициента усиления усилителя,
изменение жесткости мембраны датчика
манометра или пружины прибора, изменение
опорного напряжения в цифровом вольтметре.

По влиянию внешних условий различают
основную и дополнительную погрешности
СИ.

Основной называется погрешность
СИ, определяемая в нормальных условиях
его применения. Для каждого СИ в
нормативно-технических документах
оговариваются условия эксплуатации –
совокупность влияющих величин (температура
окружающей среды, влажность, давление,
напряжение и частота питающей сети и
др.), при которых нормируется его
погрешность.

Дополнительной называется погрешность
СИ, возникающая вследствие отклонения
какой-либо из влияющих величин.

В зависимости от влияния характера
изменения измеряемых величин
погрешности СИ делят на статические и
динамические.

Статическая погрешность – это
погрешность СИ применяемого для измерения
ФВ, принимаемой за неизменную.

Динамической называется погрешность
СИ, возникающая дополнительно при
измерении переменной ФВ и обусловленная
несоответствием его реакции на скорость
(частоту) изменения измеряемого сигнала.

Правила округления и записи результатов
измерений.

Эмпирически были установлены следующие
правила округления рассчитанного
значения погрешности и полученного
результата измерения.

1. Погрешность результата измерения
   указывается двумя значащими цифрами,
   если первая из них равна 1 или 2, и одной
   – если первая цифра равна 3 или более.
   Пример: 0,00012; 0,0004.

2. Результат измерения округляется до
   того же десятичного знака, которым
   оканчивается округленное значение
   абсолютной погрешности. Если десятичная
   дробь в числовом значении результата
   измерений оканчивается нулями, то нули
   отбрасываются до того разряда, который
   соответствует разряду числового
   значения погрешности. Пример:
   результат 1,072000, погрешность ±0,0001.
   Результат округляют до 1,0720.

3. Если цифра старшего из отбрасываемых
   разрядов меньше 5, то остальные цифры
   числа не изменяются. Лишние цифры в
   целых числах заменяются нулями, а в
   десятичных дробях отбрасываются.
   Пример: 4567,343 округляют до 4567,34.

4. Если цифра старшего из отбрасываемых
   разрядов больше или равна 5, но за ней
   следуют отличные от нуля цифры, то
   последнюю оставляемую цифру увеличивают
   на единицу. Пример: 6783,6 округляют
   до 6784; 12,34501 до 12,35.

5. Если отбрасываемая цифра равна 5, а
   следующие за ней нули, то последнюю
   сохраняемую цифру не изменяют, если
   она четная, и увеличивают на единицу,
   если она нечетная. Пример: 1234,50
   округляют до 1234; 8765,50 – до 8766.

6. Округление производится лишь в
   окончательном ответе, а все предварительные
   вычисления проводят с одним-двумя
   лишними знаками. Пример: результат
   1,072000, погрешность ±0,0001. Вычисления
   производят с 1,07200.

Соседние файлы в папке Лекции по метрологии

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задача 1

Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности N_B
с пределом измерений U_m, ток I амперметром класса точности N_a
с пределом измерений I_m. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.

Дано:

Найти:

Решение:

1)  Найдем
мощность, потребляемую приемником

2)  Класс
точности определяет приведенную погрешность

3)  Найдем
абсолютную погрешность измерения тока и напряжения

,

.

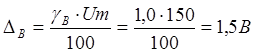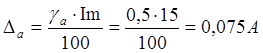4)  Найдем
абсолютную погрешность измерения мощности при косвенном измерении

5)  Найдем
относительную погрешность измерения мощности

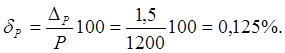
6)  Доверительный
интервал результата измерения с вероятностью .

Задача 2

Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.

Дано:

Найти:

Решение:

1)  Определим
среднее арифметическое результатов измерения

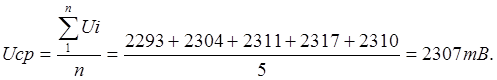
2)  Определяем
среднее квадратичное результатов измерения

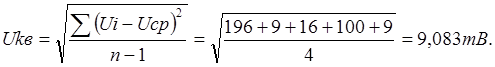
3)  Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется     , где

– коэффициент Стьюдента,

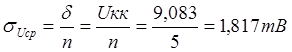 – среднее квадратичное отклонение
результата измерения.

4)  Находим
доверительный интервал

5)  Результат
измерения

Задача 3

Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление R_O  и рассчитана на предельный длительный ток I_O, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений I_m
и вольтметр с пределом измерений U_m?

Дано:

Найти: ,

Решение:

1)  Расчет
измерительной цепи амперметра

1.1 
Определяем коэффициент расширения пределов измерения по току

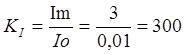
1.2     Определяем сопротивление
шунта

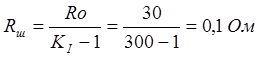
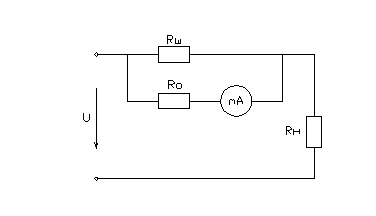
1.3 
 Схема измерительной цепи

2)  Расчет
цепи вольтметра

2.1 Определяем коэффициент
расширения пределов измерения по напряжению

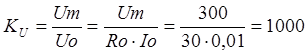
2.2  Определяем добавочное
сопротивление

2.3 
Схема включения

Задача 4

Определить
цену деления измерительных приборов:

1) амперметра, имеющего на шкале n_a делений и предел измерения I_m;

2)вольтметра, имеющего n_в делений шкалы и предел измерения U_m;

3) ваттметра, имеющего n_ВТ делений шкалы и пределы измерений по току I_{m ВТ} и напряжению U_m
ВТ.

Дано:

Найти:

Решение:

1) Цена деления
амперметра

2) Цена деления
вольтметра

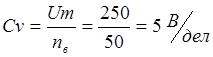
3) Цена
деления ваттметра

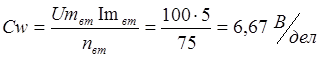
Задача 5

У вольтметра и
амперметра с пределами измерений U_m и I_m, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U₂ и I₂.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов N_a и N_в и
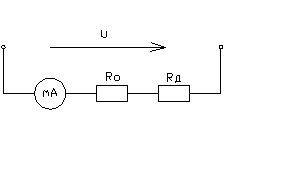
измерительных трансформаторов N_тн и N_тт. Привести схему измерения.

Дано:

Найти:

Решение:

1) Определим
коэффициенты трансформации трансформатора напряжения и тока

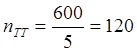
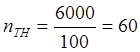
2) Определим
ток и напряжение в сети

3) Определим
абсолютные погрешности амперметра и вольтметра

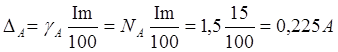
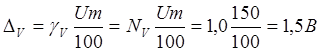
4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения

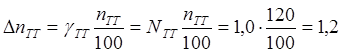
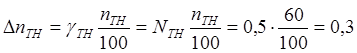
5) Результирующие
абсолютные погрешности измерения тока и напряжения равны

6)
Относительные погрешности измерения тока и напряжения

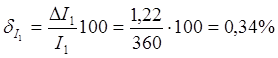
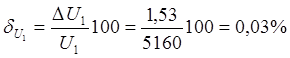
Задача 6

Определить
относительные погрешности измерения сопротивления R_x
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – R_a,
вольтметра – R_в. Сделать вывод о
целесообразности использования той или иной схемы.

Дано:

Найти: .

Решение:

Принципиальные
схемы

 

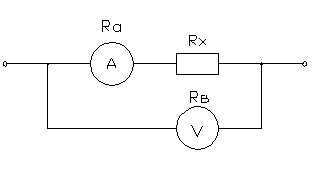
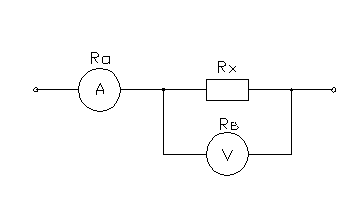
Схема
1                                              Схема 2

1)  Для
схемы включения 1.

1.1. 
Измеренное сопротивление.

1.2. 
Определяем абсолютную погрешность.

1.3. 
Определяем относительную погрешность.

Лабораторная работа № 1.

Расчет погрешностей емкости с
помощью коэффициента Стьюдента.

Расчет погрешности измерения
мощности и сопротивления

Цели занятия:

1.     Общеобразовательная – Умение решать задачи по
теме погрешности.

2.     Развивающая –  Углубление знаний .

3.     Воспитательная – Проверить сформированность
качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой
величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности
между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А                                                                                      
                          (1)

Действительная относительная погрешность  представляет собой отношение абсолютной
погрешности измерения к действительному значению измеряемой величины,
выраженное в процентах:

                                                                                                                  
       (2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению
исследуемой величины,

т
.е. к показанию прибора

                                                                      
                                               (3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности
измерения к максимальному значению измерительного прибора

                                                                                                          (4)

Для приборов с двухсторонней шкалой А_макс
определяется как сумма абсолютных величин положительного и отрицательного
пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального
значения, то А_макс равно разности между конечным и начальным
значениями шкалы.

Случайными называются
погрешности, изменяющиеся случайным образом при повторных измерениях одной и
той же величины. Случайные погрешности нельзя исключить опытным путем, т. к.
они возникают случайно. Для того, чтобы исключить случайные погрешности
производят неоднократные измерения и определяют среднее арифметическое из
полученных значений, определяемое как

 ,

где
а₁, а₂, …, а_n –
результаты отдельных измерений;

n
– число измерений.

            Для
оценки точности результата измерений необходимо знать закон распределения
случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее
квадратическое отклонение может быть выражено через случайные отклонения
результатов наблюдения Р:

где
Р₁ = а₁ – А_ср; Р₂ = а₂ –
А_ср; Р_n = а_n – А_ср.

            Этот
способ определения доверительных интервалов справедлив толко для больших
количеств измерений (>20-30). Для небольшого количества измерений для
определения доверительного интервала нужно пользоваться коэффициентами
Стьюдента t_n, которые зависят от задаваемой
доверительной вероятности Р и количества измерений n.

            Для
определения доверительного интервала среднюю квадратическую погрешность  надо умножить на коэффициент Стьюдента.
Окончательный результат измерения можно записать так:

А
= Аср  t_n

Контрольное задание

Задача 1. Для уменьшения
влияния случайных погрешностей на результат измерения, емкость конденсатора С
измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные
погрешности имеют нормальный закон распределения, определить на основании
заданного количества измерения (табл. 1, табл. 2):

• Действительное
  значение измеряемой емкости;
• Среднюю
  квадратическую и максимальную погрешности однократного измерения;
• Доверительный
  интервал для результата измерения при доверительной вероятности Р_д
  (табл.3).
• Имеется
  ли систематическая составляющая в погрешности измерения емкости и с какой
  доверительной вероятностью ее можно оценить, если принять в качестве
  действительного значения емкости значения С_ср  (таб.1, таб.2).

Таблица
1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица
2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание.
Количество и номера наблюдений значений емкости для каждого варианта
определяются данными таблицы 1 и 2, например для варианта 1 следует взять
результаты измерений 1-3 табл.2.

Указания к решению

1.     
Для удобства выполнения и проверки расчетов по
заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица
3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

2.     
Далее определить среднеквадратическую погрешность :

3.     
По таблице  (4) определить коэффициент Стьюдента.

4.     
В конце решения следует записать окончательный  (с
учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание
2._. Используя
формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей
измерения мощности и сопротивления. Расчет выполняется в соответствии с
вариантами указанными в задании.

Задача 1. Для определения
сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены
напряжение и ток. Зная основные параметры измерительных приборов (амперметра и
вольтметра), определить ошибку косвенных измерений  мощности и сопротивления.

Пример. Определить абсолютную и
относительную погрешности измерения мощности, выделяемой на резисторе, если известны
показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А =
1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем
   мощность Р = U * I  ( Вт)
2. Абсолютная
   ошибка измерения напряжения, В

1. Абсолютная
   ошибка измерения тока, _М А

1. В
   соответствии с таблицей абсолютная ошибка измерения мощности, Вт

            Относительная
ошибка

1. Формула
   для сопротивления R = U / I
2. 
3. Относительная
   погрешность

  

Примечание:

1.     
Для  вычисления погрешностей измерения мощности
используются формулы 1,2,3,4,

2.     
Для вычисления погрешностей измерения сопротивления
используются формулы 2,3,5,6,7.

Формулы для выполнения
контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

          3    Номинальная относительная погрешность

          4.Приведенная относительная погрешность

5.     
Сопротивление шунта

R_Ш = R_А / Р-1  (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1)  (Ом)

7       
Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

10   
Напряжение сети:

U_C = K_U* U (В)

11   
Активная мощность сети:

P_C = K_i * K_U *P (Вт)

12   
Реактивная мощность сети :

Q = U*I* sinφ (Вар)

13   
Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление
сети :

Z_C  = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C  / S_C

16   
Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

17   
Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

18   
Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%