| Статья является частью одноименной серии. |
| Тепловые процессы |
|---|
 |
|
| См. также «Физический портал» |
Адиабати́ческий, или адиаба́тный[1] проце́сс (от др.-греч. ἀδιάβατος «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Серьёзное исследование адиабатических процессов началось в XVIII веке[2].
В целом термин адиабатический в разных областях науки всегда подразумевает сохранение неизменным какого-то параметра. Так в квантовой химии, электронно адибатический процесс это процесс, в котором не изменяется квантовое число электронного состояния. Например, молекула всегда остается в первом возбужденном состоянии вне зависимости от изменения положения атомных ядер. Соответственно неадиабатическим называется процесс, в котором происходит изменение какого-то важного параметра.
В термодинамике, адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[3]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Равновесный адиабатный процесс является изоэнтропным процессом[4]. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы[5].
Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Также такие процессы получили ряд применений в технике.
История[править | править код]
Уравнение Пуассона позволило описать адиабатический процесс
Существование атмосферного давления было показано рядом экспериментов в XVII веке. Одним из первых доказательств гипотезы стали магдебургские полушария, сконструированные немецким инженером Герике. Из сферы, образованной полушариями, выкачивался воздух, после чего их было трудно разъединить в силу внешнего давления воздуха. Другой эксперимент в рамках исследования природы атмосферного давления поставил Роберт Бойль. Он состоял в том, что если запаять изогнутую стеклянную трубку с короткого конца, а в длинное колено постоянно подливать ртуть, она не поднимется до верха короткого колена, поскольку воздух в трубке, сжимаясь, будет уравновешивать давление ртути на него. К 1662 году данные опыты позволили прийти к формулировке закона Бойля — Мариотта[6].
В 1779 году в «Пирометрии» Ламберта был описан опыт повышения и понижения температуры в приёмнике воздушного насоса при движении поршня. Впоследствии данный эффект был подтверждён Дарвином (1788) и Пикте (1798). В 1802 году Дальтон опубликовал доклад, в котором, в числе прочего, указал, что сгущение газов сопровождается выделением тепла, а разрежение — охлаждением. Рабочий оружейного завода зажёг трут в дуле духового ружья путём сжатия воздуха, о чём сообщил в 1803 году лионский физик Моле[2].
Теоретическим обобщением накопившихся экспериментальных знаний занялся физик Пуассон. Так как при адиабатическом процессе температура непостоянна, то закон Бойля — Мариотта требует поправки, которую Пуассон обозначил как коэффициент k и выразил через соотношение теплоёмкостей. Экспериментально данный коэффициент определялся Вальтером и Гей-Люссаком (эксперимент описан в 1807 году) и затем более точно Дезормом и Клеманом в 1819 году. Практическое использование адиабатического процесса предложил С. Карно в работе «Движущая сила огня» в 1824 году[2].
Физический смысл адиабатического процесса[править | править код]
Если термодинамический процесс в общем случае представляет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии[7], то адиабатический процесс в силу отсутствия теплообмена (
где 

Изменения энтропии 
Здесь 

Работа газа[править | править код]
Совершение над газом работы на элементарном участке
dh. Совершаемая работа показана красными лампочками
Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем. Если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок 
где F — сила, с которой газ действует на поршень. Перепишем уравнение:
где s — площадь поршня. Тогда работа будет равна[11][12]
где 


Основное уравнение термодинамики примет вид[13]:

|
(1) |
Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны, она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны, скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим[14][15].
Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид:

|
(1a) |
где 



Внутренняя энергия идеального газа[править | править код]
Тепловое движение молекул одноатомного газа идёт в среднем тем интенсивнее, чем больше его внутренняя энергия. Скорость каждой отдельной молекулы при этом может изменяться даже при постоянстве внутренней энергии всего газа[Комм 2]
Внутренняя энергия является однозначной функцией состояния системы. Поэтому применительно к адиабатическому процессу её изменение имеет тот же физический смысл, что и в общем случае. Согласно экспериментально установленному закону Джоуля (закону Гей-Люссака — Джоуля) внутренняя энергия идеального газа не зависит от давления или объёма газа[16]. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, 

|
(2) |
где 
Уравнение Пуассона для идеального газа[править | править код]
Адиабата Пуассона[править | править код]
Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением[8][18][19]
где 



График адиабаты (жирная линия) на 


С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
где 
Поскольку 



Вывод уравнения[править | править код]
Согласно закону Менделеева — Клапейрона[8] для идеального газа справедливо соотношение
где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обеих частей уравнения, полагая независимыми термодинамическими переменными 

|
(3) |
Если в (3) подставить 

или, введя коэффициент 
Это уравнение можно переписать в виде
что после интегрирования даёт:
Потенцируя, получаем окончательно:
что и является уравнением адиабатического процесса для идеального газа.
Показатель адиабаты[править | править код]
| Показатели адиабаты для различных газов[20][21] | ||||||
|---|---|---|---|---|---|---|
| Темп. | Газ | k | Темп. | Газ | k | |
| −181 °C | H2 | 1,597 | 20 °C | He | 1,660 | |
| −76 °C | 1,453 | 20 °C | H2O | 1,330 | ||
| 20 °C | 1,410 | 100 °C | 1,324 | |||
| 100 °C | 1,404 | 200 °C | 1,310 | |||
| 400 °C | 1,387 | −180 °C | Ar | 1,760 | ||
| 1000 °C | 1,358 | 20 °C | 1,670 | |||
| 2000 °C | 1,318 |
При адиабатическом процессе показатель адиабаты равен

Для нерелятивистского невырожденного одноатомного идеального газа 




Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно при низких температурах, когда большу́ю роль начинает играть межмолекулярное взаимодействие. Для его теоретического нахождения следует проводить расчёт без некоторых допущений, в частности, использованных при выводе формулы (1), и использовать формулу (1а).
Один из методов для экспериментального определения показателя был предложен в 1819 г. Клеманом и Дезормом. Стеклянный баллон вместимостью несколько литров наполняется исследуемым газом при давлении 


Энтропия и обратимость[править | править код]
В общем случае для произвольной физической системы изменение состояния при адиабатическом расширении определяется производными термодинамических параметров при постоянной энтропии. Справедливы соотношения
,
,
где Cp и Cv — теплоёмкости при постоянном давлении и объёме, которые всегда положительны по своему физическому смыслу, 



Необратимость адиабатических процессов связана с неравновесным переходом от начального состояния к конечному: система не следует адиабате Пуассона 
Примеры[править | править код]
Открытие адиабатического процесса практически сразу нашло применение в дальнейших исследованиях. Создание теоретической модели цикла Карно позволило установить пределы развития реальных тепловых машин (сам С. Карно показал, что двигатель с более высоким КПД позволил бы создать вечный двигатель[28]). Однако цикл Карно трудно осуществим для некоторых реальных процессов, так как входящие в его состав изотермы требуют определённой скорости теплообмена[29]. Поэтому были разработаны принципы циклов, частично сходных с циклом Карно (например, цикл Отто, цикл сжижения газа, цикл Ренкина), которые были бы применимы в конкретных практических задачах.
Дальнейшие исследования показали также, что некоторые процессы в природе (например, распространение звука в газе) можно с достаточной степенью приближения описывать адиабатическим процессом и выявлять их закономерности[30]. Химическая реакция внутри объёма газа в случае отсутствия теплообмена с окружающей средой также по определению будет адиабатическим процессом. Таким процессом является, например, адиабатическое горение. Для атмосферы Земли также считается адиабатическим процесс совершения газом работы на увеличение его потенциальной энергии. Исходя из этого, можно определить адиабатический градиент температуры для атмосферы Земли[31]. Теория адиабатического процесса употребляется и для других астрономических объектов с атмосферой. В частности, для Солнца наличие макроскопических конвекционных движений теоретически определяют путём сравнения адиабатического градиента и градиента лучевого равновесия[32].
Адиабатическими можно считать процессы, происходящие с применением адиабатных оболочек.
Цикл Карно[править | править код]
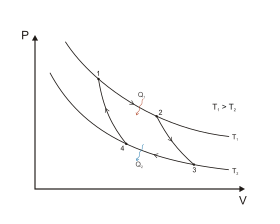
Цикл Карно в координатах P и V
Цикл Карно является идеальным термодинамическим циклом. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно[10][33].
Максимальное КПД достигается при обратимом цикле[10]. Для того, чтобы цикл был обратимым, из него должна быть исключена передача тепла при наличии разности температур. Чтобы доказать этот факт, предположим, что передача тепла при разности температур имеет место. Данная передача происходит от более горячего тела к более холодному. Если предположить процесс обратимым, то это означало бы возможность передачи тепла обратно от более холодного тела к более нагретому, что невозможно, следовательно процесс необратим[29]. Соответственно, преобразование тепла в работу может происходить только изотермически[Комм 3]. При этом обратный переход двигателя в начальную точку только путём изотермического процесса невозможен, так как в этом случае вся полученная работа будет затрачена на восстановление исходного положения. Так как выше было показано, что адиабатический процесс может быть обратимым — то этот вид адиабатического процесса подходит для использования в цикле Карно.
Всего при цикле Карно происходят два адиабатических процесса[33]:
- Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс 2→3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
- Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс 4→1). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
Цикл Отто[править | править код]
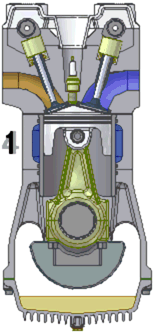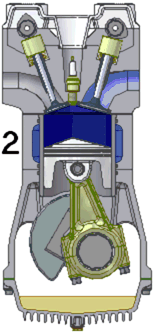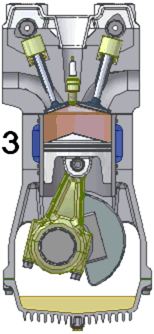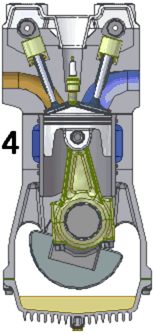
Схема работы четырёхтактного двигателя, цикл Отто
1. впуск
2. сжатие
3. рабочий ход
4. выпуск
При идеальном цикле Отто, который приближённо воспроизведён в бензиновом двигателе внутреннего сгорания, второй и третий из четырёх тактов являются адиабатическими процессами[Комм 4]. Работа, которая совершается на выходе двигателя, равна разности работы, которую произведёт газ над поршнем во время третьего такта (то есть рабочего хода), и работы, которую затрачивает поршень на сжатие газа во время второго такта. Так как в цикле Отто используется система принудительного зажигания смеси, то происходит сжатие газа в 7—12 раз[34]. Более высокая степень сжатия требует использования топлива с более высоким октановым числом (для бензиновых ДВС) во избежание детонации.
Рассчитаем пример процесса, происходящего в двигателе внутреннего сгорания при адиабатическом сжатии. Примем величину сжатия 10 и объём двигателя 10−3 м³ (1 л). Перед сжатием припишем смеси околокомнатную температуру 300 K (около 27 °C) и нормальное атмосферное давление около 100 кПа. Также примем газ смеси двухатомным и идеальным. Тогда

Рассмотрим процесс сжатия газа в десять раз — до объёма 100 мл. Константа адиабатического сжатия остаётся при этом равной 6,31. Итого получаем:

что даёт решение для P:

что составляет приблизительно 24,5 атмосферы. Однако в процессе сжатия изменилось не только давление, но и температура газа, которую можно рассчитать по закону Менделеева — Клапейрона:

Теперь, подставляя объём 100 мл и вычисленное нами ранее давление, получаем температуру:

Как видно из решения, такая температура не может привести к самоподжигу топлива[Комм 5]. Выводы из расчёта справедливы и для реальных двигателей, так как в них при данной степени сжатия самоподжига не происходит[34].
Прохождение звуковых волн в газе[править | править код]
Для небольших объёмов газа адиабатическим процессом, близким к обратимому, можно считать процессы в небольших объёмах газа при прохождении звуковой волны[8].
На основании этого можно рассчитать скорость звука в газах путём нахождения зависимости 


где 



Сжижение газов[править | править код]
Идеальный цикл сжижения газа
Пусть необходимо охладить идеальный газ путём отведения тепла в область с более высокой температурой. Тогда наименьшая затрачиваемая работа будет происходить по циклу Карно в обратном направлении 

В реальном газе при наличии большого давления и низкой температуры возможна ситуация, когда значительную роль в движении молекул начинает играть межмолекулярное притяжение. В случае адиабатического расширения газа (например в результате использования эффекта Джоуля — Томсона) из-за работы, которая тратится на преодоление межмолекулярного притяжения, температура газа резко падает, часть газа конденсируется[37]. Адиабатическое дросселирование проходит с увеличением энтропии и не сразу после изотермического сжатия[36].
Магнитное охлаждение[править | править код]
Магнитокалорический эффект. Адиабатической здесь является фаза размагничивания
С помощью адиабатического размагничивания парамагнетиков можно достичь температуры в сотые доли кельвина, а для некоторых веществ (так называемые ванфлековские или поляризационные парамагнетики) даже нанокельвинов. Метод был предложен Петером Дебаем и Уильямом Джиоком в 1926 году[38]. Парамагнитный образец для эффективного охлаждения должен иметь малую удельную теплоёмкость кристаллической решётки и большую удельную теплоёмкость магнитной подсистемы, его внутренние магнитные поля должны быть малы, а спин-решёточная связь достаточно сильной. Этим условиям удовлетворяют медь и один из интерметаллидов празеодима с никелем (празеодимпентаникель, 
При температуре порядка одного кельвина спины электронов, как правило, упорядочены, в отличие от ядерных спинов I[40]. При этом связь между ядерными спинами различных атомов практически отсутствует. При магнитном охлаждении образец вначале намагничивают в сильном магнитном поле B (до нескольких Тл), которое упорядочивает его магнитную подсистему. Далее происходит адиабатическое размагничивание, которое сохраняет постоянной энтропию системы. Энтропия одного моля меди зависит от ядерных спинов I, поля B и температуры T (в кельвинах) как
где R — газовая постоянная, b — внутреннее магнитное поле вещества, 
где g и g0 — факторы Ланде для направлений полей с напряжённостями H и H0 соответственно[42].
См. также[править | править код]
- Адиабатическое горение
- Адиабатическое приближение
- Адиабатический инвариант
- Адиабатический градиент температуры
- Система адиабатического увлажнения воздуха
Примечания[править | править код]
Комментарии[править | править код]
- ↑ Если в уравнении
считать работой внешних сил над системой, то уравнение будет иметь вид
- ↑ Что можно наглядно проследить на этом рисунке, если наблюдать за любой помеченной красным молекулой
- ↑ В соответствии с определением изотермический процесс происходит при постоянной температуре (см. например, Савельев, 2001, с 30). Если же процесс другой, то при постоянной температуре нагревателя/холодильника, очевидно в какой-то момент будет разность температур. Если же теплообмен происходит с телом переменной температуры, как в цикле Стирлинга, то это условие необязательно.
- ↑ Чтобы соответствовать циклу Отто, процесс сгорания топлива между вторым и третьим тактом должен быть быстрым по сравнению со временем такта.
- ↑ Рабочая температура для дизельных двигателей, работающих по системе самовоспламенения, составляет 820—870 K.
- ↑ Так как такой процесс будет сопровождаться передачей тепла между частями газа и, следовательно, будет необратимым (как любой процесс с передачей от более горячего тела к холодному — см. Савельев, 2001, с 106), а для обратимого адиабатического процесса dS = 0.
Источники[править | править код]
- ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 14.
- ↑ 1 2 3 Кудрявцев, 1956, с. 396—399.
- ↑ Савельев, 2001, с. 33-34.
- ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 6.
- ↑ Ландау, Лифшиц V, 1976, с. 55.
- ↑ Кудрявцев, 1956, с. 185—186.
- ↑ Савельев, 2001, с. 17.
- ↑ 1 2 3 4 Савельев, 2001, с. 30—32.
- ↑ Сивухин, 1975, с. 54.
- ↑ 1 2 3 4 Савельев, 2001, с. 109—113.
- ↑ 1 2 3 Савельев, 2001, с. 19—20.
- ↑ 1 2 Ландау Л.Д., Ахиезер А.И., 1965, с. 181—182.
- ↑ Ландау Л.Д., Ахиезер А.И., 1965, с. 196—198.
- ↑ Савельев, 2001, с. 13.
- ↑ Ландау, Лифшиц V, 1976, с. 56.
- ↑ Герасимов Я. И., 1970, с. 50—51.
- ↑ Ландау Л.Д., Ахиезер А.И., 1965, с. 185.
- ↑ Ландау Л.Д., Ахиезер А.И., 1965, с. 196-198.
- ↑ Ландау, Лифшиц V, 1976, с. 144.
- ↑ White, Frank M. Fluid Mechanics. — 4th. — McGraw-Hill, New York., 1998. — ISBN 978-0072281927.
- ↑ Lange, N. A.; Dean, J. A. Lange’s Handbook of Chemistry. — 10th. — McGraw-Hill, New York., 1967. — С. 1524.
- ↑ 1 2 Адиабата // А — Ангоб. — М. : Советская энциклопедия, 1969. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 1).
- ↑ Сивухин, 1975, с. 78—79.
- ↑ Ландау, Лифшиц V, 1976, с. 70.
- ↑ 1 2 Глаголев К. В., Морозов А. Н. Применение термодинамических потенциалов для описания эффекта Джоуля-Томсона (недоступная ссылка — история). Физическая термодинамика. МГТУ им. Н. Э. Баумана. Дата обращения: 4 января 2012. Архивировано 1 февраля 2012 года.
- ↑ K. C. Pal. Heat Power. — Orient Blackswan, 1990. — P. 85—88. — 480 p. — ISBN 9780861319596.
- ↑ David R. Gaskell. Introduction to the thermodynamics of materials. — 4th Ed. — Taylor & Francis, 2003. — P. 47. — 618 p. — ISBN 9781560329923.
- ↑ Кудрявцев, 1956, с. 400—401.
- ↑ 1 2 Савельев, 2001, с. 106.
- ↑ 1 2 3 Савельев Т.4, 2001, с. 32—36.
- ↑
Paul E. Lyndorph. Weather and Climate. — 3-е изд. — New Jersey: Rowman & Allanheld Publishers, 1985. — С. 95—97. - ↑
Соболев В. В. Курс теоретической астрофизики. — 3-е изд. — М.: Наука, 1985. — С. 170—172. — 504 с. - ↑ 1 2 Ландау Л.Д., Ахиезер А.И., 1965, с. 209.
- ↑ 1 2 Кириллин, 2008.
- ↑ Сивухин, 1975, с. 98—99.
- ↑ 1 2 3 Сжижение газов / А. Б. Фрадков // Сафлор — Соан. — М. : Советская энциклопедия, 1976. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 23).
- ↑ Адиабатный процесс // А — Ангоб. — М. : Советская энциклопедия, 1969. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 1).
- ↑ 1 2 Магнитное охлаждение — статья из Физической энциклопедии
- ↑ Anthony Kent. Experimental low temperature physics. — Springer, 1993. — P. 141. — 212 p. — (Macmillan physical science). — ISBN 9781563960307.
- ↑ Luke C. L., Wu Yan, Chien-Shieng. Part B // Nuclear Physics. — Academic Press, 1963. — Vol. 5. — P. 187. — 886 p. — (Methods in Experimental Physics). — ISBN 9780124759459.
- ↑ Магнитное охлаждение / А. Б. Фрадков // Ломбард — Мезитол. — М. : Советская энциклопедия, 1974. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 15).
- ↑ Luke C. L., Wu Yan, Chien-Shieng. Part B // Nuclear Physics. — Academic Press, 1963. — Vol. 5. — P. 189. — 886 p. — (Methods in Experimental Physics). — ISBN 9780124759459.
Литература[править | править код]
- Савельев И. В. Курс общей физики: Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
- Савельев И. В. Курс общей физики: Волны. Оптика. — М.: Астрель, 2001. — Т. 4. — 256 с. — 7000 экз. — ISBN 5-17-004586-7.
- Ландау Л. Д., Ахиезер А. И., Лифшиц Е. М. Курс общей физики: Механика. Молекулярная физика. — М.: Наука, 1965.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1 // Теоретическая физика. — М.: Наука, 1976. — Т. V. — 584 с. — 45 000 экз.
- Сивухин Д. В. Общий курс физики. — М.: МФТИ, 2005. — Т. I. Механика. — 560 с.
- Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
- Кудрявцев П. С. История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
- Кириллин В. А., Сычёв В. В., Шейндлин А. Е. Техническая термодинамика: учебник для вузов. — М.: Издательство МЭИ, 2008. — 496 с. Архивная копия от 24 ноября 2011 на Wayback Machine
- Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М.: Химия, 1970. — Т. I. — 592 с.
- Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
Адиабатный процесс

4.7
Средняя оценка: 4.7
Всего получено оценок: 148.
4.7
Средняя оценка: 4.7
Всего получено оценок: 148.
Среди различных явлений, происходящих с газами, важную роль играет адиабатный процесс. Он широко используется в технике и часто встречается в Природе. Рассмотрим его суть более подробно.
Адиабатный процесс
При изучении законов газовых процессов (изопроцессов) для изменения внутренней энергии газа используется обмен теплом с внешними источниками. Например, в изохорическом процессе, когда объем газа не меняется, увеличение внутренней его энергии возможно за счет внешнего нагрева. Обмен теплом также происходит и в изобарическом и изотермическом процессах.
Однако, состояние газа и его внутренняя энергия могут меняться и без теплового обмена с внешними источниками. Такой процесс, для которого количество подведенного тепла равно нулю ($Q=0$), называется адиабатным.
Для того, чтобы газовый процесс был приближен к адиабатному в реальных условиях, существует два способа (и их комбинация). Во-первых, можно окружить систему толстой теплоизолирующей оболочкой, сильно замедляющей обмен теплом. Во-вторых, процесс можно проводить очень быстро, при этом теплообмен просто не успеет произойти.
На первый взгляд, может показаться, что если к системе не подводится тепло, то она не может совершать работу. Однако, это не так. Согласно Первому Закону термодинамики, изменение внутренней энергии системы равно сумме работы внешних сил и количества тепла переданного системе:
$$ΔU=A+Q$$
А это значит, что в адиабатном процессе совершение работы возможно. Но вся эта работа будет произведена за счет изменения внутренней энергии газа.
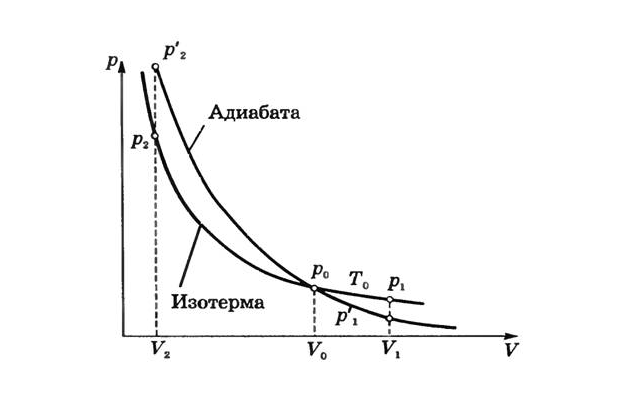
График адиабаты
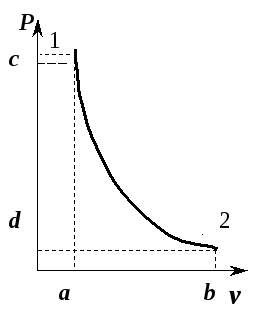
Характеристикой внутренней энергии газа является его температура. То есть, если в адиабатном процессе производится работа, то это происходит с обязательным изменением температуры. Например, если работа положительна, и внешние силы сжимают газ, то его температура увеличится, газ нагреется.
Отсюда следует, что давление газа при сжатии в адиабатном процессе будет расти быстрее, чем в изотермическом. В адиабатном процессе давление будет повышаться не только за счет уменьшения объема, но и за счет увеличения температуры. То есть, график адиабаты в координатах $p-V$ внешне будет похож на график изотермы, но пройдет более круто.
Можно вывести математические уравнения данных процессов:
- Изотерма: $pV=const$;
- Адиабата: $pV^gamma=const$.
Параметр $gamma$ в формуле адиабатного процесса называется показателем адиабаты. Для реальных газов в нормальных условиях показатели адиабаты несколько больше единицы, и равны:
|
Газ |
Показатель |
|
Пропан |
1.13 |
|
Метан |
1.32 |
|
Воздух |
1.40 |
|
Аргон |
1.67 |
Фактически, изотерму можно представить адиабатой, с показателем адиабаты $gamma=1$.
Адиабатные процессы в Природе и технике
Поскольку при быстром сжатии и расширении газа теплообмен очень невелик, адиабатные процессы широко используются в технике, и играют большую роль в атмосферных явлениях в Природе.
Например, в двигателях внутреннего сгорания горючая смесь после впуска в цилиндр в течение короткого времени сжимается, а затем, после воспламенения смеси в течении короткого времени расширяется. Таким образом, такты сжатия и рабочего хода в двигателях являются хорошими примерами адиабатного процесса.
Значительный нагрев газа при адиабатном процессе используется в дизельных двигателях. В этих двигателях нет систем для поджигания сжатой топливовоздушной смеси. В дизеле происходит сжатие атмосферного воздуха, сильнее, чем в бензиновом карбюраторном двигателе. А в конце сжатия топливо впрыскивается в цилиндр с помощью специальной форсунки. В этот момент воздух имеет температуру, достаточную для самовоспламенения впрыснутой горючей смеси, температура сгоревшей топливовоздушной смеси резко возрастает, смесь расширяется, толкая поршень и совершая полезную работу.
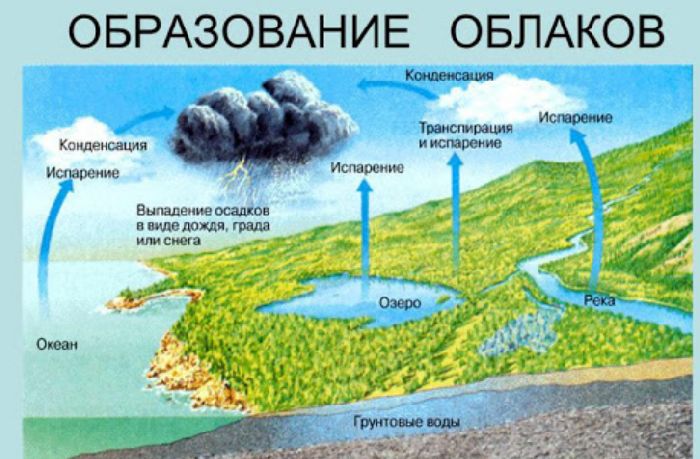
Природные адиабатные процессы играют значительную роль в формировании погоды. Нагретые массы воздуха быстро поднимаются вверх и расширяются. В результате их температура падает ниже точки росы, и влага, содержащаяся в воздухе, конденсируется в облака. Однако, при снижении снова происходит адиабатное сжатие, температура повышается, и облачные капли у нижней границы облаков снова превращаются в пар.
Что мы узнали?
Адиабатный процесс – это газовый процесс, при котором не происходит теплообмена с внешней средой. Работа при адиабатном процессе может быть совершена только за счет изменения внутренней энергии. На графике $p-V$ график адиабаты похож на график изотермы, но пройдет более круто.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 148.
А какая ваша оценка?
Адиабатическое сжатие это термодинамический процесс, при котором внутренняя энергия системы увеличивается из-за повышения температуры.
Адиабатическое сжатие характеризуется отсутствием передачи тепла между системой и окружающей средой. Повышение температуры во время адиабатического сжатия приводит к увеличению давления, которое обычно намного сильнее, чем скорость уменьшения объема.
Адиабатический процесс можно определить выражением:
PVꝩ = Постоянный
Где,
P = Давление в системе
V: объем системы
ꝩ = Отношение удельной теплоемкости газа (Cp / Cv)
Здесь Cp – удельная теплоемкость при постоянном давлении, а Cv – удельная теплоемкость при постоянном объеме. В приведенном выше уравнении считается, что система идеально изолирована от окружающей среды, так что dQ = 0, или нет передачи тепла с окружающей средой. Другое предположение приведенных выше выражений состоит в том, что газ должен быть идеальным газом (коэффициент сжимаемости = 1).
На практике идеальное поведение демонстрирует небольшое количество газов или состав газов. Кроме того, всегда есть потери тепла в окружающую среду, когда работа фотоэлектрических систем выполняется системой. Однако для всех практических целей поведение большинства газов близко к идеальному при давление и температура выше их точки кипения. В этих условиях столкновения между газами абсолютно упругие, а межмолекулярные силы между сталкивающимися атомами почти отсутствуют.

Изображение |: упругое столкновение
источник: https://www.nuclear-power.com/nuclear-engineering/thermodynamics/ideal-gas-law/what-is-ideal-gas/
Еще один практический пример адиабатического процесса – газовая турбина операции, где процесс изменения очень рейд. В этих процессах потери тепла происходят, но их количество довольно мало по сравнению с теплом, передаваемым в процессе, что делает их незначительными. Другой пример адиабатический процесс – такты сжатия и расширения двигателя внутреннего сгорания.

PV диаграмма тактов в двигателе внутреннего сгорания
Image Source: https://engineeringinsider.org/adiabatic-process-types/
Что такое адиабатическое сжатие?
В термодинамике адиабатический процесс характеризуется dQ = 0, где Q – сердце, перенесенное с окружающим.
Адиабатическое сжатие – это процесс, при котором работа фотоэлектрической системы отрицательна, что приводит к повышению температуры системы. Это повышение температуры увеличивает внутреннюю энергию системы.
Адиабатическое сжатие предполагает идеальную изоляцию, что чисто теоретически. Однако инженеры могут безопасно сделать адиабатическое допущение для всех практических целей в процессах, которые достаточно хорошо изолированы или которые являются очень быстрыми.
Адиабатическое сжатие, как это работает?
Адиабатическое сжатие работает по тем же принципам, что и первый закон термодинамики.
Первый закон термодинамики гласит, что
dQ = dU + dW
In адиабатическое сжатие, поскольку теплопередача с окружающей средой равна нулю, приведенное выше уравнение можно записать как:
dU = -PdV
Из сказанного следует, что увеличение внутренней энергии соответствует уменьшению объема. На увеличение внутренней энергии указывает повышение температуры системы.

PV Схема адиабатического процесса
источник: https://engineeringinsider.org/adiabatic-process-types/
Всегда ли сжатие адиабатично?
Сжатие осуществляется для сжимаемых жидкостей, которые в основном представляют собой газ, и это происходит по различным термодинамическим путям.
Процесс сжатия газа термодинамически может быть трех типов: – изотермическое, адиабатическое и политропическое сжатие. Все эти различные типы сжатия могут привести к различным конечным условиям при одинаковом объеме выполненной работы.
Изотермическое сжатие: как следует из названия, этот тип сжатия происходит при постоянной температуре. Это достигается за счет обеспечения охлаждающей жидкости над корпусом компрессора и / или межступенчатого охлаждения. Однако на практике добиться полного изотермического сжатия очень сложно. Сжатие, близкое к изотермическому, может быть достигнуто, если процесс сжатия протекает в очень медленном темпе с достаточным временем для отвода тепла, образующегося в процессе. Изотермическое сжатие дается выражением
PV = постоянный
Адиабатическое сжатие: этот тип сжатия требует, чтобы сжатие осуществлялось без потери или увеличения тепла из окружающей среды. Для этого требуется идеально изолированная система. Другой способ добиться адиабатическое сжатие заключается в том, чтобы производить сжатие в очень быстром темпе, чтобы не было времени для передачи тепла от системы к окружающей среде. Адиабатическое сжатие выражается выражением:
PVꝩ= константа, где ꝩ – отношение удельной теплоты сжимаемого газа.
Политропное сжатие: Политропное сжатие определяет фактические процессы сжатия, происходящие в реальных системах сжатия, например, в газовом компрессоре. А процесс политропного сжатия задается выражением:
PVn = Константа, где n изменяется от 1 до 1.4.
Формула адиабатического сжатия
Формула адиабатического сжатия выводится из первого закона термодинамики с учетом отсутствия передачи тепла в систему и из системы.
Формула для адиабатического сжатия может быть выражена в различных формах, например, в форме PV, в форме TV и в форме PT, где P, V и T – это давление, объем и температура соответственно.
Адиабатическое сжатие в форме давления и температуры определяется как:
P1-Ꝩ Tꝩ = Постоянный
Адиабатическое сжатие в объемно-температурной форме:
TVꝩ-1= Постоянный
Адиабатическое сжатие в форме давления и объема определяется как:
PVꝩ= Постоянный
Как рассчитать адиабатическое сжатие?
Адиабатическое сжатие можно рассчитать по формуле PVꝩ= Константа.
Поршень, сжимающий газ в цилиндре, назовем адиабатическим процессом, когда передача тепла в окружающую среду равна нулю. В таком случае, если известны начальные условия (P1 и V1), а также отношение удельной теплоемкости газа (), можно получить любое из конечных условий (P2, V2), если оно задано. Таким образом, формула принимает следующий вид:
P1V1ꝩ= P2V2ꝩ
Что вызывает адиабатическое сжатие (не имеет значения)
Работа, проделанная при адиабатическом сжатии
Работа, проделанная в адиабатическом процессе, может быть получена из формулы для адиабатического процесса
PVꝩ= Константа (K). Эту формулу можно переписать как P = KV–
Чтобы рассчитать работу, совершенную в адиабатический процесс , будем считать, что система сжата от начального положения P1, V1 и T1 до конечного положения P2, V2 и T2. Совершенная работа определяется
Выполненная работа (Вт) = Сила x смещение
W = Fdx
W = PAdx
W = P (Adx)
W = PdV
Чтобы рассчитать работу, проделанную во время сжатия от V1 до V2, PdV необходимо интегрировать с пределами V1 и V2.
Или W =
Или W =dV Где P = KV–
Это можно представить как работа, выполненная в адиабатическом процессе.
Интегрируя дальше, мы получаем окончательное выражение для проделанной работы как
W=1/(1−γ) {P2V2−P1V1}
Какая работа выполняется в адиабатическом процессе
Адиабатический процесс может быть адиабатическим сжатием или адиабатическим расширением.
В случае при адиабатическом сжатии работа совершается окружающей средой над системой и при адиабатическом расширении работа совершается системой над окружающей средой. Работа, совершаемая в адиабатическом процессе, аналогична работе, совершаемой при адиабатическом сжатии или расширении.
Пример адиабатический расширение – это подъем горячего воздуха в атмосферу, который адиабатически расширяется из-за более низкого атмосферного давления и в результате остывает. В этом случае работа совершается поднимающимся горячим воздухом, а работа совершается системой.
Отрицательная ли работа при адиабатическом сжатии?
Да, работа, совершаемая системой при адиабатическом сжатии отрицательно.
Адиабатическое сжатие происходит с увеличением внутренней энергии системы. Мы знаем из первого закона термодинамика что, поскольку dQ при адиабатическом сжатии равно нулю,
dU + dW = 0
или dU = -dW
dU и dW имеют отрицательное отношение друг к другу. Таким образом, поскольку изменение внутренней энергии положительное, проделанная работа отрицательна.
Связь можно также подтвердить тем фактом, что при адиабатическом сжатии внутренняя энергия поднимается, работа над системой совершается окружающей средой, следовательно, работа, совершаемая системой над окружающей средой, отрицательна.
Напротив, работа, совершаемая системой над окружающей средой при адиабатическом расширении положительно.
Как вы рассчитываете работу, проделанную в адиабатическом процессе?
Адиабатический процесс может быть достигнут, если расширение или сжатие газа осуществляется в идеально изолированной системе или происходит так быстро, что передача тепла в окружающую среду незначительна.
Математически нет никакой разницы между адиабатическим расширением и адиабатическим сжатием, и, следовательно, они следуют одним и тем же формулам и выводам.
Таким образом, все приведенные выше формулы для адиабатического сжатия справедливы для любого адиабатического процесса.
Обратимо ли адиабатическое сжатие?
Адиабатическое сжатие обратимо, если нет изменения энтропии
Процесс называется обратимым, если он изоэнтропический, либо энтропия системы не изменяется, либо dS=0. Адиабатическое сжатие – это такое сжатие, при котором не происходит изменения теплопередача с окрестностями. Чтобы адиабатическое сжатие было обратимым, процесс сжатия должен быть без трения.
An пример обратимой адиабаты сжатие, которое также называют изоэнтропическим сжатием, можно найти в газовой турбине или современных реактивных двигателях. Этот газ турбины работают по циклу Брайтона как показано ниже.

На приведенном выше рисунке идеал Цикл Брайтона состоит из четырех термодинамических процессов.
Этап 1-> этап 2: изоэнтропическое сжатие
Этап 2-> этап 3: Изобарический нагрев
Этап 3-> этап 4: Изоэнтропийное расширение
-
Адиабатный процесс
Адиабатный
процесс- это процесс без теплообмена с
внешней средой. При адиабатном процессе
энергообмен рабочего тела с окружающей
средой происходит только в форме работы,
энергообмена в форме теплоты нет. Эти
условия выражаются соотношением:
.
Тогда уравнение первого закона
термодинамики для адиабатного процесса
имеет вид:
.
(5.4)
Из
этого уравнения видно, что работа
адиабатного процесса расширения
совершается вследствие уменьшения
внутренней энергии газа и, следовательно,
температура газа уменьшается. Работа
адиабатного сжатия полностью идет на
увеличение внутренней энергии газа, то
есть на повышение его температуры. Таким
образом, изменение внутренней энергии
и работа в адиабатном процессе эквивалентны
по величине и противоположны по знаку.
Выведем
уравнение адиабаты для идеального газа.
Воспользуемся уравнением первого закона
термодинамики:
т.к.
,
то
(5.5)
Разделив
переменные, получим:
(5.6)
Интегрируя
(5.6) при k
= const,
получим
,
откуда
(5.7)
Уравнение
(5.7) является уравнением адиабаты.
На
рис. 5.10 приведен адиабатный процесс
расширения газа в
-диаграмме.
Из
уравнения (5.7) следует:

то
есть при адиабатном расширении давление
падает, а при сжатии возрастает.
Рис.
5.10. Адиабата идеального газа
Учитывая,
что в адиабатном процессе изменяются
все три параметра состояния, необходимо
выявить зависимости между v
и T,
p
и T.
Зависимость
между температурой T
и объемом
v
можно получить из уравнения (5.8) и
уравнений состояния, записанных для
точек процесса 1
и 2:
Р1v1
= RT1
и Р2v2=RT2,
откуда
(5.9)
Из
уравнений (5.8) и (5.9) следует:
(5.10)
Далее
из уравнений (5.8) и (5.10) следует:
(5.11)
При
k
= const
для вычисления работы адиабатного
процесса можно записать несколько
формул. Из уравнения
приcv
= const
имеем:

Учитывая
соотношения (5.10) и (5.11), уравнение (5.12)
запишем в виде:
(5.13)
Располагаемая
работа в адиабатном процессе определим
из соотношения
,
то есть
(5.14)
Для
обратимого адиабатного процесса
,
поэтому
,
то есть обратимый адиабатный процесс
будет изоэнтропным и в
-диаграмме
изображается прямой линией, параллельной
оси(рис. 5.11). Процесс адиабатного расширения
изображается вертикальной прямой 2-1,
идущей вниз, а процесс адиабатного
сжатия 1-2 – вертикальной прямой, идущей
вверх.
Рис.
5.11. Адиабатный процесс в
-диаграмме
Теплоемкость
в адиабатном процессе равна нулю:
.
-
a
a
Рис.
5.12. Схема распределения энергии в
адиабатном процессе:
а-
при расширении газа; б – при сжатии газа
-
Политропный процесс
Политропный
процесс – любой произвольный процесс
изменения состояния рабочего тела,
протекающий при постоянной теплоемкости
сx,
то есть
c =
cx
= const. Линия
процесса называется политропой.
Из
определения политропного процесса
следует, что основные термодинамические
процессы (изохорный, изобарный,
изотермический, адиабатный, если они
протекают при постоянной удельной
теплоемкости, являются частными случаями
политропного процесса.
Другими
словами, политропный процесс характеризуется
одной и той же долей количества подводимой
теплоты, расходуемой на изменение
внутренней энергии системы.
Уравнение
политропного процесса можно получить
из уравнений первого закона термодинамики
для идеального газа:
далее
имеем:
Разделим
первое уравнение на второе
и
обозначим
,
тогда
Интегрируя
полученное соотношение в пределах от
начала до конца процесса, находим:
,
или
после потенцирования
получаем
уравнение политропного процесса
Поскольку
уравнение политропы отличается от
уравнения адиабаты только значением
показателя n,
то все соотношения между основными
параметрами могут быть представлены
формулами, аналогичными формулам для
адиабатного процесса:
Удельная
теплоемкость политропного процесса
может быть определена из выражения для
показателя политропы
,
откуда
,
где
k
– показатель адиабаты.
Последнее
уравнение позволяет определить удельную
теплоемкость политропного процесса
для любого значения n.
Если в это уравнение подставить значения
для частных случаев, то можно получить:
|
Изохорный |
n |
c |
v |
|
Изобарный |
n |
c |
p |
|
Изотермический |
n |
c |
T |
|
Адиабатный |
n |
c |
pvk |
Характер
зависимости
от показателя политропыn
графически показан на рис. 5.13.
Рис.5.13.
Зависимость теплоемкости от показателя
политропы.
Уравнение
удельной работы изменения объема,
совершаемой телом при политропном
процессе, имеет аналогичный вид с
уравнением удельной работы в адиабатном
процессе
или

Располагаемая
работа равна:
Изменение
удельной внутренней энергии газа и
теплота в политропном процессе
определяются из уравнений:
.
Изменение
удельной энтальпии определяется по
формуле, справедливой для всех процессов
идеального газа, включая политропный
процесс:
.
Изменение
удельной энтропии газа в политропном
процессе равно:
или
для конечного изменения состояния
.
Значение
показателя политропы в любом политропном
процессе может быть определено по
координатам любых двух точек графика:



Если
в vP–
и sT
– координатах
выбрать некоторую произвольную точку
и провести из нее все рассмотренные
термодинамические процессы, то все поле
построенной таким образом диаграммы
делится на восемь областей, характеризующихся
определенными признаками (рис. 5.14).
Рис.
5.14. Взаимное расположение политроп в
зависимости от величины показателя n
Соседние файлы в папке Термодинамика
- #
- #
- #
- #
- #
- #
- #
- #
Определить температуру и работу при адиабатном сжатии 0,01 азота до 1/10 его первоначального объема, если начальные температура 26,8° С и давление [c.12]
Изменение температуры газа в полости за счет адиабатного сжатия определяется по уравнению [c.70]
Цикл Карно—это обратимый цикл, состоящий из четырех процессов изотермического расширения при температуре Т , изотермического сжатия при температуре Т , адиабатного расширения и адиабатного сжатия газа. Этот цикл схематически изображен на рис. I, 3, его проекция на координатную плоскость р—и представлена на рис. 1,4. [c.43]
Работа, затраченная на адиабатное сжатие 3 кг воздуха, равна 471 кДж. Начальная температура 15° С. Определить изменение внутренней энергии и конечную температуру. Среднюю теплоемкость Сг. воздуха при сжатии принять равной 0,732 кДж/(кг-К). [c.41]
Поясним это на примере адиабатного процесса сжатия. Работу компрессора в этом процессе можно рассматривать как сумму работ изотермического сжатия (линия 1—2) и цикла 2—1—2 —2 теплового насоса (рис. 12, а) при этом источником низкой температуры является тепло, отводимое в изотермическом сжатии, а нагреваемый источник меняет температуру в пределах начальной и конечной температур адиабатного сжатия. В идеальном случае процессы сжатия компрессора 1—2 и подвода тепла 2—1 в цикле теплового насоса взаимно исключают друг друга. В результате получается сжатый газ при наименьшей затрате работы и количество тепла 9=Ср(Т2–Т1) с затратой работы [c.41]
Определить работу адиабатного сжатия 1 моль двухатомного идеального газа при повышении температуры от 15 до 25° С. [c.12]
Нагрев газа, подсчитываемый по (7-51) и (7-52), соответствует расходу мощности вентилятора, определяемому по общепринятой формуле (7-49), которая основана на том допущении, что плотность газа в машине не изменяется. Погрешность определения становится значительной при больших напорах вентилятора, так как в действительности при адиабатном процессе плотность газа изменяется, а процесс в машине близок к адиабатному. Для оценки этой погрешности принимаем, что в вентиляторе идет процесс адиабатного сжатия и температура газа изменяется в соответствии с формулой [c.229]
Пример 5.3. Компрессор всасывает 100 м ч воздуха при давлении />1 = 0, МПа и температуре /[ = 27 С. Конечное давление воздуха составляет 0,8 МПа. Найти теоретическую мощность двигателя для привода компрессора и расход охлаждающей воды, если температура ее повышается на 13 С. Расчет произвести для изотермического и адиабатного сжатия. Теплоемкость воды принять равной 4,19 кДж/(кг К). [c.148]
Оценка точности метода условных температур. Для оценки точности метода условных температур выполнялись численные расчеты с использованием уравнения состояния Боголюбова— Майера (1.32) применительно к хладагенту R12, свойства которого наиболее сильно отличаются от свойств идеального газа [17]. Расчетной проверке подвергались политропные процессы, соответствующие адиабатному сжатию с потерями, протекающие в непосредственной близости от линии насыщения. В этой области [c.116]
Считая процесс сжатия в насосе адиабатным, а газовую смесь — двухатомным идеальным газом, найти температуру после сжатия, если до сжатия t = 15. Газ поступает в насос под давлением 270 атм давление выходящего из насоса газа 300 атм. Для расчета воспользоваться уравнением, приведенным в условии задачи 1. [c.14]
Быстрое повышение температуры при воспламенении и взрыве увеличивает давление газов. Если давление не успевает передаться окружающей среде, то возникает сильное адиабатное сжатие, в результате чего соседние зоны нагреваются до температуры воспламенения и загораются. [c.360]
При температуре теплоприемника Гг в результате соприкосновения газа с теплоприемником осуществляется изотермическое сжатие газа до объема У4, чтобы при последующем адиабатном сжатии газ достиг точно исходной температуры Т,. Вся работа Шз, затрачиваемая на сжатие, переходит в теплоту Оа, которая и [c.67]
В связи с. этим при адиабатном изменении объема давление изменяется быстрее, чем при постоянной температуре. Если газ расширять адиабатно, начиная от точки я, то кривая 2 пройдет круче изотермы / и равное давление будет достигнуто при меньшем объеме, так как адиабатное расширение сопровождается охлаждением. Наоборот, если исходя из состояния точки b вести адиабатное сжатие, то равное давление будет достигнуто прн большем, по сравнению с изотермой, объеме причина — нагревание газа. Приближенно условиям адиабаты отвечает быстрое проведение процессов сжатия или расширения, когда сравнительно медленно протекающий теплообмен мало влияет в пределах интересующего нас времени на изменение внутренней энергии газа и его температуру. [c.40]
Последний процесс — адиабатное сжатие газа — мы проведем, отъединив газ от теплоприемника, изолировав его полностью от теплообмена с окружающей средой и подвергнув адиабатному сжатию до исходного объема Vi, т. е. приведя его опять к исходному состоянию, характеризующемуся температурой Ti, давлением Pi и объемом V. В этом последнем процессе внутренняя энергия газа возрастает на величину, равную затраченной работе сжатия, и, следовательно [c.139]
Единственная возможность осуществления в этих условиях цикла, состоящего только из равновесных процессов, заключается в следующем. Теплоту от горячего источника к рабочему телу нужно подводить изотермически. В любом другом случае температура рабочего тела будет меньше температуры источника 7 ], т.е. теплообмен между ними будет неравновесным. Равновесно охладить рабочее тело от температуры горячего до температуры холодного источника Т2, не отдавая теплоту другим телам (которых по условию нет), можно только адиабатным расширением с совершением работы. По тем же соображениям процесс теплоотдачи от рабочего тела к холодному источнику тоже должен быть изотермическим, а процесс повышения температуры рабочего тела от до Т — адиабатным сжатием с затратой работы. Такой цикл, состоящий из двух изотерм и двух адиабат, называется циклом Карно. [c.152]
В качестве основного термодинамического холодильного цикла обычно рассматривают обратный цикл Карно (рис. 18), состоящий из четырех последовательных обратимых процессов двух изотермических и двух адиабатных. Рабочее тело отнимает тепло у охлаждаемого тела при постоянной температуре Гд, подвергается адиабатному сжатию до температуры окружающей среды, передает теило (< = ( о + ) окружающей среде при постоянной температуре и далее подвергается адиабатному расширению в расширительной машине до температуры охлаждаемого тела. В процессе теплообмена между рабочим телом и источниками (охлаждаемым телом и окружающей средой) разности температур принимаются бесконечно малыми. [c.52]
Для исследований плотности газов при весьма высоких давлениях и температурах может быть применен метод адиабатного сжатия. Быстро движущийся поршень 5 (рис. 9.9) сжимает вещество в стволе /. при этом развиваются высокие давления и температуры. После сжатия поршень возвращается в исходное состояние, выталкивая разгонявший его газ в атмосферу. Давление газа измеря.ют манганиновым манометром, размещенном в корпусе 4. Температура в опытах, определяемая по уравнению адиабаты расчетным путем, достигает 7000 К. Подробное описание этого метода можпо найти в [20, 21]. [c.438]
Смолистый туман имеет температуру газа и теплоемкость 0,5 ккал/кг-град-, он оказывает охлаждающее действие при сжатии газовой смеси, уменьшая тем самым расход энергии по сравнению с адиабатным сжатием идеального газа в пределах тех же давлений. [c.169]
Температура при адиабатном сжатии находится в следующей зависимости от степени сжатия [c.187]
Рис. Vni. 12 иллюстрирует повышение температуры при обратимом адиабатном сжатии газа (или понижение — при расширении). [c.176]
По диаграмме рис. VHI. 15 можно определить работу А цикла адиабатного сжатия любого газа при любых значение k == Ср/С (от 1,67 до 1) в расчете для одной температуры засасываемого газа в одноступенчатом компрессоре. Для определения идеальной работы в n ступенях надо вычислить отношение давлений на одну [c.178]
Уравнения Пуассона по смыслу их вывода приложимы только к равновесному адиабатному процессу. Для расчета быстрого (а значит, и неравновесного) адиабатного сжатия или расширения уравнениями Пуассона, по сути дела, пользоваться нельзя. Резко, ударом увеличивая нагрузку на поршень, удерживающий газ в цилиндре, мы затрачиваем на сжатие газа больше работы, чем потребовалось бы при осторожном, постепенном увеличении нагрузки в связи с этим температура газа будет возрастать быстрее, чем это следует по уравнению Пуассона. При неравновесном расширении газ производит меньщую работу, чем мог бы произвести (при равновесном расширении), и поэтому температура будет падать медленнее. [c.30]
Представим себе газ, заключенный в цилиндр, который термически изолирован, и будем подвергать этот газ равновесному адиабатному сжатию. Известно, что температура газа повышается. Спрашивается, почему она возрастает, как это понять с молекулярной точки зрения Молекулы газа находятся в движении. Ударяясь о стенки и о поршень, они изменяют направление своего движения, причем каждый раз, когда какая-либо молекула ударяется о движущийся поршень, эта молекула приобретает некоторый прирост скорости, заимствованный от поршня. При каждом таком соударении этот прирост скорости, конечно, весьма мал. Однако он не равен нулю. Допустим, что мы стали двигать поршень в два раза медленнее тогда раньше, чем он пройдет определенное расстояние, та же, какая-то замеченная нами молекула успеет в два раза большее число раз удариться о поршень, и поэтому (хотя каждый раз она получит теперь в два раза меньший прирост скорости, но так как число ударов также в два раза возрастет) общий прирост скорости, а стало быть, в итоге и общее повышение температуры, вызванное определенным перемещением поршня, останутся без изменения. Поэтому, когда мы переходим в пределе к бесконечно медленному перемещению поршня, эффект повышения температуры сохраняется и равновесное адиабатное сжатие приводит к разогреву газа. Эти простые соображения об адиабатно сжимаемом газе полезно иметь в виду, анализируя содержание закона Нернста. [c.184]
Мне кажется, что вышеприведенное рассуждение, касающееся молекулярного механизма равновесного адиабатного сжатия при абсолютном нуле, интересно и поучительно в том отношении, что, с одной стороны, оно ведет к закону Нернста и в то же время вскрывает противоречивость классических взглядов на свойства веществ при температурах, близких к абсолютному нулю. [c.186]
Далее, существенно отметить, что упомянутое рассуждение успешно только для температуры абсолютного нуля, но не для температур, близких к абсолютному нулю. Действительно, рассматривая адиабатное сжатие кристалла, имеющего температуру, близкую к абсолютному нулю (но не равную нулю), мы уже не можем на основании молекулярной картины сжатия предугадать, что в этом случае сжатие почти не приведет к повышению температуры. [c.186]
Большой вклад в изучение в СССР вихревого эффекта внес А.П. Меркулов. В предложенной им гипотезе процесса энергетического разделения большое внимание уделено турбулентному энер-гообмену. Энергия турбулентности используется для осуществления работы охлаждения вынужденного вихря, так как за счет радиальной составляющей турбулентной пульсационной скорости элементарные турбулентные моли перемещаются по радиусу в поле высокого радиального градиента статического давления . При адиабатном сжатии или расширении турбулентные моли изменяют свою температуру, соответственно вызывая нафев или охлаждение газа при смешении со своим слоем. Передавая тепло из зоны низкого в зону высокого статического давления, они осуществляют элементарные турбулентные циклы. Охлаждение имеет место только в приосевом потоке, так как в нем и статическая температура, и окружающая скорость падают, обеспечивая снижение полной температуры . Основная доля кинетической энергии исходного потока зафачивается на закрутку вынужденного вихря и дисси-пирует в турбулентность. Энергия на закрутку передается до тех пор, пока не наступит равновесие со свободным вихрем в сопловом сечении . Считается, что формирование центрального потока происходит по всей длине фубы и завершается в сопловом сечении. Учет поля центробежных сил проводится через радиальный фадиент статического давления. Передача кинетической энергии направлена от периферии к оси, и часть ее расходуется на турбулентность. Термодинамическая температура в приосевой области ниже, чем в периферийной области вихревой трубы. [c.23]
Закон Нернста чрезвычайно упростил вычисление энтропии. Желая вычислить энтропию какого-либо тела в состоянии 1 по отношению к его нулевому состоянию Со (кристалл при р = 0иГ = 0)и учитывая, что энтропия как сумма приведенных теплот не зависит от пути процесса, мы можем избрать любой путь перехода из Со в /. Для применения закона Нернста проще всего избрать такой путь перехода исходя из нулевого состояния Со, адиабатно сжать тело до требуемого давления и затем изобарно нагреть его до требуемой температуры (см. рис. 15). [c.188]
Полная удельная энергия жидкости складывается из механической удельной энергии и удельного теплосодержания. Поэтому, строго говоря, напор насосав равен приращению полной удельной энергии жидкости в насосе W только при изотермном процессе, т. е. при одинаковой температуре жидкости на входе и на выходе насоса. Если в результате политропного или адиабатного сжатия жидкости в насосе, а также в результате потерь механической энергии жидкости происходит нагрев последней, то [c.16]
Тем не менее наблюдение за температурой перегрева пара на нагнетательной стороне компрессора является полезным. Сравнение температуры пара в конце адиабатного сжатия в компрессоре с действительной температурой пара, выходящего из компрессора, позволяет с некоторым приближением определить состояние пара, всасываемого в компрессор в тех случаях, когда отсутствует непосредственное наблюдение за перегревом всасываемого пара резкое падение температуры на нагнетательной стороне компрессора является признаком наступления влажного хода. Кроме того, по температуре перегрева могут быть обнаружены некоторые нарушения нормальной работы установки, о которых говорится ниже. [c.494]
При отсутствии под рукой диаграммы для аммиака можно приблизительно определить температуру 1 в конце адиабатного сжатия в компрессоре в интервале температур кипения и конденсации t (в случае всасывания сухого насыщенного пара), по эмпирической формуле [c.495]
Высокая температура пара на выходе из компрессора не всегда может быть результатом ненормальной работы установки. Так, в летнее время при относительно высокой температуре конденсации и низкой температуре кипения аммиачный компрессор даже теоретически должен работать с высоким перегревом на нагнетании (например, при = —30° С и / = 22° С температура в конце адиабатного сжатия пара, поступившего в компрессор в сухом насыщенном состоянии, равна 127° С) это явление несомненно нежелательное, но независящее от состояния оборудования. [c.501]
В табл. 6 приведены значения температур нагнетания для аммиачных одноступенчатых компрессоров, работающих сухим, насыщенным, перегретым (перегрев на 10° С) и влажным (х = 0,95) паром. Таблица составлена по тепловой диаграмме для адиабатного сжатия агента. [c.185]
Действительная температура адиабатного сжатия находится по форцуле, приведенной в / 1 7 [c.39]
Это значит, что при адиабатном расширении газа (работа ноло-жи- ельпа) его температура падает и, наоборот, при адиабатном сжатии температура газа повышается. [c.29]
На осуществление сжатия расходуется энергия приводного двигателя машины. Сжатие газа сопровождается повышением его температуры. В каждой ступени центробежной компрессорной машины идеальным является процесс адиабатного сжатия газа. Действительное количество подводимой энерпин от двигателя больше, чем требуется для адиабатного сжатия газа. Дополнительная энергия затрачивается на преодоление трения в каналах рабочего колеса, диффузора и корпусе, а также тренпя колесных дисков в среде сжимаемого газа. Вся дополнительно подводимая энергия превращается в тепло, что ведет к дополнительному повышению температуры газа. [c.265]
Весьма перспективным хладагентом является 1 502, представляющий собой азеотропную смесь Н22(48,8% массы) и Н115(51,2% массы). Он имеет существенные преимущества перед Н22 более низк/ю температуру конца адиабатного сжатия, меньшее отношение давлений при заданных температурах конденсации и кипения хладагента, наиболее высокие значения объемной холодопроизводительности в широком интервале температур кипения (табл. IV.2), возможность получения температур до —40°С при нормальном давлении в картере компрессора. Эти достоинства К502 позволяют создавать простые, компактные и надежные в эксплуатации одноступенчатые низкотемпературные хо-/юдильные установки. [c.59]
Имея этот же источник т, можно совершить и цикл АВ О А, в котором АВ — обратимо-адиабатное сжатие газа, ВО — необратимое изохорное понижение температуры от tв до т, а О А — обратимое изотермическое расширение (см. рис. 34). В этом необратимом цикле с одним источ- ником также положительна внешняя работа, так как И еЛВ > О, 1 еВ В = О и We.D A < О, но ШеЛВ > еВ А СоВбрШИТЬ этот ЦИКЛ В противоположном направлении, т. е. осуществить цикл АО В А невозможно, так как, имея тот же источник, нельзя вызвать изохорное повышениеО В температуры газа. [c.113]
Рассмотрим диаграмму V—P (рис. VIII. 13), характеризующую происходящее при непрерывном сжатии (расширении) в идеальном одноступенчатом компрессоре. При адиабатном сжатии температура повышается и ход этого сжатия изображается кривой ВЕ адиабатная работа А при этом несколько больше, чем изотермическая (разность выражается площадью ВЕС). [c.177]
Изотермическое сжатие мы осушествим, вводя газ в соприкосновение с теплопрнемником, температура которого равна точно Гг, и сжимая газ при этой температуре до объема Va, определяемого тем, чтобы при последующем адиабатном сжатии газ достиг точно температуры Т. [c.139]
На основе обобщенного уравнения состояния, справедливого в области температур 200+400 К и давлений до 40 бар, с использованием введенных авторами параметров корреляции компонентов смеси И разработан алгоритм и составлена программа расчета адиабатного процесса природного газа и газа пиролиза на ЭЦВМ. В качестве прюде-ра приведены результаты расчета процесса адиабатного сжатия газовой смеси из двенадцати компонентов. Коэффициенты, необходимые для расчетов, представлены в таблице. [c.253]
При двухступенчатом сжатии работа адиабатного сжатия в первой ступени будет характеризоваться площадью Ыйек. После сжатия до промежуточного давления но адиабате газ поступает в промежуточный холодильник, где охлаждается при постоянном давлении до первоначальной температуры. Вследствие охлаждения газа объем его сокращается на величину г/, равную у, благодаря чему точка начала сжатия возвращается на исходную изотерму йЪ. Адиабатное сжатие во II ступени будет изображаться адиабатной /г, и работа сжатия II ступени будет изображаться площадью аЦка. Таким образом, при двухступенчатом сжатии мы выигрываем работу, равную площади заштрихованной на диаграмме. [c.186]