Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
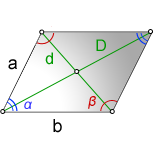
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
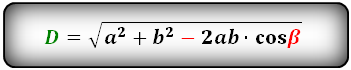
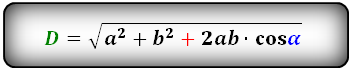
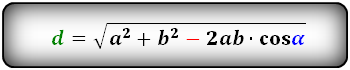

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
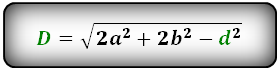
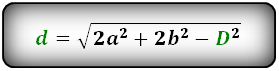
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.

D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
S – площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
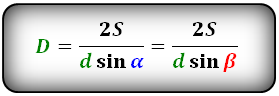
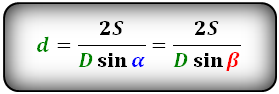
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
Посчитать диагональ прямоугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Посчитать диагональ прямоугольника
Чтобы посчитать диагональ прямоугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).
Просто подставьте их в калькулятор и получите результат.
Чему равна диагональ прямоугольника если сторона
a = ,
а сторона
b = ?
Ответ: d =
0
Теория
Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?
Формула
d = √a2 + b2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
d = √102 + 52 = √100 + 25 ≈ 11.18 см
См. также
Загрузить PDF
Загрузить PDF
Диагональ — это отрезок, который соединяет две противолежащие вершины прямоугольника.[1]
В прямоугольнике две равные диагонали.[2]
Если известны стороны прямоугольника, диагональ можно найти по теореме Пифагора, потому что диагональ делит прямоугольник на два прямоугольных треугольника. Если стороны не даны, но известны другие величины, например, площадь и периметр или отношение сторон, можно найти стороны прямоугольника, а затем по теореме Пифагора вычислить диагональ.
-

1
-

2
-

3
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-

4
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[5]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
-

1
Запишите формулу для вычисления площади прямоугольника. Формула:
, где
— площадь прямоугольника,
— длина прямоугольника,
— ширина прямоугольника.[6]
(На рисунке вместо S использовано обозначение А.) -

2
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
-

3
Перепишите формулу так, чтобы обособить
. Для этого разделите обе стороны уравнения на
. Затем полученное выражение нужно подставить в формулу для вычисления периметра.
-

4
Запишите формулу для вычисления периметра прямоугольника. Формула:
, где
— длина прямоугольника,
— ширина прямоугольника.[7]
-

5
В формулу подставьте значение периметра прямоугольника. Это значение подставляется вместо
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
-

6
Разделите обе стороны уравнения на 2. Вы получите сумму сторон прямоугольника, а именно
.
-

7
В формулу подставьте выражение для вычисления
. Это выражение, полученное при обособлении
.
-

8
Избавьтесь от дроби. Для этого обе части уравнения умножьте на
.
-

9
Приравняйте уравнение к 0. Для этого из обеих сторон уравнения вычтите член с переменной первого порядка.
-

10
Упорядочьте члены уравнения. Первым членом будет член с переменной второго порядка, затем член с переменной первого порядка, а затем свободный член. При этом не забудьте про знаки («плюс» и «минус»), которые стоят перед членами. Обратите внимание, что уравнение запишется в виде квадратного уравнения.
-

11
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-

12
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (это корни уравнения), которые в случае прямоугольника являются его длиной и шириной.
-

13
-

14
-

15
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-

16
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[10]
Вы найдете, то есть гипотенузу треугольника, а значит, и диагональ прямоугольника.
Реклама
-

1
-

2
-

3
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
-

4
В формулу подставьте выражение, характеризующее отношение сторон. В случае прямоугольника можно подставить выражение для вычисления
или
.
-

5
Запишите квадратное уравнение. Для этого раскройте скобки и приравняйте уравнение к нулю.
-

6
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-

7
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (так называемые корни уравнения).
-

8
Подставьте найденное значение ширины (или длины) в уравнение, характеризующее отношение сторон. Так можно найти другую сторону прямоугольника.
-

9
-

10
-

11
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-

12
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[16]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
Об этой статье
Эту страницу просматривали 557 104 раза.
Была ли эта статья полезной?
|
Длину d диагонали квадрата по отношению к длине b его стороны находят по теореме Пифагора на основании того, что все стороны квадрата равны и все углы, образованные сторонами квадрата, прямые. Поэтому сумма квадратов двух сторон равна квадрату диагонали, являющейся гипотенузой прямоугольного треугольника: 2b^2=d^2, d= b√2. Если принять сторону квадрата за единицу, то d= √2=1,414… . автор вопроса выбрал этот ответ лучшим
Степан-16 5 лет назад Диагональ (с) – это гипотенуза треугольника, у которого катеты (а и а, поскольку они равны) – это две стороны квадрата. Два способа решения.
Алиса в Стране 5 лет назад Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой “а”, а длину гипотенузы латинской буквой “с”, получаем формулу: c² = a² + a² = 2 a² с = √2a. Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон.
Ксарфакс 5 лет назад Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины. В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника. Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора. a² + b² = c². Пусть c – это диагональ, a и b – стороны квадрата, которые по определению равны между собой. Перепишем формулу в виде: 2a² = c². Выразим диагональ c: c = √2 * a. Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2.
Пример Сторона квадрата равна 10 см. Диагональ будет равна 10 * √2 см ≈ 14 см.
terli4eno4ka 5 лет назад Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр:
К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле √2*a = √2*100 = 1,4142*100 = 141,42 см.
Zolotynka 5 лет назад Исходя из того, что, согласно теореме Пифагора, диагональ делит квадрат на два конгруэнтных прямоугольных треугольника, мы можем использовать длину стороны квадрата, чтобы найти длину диагонали (которая будет являться гипотенузой треугольника). Следовательно, d=b√2, где d – длина диагонали, а b – длина одной из сторон. ** Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07. ** Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул.
Так же как и найти гипотенузу у равнобедренного треугольника. Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны. Имея в условии слово “квадрат” можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй. Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали.
Alexgroovy 5 лет назад Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата. d = √2 * a, где a – длина стороны квадрата. d = √2S, здесь S – площадь квадрата. d = P / 2√2, где P – периметр.
Татьяна-Татьяна 9 лет назад На основании теоремы Пифагора – сумма квадратов катетов равна квадрату гипотенузы. То есть, если сторона квадрата равна “а”, то диагональ его (“в”) равна корню квадратному из выражения (2a^2). То есть вот так: а^2=b^2+b^2 а^2= 2b^2 a=√2b^2 a=b√2
gematogen 8 лет назад Если взять любой квадрат и принять его сторону за букву – a, то диагональ будет равна √2а. Это можно вычислить так же по теореме Пифагора, при которой сторона a*a+a*a=2a*a, из этого извлекаем корень и получаем √2а. Знаете ответ? |
При решении задач по физико-математическим дисциплинам иногда необходимо найти диагонали прямоугольника. Формула в интернете не всегда является достоверной. Очень важно на начальных стадиях вычислений правильно идентифицировать фигуру, чтобы применить к ней нужные свойства и соотношения. Специалисты рекомендуют не приступать сразу к практике, а разобраться с теорией.
Оглавление:
- Общая информация
- Формулы и соотношения
- Пример расчета параметров
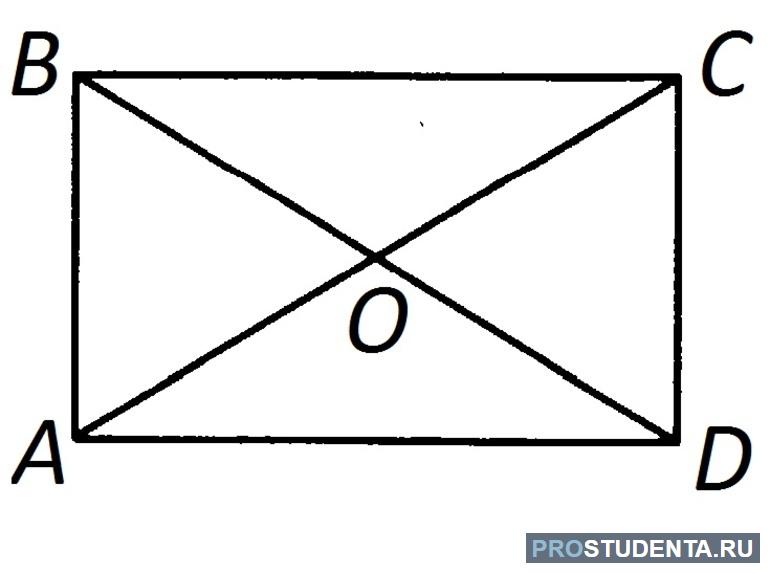
Общая информация
Прямоугольник — геометрическая плоская фигура, состоящая из четырех попарно параллельных сторон, между которыми образованы прямые углы. Ее можно перепутать с квадратом, имеющим похожие свойства и тождества. При решении задачи очень важно правильно найти фигуру, имеющую определенные признаки определения. Некоторые учащиеся путают последние со свойствами. Эти два термина отличаются между собой.
Методика идентификации
Признак — совокупность некоторых критериев, позволяющих правильно различать фигуры. Прямоугольник возможно идентифицировать по таким правилам:

- Неравенство сторон, являющихся смежными.
- Диагонали при пересечении не образуют угол в 90 градусов.
- Диагонали не являются биссектрисами углов больших треугольников, полученных при пересечении.
- Окружность можно только описать, а не вписать.
Если для искомой фигуры применим хотя бы один из признаков, то ее возможно классифицировать как прямоугольник.
После успешной идентификации необходимо перейти к рассмотрению свойств, которые рекомендовано специалистами использовать при расчетах параметров и доказательстве утверждений (тождеств и теорем).
Важные свойства
Свойства — набор или список утверждений и тождеств, используемых при вычислениях требуемых величин, а также для доказательства теорем, а именно:
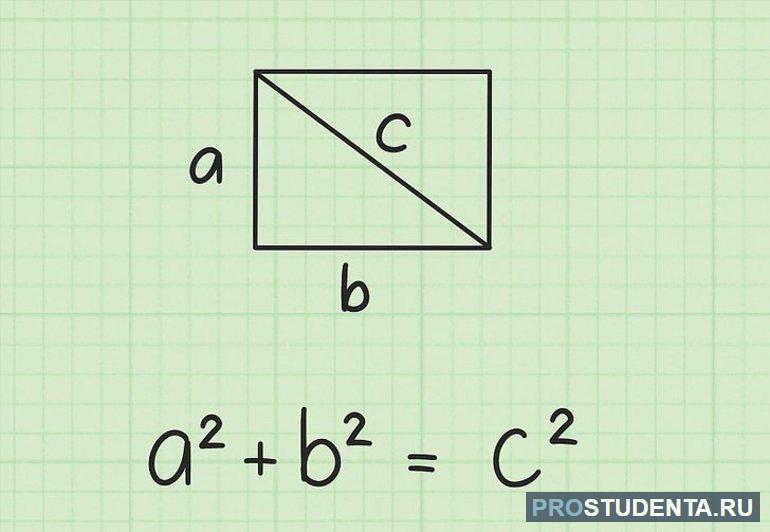
- Все углы прямые, а их алгебраическая сумма равна 360.
- Несмежные стороны параллельны и равны.
- Точка пересечения диагоналей – центр симметрии и делит их на две части. Кроме того, средняя линия проходит через нее.
- Формула диагонали (m) прямоугольника через стороны p и t: m=(рp+tt]^1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение.
- Подобность малого и большого треугольников, образованных диагоналями.
- Существует только описанная окружность, диаметр которой эквивалентен диагонали прямоугольника.
- При проведении диагонали образуются два равных треугольника, являющиеся прямоугольными.
Следует отметить, что вышеописанные свойства – это требуемый минимум, которого недостаточно для выполнения вычислений и доказательства других тождеств.
Формулы и соотношения
Чтобы ориентироваться в формулах, нужно ввести некоторые обозначения. К ним принадлежат следующие:

- Диагональ – m.
- Стороны – k и l.
- Периметр – P.
- Полупериметр – р.
- Площадь – S.
- Острый угол, который образуют две диагонали – Z, а тупой – Y.
- Диаметр – D.
После этого необходимо рассмотреть основные тождества. Их рекомендуется применять при вычислениях различных параметров фигуры.
К ним относятся такие выражения:
- Периметр: P=2S/к + (2/к)k 2 =2k+2(m 2 -k 2 )^(1/2))=2k+2(D 2 -k 2 )^(1/2)).
- Площадь: S=[Pк — 2к 2 ]/2=[Pl — 2l 2 ]/2=k[m 2 -k 2 ]=[sin(Z)/2]m^2 .
- Диагонали: m=[k 2 +l 2 ]^(1/2)=(1/k)(S 2 +k 4 )^(1/2).
Кроме того, найти диагональ прямоугольника возможно, используя формулу такого вида: m=((2k+2l) 2 -4(2k(k+l)+8k 2 )^(1/2) * 0,5. Величины «(2k+2l)» можно заменить периметром Р, когда он известен.
Следует отметить, что найти длину диагонали прямоугольника возможно при известном D. Соотношение имеет следующий вид: m=2R=D.
Пример расчета параметров
У прямоугольника известна диагональ (m=10) и периметр (Р=28). Необходимо узнать длину его сторон. Решать задачу нужно по такому алгоритму:

- Диагональ находится по следующему выражению: m^2=k^2+l^2.
- Формула для вычисления периметра: P=2(k+l).
- Составить систему уравнений для нахождения сторон: 100=k^2+l^2 и 28=2(k+l).
- Выразить из второго уравнения одну из сторон: k=14-l.
- Подставить в первое: (14-l)^2+l^2=100.
- Раскрыть скобки: 196-28l+l^2+l^2=2l^2-28l+196=100.
- Уравнение имеет такой вид: l^2-14l+48=0.
- Вычислить его корни: l1=6 и l2=8.
- Подставить в четвертый пункт и посчитать стороны: l=6 и к=8.
Следует отметить, что расчет корней производится подстановкой, при которой возникают дубли решений. Среди них требуется выбрать любых две пары. Исходя из девятого пункта, можно рассчитать значение площади, зная две стороны. Используя формулы, можно находить и другие параметры. Например, высчитать значение острого угла.
Таким образом, перед решением задач по геометрии математики рекомендуют правильно идентифицировать геометрическую фигуру при помощи признаков, а затем использовать какие-либо соотношения.


