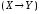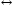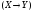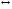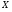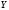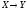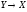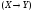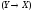Запись утверждений на языке алгебры высказываний. Формулы алгебры высказываний
Простые и составные высказывания
Бывают два вида высказываний: простые и составные. Составные высказывания получаются из простых с помощью логических символов %%overline, land, lor, rightarrow, leftrightarrow%%. Рассмотрим высказывание «Иванов окончил школу и поступил в институт». Оно образовано из простых высказываний «Иванов окончил школу» и «Иванов поступил в институт» с помощью операции конъюнкции. Обозначим эти высказывания через %%A%% и %%B%% соответственно, тогда сложное высказывание «Иванов окончил школу и поступил в институт» имеет вид %%A land B%%. При этом высказывания %%A%% — «Иванов окончил школу» и %%B%% — «Иванов поступил в институт» нельзя представить ввиде составных высказываний. Поэтому они простые (элементарные).
Пример
Дано высказывание «Если число %%a%% делится на число %%c%% и число %%b%% делится на число %%c%%, то их сумма %%a+b%% делится на число %%c%%». Обозначить буквами простые высказывания и, используя логические символы, выразить данное высказывание через простые.
Обозначим:
- %%A%%: «число %%a%% делится на число %%c%%»;
- %%B%%: «число %%b%% делится на число %%c%%»;
- %%C%%: «сумма %%a+b%% делится на число %%c%%».
Тогда высказывание, с учетом замены, примет вид: «Если %%A%% и %%B%%, то %%C%%», которое на языке алгебры высказываний выглядит
$$
(A land B) rightarrow C.
$$
Формулы алгебры высказываний
Для определения понятия формулы нам необходимо понять, какие переменные используются в алгебре высказываний.
Пропозициональная переменная, или переменная для высказываний, — переменная, котороя может принимать одно из двух истинностных значений: «истина» или «ложь». Далее будем их называть просто переменными.
С помощью логических знаков (%%overline{ }, land, lor, rightarrow, leftrightarrow%%) и переменных можно составлять сложные высказывания, которые и будем называть формулами алгебры высказываний.
Например, формула %%X = (A land B) rightarrow (A lor B)%% получена так: сначала построены формулы %%A land B%% и %%A lor B%%, затем из этих двух формул получена исходная с помощью применения знака %%rightarrow%%.
Вместо переменных в формулу можно подставлять произвольные значения переменных. При вычислении значения формулы неважно как сформулированы входящие в нее высказывания, важно лишь их значения: «истина» или «ложь».
Порядок построения формулы позволяет составить таблицу истинности для формулы %%X%%. Для этого переберем всевозможные комбинации значений переменных %%A%% и %%B%% (каждая строка в таблице) и найдем значение интересующей нас формулы.
| %%A%% | %%B%% | %%A land B%% | %%A lor B%% | %%(A land B) rightarrow (A lor B)%% |
|---|---|---|---|---|
| %%0%% | %%0%% | %%0%% | %%0%% | %%1%% |
| %%0%% | %%1%% | %%0%% | %%1%% | %%1%% |
| %%1%% | %%0%% | %%0%% | %%1%% | %%1%% |
| %%1%% | %%1%% | %%1%% | %%1%% | %%1%% |
Таблица истинности для формулы %%X%%
В курсе математической логики дается следующее определение формулы алгебры высказываний:
- Переменные являются формулами.
- Если %%A%% и %%B%% — формулы, то выражения
$$
overline{A}, A land B, A lor B, A rightarrow B, A leftrightarrow B
$$
являются формулами. - Всякая формула есть либо переменная или образуется из переменных последовательным применением правила %%2%%.
Пример
Показать, что выражение %%X = (A lor B) rightarrow ((C land D) leftrightarrow overline{A})%% является формулой.
Действительно, %%A, B, C, D%% — переменные, следовательно, формулы по правилу %%1%%. Так как %%A%% — формула, то %%overline{A}%% — формула по правилу %%2%%. Так как %%A,B,C,D%% формулы, %%A lor B%% и %%C land D%% — формулы по правилу %%2%%. Так как %%C land D%% и %%overline{A}%% формулы, то %%(C land D) leftrightarrow overline{A}%% формула по правилу %%2%%. Так как %%A lor B%% и %%(C land D) leftrightarrow overline{A}%% формулы, то %%X%% — формула по правилу %%2%%.
Подформулы
Выражения, полученные при «сборке» формулы называются ее частями или подформулами. Например, формула %%X = (A lor B) rightarrow ((C land D) leftrightarrow overline{A})%% имеет следующие подформулы:
$$
A,B,C,D, overline{A}, A lor B, C land D, (C land D) leftrightarrow overline{A}, (A lor B) rightarrow ((C land D) leftrightarrow overline{A})
$$
Правила записи формул
При записи формул придерживаются следующих правил.
- Внешние скобки в формуле можно опускать. Например, вместо %%(A lor B)%% пишем %%A lor B%%.
-
Как и в арифметике, в алгебре высказываний у каждой операции есть свой приоритет. Приоритеты логических знаков, расположенные в порядке убывания, следующие:
$$
overline{ }, land, lor, rightarrow, leftrightarrow.
$$Приоритеты логических операций можно изменить, используя скобки.
Каждый предшествующий знак является «сильнее» последующего. Поэтому вместо записи %%(A land B) lor C%% можно писать %%A land B lor C%%, вместо записи %%A leftrightarrow (B lor C)%% — %%A leftrightarrow B lor C%%.
3. Если в формуле %%X = A land B land C land ldots land Z%% опущены скобки, то подрузамевается левосторонняя расстановка скобок и считается, что %%X = bigg(Big((A land B) land CBig) land ldotsbigg)land Z%%. Аналогично для подобных формул, имеющих знак %%lor%%, %%rightarrow%% или %%leftrightarrow%%.
Примеры
Пользуясь правилами %%1-3%% восстановить скобки в формуле
$$
X = A lor B land C leftrightarrow A rightarrow B rightarrow C
$$
По правилам %%1-3%% имеем %%X = Bigg(Big(A lor (B land C)Big) leftrightarrow Big((A rightarrow B) rightarrow CBig)Bigg)%%.
Пользуясь правилами %%1-3%% опустить лишние скобки в формуле
$$
X = Bigg((A leftrightarrow B) lor Big((A land B) land CBig) rightarrow Big((B lor C) land ABig)Bigg)
$$
Решение, над знаком равно будут указаны номера правил которые применяются.
$$
begin{array}{ll}
X &= Bigg((A leftrightarrow B) lor Big((A land B) land CBig) rightarrow Big((B lor C) land ABig)Bigg) overset{1}{=}\
&overset{1}{=} (A leftrightarrow B) lor Big((A land B) land CBig) rightarrow Big((B lor C) land ABig) overset{3}{=}\
&overset{3}{=} (A leftrightarrow B) lor (A land B land C) rightarrow Big((B lor C) land ABig) overset{2}{=}\
&overset{2}{=} (A leftrightarrow B) lor A land B land C rightarrow Big((B lor C) land ABig) overset{2}{=}\
&overset{2}{=} (A leftrightarrow B) lor A land B land C rightarrow (B lor C) land A.
end{array}
$$
Виды формул
Формула %%X%% называется тождественно истинной (или тавтологией), если она принимает значение «истина» при любых значениях входящих в нее переменных.
Например, формула %%X = (A land B) rightarrow (A lor B)%% является тождественно истинной, т.к. при любых значениях %%A%% и %%B%% она является истинной.
Существует две причины, по которым мы считаем высказывание истинным или ложным. Первое, на основе различных свойств объекта. Например, «Москва — столица Австрии» ложно, так как она ею не является. Точно также в случае «%%2 cdot 3 = 6%%» значение «истина» установлено из свойств рассматриваемых объектов. Второе, когда приписывается значение «истина» или «ложь» вне зависимости от свойств обсуждаемых объектов. Это и есть логическая истинность.
Рассмотрим утверждение «верно, что завтра пойдет дождь или завтра не пойдет дождь». Очевидно, что это утверждение является истинным, даже не зная погоды на завтрашний день. В данном случае мы имеем дело с утверждениями вида %%A lor overline{A}%%. Так как формула %%A lor overline{A}%% является тождественно истинной, то независимо от переменной %%A%%, утверждение истинно.
Формула %%X%% называется тождественно ложной, если она принимает значение «ложь» при любых значениях входящих в нее переменных.
Формула, не являющаяся тождественно ложной и тождественно истинной, называется выполнимой.
Пример
Определить вид (тождественно истинная, тождественно ложная, выполнимая) формулы:
$$
X = A lor B rightarrow A land B
$$
Составим таблицу истинности для формулы %%X%%.
| %%A%% | %%B%% | %%A land B%% | %%A lor B%% | %%(A lor B) rightarrow (A land B)%% |
|---|---|---|---|---|
| %%0%% | %%0%% | %%0%% | %%0%% | %%1%% |
| %%0%% | %%1%% | %%0%% | %%1%% | %%0%% |
| %%1%% | %%0%% | %%0%% | %%1%% | %%0%% |
| %%1%% | %%1%% | %%1%% | %%1%% | %%1%% |
Поскольку формула не является тождественно истинной или тождественно ложной, то %%X%% — выполнимая формула.
2.1 Формулы алгебры
логики. С помощью логических операций
над высказываниями из простейших
высказываний можно строить высказывания
более сложные. При этом порядок
выполнения операций указывается
скобками. Например, можно построить
такое высказывание: «Если Омск находится
на берегу Волги и кислород – газ, то
2+3=5». Построенное высказывание
символически записывается так:(А
/В)
интересует не содержание этого
высказывания, а его логическое значение.
Логическое значение составного
высказывания может быть определено,
исходя из логических значений исходных
высказыванийА, В, С
и схемы по которой из исходных
высказываний построено сложное
высказывание.
Такая схема
построения составного высказывания
может быть применена к различным
конкретным высказываниям, а не только
к высказываниям А, В, С.Поэтому ее можно записать в виде(X/Y)
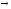
переменные, вместо которых можно
подставить любые элементарные
высказывания. Переменные, вместо
которых можно подставлять любые
элементарные высказывания, называютвысказывательнымиили
пропозициональными переменными. С
помощью высказывательных переменных
и символов логических операций любое
сложное высказывание можно формализовать,
то есть заменить формулой, выражающей
его логическую структуру. Эта формула
называется формулой алгебры логики.
Теперь сформулируем
точное определение формулы алгебры
высказываний.
Определение
формулы алгебры высказываний.
1. Каждая отдельно
взятая пропозициональная переменная
есть формула алгебры высказываний.
2. Если
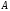
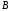
выражения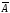
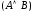
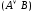
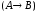
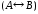
высказываний.
3. Никаких других
формул алгебры высказываний, кроме
получающихся согласно пунктам 1 и 2, нет.
Для составления
формулы сложного высказывания нужно:
1) выделить все
элементарные высказывания и логические
связки, образующие данное составное
высказывание;
2) заменить их
соответствующими символами;
3) расставить скобки
в соответствии со смыслом данного
высказывания.
Для упрощения
записи формул принят ряд соглашений:
1) скобки можно
опускать, если над формулой стоит знак
отрицания;
2) можно не заключать
в скобки формулы, не являющиеся частями
других формул;
3) скобки можно
опускать, если придерживаться следующего
порядка действий: первой выполняется
операция отрицания, затем выполняется
конъюнкция, дизъюнкция, импликация и
эквиваленция.
Пример.
Формализовать
составное высказывание «Две плоскости
параллельны тогда и только тогда, когда
они не имеют общих точек или совпадают».
Выделим и обозначим элементарные
высказывания, образующие данное составное
высказывание:
А: «Две плоскости
параллельны»;
В: «Две плоскости
имеют общие точки»;
С: «Две плоскости
совпадают».
Тогда данное
высказывание в виде формулы записывается
так:
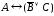
2.2 Таблица
истинности. Логическое значение
формулы алгебры логики можно определить,
если вместо элементарных высказываний
вставить символы их логических значений
(0 или 1), а затем выполнить над этими
символами последовательно все
предписываемые формулой операции. Все
вероятные логические значения формулы,
в зависимости от комбинаций значений
входящих в нее переменных, могут быть
описаны полностью с помощью таблицы
истинности.
Пример. Составить
таблицу истинности для формулы
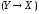
всевозможные пары логических значений,
которые могут принимать переменныеXиY(точнее, те
высказывания, которые могут быть
подставлены в формулу вместо переменныхXиY). В последующих столбцах выписываем
логические значения формул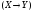
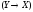
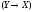
операций импликации и эквиваленции.
В результате
получим таблицу:
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
Первые два столбца
и последний столбец этой таблицы задают
соответствие между логическими
значениями элементарных высказываний
и логическим значением составного
высказывания, получаемого по данной
формуле. Эти три столбца образуют таблицу
истинности данной формулы.Остальные два столбца, для логических
значений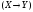
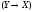
носят вспомогательный, промежуточный,
характер.
Если формула
содержит n элементарных
высказываний, то таблица содержит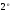
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
КУРС ЛЕКЦИЙ
Элементы математической логики
ВЫСКАЗЫВАНИЕ И ЕГО ЛОГИЧЕСКОЕ ЗНАЧЕНИЕ
Основным понятием
математической логики является понятие «простого высказывания». Под высказыванием
обычно понимают всякое повествовательное предложение, утверждающее что-либо о
чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях
места и времени. Логическими значениями высказываний являются «истина» и
«ложь».
Примеры
высказываний:
1) Москва стоит
на Неве.
2) Лондон —
столица Англии.
3) Сокол не рыба.
4) Число 6
делится на 2 и на 3.
Высказывания 2),
3), 4) истинны, а высказывание 1) ложно. Очевидно, предложение «Да здравствует
Россия!» не является высказыванием.
Высказывание, представляющее
собой одно утверждение, принято называть простым или элементарным.
Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических
связок «не», «и», «или», «если …. то …», «тогда и только тогда», принято
называть сложными или составными. Так, высказывание 3) получается
из простого высказывания «Сокол – рыба» с помощью отрицания «не», высказывание
4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6
делится на З», соединенных союзом «и». Аналогично сложные высказывания могут
быть получены из простых высказываний с помощью грамматических связок «или»,
«тогда и только тогда». В алгебре логики все высказывания рассматриваются
только с точки зрения их логического значения, а от их житейского содержания
отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно
высказывание не может быть одновременно истинным и ложным. Элементарные
высказывания обозначаются малыми буквами латинского алфавита: х, у, z, …, а,
b, с, …; истинное значение высказывания цифрой 1, а ложное значение – буквой
цифрой 0. Если высказывание а истинно, то будем писать а = 1, а если а ложно,
то а = 0.
Типовая задача 1:
Пусть х =0, y =1,
z =1. Определить логические значения нижеследующих сложных высказываний:
Контрольные вопросы:
1. Что называется высказыванием
алгебры логики?
2. Приведите примеры не
высказываний
3. Что такое высказывательная
форма?
4. Какие значения принимают
высказывания?
5. Что такое составное
высказывание?
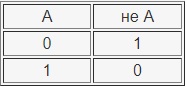
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Отрицанием высказывания х называется новое
высказывание , которое является истинным,
если высказывание х ложно, и ложным, если высказывание х истинно. Отрицание высказывания х обозначается и читается «не х» или
«неверно, что х». Логические значения высказывания можно описать с помощью
таблицы.
Таблицы такого вида
принято называть таблицами истинности. Пусть х высказывание. Так как
также является высказыванием,
то можно образовать отрицание высказывания , то есть высказывание
, которое называется двойным
отрицанием высказывания х. Ясно, что логические значения высказываний х и совпадают. Например,
для высказывания «Путин президент России» отрицанием будет высказывание «Путин не
президент России», а двойным отрицанием будет высказывание «Неверно, что Путин не
президент России».
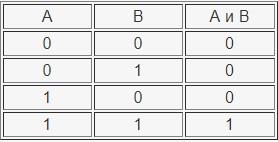
Конъюнкцией (логическим умножением) двух
высказываний х и у называется новое высказывание, которое считается истинным, если
оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно Конъюнкция
высказываний х и у обозначается символом х&у ( , ху ), читается «х и у». Высказывания
х и у называются членами конъюнкции. Логические значения конъюнкции описываются
следующей таблицей истинности:
Например, для высказываний
«6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится
на 2 и 6 делится на 3», которое, очевидно, истинно. Из определения операции конъюнкции
видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной
речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких
друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух
любых высказываний.
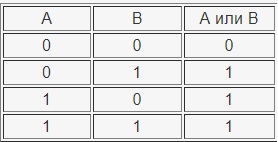
Дизъюнкцией (логическим сложением) двух
высказываний х и у называется новое высказывание, которое считается истинным,
если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны.
Дизъюнкция высказываний х, у обозначается символом «x V у» , читается «х или у»
. Высказывания х, у называются членами дизъюнкции. Логические значения
дизъюнкции описываются следующей таблицей истинности:
В повседневной речи
союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре
логики союз «или» всегда употребляется в не исключающем смысле.
Импликацией двух высказываний х и у
называется новое высказывание, которое считается ложным, если х истинно, а у –
ложно, и истинным во всех остальных случаях. Импликация высказываний х, у
обозначается символом , читается«если х, то у»
или «из х следует у». Высказывание х называют условием или посылкой,
высказывание у – следствием или заключением, высказывание следованием или
импликацией. Логические значения операции импликации описываются следующей
таблицей истинности:
Употребление слов
«если …. то …» в алгебре логики отличается от употребления их в обыденной речи,
где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «Если
х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то
у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения
х . Употребление слов «если …, то …» в математической логике не требует этого,
поскольку в ней смысл высказываний не рассматривается. Импликация играет важную
роль в математических доказательствах, так как многие теоремы формулируются в условной
форме «Если х, то у». Если при этом известно, что х истинно и доказана истинность
импликации , то мы вправе сделать вывод
об истинности заключения у .
Эквивалентностью двух высказываний х и у
называется новое высказывание, которое считается истинным, когда оба
высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным
во всех остальных случаях. Эквивалентность высказываний х, у обозначается
символом , читается«для того,
чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда
у». Высказывания х, у называются членами эквивалентности. Логические значения
операции эквивалентности описываются следующей таблицей истинности:
Эквивалентность играет
важную роль в математических доказательствах. Известно, что значительное число теорем
формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности.
В этом случае, зная об истинности или ложности одного из двух членов эквивалентности
и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности
второго члена эквивалентности.
Контрольные вопросы:
1. Какие операции необходимы для
описания логических высказываний?
2. Как определяется порядок
выполнения логических операций?
3. Что включают в себя
логические выражения?
4. Что такое высказывательная
форма?
формулЫ
АЛГЕБРЫ ЛОГИКИ
Выражение, составленное из логических
переменных с помощью операций над высказываниями и обращающееся в конкретное
высказывание при подстановке вместо логических переменных конкретных
высказываний, называется формулой высказываний. Таким образом,
появляется возможность применять логические операции многократно, получая с их
помощью всё более сложные высказывания. При этом возникает одно затруднение:
при записи сложных высказываний может оказаться неясным порядок,
в котором следует проводить операции. Если формула не содержит скобки, то
прослеживается следующий приоритет логических операций: инверсия, конъюнкция,
дизъюнкция, импликация (эквиваленция).
Логические функции, истинные
на всех наборах значений входных переменных, называются тождественно-истинными
(тавтологией). Логические функции, ложные на всех наборах значений
входных переменных, называются тождественно-ложными. Если у двух
логических функций (формул) совпадают таблицы истинности, то есть на всех
наборах значений входных переменных они принимают одинаковые значения, то их
называют равносильными.
Таблица истинности – это табличное
представление логической формулы, в котором перечислены все возможные сочетания
значений истинности входных сигналов вместе со значением истинности выходного
сигнала (результата операции) для каждого из этих сочетаний. Согласно
определению, таблица истинности логической формулы выражает соответствие между
всевозможными наборами значений переменных и значений формулы.
Порядок выполнения логических операций в
сложном логическом выражении. Для изменения указанного порядка выполнения
операций используются круглые скобки:
Инверсия→Конъюнкция→Дизъюнкция→Импликация→Эквивалентность
Алгоритм построения
таблиц истинности для сложных выражений:
1. Определить
количество строк:
количество строк = 2n+ строка для заголовка, n – кол-во
простых высказываний.
2. Определить
количество столбцов:
количество столбцов = кол-во переменных + кол-во логических
операций
o
определить количество переменных (простых выражений);
o
определить количество логических операций и последовательность их
выполнения.
3. Заполнить столбцы
результатами выполнения логических операций в обозначенной последовательности с
учетом таблиц истинности основных логических операций.
Вопросы
для самоконтроля:
1.Привести
примеры высказываний.
2.Что
содержат ТИ и каков порядок их построения?
3. Какие
логические выражения называются равносильными?
4.
Какое логическое выражение называется тавтологией?
5.
Как определить, что логическое выражение тождественно-ложно?
РавносильнОСТЬ ФОРМУЛ алгебры логики
Выражение, составленное из логических
переменных с помощью операций над высказываниями и обращающееся в конкретное
высказывание при подстановке вместо логических переменных конкретных
высказываний, называется формулой высказываний.
Таким образом,
появляется возможность применять логические операции многократно, получая с их
помощью всё более сложные высказывания. При этом возникает одно затруднение:
при записи сложных высказываний может оказаться неясным порядок,
в котором следует проводить операции. Если формула не содержит скобки, то
прослеживается следующий приоритет логических операций: инверсия, конъюнкция,
дизъюнкция, импликация (эквиваленция).
Логические
функции, истинные на всех наборах значений входных переменных, называются тождественно-истинными
(тавтологией). Логические функции, ложные на всех наборах значений
входных переменных, называются тождественно-ложными. Если у двух
логических функций (формул) совпадают таблицы истинности, то есть на всех
наборах значений входных переменных они принимают одинаковые значения, то их
называют равносильными.
Типовая
задача 1
Проверить
функцию на тождественную истинность
и на тождественную ложность:
Решение:
1. Составим таблицу истинности
для заданной формулы, которая содержит две переменные х и у. В
первых двух столбцах таблицы запишем четыре возможных пары значений этих
переменных, в последующих столбцах – значения промежуточных формул и в
последнем столбце – значение формулы. В результате получим таблицу:
2. Делаем вывод, анализируя
полученную таблицу. Из нее видно, что при все наборах значений переменных х
и у формулы принимает значение 1, то есть является тождественно
истинной или тавтологией.
Типовая задача
2
Докажите равносильность формул алгебры логики
с помощью таблиц истинности:
·
·
Контрольные вопросы:
5. Что называется формулой алгебры
логики?
6. Какие операции необходимы для
описания логических высказываний?
7. Как определяется порядок
выполнения логических операций?
8. Каким образом можно упростить
логические формулы?
9. Какая формула называется
тавтологией?
10. Что называют таблицей истинности?
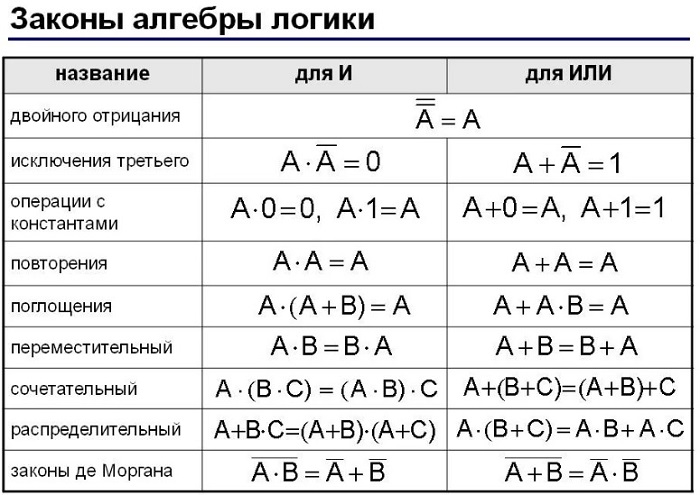
ЗАКОНЫ алгебры логики
Упрощение формул логики
Проверка формул логики на равносильность
Равносильность
высказываний можно устанавливать и другим способом, используя законы алгебры
логики. При этом проводится цепочка равносильных преобразований для каждого
высказывания, которая делает их более простыми, минимизирует их. Если
минимизированные выражения обоих высказываний совпадают, то можно говорить о их
равносильности.
Импликацию и эквиваленцию
можно выразить через основные операции алгебры логики (инверсию, конъюнкцию,
дизъюнкцию):
·
·
Типовые задания:
№1 Упростить функцию, используя равносильные
преобразования. Выполнить проверку с помощью таблиц истинности:
F=
Решение:
1. Проводим цепочку равносильных
преобразований, пока формула не станет минимальной:
В ходе преобразовании
использовали:
1
распределительный
закон (вынесли общий множитель)
2
свойство
дизъюнкции (закон исключения третьего)
3
свойство
конъюнкции (умножение на 1)
2. Используя таблицу истинности,
выполним проверку нашего упрощения. Для построения таблицы истинности
воспользуемся следующим алгоритмом:
1) Определим количество входных
переменных (простых высказываний – 3) и по формуле (n – количество переменных) вычислим
количество строк (наборов переменных – 8)
2) Методом половинного деления
заполним значения входных переменных (первый столбец делим на две одинаковые
группы 0 и 1, в каждом последующем столбце все группы вновь делятся на две
одинаковые группы 0 и 1)
3) Проставим порядок действий и
заполняем таблицу слева на право, где в каждом столбце по определению выполняем
одну операцию алгебры логики. Последнее действие – это значения, которые
принимает заданная функция на всех наборах переменных
|
А |
B |
C |
|
А Ù B Ù С |
А Ù B Ù |
(А Ù B Ù С)Ú( А Ù B Ù |
А Ù B |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
Значения заданной
в условии задачи функции и полученного минимального выражения совпали на всех
наборах переменных. Делаем вывод, что преобразования выполнены, верно.
№2 Проверить функцию на тождественную
истинность
и на тождественную ложность:
Решение:
3. (1 способ) Выполнить
цепочку равносильных преобразований и минимизировать формулу. Если в результате
преобразований получаем 1, как в нашем случае, то формула является
тождественно истинной:
В ходе преобразовании
использовали:
1
закон
де Моргана (избавляемся от общей инверсии)
2
формула
склеивания
3
свойство
дизъюнкции (закон исключения третьего)
4. (2 способ) Составим
таблицу истинности для заданной формулы, которая содержит две переменные х
и у. В первых двух столбцах таблицы запишем четыре возможных пары
значений этих переменных, в последующих столбцах – значения промежуточных
формул и в последнем столбце – значение формулы. В результате получим таблицу:
5. Делаем вывод, анализируя
полученную таблицу. Из нее видно, что при все наборах значений переменных х
и у формула принимает значение 1, то есть является тождественно
истинной или тавтологией.
№3 Минимизировать
функцию:
Вопросы
для самоконтроля:
1. Что называется формулой
алгебры логики?
2. Что такое минимизация формулы
алгебры логики?
3. Какие типы формул ты знаешь?
4. Как проверить равносильность
двух формул логики?
МНОЖЕСТВО. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Множеством называется совокупность каких-либо объектов,
обладающим общим для всех характеристическим свойством. Это определение нельзя
считать строгим, так как понятие множества является исходным понятием
математики и не может быть определено через другие математические объекты. Один
из основателей теории множеств Г. Кантор определял множество так:
“Множество есть многое, мыслимое как целое”. Следующие совокупности
объектов являются множествами: множество деревьев в лесу, множество целых
чисел, множество корней уравнения exsinx = 0.5.
Всякое
множество состоит из элементов. Множества обозначают большими
буквами А, В, С, а элементы – маленькими буквами а, b, c.
А = {a1, a2, a3}
– множество, состоящее из трех элементов;
А = {a1, a2, …} –
множество, состоящее из бесконечного числа элементов.
Если элемент a принадлежит
множеству А – a Î А
Если элемент a не
принадлежит множеству А- a Ï А.
Если все элементы множества А являются
элементами множества В и наоборот, т. е. множества А и В совпадают,
то говорят, что А = В.
Если каждый элемент множества А
является элементом множества В, говорят, что множество А является
подмножеством множества В, и записывают А Í В или В Ê А. Отметим,
что по определению само множество А является своим подмножеством, т.е. А
Í А.
Если А Í В и В Í А, то по ранее введенному определению А =
В.
Пусть А – множество четных
чисел, В – множество целых чисел, С – множество нечетных
чисел. Тогда А Ì В, С Ì В, А Ë С, В Ë А.
Множество, не содержащее ни
одного элемента, называется пустым множеством и
обозначается Æ. Множество корней
уравнения sinx = 2 является пустым.
Существуют
следующие способы задания множеств:
1. Перечислением элементов множества.
A = {1, 3, 5, 7, 9} – конечное множество;
B = {1, 2, …, n, …} – бесконечное множество.
2. Указанием свойств элементов множества. Для этого
способа пользуются следующим форматом записи: A = {açуказание свойства элементов}. Здесь a является
элементом множества A, a Î А.
A = {a ça – простое число} – множество простых чисел;
B = {b çb2 – 1 = 0, b – действительное число} – множество, состоящее из
двух элементов, B = {– 1, 1};
Z = {x ç = 1}– множество, состоящее из одного числа, x = 0.
Операции над
множествами
Объединением множеств А и В называется
множество АÈВ, все элементы которого являются элементами
хотя бы одного из множеств А или В:
АÈВ =
{x ç xÎ А
или xÎВ}.
а) Пусть А = {4, 5, 6}, В = {2, 4,
6}.Тогда АÈВ = {2, 4, 5, 6}.
б) Пусть А – множество чисел, которые делятся на
2, а В – множество чисел, которые делятся на 3:
А = {2, 4, 6, …}, В
= {3, 6, 9, …}.
Тогда АÈВ
множество чисел, которые делятся на 2 или на 3:
АÈВ =
{2, 3, 4, 6, 8, 9, 10, …}.
Пересечением множеств А и В называется
множество АÇВ, все элементы которого являются элементами
обоих множеств А и В:
АÇВ =
{x ç xÎ А
и xÎВ}.
а) Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда
АÇВ = {4, 6}.
б) Пусть А – множество чисел, которые делятся на
2, а В – множество чисел, которые делятся на 3:
А = {2, 4, 6, …}, В
= {3, 6, 9, …}.
Тогда АÇВ множество
чисел, которые делятся и на 2 и на 3:
АÈВ =
{6, 12, 18, …}.
Может оказаться, что множества не
имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются
или что их пересечение – пустое множество.
Относительным дополнением множества В до множества А называется
множество А В, все элементы которого являются элементами
множества А, но не являются элементами множества В:
А В = {x ç xÎ А и xÏВ}.
а) А = {4, 5, 6}, В = {2, 4, 6}. А
В = {4, 5}, В А= {2}.
б) А = {2, 4, 6, …}, В = {3, 6, 9, …}.
Тогда А В – множество
чисел, которые делятся на 2, но не делятся на 3, а В А –
множество чисел, которые делятся на 3, но не делятся на 2:
А В = {2, 4, 8, 10, 14, …}.
В А= {3, 9, 15, 21, 27, …}.
Универсальным множеством называется такое множество U, что все рассматриваемые в
данной задаче множества являются его подмножествами.
Абсолютным дополнением множества А называется множество всех таких элементов x Î U, которые не принадлежат множеству А:
= U A.
Пусть А – множество
положительных четных чисел. Тогда U – множество всех натуральных чисел и
– множество положительных нечетных чисел.
Счетные множества
Можно сказать также, что множество счетно,
если его элементы можно перенумеровать.
1. A1 = {–1, –2, …, – n,
…};
2. A2 = {2, 22, …, 2n,…};
3. A3 = {2, 4, …, 2n,…};
4. A4 = {…, – n, …, – 1, 0, 1, …, n,…};
Чтобы установить счетность некоторого множества,
достаточно указать взаимно однозначное соответствие между элементами данного
множества и множества натуральных чисел.
Существуют бесконечные множества,
элементы которых нельзя перенумеровать. Такие множества называются несчетными.
Вопросы для самоконтроля:
1. Пусть a Î А. Следует ли отсюда, что {a} А?
2. В каком случае ААÇВ?
3. Назовите множество, которое
является подмножеством любого множества.
4. Может ли быть множество эквивалентно своему
подмножеству?
5. Мощность какого множества больше: множества
натуральных чисел или множества точек отрезка [0, 1]?
диаграмм Эйлера-Венна
Эйлеровы круги (круги Эйлера) — принятый в
логике способ моделирования, наглядного изображения отношений между объемами
понятий с помощью кругов, предложенный знаменитым математиком
Л. Эйлером (1707–1783).

какого-нибудь понятия. Объем же понятия отображает совокупность предметов того
или иного класса предметов. Поэтому каждый предмет класса предметов можно
изобразить посредством точки, помещенной внутри круга:

предметов, изображается в виде меньшего круга, нарисованного внутри большего
круга. Такое именно отношение существует между объемами понятий «небесное тело»
(А) и «комета» (B). Объему понятия «небесное тело» соответствует больший круг,
а объему понятия «комета» — меньший круг. Это означает, что все кометы являются
небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное
тело».

двух понятий совпадают только частично, отношение между объемами таких понятий
изображается посредством двух перекрещивающихся кругов. Такое именно отношение
существует между объемом понятий «учащийся» и «комсомолец». Некоторые (но не
все) учащиеся являются комсомольцами; некоторые (но не все) комсомольцы являются
учащимися. Незаштрихованная часть круга А отображает ту часть объема понятия
«учащийся», которая не совпадает с объемом понятия «комсомолец»;
незаштрихованная часть круга B отображает ту часть объема понятия «комсомолец»,
которая не совпадает с объемом понятия «учащийся». 3аштрихованиая часть,
являющаяся общей для обоих кругов, обозначает учащихся, являющихся
комсомольцами, и комсомольцев, являющихся учащимися.
Когда же ни один
предмет, отображенный в объеме понятия A, не может одновременно отображаться в
объеме понятия B, то в таком случае отношение между объемами понятий
изображается посредством двух кругов, нарисованных один вне другого. Ни одна
точка, лежащая на поверхности одного круга, не может оказаться на поверхности
другого круга. Такое именно отношение существует, например, между понятиями
«тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия
«тупоугольный треугольник» не отображается ни один остроугольный треугольник, а
в объеме понятия «остроугольный треугольник» не отображается ни один
тупоугольный треугольник.

равнозначащими понятиями, объемы которых совпадают, отображаются наглядно
посредством одного круга, на поверхности которого написаны две буквы,
обозначающие два понятия, имеющие один и тот же объем. Такое отношение
существует, например, между понятиями «родоначальник английского материализма»
и «автор „Нового Органона“». Объемы этих понятий одинаковы, в них отобразилось
одно и то же историческое лицо — английский философ Ф. Бэкон.

сразу несколько видовых понятий, которые в таком случае называются
соподчиненными. Отношение между такими понятиями изображается наглядно
посредством одного большого круга и нескольких кругов меньшего размера, которые
нарисованы на поверхности большего круга. Такое именно отношение существует
между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия
в равной мере подчинены одному общему родовому понятию «музыкальные
инструменты».
Круги,
изображающие соподчиненные понятия, не должны касаться друг друга и
перекрещиваться, так как объемы соподчиненных понятий несовместимы; в
содержании соподчиненных понятий имеются, наряду с общими, различающие
признаки. Эта схема отображает общее, что характерно для отношения любых
соподчиненных понятий, взятых из различных областей знания. Это применимо к
понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к
понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию
«насекомое» и т. д.

противоположности, отношение между объемами таких понятий отображается
посредством одного круга, обозначающего общее для обоих противоположных понятий
родовое понятие, а отношение между противоположными понятиями обозначается так:
А — родовое понятие, B и C — противоположные понятия. Противоположные понятия
исключают друг друга, но входят в один и тот же род. При этом видно, что между
противоположными понятиями возможно третье, среднее, так как они не исчерпывают
полностью объема родового понятия. Такое именно отношение существует между
понятиями «легкий» и «тяжелый». Они исключают друг друга. Нельзя об одном и том
же предмете, взятом в одно и то же время и в одном и том же отношении, сказать,
что он и легкий, и тяжелый. Но между данными понятиями есть среднее, третье:
предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
Когда же между
понятиями существует противоречащее отношение, тогда отношение между объемами
понятий изображается иначе: круг делится 
понятие, B и не-B (обозначается как ¬B) — противоречащие понятия.
Противоречащие понятия, исключают друг друга и входят в один и тот же род. При
этом видно, что между противоречащими понятиями третье, среднее, невозможно,
так как они полностью исчерпывают объем родового понятия. Такое отношение
существует, например, между понятиями «белый» и «небелый». Они исключают друг
друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном
и том же отношении, сказать, что он и белый и небелый.
Вопросы для самоконтроля:
1. Что называется диаграммой
Эйлера-Венна?
2. Какие типовые диаграммы можно
перечислить?
3. Что такое универсальное
множество?
4. Когда пересечение диаграмм будет равно пустому
множеству?
Законы алгебры множеств
Соответствие между операциями алгебры множеств и
алгебры логики
Проведем аналогию
с алгеброй логики. Используя определения множественных операций, сопоставим их
операциям алгебры логики. Вспомните законы алгебры логики, и «переведите» их на
язык алгебры множеств.
Любой из этих
законов легко доказывается с помощью известного нам метода – с помощью диаграмм
Эйлера-Венна. Мы доказывать все эти законы не будем (это элементарные вещи),
оставьте страницу и докажите их самостоятельно. Но чтобы не быть голословными,
давайте выберем любой из законов и проверим.
С помощью
кругов Эйлера можно доказать следующие свойства множеств, справедливые для
произвольных множеств А, В, С и D:1) (коммутативность объединения);
2) (коммутативность
пересечения);
3) (ассоциативность
объединения);
4) (ассоциативность
пересечения);
5) (дистрибутивность объединения);
6) (дистрибутивность пересечения);
Декартовым (или прямым)
произведением множеств А и В называется — множество, элементами которого
являются все возможные упорядоченные пары элементов исходных двух множеств А и
В:
АхВ ={(x,y)|(x ∈ A) (y ∈ B)}
Пример:
если А={a1,a2} и B={b1,b2,b3},
то АхВ ={(a1,b1),
(a1,b2), (a1,b3),
(a2,b1), (a2,b2),
(a2,b3)}
Разность между универсальным
множеством U и множеством В называется дополнением множества В.
Обозначается
CВ=UВ={x | x В)}
Пусть ВА.
Дополнением множества В до множества А называется множество, содержащее все
элементы множества А, которые не принадлежат множеству В.
CB={x|(x ∈
A) (x
B)}
Вычитание множества А и В в случаях, когда одно из них является
подмножеством другого, называется дополнением множества В до
множества А.
С помощью диаграмм Эйлера-Венна дополнение множества В до
множества А обозначают:
Обозначим число элементов конечного множества А символом n(А) – это мощность
данного множества.
Например, если A={m ,p, r, s}, то можно записать, что n(А)=4, и
сказать, что мощность множества А равна 4 или в множестве А четыре элемента.
Типовая задача
1
Доказать с
помощью диаграмм Эйлера:
·
·
Типовая задача
2
Вспомнить
законы поглощения алгебры логики. Доказать аналогичные законы поглощения
алгебры множеств, используя доказательство по определению и доказательство с
помощью диаграмм:
·
·
Для заданных
множеств А, В, С найти следующие множества:
а) А∩В; б) АUС;
в) А∩ВUС; г) СВ; д) ВА; е) А(В∩С); ж)
(В∩С)С.
|
№ |
А |
В |
С |
|
1. |
{1,3,5,7,9,11} |
{0,2,3,5} |
{0,1,2} |
|
2. |
{0,4,5,6,7,9} |
{4,5,7,9} |
{1,2,4} |
|
3. |
{3,4,6,7,8,9} |
{0,2,4,8,9} |
{2,5,8} |
|
4. |
{0,1,2,3,4,5} |
{2,4,8} |
{2,6,7,8} |
|
5. |
{3,4,6,8,9,13} |
{6,7,8} |
{0,2,6} |
|
6. |
{1,2,3,4,5,6,} |
{3,6,7,} |
{3,7,0} |
|
7. |
{2,3,4,5,6,7} |
{4,7,8} |
{1,4,9} |
|
8. |
{3,4,5,6,7,8} |
{5,8,9} |
{4,8,1} |
|
9. |
{4,5,6,7,8,,9} |
{1,6,9} |
{2,5,9} |
|
10. |
{5,7,8,9,0} |
{0,5,7,} |
{0,3,6} |
Задать с
помощью операций над множествами выделенную часть
Вопросы для самоконтроля:
1. Что является множеством
алгебры логики?
2. Какие множества являются
равносильными?
3. Как доказать равносильность
множеств?
4. Какие операции логики и множеств являются
соответствующими?
бинарнОЕ отношениЕ. ОТОБРАЖЕНИЕ. ФУНКЦИЯ
Пусть среди трех людей: Андрей (А), Василий (В) и
Сергей (С) двое знакомы друг с другом (Андрей и Василий) и знают третьего –
Сергея, но Сергей их не знает. Как описать отношения между этими людьми?
Имеем исходное множество Х = {А, В, С}.
Далее из элементов множества Х составим упорядоченные пары: (А, В),
(В, А), (А, С), (В, С). Это множество пар и описывает связи
между элементами множества X. Кроме того, множество этих пар есть подмножество
декартова произведения X ´ X.
На множестве X задано бинарное отношение R,
если задано подмножество декартова произведения X ´ X (т. е. R Ì X ´ X).
Пример. Пусть X = {1, 2, 3, 4}. Зададим
на X следующие
отношения:
Т = {(х, у) | х, у Î Х; х = у} – отношение равенства;
Р = {(х, у) | х, у Î Х; х = у – 1} –
отношение предшествования;
Q = {(х, у) | х, у Î Х; х делится на у} –
отношение делимости.
Все эти отношения заданы с помощью
характеристического свойства. Перечислим элементы этих отношений для заданного
множества X = {1,2,3,4}:
Т = {(1,1), (2,2), (3,3), (4,4)};
P =
{(1,2), (2,3), (3,4) };
Q = {(4,4), (4,2), (4,1), (3,3),
(3,1), (2,2), (2,1), (1,1)}.
Областью определения Dr бинарного отношения R называется множество DR = {x | (х, у) Î R}.
Областью значений ЕR бинарного отношения R называется множество ЕR = {у| (х, у) Î R}.
В примере для отношения Р областью определения
является множество DR = {1,2,3}, а областью значений является множество
ЕR = {2,3,4}.
Способы задания бинарного отношения
Бинарное отношение можно задать, указав характеристическое
свойство или перечислив все его элементы. Существуют и
более наглядные способы задания бинарного отношения: график отношения,
схема отношения, граф отношения, матрица
отношения.
График отношения изображается в
декартовой системе координат: на горизонтальной оси отмечается область
определения, на вертикальной – область значений отношения. Элементу отношения
(х, у) соответствует точка плоскости с этими координатами.
a б
Рисунок 1. График отношения
Q (а)
и схема отношения Q (б)
Схема отношения изображается с помощью двух вертикальных прямых, левая из которых
соответствует области определения отношения, а правая – множеству значений
отношения. Если элемент (х, у) принадлежит отношению R, то соответствующие
точки из DR и ЕR соединяются прямой.
Граф
отношения R Ì X ´ X строится следующим образом. На
плоскости в произвольном порядке изображаются точки – элементы множества X.
Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда,
когда пара (х, у) принадлежит отношению R.
Матрица
отношения R Ì X ´ X – это квадратная таблица, каждая
строка и столбец которой соответствует некоторому элементу множества X. На
пересечении строки х и столбца у ставится 1, если пара (х, у) Î R; все остальные элементы матрицы
заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен
номеру строки, второй – номеру столбца.
Риунок 2. Граф отношения Q (а) и матрица отношения Q (б)
Свойства бинарных отношений
1. Отношение R на множестве X называется рефлексивным, если
для всех х Î X выполняется условие
(х, х) Î R. Отношение R на множестве Х называется нерефлексивным,
если условие (х, х) Î R не
выполняется хотя бы при одном х Î X .
2. Отношение R на множестве X называется симметричным, если
из условия (х, у) Î R следует (у, х) Î R. Отношение R на множестве X называется несимметричным,
если для любых х, у Î X из
условия (х, y) Î R следует (у, х) Ï R.
3. Отношение R на множестве X называется транзитивным, если
для любых х, у, z Î R из одновременного выполнения условий
(x, y) Î R и (у, z) Î R следует (х, z) Î R .
Отношение R на
множестве X называется отношением эквивалентности,
если оно обладает свойствами рефлексивности, симметричности и транзитивности.
Композицией отношений r1 и r2 называется отношение
r2°r1={<x,z>|, существует y такое,
что <x,y>Îr1 и <y,z>Îr2}.
Матрица отношения r2°r1 получается путем умножения матрицы r1 на матрицу r2. Чтобы получить граф композиции r2°r1 надо к графу отношения r1 достроить граф отношения r2 и включить вершины множества Y,
заменив маршруты, которые проходят через них из множества Х в Y одной дугой.
1.(r-1)-1=r;
2. (r2°r1)-1=r1-1 ° r2-1.
Пример. Рассмотрим следующие отношения на
множестве X = {1,2,3,4,5,6,7}:
G = {(x, y) | х, у Î Х; х > у};
L = {(х, у) | х, у Î Х; х £ у};
M = {(x, y) | х, у Î X; (х – у) делится на 3};
К = {(х, y) | х, у Î
Х; х2 + у2 £ 20}.
Исследуем, какими свойствами они обладают.
Среди приведенных в примере
отношений рефлексивными являются отношение L
(т. к. х £ х справедливо при
всех х Î X) и отношение М (т. к. х – х = 0 делится
на 3, поэтому пара (х, х) принадлежит отношению М при всех х Î X).
Симметричными являются отношения М (если х – у
делится на 3, то и у – х делится на 3) и К (если х2 + у2 £ 20, то и у2 + х2 £ 20).
Транзитивными являются отношения G, L, М.
булевА функциЯ
Функцию, принимающую одно из двух значений 0 или 1, от
n переменных, каждая из которых принимает одно из двух значений 0 или 1
называют булевой функцией. Любое сложное высказывание алгебры логики
можно считать булевой функцией.
Сложное высказывание можно представить в виде выражения, в которое
входят простые высказывания (переменные) xi
операции дизъюнкции, конъюнкции, отрицания и, быть может, скобки. Рассмотрим,
каким свойствам должны удовлетворять операции, с помощью которых можно выражать
любое сложное выражение. Булеву функцию от n переменных можно задать таблицей истинности.
Построим всевозможные булевы функции для двух
переменных.
|
переменные |
Булевы функции |
||||||||||||||||
|
x1 |
x2 |
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Основные типы булевых функций
f0(x1,x2)=0 – константа 0;
f1(x1,x2)= – конъюнкция;
f2(x1,x2)= – левая коимпликация
f3(x1,x2)= ;
f4(x1,x2)= – правая коимпликация;
f5(x1,x2)=
f6(x1,x2)= – функция неравнозначности, неэквивалентности,
сумма Жегалкина;
f7(x1,x2)= – дизъюнкция;
f8(x1,x2)= – функция Вебба;
f9(x1,x2)= – функция эквивалентности, равнозначности;
f10(x1,x2)= – отрицание;
f11(x1,x2)= – правая импликация (читается «если x2, то x1»);
f12(x1,x2)= – отрицание;
f13(x1,x2)= левая импликация (читается «если x1, то x2»);
f14(x1,x2)= – функция Шеффера;
f15(x1,x2)=1– константа 1.
Правила
построения логической функции по ее таблице истинности:
- Выделить
в таблице истинности те строки, в которых значение функции равно 1. - Выписать
искомую формулу в виде дизъюнкции нескольких логических элементов. Число
этих элементов равно числу выделенных строк. - Каждый
логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов
функции. - Если
значение какого-либо аргумента функции в соответствующей строке таблице
равно 0, то этот аргумент взять с отрицанием.
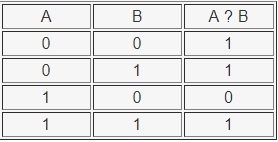
Типовая задача №1
Построить
логическую функцию по ее таблице истинности:
|
X |
Y |
Z |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Решение:
1. В первой и
третьей строках таблицы истинности значение функции равно 1.
2. Так как строки
две, получаем дизъюнкцию двух элементов: ( )
V ( ).
3. Каждый логический элемент
в этой дизъюнкции запишем в виде конъюнкции аргументов
функции X и Y: (X & Y) V
(X & Y).
4. Берем аргумент
с отрицанием если его значение в соответствующей строке таблицы равно 0 и
получаем искомую функцию:
Z (X, Y) =(¬ X & ¬Y) V (X & ¬Y).
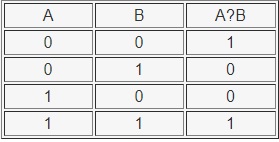
Типовая задача №2
Найти
формулу, определяющую функцию, по заданной таблице истинности:
Вопросы
для самоконтроля:
1. Докажите с помощью таблиц истинности основные законы алгебры Буля.
2. Перечислите основные булевы функции.
3. Какая функция называется Стрелка Пирса, Штрих
Шеффера?
ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
конънктивные НОРМАЛЬНЫЕ ФОРМЫ
Исчисление высказываний можно построить, используя соответствующие
таблицы истинности. Алгебра Буля простейшая в классе булевых алгебр; она
является двухэлементной булевой алгеброй. Каждое высказывание и
соответствующую ему булеву функцию f (x1,x2,…xn)
можно представить в виде дизъюнкции элементарных произведений. Элементарной
конъюнкцией называется
конъюнкция, состоящая из переменных или их отрицаний.
Формула, равносильная данной
формуле алгебры высказываний и являющаяся дизъюнкцией элементарных произведений,
называется дизъюнктивной нормальной формой (ДНФ) данной формулы.
Формула, равносильная данной формуле
алгебры высказываний и являющаяся конъюнкцией элементарных сумм, называется конъюнктивной
нормальной формой (КНФ) данной формулы.
Совершенной дизъюнктивной
(конъюнктивной) нормальной формой СДНФ (СКНФ) называется ее ДНФ (КНФ),
обладающая следующими свойствами:
1. Все элементарные конъюнкции
(дизъюнкции) различны.
2. Нет нулевых конъюнкций
(дизъюнкций).
3. Ни одна из элементарных
конъюнкций (дизъюнкций) не содержит одинаковых членов.
4. Каждая элементарная
конъюнкция (дизъюнкция) содержит все переменные.
Для получения СДНФ необходимо
сначала найти минимальную ДНФ, а затем путем ввода
дополнительных множителей добиться выполнения условия 4.
Пример:
Представление булевой функции в виде СДНФ (СКНФ) по
таблице истинности формулы
Чтобы построить СДНФ (СКНФ) по
заданной таблице истинности, нужно выбрать все встречающиеся в ней значения
функции равные 1 (0) и рассмотреть соответствующие наборы значений переменных.
СДНФ (СКНФ) содержит столько
слагаемых (сомножителей), сколько единиц (нулей) имеет таблица истинности,
заданной функции. Эти единицы (нули) соответствуют тем наборам переменных, при
которых каждое слагаемое (сомножитель) обращается в единицу (нуль), т.е.
переменным, входящим в элементарное произведение (элементарную сумму) без знака
отрицания соответствует 1 (0), а со знаком отрицания – 0 (1)
Каждая формула алгебры логики имеет
единственную СКНФ, единственную СДНФ. Тоджественно-истинная формула не имеет
СКНФ. Тождественно-ложная формула не имеет СДНФ.
Понятие двойственности
Пусть дана булева функция f (x1, x2,
..,xn), тогда f *(x1, x2, ..,xn) называется двойственной f (x1,
x2, ..,xn), если

двойственности
Типовая
задача №1
Функция f(x1,x2,x3), задана таблицей истинности.
Составить ее СДНФ.
|
x1 |
X2 |
x3 |
f(x1,x2,x3) |
x1 |
x2 |
x3 |
f(x1,x2,x3) |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Согласно предыдущему утверждению
функция f(x1,x2,x3) может быть представлена в виде: f(x1,x2,x3)= .
Типовая
задача №2
Следующую формулу привести к
СДНФ, предварительно приведя ее равносильными преобразованиями к ДНФ.
Типовая
задача №3
Для формулы из примера 2
найти СДНФ путем составления таблицы истинности.
Типовая
задача №4
Для формулы из примера 2
найти СКНФ путем равносильных преобразований, приведя ее к КНФ.
Типовая
задача №5
Для формулы из примера 2
найти СКНФ, записав предварительно СДНФ ее отрицания, а потом воспользовавшись
формулой двойственности.
Типовая
задача №6
Будет ли формула
тождественно-ложной, тождественно-истинной или выполнимой?
Это произведение не является тожественно-истинным,
так как полученная элементарная сумма не тождественно-истинна. Таким образом,
исходная формула не тождественно-ложна и не тождественно-истинна,
следовательно, она выполнима.
Вопросы
для самоконтроля:
1. Что называется булевой функцией?
2. Что называют совершенной дизъюнктивной нормальной формой? Как
выполняется ее построение?
2. Что называют совершенной конъюнктивной нормальной
формой? Как выполняется ее построение?
релейно-контактныЕ схемЫ
Релейно-контактной схемой (РКС) или переключательной схемой называется
схематическое изображение устройства, состоящего из следующих элементов:
1) переключателей (контактов,
реле, ламп и др.);
2) соединительных проводников;
3) входов-выходов (полюсов РКС).
Рассмотрим простейшую РКС,
содержащую один переключатель Р. Если переключателю Р поставить в соответствие
высказывание х: «Переключатель Р замкнут», то истинному значению х (х = 1)
будет соответствовать замкнутое состояние переключателя, при котором РКС проводит
ток, т.е. импульс, поступающий на вход, может быть снят на выходе. Значению х =
0 будет соответствовать разомкнутое состояние РКС (ток не проводится).
Каждой РКС, состоящей из
нескольких переключателей, можно поставить в соответствие высказывание,
выраженное некоторой формулой А, таким образом, что истинному значению формулы
(А = 1) будет соответствовать замкнутое состояние РКС, а значению А = 0 –
разомкнутое состояние.
Обозначения
на схемах
|
РКС |
Формула |
Значения |
|
Переключатель х: |
Простейшее |
х = 1, если х = 0, если |
|
Переключатель |
Отрицание простейшего |
|
|
Последовательное соединение: (схема замкнута, когда оба переключателя |
Конъюнкция xÙy |
|
|
Параллельное соединение: (схема разомкнута, оба переключателя |
Дизъюнкция xÚy |
|
|
Схема, которая всегда |
xÙ |
xÙ |
|
Схема, которая всегда |
xÚ |
xÚ |
Из простейших РКС путем их
последовательного и параллельного соединения могут быть построены более сложные
переключательные схемы.
Доказано, что любая формула
алгебры логики может быть преобразована к виду, содержащему только операции
отрицания, конъюнкции и дизъюнкции. Это позволяет изображать логические формулы
при помощи РКС, а РКС задавать формулами.
Например, согласно формулам
основных равносильностей
x ® y º Ú y и x « y º (x ® y) Ù (y ® x),
следовательно, логическим операциям импликации
и эквиваленции соответствуют РКС, изображенные рис. 1.
Алгоритм построения
контактных схем
1) определить число переменных;
2) определить количество логических операций и их порядок;
3) построить для каждой логической операции свою
схему (если это возможно);
4) объединить схемы в порядке выполнения логических
операций.
Используя равносильные
преобразования логической формулы, соответствующей некоторой РКС, можно
упростить РКС, т.е. привести ее к виду, содержащему меньшее число переключателей.
Образец
решения типовых задач
1 пример: Записать формулу алгебры логики,
соответствующую данной релейно-контактной схеме, упростить ее, если это
возможно и нарисовать новую схему по упрощенной формуле.
Решение:
Запишем соответствующую РКС
формулу, используя таблицу простейших РКС и соответствующих им формул логики:
Упростим формулу, используя
основные равносильности:
Таким образом, . Построим РКС, соответствующую упрощенной
формуле.
2 пример: Задать релейно-контактной
схемой формулу, соответствующую таблице истинности.
|
x |
y |
z |
F |
|
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
Решение:
Запишем по таблице истинности
соответствующую СКНФ или СДНФ для заданной булевой функции (в зависимости от
количества 0 и 1 для значений F):
Построим контактную схему по
алгоритму (определяем число переменных;
определяем количество логических операций и их порядок; строим для каждой
логической операции свою схему; объединяем схемы в порядке выполнения
логических операций):
Таким образом, полученная
схема будет соответствовать заданной таблице истинности.
3
пример: Проверить
являются ли заданные контактные схемы взаимозаменяемыми (равносильными).
|
|
|
Решение:
Запишем соответствующие контактным
схемам формулы, используя таблицу простейших РКС и соответствующих им формул логики:
Проверим равносильность
формул, используя основные преобразования алгебры логики. Для этого
минимизируем формулы А и В:
Таким образом, , так как их минимизированные формы
совпали. Соответствующие этим формулам заданные контактные схемы будут
равносильны между собой, то есть взаимозаменяемы.
Контрольные вопросы:
1. Что такое релейно-контактная
схема?
2. Где применяются
релейно-контактные схемы?
3. Таблица состояния и таблицы
истинности одно и тоже или имеются различия?
4. Методика построения РКС.
ПРЕДИКАТ. ОПЕРАЦИИ НАД ПРЕДИКАТАМИ
Одноместным предикатом Р(х) называется произвольная функция переменной
х, определенная на множестве М и принимающая значения из множества
{1,0}.
Множество М, на котором определен предикат P(х),
называется областью определения предиката.
Множество всех элементов х Î М , при которых предикат принимает значение «истина», называется множеством
истинности предиката Р(х).
Iр = {х| х Î М, Р(х) = 1} – множество
истинности предиката Р(х)
Примеры
предикатов:
1) Р(х) = «х – простое число» определен на множестве N, а
множество истинности
Iр для него есть множество
всех простых чисел.
2) Q{x} = « sin х = 0 » определен на
множестве R, а его множество истинности
Iq= {x| x = pk; kÎ Z}.
3) F(x) = «Диагонали
параллелограмма х перпендикулярны» определен на множестве всех
параллелограммов, а его множеством истинности является множество всех ромбов.
4) Р(х) = «х2 + 1> 0, xÎ R»; область
определения предиката М = R и область истинности – тоже R, т.к. неравенство верно для всех действительных чисел. Таким образом,
для данного предиката М = Ip . Такие предикаты
называются тождественно истинными.
5) В(х) = «х2 + 1< 0, xÎ R»; область истинности Ip =Æ, т.к. не существует
действительных чисел, для которых выполняется неравенство. Такие предикаты
называются тождественно ложными.
Предикат
Р(х), определенный на множестве М, называется тождественно
истинным (тождественно ложным), если Iр = М (Iр
= Æ).
предикат sin2x+cos2x=1 –
тождественно истинный
предикат – тождественно ложный
Двухместным предикатом Р(х,у) называется
функция двух переменных х и у, определенная на множестве М
=М1 ´ М2 (хÎ М1
, уÎ М2 ) и принимающая значения из
множества {1,0}.
Примеры предикатов:
1)
Р(х, у) = «х < у» определен на
множестве пар (2,1), (4,4), (3,7).
Вместо
х и у подставим указанные значения: Р(2,1) = 0; Р(4,4)=0;
Р(3,7)=1. Областью истинности этого предиката является множество,
состоящее из пары (3,7).
2) Р(х,
у) = «х < у» с областью определения M = R2,
тогда область его истинности можно представить графически: это
все точки части плоскости (открытая, бесконечная область), лежащей ниже прямой
у = х.
3)
Q(х, у) = « х = у » определенный
на множестве M = R2, область истинности
которого – все точки прямой у = х.
n – местным предикатом называется функция Q(x1, x2,…,xn),
определенная на множестве М = М1´ М2´…´Мn и принимающая на этом множестве значение из
множества {1, 0}.
Предикат
Р(х) является следствием предиката Q(x), если IQÌIP.
Предикаты
P(x) и Q(x) равносильны, если IQ=IP
.
Типовая задача №1
На
множестве М= {3,4,5,6,7,8} заданы предикаты P(x) =«х – простое число», Q(x)= «х
– нечетное число». Равносильны ли предикаты на множестве:
а) М; б) L = {2,3,4,5,6,7,8}; в) К = {3,4,5,6,7,8,9}?
Решение: Составим таблицы истинности
предикатов на данных множествах:
|
М |
Р(х) |
Q(x) |
L |
Р(х) |
Q(x) |
K |
Р(х) |
Q(x) |
|
3 |
1 |
1 |
2 |
1 |
0 |
3 |
1 |
1 |
|
4 |
0 |
0 |
3 |
1 |
1 |
4 |
0 |
0 |
|
5 |
1 |
1 |
4 |
0 |
0 |
5 |
1 |
1 |
|
6 |
0 |
0 |
5 |
1 |
1 |
6 |
0 |
0 |
|
7 |
1 |
1 |
6 |
0 |
0 |
7 |
1 |
1 |
|
8 |
0 |
0 |
7 |
1 |
1 |
8 |
0 |
0 |
|
8 |
0 |
0 |
9 |
0 |
1 |
На множестве М IP =
IQ, следовательно на этом множестве предикаты равносильны.
На множествах L и К условие равносильности не соблюдается.
Предикаты,
так же, как высказывания, принимают два значения истина и ложь, поэтому к ним применимы
все операции логики высказываний.
Примеры:
1)
Р(х) = «х –
четное число» и Q(x) = «х кратно 3»
– P(x)LQ(x) = «х – четное
число и х кратно 3», область истинности IPLQ = IP Ç IQ = {2, 4, 6,…,2n, …}Ç {3, 6, 9, 12,…, 3n,
…}={6, 12, 18, …, 6n, …}.
– P(x)VQ(x) = «х – четное число или х кратно 3», область истинности IPVQ
= Iр È Iq={2, 4, 6,…,2n, …}È {3, 6, 9, 12,…, 3n,
…}={2,3,4,6,…,2n, 3n, …}
– = «х – нечетное число»,
его область истинности:
–
Типовая задача №2
На
множестве М= {1,2,3,4,…,20} заданы предикаты А(x) =« х
не делится на5», В(x)= «х- простое число», С(x)= «х кратно 3». Найти множество
истинности предиката
Решение: Найдем области истинности предикатов
А(х), В(х) и :
IA = {1,2,3,4,6,7,8,9,11,12,13,1,14,16,17,18,19};
IB = {2,3,5,7,11,13,17,19};
CIc = {1,2,4,5,7,8,10,11,13,14,16,17,19,20}.
В предикате заменим импликацию :
Типовая задача №3
Изобразить на диаграмме Эйлера – Венна область истинности предиката
Решение:
Сначала выполним
преобразования, рассматривая предикат как высказывание:
Изобразить
на диаграмме Эйлера – Венна область истинности предиката
Решение:
Выполним преобразования:
Типовая задача №4
Записать предикат, полученный
в результате логических операций над предикатами P(x), Q(x), R(x), область истинности
которого заштрихована
Решение:
Типовая задача №5
Изобразить
на координатной плоскости область истинности предиката
Решение:
Выполним преобразования:
Область
истинности предиката х £ 2 – часть плоскости, расположенная
левее прямой х = 2 и все точки этой прямой (изобразим ее сплошной
линией).
Область
истинности предиката x < y – часть плоскости, расположенная выше
прямой у = х без этой прямой (изобразим ее пунктирной линией).
Область истинности данного предиката
– пересечение описанных областей истинности:
Типовая задача №6
Изобразить
на координатной плоскости область истинности предиката ((х>2)(y³1))V((x<-1)(y<-2))
Решение:
Составим соответствующую
формулу алгебры множеств, обозначив:
P(x,y)= (x>2)
Q(x,y) =(y³1) R(x,y)
=(x<-1) S(x,y) =(y<-2)
Область истинности данного
предиката: I= IPÇIQÈIRÇIS.
Контрольные вопросы:
1. Определение одноместного
предиката.
2. Область истинности
одноместного предиката.
3. Определение тождественно
истинного (тождественно ложного) предиката.
4. Определение двухместного
предиката.
5. Определение n – местного
предиката.
6. Какие предикаты являются
равносильными? В каком случае предикат Р(х) является следствием предиката Q(x)?
7. Перечислить логические
операции над предикатами и показать области истинности на диаграммах Эйлера-
Венна.
ФОРМУЛЫ ЛОГИКИ ПРЕДИКАТОВ
Наряду с обычными операциями в логике предикатов рассматривается еще
две операции, которые превращают одноместный предикат в высказывание. Такие
операции называются кванторными.
Квантор всеобщности. Пусть Р(х) — предикат,
определенный на множестве М. Под выражением “ х Р(х) понимают высказывание, истинное, когда Р(х) истинно для
каждого элемента х из множества М и ложное, в противном
случае. Это высказывание уже не зависит от х. Соответствующее ему словесное
выражение будет: «Для всякого х Р(х) истинно». Символ “ называют квантором всеобщности.
Переменную х в предикате Р(х) называют свободной (ей
можно придавать различные значения из М), в высказывании “ х Р(х) переменную х называют связанной
квантором “.
Квантор существования. Пусть Р(х) — предикат, определенный на
множестве М. Под выражением $х
Р(х) понимают высказывание,
которое является истинным, если существует элемент х Î М, для которого Р(х) истинно, и ложным в противном случае. Это
высказывание уже не зависит от х. Соответствующее ему словесное
выражение будет: «Существует х, при котором Р(х) истинно». Символ
$ называют квантором существования.
В высказывании $х Р(х) переменная
х связана квантором $.
Примеры
употребления кванторов:
1) Р(х) = «число х кратно 5» определен на множестве N. Используя
кванторы, из данного предиката можно получить высказывания: “хÎ N Р(х) = «Все натуральные числа кратны 5»=0; $хÎN P(x) = «Существует натуральное число, кратное 5»=1.
Ясно, что высказывание “
х Р(х) истинно
только в том единственном случае, когда Р(х) – тождественно истинный
предикат, а высказывание $х
Р(х) ложно только в
том единственном случае, когда Р(х) — тождественно ложный предикат.
Кванторные операции применяются и к многоместным предикатам.
Пусть, например, на множестве М задан двухместный предикат Р(х,у).
Применение кванторной операции к предикату Р(х,у) по переменной х
ставит в соответствие двухместному предикату Р(х,у) одноместный
предикат “x P(x, у) (или одноместный предикат $х Р(х, у)), зависящий от переменной у и не зависящий от переменной х.
К ним можно применить кванторные операции по переменной у, которые
приведут уже к высказываниям следующих видов:
“y“xP(x,y)
$y“xP(x,y) “y$xP(x,y) $у$хР(х,у).
Примеры
употребления кванторов:
1) Р(х,у) = «число х кратно у» определен на множестве N. Применение
кванторных операций к предикату Р(х,у) приводит к восьми возможным
высказываниям:
1.
“y“xP(x,y) = «Для всякого у и для всякого х у
является делителем х»=0.
2.
$y“xP(x,y) = «Существует у, которое является делителем всякого х»=1.
3.
“y$xP(x,y)= «Для всякого у существует х такое, что х делится на у»=1.
4.
$у$хР(х,у) = «Существует у и существует х такие, что у является делителем х»=1.
5.
“х“уP(x,y) = «Для всякого х и для всякого у у
является делителем х»=0.
6.
“х$уP(x,y) = «Для всякого х существует такое у, что х делится на у»=1.
7.
$х$уP(x,y) = «Существует х и существует у такие, что у является делителем х»=1.
8.
$х“уР(х,у) = «Существует х такое, что для всякого у х делится на у»=0.
Из рассмотренных примеров видно, что в общем случае
изменение порядка следования кванторов изменяет смысл высказывания, а значит, и
его логическое значение.
“хР(х) º P(a1)
P(a2)… P(an)
$хР(х) º P(a1)V P(a2)V…VP(an)
Типовая задача №1
Какие
из следующих высказываний тождественно ложные, а какие тождественно истинные,
если область определения М = R?
1)
$х (х +5 = х + 3) – тождественно ложное
высказывание, т.к. ни при каком х равенство неверно;
2)
“х (х2 +х + 1
> 0) – тождественно истинное высказывание:
левую часть неравенства перепишем в виде (х + ½)2 + ¾ , эта сумма
больше нуля при любом х;
3)
$х ((х2 – 5х +6 ³ 0)(х2 – 2х + 1 >0)) – высказывание тождественно истинное, если пересечение областей
истинности логически умножаемых предикатов не пусто, и ложное, в противном
случае.
Первое неравенство представим в виде (х –2)(х – 3)³ 0, решением которого являются хÎ(-¥; 2]È [3; +¥).
Второе неравенство представим в виде (х – 1)2> 0,
решением которого являются все
х ¹ 0.
Пересечение
областей истинности: (-¥; 0)È(0; 2]È[3; +¥)¹Æ, значит, высказывание тождественно истинное.
Формула логики предикатов:
1.
Каждое высказывание как переменное, так и
постоянное, является формулой (элементарной).
2.
Если F( .,.,…,.)
– n– местная предикатная переменная или постоянный
предикат, а х1, х2, …, хn
– предметные переменные или предметные постоянные (не
обязательно все различные), то F(х1, х2, …, хn) есть формула. Такая формула называется элементарной, в ней предметные
переменные являются свободными, не связанными кванторами.
3.
Если А и В — формулы, причем такие,
что одна и та же предметная переменная не является в одной из них связанной, а
в другой – свободной, то слова А v В , А& В, А®В есть формулы. В этих формулах те переменные, которые в исходных
формулах были свободными, являются свободными, а те, которые были связанными,
являются связанными.
4.
Если А – формула, то – формула, и характер предметных переменных при переходе от формулы А
к формуле не
меняется.
5.
Если А(х) – формула, в которую предметная
переменная х входит свободно, то слова “xA(х) и $хА(х) являются формулами,
причем предметная переменная входит в них связанно.
6.
Всякое слово, отличное от тех, которые названы
формулами в пунктах 1-5, не является формулой.
Примеры формул
логики предикатов:
1)
“хР(х)® $xQ(x, у) – формула
2)
“xQ(x, y) ® Р(х) – не формула (так как в формулу“xQ(x, y) переменная х входит связано, а в формулу Р(х) переменная х
входит свободно)
3)
“у($уР(х,у))VQ(x) – не формула (квантор
всеобщности на у навешан на формулу $уР(х,у), в которой переменная у уже связана
квантором существования)
4)
“у хР(х, у) – не формула (переменной х не присвоен квантор)
О логическом значении формулы логики предикатов можно говорить лишь
тогда, когда задано множество М, на котором определены входящие в эту
формулу предикаты. Логическое значение формулы логики предикатов зависит
от значений трех видов переменных: 1) значений входящих
в формулу переменных высказываний, 2) значений свободных
предметных переменных из множества М, 3) значений предикатных
переменных. При конкретных
значениях каждого из трех видов переменных формула логики предикатов становится
высказыванием, имеющим истинное или ложное значение.
Пример вычисления
значения формулы предикатов:
1)
“x(P(x)Q(x)®R(x)) предикаты
определены на множестве N. P(x) = «х делится на 3», Q(x) = «х
делится на 4», R(x) = «х делится на 2». Данная формула является высказыванием, т.к. х
связанная переменная. Следовательно, значение формулы будет зависеть только от
значений предикатных переменных. P(x)Q(x)– означает, что х делится на 12. Тогда
предикат P(x)Q(x)®R(x) = «если х делится на 12, то х делится на 2»
– тождественно истинный, следовательно формула “x(P(x)Q(x)®R(x)=1.
Две формулы логики предикатов А и В называются равносильными
на области М, если они принимают одинаковые логические значения при всех
значениях входящих в них переменных, отнесенных к области М. Для равносильных
формул принято обозначение А º
В.
Основные формулы
предикатов:
Контрольные вопросы:
1. Как одноместный предикат
можно превратить в единичное высказывание?
2. Что понимают под выражением “хР(х)?
3. Что понимают под выражением $хР(х)?
алгоритм
Основные алгоритмические конструкции
Одним из фундаментальных понятий в информатике является понятие алгоритма.
Происхождение самого термина «алгоритм» связано с математикой. Это слово
происходит от Algorithmi — латинского написания имени Мухаммеда аль-Хорезми
(787 — 850), выдающегося математика средневекового Востока. В XII в. был
выполнен латинский перевод его математического трактата, из которого европейцы
узнали о десятичной позиционной системе счисления и правилах арифметики
многозначных чисел. Именно эти правила в то время называли алгоритмами.
Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел —
вот первые алгоритмы в математике.Правила алгебраических преобразований,
способы вычислений корней уравнений также можно отнести к математическим
алгоритмам.
В наше время понятие алгоритма трактуется
шире. Алгоритм — это последовательность команд управления каким-либо
исполнителем. В школьном курсе информатики с понятием алгоритма, с методами
построения алгоритмов ученики знакомятся на примерах учебных исполнителей:
Робота, Черепахи, Чертежника и т.д. Эти исполнители ничего не вычисляют. Они создают
рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на
место. Таких исполнителей принято называть исполнителями, работающими в
обстановке.
Под алгоритмом будем понимать общую,
выполняемую шаг за шагом процедуру решения задачи. Для определенности можно
считать ее программой. Алгоритмы бывают:
–
точные, которые для любой индивидуальной задачи
всегда дают точное решение;
–
приближенные с гарантированной оценкой точности;
–
аппроксимационные
схемы — семейство
алгоритмов, позволяющих получать решения с любой наперед заданной точностью e > 0, время работы которых растет с
ростом величины 1/e ;
–
итерационные
методы локального поиска (метаэвритстики), для которых вероятность получить точное решение
растет с ростом числа итераций;
–
быстрые
конструктивные эвристики без гарантии получить точное решение или решение с заданной
погрешностью.
Понятие алгоритма, можно назвать
понятием алгоритма в интуитивном смысле. Оно имеет нечеткий, неформальный
характер, ссылается на некоторые точно не определенные, но интуитивно понятные
вещи. На основе обобщения свойств алгоритмов различной природы и имеют
прикладной характер. Этих свойств достаточно для практического
программирования, для создания обширного круга программ для компьютеров,
станков с ЧПУ, промышленных роботов и т.д. Однако, как фундаментальное научное
понятие алгоритм требует более обстоятельного изучения. Оно невозможно без
уточнения понятия «алгоритм», более строгого его описания или, как еще говорят,
без его формализации.
Известно несколько подходов к формализации понятия «алгоритм»:
–
теория
конечных и бесконечных автоматов;
–
теория
вычислимых (рекурсивных) функций;
–
λ-исчисление
Черча.
Главная цель формализации понятия
алгоритма такова: подойти к решению проблемы алгоритмической разрешимости
различных математических задач, т.е. ответить на вопрос, может ли быть
построен алгоритм, приводящий к решению задачи.
Этапы решения задачи на ЭВМ
Работа по решению любой задачи с использованием компьютера делится
на следующие этапы:
1.
Постановка задачи.
2. Формализация задачи.
3. Построение алгоритма.
4. Составление программы на языке программирования.
5. Отладка и тестирование программы.
6. Проведение расчетов и анализ полученных результатов.
Часто эту последовательность называют технологической
цепочкой решения задачи на ЭВМ. Непосредственно к программированию в этом
списке относятся пункты 3, 4, 5.
На этапе постановки задачи должно быть
четко сформулировано, что дано и что требуется найти. Здесь очень важно
определить полный набор исходных данных, необходимых для получения решения.
Второй этап — формализация задачи.
Здесь чаще всего задача переводится на язык математических формул, уравнений,
отношений. Если решение требует математического описания какого-то реального
объекта, явления или процесса, то формализация равносильна получению
соответствующей математической модели.
Третий этап — построение алгоритма.
Опытные программисты часто сразу пишут программы на языках, не прибегая к
каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам).
Однако в учебных целях полезно использовать эти средства, а затем переводить
полученный алгоритм на язык программирования.
Первые три этапа предусматривают работу без
компьютера. Дальше следует собственно программирование на определенном языке,
в определенной системе программирования.
Последний (шестой) этап — это использование
уже разработанной программы в практических целях.
Таким образом, программист должен обладать
следующими знаниями и навыками:
1.
уметь строить алгоритмы;
2. знать языки программирования;
3. уметь работать в соответствующей системе программирования.
Первый подход к формализации алгоритма связан с формализацией
понятия вычислителя, т. е. к построению очень простого, но функционально
полного вычислителя. Таким вычислителем является машина Поста. Машина Поста состоит из:
–
бесконечной в обе стороны ленты;
–
вычислительной головки.
В каждый момент времени (такт) головка
находится в некотором состоянии и обозревает одну позицию на ленте, в которой
находится символ (обозреваемый символ). Головка может выполнить одно из четырех действий:
–
записать в обозреваемую позицию на ленте новый символ.
–
переместиться на одну позицию влево по ленте.
–
переместиться на одну позицию вправо по ленте.
–
больше ничего не делать.
Действие головки однозначно определяется
парой: (<текущее состояние головки> <обозреваемый символ>)
и задается программой. Если в программе текущая пара не существует, то головка
останавливается.
Вопросы для
самоконтроля:
1.
Каковы
назначение и возможности системы алгоритмических конструкций?
2. Что такое блок-схема?
3. Какие основные элементы
блок-схем существуют?
4. Какие алгоритмические
конструкции бывают?
5. Что такое алгоритм линейной
структуры?
6. Что такое алгоритм
разветвляющейся структуры?
7. Что такое алгоритм
циклической структуры?
8. Что такое алгоритм сложной
структуры?
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.
Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.
Переместительный закон – предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон – применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон – имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) – основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.
Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Примеры:
-
Нью-Йорк — столица США (ложное);
-
в России 1117 городов (верное).
Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Пример:
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
-
если исходное выражение истинно, то результат его отрицания будет ложным;
-
если исходное выражение ложно, то результат его отрицания будет истинным.
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.
Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.
Таблица истинности операции ИЛИ:
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
Логическое следование (импликация) — ЕСЛИ ТО
Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если…, то».
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if…then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
Операция эквивалентности (равнозначности) – А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
>
Содержание:
- Логические операции. Таблицы истинности
- Примеры с решением
- Логические формулы. Законы алгебры логики
Алгебра логики является частью, разделом бурно развивающейся сегодня науки — дискретной математики. Дискретная математика занимается изучением свойств структур конечного характера, которые возникают как внутри математики, так и в ее приложениях.
- Заметим, что классическая математика, в основном, занимается изучением свойств объектов непрерывного характера, хотя само деление математики на классическую и дискретную в значительной мере условно, поскольку между ними происходит активная циркуляция идей и методов, часто возникает необходимость исследовать модели, обладающие как дискретными, так и непрерывными свойствами.
К числу структур, изучаемых дискретной математикой, могут быть отнесены конечные группы, конечные графы, математические модели преобразователей информации типа конечных автоматов или машин Тьюринга и др. Математический аппарат алгебры логики широко используется в информатике, в частности, в таких ее разделах, как проектирование ЭВМ, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование и т. д. Алгебра логики.
Понятие высказывания Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например,
Именно он построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.
Существуют алгебры натуральных чисел, многочленов, векторов, матриц, множеств и т. д. Дж. Буль (1815-1864) Долгое время алгебра логики была известна достаточно узкому классу специалистов.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон (1916-2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования ре-лейно-контактных и электронно-ламповых схем. Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).
- С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примерами высказываний на естественном языке являются предложения «Сегодня светит солнце» или «Трава растет». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в нашем примере погоды и окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь».
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 

Определение 1. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Возможно вам будут полезны данные страницы:
Это словесное определение, не являющееся математически точным, только на первый взгляд кажется удовлетворительным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению «Это предложение является ложным» невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его смыслу. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно.
- Как видно, этому предложению осмысленно нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием. Причина этого парадокса лежит в структуре построения указанного предложения: оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя и, следовательно, устранены возникающие отсюда парадоксы.
Определение 2. Высказывание называется простым (элементарным)I, если никакая его часть не является высказыванием.
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывание, соединив их знаком равенства или неравенства. Сами числовые выражения высказываниями не являются. Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «

Мы можем договориться, что абсурдное по смыслу высказывание «Крокодилы летают» является истинным, и с этим значением высказывания будем работать. Вопрос о том, летают крокодилы или нет, может волновать зоологов, но никак не математиков: им этот потрясающий факт безразличен. Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания. В информатике для точного определения понятия высказывания строятся ограниченные системы форм высказываний (формальный язык), которые используются при описании алгоритмических языков, в информационных системах, для строгого формального описания алгоритмов и т. д.
Логические операции. Таблицы истинности
Употребляемые в обычной речи связки «и», «или», «не», «если …, то …», «тогда и только тогда, когда …» и т. п. позволяют из уже заданных высказываний строить новые сложные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как логических операций над высказываниями. Для обозначения истинности, как правило, используются символы «И» и «1», а для обозначения ложности — символы «Л» и «0».
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний. В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:

Введем перечисленные логические операции формальным образом. Высказывание, составленное из двух высказываний путем объединения их связкой «и», называется конъюнкцией или логическим умножением. Высказывая конъюнкцию, мы утверждаем, что выполняются оба события, о которых идет речь в составляющих высказываниях.
Например, сообщая: {Ивановы привезли на зиму уголь и закупили дрова на растопку камина}, мы выражаем в одном высказывании свое убеждение в том, что произошли оба этих события.
Определение 3. Конъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Логическая операция конъюнкция определяется следующей таблицей, которую называют таблицей истинности:

Рассмотрим два высказывания 



Высказывание 
Высказывание, состоящее из двух высказываний, объединенных связкой «или», называется дизъюнкцией или логическим сложением, нестрогой дизъюнкцией.
В высказываниях, содержащих связку «или», указывается на существование двух возможных событий, из которых хотя бы одно должно быть осуществлено. Например, сообщая: {Петя читает книгу или пьет чай), мы имеем в виду, что хотя бы что-либо одно Петя делает. При этом Петя может одновременно читать книгу и пить чай. И в этом случае дизъюнкция будет истинна.
Определение 4. Дизъюнкция — логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Логическая операция дизъюнкция определяется следующей таблицей истинности:

Дизъюнкция истинна, когда хотя бы одно из двух образующих ее высказываний истинно. Рассмотрим два высказывания 


Союз «или» может применяться в речи и в другом, «исключающем» смысле. Тогда он соответствует другому высказыванию — разделительной, или строгой дизъюнкции. 3.2.3. Высказывание, образованное из двух высказываний, объединенных связкой «либо» (точнее: «либо только …, либо только …»), называется разделительной (строгой) дизъюнкцией, исключающим ИЛИ, сложением по модулю 2.
В отличие от обычной дизъюнкции (связка «или»), в высказывании, являющемся разделительной дизъюнкцией, мы утверждаем, что произойдет только одно событие из двух. Например, сообщая: {Петя сидит на трибуне А либо на трибуне Б}, мы утверждаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б.
Определение 5. Строгая, или разделительная дизъюнкция — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда ровно одно из двух высказываний является истинным.
Логическая операция разделительная дизъюнкция определяется следующей таблицей истинности:

Рассмотрим два высказывания 


Определение 6. Импликация — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (посылка) — истинно, а следствие (заключение) — ложно.
Логическая операция импликация задается следующей таблицей истинности:

Мы видим, что импликация заведомо истинна, если условие 

Примеры с решением
Пример 1.
Истинным высказыванием {Если на каникулах мы поедем в Петербург, то посетим Исаакиевский собор) мы утверждаем, что в случае приезда на каникулах в Петербург Исаакиевский собор мы посетим обязательно. В соответствии с определением импликации истинны следующие высказывания:
а) {Если 
б) {Если через Смоленск протекает Енисей, то 
в) {Если через Смоленск протекает Енисей, то 
г) {Если все ученики класса напишут контрольную работу по физике на отлично, то слоны в Африке живут).
д) {Если через Смоленск протекает Енисей, то все ученики класса напишут контрольную работу по физике на отлично).
Отметим, что высказывания г) и д) являются истинными импликациями и в том случае, если высказывание {все ученики класса напишут контрольную работу по физике на отлично) является истинным, и в том случае, если оно является ложным.
Следующие две импликации являются ложными, так как в них посылки истинны, а заключения ложны:
е) {Если 
ж) {Если через Смоленск протекает Днепр, то Луна сделана из теста). Импликация, образованная из высказываний А к В, может быть записана на естественном языке при помощи следующих предложений: «Если А, то Б», «Из Л следует В», «А влечет В».
Может показаться странным, что высказывание «Если А, то В>> всегда истинно, если посылка (высказывание Л) ложна. Но для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение. Допустим, что 1 = 2, тогда и 2 = 1. Складывая эти равенства, получим 3 = 3, т. е. из ложной посылки путем тождественных преобразований мы получили истинное высказывание.
Большинство математических теорем являются импликациями. Однако те импликации, в которых посылки (условия) и заключения (следствия) являются предложениями без взаимной (по существу) связи, не могут играть в науке важной роли. Они являются бесплодными предложениями, так как не ведут к выводам более глубокого содержания.
Логические формулы. Законы алгебры логики
Математики под словом «алгебра» подразумевают науку, которая изучает некие объекты и операции над ними. Например, школьная алгебра (алгебра действительных чисел) изучает действительные числа и операции над ними. Предметом же нашего изучения являются высказывания, операции над ними, а также логические функции. В предыдущих параграфах для обозначения высказываний мы использовали буквы. Как и в алгебре действительных чисел, введем следующие определения.
Определение 9. Логической переменной называется переменная, значением которой может быть любое высказывание.
Логические переменные (далее «переменные») обозначаются латинскими буквами, иногда снабженными индексами, как обычные алгебраические переменные: 
Понятие логической формулы является формализацией понятия сложного высказывания. Введем его индуктивно. Определение 10. Логической формулой является: 1) любая логическая переменная, а также каждая из двух логических констант — 0 (ложь) и 1 (истина); 2) если А и В — формулы, то В и А*В — тоже формулы, где знак «*» означает любую из логических бинарных операций. Формулой является, например, следующее выражение:
Определение 11. Формулы А и В, зависящие от одного и того же набора переменных 

Для обозначения равносильности формул используется знак равенства, например А В. В дальнейшем будет показано, что любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введенные операции 
1) законы коммутативности 
2) законы ассоциативности 
3) законы поглощения (нуля и единицы) 
4) законы дистрибутивности 
5) закон противоречия 
6) закон исключенного третьего 
7) законы идемпотентности 
8) закон двойного отрицания 
9) законы де Моргана 
10) законы поглощения 
Любой из этих законов может быть легко доказан с помощью таблиц истинности.
Пример 2.
Докажем первый закон де Моргана с использованием таблиц истинности. Построим таблицу истинности для левой и правой частей закона.

Так как результирующие столбцы совпали, то формулы, стоящие в левой и правой частях закона, равносильны. Любой из законов алгебры логики может быть доказан путем логических рассуждений.
Пример 3.
Докажем первый закон поглощения 
Пусть истинна правая часть, т. е. 

Пусть истинна левая часть. Тогда по определению дизъюнкции истинна или формула 

Если 


Методы решения логических задач Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.
Рассмотрим, как можно использовать данный способ для решения задач.
Пример 4.
Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?
Решение. Обозначим через 



Высказывание 


Пример 5.
Задача «Кто виноват?» По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено: 1) если Иванов не виновен или Петров виновен, то Сидоров виновен; 2) если Иванов не виновен, то Сидоров не виновен. Виновен ли Иванов? Решение. Рассмотрим простые высказывания: А = {Иванов виновен}, В = {Петров виновен}, С = {Сидоров виновен}. Запишем на языке алгебры логики факты, установленные следствием: 


Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание F истинно. Для этого необходимо проанализировать все строки таблицы истинности, где 



Лекции:
- Эластичность функции
- Разностные уравнения
- Случайная вероятность
- Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций
- Решение определённых интегралов
- Теорема о разложении на множители
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур