Алгебраическая прогрессия как найти сумму – Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Прогрессия.

Арифмети́ческая прогре́ссия — числовая последовательность вида

${displaystyle a_{1}, a_{1}+d, a_{1}+2d, ldots , a_{1}+(n-1)d, ldots ,}$

то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа $d$ (шага, или разности прогрессии):

${displaystyle a_{n}=a_{n-1}+d.}$ ^[1]

Любой член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому, т. е. он выражается формулой^[2]:

${displaystyle a_{n}=a_{1}+(n-1)d.}$

Арифметическая прогрессия является монотонной последовательностью. При $d>0$ она является возрастающей, а при $d<0$ — убывающей. Если $d=0$ , то последовательность будет стационарной. Эти утверждения следуют из соотношения $a_{n+1}-a_n=d$ для членов арифметической прогрессии.

Свойства[править | править код]

Общий член арифметической прогрессии[править | править код]

Член арифметической прогрессии с номером $n$ может быть найден по формулам

$a_n=a_1+(n-1)d$
${displaystyle a_{n}=a_{m}-(m-n)d}$

где $a_{1}$ — первый член прогрессии, $d$ — её разность, $a_m$ — член арифметической прогрессии с номером $m$ .

Доказательство формулы общего члена арифметической прогрессии

Пользуясь соотношением $a_{n+1}=a_n+d$ выписываем последовательно несколько членов прогрессии, а именно:

$a_2=a_1+d$

$a_3=a_2+d=a_1+d+d=a_1+2d$

$a_4=a_3+d=a_1+2d+d=a_1+3d$

$a_5=a_4+d=a_1+3d+d=a_1+4d$

Заметив закономерность, делаем предположение, что $a_n=a_1+(n-1)d$ . С помощью математической индукции покажем, что предположение верно для всех $n in mathbb N$ :

База индукции $(n=1)$ :

$a_1=a_1+(1-1)d=a_1$ — утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при $n=k$ , то есть $a_k=a_1+(k-1)d$ . Докажем истинность утверждения при $n=k+1$ :

$a_{k+1}=a_k+d=a_1+(k-1)d+d=a_1+kd$

Итак, утверждение верно и при $n=k+1$ . Это значит, что $a_n=a_1+(n-1)d$ для всех $n in mathbb N$ .■

Отметим, что в формулах общего члена $n$ -й член прогрессии есть линейная функция. Об этом говорит следующая теорема.

Для того чтобы последовательность ${displaystyle left{a_{n}right}}$ являлась арифметической прогрессией, необходимо и достаточно, чтобы $a_n$ являлась линейной функцией (от $n$ )^[3].

Доказательство

Необходимость. Пусть ${displaystyle left{a_{n}right}}$ арифметическая прогрессия. Тогда, как было уже показано, $a_n=a_1+(n-1)d$ , то есть ${displaystyle a_{n}=nd+a_{1}-d}$ . Так как ${displaystyle fleft(xright)=ax+b}$ есть линейная функция и ${displaystyle xin mathbb {N} }$ , это значит, что ${displaystyle a=d}$ и ${displaystyle b=a_{1}-d}$ , т. е. $a_n$ — линейная функция, где ${displaystyle fleft(nright)=nd+a_{1}-d}$ .

Достаточность. Пусть $a_n$ есть линейная функция, т. е. ${displaystyle a_{n}=acdot x+b}$ . Так как ${displaystyle xin mathbb {N} }$ и ${displaystyle x=n}$ , то ${displaystyle a_{n}=acdot n+b}$ , тогда ${displaystyle a_{n+1}=acdot left(n+1right)+b}$ .
Рассмотрим ${displaystyle a_{n+1}-a_{n}=left(acdot left(n+1right)+bright)-left(an+bright)}$ .
Отсюда следует, что ${displaystyle a_{n+1}-a_{n}=a}$ , где $a$ — величина постоянная. Тогда ${displaystyle a_{n+1}=a_{n}+a}$ , а это значит по определению, что ${displaystyle left{a_{n}right}}$ — арифметическая прогрессия.■

Суммы членов арифметической прогрессии с равными суммами номеров равны, т. е. ${displaystyle a_{n}+a_{m}=a_{k}+a_{l}Longleftrightarrow n+m=k+lquad vert ;forall left(n,,m,,k,,lin mathbb {N} right)}$ .

Характеристическое свойство арифметической прогрессии[править | править код]

Последовательность $a_1, a_2, a_3, ldots$ есть арифметическая прогрессия $Longleftrightarrow$ для любого её элемента выполняется условие

${displaystyle a_{n}={dfrac {a_{n-1}+a_{n+1}}{2}},ngeqslant 2.}$

Доказательство характеристического свойства арифметической прогрессии

Необходимость.

Поскольку $a_1, a_2, a_3, ldots$ — арифметическая прогрессия, то для $n geqslant 2$ выполняются соотношения:

$a_n=a_{n-1}+d$

$a_n=a_{n+1}-d$ .

Сложив эти равенства и разделив обе части на 2, получим ${displaystyle a_{n}={dfrac {a_{n-1}+a_{n+1}}{2}}}$ .

Достаточность.

Имеем, что для каждого элемента последовательности, начиная со второго, выполняется $a_n=frac{a_{n-1}+a_{n+1}}2$ . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду $a_{n+1}-a_n=a_n-a_{n-1}$ . Поскольку соотношения верны при всех $n geqslant 2$ , с помощью математической индукции покажем, что $a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n$ .

База индукции $(n=2)$ :

$a_2-a_1=a_3-a_2$ — утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при $n=k$ , то есть $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k$ . Докажем истинность утверждения при $n=k+1$ :

$a_{k+1}-a_{k}=a_{k+2}-a_{k+1}$

Но по предположению индукции следует, что $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k$ . Получаем, что $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k=a_{k+2}-a_{k+1}$

Итак, утверждение верно и при $n=k+1$ . Это значит, что $a_n=frac{a_{n-1}+a_{n+1}}2, n geqslant 2 Rightarrow a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n$ .

Обозначим эти разности через $d$ . Итак, $a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n=d$ , а отсюда имеем $a_{n+1}=a_n+d$ для $n in mathbb N$ . Поскольку для членов последовательности $a_1, a_2, a_3, ldots$ выполняется соотношение $a_{n+1}=a_n+d$ , то это есть арифметическая прогрессия.■

Тождество арифметической прогрессии[править | править код]

Пусть ${displaystyle a_{k},a_{l},a_{m}}$ — соответственно $k$ -й, $l$ -й, $m$ -й члены арифметической прогрессии, где ${displaystyle k,,l,,min mathbb {N} }$ . Тогда для всякой такой тройки выполняется комплементарное свойство арифметической прогрессии^{[нет в источнике]}, называемое тождеством арифметической прогрессии:

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0.}$

Доказательство тождества арифметической прогрессии

С помощью формулы общего члена выразим $k$ -й, $l$ -й, $m$ -й члены:

${displaystyle a_{k}=a_{1}+(k-1)d,quad a_{l}=a_{1}+(l-1)d,quad a_{m}=a_{1}+(m-1)d.}$

Вычитая почленно из первого равенства второе, а из второго третьего, получим:

${displaystyle a_{k}-a_{l}=(k-l)d,quad a_{l}-a_{m}=(l-m)d.}$

Выражая из этих равенств $d$ и приравнивая полученные выражения, получим:

${displaystyle {dfrac {a_{k}-a_{l}}{k-l}}={dfrac {a_{l}-a_{m}}{l-m}}.}$

По основному свойству пропорции:

${displaystyle (l-m)(a_{k}-a_{l})=(k-l)(a_{l}-a_{m}).}$

Откуда следует доказываемое тождество:

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0.}$

■

Следствие 1. Всякий член арифметической прогрессии вырази́м^[5] через любую пару других членов.

Доказательство

Преобразовав тождество арифметической прогрессии

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0}$

к виду

${displaystyle a_{m}={dfrac {(l-m)a_{k}+(m-k)a_{l}}{l-k}},}$

можно заметить, что $m$ -й член есть линейная комбинация двух других членов ( $a_{{k}}$ и ${displaystyle a_{l}}$ ), поскольку оно равносильно

${displaystyle a_{m}={dfrac {l-m}{l-k}}a_{k}+{dfrac {m-k}{l-k}}a_{l}.}$

■

Следствие 2. Для того, чтобы число ${displaystyle a_{m}}$ являлось членом данной арифметической прогрессии с членами $a_{{k}}$ и ${displaystyle a_{l}}$ , необходимо и достаточно, чтобы было натуральным число

${displaystyle m={dfrac {(a_{l}-a_{m})k+(a_{m}-a_{k})l}{a_{l}-a_{k}}}.}$

Формулировка ещё одного признака арифметической прогрессии.

Следствие 3 [критерий]. Числовая последовательность является арифметической прогрессией в том и только в том случае, если выполняется тождество арифметической прогрессии для всех членов данной последовательности. Другими словами, чтобы каждый член был вырази́м через любую пару остальных членов последовательности.

${displaystyle left{a_{n}right}~-~div Longleftrightarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} .}$

Доказательство

Необходимость. Утверждение

${displaystyle left{a_{n}right}~-~div Rightarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} }$

очевидно (см. доказательство тождества арифметической прогрессии).

Достаточность. Докажем, что

${displaystyle left{a_{n}right}~-~div Leftarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} .}$

Равенство

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0}$

можно преобразовать к виду

${displaystyle (l-m)(a_{k}-a_{l})=(k-l)(a_{l}-a_{m}).}$

Если все три номера различны, тогда

${displaystyle {dfrac {a_{k}-a_{l}}{k-l}}={dfrac {a_{l}-a_{m}}{l-m}}.}$

Обозначим выражение, например, в левой части равенства за $d$ , то есть

${displaystyle d={dfrac {a_{k}-a_{l}}{k-l}}.}$

Откуда можно прийти к следующему предложению:

${displaystyle a_{k}=a_{l}+{left(k-lright)}d.}$

Наконец, методом математической индукции, например, по $l$ нетрудно убедиться, что данное соотношение описывает именно арифметическую прогрессию.

Действительно, при $l=1$ (база индукции) получаем формулу общего члена арифметической прогрессии:

${displaystyle a_{k}=a_{1}+{left(k-1right)}d.}$

Предположим истинность утверждения (для $l$ ): формула ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ характеризует арифметическую прогрессию. Тогда покажем, что и при $l+1$ формула верна для арифметической прогрессии (переход, или шаг, индукции). Рассмотрим левую часть формулы

${displaystyle a_{k}=a_{l+1}+{left(k-left(l+1right)right)}d.}$

По предположению индукции ( ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ ) заменим $a_{k}$ на выражение ${displaystyle a_{l}+{left(k-lright)}d}$ . Итак, получим следующее:

${displaystyle a_{l}+{left(k-lright)}d=a_{l+1}+{left(k-left(l+1right)right)}d.}$

Методом тождественных преобразований имеем равносильное предложение

${displaystyle a_{l+1}=a_{l}+d.}$

А это, в свою очередь, рекуррентное соотношение для арифметической прогрессии.

Значит, по принципу математической индукции можно утвердать, что для всякого $l$ соотношение ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ верно только и только для членов арифметической прогрессии.

Аналогичные рассуждения проводятся для формулы ${displaystyle d={dfrac {a_{l}-a_{m}}{l-m}}}$ .

Данное следствие целиком и полностью считается доказанным.■

Сумма первых n членов арифметической прогрессии[править | править код]

Сумма первых $n$ членов арифметической прогрессии ${displaystyle S_{n}=sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+ldots +a_{n}}$ может быть найдена по формулам

${displaystyle S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$ , где $a_{1}$ — первый член прогрессии, $a_n$ — член с номером $n$ , $n$ — количество суммируемых членов.

${displaystyle S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot ({dfrac {a_{n}-a_{1}}{a_{2}-a_{1}}}+1)}$ — где $a_{1}$ — первый член прогрессии, $a_{2}$ — второй член прогрессии ${displaystyle ,a_{n}}$ — член с номером $n$ .

${displaystyle S_{n}={dfrac {2a_{1}+d(n-1)}{2}}cdot n}$ , где $a_{1}$ — первый член прогрессии, $d$ — разность прогрессии, $n$ — количество суммируемых членов.

${displaystyle S_{n}=a_{frac {n+1}{2}}cdot n}$ , если $n$ — нечётное натуральное число.

Доказательство
Запишем сумму двумя способами: $S_n=a_1+a_2+a_3+ ldots +a_{n-2}+a_{n-1}+a_n$ $S_n=a_n+a_{n-1}+a_{n-2}+ ldots +a_3+a_2+a_1$ — та же сумма, только слагаемые идут в обратном порядке. Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали: $2S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+ ldots +(a_{n-2}+a_3)+(a_{n-1}+a_2)+(a_n+a_1)$ Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде $a_i+a_{n-i+1}, i=1,2,ldots,n$ . Воспользуемся формулой общего члена арифметической прогрессии: $a_i+a_{n-i+1}=a_1+(i-1)d+a_1+(n-i+1-1)d=2a_1+(n-1)d, i=1,2,ldots,n$ Получили, что каждое слагаемое не зависит от $i$ и равно $2a_1+(n-1)d$ . В частности, $a_1+a_n=2a_1+(n-1)d$ . Поскольку таких слагаемых $n$ , то ${displaystyle 2S_{n}=(a_{1}+a_{n})cdot nRightarrow S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$ Третья формула для суммы получается подстановкой $2a_1+(n-1)d$ вместо $a_1+a_n$ . Что и так непосредственно следует из выражения для общего члена. Замечание: Вместо $a_1+a_n$ в первой формуле для суммы можно взять любое из других слагаемых $a_i+a_{n-i+1}, i=2,3,ldots,n$ , так как они все равны между собой.

Доказательство

Запишем сумму двумя способами:

$S_n=a_1+a_2+a_3+ ldots +a_{n-2}+a_{n-1}+a_n$

$S_n=a_n+a_{n-1}+a_{n-2}+ ldots +a_3+a_2+a_1$ — та же сумма, только слагаемые идут в обратном порядке.

Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали:

$2S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+ ldots +(a_{n-2}+a_3)+(a_{n-1}+a_2)+(a_n+a_1)$

Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде $a_i+a_{n-i+1}, i=1,2,ldots,n$ . Воспользуемся формулой общего члена арифметической прогрессии:

$a_i+a_{n-i+1}=a_1+(i-1)d+a_1+(n-i+1-1)d=2a_1+(n-1)d, i=1,2,ldots,n$

Получили, что каждое слагаемое не зависит от $i$ и равно $2a_1+(n-1)d$ . В частности, $a_1+a_n=2a_1+(n-1)d$ . Поскольку таких слагаемых $n$ , то

${displaystyle 2S_{n}=(a_{1}+a_{n})cdot nRightarrow S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$

Третья формула для суммы получается подстановкой $2a_1+(n-1)d$ вместо $a_1+a_n$ . Что и так непосредственно следует из выражения для общего члена.

Замечание:

Вместо $a_1+a_n$ в первой формуле для суммы можно взять любое из других слагаемых $a_i+a_{n-i+1}, i=2,3,ldots,n$ , так как они все равны между собой.

Формулировка ещё одного факта: для всякой арифметической прогрессии при любом $n$ выполняется равенство:

${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n}.}$

Примечание: $S_{k}$ — сумма $k$ первых членов арифметической прогрессии.

Доказательство
1. Очевидно, что ${displaystyle {dfrac {S_{2n}}{2n}}-{dfrac {S_{n}}{n}}={dfrac {a_{1}+a_{2n}-left(a_{1}+a_{n}right)}{2}}={dfrac {a_{2n}-a_{n}}{2}},}$ или ${displaystyle S_{2n}-2S_{n}=ncdot (a_{2n}-a_{n}).}$ Прибавим к обеим частям $S_{n}$ и получим, что ${displaystyle S_{2n}-S_{n}=S_{n}+ncdot (a_{2n}-a_{n}).}$ 2. Покажем, что ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$ Это так, поскольку можно написать верное равенство: ${displaystyle {dfrac {S_{3n}}{3n}}-{dfrac {S_{n}}{n}}={dfrac {a_{3n}-a_{n}}{2}}.}$ Из него следует, что ${displaystyle {dfrac {S_{3n}}{3}}=S_{n}+{dfrac {a_{3n}-a_{n}}{2}}cdot n.}$ 3. Теперь докажем, что ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$ Перепишем последнее как ${displaystyle a_{2n}={dfrac {a_{3n}+a_{n}}{2}}.}$ Но гораздо лучше представить это равенство в виде ${displaystyle a_{2n}={dfrac {a_{2n+1}+a_{2n-1}}{2}}.}$ Видно, что это характеристическое свойство арифметической прогрессии. Значит, действительно ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$ 4. А следовательно, ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$ 5. Тем самым, ${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n},}$ что и требовалось доказать.

Доказательство

1. Очевидно, что ${displaystyle {dfrac {S_{2n}}{2n}}-{dfrac {S_{n}}{n}}={dfrac {a_{1}+a_{2n}-left(a_{1}+a_{n}right)}{2}}={dfrac {a_{2n}-a_{n}}{2}},}$ или ${displaystyle S_{2n}-2S_{n}=ncdot (a_{2n}-a_{n}).}$

Прибавим к обеим частям $S_{n}$ и получим, что ${displaystyle S_{2n}-S_{n}=S_{n}+ncdot (a_{2n}-a_{n}).}$

2. Покажем, что ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$

Это так, поскольку можно написать верное равенство:

${displaystyle {dfrac {S_{3n}}{3n}}-{dfrac {S_{n}}{n}}={dfrac {a_{3n}-a_{n}}{2}}.}$ Из него следует, что ${displaystyle {dfrac {S_{3n}}{3}}=S_{n}+{dfrac {a_{3n}-a_{n}}{2}}cdot n.}$

3. Теперь докажем, что ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$
Перепишем последнее как ${displaystyle a_{2n}={dfrac {a_{3n}+a_{n}}{2}}.}$

Но гораздо лучше представить это равенство в виде ${displaystyle a_{2n}={dfrac {a_{2n+1}+a_{2n-1}}{2}}.}$ Видно, что это характеристическое свойство арифметической прогрессии.
Значит, действительно ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$

4. А следовательно, ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$

5. Тем самым, ${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n},}$ что и требовалось доказать.

Предыдущее свойство имеет обобщение.

Для любых натуральных $k$ , $l$ , $m$ выполняется комплементарное свойство сумм:

${displaystyle {dfrac {l-m}{k}}cdot S_{k}+{dfrac {m-k}{l}}cdot S_{l}+{dfrac {k-l}{m}}cdot S_{m}=0.}$

Ещё один признак арифметической прогрессии.

Для того чтобы последовательность ${displaystyle left{a_{n}right}}$ являлась арифметической прогрессией, необходимо и достаточно, чтобы сумма первых $n$ членов последовательности была функцией не выше второй степени относительно $n$ ^[6].

Сумма членов арифметической прогрессии от n-го до m-го[править | править код]

Сумма членов арифметической прогрессии с номерами от $n$ до $m$ ${displaystyle S_{m,n}=sum _{i=n}^{m}a_{i}=a_{n}+a_{n+1}+ldots +a_{m}}$ может быть найдена по формулам

${displaystyle S_{m,n}={dfrac {a_{m}+a_{n}}{2}}cdot (m-n+1)}$ , где $a_m$ — член с номером $m$ , $a_n$ — член с номером $n$ , ${displaystyle (m-n+1)}$ — количество суммируемых членов.

${displaystyle S_{m,n}={dfrac {2a_{n}+dleft(m-nright)}{2}}cdot left(m-n+1right),}$

где $a_n$ — член с номером $n$ , $d$ — разность прогрессии, ${displaystyle (m-n+1)}$ — количество суммируемых членов.

Произведение членов арифметической прогрессии[править | править код]

Произведением первых $n$ членов арифметической прогрессии ${displaystyle left{a_{n}right}}$ называется произведение от $a_{1}$ до $a_n$ , то есть выражение вида ${displaystyle prod limits _{i=1}^{n}a_{i}=a_{1}cdot a_{2}cdot a_{3}cdot ldots cdot a_{n-2}cdot a_{n-1}cdot a_{n}.}$ Обозначение: $P_{n}$ .

Свойство произведения:

Число множителей-скобок ${displaystyle {left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ равно ${displaystyle {dfrac {n-1}{2}}}$ , а в самом произведении ${displaystyle a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ их составляет ${displaystyle {dfrac {n+1}{2}}}$ «штук».^[10]

Сходимость арифметической прогрессии[править | править код]

Арифметическая прогрессия $a_1, a_2, a_3, ldots$ расходится при $dne 0$ и сходится при $d=0$ . Причём

$lim_{nrightarrowinfty} a_n=left{ begin{matrix} +infty, d>0 \ -infty, d<0 \ a_1, d=0 end{matrix} right.$

Доказательство
Записав выражение для общего члена и исследуя предел $lim_{nrightarrowinfty} (a_1+(n-1)d)$ , получаем искомый результат.

Связь между арифметической и геометрической прогрессиями[править | править код]

Пусть $a_1, a_2, a_3, ldots$ — арифметическая прогрессия с разностью $d$ и число $a>0$ . Тогда последовательность вида $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ есть геометрическая прогрессия со знаменателем $a^d$ .

Доказательство
Проверим характеристическое свойство для образованной геометрической прогрессии: $sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}= a^{a_n}, ngeqslant 2$ Воспользуемся выражением для общего члена арифметической прогрессии: $sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}=sqrt{a^{a_1+(n-2)d}cdot a^{a_1+nd}}=sqrt{a^{2a_1+2(n-1)d}}=sqrt{(a^{a_1+(n-1)d})^2}=a^{a_1+(n-1)d}=a^{a_n}, ngeqslant 2$ Итак, поскольку характеристическое свойство выполняется, то $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения $q=frac{a^{a_2}}{a^{a_1}}=frac{a^{a_1+d}}{a^{a_1}}=a^d$ .

Доказательство

Проверим характеристическое свойство для образованной геометрической прогрессии:

$sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}= a^{a_n}, ngeqslant 2$

Воспользуемся выражением для общего члена арифметической прогрессии:

$sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}=sqrt{a^{a_1+(n-2)d}cdot a^{a_1+nd}}=sqrt{a^{2a_1+2(n-1)d}}=sqrt{(a^{a_1+(n-1)d})^2}=a^{a_1+(n-1)d}=a^{a_n}, ngeqslant 2$

Итак, поскольку характеристическое свойство выполняется, то $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения $q=frac{a^{a_2}}{a^{a_1}}=frac{a^{a_1+d}}{a^{a_1}}=a^d$ .

Следствие: если последовательность положительных чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию.

Арифметические прогрессии высших порядков[править | править код]

Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

1, 4, 9, 16, 25, 36, …

разности которых образуют простую арифметическую прогрессию с разностью 2:

3, 5, 7, 9, 11, …

Треугольные числа ${displaystyle 1,3,6,10,15,ldots }$ также образуют арифметическую прогрессию второго порядка, их разности образуют простую арифметическую прогрессию ${displaystyle 2,3,4,5,ldots }$

Тетраэдральные числа ${displaystyle 1,4,10,20,35,ldots }$ образуют арифметическую прогрессию третьего порядка, их разности являются треугольными числами.

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

Если $left[a_{{i}}right]_{{1}}^{{n}}$ — арифметическая прогрессия порядка $m$ , то существует многочлен $P_{{m}}(i)=c_{{m}}i^{{m}}+...+c_{{1}}i+c_{{0}}$ , такой, что для всех $iin left{1,....nright}$ выполняется равенство $a_{{i}}=P_{{m}}(i)$ ^[11]

Примеры[править | править код]

${displaystyle T_{n}=sum _{i=1}^{n}i=1+2+3+ldots +n={frac {n(n+1)}{2}}}$

Формула для разности[править | править код]

Если известны два члена арифметической прогрессии, а также их номера в ней, то можно найти разность как

${displaystyle {mathit {d={frac {a_{m}-a_{n}}{m-n}}}}}$ .

Сумма чисел от 1 до 100[править | править код]

Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050.
Действительно, легко видеть, что решение сводится к формуле

$frac{n(n+1)}2$

то есть к формуле суммы первых $n$ чисел натурального ряда.

См. также[править | править код]

Геометрическая прогрессия
Арифметико-геометрическая прогрессия

Примечания[править | править код]

↑ Такое соотношение называют рекуррентным соотношением первого порядка. Поэтому арифметическая прогрессия есть множество последовательностей, задающихся именно таким образом.
↑ Фильчаков П. Ф. Глава II. Алгебра и элементарные функции. Функции натурального аргумента (§ 75. Арифметическая прогрессия) // Справочник по элементарной математике: для поступающих в вузы : книга / под ред. чл.-кор. АН УССР П. Ф. Фильчакова. — Киев : «Наукова думка», 1972. — С. 303. — 528 с. — 400 000 экз. — УДК 51 (08)^(G).
↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 135. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
↑ Соотношение между любыми тремя членами арифметической прогрессии и их номерами (Мусинов В. А.) // Материалы студенческой научной сессии Института математики и информатики МПГУ. 2021–2022 учебный год : сборник статей / под общ. ред. Е. С. Крупицына. — М.: МПГУ, 2022. — С. 91—93. — 156 с. — ISBN 978-5-4263-1109-1, ББК 22.1я431+32.81я431+22.1р30я431+74.262.21я431+74.263.2я431.
↑ Это означает, что выражаемый член есть комбинация любых двух других членов данной последовательности, причём эта комбинация составлена с помощью арифметических операций и конечного набора символов. Для арифметической последовательности такая комбинация будет линейной.
↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 141. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
↑ Из доказательства необходимости следует, что ${displaystyle S_{n}=an^{2}+bn}$ , поэтому, если ${displaystyle S_{n}=an^{2}+bn+c}$ , то необходимо сделать проверку. Например, если ${displaystyle S_{n}=2n^{2}-n-6}$ — сумма первых $n$ членов последовательности, то такая последовательность НЕ является арифметической прогрессией. А последовательность, заданная суммой ${displaystyle S_{n}=2n^{2}-n}$ первых $n$ членов, будет арифметической прогрессией.
↑ При $n=1$ произведение $P_{n}$ равно ${displaystyle a_{frac {1+1}{2}}=a_{1}}$ , что безусловно верно.
↑ Эту формулу удобно использовать для выполнения итераций в программном коде, так как результат зависит от значения только двух величин: постоянного числа — разности, и члена, стоящего ровно по середине между первым и $n$ -м членом.
↑ Пример применения формулы.
Пусть ${displaystyle div left{a_{n}right}:quad underbrace {27} _{a_{1}},;underbrace {20} _{a_{2}},;underbrace {13} _{a_{3}},;underbrace {6} _{a_{4}},;underbrace {-1} _{a_{5}}}$ , где ${displaystyle d=-7}$ .

По формуле ${displaystyle P_{n}=a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ найдём произведение пяти первых членов. Количество сомножителей должно равняться ${displaystyle {dfrac {5+1}{2}}=3}$ . Причём первым сомножителем будет ${displaystyle a_{frac {5+1}{2}}=a_{3}=13}$ .

Далее ${displaystyle prod limits _{i=1}^{frac {5-1}{2}}{left(a_{frac {5+1}{2}}^{2}-{left[idright]}^{2}right)}=prod limits _{i=1}^{2}{left(a_{3}^{2}-{left[idright]}^{2}right)}=}$ ${displaystyle ={left(a_{3}^{2}-{left[dright]}^{2}right)}cdot {left(a_{3}^{2}-{left[2dright]}^{2}right)}={left(169-49right)}cdot {left(169-4cdot 49right)}=}$ ${displaystyle =120cdot {left(-27right)}}$ .

Наконец, ${displaystyle P_{n}=13cdot 120cdot {left(-27right)}=-42120}$ .
↑ Бронштейн, 1986, с. 139.

Литература[править | править код]

Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1986. — 544 с.

Ссылки[править | править код]

Арифметическая прогрессия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890. — Т. II. — С. 98.

Источник

Сумма членов арифметической прогрессии

Сумма всех членов арифметической прогрессии равна половине произведения суммы её крайних членов на количество всех её членов.

где S — это сумма всех членов, a₁ — первый член прогрессии, a_n — последний член, а n — количество членов в данной прогрессии.

Рассмотрим, почему именно с помощью данной формулы можно найти сумму всех членов арифметической прогрессии:

Если взять любую конечную арифметическую прогрессию, например:

3, 6, 9, 12, 15, 18, 21, 24, 27, 30;

то не трудно будет посчитать (складывая числа друг за другом), что сумма всех её членов равна 165. В то же время, если сгруппировать попарно все члены, равноудалённые от концов:

(3 + 30), (6 + 27), (9 + 24), (12 + 21) и (15 + 18);

то можно увидеть, что суммы таких групп равны (в данном случае сумма чисел каждой группы равна 33). Значит, вместо того, чтобы последовательно складывать все члены прогрессии, достаточно узнать сумму двух её членов — первого и последнего. Так как таких сумм получится ровно в 2 раза меньше, чем всех членов в прогрессии, то для вычисления суммы всех членов, надо умножить сумму первого и последнего члена на общее количество членов прогрессии, разделённое на два:

(3 + 30) ·	10	=	(3 + 30) · 10	= 165.
2	2

Исходя из данного примера, можно вывести общую формулу нахождения суммы всех членов прогрессии, если известен первый и последний её члены, а также количество членов:

S =	(a₁ + a_n) ·	n	=	(a₁ + a_n)n	.
2	2

Если в формулу для суммы вместо a_n вставить равное ему выражение: a₁ + (n – 1)d, то получится:

S =	(2a₁ + d(n – 1))n	.
2

По этой формуле можно определить сумму в зависимости от первого члена, разности и количества членов данной прогрессии.

Пример. Найти сумму первых 10 членов арифметической прогрессии:

1, 3, 5, 7, … .

Решение: В данной прогрессии первый член равен 1, а разность — 2, значит, сумма первых 10 членов равна:

(2 · 1 + 2(10 – 1)) · 10	= 100.
2

Источник

Арифметическая прогрессия

Понятие арифметической прогрессии
Формула n-го члена арифметической прогрессии
Свойства арифметической прогрессии
Сумма первых n членов арифметической прогрессии
Примеры

п.1. Понятие арифметической прогрессии

Арифметической прогрессией называют числовую последовательность, каждый член которой a_n, начиная со второго, равен сумме предыдущего члена a_n-1 и некоторого постоянного числа d: $$ mathrm{ a_n=a_{n-1}+d, ninmathbb{N}, nleq 2 } $$ Число d называют разностью арифметической прогрессии.

Например:
1. Последовательность 2, 5, 8, 11, 14, … является арифметической прогрессией с разностью d = 3.

2. Последовательность 12, 9, 6, 3, 0, –3, –6, … является арифметической прогрессией с разностью d = –3.

п.2. Формула n-го члена арифметической прогрессии

По определению арифметической прогрессии мы получаем рекуррентную формулу для n-го члена: a_n = a_n-1 + d. Из неё можно вывести аналитическую формулу:

a₂ = a₁ + d, $qquad$ a₃ = a₂ + d = (a₁ + d) + d = a₁ + 2d
a₄ = a₃ + d = (a₁ + 2d) + d = a₁ + 3d,…

Получаем:

a_n = a₁ + (n – 1)d

Например:
Найдём a₇, если известно, что a₁ = 5, d = 3.
По формуле n-го члена получаем: a₇ = a₁ + 6d = 5 + 6 · 3 = 23

п.3. Свойства арифметической прогрессии

Свойство 1. Линейность

Арифметическая прогрессия является линейной функцией f(n) = kn + b:

a_n = dn + (a₁ – d)

с угловым коэффициентом k = d и свободным членом b = a₁ – d.

Свойство 1

При d > 0 прогрессия линейно возрастает

При d < 0 прогрессия линейно убывает

Следствие: любую арифметическую прогрессию можно задать формулой: $$ mathrm{ a_n=dn+b, ninmathbb{N}, binmathbb{R}, dinmathbb{R}} $$ где d, b – некоторые числа.

Свойство 2. Признак арифметической прогрессии

Для того чтобы числовая последовательность была арифметической прогрессией необходимо и достаточно, чтобы каждый её член, начиная со второго, был средним арифметическим предыдущего и последующего членов: $$ mathrm{ left{a_nright} – text{арифметическая прогрессия} Leftrightarrow a_n=frac{a_{n-1}+a_{n+1}}{2}, ninmathbb{N}, n geq 2 } $$ Следствие: каждый член прогрессии является средним арифметическим двух равноудалённых от него членов: $$ mathrm{ a_n=frac{a_{n-k}+a_{n+k}}{2}, ninmathbb{N}, ninmathbb{N}, n geq k+1 } $$

Например:
Найдём a₉, если известно, что a₇ = 10, a₁₁ = 15
По следствию из признака арифметической прогрессии: (mathrm{a_9=frac{a_7+a_{11}}{2}=frac{10+15}{2}=12,5})

Свойство 3. Равенство сумм индексов

Если {a_n} – арифметическая прогрессия, то из равенства сумм индексов следует равенство сумм членов: $$ mathrm{ m+k=p+q Rightarrow a_m+a_k=a_p+a_q } $$ Следствие: сумма членов, равноудалённых от концов прогрессии, является постоянной величиной: $$ mathrm{ a_1 + a_n=a_2+a_{n-1}=a_3+a_{n-2}=… } $$

Например:
Найдём a₆, если известно, что a₂ = 5, a₄ = 10, a₈ = 20
По равенству сумм индексов a₂ + a₈ = a₄ + a₆
Откуда a₆ = a₂ + a₈ – a₄ = 5 + 20 – 10 = 15

п.4. Сумма первых n членов арифметической прогрессии

Сумма первых n членов арифметической прогрессии равна произведению среднего арифметического её крайних членов и количества членов: $$mathrm{ S_n=frac{a_1+a_n}{2}n} $$

Если учесть, что a_n = a₁ + d(n – 1), получаем ещё одну формулу для суммы: $$mathrm{ S_n=frac{2a_1+d(n-1)}{2}n} $$

Например:
Найдём сумму первых 100 натуральных чисел: 1 + 2 +…+ 100
В этом случае a₁ = 1, a₁₀₀ = 100, n = 100
(mathrm{ S_{100}=frac{1+100}{2}cdot 100=5050})

п.5. Примеры

Пример 1. Найдите первый член и разность арифметической прогрессии, если:
а) a₇ = 10, a₁₅ = 42
Найдем разность данных членов: a₁₅ – a₇ = (a₁ + 14d) – (a₁ + 6d) = 8d
Получаем разность прогрессии: 42 – 10 = 8d ⇒ d = 32 : 8 = 4
7-й член: a₇ = a₁ + 6d = a₁ + 6 · 4 = 10 ⇒ a₁ = 10 – 24 = –14
Ответ: a₁ = –14, d = 4

б) a₁₀ = 95, S₁₀ = 500
Сумма прогрессии: (mathrm{S_{10}=frac{a_1+a_{10}}{2}cdot 10Rightarrow 500=(a_1+95)cdot 5Rightarrow a_1+95=100Rightarrow a_1=5})
10-й член: (mathrm{a_{10}=a_1+9dRightarrow95=5+9dRightarrow 9d=90Rightarrow d=10})
Ответ: a₁ = 5, d = 10

Пример 2. Найдите сумму первых 100 нечётных натуральных чисел.
Чему равно последнее слагаемое этой суммы?
Ищем сумму (mathrm{underbrace{1+3+5+…}_{100 text{слагаемых}}})
По условию a₁ = 1, d = 2, n = 100. Получаем:
(mathrm{S_{100}=frac{2a_1+d(n-1)}{2}n=frac{2cdot 1+2cdot 99}{2}cdot 100=10000})
Формула n-го члена данной прогрессии: (mathrm{a_n=a_1+d(n-1)=dn+(a_1-d)=2n-1})
100-й член (mathrm{a_{100}=2cdot 100-1=199})
Ответ: S₁₀₀ = 10000, a₁₀₀ = 199

Пример 3*. Сколько членов арифметической прогрессии 10, 16, 22, … находится между числами 110 и 345?
По условию a₁ = 10, d = 16 – 10 = 6
Формула n-го члена данной прогрессии a_n = a₁ + d(n – 1) = dn + (a₁ – d) = 6n + 4
Заданные числа могут быть членами данной прогрессии или находиться по «соседству» с ними. Подставим их в формулу для n-го члена: begin{gather*} mathrm{ 6k+4=110Rightarrow 6k=106Rightarrow k=17frac23Rightarrow 17lt klt 18 }\ mathrm{ 6m+4=345Rightarrow 6m=341Rightarrow m=56frac56Rightarrow 56lt mlt 57 } end{gather*} Ближайший сосед справа к 100 – это a₁₈ = 6 · 18 + 4 = 112, k = 18
Ближайший сосед слева к 345 – это a₅₆ = 6 · 56 + 4 = 340, m = 56
Свойство 1
Количество членов прогрессии в заданном интервале:

n = m – k + 1 = 56 – 18 + 1 = 39

Ответ: 39

Пример 4. Одиннадцатый член арифметической прогрессии равен 7.
Найдите сумму её первых 21 членов.
По свойству суммы индексов: a₁₁ + a₁₁ = a₁ + a₂₁
Откуда a₁ + a₂₁ = 2a₁₁ = 14
Искомая сумма: (mathrm{S_{21}=frac{a_1+a_{21}}{2}cdot 21=frac{14}{2}cdot 21=147})
Ответ: 147

Пример 5. Величины углов выпуклого пятиугольника образуют арифметическую прогрессию. Найдите третий член этой прогрессии.
Сумма углов выпуклого пятиугольника S₅ = 180° · (5 – 2) = 540°
Если углы образуют арифметическую прогрессию, то: $$ mathrm{ S_5=frac{a_1+a_5}{2}cdot 5=540^circRightarrow a_1+a_5=216^circ } $$ По свойству суммы индексов: a₃ + a₃ = a₁ + a₅
Откуда: (mathrm{a_3=frac{a_1+a_5}{2}=108^circ})
Ответ: 108°

Пример 6. При каких значениях x числа x² – 11, 2x² + 29, x⁴ – 139 в заданной последовательности являются членами арифметической прогрессии?
Для последовательных членов получаем уравнение:

a₂ – a₁ = a₃ – a₂
(2x² + 29) – (x² – 11) = (x⁴ – 139) – (2x² + 29)
x⁴ – 3x² – 208 = 0 ⇒ (x² + 13)(x² – 16) = 0 ⇒ x² = 16 ⇒ x = ±4

Ответ: x = ±4

Пример 7. Сумма первых трёх членов убывающей арифметической прогрессии равна 9, а сумма их квадратов равна 99. Найдите седьмой член прогрессии.
По условию d < 0 и: $$ left{ begin{array}{ l } mathrm{a_1+a_2+a_3=9} & \ mathrm{a_1^2+a_2^2+a_3^2=99} & end{array}right. $$ Используем свойство прогрессии: (mathrm{a_2=frac{a_1+a_3}{2}}). Получаем из первого уравнения:

3a₂ = 9 ⇒ a_2 = 3

Тогда a₁ = a₂ – d = 3 – d, a₃ = a₂ + d = 3 + d. Подставляем во второе уравнение:

(3 – d)² + 3² + (3 + d)² = 99
9 – 6d + d² + 9 + 9 + 6d + d² = 99
2d² = 72 ⇒ d² = 36 ⇒ d = ±6

Выбираем отрицательное значение d = –6
1-й член прогрессии: a₁ = a₂ – d = 3 + 6 = 9
7-й член прогрессии: a₇ = a₁ + 6d = 9 + 6(–6) = –27
Ответ: x = –27

Источник

На этой странице вы узнаете

Как правильно расставить шары для бильярда в начале игры?
Как Карл Гаусс удивил своего учителя по математике?

Считаем ли мы овец перед сном, добавляем по монетке в копилку или достаем сухарик из упаковки — каждый раз мы интуитивно применяем законы математики, которые рассмотрим в этой статье.

Понятие арифметической прогрессии

Арифметическая прогрессия является видом «Числовых последовательностей».

У арифметической прогрессии есть особенность: каждый следующий член отличается от предыдущего на одно и то же число. В последовательности 1, 2, 3, 4 и так далее — члены отличаются друг от друга на единицу.

Арифметическая прогрессия — последовательность чисел, в которой каждый член, начиная со второго, равен сумме предыдущего члена и разности прогрессии.

Разность прогрессии — то число, на которое отличаются члены прогрессии друг от друга. Разность прогрессии обозначается буквой d.

Арифметическую прогрессию можно задать формулой.

a_n+1 = a_n + d

Например, если мы хотим найти третий член арифметической прогрессии, то нужно воспользоваться формулой: a₃ = a₂ + d

Однако бывает, что известны только первый член прогрессии и ее разность. Как быть в этом случае?

Разберемся на примере. Допустим, мы читаем книгу. Количество прочитанных страниц может быть задано с помощью арифметической прогрессии, в которой разность прогрессии и первый ее член равны 1.

Мы прочитали 10 страниц. Десятая страница будет десятым членом прогрессии. Это 1 + 1 + 1 + 1 +1 + 1 + 1 + 1 + 1 + 1 страниц, если считать их по отдельности.

Выделим первую страницу отдельно: 1 + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) = 1 + 9 = 1 + 1 * 9

Теперь заменим десятый член прогрессии, первый член прогрессии и ее разность на буквенные обозначения: a₁₀ = a₁ + 9 * d.

Заметим, что множитель перед d на один меньше, чем порядковый номер искомого члена прогрессии. Тогда получаем: a₁₀ = a₁ + (10 — 1) * d

Мы можем вывести формулу для n-го члена прогрессии. А выглядит она так.

a_n = a₁ + d(n — 1)

Как правильно расставить шары для бильярда в начале игры?

Вспомним расстановку шаров в бильярде. Они ставятся в пять рядов, причем в первом ряду один шар, а в пятом — пять.

Тогда, чтобы правильно разместить 15 шаров, нужно воспользоваться арифметической прогрессией. В каждом следующем ряду будет на один шар больше, следовательно, во втором ряду имеем 1 + 1 = 2 шара, в третьем ряду 2 + 1 = 3 шара, а в четвертом 3 + 1 = 4.

Расставленные таким образом шары образуют форму треугольника.

Допустим, мы хотим купить джинсы. В магазине представлены три ценовых категорий, которые отличаются друг от друга на одинаковую сумму. Мы знаем, что самые дешевые джинсы стоят 1000 рублей, а самые дорогие 3000 рублей. Как найти, сколько стоят джинсы во второй ценовой категории?

Попробуем найти разность арифметической прогрессии.

Джинсы во второй категории будут стоить 1000 + d, а чтобы найти стоимость третьей категории, нужно прибавить разность прогрессии ко второй категории. Получаем 1000 + d + d = 1000 + 2d.

Мы знаем, что самые дорогие джинсы стоят 3000 рублей. Получаем уравнение 1000 + 2d = 3000, откуда можем выразить разность прогрессии:

(d = frac{3000 — 1000}{2} = 1000)

Тогда джинсы во второй ценовой категории будут стоить 1000 + 1000 = 2000 рублей.

Можно ли как-то найти это значение, не прибегая к таким большим рассуждениям? Для этого достаточно найти среднее арифметическое двух соседних членов.

(a_n = frac{a_{n-1} + a_{n+1}}{2})

Докажем это. Если рассмотреть член а_n, то член до него будет равен a_{n — 1} = a_n — d, а член после него a_{n + 1} = a_n + d. Тогда их среднее арифметическое равно (frac{a_{n — 1} + a_{n+1}}{2} = frac{a_n — d + a_n + d}{2} = frac{2a_n}{2} = a_n).

Проверим на нашей задаче.

(a_2 = frac{a_1 + a_3}{2} = frac{1000 + 3000}{2} = frac{4000}{2} = 2000). Все верно.

Чтобы найти разность прогрессии, достаточно вычесть из любого члена прогрессии предыдущий к нему.

d = a_n+1 — a_n

Найдем сумму всех членов арифметической прогрессии. Разумеется, их можно сложить: a₁ + a₂ + a₃ + … + a_n. Но тогда нужно вычислять все члены прогрессии, а их может быть очень много.

В этом случае используется формула суммы арифметической прогрессии. Ее удобство в том, что используются только первый и последний член прогрессии.

(S_n = frac{a_1 + a_n}{2} * n)

Немного преобразуем формулу:

(S_n = frac{a_1 + a_n}{2} * n = frac{a_1 + a_1 + d(n — 1)}{2} * n = frac{2a_1 + d(n — 1)}{2} * n) — это формула суммы членов арифметической прогрессии через первый член и ее разность.

Решим небольшую задачу. Марина решила сделать картину из страз. По схеме у нее есть 15 рядов, в каждом из которых страз на три больше, чем в предыдущем. В первом ряду 6 страз. Сколько всего страз понадобится, чтобы выложить эти ряды?

Воспользуемся формулой арифметической прогрессии. Но прежде найдем, сколько страз в последнем, пятнадцатом ряду:

a₁₅ = 6 + 3 * (15 + 1) = 6 + 3 * 14 = 6 + 42 = 48

Тогда по формуле суммы арифметической прогрессии всего Марине понадобится:

(S_{15} = frac{6 + 48}{2} * 15 = frac{54}{2} * 15 = 27 * 15 = 405) страз.

Как Карл Гаусс удивил своего учителя по математике?

Карл Гаусс — немецкий математик, живший в 18–19 веках. На одном из уроков математики учитель задал сложить все цифры от 1 до 100.

Карл Гаусс заметил, что суммы чисел с противоположных сторон одинаковые: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101 и так далее. Всего таких сумм получилось 50. Следовательно, быстро вычислить сумму этих цифр можно было как произведение 101 * 50.

Такой способ работает для любой арифметической прогрессии.
Внимательно посмотрим на сумму арифметической прогрессии. Пусть a₁ = 1, a₁₀₀ = 100, n = 100. Тогда получаем:
(S_{100} = frac{1 + 100}{2} * 100 = 101 * 50), то есть Карл Гаусс использовал сумму арифметической прогрессии, сам того не зная.

Виды арифметических прогрессий

Существует всего три вида арифметической прогрессии.

1. Возрастающая арифметическая прогрессия.

Разность прогрессии — положительное число, то есть d > 0, а каждый следующий член прогрессии больше предыдущего.

Прогрессия 2, 4, 6, 8 является возрастающей.

2. Убывающая арифметическая прогрессия.

Разность прогрессии — отрицательное число, то есть d < 0, а каждый следующий член прогрессии меньше предыдущего.

Примером убывающей арифметической прогрессии может служить 100, 95, 90, 85 и так далее.

3. Стационарная арифметическая прогрессия.

В этой арифметической прогрессии разность будет равна 0, то есть d = 0. Следовательно, члены прогрессии не будут отличаться друг от друга.

Например, прогрессия 3, 3, 3, 3, 3 будет являться стационарной.

Фактчек

Арифметическая прогрессия — последовательность чисел, в которой каждый член, начиная со второго, равен сумме предыдущего члена и разности прогрессии.
Разность арифметической прогрессии — это число, на которое отличаются члены прогрессии.
Чтобы найти n-ый член прогрессии, необходимо воспользоваться одной из трех формул: a_n+1 = a_n + d, a_n = a₁ + d(n — 1) или (a_n = frac{a_{n-1} + a_{n+1}}{2}).
Чтобы найти разность прогрессии, достаточно из любого члена прогрессии вычесть предыдущий ему член прогрессии.
По формуле (S_n = frac{a_1 + a_n}{2} * n) можно найти сумму n членов прогрессии.
Арифметическая прогрессия может быть убывающей, возрастающей или стационарной.

Проверь себя

Задание 1.
Какая прогрессия является арифметической?

3, 7, 11, 15
1, 1, 2, 3, 5
2, 4, 8, 16
1, 4, 16, 25

Задание 2.
Первый член арифметической прогрессии равен 10, а ее разность равна -5. Найдите семнадцатый член арифметической прогрессии.

Семнадцатого члена такой арифметической прогрессии не существует
0
−70
−75

Задание 3.
Пятый член арифметической прогрессии равен 16, а седьмой член равен 20. Найдите шестой член арифметической прогрессии.

2
18
17,5
Невозможно найти шестой член арифметической прогрессии.

Задание 4.
Каждый день Миша катается на велосипеде, причем с каждым разом увеличивает расстояние на 2 км. В первый день он проехал 3 км. Сколько всего км проедет Миша за пять дней?

Ответы: 1. — 1 2. — 3 3. — 2 4. — 4

Источник

В математике любая организованная каким-либо способом совокупность чисел, которые следуют друг за другом, называется последовательностью. Из всех существующих последовательностей чисел выделяют два интересных случая: прогрессии алгебраическую и геометрическую.

Что представляет собой арифметическая прогрессия?

Сразу следует сказать, что алгебраическую прогрессию часто называют арифметической, поскольку ее свойства изучает ветвь математики – арифметика.

Вам будет интересно:Арифметическая прогрессия (9 класс): формулы, примеры

Эта прогрессия представляет собой такую последовательность чисел, в которой каждый следующий ее член отличается от предыдущего на некоторое постоянное число. Оно называется разностью алгебраической прогрессии. Для определенности обозначим его латинской буквой d.

Примером такой последовательности может быть следующая: 3, 5, 7, 9, 11 …, здесь видно, что число 5 больше числа 3 на 2, 7 больше 5 тоже на 2, и так далее. Таким образом, в представленном примере d = 5-3 = 7-5 = 9-7 = 11-9 = 2.

Какие бывают арифметические прогрессии?

Характер этих упорядоченных последовательностей чисел во многом определяется знаком числа d. Выделяют следующие виды алгебраических прогрессий:

возрастающая, когда d положительное (d>0);
постоянная, когда d = 0;
убывающая, когда d отрицательное (d<0).

В примере, который приведен в предыдущем пункте, показана возрастающая прогрессия. Примером убывающей является следующая последовательность чисел: 10, 5, 0, -5, -10, -15 … Постоянная прогрессия, как следует из ее определения, представляет собой совокупность одинаковых чисел.

n-й член прогрессии

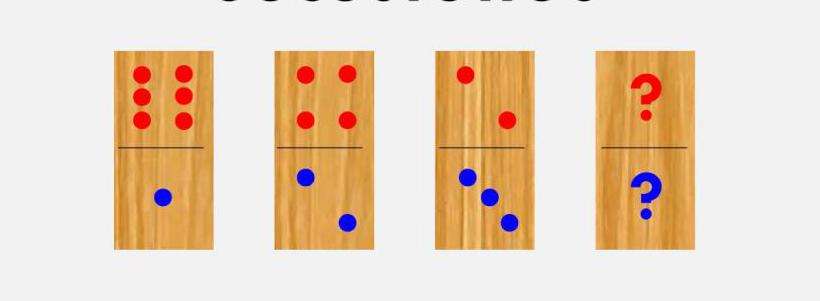
Благодаря тому, что каждое последующее число в рассматриваемой прогрессии отличается на константу d от предыдущего, можно легко определить n-й ее член. Для этого нужно знать не только d, но и a1 – первый член прогрессии. Применяя рекурсивный подход, можно получить формулу алгебраической прогрессии для нахождения n-го члена. Она имеет вид: an = a1 + (n-1)*d. Это формула является достаточно простой, и понять ее можно на интуитивном уровне.

Также не представляет никакой сложности ее использование. Например, в прогрессии, которая приведена выше (d=2, a1=3), определим 35-й ее член. Согласно формуле, он будет равен: a35 = 3 + (35-1)*2 = 71.

Формула для суммы

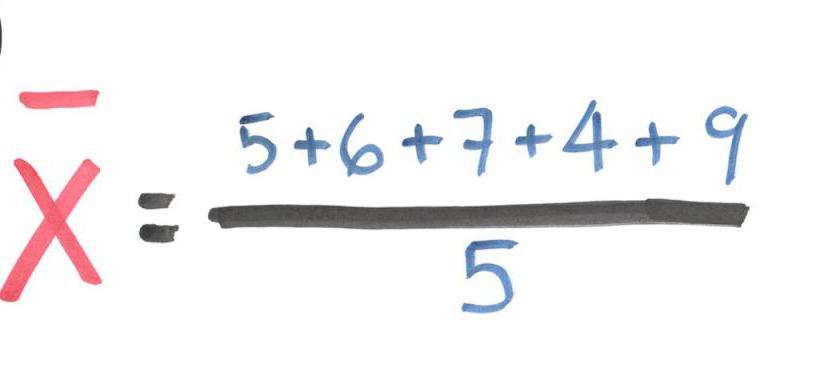
Когда дана некоторая арифметическая прогрессия, то сумма ее первых n членов является часто возникающей задачей, наряду с определением значения n-го члена. Формула суммы алгебраической прогрессии записывается в следующем виде: ∑n1 = n*(a1+an)/2, здесь значок ∑n1 говорит о том, что суммируются с 1-го по n-й член.

Приведенное выражение можно получить, прибегая к свойствам все той же рекурсии, однако существует более легкий способ доказательства его справедливости. Запишем первые 2 и последние 2 члена этой суммы, выразив их в числах a1, an и d, и получим: a1, a1+d,…,an-d, an. Теперь заметим, что если сложить первый член с последним, то он будет точно равен сумме второго и предпоследнего члена, то есть a1+an. Аналогичным способом можно показать, что эту же сумму можно получить, если сложить третий и предпредпоследний члены, и так далее. В случае парного количества чисел в последовательности получаем n/2 сумм, каждая из которых равна a1+an. То есть получаем вышеприведенную формулу алгебраической прогрессии для суммы: ∑n1 = n*(a1+an)/2.

Для непарного количества членов n получается аналогичная формула, если следовать описанным рассуждениям. Только нужно не забыть добавить оставшееся слагаемое, которое находится в центре прогрессии.

Покажем, как пользоваться приведенной формулой на примере простой прогрессии, которая была введена выше (3, 5, 7, 9, 11 …). Например, необходимо определить сумму первых 15 ее членов. Для начала определим a15. Воспользовавшись формулой для n-го члена (см. предыдущий пункт), получаем: a15 = a1 + (n-1)*d = 3 + (15-1)*2 = 31. Теперь можно применить формулу суммы алгебраической прогрессии: ∑151 = 15*(3+31 )/2 = 255.

Любопытно привести интересный исторический факт. Формулу для суммы арифметической прогрессии впервые получил Карл Гаусс (знаменитый немецкий математик XVIII века). Когда ему было всего 10 лет, то учитель задал задачу, найти сумму чисел от 1 до 100. Говорят, что маленький Гаусс решил эту задачу за несколько секунд, заметив, что попарно суммируя числа с начала и конца последовательности, всегда можно получить 101, а поскольку таких сумм 50, то он быстро выдал ответ: 50*101 = 5050.

Пример решения задачи

В качестве завершения темы алгебраической прогрессии приведем пример решения еще одной любопытной задачи, закрепив тем самым понимание рассматриваемой темы. Пусть дана некоторая прогрессия, для которой известна разность d = -3, а также ее 35-й член a35 = -114. Необходимо найти 7-й член прогрессии a7.

Как видно из условия задачи, значение a1 является неизвестным, поэтому напрямую формулой для n-го члена воспользоваться не получится. Также является неудобным способ рекурсии, который в ручную тяжело реализовать, и велика вероятность допустить ошибку. Поступим следующим образом: выпишем формулы для a7 и a35, имеем: a7 = a1 + 6*d и a35 = a1 + 34*d. Вычтем из первого выражения второе, получим: a7 – a35 = a1 + 6*d – a1 – 34*d. Откуда следует: a7 = a35 – 28*d. Осталось подставить известные данные из условия задачи и записать ответ: a7 = -114 – 28*(-3) = -30.

Геометрическая прогрессия

Чтобы раскрыть тему статьи полнее, приведем краткое описание еще одного вида прогрессии – геометрической. В математике под этим названием понимают последовательность чисел, в которой каждый последующий член отличается от предыдущего на некоторый множитель. Обозначим этот множитель буквой r. Он называется знаменателем рассматриваемого вида прогрессии. Примером этой последовательности чисел может быть следующая: 1, 5, 25, 125, …

Как видно из приведенного определения, алгебраическая и геометрическая прогрессии схожи по своей идее. Отличие между ними заключается в том, что первая изменяется медленнее, чем вторая.

Геометрическая прогрессия также может быть возрастающей, постоянной и убывающей. Ее тип зависит от значения знаменателя r: если r>1, то имеет место возрастающая прогрессия, если r<1 – убывающая, наконец, если r = 1 – постоянная, которая в этом случае может также называться постоянной арифметической прогрессией.

Формулы геометрической прогрессии

Как и в случае алгебраической, формулы геометрической прогрессии сводятся к определению ее n-го члена и суммы n слагаемых. Ниже приведены эти выражения:

an = a1*r(n-1) – эта формула следует из определения геометрической прогрессии.
∑n1 = a1*(rn-1)/(r-1). Важно отметить, если r = 1, то приведенная формула дает неопределенность, поэтому ей пользоваться нельзя. В этом случае сумма n членов будет равна простому произведению a1*n.

Например, найдем сумму всего 10 членов последовательности 1, 5, 25, 125, … Зная, что a1 = 1 и r = 5, получаем: ∑101 = 1*(510-1)/4 = 2441406. Полученное значение является наглядным примером того, насколько быстро растет геометрическая прогрессия.

Пожалуй, первым упоминанием об этой прогрессии в истории является легенда с шахматной доской, когда друг одного султана, обучив его игре в шахматы, попросил за свою услугу зерно. Причем количество зерна должно было быть следующим: на первую клетку шахматной доски необходимо положить одно зерно, на вторую в два раза больше, чем на первую, на третью в 2 раза больше, чем на вторую и так далее. Султан охотно согласился выполнить эту просьбу, но он не знал, что ему придется опустошить все закрома своей страны, чтобы сдержать данное слово.

Источник

Свойства[править | править код]

Общий член арифметической прогрессии[править | править код]

Характеристическое свойство арифметической прогрессии[править | править код]

Тождество арифметической прогрессии[править | править код]

Сумма первых n членов арифметической прогрессии[править | править код]

Сумма членов арифметической прогрессии от n-го до m-го[править | править код]

Произведение членов арифметической прогрессии[править | править код]

Сходимость арифметической прогрессии[править | править код]

Связь между арифметической и геометрической прогрессиями[править | править код]

Арифметические прогрессии высших порядков[править | править код]

Примеры[править | править код]

Формула для разности[править | править код]

Сумма чисел от 1 до 100[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Сумма членов арифметической прогрессии

Арифметическая прогрессия

п.1. Понятие арифметической прогрессии

п.2. Формула n-го члена арифметической прогрессии

п.3. Свойства арифметической прогрессии

п.4. Сумма первых n членов арифметической прогрессии

п.5. Примеры

На этой странице вы узнаете

Понятие арифметической прогрессии

Виды арифметических прогрессий

Фактчек

Проверь себя

Что представляет собой арифметическая прогрессия?

Какие бывают арифметические прогрессии?

n-й член прогрессии

Формула для суммы

Пример решения задачи

Геометрическая прогрессия

Формулы геометрической прогрессии

Вам также может понравиться

Как найти элитры в майне

Как найти периметр правильного многоугольника 9 класс

Как найти эквалайзер на телефоне хонор

Добавить комментарий Отменить ответ