| Алгоритм Флойда — Уоршелла | |
|---|---|
 |
|
| Назван в честь | Роберт Флойд и Стивен Уоршелл |
| Автор | Бернар Руа[d] |
| Предназначение | поиск в графе кратчайших путей между любыми парами вершин |
| Структура данных | граф |
| Худшее время |
 |
| Лучшее время |
 |
| Среднее время |
 |
| Затраты памяти |
 |
В информатике алгоритм Флойда-Уоршелла (также известный как алгоритм Флойда, алгоритм Роя-Уоршелла, алгоритм Роя-Флойда или алгоритм WFI) — это алгоритм поиска кратчайших путей во взвешенном графе с положительным или отрицательным весом ребер (но без отрицательных циклов). За одно выполнение алгоритма будут найдены длины (суммарные веса) кратчайших путей между всеми парами вершин. Хотя он не возвращает детали самих путей, можно реконструировать пути с помощью простых модификаций алгоритма. Варианты алгоритма также могут быть использованы для поиска транзитивного замыкания отношения 
История и именование[править | править код]
Алгоритм Флойда-Уоршелла является примером динамического программирования и был опубликован в своей ныне признанной форме Робертом Флойдом в 1962 году. Однако он по сути такой же, как алгоритмы, ранее опубликованные Бернардом Роем в 1959 году, а также Стивеном Уоршеллом в 1962 году для поиска транзитивного замыкания графа, и тесно связан с алгоритмом Клини (опубликовано в 1956 г.) для преобразования детерминированного конечного автомата в регулярное выражение. Современная формулировка алгоритма в виде трех вложенных циклов for была впервые описана Питером Ингерманом также в 1962 году
Алгоритм[править | править код]
Рассмотрим граф 




Далее рассмотрим функцию 






Для каждой из этих пар вершин 
- (1) путь, который не проходит через
(использует только вершины из набора
),
или
- (2) путь, который проходит через
(от
до
и затем от
до
, в обоих случаях используются только промежуточные вершины в
).
Мы знаем, что лучший путь от 













Если 



базовый случай
и рекурсивный случай
.
Эта формула составляет основу алгоритма Флойда-Уоршелла. Алгоритм работает, сначала вычисляя 





let dist be a |V| × |V| массив минимальных расстояний, инициализированный как ∞ (бесконечность)
for each edge (u, v) do
dist[u][v] ← w(u, v) // Вес ребра (u, v)
for each vertex v do
dist[v][v] ← 0
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if dist[i][j] > dist[i][k] + dist[k][j]
dist[i][j] ← dist[i][k] + dist[k][j]
end if
Пример[править | править код]
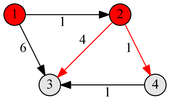
Алгоритм выше выполняется на графе слева внизу:
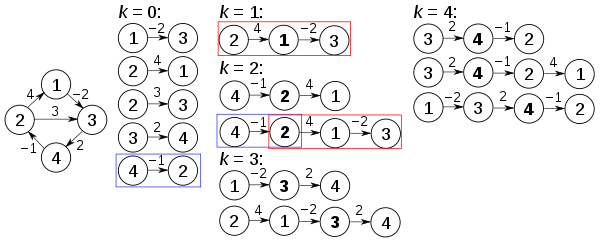
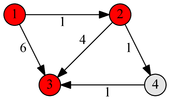
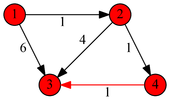
До первой рекурсии внешнего цикла, обозначенного выше k = 0, единственные известные пути соответствуют отдельным ребрам в графе. При k = 1 находятся пути, проходящие через вершину 1: в частности, найден путь [2,1,3], заменяющий путь [2,3], который имеет меньше ребер, но длиннее (с точки зрения веса). При k = 2 находятся пути, проходящие через вершины 1,2. Красные и синие прямоугольники показывают, как путь [4,2,1,3] собирается из двух известных путей [4,2] и [2,1,3], встреченных в предыдущих итерациях, с 2 на пересечении. Путь [4,2,3] не рассматривается, потому что [2,1,3] — это кратчайший путь, встреченный до сих пор от 2 до 3. При k = 3 пути, проходящие через вершины 1,2,3 найдены. Наконец, при k = 4 находятся все кратчайшие пути.
Матрица расстояний на каждой итерации k, обновленные расстояния выделены жирным шрифтом, будет иметь вид:
| k = 0 | j | ||||
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| i | 1 | 0 | ∞ | −2 | ∞ |
| 2 | 4 | 0 | 3 | ∞ | |
| 3 | ∞ | ∞ | 0 | 2 | |
| 4 | ∞ | −1 | ∞ | 0 |
| k = 1 | j | ||||
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| i | 1 | 0 | ∞ | −2 | ∞ |
| 2 | 4 | 0 | 2 | ∞ | |
| 3 | ∞ | ∞ | 0 | 2 | |
| 4 | ∞ | −1 | ∞ | 0 |
| k = 2 | j | ||||
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| i | 1 | 0 | ∞ | −2 | ∞ |
| 2 | 4 | 0 | 2 | ∞ | |
| 3 | ∞ | ∞ | 0 | 2 | |
| 4 | 3 | −1 | 1 | 0 |
| k = 3 | j | ||||
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| i | 1 | 0 | ∞ | −2 | 0 |
| 2 | 4 | 0 | 2 | 4 | |
| 3 | ∞ | ∞ | 0 | 2 | |
| 4 | 3 | −1 | 1 | 0 |
| k = 4 | j | ||||
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| i | 1 | 0 | −1 | −2 | 0 |
| 2 | 4 | 0 | 2 | 4 | |
| 3 | 5 | 1 | 0 | 2 | |
| 4 | 3 | −1 | 1 | 0 |
Поведение с отрицательными циклами[править | править код]
Отрицательный цикл — это цикл, сумма ребер которого равна отрицательному значению. Не существует кратчайшего пути между любой парой вершин 



- Алгоритм Флойда-Уоршелла итеративно просматривает длину пути
между всеми парами вершин 

- Изначально длина пути
равна нулю;
- Путь
может улучшиться только в том случае, если его длина
меньше нуля, то есть обозначает отрицательный цикл;
- Таким образом, после алгоритма,
будет отрицательным, если
существует путь отрицательной длины от 

Следовательно, чтобы обнаружить отрицательные циклы с помощью алгоритма Флойда-Уоршелла, можно проверить диагональ матрицы кратчайших путей, и наличие отрицательного числа указывает на то, что граф содержит по крайней мере один отрицательный цикл. Во время выполнения алгоритма, если есть отрицательный цикл, могут появиться экспоненциально большие числа, вплоть до 

Реконструкция путей[править | править код]
Алгоритм Флойда-Уоршелла обычно предоставляет только длины путей между всеми парами вершин. С помощью простых модификаций можно создать метод восстановления фактического пути между любыми двумя вершинами конечной точки. Хотя кто-то может быть склонен хранить 3 фактический путь от каждой вершины к каждой другой вершине, это не обязательно, и на самом деле это очень дорого с точки зрения памяти. Вместо этого дерево кратчайших путей может быть вычислено для каждого узла за 

Псевдокод[1][править | править код]
let dist be aмассив минимальных расстояний, инициализированный как
(бесконечность) let next be a
массив индексов вершин, инициализированный null procedure FloydWarshallWithPathReconstruction() is for each edge (u, v) do dist[u][v] ← w(u, v) // Вес ребра (u, v) next[u][v] ← v for each vertex v do dist[v][v] ← 0 next[v][v] ← v for k from 1 to |V| do // стандартная реализация алгоритма Флойда–Уоршелла for i from 1 to |V| for j from 1 to |V| if dist[i][j] > dist[i][k] + dist[k][j] then dist[i][j] ← dist[i][k] + dist[k][j] next[i][j] ← next[i][k]
procedure Path(u, v)
if next[u][v] = null then
return []
path = [u]
while u ≠ v
u ← next[u][v]
path.append(u)
return path
Анализ сложности Алгоритма[править | править код]
Пусть 















Приложения и обобщения[править | править код]
Алгоритм Флойда-Уоршелла может быть использован для решения следующих задач, в частности:
- Кратчайшие пути в ориентированных графах (алгоритм Флойда).
- Транзитивное замыкание ориентированных графов (алгоритм Уоршелла). В оригинальной формулировке алгоритма Уоршелла граф не взвешен и представлен булевой матрицей смежности. Затем операция сложения заменяется логической конъюнкцией (И), а минимальная операция — логической дизъюнкцией (ИЛИ).
- Нахождение регулярного выражения, обозначающего регулярный язык, принимаемый конечным автоматом (алгоритм Клини, тесно связанное обобщение алгоритма Флойда-Уоршелла)
- Обращение вещественных матриц (алгоритм Гаусса-Жордана)
- Оптимальная маршрутизация. В этом приложении нужно найти путь с максимальным потоком между двумя вершинами. Это означает, что вместо взятия минимумов, как в псевдокоде выше, используются максимумы. Веса ребер представляют фиксированные ограничения для потока. Веса путей представляют собой узкие места поэтому операция сложения, указанная выше, заменяется минимальной операцией.
- Быстрый расчет сетей Pathfinder.
- Самые широкие пути/пути с максимальной пропускной способностью
- Вычисление канонической формы матриц разностных границ (DBMs)
- Вычисление сходства между графами
Реализации[править | править код]
- Для C++, в библиотеке boost::graph
- Для C#, в QuickGraph
- Для C#, в QuickGraphPCL (Форк QuickGraph с лучшей совместимостью с проектами, использующими переносимые библиотеки классов.)
- Для Java, в библиотеке Apache Commons Graph
- Для JavaScript, в библиотеке Cytoscape
- Для MATLAB, в пакете Matlab_bgl
- Для Perl, в модуле Graph
- Для Python, в библиотеке SciPy (модуль scipy.sparse.csgraph) или в библиотеке NetworkX
- Для R, в пакете e1071 и Rfast
Сравнение с другими алгоритмами[править | править код]
Алгоритм Флойда-Уоршелла является эффективным для расчёта всех кратчайших путей в плотных графах, когда имеет место большое количество пар рёбер между парами вершин. В случае разреженных графов с рёбрами неотрицательного веса лучшим выбором считается использование алгоритма Дейкстры для каждого возможного узла. При таком выборе сложность составляет 



Также являются известными алгоритмы с применением алгоритмов быстрого перемножения матриц, которые ускоряют вычисления в плотных графах, но они обычно имеют дополнительные ограничения (например, представление весов рёбер в виде малых целых чисел)[2][3]. Вместе с тем, из-за большого константного фактора времени выполнения преимущество при вычислениях над алгоритмом Флойда-Уоршелла проявляется только на больших графах.
Примечания[править | править код]
- ↑ Free Algorithms Book. Дата обращения: 19 декабря 2020. Архивировано 12 января 2021 года.
- ↑ Zwick, Uri (May 2002), All pairs shortest paths using bridging sets and rectangular matrix multiplication, Journal of the ACM Т. 49 (3): 289–317, DOI 10.1145/567112.567114.
- ↑ Chan, Timothy M. (January 2010), More algorithms for all-pairs shortest paths in weighted graphs, SIAM Journal on Computing Т. 39 (5): 2075–2089, DOI 10.1137/08071990x.
Литература[править | править код]
- Левитин А. В. Глава 11. Преодоление ограничений: Метод деления пополам // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 349—353. — 576 с. — ISBN 978-5-8459-0987-9
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1.
- Белоусов А. И., Ткачев С. Б. Дискретная математика. — М.: МГТУ, 2006. — 744 с. — ISBN 5-7038-2886-4.
Алгоритм Флойда (алгоритм Флойда–Уоршелла) — алгоритм нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл. Алгоритм работает за времени и использует памяти. Разработан в 1962 году.
Содержание
- 1 Алгоритм
- 1.1 Постановка задачи
- 1.2 Описание
- 1.3 Код (в первом приближении)
- 1.4 Код (окончательный)
- 1.5 Пример работы
- 2 Вывод кратчайшего пути
- 2.1 Модифицированный алгоритм
- 3 Нахождение отрицательного цикла
- 4 Построение транзитивного замыкания
- 4.1 Псевдокод
- 4.2 Доказательство
- 4.3 Оптимизация с помощью битовых масок
- 5 Источники информации
Алгоритм
Постановка задачи
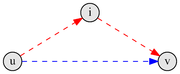
Текущий (синий) путь и потенциально более короткий (красный)
Дан взвешенный ориентированный граф , в котором вершины пронумерованы от до .
Требуется найти матрицу кратчайших расстояний , в которой элемент либо равен длине кратчайшего пути из в , либо равен , если вершина не достижима из .
Описание
Обозначим длину кратчайшего пути между вершинами и , содержащего, помимо и , только вершины из множества как , .
На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер — ) и для всех пар вершин и вычислять . То есть, если кратчайший путь из в , содержащий только вершины из множества , проходит через вершину , то кратчайшим путем из в является кратчайший путь из в , объединенный с кратчайшим путем из в . В противном случае, когда этот путь не содержит вершины , кратчайший путь из в , содержащий только вершины из множества является кратчайшим путем из в , содержащим только вершины из множества .
Код (в первом приближении)
for
for
for
В итоге получаем, что матрица и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества , что есть попросту все вершины графа. Такая реализация работает за времени и использует памяти.
Код (окончательный)
Утверждается, что можно избавиться от одной размерности в массиве , т.е. использовать двумерный массив . В процессе работы алгоритма поддерживается инвариант , а, поскольку, после выполнения работы алгоритма , то тогда будет выполняться и .
| Утверждение: |
|
В течение работы алгоритма Флойда выполняются неравенства: . |
|
После инициализации все неравенства, очевидно, выполняются. Далее, массив может измениться только в строчке 5. Докажем второе неравенство индукцией по итерациям алгоритма. Пусть также — значение сразу после итерации. Покажем, что , зная, что . Рассмотрим два случая:
Докажем первое неравенство от противного. Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была -ая итерация и в этот момент изменилось значение и выполнилось . Так как изменилось, то (так как ранее ) (по неравенству треугольника) . Итак — противоречие. |
func floyd(w):
d = // изначально
for
for
for
d[u][v] = min(d[u][v], d[u][i] + d[i][v])
Данная реализация работает за время , но требует уже памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении весьма мала.
Пример работы
 |
 |
 |
 |
|
Вывод кратчайшего пути
Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив , в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из в по кратчайшему пути.
Модифицированный алгоритм
func floyd(w):
d = // изначально
for
for
for
if d[u][i] + d[i][v] < d[u][v]
d[u][v] = d[u][i] + d[i][v]
next[u][v] = next[u][i]
func getShortestPath(u, v):
if d[u][v] ==
print "No path found" // между вершинами u и v нет пути
c = u
while c != v
print c
c = next[c][v]
print v
Нахождение отрицательного цикла
| Утверждение: |
|
При наличии цикла отрицательного веса в матрице появятся отрицательные числа на главной диагонали. |
| Так как алгоритм Флойда последовательно релаксирует расстояния между всеми парами вершин , в том числе и теми, у которых , а начальное расстояние между парой вершин равно нулю, то релаксация может произойти только при наличии вершины такой, что , что эквивалентно наличию отрицательного цикла, проходящего через вершину . |
Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину , для которой , и вывести кратчайший путь между парой вершин . При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной , либо проверять наличие отрицательных чисел на главной диагонали во время подсчета.
Построение транзитивного замыкания
Сформулируем нашу задачу в терминах графов: рассмотрим граф , соответствующий отношению . Тогда необходимо найти все пары вершин , соединенных некоторым путем.
Иными словами, требуется построить новое отношение , которое будет состоять из всех пар таких, что найдется последовательность , где .
Псевдокод
Изначально матрица заполняется соответственно отношению , то есть . Затем внешним циклом перебираются все элементы множества и для каждого из них, если он может использоваться, как промежуточный для соединения двух элементов и , отношение расширяется добавлением в него пары .
for k = 1 to n
for i = 1 to n
for j = 1 to n
W[i][j] = W[i][j] or (W[i][k] and W[k][j])
Доказательство
<wikitex>Назовем промежуточной вершину некоторого пути $p = left langle v_0, v_1, dots, v_k right rangle$, принадлежащую множеству вершин этого пути и отличающуюся от начальной и конечной вершин, то есть принадлежащую $left { v_1, v_2, dots, v_{k-1} right }$. Рассмотрим произвольную пару вершин $i, j in V$ и все пути между ними, промежуточные вершины которых принадлежат множеству вершин с номерами $left { 1, 2, dots, k right }$. Пусть $p$ — некоторый из этих путей. Докажем по индукции (по числу промежуточных вершин в пути), что после $i$-ой итерации внешнего цикла будет верно утверждение — если в построенном графе между выбранной парой вершин есть путь, содержащий в качестве промежуточных только вершины из множества вершин с номерами $left { v_1, v_2, dots, v_{i} right }$, то между ними будет ребро.
- База индукции. Если у нас нет промежуточных вершин, что соответствует начальной матрице смежности, то утверждение выполнено: либо есть ребро (путь не содержит промежуточных вершин), либо его нет.
- Индуктивный переход. Пусть предположение выполнено для $i = k – 1$. Докажем, что оно верно и для $i = k$ Рассмотрим случаи (далее под вершиной будем понимать ее номер для простоты изложения):
- $k$ не является промежуточной вершиной пути $p$. Тогда все его промежуточные пути принадлежат множеству вершин с номерами $left { 1, 2, dots, k-1 right } subset left { 1, 2, dots, k right }$, то есть существует путь с промежуточными вершинами в исходном множестве. Это значит $W[i][j]$ будет истиной. В противном случае $W[i][j]$ будет ложью и на k-ом шаге ею и останется.
- $k$ является промежуточной вершиной предполагаемого пути $p$. Тогда этот путь можно разбить на два пути: $i xrightarrow{p_1} k xrightarrow{p_2} j$. Пусть как $p_1$, так и $p_2$ существуют. Тогда они содержат в качестве промежуточных вершины из множества $left { 1, 2, dots, k-1 right } subset left { 1, 2, dots, k right }$ (так как вершина $k$ — либо конечная, либо начальная, то она не может быть в множестве по нашему определению). Тогда $W[i][k]$ и $W[k][j]$ истинны и по индуктивному предположению посчитаны верно. Тогда и $W[i][j]$ тоже истина. Пусть какого-то пути не существует. Тогда пути $p$ тоже не может существовать, так как добраться, например, от вершины $i$ до $k$ по вершинам из множества $left { 1, 2, dots, k right }$ невозможно по индуктивному предположению. Тогда вся конъюнкция будет ложной, то есть такого пути нет, откуда $W[i][j]$ после итерации будет ложью.
Таким образом, после завершения внешнего цикла у нас будет $W[i][j] = true$, если между этими вершинами есть путь, содержащий в качестве промежуточных вершин из множества всех остальных вершин графа, что и есть транзитивное замыкание.
</wikitex>
Оптимизация с помощью битовых масок
Строки матрицы можно хранить с помощью массива битовых масок длиной . Тогда последний цикл будет выполняться в раз быстрее и сложность алгоритма снижается до .
Пример реализации оптимизации с помощью битмасок:
unsigned int W[N][N / 32 + 1]
func transitiveClosure(W):
for k = 1 to n
for i = 1 to n
if бит с номером (k % 32) в маске a[i][k / 32] единичный
for j = 1 to n / 32 + 1
W[i][j] = W[i][j] or W[k][j]
В данной реализации длина битовой маски равна битам. Последний цикл делает в раза меньше операций — сложность алгоритма .
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд — М.: Издательский дом «Вильямс», 2009. — ISBN 978-5-8459-0857-5.
- Романовский И. В. Дискретный анализ: Учебное пособие для студентов, специализирующихся по прикладной математике и информатике. Изд. 3-е. — СПб.: Невский диалект, 2003. — 320 с. — ISBN 5-7940-0114-3.
- Википедия – Алгоритм Флойда — Уоршелла
- Wikipedia – Floyd–Warshall algorithm
Алгоритм Флойда — Уоршелла
Время на прочтение
6 мин
Количество просмотров 153K
 Алгоритм Флойда — Уоршелла — алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами с использованием метода динамического программирования. Это базовый алгоритм, так что тем кто его знает — можно дальше не читать.
Алгоритм Флойда — Уоршелла — алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами с использованием метода динамического программирования. Это базовый алгоритм, так что тем кто его знает — можно дальше не читать.
Этот алгоритм был одновременно опубликован в статьях Роберта Флойда (Robert Floyd) и Стивена Уоршелла (Stephen Warshall) в 1962 г., хотя в 1959 г. Бернард Рой (Bernard Roy) опубликовал практически такой же алгоритм, но это осталось незамеченным.
Ремарка
Если граф не содержит рёбер с отрицательным весом, то для решения этой проблемы можно использовать алгоритм Дейкстры для нахождения кратчайшего пути от одной вершины до всех остальных, запустив его на каждой вершине. Время работы такого алгоритма зависит от типа данных, который мы будем использовать для алгоритма Дейкстры, это может быть как простая очередь с приоритетом, так и бинарная или фибоначчиева Куча, соответственно время работы будет варьироваться от O(V3) до O(V*E*log(V)), где V количество вершин, а E — рёбер. («О»-большое).
Если же есть рёбера с отрицательным весом, можно использовать алгоритм Беллмана — Форда. Но этот алгоритм, запущенный на всех вершинах графа, медленнее, время его работы O(V2*E), а в сильно «густых» графах аж O(V4).
Динамическое программирование
Что значит динамический алгоритм? Динамическое программирование — это альтернатива решению задач методом «в лоб», то есть brute forc’ом или жадными алгоритмами. Используется там, где оптимальное решение подзадачи меньшего размера может быть использовано для решения исходной задачи. В общем виде метод выглядит так:
1. Разбиение задачи на подзадачи меньшего размера.
2. Нахождение оптимального решения подзадач рекурсивно.
3. Использование полученного решения подзадач для конструирования решения исходной задачи.
Для нахождения кратчайших путей между всеми вершинами графа используется не перебор всех возможностей, что приведет к большому времени работы и потребует больше памяти, а восходящее динамическое программирование, то есть все подзадачи, которые впоследствии понадобятся для решения исходной задачи, просчитываются заранее и затем используются.
Структура кратчайшего пути
В основе алгоритма лежат два свойства кратчайшего пути графа. Первое:
Имеется кратчайший путь p1k=(v1,v2,… ,vk) от вершины v1 до вершины vk, а также его подпуть p'(vi,vi+1,… ,vj), при этом действует 1 <= i <= j <= k.
Если p — кратчайший путь от v1 до vk, то p’ также является кратчайшим путем от вершины vi до vj
Это можно легко доказать, так как стоимость пути p складывается из стоимости пути p’ и стоимости остальных его частей. Так вот представив что есть более короткий путь p’, мы уменьшим эту сумму, что приведет к противоречию с утверждением, что эта сумма и так уже была минимальной.
Второе свойство является основой алгоритма. Мы рассматриваем граф G с пронумерованными от 1 до n вершинами {v1,v2,… ,vn} и путь pij от vi до vj, проходящий через определенное множество разрешенных вершин, ограниченное индексом k.
То есть если k=0, то мы рассматриваем прямые соединения вершин друг с другом, так как множество разрешенных промежуточных вершин рано нулю. Если k=1 — мы рассматриваем пути, проходящие через вершину v1, при k=2 — через вершины {v1, v2}, при k=3 — {v1, v3, v3} и так далее.
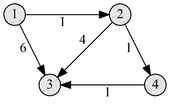
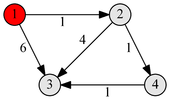
 Например у нас есть такой граф (слева) и k=1, то есть в качестве промужуточных узлов разрешен только узел «1». В этом графе при k=1 нет пути p43, но есть при k=2, тогда можно добраться из «4» в «3» через «2» или через «1» и «2».
Например у нас есть такой граф (слева) и k=1, то есть в качестве промужуточных узлов разрешен только узел «1». В этом графе при k=1 нет пути p43, но есть при k=2, тогда можно добраться из «4» в «3» через «2» или через «1» и «2».
Рассмотрим кратчайший путь pij с разрешенными промужуточными вершинами {1..k-1} стоимостью dij. Теперь расширим множество на k- тый элемент, так что множество разрешенных вершин станет {1..k}. При таком расширении возможно 2 исхода:
Случай 1. Элемент k не входит в кратчайший путь pij, то есть от добавления дополнительной вершины мы ничего не выиграли и ничего не изменили, а значит стоимость кратчайшего пути dkij не изменился, соответственно
dkij = dk-1ij — просто перенимаем значение до увеличения k.
Случай 2. Элемент k входит в кратчайший путь pij, то есть после добавления новой вершины в можество разрешенных, кратчайший путь изменился и проходит теперь через вершину vk. Какую стоимость получит новый путь?
Новый кратчайший путь разбит вершиной vk на pik и pkj, используем первое свойство, согласно ему, pik и pkj также кратчайшие пути от vi до vk и от vk до vj соответственно. Значит
dkij = dkik + dkkj
А так как в этих путях k либо конечный, либо начальный узел, то он не входит в множество промежуточных, соответственно его из него можно удалить:
dkij = dk-1ik + dk-1kj
Алгоритм
Посмотрим на значение dkij в обоих случаях — верно! оно в обоих случаях складывается из значений d для k-1, а значит имея начальные (k=0) значения для d, мы сможем расчитать d для всех последующих значений k. А значения d для k=0 мы знаем, это вес/стоимость рёбер графа, то есть соединений без промужуточных узлов.
При k=n (n — количество вершин) мы получим оптимальные значения d для всех пар вершин.
При увеличении с k-1 до k, какое значение мы сохраним для dkik? Минимумом значений случая 1 и 2, то есть смотрим дешевле ли старый путь или путь с добавлением дополнительной вершины.

Псевдокод
Наконец сам алгоритм. Мы используем представление графа в виде матрицы cмежностей.

Как видно алгоритм очень прост — сначала происходит инициализация матрицы кратчайших расстояний D0, изначально она совпадает с матрицей смежности, в цикле увеличиваем значение k и пересчитываем матрицу расстояний, из D0 получаем D1, из D1 — D2 и так далее до k=n.
Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно. Правда, если не принять специальных мер, то при наличии в графе рёбер отрицательного веса, в результирующей матрице могут появиться числа вида ∞-1, ∞-2, и т.д., которые, конечно, по-прежнему означают, что между соответствующими вершинами вообще нет пути. Поэтому при наличии в графе отрицательных рёбер алгоритм Флойда лучше написать так, чтобы он не выполнял переходы из тех состояний, в которых уже стоит «нет пути»
Пример

Первый пересчет матрицы — изменяется одно значение, из-за расширения множества разрешенных вершин на вершину «1» мы смогли добраться от вершины «4» до «2», используя более дешевый путь.
dkij = min( dk-1ij; dk-1ik + dk-1kj )
d142 = min( d042, d041 + d012)
d142 = min( 4, -1)
Вторая итерация, улучшили значение для p43

Результат

Тут и там можно поиграть с аплетом и посмотреть как в живую работает алгоритм.
Анализ времени работы и использования памяти
Алгоритму требуется O(n3) памяти, для сохранения матриц. Однако количество матриц можно легко сократить до двух, каждый раз переписывая ненужную матрицу или вообще перейти к двухмерной матрице, убрав индекс k у dkij. Лучший вариант, который чаще всего используется — писать сразу в матрицу смежности, тогда нам совсем не нужна дополнительная память, правда если сразу переписывать изначальную матрицу, то нужно дополнительно показать корректность алгоритма, так как классическое академическоле доказательство верно только для случая, когда матрица предыдущей итерации не изменяется.
Что касается времени работы — три вложенных цикла от 1 до n — Θ(n3).
Случай отрицательных циклов
Если в графе есть циклы отрицательного веса, то формально алгоритм Флойда-Уоршелла к такому графу неприменим. Но на самом деле алгоритм корректно сработает для всех пар, пути мужду которыми никогда не проходят через цикл негативной стоимости, а для остальных мы получим какие-нибудь числа, возможно сильно отрицательные. Алгоритм можно научить выводить для таких пар некое значение, соответствующее -∞
Кстати после отработки такого графа на диагонале матрицы кратчайших путей возникнут отрицательные числа — кратчайшее расстояние от вершины в этом цикле до неё самой будет меньше нуля, что соответствует проходу по этому циклу, так что алгоритм можно использовать для определения наличия отрицательных циклов в графе.
Реконструирование пути
Матрица расстояний покажет нам кратчайшее (самое дешевое) растояние для любой пары вершин, а как же узнать путь? Очень просто, при расчете dkij нужно расчитать еще и πkij. πkij при этом — предшественник вершины vj на пути от vi с множеством разрешенных промежуточных вершин {1..k}.
Я просто оставлю это сдесь, остально додумать может каждый сам

Применение
 Как и любой базовый алгоритм, алгоритм Флойда — Уоршелла используется очень широко и много где, начиная от поиска транзитивного замыкания графа, заканчивая генетикой и управлением проектами. Но первое что приходит в голову конечно же транспортные и всякие другие сети.
Как и любой базовый алгоритм, алгоритм Флойда — Уоршелла используется очень широко и много где, начиная от поиска транзитивного замыкания графа, заканчивая генетикой и управлением проектами. Но первое что приходит в голову конечно же транспортные и всякие другие сети.
Скажем если вы возьмете карту города — её транспортная система это граф, соответственно присвоив каждому ребру некую стоимость, расчитанную скажем из пропускной способности и других важный параметров — вы сможете подвести попутчика по самому короткому/быстрому/дешевому пути.
На этом всё, написано не очень, так что если укажите на ошибки, несостыковки, непонятки и прочее, буду благодарен, текст мне этот еще нужен будет 🙂
Спасибо Rustam’у и mastersobg’у за поправки
Given a graph and two nodes u and v, the task is to print the shortest path between u and v using the Floyd Warshall algorithm.
Examples:
Input: u = 1, v = 3
Output: 1 -> 2 -> 3
Explanation:
Shortest path from 1 to 3 is through vertex 2 with total cost 3.
The first edge is 1 -> 2 with cost 2 and the second edge is 2 -> 3 with cost 1.Input: u = 0, v = 2
Output: 0 -> 1 -> 2
Explanation:
Shortest path from 0 to 2 is through vertex 1 with total cost = 5
Approach:
- The main idea here is to use a matrix(2D array) that will keep track of the next node to point if the shortest path changes for any pair of nodes. Initially, the shortest path between any two nodes u and v is v (that is the direct edge from u -> v).
- Initialising the Next array
If the path exists between two nodes then Next[u][v] = v
else we set Next[u][v] = -1
- Modification in Floyd Warshall Algorithm
Inside the if condition of Floyd Warshall Algorithm we’ll add a statement Next[i][j] = Next[i][k]
(that means we found the shortest path between i, j through an intermediate node k).
- This is how our if condition would look like
if(dis[i][j] > dis[i][k] + dis[k][j])
{
dis[i][j] = dis[i][k] + dis[k][j];
Next[i][j] = Next[i][k];
}
- For constructing path using these nodes we’ll simply start looping through the node u while updating its value to next[u][v] until we reach node v.
path = [u]
while u != v:
u = Next[u][v]
path.append(u)
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100
const int INF = 1e7;
int dis[MAXN][MAXN];
int Next[MAXN][MAXN];
void initialise(int V,
vector<vector<int> >& graph)
{
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
dis[i][j] = graph[i][j];
if (graph[i][j] == INF)
Next[i][j] = -1;
else
Next[i][j] = j;
}
}
}
vector<int> constructPath(int u,
int v)
{
if (Next[u][v] == -1)
return {};
vector<int> path = { u };
while (u != v) {
u = Next[u][v];
path.push_back(u);
}
return path;
}
void floydWarshall(int V)
{
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dis[i][k] == INF
|| dis[k][j] == INF)
continue;
if (dis[i][j] > dis[i][k]
+ dis[k][j]) {
dis[i][j] = dis[i][k]
+ dis[k][j];
Next[i][j] = Next[i][k];
}
}
}
}
}
void printPath(vector<int>& path)
{
int n = path.size();
for (int i = 0; i < n - 1; i++)
cout << path[i] << " -> ";
cout << path[n - 1] << endl;
}
int main()
{
int V = 4;
vector<vector<int> > graph
= { { 0, 3, INF, 7 },
{ 8, 0, 2, INF },
{ 5, INF, 0, 1 },
{ 2, INF, INF, 0 } };
initialise(V, graph);
floydWarshall(V);
vector<int> path;
cout << "Shortest path from 1 to 3: ";
path = constructPath(1, 3);
printPath(path);
cout << "Shortest path from 0 to 2: ";
path = constructPath(0, 2);
printPath(path);
cout << "Shortest path from 3 to 2: ";
path = constructPath(3, 2);
printPath(path);
return 0;
}
Java
import java.util.*;
class GFG{
static final int MAXN = 100;
static int INF = (int) 1e7;
static int [][]dis = new int[MAXN][MAXN];
static int [][]Next = new int[MAXN][MAXN];
static void initialise(int V,
int [][] graph)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
dis[i][j] = graph[i][j];
if (graph[i][j] == INF)
Next[i][j] = -1;
else
Next[i][j] = j;
}
}
}
static Vector<Integer> constructPath(int u,
int v)
{
if (Next[u][v] == -1)
return null;
Vector<Integer> path = new Vector<Integer>();
path.add(u);
while (u != v)
{
u = Next[u][v];
path.add(u);
}
return path;
}
static void floydWarshall(int V)
{
for(int k = 0; k < V; k++)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
if (dis[i][k] == INF ||
dis[k][j] == INF)
continue;
if (dis[i][j] > dis[i][k] +
dis[k][j])
{
dis[i][j] = dis[i][k] +
dis[k][j];
Next[i][j] = Next[i][k];
}
}
}
}
}
static void printPath(Vector<Integer> path)
{
int n = path.size();
for(int i = 0; i < n - 1; i++)
System.out.print(path.get(i) + " -> ");
System.out.print(path.get(n - 1) + "n");
}
public static void main(String[] args)
{
int V = 4;
int [][] graph = { { 0, 3, INF, 7 },
{ 8, 0, 2, INF },
{ 5, INF, 0, 1 },
{ 2, INF, INF, 0 } };
initialise(V, graph);
floydWarshall(V);
Vector<Integer> path;
System.out.print("Shortest path from 1 to 3: ");
path = constructPath(1, 3);
printPath(path);
System.out.print("Shortest path from 0 to 2: ");
path = constructPath(0, 2);
printPath(path);
System.out.print("Shortest path from 3 to 2: ");
path = constructPath(3, 2);
printPath(path);
}
}
Python3
def initialise(V):
global dis, Next
for i in range(V):
for j in range(V):
dis[i][j] = graph[i][j]
if (graph[i][j] == INF):
Next[i][j] = -1
else:
Next[i][j] = j
def constructPath(u, v):
global graph, Next
if (Next[u][v] == -1):
return {}
path = [u]
while (u != v):
u = Next[u][v]
path.append(u)
return path
def floydWarshall(V):
global dist, Next
for k in range(V):
for i in range(V):
for j in range(V):
if (dis[i][k] == INF or dis[k][j] == INF):
continue
if (dis[i][j] > dis[i][k] + dis[k][j]):
dis[i][j] = dis[i][k] + dis[k][j]
Next[i][j] = Next[i][k]
def printPath(path):
n = len(path)
for i in range(n - 1):
print(path[i], end=" -> ")
print (path[n - 1])
if __name__ == '__main__':
MAXM,INF = 100,10**7
dis = [[-1 for i in range(MAXM)] for i in range(MAXM)]
Next = [[-1 for i in range(MAXM)] for i in range(MAXM)]
V = 4
graph = [ [ 0, 3, INF, 7 ],
[ 8, 0, 2, INF ],
[ 5, INF, 0, 1 ],
[ 2, INF, INF, 0 ] ]
initialise(V)
floydWarshall(V)
path = []
print("Shortest path from 1 to 3: ", end = "")
path = constructPath(1, 3)
printPath(path)
print("Shortest path from 0 to 2: ", end = "")
path = constructPath(0, 2)
printPath(path)
print("Shortest path from 3 to 2: ", end = "")
path = constructPath(3, 2)
printPath(path)
C#
using System;
using System.Collections.Generic;
class GFG{
static readonly int MAXN = 100;
static int INF = (int)1e7;
static int [,]dis = new int[MAXN, MAXN];
static int [,]Next = new int[MAXN, MAXN];
static void initialise(int V,
int [,] graph)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
dis[i, j] = graph[i, j];
if (graph[i, j] == INF)
Next[i, j] = -1;
else
Next[i, j] = j;
}
}
}
static List<int> constructPath(int u, int v)
{
if (Next[u, v] == -1)
return null;
List<int> path = new List<int>();
path.Add(u);
while (u != v)
{
u = Next[u, v];
path.Add(u);
}
return path;
}
static void floydWarshall(int V)
{
for(int k = 0; k < V; k++)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
if (dis[i, k] == INF ||
dis[k, j] == INF)
continue;
if (dis[i, j] > dis[i, k] +
dis[k, j])
{
dis[i, j] = dis[i, k] +
dis[k, j];
Next[i, j] = Next[i, k];
}
}
}
}
}
static void printPath(List<int> path)
{
int n = path.Count;
for(int i = 0; i < n - 1; i++)
Console.Write(path[i] + " -> ");
Console.Write(path[n - 1] + "n");
}
public static void Main(String[] args)
{
int V = 4;
int [,] graph = { { 0, 3, INF, 7 },
{ 8, 0, 2, INF },
{ 5, INF, 0, 1 },
{ 2, INF, INF, 0 } };
initialise(V, graph);
floydWarshall(V);
List<int> path;
Console.Write("Shortest path from 1 to 3: ");
path = constructPath(1, 3);
printPath(path);
Console.Write("Shortest path from 0 to 2: ");
path = constructPath(0, 2);
printPath(path);
Console.Write("Shortest path from 3 to 2: ");
path = constructPath(3, 2);
printPath(path);
}
}
Javascript
<script>
let MAXN = 100;
let INF = 1e7;
let dis = new Array(MAXN);
let Next = new Array(MAXN);
for(let i = 0; i < MAXN; i++)
{
dis[i] = new Array(MAXN);
Next[i] = new Array(MAXN);
}
function initialise(V, graph)
{
for(let i = 0; i < V; i++)
{
for(let j = 0; j < V; j++)
{
dis[i][j] = graph[i][j];
if (graph[i][j] == INF)
Next[i][j] = -1;
else
Next[i][j] = j;
}
}
}
function constructPath(u, v)
{
if (Next[u][v] == -1)
return null;
let path = [];
path.push(u);
while (u != v)
{
u = Next[u][v];
path.push(u);
}
return path;
}
function floydWarshall(V)
{
for(let k = 0; k < V; k++)
{
for(let i = 0; i < V; i++)
{
for(let j = 0; j < V; j++)
{
if (dis[i][k] == INF ||
dis[k][j] == INF)
continue;
if (dis[i][j] > dis[i][k] +
dis[k][j])
{
dis[i][j] = dis[i][k] +
dis[k][j];
Next[i][j] = Next[i][k];
}
}
}
}
}
function printPath(path)
{
let n = path.length;
for(let i = 0; i < n - 1; i++)
document.write(path[i] + " -> ");
document.write(path[n - 1] + "<br>");
}
let V = 4;
let graph = [ [ 0, 3, INF, 7 ],
[ 8, 0, 2, INF ],
[ 5, INF, 0, 1 ],
[ 2, INF, INF, 0 ] ];
initialise(V, graph);
floydWarshall(V);
let path;
document.write("Shortest path from 1 to 3: ");
path = constructPath(1, 3);
printPath(path);
document.write("Shortest path from 0 to 2: ");
path = constructPath(0, 2);
printPath(path);
document.write("Shortest path from 3 to 2: ");
path = constructPath(3, 2);
printPath(path);
</script>
Output:
Shortest path from 1 to 3: 1 -> 2 -> 3 Shortest path from 0 to 2: 0 -> 1 -> 2 Shortest path from 3 to 2: 3 -> 0 -> 1 -> 2
Complexity Analysis:
- The time complexity for Floyd Warshall Algorithm is O(V3)
- For finding shortest path time complexity is O(V) per query.
Note: It would be efficient to use the Floyd Warshall Algorithm when your graph contains a couple of hundred vertices and you need to answer multiple queries related to the shortest path.
Last Updated :
18 Aug, 2021
Like Article
Save Article
Алгоритм Флойда
Рассматриваемый алгоритм иногда называют алгоритмом Флойда-Уоршелла. Алгоритм Флойда-Уоршелла является алгоритмом на графах, который разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом. Он служит для нахождения кратчайших путей между всеми парами вершин графа.
Метод Флойда непосредственно основывается на том факте, что в графе с положительными весами ребер всякий неэлементарный (содержащий более 1 ребра) кратчайший путь состоит из других кратчайших путей.
Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя вершинами графа.
В алгоритме Флойда используется матрица A размером nxn, в которой вычисляются длины кратчайших путей. Элемент A[i,j] равен расстоянию от вершины i к вершине j, которое имеет конечное значение, если существует ребро (i,j), и равен бесконечности в противном случае.
Алгоритм Флойда
Основная идея алгоритма. Пусть есть три вершины i, j, k и заданы расстояния между ними. Если выполняется неравенство A[i,k]+A[k,j]<A[i,j], то целесообразно заменить путь i->j путем i->k->j. Такая замена выполняется систематически в процессе выполнения данного алгоритма.
Шаг 0. Определяем начальную матрицу расстояния A0 и матрицу последовательности вершин S0. Каждый диагональный элемент обеих матриц равен 0, таким образом, показывая, что эти элементы в вычислениях не участвуют. Полагаем k = 1.
Основной шаг k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения замены описанной выше, ко всем элементам A[i,j] матрицы Ak-1. Если выполняется неравенство ![A[i,k]+A[k,j]<A[i,j], (ine k, jne k, ine j)](https://intuit.ru/sites/default/files/tex_cache/c035f5c4524f40d3799ae6e240e257b4.png) , тогда выполняем следующие действия:
, тогда выполняем следующие действия:
- создаем матрицу Ak путем замены в матрице Ak-1 элемента A[i,j] на сумму A[i,k]+A[k,j] ;
- создаем матрицу Sk путем замены в матрице Sk-1 элемента S[i,j] на k. Полагаем k = k + 1 и повторяем шаг k.
Таким образом, алгоритм Флойда делает n итераций, после i -й итерации матрица А будет содержать длины кратчайших путей между любыми двумя парами вершин при условии, что эти пути проходят через вершины от первой до i -й. На каждой итерации перебираются все пары вершин и путь между ними сокращается при помощи i -й вершины (
рис.
45.2).

Рис.
45.2.
Демонстрация алгоритма Флойда
//Описание функции алгоритма Флойда
void Floyd(int n, int **Graph, int **ShortestPath){
int i, j, k;
int Max_Sum = 0;
for ( i = 0 ; i < n ; i++ )
for ( j = 0 ; j < n ; j++ )
Max_Sum += ShortestPath[i][j];
for ( i = 0 ; i < n ; i++ )
for ( j = 0 ; j < n ; j++ )
if ( ShortestPath[i][j] == 0 && i != j )
ShortestPath[i][j] = Max_Sum;
for ( k = 0 ; k < n; k++ )
for ( i = 0 ; i < n; i++ )
for ( j = 0 ; j < n ; j++ )
if ((ShortestPath[i][k] + ShortestPath[k][j]) <
ShortestPath[i][j])
ShortestPath[i][j] = ShortestPath[i][k] +
ShortestPath[k][j];
}
Заметим, что если граф неориентированный, то все матрицы, получаемые в результате преобразований симметричны и, следовательно, достаточно вычислять только элементы, расположенные выше главной диагонали.
Если граф представлен матрицей смежности, то время выполнения этого алгоритма имеет порядок O(n3), поскольку в нем присутствуют вложенные друг в друга три цикла.
Переборные алгоритмы
Переборные алгоритмы по сути своей являются алгоритмами поиска, как правило, поиска оптимального решения. При этом решение конструируется постепенно. В этом случае обычно говорят о переборе вершин дерева вариантов. Вершинами такого графа будут промежуточные или конечные варианты, а ребра будут указывать пути конструирования вариантов.
Рассмотрим переборные алгоритмы, основанные на методах поиска в графе, на примере задачи нахождения кратчайшего пути в лабиринте.
Постановка задачи.
Лабиринт, состоящий из проходимых и непроходимых клеток, задан матрицей A размером mxn. Элемент матрицы A[i,j]=0, если клетка (i,j) проходима. В противном случае ![A[i,j]=infty](https://intuit.ru/sites/default/files/tex_cache/db2c035e62916aae55881f5dd7d3f700.png) .
.
Требуется найти длину кратчайшего пути из клетки (1, 1) в клетку (m, n).
Фактически дана матрица смежности (только в ней нули заменены бесконечностями, а единицы – нулями). Лабиринт представляет собой граф.
Вершинами дерева вариантов в данной задаче являются пути, начинающиеся в клетке (1, 1). Ребра – показывают ход конструирования этих путей и соединяют два пути длины k и k+1, где второй путь получается из первого добавлением к пути еще одного хода.
Перебор с возвратом
Данный метод основан на методе поиска в глубину. Перебор с возвратом считают методом проб и ошибок (“попробуем сходить в эту сторону: не получится – вернемся и попробуем в другую”). Так как перебор вариантов осуществляется методом поиска в глубину, то целесообразно во время работы алгоритма хранить текущий путь в дереве. Этот путь представляет собой стек Way.
Также необходим массив Dist, размерность которого соответствует количеству вершин графа, хранящий для каждой вершины расстояние от нее до исходной вершины.
Пусть текущей является некоторая клетка (в начале работы алгоритма – клетка (1, 1) ). Если для текущей клетки есть клетка-сосед Neighbor, отсутствующая в Way, в которую на этом пути еще не ходили, то добавляем Neighbor в Way и текущей клетке присваиваем Neighbor, иначе извлечь из Way.
Приведенное выше описание дает четко понять, почему этот метод называется перебором с возвратом. Возврату здесь соответствует операция “извлечь из Way “, которая уменьшает длину Way на 1.
Перебор заканчивается, когда Way пуст и делается попытка возврата назад. В этой ситуации возвращаться уже некуда (
рис.
45.3).
Way является текущим путем, но в процессе работы необходимо хранить и оптимальный путь OptimalWay.
Усовершенствование алгоритма можно произвести следующим образом: не позволять, чтобы длина Way была больше или равна длине OptimalWay. В этом случае, если и будет найден какой-то вариант, он заведомо не будет оптимальным. Такое усовершенствование в общем случае означает, что как только текущий путь станет заведомо неоптимальным, надо вернуться назад. Данное улучшение алгоритма позволяет во многих случаях сильно сократить перебор.

Рис.
45.3.
Демонстрация алгоритма перебора с возвратом
/*Описание функции переборного алгоритма методом поиска в глубину */
void Backtracking(int n, int m, int **Maze){
int Begin, End, Current;
Begin = (n - 1) * m;
End = m - 1;
int *Way, *OptimalWay;
int LengthWay, LengthOptimalWay;
Way = new int[n*m];
OptimalWay = new int[n*m];
LengthWay = 0;
LengthOptimalWay = m*n;
for (int i = 0 ; i < n*m ; i++ )
Way[i] = OptimalWay[i] = -1;
int *Dist;
Dist = new int[n*m];
for (int i = 0 ; i < n ; i++ )
for (int j = 0 ; j < m ; j++ )
Dist[i * m + j] = ( Maze[i][j] == 0 ? 0 : -1 );
Way[LengthWay++] = Current = Begin;
while ( LengthWay > 0 ){
if(Current == End){
if (LengthWay < LengthOptimalWay){
for (int i = 0 ; i < LengthWay ; i++ )
OptimalWay[i] = Way[i];
LengthOptimalWay = LengthWay;
}
if (LengthWay > 0) Way[--LengthWay] = -1;
Current = Way[LengthWay-1];
}
else{
int Neighbor = -1;
if ((Current/m - 1) >= 0 && !Insert(Way, Current - m) &&
(Dist[Current - m] == 0 || Dist[Current - m] > LengthWay)
&& Dist[Current] < LengthOptimalWay)
Neighbor = Current - m;
else
if ((Current%m - 1) >= 0 && !Insert(Way,Current - 1)&&
(Dist[Current - 1]== 0 || Dist[Current - 1] > LengthWay)
&& Dist[Current] < LengthOptimalWay )
Neighbor = Current - 1;
else
if ((Current%m + 1) < m && !Insert(Way,Current + 1) &&
(Dist[Current + 1]== 0 || Dist[Current + 1] > LengthWay)
&& Dist[Current] < LengthOptimalWay )
Neighbor = Current + 1;
else
if ((Current/m + 1) < n && !Insert(Way,Current + m) &&
(Dist[Current + m]== 0 || Dist[Current + m] > LengthWay)
&& Dist[Current] < LengthOptimalWay )
Neighbor = Current + m;
if ( Neighbor != -1 ){
Way[LengthWay++] = Neighbor;
Dist[Neighbor] = Dist[Current] + 1;
Current = Neighbor;
}
else {
if (LengthWay > 0) Way[--LengthWay] = -1;
Current = Way[LengthWay-1];
}
}
}
if ( LengthOptimalWay < n*m )
cout << endl << "Yes. Length way=" << LengthOptimalWay<< endl;
else cout << endl << "No" << endl;
}
Листинг
.
Волновой алгоритм
Этот переборный алгоритм, который основан на поиске в ширину, состоит из двух этапов:
- распространение волны;
- обратный ход.
Распространение волны и есть собственно поиск в ширину, при котором клетки помечаются номером шага метода, на котором клетка посещается. При обратном ходе, начиная с конечной вершины, идет восстановление пути, по которому в нее попали путем включения в него клеток с минимальной пометкой (
рис.
45.4). Важной особенностью является то, что восстановление начинается с конца (с начала оно зачастую невозможно).

Рис.
45.4.
Демонстрация волнового алгоритма
Заметим, что перебор методом поиска в ширину по сравнению с перебором с возвратом, как правило, требует больше вспомогательной памяти, которая необходима для хранения информации, чтобы построить путь при обратном ходе и пометить посещенные вершины. Однако он работает быстрее, так как совершенно исключается посещение одной и той же клетки более чем один раз.
Ключевые термины
Алгоритм Дейкстры – это алгоритм нахождения кратчайшего пути от одной из вершин графа до всех остальных, который работает только для графов без ребер отрицательного веса.
Алгоритм Флойда – это алгоритм поиска кратчайшего пути между любыми двумя вершинами графа.
Волновой алгоритм – это переборный алгоритм, который основан на поиске в ширину и состоит из двух этапов: распространение волны и обратный ход.
Кратчайший путь – это путь в графе, то есть последовательность вершин и ребер, инцидентных двум соседним вершинам, и его длина.
Переборный алгоритм – это алгоритм обхода графа, основанный на последовательном переборе возможных путей.
Краткие итоги
- Нахождение кратчайшего пути на сегодняшний день является актуальной задачей
- К наиболее эффективным алгоритмам нахождения кратчайшего пути в графах относятся алгоритм Дейкстры, алгоритм Флойда и переборные алгоритмы. Эти алгоритмы эффективны при достаточно небольших количествах вершин.
- В реализации алгоритма Дейкстры строится множество вершин, для которых кратчайшие пути от начальной вершины уже известны. Следующие шаги основаны на добавлении к имеющемуся множеству по одной вершине с сохранением длин оптимальных путей.
- Сложность алгоритма Дейкстры зависит от способа нахождения вершины, а также способа хранения множества непосещенных вершин и способа обновления длин.
- Метод Флойда основывается на факте, что в графе с положительными весами ребер всякий неэлементарный кратчайший путь состоит из других кратчайших путей.
- Если граф представлен матрицей смежности, то время выполнения алгоритма Флойда имеет порядок O(n3).
- Переборные алгоритмы являются алгоритмами поиска оптимального решения.
- Волновой алгоритм является переборным алгоритмом, который основан на поиске в ширину и состоит из двух этапов: распространение волны и обратный ход.
- Перебор методом поиска в ширину, по сравнению с перебором с возвратом, требует больше вспомогательной памяти для хранения информации, однако, он работает быстрее, так как исключается посещение одной и той же вершины более чем один раз.




