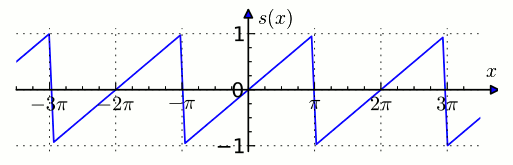
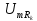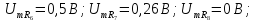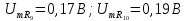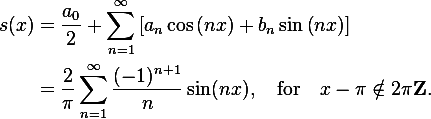МИНИСТЕРСТВО
ОБРАЗОВАНИЯ НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНО
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ
И ИНФОРМАТИКИ
В.
В. Филинов
Электроника
и схемотехника.
Расчёт
спектров электрических сигналов.
Учебно-методическое
пособие
Москва
– 2014
УДК
621.38
ББК
32.85
Рекомендовано
к изданию в качестве учебно-методического
пособия редакционно-издательским
советом МГУПИ
Рецензент:
д.т.н.
профессор Шкатов П. Н. (МГУПИ)
Филинов
В.В.
Электроника
и схемотехника. Расчет спектров
электрических сигналов.
Учебно-методическое пособие. М.: МГУПИ,
2014
Учебно-методическое
пособие предназначено для студентов
(бакалавров и специалистов) специальностей
по радиоэлектронике и информационной
безопасности, изучающих курс лекций
“Электроника и схемотехника”,
предназначено при подготовке к выполнению
практических и расчетно-графических
работ (РГР) по теме “Расчет спектров
электрических сигналов”. Приведены
примеры расчета спектров периодических
и непериодических сигналов, а также
задания для выполнения РГР. Полезно для
магистров и аспирантов технических
направлений МГУПИ.
Утверждено
и рекомендовано решением УМС факультета
«Приборостроения и радиоэлектроники»
МГУПИ в качестве учебно-методического
пособия.
©
Московский Государственный Университет
Приборостроения и Информатики, 2014
©
Филинов В.В., 2014
Оглавление
Стр.
Введение.
Необходимые формулы
………………………………………4
-
Спектры
амплитуд и фаз периодических сигналов
..…………6
Пример
1 ……………………………………………………………………6
Пример
2 …………………………………………………………………..10
Пример
3 …………………………………………………………………..11
Пример
4 …………………………………………………………………..12
Пример
5 …………………………………………………………………..13
Пример
6 …………………………………………………………………..14
Пример
7 …………………………………………………………………..16
Пример
8 …………………………………………………………………..17
Пример
9 …………………………………………………………………..18
Пример
10 …………………………………………………………………23
Пример
11 …………………………………………………………………24
-
Спектральная
плотность амплитуд и фаз периодических
сигналов
……..….…………..………………………..…….………………27
Пример
12 …………………………..……………………….……………27
Пример
13 …………………………..……………………….……………29
Пример
14 …………………………..……………………….……………31
Пример
15 …………………………..……………………….……………31
Пример
16 …………………………..……………………….……………33
Пример
17 …………………………..……………………….……………34
Пример
18 …………………………..……………………….……………36
Пример
19 …………………………..……………………….……………37
-
Литература
……………………………………………………………….39 -
Задания
для расчетно-географических
работ…………..………39
Необходимые
формулы.
Применительно
к периодическому гармоническому
напряжению
можно использовать разложение в ряд
Фурье:
(1)
Простейшим
периодическим сигналом является
гармоническое колебание вида
Разложение
последовательности прямоугольных
импульсов рис. 1.1 имеет вид:
(2)
Разложение
последовательности пилообразных
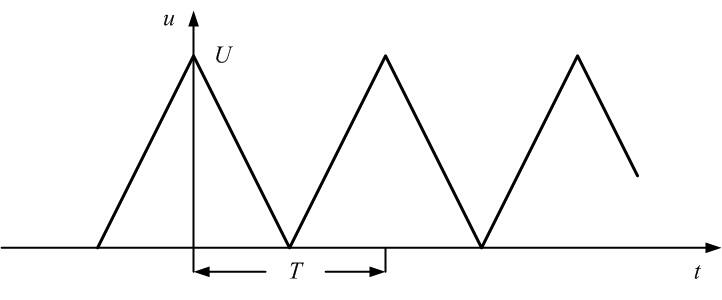
импульсов рис. 1.2 имеет вид:
(3)
Две
равнозначные записи ряда Фурье:
Ряд Фурье в
комплексной форме:
Выражение
для комплексного спектра сигнала:
Ряд
Фурье периодической последовательности
прямоугольных импульсов амплитудой U
(рис. 1.5а)
имеет вид:
Напряжение
на участках цепи находят, используя
принцип суперпозиции, например напряжение
на резисторах:
Расчет
цепи от отдельных постоянной и
гармонических составляющих напряжения
проводится в символической форме. При
этом нужно иметь в виду, что на k-й
гармонике сопротивление индуктивности

а сопротивление емкости
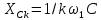
Интеграл
Фурье:
Уравнения
(10) и (11) являются основными в теории
спектров непериодических сигналов,
причем (10) называется прямым,
а (11) –
обратным
преобразованием Фурье (интегралом
Фурье).
Комплексная
придаточная функция по напряжению:
Из
выражений:
следует,
что спектральная плотность амплитуд
реакции цепи равна произведению
спектральной плотности амплитуд
воздействия АЧХ
цепи, а спектральная плотность фаз
реакции цепи равна сумме спектральной
плотности фаз
воздействия и ФЧХ
цепи.
-
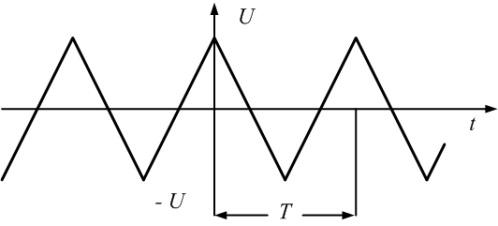
Спектры амплитуд и фаз периодических сигналов.
Пример
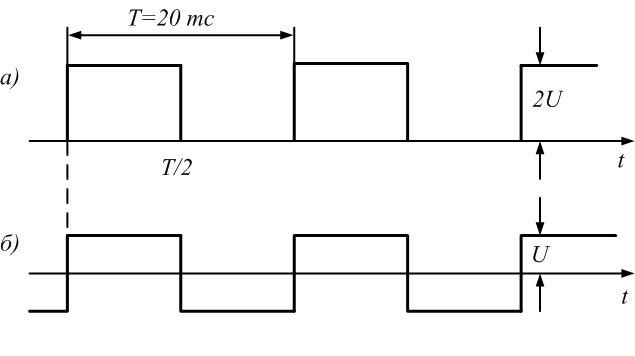
1.
Определим параметры синусоид, формирующих
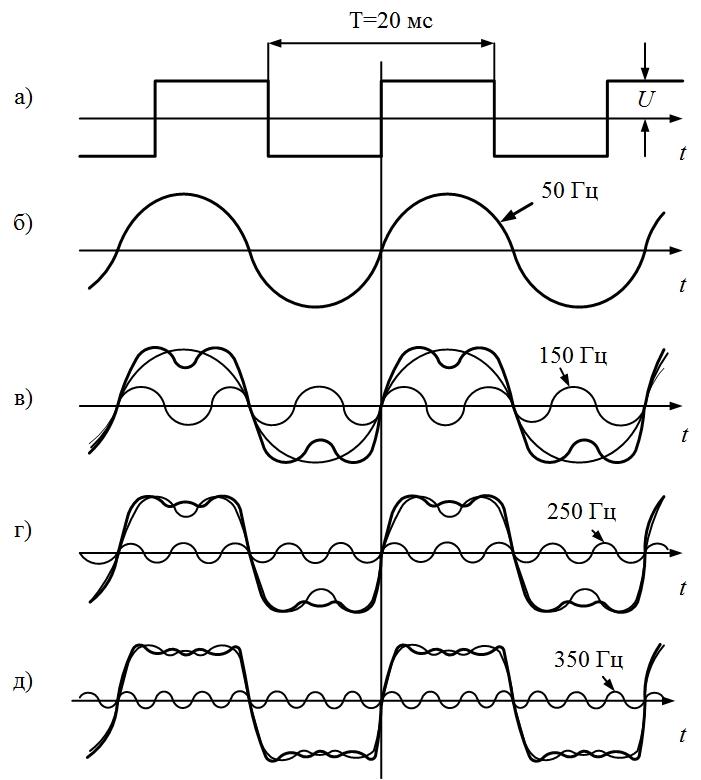
последовательности прямоугольных (рис.
1.1, а) и пилообразных (рис. 1.2, а) импульсов,
имеющих амплитуду U = 10 В
и период Т = 20 мс.
а)
Для формирования периодической
последовательности прямоугольных
импульсов амплитуда основной синусоиды
должна быть
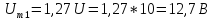
Частота
колебаний этой синусоиды обратно
пропорциональна периоду:
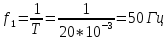
Круговая
частота

Таким образом, основная синусоида
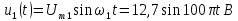
Все
последующие синусоиды в соответствии
с (2) должны иметь амплитуды в нечетное
количество раз меньшие, а частоты – в
это же нечетное количество раз большие,
чем у основной синусоиды:

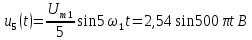
и
т.д.
Последовательность
прямоугольных импульсов, изображенных
на рис. 1.1, а,
–
это сумма синусоид:
.
Сигнал
изображен
на рис. 1.1, д.
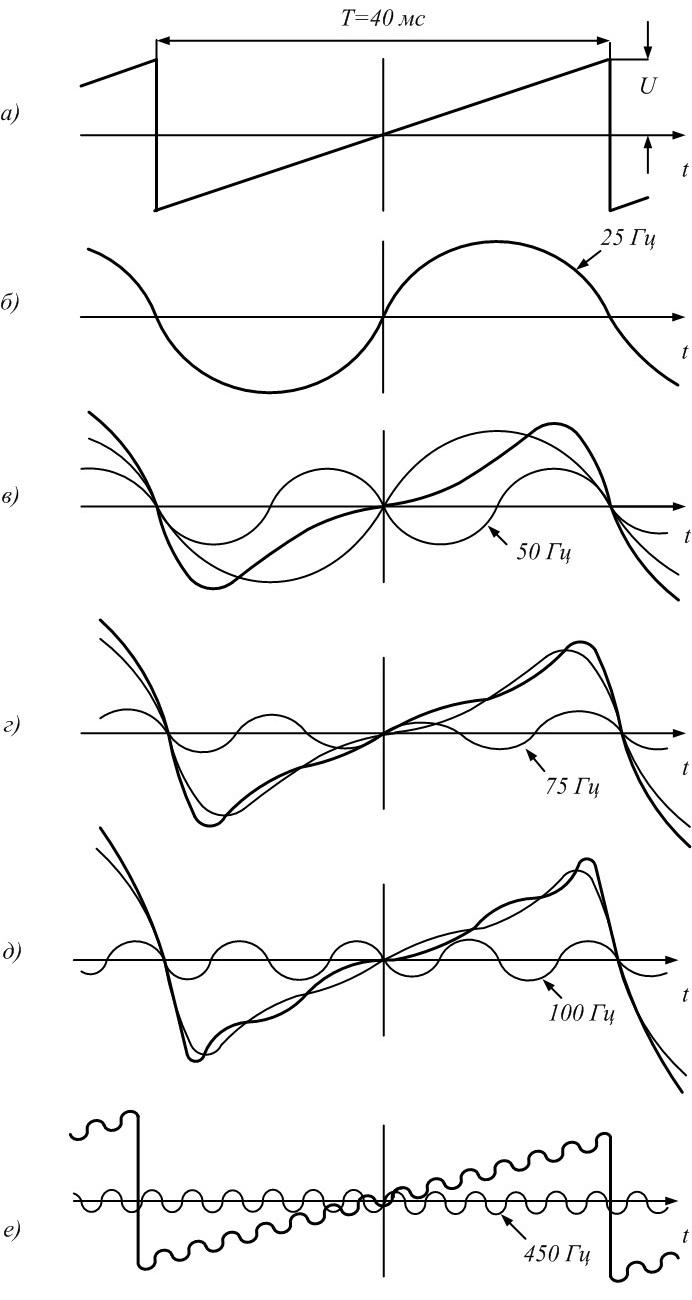
6)
Для формирования последовательности
пилообразных импульсов необходимо,
чтобы амплитуда основной синусоиды
была, как мы уже знаем [1, 3], равна
Частота
основной синусоиды

Таким
образом,
Рис.
1.1. Последовательность прямоугольных
импульсов и образующие ее синусоиды
Рис.
1.2. Последовательность пилообразных
импульсов и образующие ее синусоиды
Таблица
1.1. Ряды Фурье наиболее часто встречающихся
сигналов
|
Сигнал |
Ряд |
|
|
|
|
|
|
|
|
|
|
|
k-четные; |
|
|
k-четные; |
|
|
|
Последующие
синусоиды в соответствии с (3) будут
иметь вид
и
т.д.
Последовательность
пилообразных импульсов – это сумма
синусоид:
.
Чем
больше синусоид используется при
формировании сигнала, тем ближе его
форма к пилообразной (рис. 1.е).
Пример
2.
Определим гармонический состав
последовательности треугольных
импульсов, изображенных на рис. 1.3,
имеющих амплитуду, U
= 10 B
и период Т = 10 мс.
Периодический
сигнал на рис. 1.3 отличается от сигнала
во второй строке табл. 1.1 на величину
постоянной составляющей
Частота
основной составляющей сигнала
или
Амплитуда
основной составляющей сигнала
рассчитывается по формуле, приведенной
в табл. 1.1, или по одной из формул (1):
Четная
функция (рис. 1.3) содержит только
косинусоиды, амплитуды и частоты
которых определяются по формулам,
приведенным во второй строке табл. 1.1.
Амплитуда
и частота третьей гармоники:
Рис.
1.3. Последовательность треугольных
импульсов
Амплитуда
и частота пятой гармоники:
Амплитуда
и частота седьмой гармоники:
и
т.д.
Гармонический
состав последовательности треугольных
импульсов (рис.1.3) имеет вид:
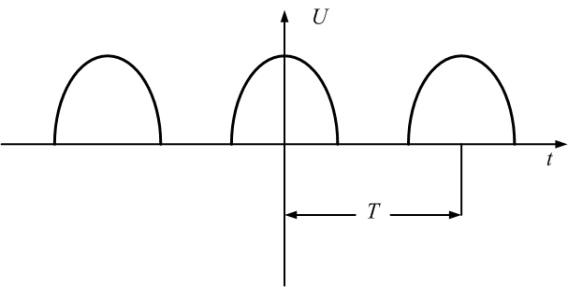
Пример
3.
Представим переменное напряжение,
выпрямленное двухполупериодным
выпрямителем (пятая строка табл. 1.1),
рядом Фурье в тригонометрической форме
(5).
Из
табл. 1.1 следует, что переменное напряжение
u(t) представлено рядом Фурье:
k
– четные.
Постоянная
составляющая напряжения u(
t)
рассчитывается по формуле

0,635U.
Нечетные
гармоники отсутствуют в ряде Фурье,
поскольку функция u(
t)–
четная.
Для
расчета амплитуд четных гармоник
нео6ходимо определить

1,27U.
Тогда амплитуда второй гармоники
Начальная
фаза второй гармоники равна нулю:
Амплитуда
четвертной гармоники
Фаза
четвертой гармоники
, так как в ряде Фурье перед слагаемым
стоит знак «минус».
Амплитуда
шестой гармоники
а
ее фаза, а также фазы десятой, четырнадцатой
и т.д. гармоник равны нулю.
Амплитуда
восьмой гармоники
а
ее начальная фаза, так же как и фазы
гармоник с номерами 12, 16, 20 и т.д., равна
180˚.
Тригонометрическая
форма ряда Фурье рассматриваемого
напряжения имеет вид:
.
Пример
4.
Представим ряд Фурье, полученный в
примере 3, в комплексной форме, ограничив
его восьмой гармоникой.
В
соответствии с (6) значения постоянной
составляющей и амплитуд гармоник
уменьшаются в 2 раза по сравнению со
значениями, которые 6ыли рассчитаны в
примере 3. Поэтому ряд Фурье в комплексной
форме имеет вид
Пример
5.
Построим спектр амплитуд и фаз
выпрямленного напряжения
(строка
5 табл, 1.1), имеющего амплитуду U
= 10 В и период Т = 10 мс.
При
решении примера 3 была получена
тригонометрическая форма ряда Фурье,
соответствующая выпрямленному напряжению:
.
Частота
основной составляющей сигнала
определяется
периодом колебаний:
В
спектре сигнала отсутствуют нечетные
гармоники, так как само колебание
является четной функцией. Частоты высших
гармоник с четными номерами кратны этим
номерам: частота второй гармоники равна
2
= 200 Гц, четвертой, шестой, восьмой гармоник
– 400, 600, 800 Гц соответственно и т.д.
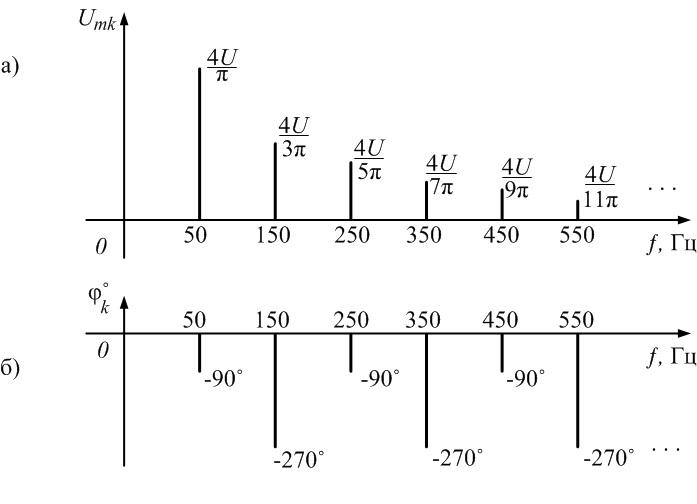
Постоянная
составляющая
Амплитуды
четных гармоник спектра в соответствии
с выражениями, полученными для ряда
Фурье, имеют следующие значения:
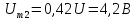

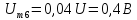
и
т.д.
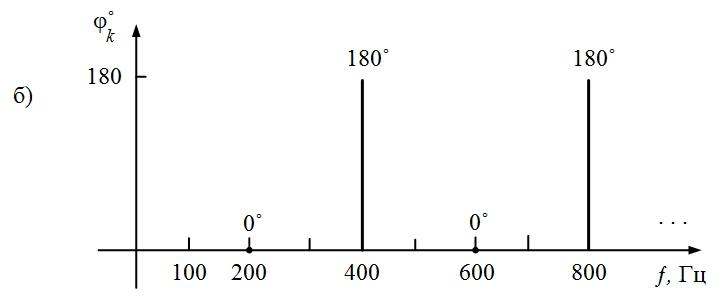
Фазы
гармоник поочередно принимают значения
0 и 180˚.
Рис.
1.4. Спектры амплитуд и фаз выпрямленного
напряжения
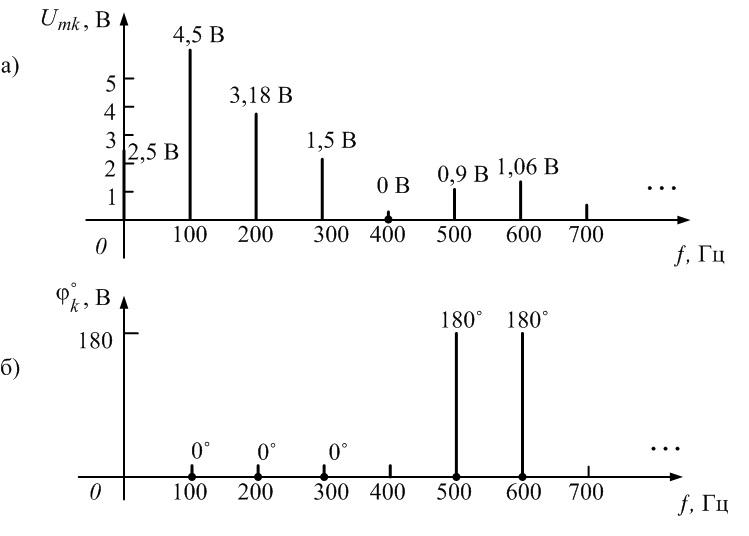
Пример
6.
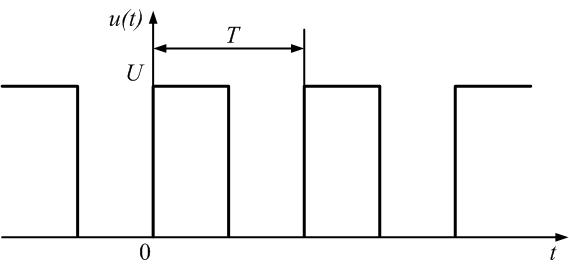
Рассмотрим периодическую последовательность
прямоугольных импульсов, показанную
на рис. 1.5, а:
Рис.
1.5. Последовательности прямоугольных
импульсов
Она
имеет постоянную составляющую, равную
в соответствии с (1)
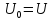
Коэффициенты
вычисляются
по формуле (1):
Здесь
6ыло учтено, что

1/Т.
Коэффициенты
вычисляются по формуле (1):
Выражение
удовлетворяет соотношению
Поэтому
Форма
ряда Фурье будет содержать только
синусоиды с нечетными гармоническими
частотами:
что,
естественно, с точностью до постоянной
составляющей U
совпадает с полученным ранее выражением
(2).
Переход
к форме ряда Фурье (5) дает
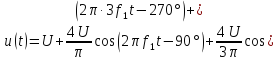
Спектр
такого сигнала без постоянной составляющей
показан на рис. 1.6:
Рис.
1.6. Спектры амплитуд и фаз сигнала рис.
1.5а
Пример
7.
Представим спектр сигнала
из примера 6 в комплексной форме.
Комплексный
спектр периодической последовательности
прямоугольных импульсов рассчитывается
по формуле (7):
Функция
имеет значения
Это
значит, что комплексный спектр
существует только для нечетных гармоник:
Заметим,
что в спектре
нет постоянной составляющей

которая рассчитывается по формуле (1) и
равна U.
Полученный
комплексный спектр
соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
Пример
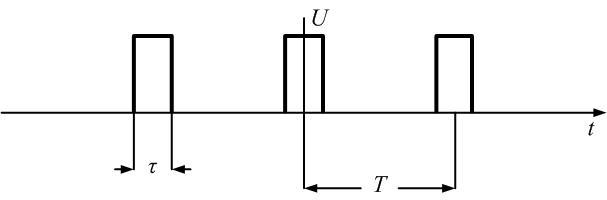
8.
Найдем спектр последовательности
прямоугольных импульсов, изображенных
на рис. 1.7.
Сигнал,
изображенный на рис. 1.7, имеет следующие
параметры: амплитуда U
= 10 В, длительность импульса τ= 10 мс,
период повторения импульсов Т
= 40 мс, скважность q
= Т/τ = 4. Спектр этого сигнала в форме
(Табл. 1.1, строка 6) имеет вид
Постоянная
составляющая
Частота
первой гармоники
Частоты
высших гармоник кратны 100 Гц. Амплитуды
первых шести гармоник, рассчитываемые
по формуле (3.28)
имеют
следующие значения:
Фазы
первой, второй, третьей гармоник равны
0˚, фазы пятой и шестой гармоник равны
180˚, так как при расчете
и
получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
Рис.
1.7. Последовательность прямоугольных
импульсов со скважностью q = 4
Рис.
1.8. Спектр последовательности прямоугольных
импульсов со скважностью q = 4
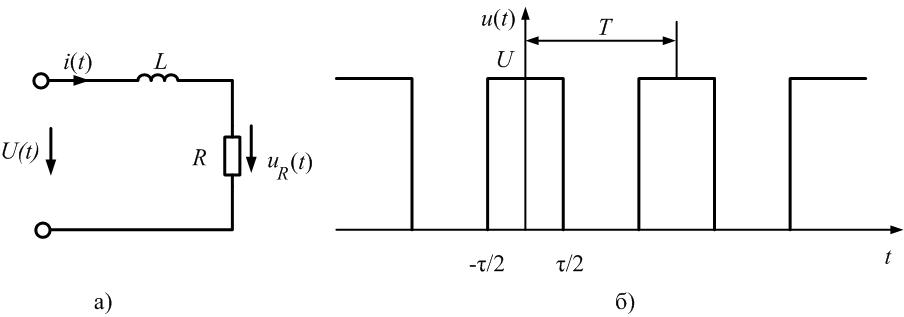
Пример
9.
Определим напряжение на резисторе
в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
Найдем
параметры постоянной и гармонических
составляющих сигнала (рис. 1.10),
представленного рядом Фурье (8). Частота
первой гармоники
или
Частоты
третьей, пятой и т.д. гармоник равны
соответственно: 3
= 18,84 рад/с; 3
= 3 кГц; 5
= 31,4 рад/с; 5
= 5 кГц; … .
Амплитуды
четных гармоник равны нулю. Амплитуды
нечетных гармоник рассчитываются по
формуле (1):
.
Ряд
Фурье сигнала имеет вид:
Рис.
1.9. Последовательный колебательный
контур с источником периодического
сигнала
Рис.
1. 10. Последовательность прямоугольных
импульсов
Определим
резонансную частоту
и
контура
(рис. 1.9):
Резонанс
в контуре наступает на частоте третьей
гармоники входного напряжения.
Добротность
контура
Определим
гармонические составляющие тока в цепи
и напряжения на резисторе в каждой из
составляющих ряда Фурье схем, изображенных
на рис. 1.9.
Схема
последовательного колебательного
контура с источником постоянного
напряжения

= 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
= 0;
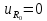
В
цепи, изображенной на рис. 1.12, в контур
включен источник напряжения, соответствующий
напряжению первой гармоники. Синусоидальное
напряжение
заменено
на комплексное

На частоте
= 1 кГц (
)
сопротивление индуктивности
а
сопротивление емкости
Рис.
1.11. Контур с источником постоянного
напряжения
Рис.
1.12. Контур с источником напряжения
первой гармоники
Комплексное
сопротивление цепи
Определим
комплексные значения тока
и напряжение
:
Это
соответствует составляющей синусоидального
напряжения (9) в исходной цепи:
На
третьей гармонике синусоидальный
источник заменяется источником
комплексного напряжения
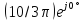
В результате имеем цепь, изображенную
на рис. 1.13.
На
частоте
= 3 кГц (
)
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
Комплексное
сопротивление цепи
= R = 2 Ом. Ток
Рис.
1.13. Контур с источником третьей гармоники
Рис.
1.14. Контур с источником напряжения
пятой гармоники
Напряжение
на резисторе
равно входному напряжению:

пятой гармонике синусоидальный источник
заменяется
источником комплексного напряжения
(рис. 1.14). На частоте
= 5 кГц (
)
сопротивления индуктивности и емкости
равны соответственно
и
Комплексное
сопротивление цепи
рассчитаем
по формуле:
Напряжение
на резисторе
Таким
образом, ряд Фурье напряжения на резисторе
имеет вид,
Рис.
1.15. Спектры амплитуд и фаз входного
напряжения и напряжения на резисторе
в колебательном контуре
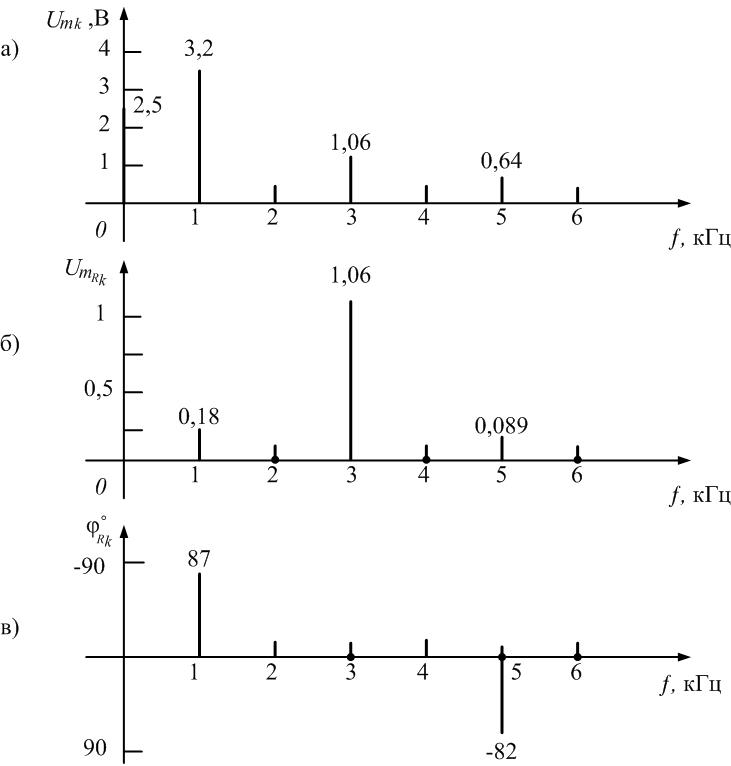
Спектры
амплитуд и фаз этого напряжения изображены
на рис. 1.15
( 6, в).
Анализ спектра
показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
Пример
10.
Сравним спектры амплитуд (рис. 1.15) входной
последовательности прямоугольных
импульсов
и напряжения
на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
В
соответствии с формулой и рис. 1.15 (а),
постоянная составляющая
в спектре напряжения
равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
Постоянная
составляющая в спектре напряжения
на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
Коэффициенты
передачи по напряжению
на частотах гармоник рассчитаем по
формуле
На
частоте f
= 0 кГц получаем
= 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
= 0,18/3,2 = 0,056.
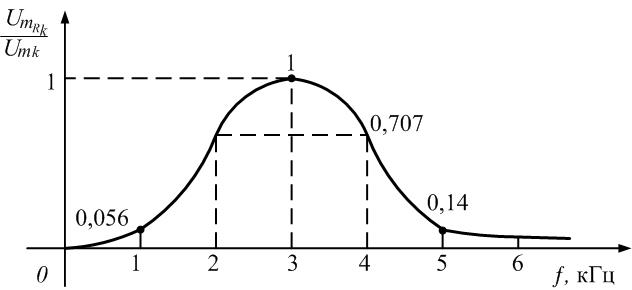
Рис.
1.16. Коэффициенты передачи по напряжению
на резисторе R на частотах гармоник
На
частоте
f=3
кГц (третья гармоника)
= 1,06/1,06 = 1.
На
частоте f=
5 кГц (пятая гармоника)
= 0,089/0,64= 0,14.
На
рис. 1.16 приведен график зависимости
коэффициента передачи контура от частоты
гармоник. На частоте резонанса коэффициент
передачи максимален и равен 1. На частотах
первой и пятой гармоник коэффициент
передачи резко уменьшается.
Пример
11.
Определим спектр амплитуд напряжения
на резисторе в цепи, изображенной на
рис. 1.17, а,
на вход которой поступает периодическая
последовательность прямоугольных
импульсов (рис. 1.17, б),
если заданы R
= 50 Ом, L
= 10 мГн, U
= 10 В, τ = 1 мс, Т = 4 мс.
Рис.
1.17. RL-цепь
и сигнал на ее входе
Найдем
комплексный спектр входного сигнала
u(t),
воспользовавшись (7):
Применив
формулу Эйлера, получим
Вычислим
амплитуды спектральных составляющих
Амплитуда
постоянной составляющей
Частота
основной составляющей
а
ее амплитуда
Аналогичным
образом определяются частоты и амплитуды
высших гармоник:
|
При |
k=2 |
2 |
|
|
k=3 |
3 |
|
|
|
k=4 |
4 |
|
|
|
k=5 |
5 |
|
|
|
k=6 |
6 |
|
|
|
k=7 |
7 |
|
|
|
k=8 |
8 |
|
|
|
k=9 |
9 |
|
|
|
k=10 |
10 |
|
Спектр
амплитуд
входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону

нули спектра расположены на частотах,
кратных
=1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
|
При |
k=0 |
|
|
k=1 |
|
|
|
k=2 |
|
|
|
k=3 |
|
|
|
k=4 |
|
|
|
k=5 |
|
|
|
k=6 |
|
|
|
k=7 |
|
|
|
k=8 |
|
|
|
k=9 |
|
|
|
k=10 |
|
Рис.
1.18. Спектры амплитуд последовательности
прямоугольных импульсов и напряжения
на резисторе в RL-цепи
и коэффициенты передачи цепи
График
зависимости коэффициента передачи
RL-цепи
от частоты изображен на рис. 3.18 (б).
Спектр
амплитуд
напряжения на резисторе, рассчитываем
в виде:
принимает
значения:
и
приведен на рис. 1.18 (в).
7. Спектральный анализ периодических сигналов
7.1. Разложение периодических сигналов
по ортогональным функциям
Электрический сигнал 







Рис. 7.1
При расчете разнообразных сигналов удобно представить их взвешенной суммой заданных функций времени вида

где 



Рекомендуемые материалы
Чтобы разложение в ряд (7.1) было взаимно однозначным
144
функции 

где момент начала интегрирования 


Для ортогонального базиса коэффициенты разложения 

В математике и технике широко используются различные ортогональные наборы функций (базисы) и прежде всего гармонический базис

полиномы Чебышева, Лагранжа, Эрмита и др. В цифровой технике применяют ортогональные дискретные функции Уолша, Радамахера.
7.2. Ряд Фурье
Ряд Фурье для действительной периодической функции времени 
145

Компоненту ряда Фурье вида

называют 

– частота первой гармоники, 








146

Величины 


7.3. Спектры амплитуд и фаз периодического сигнала
Периодический сигнал 

то есть двумя в общем случае бесконечными наборами чисел.
Первый из них называют спектром амплитуд сигнала,

а второй – спектром фаз,

Спектры амплитуд и фаз не зависят от времени, а определяются формой сигнала 



147
не зависят от формы сигнала и определяются только периодом его повторения 

Рис. 7.2 тельности прямоугольных
импульсов с амплитудой 




а амплитуды синфазной и квадратурной составляющих –


Для амплитуды и начальной фазы 


148
Графики спектров амплитуд и фаз при условии 


Рис. 7.3
Переменная 

и спектральные диаграммы можно строить в координатах частоты гармоники, как показано на рис. 7.4 для спектра амплитуд.
Спектры имеют дискретный (линейчатый) характер, интервал частот между соседними гармониками одинаков и
149
равен 



Рис. 7.4 амплитуд гармоник. Формулу
огибающей можно получить из выражения для спектра амплитуд, подобного (7.20), при замене номера гармоники 

где 
В примере (7.20) получим

график показан на рис. 7.3а пунктирной линией. Характерной особенностью огибающей спектра амплитуд сигнала рис. 7.2 является наличие точек с нулевым значением (нулей огибающей), определяемых из уравнения

решение которого имеет вид
150

где 

7.4. Синтез сигнала по его спектру
Если известны спектры амплитуд и фаз, то с помощью ряда Фурье (7.13) можно получить сигнал как функцию времени. Бесконечная сумма на практике не реализуема и сигнал описывается конечной суммой гармоник,

Соответствующие кривые при 


Как видно, с увеличением 
7.5. Ряд Фурье в комплексной форме
Гармоники сигнала могут быть представлены своими комплексными амплитудами в виде

тогда исходный сигнал можно представить в виде ряда Фурье,

151
Рис. 7.5
Амплитуда 


а ее начальная фаза 

152

Комплексная амплитуда гармоники (2.27) позволяет существенно упростить расчеты спектров амплитуд и фаз за счет сокращения числа интегралов и с учетом того, что подынтегральное выражение с экспонентой часто интегрируется проще, чем с тригонометрической функцией.
Рассмотрим сигнал, показанный на рис. 7.6, тогда

Как видно, в данном примере комплексная амплитуда является действительной величиной, что обусловлено формой сигнала на рис. 7.2..Спектры амплитуд и фаз совпадают с ранее полученными значениями.
7.6. Влияние формы сигнала на спектры амплитуд и фаз
Спектры амплитуд и фаз сигнала взаимно однозначно связаны с его формой, которая определяется формой импульсов и их длительностью на периоде повторения.
На рис. 7.6 показана последовательность прямоугольных импульсов 



153
тельностью) фронт и срез импульса. Величину

называют скважностью импульсов. На рис. 7.7 приведены спектры амплитуд (рис. 7.7а) и фаз (рис. 7.7б)
Рис. 7.6 при 
Рис. 7.7
На рис. 7.8 приведены аналогичные зависимости при 
Рис. 7.8.
154
При фиксированном периоде повторения импульсов 

 |
Рассмотрим трапециидальный импульс, программа исследование которого в среде MathCAD показана на рис. 7.9. Спектральный анализ проводится с помощью стандартной процедуры спектрального анализа fft(s). Она построена на основе алгоритма быстрого преобразования Фурье (БПФ) и позволяет получить комплексные коэффициенты 


Период 

Как видно при сравнении графиков спектров амплитуд на рис. 7.7 и рис. 7.9, увеличение длительности фронта и среза импульса приводит к значительному ослаблению высших гармоник сигнала.
155
На рис. 7.10 показан пример программы расчета спектра амплитуд колоколообразного сигнала вида

для которого характерно наиболее плавное изменение значений во всем интервале времени.
Рис. 7.9.
График сигнала и его спектр амплитуд показаны в листинге программы на рис. 7.10. Как видно, спектр «гладкого» сигнала сосредоточен в области нижних частот, высшие гармоники практически отсутствуют.
Полученные выводы подтверждают результаты синтеза прямоугольных импульсов по ограниченному числу 
156
Рис. 7.10.
7.7. Свойства спектров сигналов
Свойства спектров сигналов часто формулируются в виде теорем.
Спектральное преобразование сигнала линейно, то есть комплексная амплитуда суммы сигналов равна сумме комплексных амплитуд гармоник каждого из суммируемых сигналов. На практике особый интерес представляет свойство (теорема) смещения сигнала во времени. Ее можно сформулировать следующим образом.
 |
157
Взяв модули левой и правой частей (7.30), получим

то есть спектр амплитуд не изменяется при задержке сиг-
нала во времени.
Вычислим аргументы обеих частей выражения (7.30),

то есть начальные фазы гармоник сигнала при временной задержке уменьшаются на величину 

Для доказательства теоремы смещения запишем

Проведем замену переменных 

На спектральные характеристики влияют свойства симметрии сигнала.
Рассмотрим четные функции времени, удовлетворяющие условию 


158
комплексная амплитуда 


а начальная фаза равна 0 или 

Для нечетной функции, удовлетворяющей условию 


комплексная амплитуда 


а начальная фаза равна 0 или 

Эти свойства иллюстрирует пример четного сигнала на рис. 7.2, для которого имеет место равенство (7.19). Его фазовый спектр со значениями 0 или 
Рассмотрим комплексные спектры двух сигналов 


Рис. 7.11.
Сигнал 

159
величину 


Комплексная амплитуда 


По теореме смещения можно найти комплексную амплитуду 


Тогда согласно свойству линейности комплексная амплитуда 


160
С другой стороны, при прямом вычислении (проведите расчеты самостоятельно) комплексная амплитуда 


что полностью совпадает с (7.46).
7.8. Мощность периодического сигнала
Пусть имеется сигнал 


Эту же величину можно выразить через гармоники сигнала с помощью равенства (теоремы) Парсеваля в виде

С помощью спектральных характеристик можно определить действующее значение 

7.9. Ширина спектра
Как видно по графикам спектров амплитуд рассмотренных сигналов, в целом наблюдается тенденция уменьшения
161
амплитуд гармоник с ростом их номера (частоты). Графики на рис. 7.5 показывают, что форма сигнала определяется сравнительно небольшим числом гармоник. Все это свидетельствует
о том, что для представления (даже достаточно точного) сигнала необходимо учитывать ограниченное число гармоник, которые занимают конечный интервал частот.
 |
Мощность сигнала определяется выражением (7.39). Для рассматриваемых видеосигналов наиболее интенсивные гармоники имеют номера от 1 до некоторой величины N, при этом их суммарная мощность равна

Как видно, с ростом 



Тогда можно определить число гармоник 


выражения

В результате можно определить ширину спектра 

162
В качестве примера рассмотрим последовательность прямоугольных импульсов, показанную на рис. 7.2 со спектром амплитуд, показанном на рис. 7.3а. (скважность импульсов 






Рис. 7.12
Этот же график в области значений от 0,9 до 1 показан на рис. 7.13. С ростом 


В инженерной практике рассмотренный расчет ширины спектра проводится редко, а используется ее инженерная оценка. Для импульсных сигналов с длительностью 
163
пример, рис. 7.2) ширина спектра определяется выражением


(сравните эти величины со значениями нулей огибающей спектра амплитуд).
Рис. 7.13
Множитель от 1 до 3 косвенно характеризует долю мощности сигнала, заключенную в полосе пропускания (единица примерно соответствует 

Оценки ширины спектра можно выразить через число гармоник,

где 

164
На практике чаще всего используются соотношения с единичным множителем вида
 |
В рассмотренном примере сигнала на рис. 7.2 скважность 

7.10. Задания для самостоятельного решения
Задание 7.1. Определите и постройте графики спектров амплитуд и фаз сигналов вида:





Задание 7.2. Определите спектры амплитуд и фаз сигналов, показанных на рис. 7.14, постройте их графики. Проведите расчет ширины спектра при 


165
Рис. 7.14
Задание 7.3. С помощью теоремы смещения проведите расчет спектров амплитуд и фаз сигнала, показанного на рис. 7.14а, воспользовавшись результатами, полученными для сигнала на рис.7.2.
Задание 7.4. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.15, постройте их графики. Сравните спектр амплитуд со спектром гармонического сигнала, проанализируйте результаты.
Вычислите ширину спектра сигнала при 
Рис. 7.15
Задание 7.5. Определите спектры амплитуд и фаз сигналjd, показанного на рис.7.16, постройте их графики.
166
Рис. 7.16
Люди также интересуются этой лекцией: 2 Нефть и получение нефтепродуктов.
Задание 7.6. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.17, постройте их графики.
Рис. 7.17
Проведите тот же расчет, представив сигнал на рис. 7.17 в виде суммы двух импульсных последовательностей, показанных на рис. 7.18, и используя свойство линейности.
Рис. 7.18
Макеты страниц
В этом методе по сложному закону изменяющиеся токи и напряжения на нелинейном элементе заменяют их первыми гармониками. В расчете используют ВАХ по первым гармоникам в аналитической форме или в виде графической зависимости.
Основные этапы расчета в аналитическом варианте:
1) выражают аналитически ВАХ нелинейного элемента для мгновенных значений;
2) путем подстановки в нее первой гармоники напряжения или тока получают формулу, которая дает нелинейную связь между амплитудой первой гармоники тока через нелинейный элемент и амплитудой первой гармоники напряжения на нем [в качестве примера такой связи можно назвать формулу (15.19)];
3) в уравнение, составленное для исследуемой цепи по второму закону Кирхгофа, подставляют вместо мгновенных значений тока и напряжения на нелинейном элементе мгновенные значения их первых гармоник, а высшими гармониками пренебрегают;
4) уравнение разбивают на два уравнения: одно из них выражает собой равенство коэффициентов при синусных слагаемых левой и правой частей уравнения, другое — равенство коэффициентов при косинусных слагаемых обеих частей уравнения;
5) совместно решают эти два уравнения.
Основные этапы расчета в графическом варианте:
1) в качестве зависимости между амплитудой первой гармоники напряжения на нелинейном элементе и амплитудой первой гармоники тока через него берется нелинейная зависимость в виде графика. Эта зависимость может быть получена любым путем, в том числе и опытным;
2) произвольно задаются амплитудой 

3) путем построения нескольких векторных диаграмм для различных значений 


Данный метод позволяет рассматривать такие нелинейные явления, как преобразование постоянного тока в переменными обратное преобразование, явление резонанса на основной гармонике, триггерный эффект на первой гармонике, некоторые типы автомодуляционных процессов. Но он не позволяет исследовать более сложные явления, как, например, резонанс на высших, низших или дробных гармониках и др.
Если пользоваться аналитическим вариантом этого метода, то решение можно получить в общем виде, что существенно, так как становится возможным исследовать решение при изменении любого из параметров цепи. Этот метод будет применен для анализа работы автогенератора (см. § 15.54) и для анализа работы разветвленной цепи с нелинейной индуктивной катушкой (см. пример 159).
Гармонические колебания
Время на прочтение
10 мин
Количество просмотров 255K
На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.
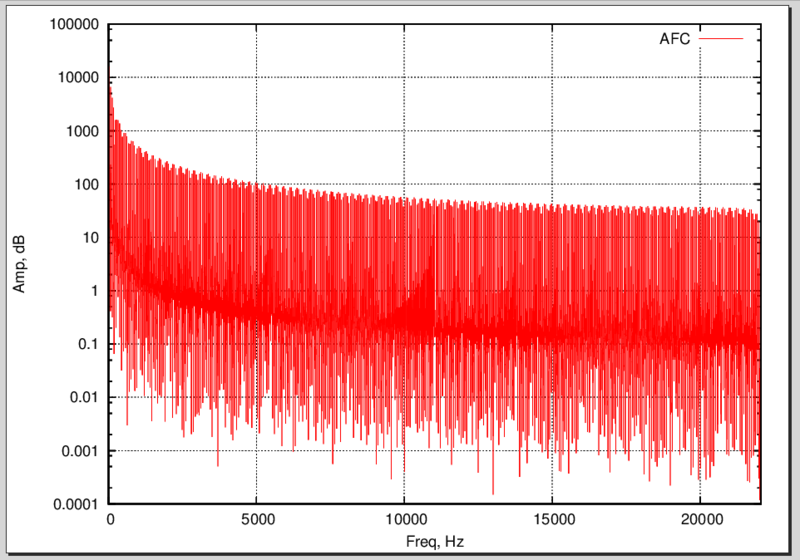
АЧХ шума.
Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).
Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.
Пару слов о матчасти
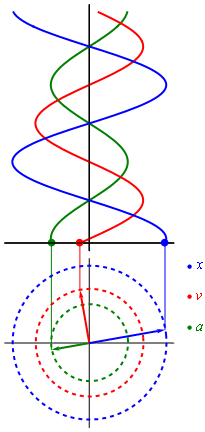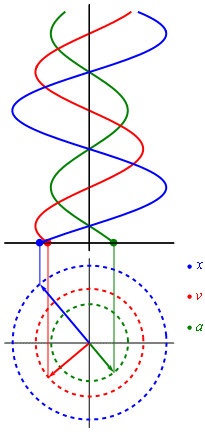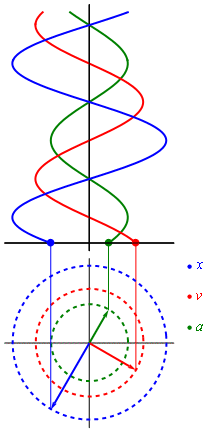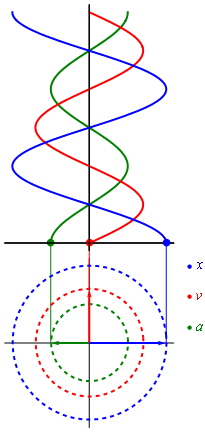
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии
Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
f(x) = A sin (ωt + φ),
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
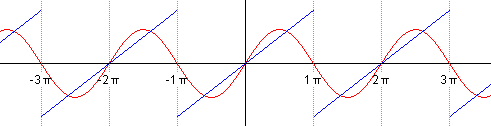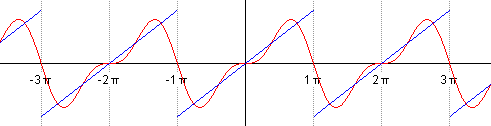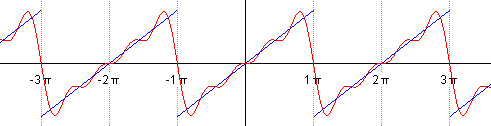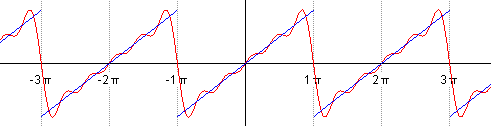
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.
Пилообразный сигнал
Его сумма будет представлена следующей формулой:
Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
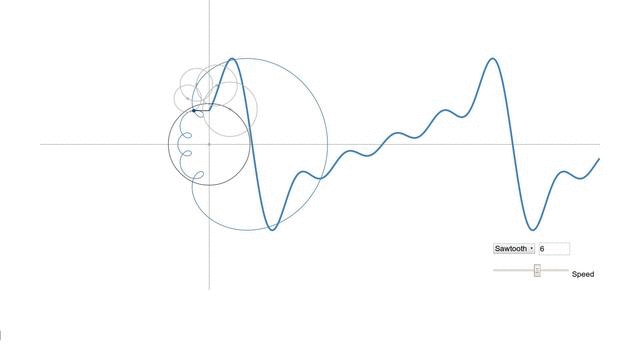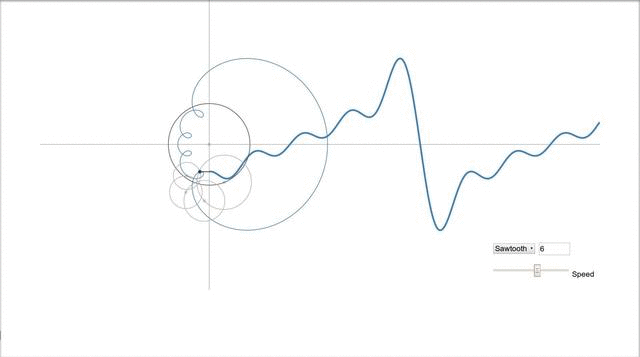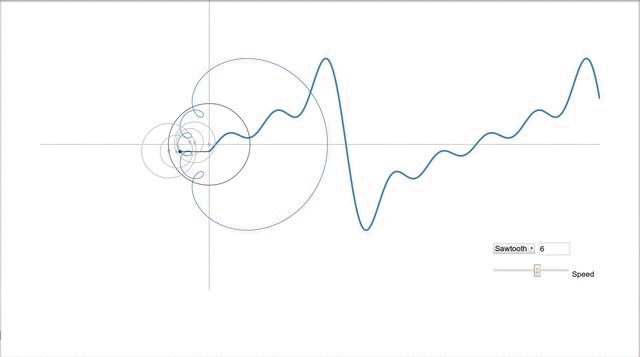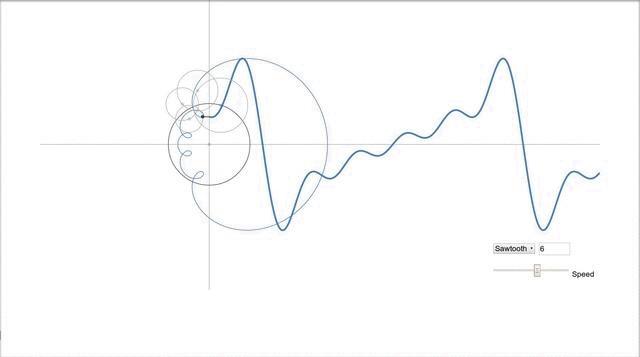
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:
Вектора рисуют пилу.
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.
Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.
Переходим к практическим упражнениям!
Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).
Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.
Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.
Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут
github.com/dlinyj/generate_wav
Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:
#define S_RATE (44100) //частота дискретизации
#define BUF_SIZE (S_RATE*10) /* 2 second buffer */
….
int main(int argc, char * argv[])
{
...
float amplitude = 32000; //берём максимальную возможную амплитуду
float freq_Hz = 100; //частота сигнала
/* fill buffer with a sine wave */
for (i=0; i<BUF_SIZE; i++)
{
buffer[i] +=(int)(amplitude * sin((float)(2*M_PI*i*freq_Hz/S_RATE)));
}
write_wav("test.wav", BUF_SIZE, buffer, S_RATE);
return 0;
}
Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).
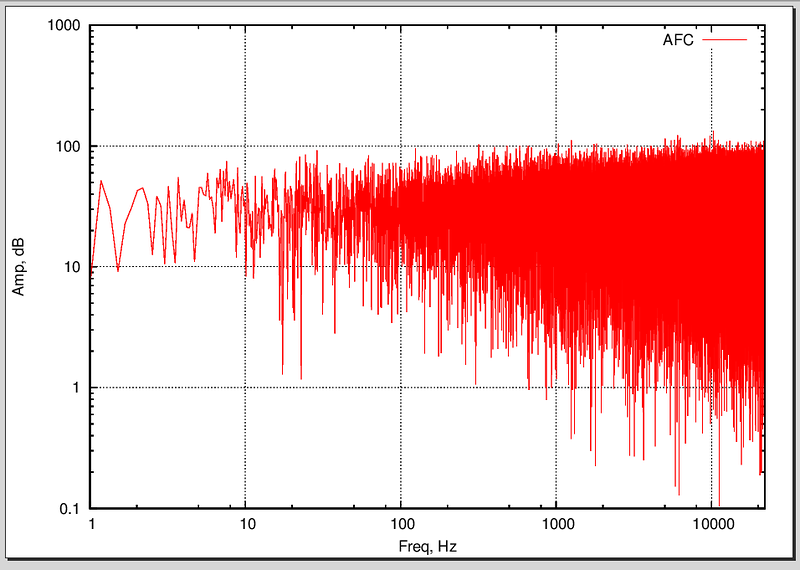
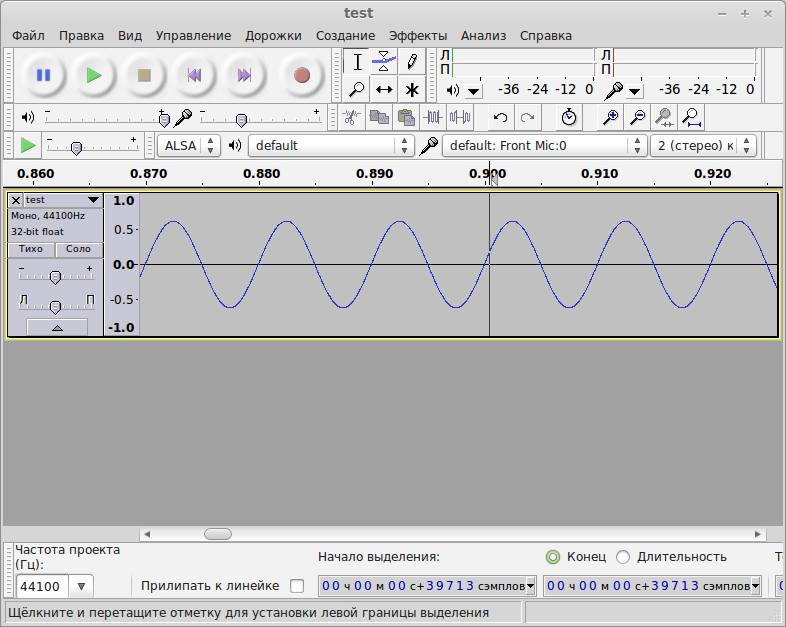
В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:
Чистый ламповый синус
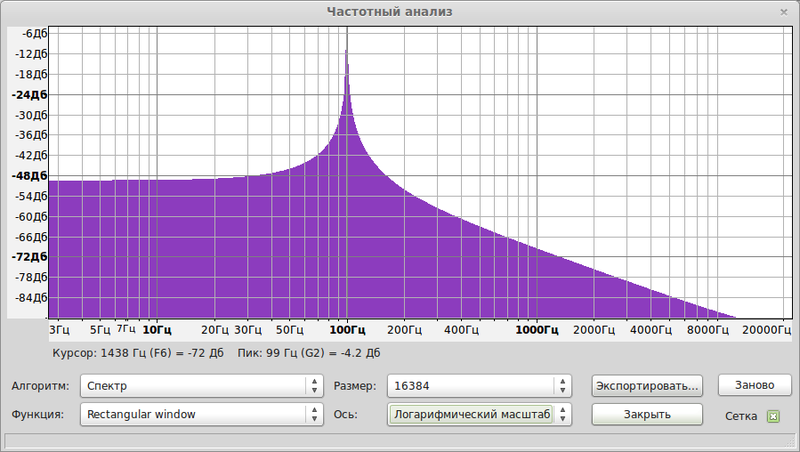
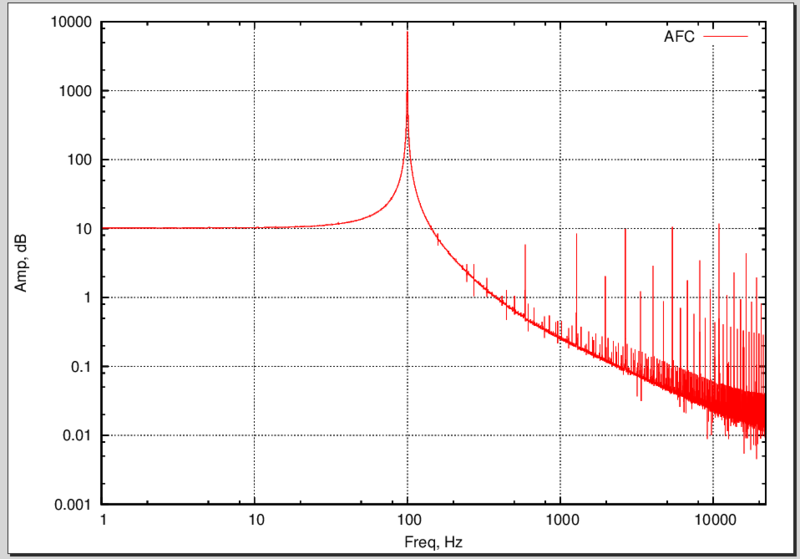
Поглядим спектр этого синуса (Анализ->Построить график спектра)
График спектра
Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.
В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.
Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой
с блекджеком и шлюхами
, тем более, что это несложно.
Пишем свой анализатор спектра
Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.
Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.
Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.
Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек
вектора
исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.
Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.
Для начала алокируем массивы:
c = calloc(size_array*2, sizeof(float)); // массив поворотных множителей
in = calloc(size_array*2, sizeof(float)); //входный массив
out = calloc(size_array*2, sizeof(float)); //выходной массив
Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).
while( fread(&value,sizeof(value),1,wav) ) {
in[j]=(float)value;
j+=2;
if (j > 2*size_array) break;
}
Массив для быстрого преобразования Фурье должен представлять собой последовательность {re[0], im[0], re[1], im[1],… re[fft_size-1], im[fft_size-1]}, где fft_size=1<< p — число точек БПФ. Объясняю нормальным языком:
это массив комплексных чисел. Я даже боюсь представить, где используется комплексное преобразование Фурье, но в нашем случае мнимая часть у нас равна нулю, а действительная равна значению каждой точке масива.
Ещё одна особенность именно быстрого преобразования Фурье, что оно обсчитывает массивы, кратные только степени двойки. В результате мы должны вычислить минимальную степень двойки:
int p2=(int)(log2(header.bytes_in_data/header.bytes_by_capture));
Логарифм от количество байт в данных, делённых на количество байт в одной точке.
После этого считаем поворотные множители:
fft_make(p2,c);// функция расчёта поворотных множителей для БПФ (первый параметр степень двойки, второй алокированный массив поворотных множителей).
И скармливаем наш считанный массив в преобразователь Фурье:
fft_calc(p2, c, in, out, 1); //(единица означает, что мы получаем нормализованный массив).
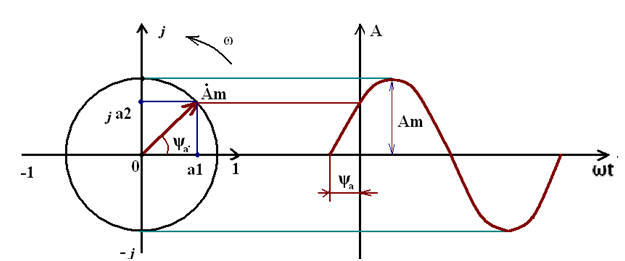
На выходе мы получаем комплексные числа вида {re[0], im[0], re[1], im[1],… re[fft_size-1], im[fft_size-1]}. Для тех, кто не знает, что такое комплексное число, поясню. Я не зря начал эту статью с кучи вращающихся векторов и кучи гифок. Так вот, вектор на комплесной плоскости определяется действительной координатой a1 и мнимой координатой a2. Или длиной (это у нас амплитуда Am) и углом Пси (фаза).
Вектор на комплексной плоскости
Обратите внимание, что size_array=2^p2. Первая точка массива соответствует частоте 0 Гц (постоянная), последняя точка соответствует частоте дискретизации, а именно 44100 Гц. В результате мы должны рассчитать частоту, соответствующей каждой точке, которые будут отличаться на частоту дельта:
double delta=((float)header.frequency)/(float)size_array; //частота дискретизации на размер массива.
Алокируем массив амплитуд:
double * ampl;
ampl = calloc(size_array*2, sizeof(double));
И смотрим на картинку: амплитуда — это длина вектора. А у нас есть его проекции на действительную и мнимую ось. В результате у нас будет прямоугольный треугольник, и тут мы вспоминаем теорему Пифагора, и считаем длину каждого вектора, и сразу пишем её в текстовый файл:
for(i=0;i<(size_array);i+=2) {
fprintf(logfile,"%.6f %fn",cur_freq, (sqrt(out[i]*out[i]+out[i+1]*out[i+1])));
cur_freq+=delta;
}
В результате получаем файл примерно такого вида:
…
11.439514 10.943008
11.607742 56.649738
11.775970 15.652428
11.944199 21.872342
12.112427 30.635371
12.280655 30.329171
12.448883 11.932371
12.617111 20.777617
...
Окончательная версия программы обитает на гитхабе вот тут:
github.com/dlinyj/fft
Пробуем!
Теперь скармливаем получившейся программе тот звуковой файл синуса
./fft_an ../generate_wav/sin 100 Hz.wav
format: 16 bits, PCM uncompressed, channel 1, freq 44100, 88200 bytes per sec, 2 bytes by capture, 2 bits per sample, 882000 bytes in data
chunk=441000
log2=18
size array=262144
wav format
Max Freq = 99.928 , amp =7216.136
И получаем текстовый файл АЧХ. Строим его график с помощью гнуплота
Скрипт для построения:
#! /usr/bin/gnuplot -persist
set terminal postscript eps enhanced color solid
set output "result.ps"
#set terminal png size 800, 600
#set output "result.png"
set grid xtics ytics
set log xy
set xlabel "Freq, Hz"
set ylabel "Amp, dB"
set xrange [1:22050]
#set yrange [0.00001:100000]
plot "test.txt" using 1:2 title "AFC" with lines linestyle 1
Обратите внимание на ограничение в скрипте на количество точек по X: set xrange [1:22050]. Частота дискретизации у нас 44100, а если вспомнить теорему Котельникова, то частота сигнала не может быть выше половины частоты дискретизации, следовательно сигнал выше 22050 Гц нас не интересует. Почему так, советую прочитать в специальной литературе.
Итак (барабанная дробь), запускаем скрипт и лицезреем:
Спектр нашего сигнала
Обратите внимание на резкий пик на частоте 100 Гц. Не забывайте, что по осям — логарифмический масштаб! Шерсть справа, как я думаю, ошибки преобразования Фурье (тут на память приходят окна).
А давайте побалуем?
А давайте! Давайте поглядим спектры других сигналов!
Вокруг шум…
Для начала построим спектр шума. Тема про шумы, случайные сигналы и т.п. достойна отдельного курса. Но мы её коснёмся слегка. Модифицируем нашу программу генерации wav-файла, добавим одну процедуру:
double d_random(double min, double max)
{
return min + (max - min) / RAND_MAX * rand();
}
она будет генерировать случайное число в заданном диапазоне. В результате main будет выглядеть так:
int main(int argc, char * argv[])
{
int i;
float amplitude = 32000;
srand((unsigned int)time(0)); //инициализируем генератор случайных чисел
for (i=0; i<BUF_SIZE; i++)
{
buffer[i] +=(int)amplitude*d_random(-1.0, 1.0); //nois
}
write_wav("test.wav", BUF_SIZE, buffer, S_RATE);
return 0;
}
Сгенерируем файл, (рекомендую к прослушиванию). Поглядим его в audacity.
Сигнал в audacity
Поглядим спектр в программе audacity.
Спектр
И поглядим спектр с помощью нашей программы:
Наш спектр
Хочу обратить внимание на очень интересный факт и особенность шума — он содержит в себе спектры всех гармоник. Как видно из графика, спектр вполне себе ровный. Как правило, белый шум используется для частотного анализа пропускной способности, например, аудиоаппаратуры. Существуют и другие виды шумов: розовый, синий и другие. Домашнее задание — узнать, чем они отличаются.
А компот?
А теперь давайте посмотрим другой интереснейший сигнал — меандр. Я там выше приводил табличку разложений различных сигналов в ряды Фурье, вы поглядите как раскладывается меандр, выпишите на бумажку, и мы продолжим.
Для генерации меандра с частотой 25 Гц мы модифицируем в очередной раз наш генератор wav-файла:
int main(int argc, char * argv[])
{
int i;
short int meandr_value=32767;
/* fill buffer with a sine wave */
for (i=0; i<BUF_SIZE; i++)
{
//meandr
if (!(i%(S_RATE/((int)freq_Hz/2)))) {
if (meandr_value==32767) {
meandr_value=-32767;
} else {
meandr_value=32767;
}
}
buffer[i]=meandr_value;
}
write_wav("test.wav", BUF_SIZE, buffer, S_RATE);
return 0;
}
В результате получим звуковой файл (опять же, советую послушать), который сразу надо посмотреть в audacity
Его величество — меандр или меандр здорового человека
Не будем томиться и поглядим его спектр:
Спектр меандра
Пока не очень что-то понятно, что такое… А давайте поглядим несколько первых гармоник:
Первые гармоники
Совсем другое дело! Ну-ка поглядим табличку. Смотрите-ка, у нас есть только 1, 3, 5 и т.д., т.е. нечётные гармоники. Мы так и видим, что у нас первая гармоника 25 Гц, следующая (третья) 75 Гц, затем 125 Гц и т.д., при этом у нас амплитуда постепенно уменьшается. Теория сошлась с практикой!
А теперь внимание! В реальной жизни сигнал меандра у нас имеет бесконечную сумму гармоник всё более и более высокой частоты, но как правило, реальные электрические цепи не могут пропускать частоты выше какой-то частоты (в силу индуктивности и ёмкости дорожек). В результате на экране осциллографа можно часто увидеть вот такой сигнал:
Меандр курильщика
Эта картинка прям как картинка из википедии, где для примера меандра берутся не все частоты, а только первые несколько.
Сумма первых гармоник, и как меняется сигнал
Меандр так же активно используется в радиотехнике (надо сказать, что — это основа всей цифровой техники), и стоит понимать что при длинных цепях его может отфильтровать так, что, родная мама не узнает. Его так же используют для проверки АЧХ различных приборов. Ещё интересный факт, что глушилки телевизоров работали именно по принципу высших гармоник, когда сама микросхема генерировала меандр десятки МГц, а его высшие гармоники могли иметь частоты сотни МГц, как раз на частоте работы телевизора, и высшие гармоники успешно глушили сигнал вещания телевизора.
Вообще тема подобных экспериментов бесконечная, и вы можете теперь сами её продолжить.
Рекомендации по прочтению
Книга
Для тех, кто нифига не понял, что мы тут делаем, или наоборот, для тех, кто понял, но хочет разобраться ещё лучше, а так же для студентам, изучающим ЦОС, крайне рекомендую эту книгу. Это ЦОС для чайников, которым является автор данного поста. Там доступным даже для ребёнка языком рассказываются сложнейшие понятия.
Заключение
В заключении хочу сказать, что математика — царица наук, но без реального применения многие люди теряют к ней интерес. Надеюсь, данный пост подстегнёт вас к изучению такого замечательного предмета, как обработка сигналов, и вообще аналоговой схемотехнике (затыкайте уши, чтобы не вытекали мозги!). 🙂
Удачи!
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы, и как с ними работать? В этом нам и предстоит сегодня разобраться. Кроме того, мы рассмотрим важнейшее понятие – амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса – гармонические и негармонические. Гармонический сигнал – это сигнал, который можно описать следующей функцией:
Здесь A – амплитуда сигнала, w – циклическая частота, а phi – начальная фаза. Может возникнуть логичный вопрос – разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sinalpha = cos(frac{pi}{2}medspace-medspace alpha) – то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
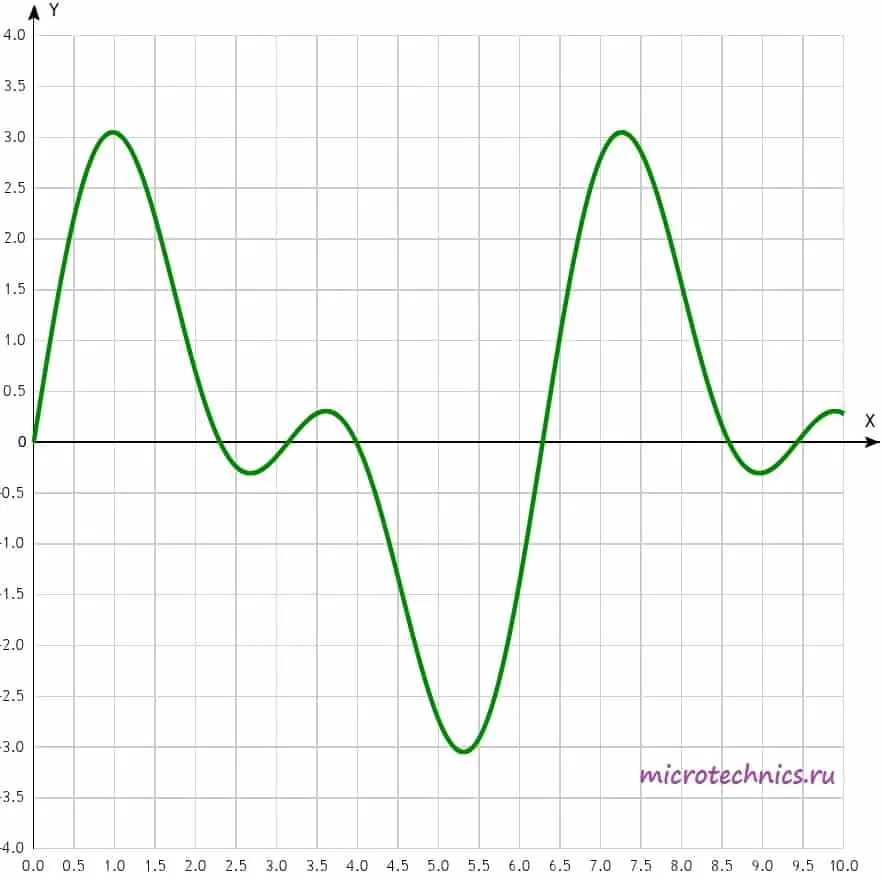
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
Давайте изобразим все эти сигналы на одном графике:
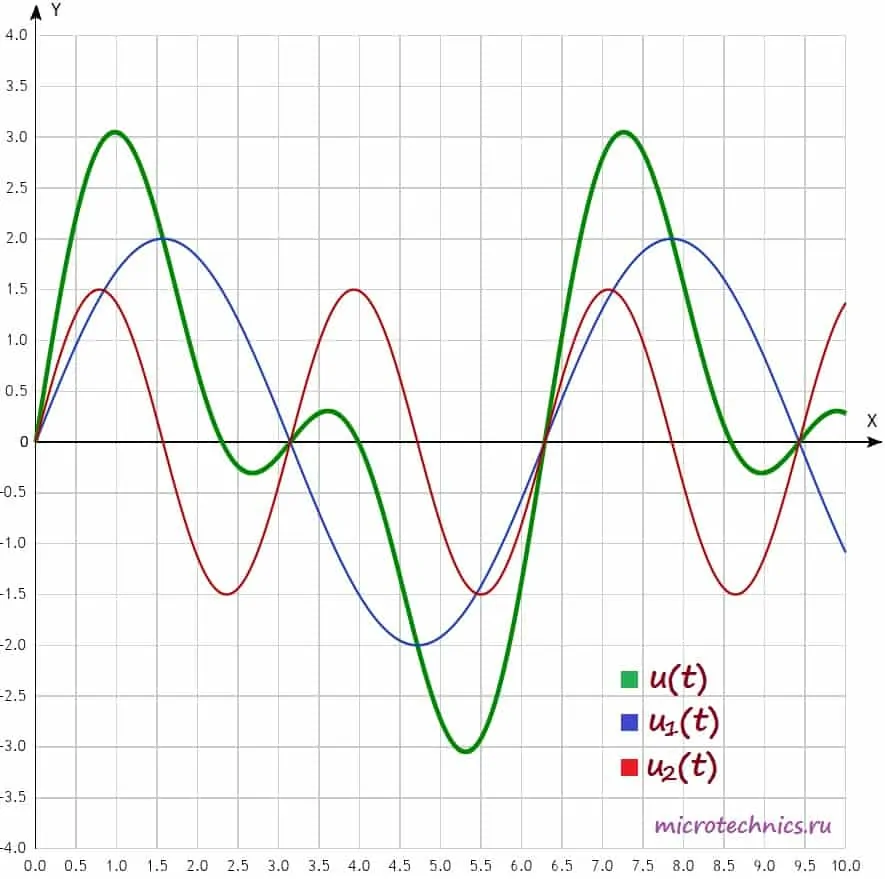
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:
u(t) = U_0 + sum_{i=0}^{infty}{U_{k}thinspace sin(thinspace kwt + phi_kthinspace )}
Здесь U_k – амплитуда, а phi_k – начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 – это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите – среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0 👍
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
- фазовый спектр сигнала – совокупность начальных фаз всех гармоник
- амплитудный спектр сигнала – амплитуды всех гармоник, из которых складывается негармонический сигнал
Давайте рассмотрим амплитудный спектр подробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
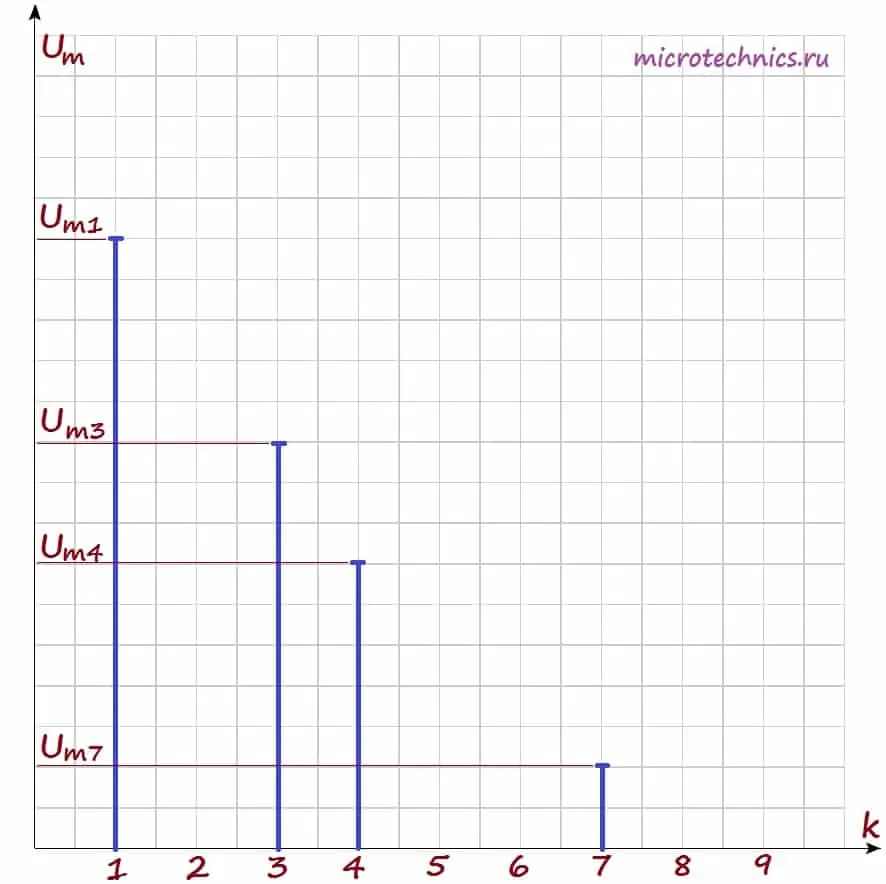
При этом на горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси – амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
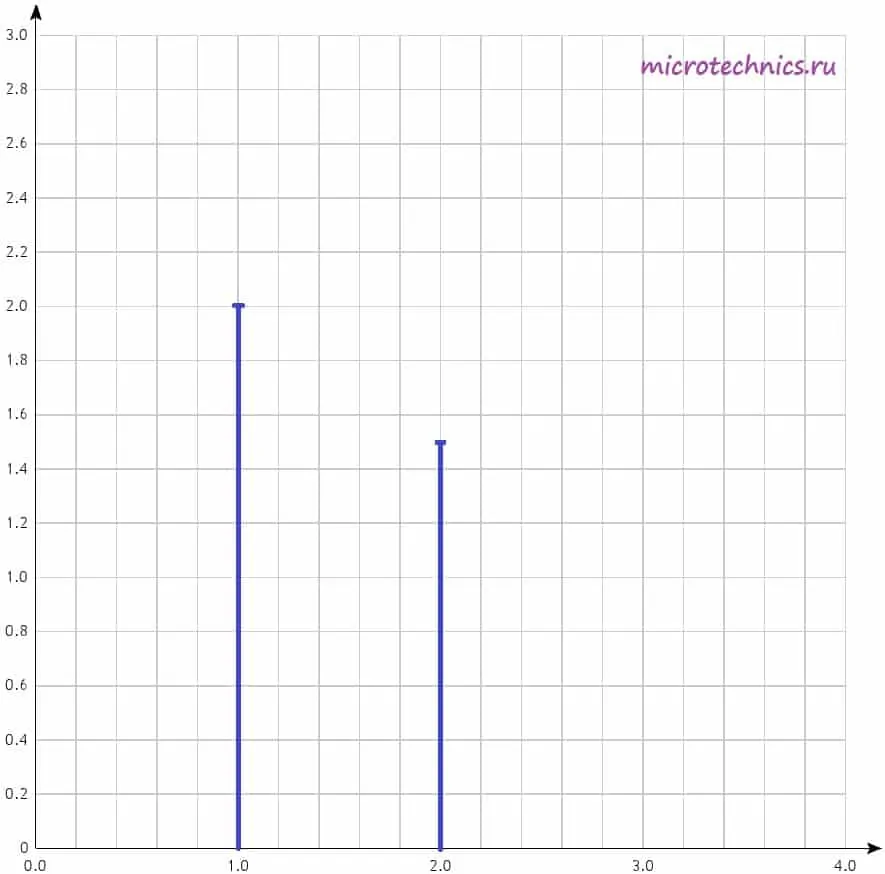
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались. Давайте перейдем к следующей теме сегодняшней статьи – к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств – фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Проанализируем, какой смысл она в себе несет…
АЧХ – это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но мы сейчас рассмотрим, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
Как видите, ни о какой периодичности здесь не идет и речи. Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи. Просто примем тот факт, что они позволяют нам осуществить такое преобразование.
Соответственно, мы можем построить диаграмму амплитудного спектра такого сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте детально обсудим этот момент.
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
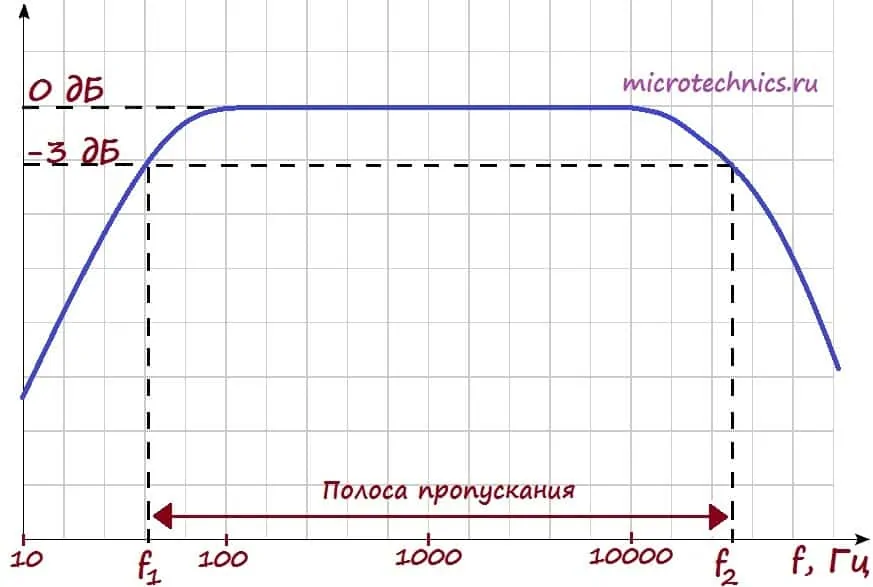
Разбираем поэтапно, что тут изображено. Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы считаем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация – сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
- 20 Гц – 160 Гц – область низких частот
- 160 Гц – 1.28 КГц – область средних частот
- 1.28 КГц – 20.5 КГц – область высоких частот
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье. И в завершение статьи посмотрим на пару примеров АЧХ:
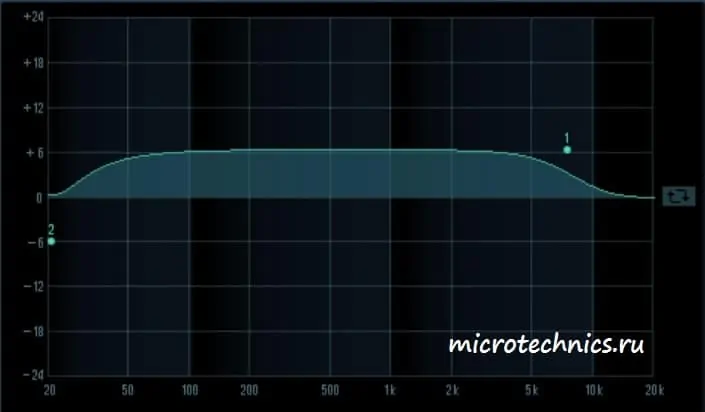
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
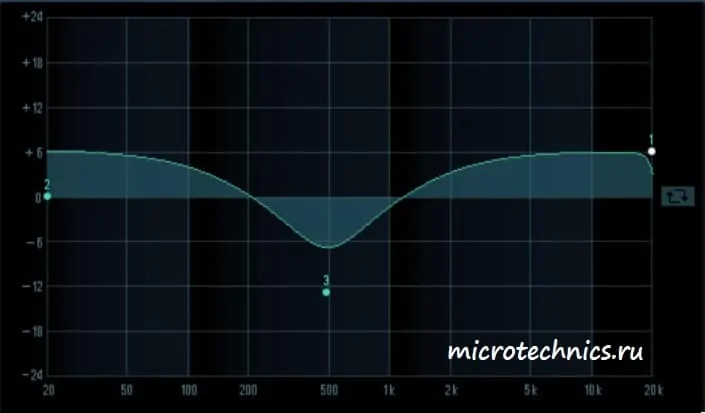
Во втором случае ситуация совсем другая – низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
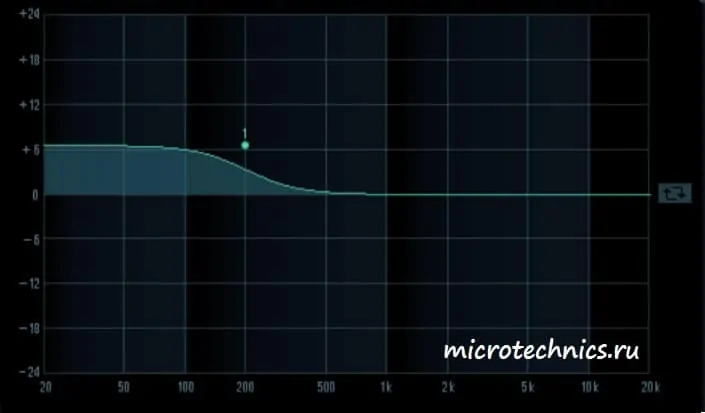
А теперь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов.
На этом мы и заканчиваем нашу сегодняшнюю статью. Спасибо за внимание и ждем вас на нашем сайте снова 🤝

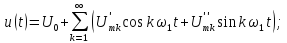
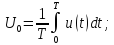
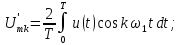

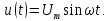
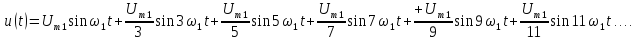
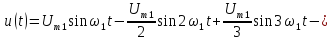
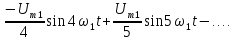


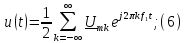

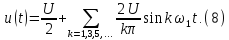

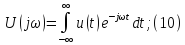
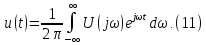
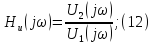
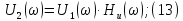
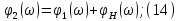


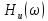
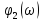

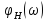

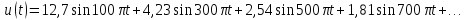

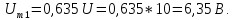



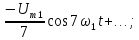
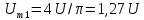
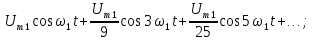


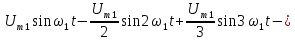

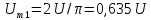
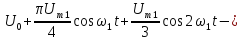
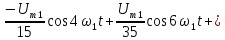


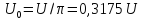

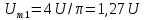

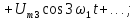
 ;
; ;
;
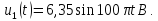

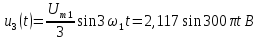
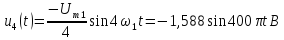
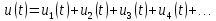

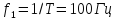
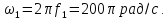
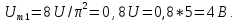



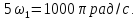
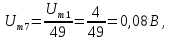


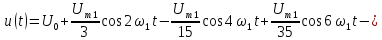
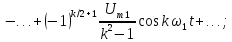
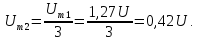

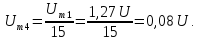


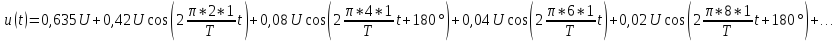
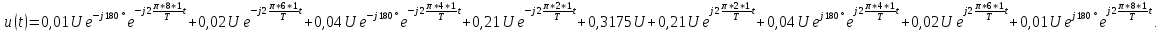
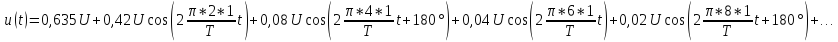
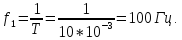
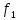
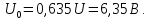


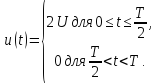
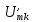



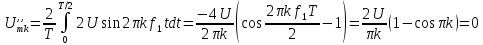
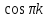
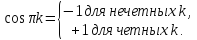
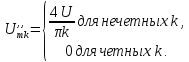
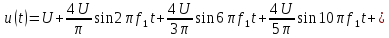



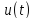





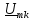
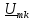
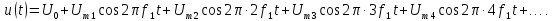
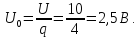

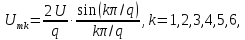

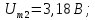

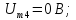
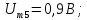
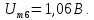


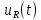
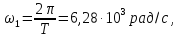
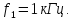

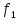



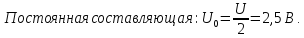
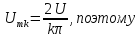
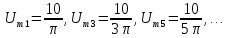

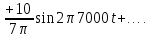




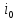
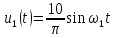
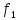
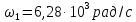
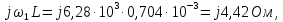
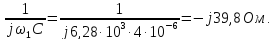


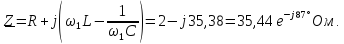






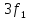
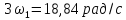


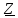

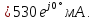




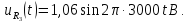
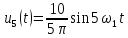





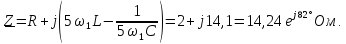
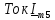
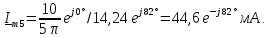
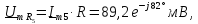
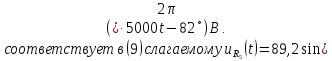

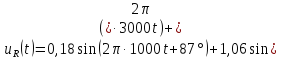

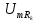
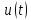

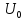

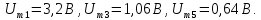
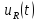
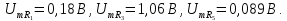

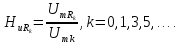

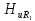

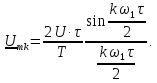
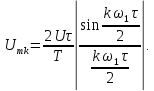
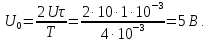

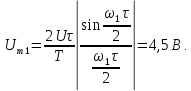
 =0,5
=0,5 =3,28
=3,28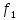 =0,75
=0,75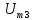 =1,5
=1,5 =1
=1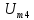 =0
=0 =1,25
=1,25 =0,9
=0,9 =1,5
=1,5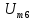 =1,06
=1,06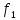 =1,75
=1,75 =0,64
=0,64 =2,0
=2,0 =0
=0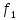 =2,25
=2,25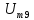 =0,5
=0,5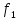 =2,5
=2,5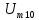 =0,64
=0,64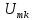

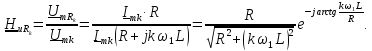
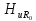 =1;
=1; =0,95;
=0,95;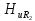 =0,85;
=0,85;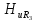 =0,73;
=0,73; =0,62;
=0,62; =0,54;
=0,54;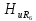 =0,47;
=0,47;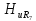 =0,41;
=0,41;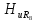 =0,37;
=0,37;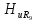 =0,33;
=0,33; =0,3.
=0,3.