Амплитуда в алгебре как найти

автор вопроса выбрал этот ответ лучшим

Амплитуда (лат. amplitudo значительность, обширность, величие, обозначается большей буквой А) наибольшее значение смещения либо конфигурации переменной величины от среднего значения при колебательном либо волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.

В общем случае гармоническое колебание математически записывается в виде:

displaystyle x(t)=A(t)sin(omega t+varphi ) displaystyle x(t)=A(t)sin(omega t+varphi )

или

displaystyle x(t)=A(t)cos(omega t+varphi ) displaystyle x(t)=A(t)cos(omega t+varphi ),

где displaystyle x(t) x(t) отклонение колеблющейся величины в текущий момент медли displaystyle t t от среднего арифметического за период значения (к примеру, в кинематике смещение, отклонение колеблющейся точки от положения равновесия, в электротехнике мгновенное значение напряжения либо силы тока от среднего значения и др.);

displaystyle A(t) A(t) амплитуда колебания, то есть максимальное за период отклонение колеблющейся величины от среднего за период значения, размерность displaystyle A(t) A(t) совпадает с размерностью displaystyle x(t), x(t), в общем случае амплитуда зависит от медли, например, при затухающем своем колебании осциллятора;

displaystyle omega omega  (радиан/с, градус/с) циклическая частота, показывающая, на сколько радиан (градусов) меняется фаза колебания за 1 с;

displaystyle varphi varphi  (радиан, градус) исходная фаза колебания.

The largest deviation of a variable from its mean value is referred to as amplitude. It is the largest displacement from a particle’s mean location in to and fro motion around a mean position. Periodic pressure variations, periodic current or voltage variations, periodic variations in electric or magnetic fields, and so on all have amplitudes.

Amplitude does not have a specific formula. It can be obtained by equations or graphical representations of such variations.

What is an Amplitude?

The highest displacement of the waves is referred to as amplitude. In addition, you will learn about amplitude, amplitude formula, formula derivation, and a solved example in this course. Furthermore, you will be able to comprehend amplitude after completing the topic.

Amplitude refers to the greatest deviation from equilibrium that an item in periodic motion might display. A pendulum, for example, swings past its equilibrium point (straight down) before reaching its maximum distance from the centre.

Furthermore, the amplitude’s distance is A. Furthermore, the pendulum’s complete range has a magnitude of 2A. Waves and springs, for example, follow a periodic motion. Furthermore, because the sine function oscillates between +1 and -1, it may be used to depict periodic motion.

SI Unit: The metre is the most notable amplitude unit (m).

Formula for Amplitude

The amplitude of a variable is the biggest variation from its mean value. The amplitude formula can be used to calculate the sine and cosine functions. Amplitude is represented by the letter A. The sine (or cosine) function has the following formula:

x = A sin (ωt + ϕ)   

or   

x = A cos (ωt + ϕ)

where,

• x = displacement of wave (meter)
• A = amplitude
• ω = angular frequency (rad/s)
• t = time period
• ϕ = phase angle

The amplitude formula is also known as the average of the maximum and minimum values of a sine or cosine function. The absolute amplitude value is always used.

Sample Problems

Problem 1: Consider a pendulum that swings back and forth. In addition, the phase shift is 0 radians. Furthermore, the pendulum is 14.0 cm or x = 0.140 m, and the time is t = 8.50 s. So, what is the oscillation’s amplitude?

Solution:

Given that,

x = 0.140 m

ω = π radians/s

ϕ = 0

t = 8.50 s

So, we can find the value of amplitude by rearranging the formula:

x = A sin (ωt+ϕ) → A = xsin(ωt+ϕ)

A = xsin(ωt+ϕ)

So, A = 0.14msin[(πradians/s)(8.50s)+0]

A = 0.140msin(8.50π)

Moreover, the sine of 8.50 π can be solved (by keeping in mind that the values is in radians) with a calculator:

Sin(8.50 π) = 1

So, the amplitude at time t is 8.50s is:

A = 0.140msin(8.50π)

A = 0.140m1

A = 0.140 m

Therefore, the amplitude of the pendulum’s oscillation is A =0.140 m = 14.0 cm.

Problem 2: Assume a spring is bouncing the head of a jack-in-the-box toy upward and downward. In addition, the oscillation’s angular frequency is π/6 radians/s, with a phase shift (ϕ) of 0 radians. The bouncing also has a 5.00 cm amplitude. Where does the Jack-in-the-head stand in relation to the equilibrium position in 6 s?

Solution:

Since, as we know that:

x = A sin (ωt+ϕ)

x = (0.500 m) sin [(π/6radians/s)(6.00s) + 0]

x = (0.500 m) sin (π/6radians/s)

x = (0.500 m) (0.00)

x = 0.00 m

So, at time t =6.00 s, the head of the-jack-in-the-box is at position 0.00 m that is the equilibrium position.

Problem 3: If y = 6 cos (7t + 1) is a wave. Find its amplitude.

Solution:

Given: equation of wave y = 6cos(7t + 1)

Using amplitude formula,

x= A cos (ωt + ϕ)

On comparing it with the wave equation:

A = 6

ω = 7

ϕ = 1

Therefore, the amplitude of the wave = 6 units. 

Problem 4: A wave is y = 2sin(4t). Find out its amplitude.

Solution:

The wave equation y = 2sin(4t)

Using the formula for amplitude,

x = A sin(ωt + ϕ)

When comparing the wave equation to the equation of motion,

A = 2

ω = 4

ϕ = 0

As a result, the amplitude of the wave is 2 units.

Problem 5: Consider a jack-in-the-box toy with its head bouncing up and down on a spring. Furthermore, the oscillation’s angular frequency is = π/6radians/s, and the phase shift is ϕ= 0 radians. Furthermore, the bouncing has a 5.00 cm amplitude. So, where does the Jack-in-the-head stand in relation to the equilibrium position in 1s.

Answer:

x = A sin (ωt+ϕ)

x = (0.500 m) sin [(π/6radians/s)(1.00s) + 0]

x = (0.500 m) sin (π/6radians/s)

x = (0.500 m) (0.500)

x = 0.250 m

x = 2.50 cm

So, at time 1.00 s the head of the jack-in-the-box is 2.5 cm above the equilibrium position.

Last Updated :
01 Feb, 2022

Like Article

Save Article

Начиная с седьмого класса в школах начинают преподавать такую тему, как “Механические колебания”. Начиная с ОГЭ и заканчивая ЕГЭ, эта тема прослеживается во многих экзаменах и вступительных испытаниях. Важной частью ее является изучение понятия амплитуды колебаний. Поэтому для начала ознакомимся с тем, что такое амплитуда колебаний и как обозначается амплитуда колебаний в физике, ведь со временем многое забывается, а именно данной переменной почему-то во многих школах уделяют меньше всего внимания.

Что такое амплитуда колебаний?

Амплитуда колебаний – это максимально возможное отклонение или смещение величины в большую или меньшую сторону от положения равновесия или от среднего значения. К примеру, для пружинного маятника положение равновесия – это покоящийся на пружине груз, а когда он начинает двигаться, то обретает определенную амплитуду, которая определяется растяжением или сжатием пружины.

Для математического же маятника немного проще – максимальное отклонения груза от положения покоя – это и есть амплитуда колебаний.

В то время как амплитуда колебаний радиоволн считается именно по отклонению от среднего значения.

Теперь перейдем к тому, какой буквой обозначается амплитуда колебаний.

Обозначение

В седьмом классе детей приучают обозначать амплитуду колебаний простой буквой “А”. Например: А=4 см, то есть амплитуда равна четырем сантиметрам.

Но уже в восьмом классе ученики изучают такое понятие, как механическая работа, и именно она в физике обозначается буквой “А”. Ученики начинают путаться в этих значениях, и к 10-11-у классу не имеют четкого представления о том, как обозначается амплитуда колебаний в физике.

В случае с пружинными и математическими маятниками лучше всего записывать амплитуду через максимальные значения. То есть Хмакс. означает максимальное отклонения от положения равновесия. Например Хмакс.=10 см, то есть пружина, как вариант, растянется максимум на 10 см. Это и будет амплитудой колебаний.

В 11-м классе выпускники изучают электромагнитные колебания. И там встречаются колебания заряда, напряжения и силы тока. Для того чтобы записать амплитуду напряжения, принято обозначать ее как максимальное значение. Для заряда и прочих величин соответственно.

Как найти амплитуду колебаний?

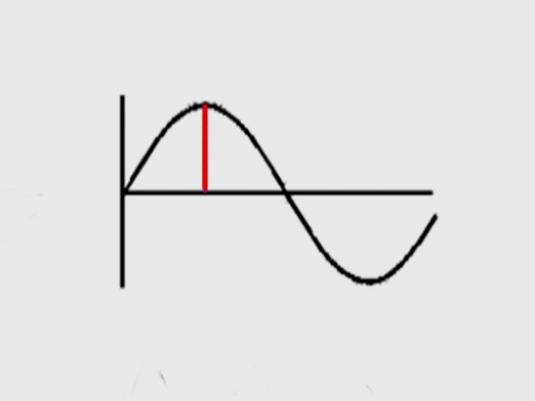
Обычно в задачах на нахождение амплитуды представлен график, подобный тому, что нарисован на картинке выше. В таком случае амплитудой будет являться максимальное значение по вертикальной оси Y. Амплитуда показано красной чертой.

Например, на данном рисунке изображен график колебаний математического маятника.

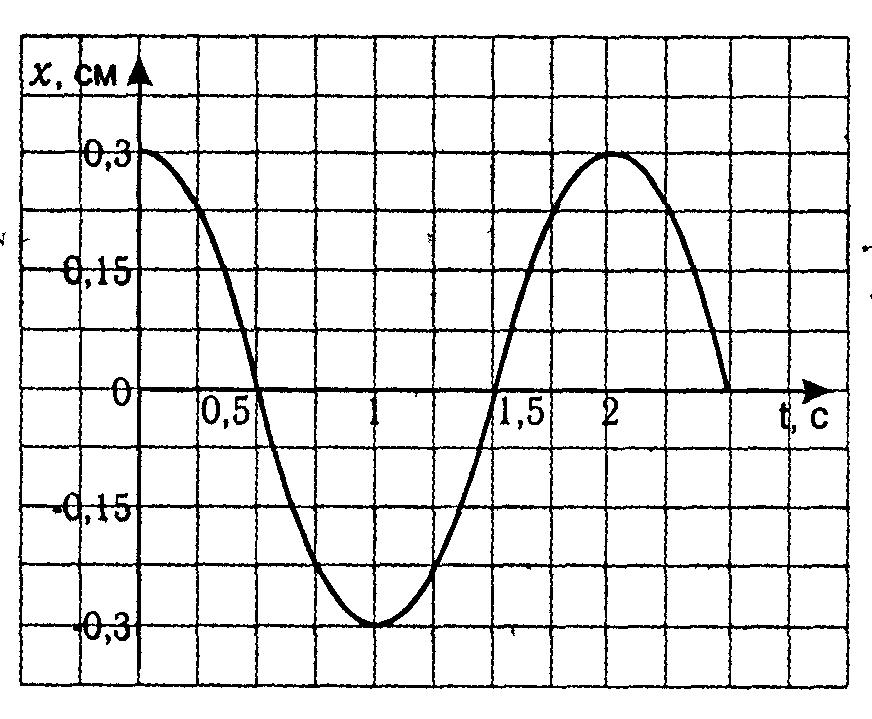
Зная, что амплитуда колебаний математического маятника – это максимальное удаление от положение равновесия, можем определить, что максимальное значение Х=0,3 см.

Найти амплитуду с помощью вычислений можно следующими способами:

1. Если груз совершает гармонические колебания и в задаче известны путь, который проходит тело, и количество колебаний, то амплитуда находится как отношение пути к количеству колебаний, умноженному на 4.

2. Если в задаче дан математический маятник, то при известных максимальной скорости и длине нити можно найти амплитуду, которая будет равна произведению максимальной скорости на квадратный корень из отношения длины к ускорению свободного падения. Эта формула похожа на формулу периода математического маятника.

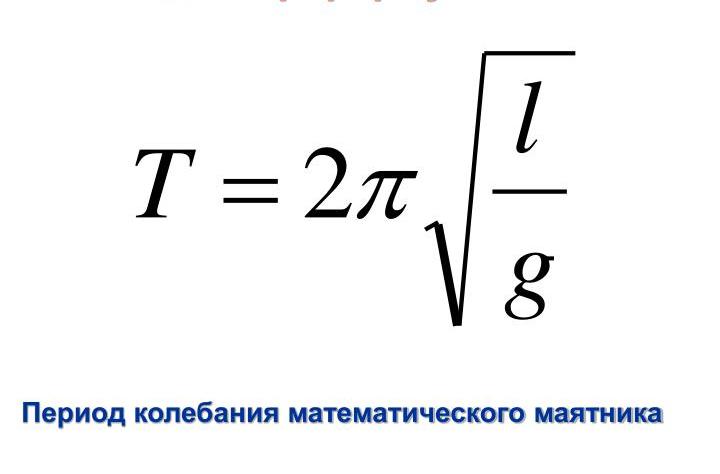
Только вместо 2п используется максимальная скорость.

В уравнениях же амплитудой является все то, что записано до косинуса, синуса или переменной омеги.

Заключение

В этой статье было сказано о том, как обозначается амплитуда колебаний и как она находится. Данная тема является лишь малой долей большого раздела колебательных процессов, но это не снижает ее важности. Ведь не понимая, что такое амплитуда, невозможно работать с графиками правильно и решать уравнения.