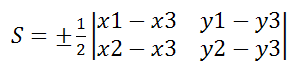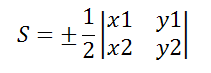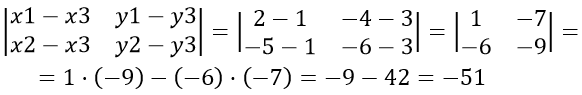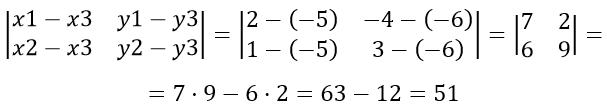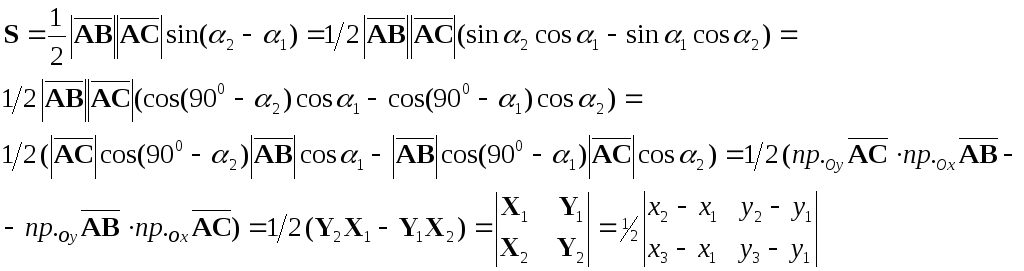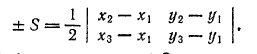Аналитическая геометрия как найти площадь треугольника

Площадь треугольника на плоскости

Пусть точки A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) – вершины треугольника, тогда площадь треугольника выражается формулой

В формуле правая сторона — это определитель второго порядка.

Площадь треугольника является положительной величиной и поэтому перед определителем берём знак «плюс», в случае, если значение положительно, и минус в противном случае, то есть отрицательно.

Примечание
Если вершина C треугольника совпадает с началом координат, то есть x₃=y₃=0, то формула площади треугольника примет вид

Пример
Найти площадь треугольника с вершинами A(2;-4), B(-5;-6) и C(1;3)

Решение
Пусть примем A за первую вершину, B — за вторую и C — за третью, тогда находим:

,так как получился отрицательный знак, следовательно перед определителем берём знак «минус»

[S = ( — frac<1><2>)cdot( — 51) = 25,5]

Если вершины треугольника переобозначим немного в другом порядке, допустим, первой вершиной A, второй вершиной C и третьей вершиной B, тогда получим выражение:

В этом случае, необходимо взять знак « плюс « и получим снова площадь треугольника S=25,5

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.5 / 5. Количество оценок: 2

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Онлайн калькулятор. Площадь треугольника построенного на векторах.

Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал.

Калькулятор для вычисления площади треугольника построенного на векторах

Выберите каким образом задается треугольник:

Введите значения векторов: Введите координаты точек:

Инструкция использования калькулятора для вычисления площади треугольника построенного на векторах

Ввод данных в калькулятор для вычисления площади треугольника построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Теория. Площадь треугольника построенного на векторах

Определение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://www.matburo.ru/ex_ag.php?p1=agtr

http://ru.onlinemschool.com/math/assistance/vector/triangle_area/

[/spoiler]

Треугольник
– одна из самых распространенных фигур
и надо уметь вычислять площадь треугольника
средствами аналитической геометрии.

Пусть
даны вершины треугольника А(х₁,
у₁),
В(х₂,
у₂),
С(х₃,у₃).
Надо найти формулу, которая бы выражала
площадь S
треугольника АВС
через координаты его вершин.

О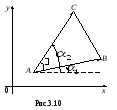бозначим
стороныАВ
и АС
треугольника как векторы, имеющие общее
начало в точке А
и следующие координаты
,.
Пусть угол между вектороми осью Ох равен,
угол между вектороми осьюОх
равен
,
а угол между самими векторамииравен
(рис. 3.10).

Из
элементарной геометрии известно, что
площадь S
треугольника равна половине произведения
длин двух сторон треугольника на синус
угла между ними:
.
Если воспользуемся формулой синуса
разности двух углов и определением
проекции вектора на ось (2.2), то получим

Этот
определитель может оказаться как
положительным, так и отрицательным
(если
>),
поэтому(3.23)

Итак,
в 3-й лекции мы познакомились с некоторыми
важными понятиями аналитической
геометрии. В основе последней лежит
метод координат, введенный в науку
французским математиком и философом
Р. Декартом, а главная ее идея заключается
в возможности представлять геометрические
объекты в виде алгебраических уравнений
и переводить геометрические задачи на
язык алгебры.

Лекция 4. Введение в анализ

Обратимся теперь
к математике непрерывных величин.
Величиною будем называть все то, что
может быть выражено числом. Будем
рассматривать величины, которые
выражаются только действительными
числами: натуральными, целыми,
рациональными, иррациональными.

Величины
могут быть постоянными и переменными.
Среди постоянных будем различать
абсолютные постоянные, например,
отношение длины окружности к ее диаметру
(число );
отношение
диагонали квадрата к его стороне ()
идругие,
и постоянные в условиях данной задачи,
например, высота данной пирамиды
равна 30 см; площадь данной трапеции
равна 24 кв. см и тому подобное. Обозначать
постоянные величины будем большими и
малыми начальными
буквами латинского алфавита: А, В, С, …,
а, b,
с, …

Переменная
величина – величина, которая принимает
различные числовые
значения. Например, температура воздуха
в каждой точке пространства
меняется в течение суток, проходя
бесконечное множество значений
от наименьшего до наибольшего. Переменные
величины будем обозначать конечными
буквами латинского алфавита X,
Y,
Z,
…
, х, у, z,
…

4.1. Функция

Если
каждому значению переменной величины
х,
принадлежащему
некоторой области, по определенному
правилу (закону) ставится в соответствие
одно и только одно определенное значение
другой переменной
величины у,
то
говорят, что у
является
функцией
от
х и
обозначают
так: у
= f(x),
причем х
называют
независимой переменной или аргументом,
а у
называют
зависимой переменной или функцией.
Символ f
указывает вид зависимости у
от
х.
Иногда
пишут и так у
= у(х).

Функции
могут зависеть от одного, двух, трех и
более аргументов. Например,
площадь круга зависит только от величины
радиуса, площадь прямоугольника
от двух переменных – длины и ширины,
объем параллелепипеда
– от трех переменных: длины, ширины,
высоты, цена продукта
– от многих переменных.

Основные
способы
задания функции:
табличный,
графический
и аналитический, (в виде формулы).

Различают
следующие основные
элементарные функции;

–
степенная;

–
показательная;

–
логарифмическая;

–
тригонометрические;

–
обратные
тригонометрические.

Из
этих функций при помощи арифметических
операций можно составить
множество элементарных функций. Например,
,,и т.д.

Функция
от функции вида
называетсясложной
функцией, где
является промежуточным аргументом.

Выражение
функциональной зависимости между
несколькими переменными
через вспомогательную переменную –
параметр, называется параметрической
функцией:,,где
t
– параметр. Например,
,-параметрическое
уравнение эллипса –замкнутой
симметричной относительно осей координат
кривой – равномерно растянутой
(сжатой) вдоль одной из осей координат
окружности.

Соседние файлы в папке математика

• #
• #
• #
• #
• #
• #

Каковы бы ни были три точки А(х₁; y₁), B(x₂; у₂) и С(x₃; у₃) площадь S треугольника ABC дается формулой

Правая часть этой формулы равна +S в том случае, когда кратчайший поворот отрезка АB к отрезку АC положителен, и -S в том случае, когда такой поворот отрицателен.

116. Вычислить площадь треугольника, вершинами которого являются точки: 1) А(2; -3), B(3; 2) и С(-2; 5); 2) М₁(-З; 2), М₂(5; -2) и М₃( 1; 3); 3) М(3; -4), N(-2; 3) и Р(4; 5).

117. Вершины треугольника суть точки A(3; 6), B( – 1; 3) и С(2; -1). Вычислить длину его высоты, проведенной из вершины С.

118. Определить площадь параллелограмма, три вершины которого суть точки А (-2; 3), 5(4; -5) и С(-3; 1).

119. Три вершины параллелограмма суть точки A(3; 7), B(2; -3) и С(- 1; 4). Вычислить длину его высоты, опущенной из вершины B на сторону АС.

120. Даны последовательные вершины однородной четырехугольной пластинки A(2; 1), B(5; 3), С(- 1; 7) и D(-7; 5). Определить координаты ее центра тяжести.

121. Даны последовательные вершины однородной пятиугольной пластинки A(2; 3), B(0; 6), С(-1; 5), D(0; 1) и E(1; 1). Определить координаты ее центра тяжести.

122. Площадь треугольника S = 3, две его вершины суть точки A(3; 1) и B(1; -3), а третья вершина С лежит на оси Оу. Определить координаты вершины С.

123. Площадь треугольника S = 4, две его вершины суть точки A(2; 1) и B(3; -2), а третья вершина С лежит на оси Ох. Определить координаты вершины С.

124. Площадь треугольника S = 3, две его вершины суть точки A(3; 1) и B(1; -3), центр тяжести этого треугольника лежит на оси Ох. Определить координаты третьей вершины С.

125. Площадь параллелограмма S = 12 кв. ед.; две его вершины суть точки А(-1; 3) и B(-2; 4). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси абсцисс.

126. Площадь параллелограмма S = 17 кв. ед.;- две его вершины суть точки A(2; 1) и B(5; -3). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси ординат.

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Другие решения по аналитической геометрии на плоскости

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.