Арифметическая прогрессия как найти шаг - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Прогрессия.

Арифмети́ческая прогре́ссия — числовая последовательность вида

${displaystyle a_{1}, a_{1}+d, a_{1}+2d, ldots , a_{1}+(n-1)d, ldots ,}$

то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага, или разности прогрессии):

${displaystyle a_{n}=a_{n-1}+d.}$ ^[1]

Любой член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому, т. е. он выражается формулой^[2]:

${displaystyle a_{n}=a_{1}+(n-1)d.}$

Арифметическая прогрессия является монотонной последовательностью. При d>0 она является возрастающей, а при d<0 — убывающей. Если d=0 , то последовательность будет стационарной. Эти утверждения следуют из соотношения $a_{n+1}-a_n=d$ для членов арифметической прогрессии.

Свойства[править | править код]

Общий член арифметической прогрессии[править | править код]

Член арифметической прогрессии с номером может быть найден по формулам

${displaystyle a_{n}=a_{m}-(m-n)d}$

где $a_{1}$

— первый член прогрессии,

— её разность, a_m

— член арифметической прогрессии с номером

Доказательство формулы общего члена арифметической прогрессии

Пользуясь соотношением $a_{n+1}=a_n+d$ выписываем последовательно несколько членов прогрессии, а именно:

Заметив закономерность, делаем предположение, что . С помощью математической индукции покажем, что предположение верно для всех :

База индукции (n=1) :

— утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при n=k , то есть . Докажем истинность утверждения при n=k+1 :

$a_{k+1}=a_k+d=a_1+(k-1)d+d=a_1+kd$

Итак, утверждение верно и при n=k+1 . Это значит, что для всех .■

Отметим, что в формулах общего члена -й член прогрессии есть линейная функция. Об этом говорит следующая теорема.

Для того чтобы последовательность ${displaystyle left{a_{n}right}}$ являлась арифметической прогрессией, необходимо и достаточно, чтобы являлась линейной функцией (от )^[3].

Доказательство

Необходимость. Пусть ${displaystyle left{a_{n}right}}$ арифметическая прогрессия. Тогда, как было уже показано, , то есть ${displaystyle a_{n}=nd+a_{1}-d}$ . Так как есть линейная функция и , это значит, что и ${displaystyle b=a_{1}-d}$ , т. е. a_n — линейная функция, где ${displaystyle fleft(nright)=nd+a_{1}-d}$ .

Достаточность. Пусть a_n есть линейная функция, т. е. ${displaystyle a_{n}=acdot x+b}$ . Так как и , то ${displaystyle a_{n}=acdot n+b}$ , тогда ${displaystyle a_{n+1}=acdot left(n+1right)+b}$ .
Рассмотрим ${displaystyle a_{n+1}-a_{n}=left(acdot left(n+1right)+bright)-left(an+bright)}$ .
Отсюда следует, что ${displaystyle a_{n+1}-a_{n}=a}$ , где — величина постоянная. Тогда ${displaystyle a_{n+1}=a_{n}+a}$ , а это значит по определению, что ${displaystyle left{a_{n}right}}$ — арифметическая прогрессия.■

Суммы членов арифметической прогрессии с равными суммами номеров равны, т. е. ${displaystyle a_{n}+a_{m}=a_{k}+a_{l}Longleftrightarrow n+m=k+lquad vert ;forall left(n,,m,,k,,lin mathbb {N} right)}$ .

Характеристическое свойство арифметической прогрессии[править | править код]

Последовательность есть арифметическая прогрессия для любого её элемента выполняется условие

${displaystyle a_{n}={dfrac {a_{n-1}+a_{n+1}}{2}},ngeqslant 2.}$

Доказательство характеристического свойства арифметической прогрессии

Необходимость.

Поскольку — арифметическая прогрессия, то для выполняются соотношения:

$a_n=a_{n-1}+d$

$a_n=a_{n+1}-d$ .

Сложив эти равенства и разделив обе части на 2, получим ${displaystyle a_{n}={dfrac {a_{n-1}+a_{n+1}}{2}}}$ .

Достаточность.

Имеем, что для каждого элемента последовательности, начиная со второго, выполняется $a_n=frac{a_{n-1}+a_{n+1}}2$ . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду $a_{n+1}-a_n=a_n-a_{n-1}$ . Поскольку соотношения верны при всех , с помощью математической индукции покажем, что $a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n$ .

База индукции (n=2) :

— утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при n=k , то есть $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k$ . Докажем истинность утверждения при n=k+1 :

$a_{k+1}-a_{k}=a_{k+2}-a_{k+1}$

Но по предположению индукции следует, что $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k$ . Получаем, что $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k=a_{k+2}-a_{k+1}$

Итак, утверждение верно и при n=k+1 . Это значит, что $a_n=frac{a_{n-1}+a_{n+1}}2, n geqslant 2 Rightarrow a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n$ .

Обозначим эти разности через . Итак, $a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n=d$ , а отсюда имеем $a_{n+1}=a_n+d$ для . Поскольку для членов последовательности выполняется соотношение $a_{n+1}=a_n+d$ , то это есть арифметическая прогрессия.■

Тождество арифметической прогрессии[править | править код]

Пусть ${displaystyle a_{k},a_{l},a_{m}}$ — соответственно -й, -й, -й члены арифметической прогрессии, где . Тогда для всякой такой тройки выполняется комплементарное свойство арифметической прогрессии^{[нет в источнике]}, называемое тождеством арифметической прогрессии:

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0.}$

Доказательство тождества арифметической прогрессии

С помощью формулы общего члена выразим -й, -й, -й члены:

${displaystyle a_{k}=a_{1}+(k-1)d,quad a_{l}=a_{1}+(l-1)d,quad a_{m}=a_{1}+(m-1)d.}$

Вычитая почленно из первого равенства второе, а из второго третьего, получим:

${displaystyle a_{k}-a_{l}=(k-l)d,quad a_{l}-a_{m}=(l-m)d.}$

Выражая из этих равенств и приравнивая полученные выражения, получим:

${displaystyle {dfrac {a_{k}-a_{l}}{k-l}}={dfrac {a_{l}-a_{m}}{l-m}}.}$

По основному свойству пропорции:

${displaystyle (l-m)(a_{k}-a_{l})=(k-l)(a_{l}-a_{m}).}$

Откуда следует доказываемое тождество:

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0.}$

■

Следствие 1. Всякий член арифметической прогрессии вырази́м^[5] через любую пару других членов.

Доказательство

Преобразовав тождество арифметической прогрессии

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0}$

к виду

${displaystyle a_{m}={dfrac {(l-m)a_{k}+(m-k)a_{l}}{l-k}},}$

можно заметить, что -й член есть линейная комбинация двух других членов ( $a_{{k}}$ и ${displaystyle a_{l}}$ ), поскольку оно равносильно

${displaystyle a_{m}={dfrac {l-m}{l-k}}a_{k}+{dfrac {m-k}{l-k}}a_{l}.}$

■

Следствие 2. Для того, чтобы число ${displaystyle a_{m}}$ являлось членом данной арифметической прогрессии с членами $a_{{k}}$ и ${displaystyle a_{l}}$ , необходимо и достаточно, чтобы было натуральным число

${displaystyle m={dfrac {(a_{l}-a_{m})k+(a_{m}-a_{k})l}{a_{l}-a_{k}}}.}$

Формулировка ещё одного признака арифметической прогрессии.

Следствие 3 [критерий]. Числовая последовательность является арифметической прогрессией в том и только в том случае, если выполняется тождество арифметической прогрессии для всех членов данной последовательности. Другими словами, чтобы каждый член был вырази́м через любую пару остальных членов последовательности.

${displaystyle left{a_{n}right}~-~div Longleftrightarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} .}$

Доказательство

Необходимость. Утверждение

${displaystyle left{a_{n}right}~-~div Rightarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} }$

очевидно (см. доказательство тождества арифметической прогрессии).

Достаточность. Докажем, что

${displaystyle left{a_{n}right}~-~div Leftarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} .}$

Равенство

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0}$

можно преобразовать к виду

${displaystyle (l-m)(a_{k}-a_{l})=(k-l)(a_{l}-a_{m}).}$

Если все три номера различны, тогда

${displaystyle {dfrac {a_{k}-a_{l}}{k-l}}={dfrac {a_{l}-a_{m}}{l-m}}.}$

Обозначим выражение, например, в левой части равенства за , то есть

${displaystyle d={dfrac {a_{k}-a_{l}}{k-l}}.}$

Откуда можно прийти к следующему предложению:

${displaystyle a_{k}=a_{l}+{left(k-lright)}d.}$

Наконец, методом математической индукции, например, по нетрудно убедиться, что данное соотношение описывает именно арифметическую прогрессию.

Действительно, при l=1 (база индукции) получаем формулу общего члена арифметической прогрессии:

${displaystyle a_{k}=a_{1}+{left(k-1right)}d.}$

Предположим истинность утверждения (для ): формула ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ характеризует арифметическую прогрессию. Тогда покажем, что и при l+1 формула верна для арифметической прогрессии (переход, или шаг, индукции). Рассмотрим левую часть формулы

${displaystyle a_{k}=a_{l+1}+{left(k-left(l+1right)right)}d.}$

По предположению индукции ( ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ ) заменим $a_{k}$ на выражение ${displaystyle a_{l}+{left(k-lright)}d}$ . Итак, получим следующее:

${displaystyle a_{l}+{left(k-lright)}d=a_{l+1}+{left(k-left(l+1right)right)}d.}$

Методом тождественных преобразований имеем равносильное предложение

${displaystyle a_{l+1}=a_{l}+d.}$

А это, в свою очередь, рекуррентное соотношение для арифметической прогрессии.

Значит, по принципу математической индукции можно утвердать, что для всякого соотношение ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ верно только и только для членов арифметической прогрессии.

Аналогичные рассуждения проводятся для формулы ${displaystyle d={dfrac {a_{l}-a_{m}}{l-m}}}$ .

Данное следствие целиком и полностью считается доказанным.■

Сумма первых n членов арифметической прогрессии[править | править код]

Сумма первых членов арифметической прогрессии ${displaystyle S_{n}=sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+ldots +a_{n}}$ может быть найдена по формулам

${displaystyle S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$

, где $a_{1}$

— первый член прогрессии, a_n

— член с номером

— количество суммируемых членов.

${displaystyle S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot ({dfrac {a_{n}-a_{1}}{a_{2}-a_{1}}}+1)}$

— где $a_{1}$

— первый член прогрессии, $a_{2}$

— второй член прогрессии ${displaystyle ,a_{n}}$

— член с номером

${displaystyle S_{n}={dfrac {2a_{1}+d(n-1)}{2}}cdot n}$

, где $a_{1}$

— первый член прогрессии,

— разность прогрессии,

— количество суммируемых членов.

${displaystyle S_{n}=a_{frac {n+1}{2}}cdot n}$

, если

— нечётное натуральное число.

Доказательство
Запишем сумму двумя способами: $S_n=a_1+a_2+a_3+ ldots +a_{n-2}+a_{n-1}+a_n$ $S_n=a_n+a_{n-1}+a_{n-2}+ ldots +a_3+a_2+a_1$ — та же сумма, только слагаемые идут в обратном порядке. Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали: $2S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+ ldots +(a_{n-2}+a_3)+(a_{n-1}+a_2)+(a_n+a_1)$ Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде $a_i+a_{n-i+1}, i=1,2,ldots,n$ . Воспользуемся формулой общего члена арифметической прогрессии: $a_i+a_{n-i+1}=a_1+(i-1)d+a_1+(n-i+1-1)d=2a_1+(n-1)d, i=1,2,ldots,n$ Получили, что каждое слагаемое не зависит от и равно . В частности, . Поскольку таких слагаемых , то ${displaystyle 2S_{n}=(a_{1}+a_{n})cdot nRightarrow S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$ Третья формула для суммы получается подстановкой вместо . Что и так непосредственно следует из выражения для общего члена. Замечание: Вместо в первой формуле для суммы можно взять любое из других слагаемых $a_i+a_{n-i+1}, i=2,3,ldots,n$ , так как они все равны между собой.

Доказательство

Запишем сумму двумя способами:

$S_n=a_1+a_2+a_3+ ldots +a_{n-2}+a_{n-1}+a_n$

$S_n=a_n+a_{n-1}+a_{n-2}+ ldots +a_3+a_2+a_1$ — та же сумма, только слагаемые идут в обратном порядке.

Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали:

$2S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+ ldots +(a_{n-2}+a_3)+(a_{n-1}+a_2)+(a_n+a_1)$

Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде $a_i+a_{n-i+1}, i=1,2,ldots,n$ . Воспользуемся формулой общего члена арифметической прогрессии:

$a_i+a_{n-i+1}=a_1+(i-1)d+a_1+(n-i+1-1)d=2a_1+(n-1)d, i=1,2,ldots,n$

Получили, что каждое слагаемое не зависит от и равно . В частности, . Поскольку таких слагаемых , то

${displaystyle 2S_{n}=(a_{1}+a_{n})cdot nRightarrow S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$

Третья формула для суммы получается подстановкой вместо a_1+a_n . Что и так непосредственно следует из выражения для общего члена.

Замечание:

Вместо a_1+a_n в первой формуле для суммы можно взять любое из других слагаемых $a_i+a_{n-i+1}, i=2,3,ldots,n$ , так как они все равны между собой.

Формулировка ещё одного факта: для всякой арифметической прогрессии при любом выполняется равенство:

${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n}.}$

Примечание: $S_{k}$ — сумма первых членов арифметической прогрессии.

Доказательство
1. Очевидно, что ${displaystyle {dfrac {S_{2n}}{2n}}-{dfrac {S_{n}}{n}}={dfrac {a_{1}+a_{2n}-left(a_{1}+a_{n}right)}{2}}={dfrac {a_{2n}-a_{n}}{2}},}$ или ${displaystyle S_{2n}-2S_{n}=ncdot (a_{2n}-a_{n}).}$ Прибавим к обеим частям $S_{n}$ и получим, что ${displaystyle S_{2n}-S_{n}=S_{n}+ncdot (a_{2n}-a_{n}).}$ 2. Покажем, что ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$ Это так, поскольку можно написать верное равенство: ${displaystyle {dfrac {S_{3n}}{3n}}-{dfrac {S_{n}}{n}}={dfrac {a_{3n}-a_{n}}{2}}.}$ Из него следует, что ${displaystyle {dfrac {S_{3n}}{3}}=S_{n}+{dfrac {a_{3n}-a_{n}}{2}}cdot n.}$ 3. Теперь докажем, что ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$ Перепишем последнее как ${displaystyle a_{2n}={dfrac {a_{3n}+a_{n}}{2}}.}$ Но гораздо лучше представить это равенство в виде ${displaystyle a_{2n}={dfrac {a_{2n+1}+a_{2n-1}}{2}}.}$ Видно, что это характеристическое свойство арифметической прогрессии. Значит, действительно ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$ 4. А следовательно, ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$ 5. Тем самым, ${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n},}$ что и требовалось доказать.

Доказательство

1. Очевидно, что ${displaystyle {dfrac {S_{2n}}{2n}}-{dfrac {S_{n}}{n}}={dfrac {a_{1}+a_{2n}-left(a_{1}+a_{n}right)}{2}}={dfrac {a_{2n}-a_{n}}{2}},}$ или ${displaystyle S_{2n}-2S_{n}=ncdot (a_{2n}-a_{n}).}$

Прибавим к обеим частям $S_{n}$ и получим, что ${displaystyle S_{2n}-S_{n}=S_{n}+ncdot (a_{2n}-a_{n}).}$

2. Покажем, что ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$

Это так, поскольку можно написать верное равенство:

${displaystyle {dfrac {S_{3n}}{3n}}-{dfrac {S_{n}}{n}}={dfrac {a_{3n}-a_{n}}{2}}.}$

Из него следует, что ${displaystyle {dfrac {S_{3n}}{3}}=S_{n}+{dfrac {a_{3n}-a_{n}}{2}}cdot n.}$

3. Теперь докажем, что ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$
Перепишем последнее как ${displaystyle a_{2n}={dfrac {a_{3n}+a_{n}}{2}}.}$

Но гораздо лучше представить это равенство в виде ${displaystyle a_{2n}={dfrac {a_{2n+1}+a_{2n-1}}{2}}.}$ Видно, что это характеристическое свойство арифметической прогрессии.
Значит, действительно ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$

4. А следовательно, ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$

5. Тем самым, ${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n},}$ что и требовалось доказать.

Предыдущее свойство имеет обобщение.

Для любых натуральных , , выполняется комплементарное свойство сумм:

${displaystyle {dfrac {l-m}{k}}cdot S_{k}+{dfrac {m-k}{l}}cdot S_{l}+{dfrac {k-l}{m}}cdot S_{m}=0.}$

Ещё один признак арифметической прогрессии.

Для того чтобы последовательность ${displaystyle left{a_{n}right}}$ являлась арифметической прогрессией, необходимо и достаточно, чтобы сумма первых членов последовательности была функцией не выше второй степени относительно ^[6].

Сумма членов арифметической прогрессии от n-го до m-го[править | править код]

Сумма членов арифметической прогрессии с номерами от до ${displaystyle S_{m,n}=sum _{i=n}^{m}a_{i}=a_{n}+a_{n+1}+ldots +a_{m}}$ может быть найдена по формулам

${displaystyle S_{m,n}={dfrac {a_{m}+a_{n}}{2}}cdot (m-n+1)}$

, где

— член с номером

— член с номером

— количество суммируемых членов.

${displaystyle S_{m,n}={dfrac {2a_{n}+dleft(m-nright)}{2}}cdot left(m-n+1right),}$

где a_n — член с номером , — разность прогрессии, — количество суммируемых членов.

Произведение членов арифметической прогрессии[править | править код]

Произведением первых членов арифметической прогрессии ${displaystyle left{a_{n}right}}$ называется произведение от $a_{1}$ до a_n , то есть выражение вида ${displaystyle prod limits _{i=1}^{n}a_{i}=a_{1}cdot a_{2}cdot a_{3}cdot ldots cdot a_{n-2}cdot a_{n-1}cdot a_{n}.}$ Обозначение: $P_{n}$ .

Свойство произведения:

Число множителей-скобок ${displaystyle {left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ равно ${displaystyle {dfrac {n-1}{2}}}$ , а в самом произведении ${displaystyle a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ их составляет ${displaystyle {dfrac {n+1}{2}}}$ «штук».^[10]

Сходимость арифметической прогрессии[править | править код]

Арифметическая прогрессия расходится при dne 0 и сходится при d=0 . Причём

$lim_{nrightarrowinfty} a_n=left{ begin{matrix} +infty, d>0 \ -infty, d<0 \ a_1, d=0 end{matrix} right.$

Доказательство
Записав выражение для общего члена и исследуя предел $lim_{nrightarrowinfty} (a_1+(n-1)d)$ , получаем искомый результат.

Связь между арифметической и геометрической прогрессиями[править | править код]

Пусть — арифметическая прогрессия с разностью и число a>0 . Тогда последовательность вида $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ есть геометрическая прогрессия со знаменателем a^d .

Доказательство
Проверим характеристическое свойство для образованной геометрической прогрессии: $sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}= a^{a_n}, ngeqslant 2$ Воспользуемся выражением для общего члена арифметической прогрессии: $sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}=sqrt{a^{a_1+(n-2)d}cdot a^{a_1+nd}}=sqrt{a^{2a_1+2(n-1)d}}=sqrt{(a^{a_1+(n-1)d})^2}=a^{a_1+(n-1)d}=a^{a_n}, ngeqslant 2$ Итак, поскольку характеристическое свойство выполняется, то $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения $q=frac{a^{a_2}}{a^{a_1}}=frac{a^{a_1+d}}{a^{a_1}}=a^d$ .

Доказательство

Проверим характеристическое свойство для образованной геометрической прогрессии:

$sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}= a^{a_n}, ngeqslant 2$

Воспользуемся выражением для общего члена арифметической прогрессии:

$sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}=sqrt{a^{a_1+(n-2)d}cdot a^{a_1+nd}}=sqrt{a^{2a_1+2(n-1)d}}=sqrt{(a^{a_1+(n-1)d})^2}=a^{a_1+(n-1)d}=a^{a_n}, ngeqslant 2$

Итак, поскольку характеристическое свойство выполняется, то $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения $q=frac{a^{a_2}}{a^{a_1}}=frac{a^{a_1+d}}{a^{a_1}}=a^d$ .

Следствие: если последовательность положительных чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию.

Арифметические прогрессии высших порядков[править | править код]

Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

1, 4, 9, 16, 25, 36, …

разности которых образуют простую арифметическую прогрессию с разностью 2:

3, 5, 7, 9, 11, …

Треугольные числа также образуют арифметическую прогрессию второго порядка, их разности образуют простую арифметическую прогрессию

Тетраэдральные числа образуют арифметическую прогрессию третьего порядка, их разности являются треугольными числами.

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

Если $left[a_{{i}}right]_{{1}}^{{n}}$ — арифметическая прогрессия порядка , то существует многочлен $P_{{m}}(i)=c_{{m}}i^{{m}}+...+c_{{1}}i+c_{{0}}$ , такой, что для всех выполняется равенство $a_{{i}}=P_{{m}}(i)$ ^[11]

Примеры[править | править код]

${displaystyle T_{n}=sum _{i=1}^{n}i=1+2+3+ldots +n={frac {n(n+1)}{2}}}$

Формула для разности[править | править код]

Если известны два члена арифметической прогрессии, а также их номера в ней, то можно найти разность как

${displaystyle {mathit {d={frac {a_{m}-a_{n}}{m-n}}}}}$

Сумма чисел от 1 до 100[править | править код]

Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050.
Действительно, легко видеть, что решение сводится к формуле

$frac{n(n+1)}2$

то есть к формуле суммы первых чисел натурального ряда.

См. также[править | править код]

Геометрическая прогрессия
Арифметико-геометрическая прогрессия

Примечания[править | править код]

↑ Такое соотношение называют рекуррентным соотношением первого порядка. Поэтому арифметическая прогрессия есть множество последовательностей, задающихся именно таким образом.
↑ Фильчаков П. Ф. Глава II. Алгебра и элементарные функции. Функции натурального аргумента (§ 75. Арифметическая прогрессия) // Справочник по элементарной математике: для поступающих в вузы : книга / под ред. чл.-кор. АН УССР П. Ф. Фильчакова. — Киев : «Наукова думка», 1972. — С. 303. — 528 с. — 400 000 экз. — УДК 51 (08)^(G).
↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 135. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
↑ Соотношение между любыми тремя членами арифметической прогрессии и их номерами (Мусинов В. А.) // Материалы студенческой научной сессии Института математики и информатики МПГУ. 2021–2022 учебный год : сборник статей / под общ. ред. Е. С. Крупицына. — М.: МПГУ, 2022. — С. 91—93. — 156 с. — ISBN 978-5-4263-1109-1, ББК 22.1я431+32.81я431+22.1р30я431+74.262.21я431+74.263.2я431.
↑ Это означает, что выражаемый член есть комбинация любых двух других членов данной последовательности, причём эта комбинация составлена с помощью арифметических операций и конечного набора символов. Для арифметической последовательности такая комбинация будет линейной.
↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 141. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
↑ Из доказательства необходимости следует, что ${displaystyle S_{n}=an^{2}+bn}$ , поэтому, если ${displaystyle S_{n}=an^{2}+bn+c}$ , то необходимо сделать проверку. Например, если ${displaystyle S_{n}=2n^{2}-n-6}$ — сумма первых членов последовательности, то такая последовательность НЕ является арифметической прогрессией. А последовательность, заданная суммой ${displaystyle S_{n}=2n^{2}-n}$ первых членов, будет арифметической прогрессией.
↑ При произведение $P_{n}$ равно ${displaystyle a_{frac {1+1}{2}}=a_{1}}$ , что безусловно верно.
↑ Эту формулу удобно использовать для выполнения итераций в программном коде, так как результат зависит от значения только двух величин: постоянного числа — разности, и члена, стоящего ровно по середине между первым и -м членом.
↑ Пример применения формулы.
Пусть ${displaystyle div left{a_{n}right}:quad underbrace {27} _{a_{1}},;underbrace {20} _{a_{2}},;underbrace {13} _{a_{3}},;underbrace {6} _{a_{4}},;underbrace {-1} _{a_{5}}}$ , где .

По формуле ${displaystyle P_{n}=a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ найдём произведение пяти первых членов. Количество сомножителей должно равняться ${displaystyle {dfrac {5+1}{2}}=3}$ . Причём первым сомножителем будет ${displaystyle a_{frac {5+1}{2}}=a_{3}=13}$ .

Далее ${displaystyle prod limits _{i=1}^{frac {5-1}{2}}{left(a_{frac {5+1}{2}}^{2}-{left[idright]}^{2}right)}=prod limits _{i=1}^{2}{left(a_{3}^{2}-{left[idright]}^{2}right)}=}$ ${displaystyle ={left(a_{3}^{2}-{left[dright]}^{2}right)}cdot {left(a_{3}^{2}-{left[2dright]}^{2}right)}={left(169-49right)}cdot {left(169-4cdot 49right)}=}$ .

Наконец, ${displaystyle P_{n}=13cdot 120cdot {left(-27right)}=-42120}$ .
↑ Бронштейн, 1986, с. 139.

Литература[править | править код]

Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1986. — 544 с.

Ссылки[править | править код]

Арифметическая прогрессия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890. — Т. II. — С. 98.

Источник

Вопрос, как решать арифметическую прогрессию, ставит поначалу в тупик многих учеников. Быть может, это происходит от того, что кажется сложным само название, а может, оттого, что формулы арифметической прогрессии выглядят устрашающе.

На самом деле, арифметическую прогрессию решать совсем несложно, если хорошо понять, что это такое.

А суть арифметической прогрессии состоит в том, что каждый последующий член прогрессии равен сумме предыдущего с неким постоянным числом. Математически это можно выразить формулой:

Эта формула позволяет найти любой член арифметической прогрессии.

Давайте проверим. Допустим, число d, которое называется разностью арифметической прогрессии, равно 3.

А первое число прогрессии равно 1. Тогда 4-й член арифметической прогрессии равен:

a4= 1 + 3(4-1)= 10

Давайте проверим, просто суммируя каждый член прогрессии:

а2=1+3=4

а3=4+3=7

а4=7+3=10

Все сошлось.

Как видите, решать арифметическую прогрессиию несложно, если понять ее смысл.

автор вопроса выбрал этот ответ лучшим

Эления
[445K]

3 года назад

Сначала вспомним, что есть арифметическая прогрессия. Это определенная, закономерная последовательность чисел, которая поддается описанию формулой. К каждому из членов прогрессии, кроме самого первого, добавляется определенное число, одинаковое каждый раз, поэтому каждый шаг прогрессии закономерен. Каждый шаг – это добавление числа “d” к предыдущему члену прогрессии, данное число так и называют “шагом” прогрессии или еще говорят “разность” арифметической прогрессии.

Всю последовательность членов прогрессии можно обозначить следующим математическим выражением:

в этой формуле каждый последующий член представлен латинской буквой “a”. Кроме первого члена прогрессии, к каждому последующему суммируется шаг с определенным значением “d”. Таким образом, третий член прогрессии – это число “a”, к которому добавили два значения “d” или “2d”, третий шаг – “3d” и т. д.

Любое n-нное по счету число “a” можно представить следующей формулой:

Или:

Сумму всех первых членов прогрессии можно представить, как формулу:

Все сказанное можно представить:

Существует возрастающая или убывающая арифметическая прогрессия, смотря выше или ниже нуля значение шага “d”.

Посчитаем убывающую арифметическую прогрессию, если известно значение первых двух членов прогрессии. Сначала найдем “шаг” прогрессии, затем все остальные члены прогрессии, схема расчета ниже.

Кареля Топин
[182K]

9 лет назад

Арифметическая прогрессия – это ряд чисел, последующее число которого получается в результате сложения предыдущего числа и коэффициента арифметической прогрессии. Например, 2, 6, 10, 14, и т. д. Коэффициент арифметической прогрессии в данном случае равняется 4.

Галина Скулкина
[64K]

9 лет назад

Чтобы решать задачи по арифметической прогрессии, надо хорошо понять, что же это такое.

Последовательность, у которой каждый её член, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией (далее – АП).

Чаще всего в задачах подобного рода ставятся такие вопросы: нахождение первого члена АП, n-го члена, разности АП, суммы всех членов АП.

Из определения АП можно определить связь соседних членов АП

An+1=An+d, например, A5=6, а d=2, то A6=A5+d=6+2=8

При известном первом члене и разности АП находится любой её член по формуле

(An): An=A1+d(n-1)

Используя эту же формулу, можно найти первый член АП

A1=An-d(n-1)

Формула разности (при известных первом и n-ом члене АП)

d=(An-A1)/(n-1)

Сумма членов АП

Sn=(A1+An)n/2

Или, если не известен n-ый член АП, но знаем шаг d и номер n-ого члена АП

Sn=(2A1+(n-1)dn)/2

Лучше разобраться в этом вопросе поможет видеоурок

Galina7v7
[120K]

7 лет назад

Основные формулы арифметической прогрессии:1)для n-го члена прогрессии:an=a1+d(n-1),где an и a1 -1-й и n-й члены прогрессии,d-разность прогрессии,2)Сумма n членов прогрессии:Sn=(a1+an)*n2.Все остальные формулы -это следствие этих 2-х формул.В каждой задаче по известным параметрам из формул находится какой-то неизвестный параметр.Известна самая знаменитая задача с использованием арифметической прогрессии:Учитель задал задачу ученикам:Просуммировать все числа от 1 до 100.И пока все ученики старательно считали,один из учеников за минуту высчитал сумму:5050!И это был маленький Гаусс!Он догадался-как быстро сосчитать эту непростую сумму:S100=(1+100)*1002=5050!

Знаете ответ?

Источник

Как решать арифметические прогрессии

Арифметическая прогрессия – это такая последовательность, у которой каждый ее член, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом d (шагом или разностью арифметической прогрессии). Чаще всего в задачах с арифметическими прогрессиями ставятся такие вопросы, как нахождение первого члена арифметической прогрессии, n-го члена, нахождение разности арифметической прогрессии, суммы всех членов арифметической прогрессии. Рассмотрим каждый из этих вопросов более подробно.

Вам понадобится

Умение выполнять основные математические действия.

Инструкция

Из определения арифметической прогрессии следует следующая связь соседних членов арифметической прогрессии – An+1=An+d, например, A5=6, а d=2, то A6=A5+d=6+2=8.

Если известен первый член (A1) и разность (d) арифметической прогрессии, то можно найти любой ее член, использую формулу n-го члена арифметической прогрессии (An): An=A1+d(n-1). Например, пусть A1=2, d=5. Найдем, A5 и A10. A5=A1+d(5-1)=2+5(5-1)=2+5*4=2+20=22, а A10=A1+d(10-1)=2+5(10-1)=2+5*9=2+45=47.

Используя предыдущую формулу можно найти первый член арифметической прогрессии. A1 тогда будет находиться по формуле A1=An-d(n-1), то есть если предположить, что A6=27, а d=3, A1=27-3(6-1)=27-3*5=27-15=12.

Чтобы найти разность (шаг) арифметической прогрессии, необходимо знать первый и n-ый член арифметической прогрессии, зная их, разность арифметической прогрессии находится по формуле d=(An-A1)/(n-1). Например, A7=46, A1=4, тогда d=(46-4)/(7-1)=42/6=7. Если d>0, то прогрессия называется возрастающей, если d<0 – убывающей.

Сумму первых n членов арифметической прогрессии можно найти по следующей формуле. Sn=(A1+An)n/2, где Sn – сумма n членов арифметической прогрессии, A1, An – 1-ый и n-ый член арифметической прогрессии соответственно. Воспользуемся данными из предыдущего примера, тогда Sn=(4+46)7/2=50*7/2=350/2=175.

Если же n-ый член арифметической прогрессии неизвестен, но зато известен шаг арифметической прогрессии и номер n-го члена, то, чтобы найти сумму арифметической прогрессии, можно воспользоваться формулой Sn=(2A1+(n-1)dn)/2. Например, A1=5, n=15, d=3, тогда Sn=(2*5+(15-1)*3*15)/2=(10+14*45)/2=(10+630)/2=640/2=320.

Видео по теме

Обратите внимание

Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии: An=(An-1+An+1)/2.

Источники:

как решать задачи арифметической прогрессии

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.

Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

Источник

Данный калькулятор предназначен для нахождения шага или разности арифметической прогрессии онлайн.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен сумме предыдущего числа и определенного фиксированного числа. Это неизменное число называется разностью арифметической прогрессии. Другими словами, разность (шаг) арифметической прогрессии – разность между последующим и предыдущим членом.

Если разность арифметической прогрессии положительная, то такую прогрессию называют возрастающей, если же разность отрицательная, то имеет место убывающая арифметическая прогрессия.

Разность арифметической прогрессии можно вычислить по следующим формулам

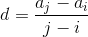
где a_i и a_j элементы прогрессии

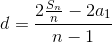
где S_n сумма n первых элементов прогрессии, a₁ – первый элемент прогрессии.

Заполните ячейки калькулятора соответствующими значениями, чтобы найти разность арифметической прогрессии онлайн.

Источник

Свойства[править | править код]

Общий член арифметической прогрессии[править | править код]

Характеристическое свойство арифметической прогрессии[править | править код]

Тождество арифметической прогрессии[править | править код]

Сумма первых n членов арифметической прогрессии[править | править код]

Сумма членов арифметической прогрессии от n-го до m-го[править | править код]

Произведение членов арифметической прогрессии[править | править код]

Сходимость арифметической прогрессии[править | править код]

Связь между арифметической и геометрической прогрессиями[править | править код]

Арифметические прогрессии высших порядков[править | править код]

Примеры[править | править код]

Формула для разности[править | править код]

Сумма чисел от 1 до 100[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Как решать арифметические прогрессии

Вам также может понравиться

Как найти 750 рублей

Как найти неизвестное слагаемое ответы

Как можно найти объем кубика

Добавить комментарий Отменить ответ