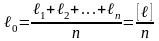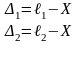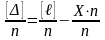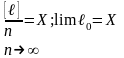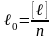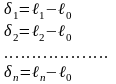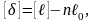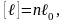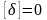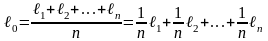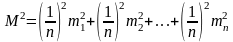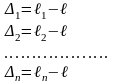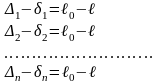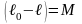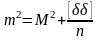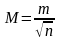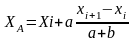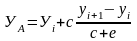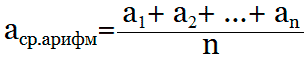Арифметическая середина как найти

Пусть
ℓ₁,
ℓ₂,…
ℓ_n
– ряд измерений некоторой величины Х.
За наилучшее приближение к значению
неизвестной величины принимают
арифметическую середину ℓ₀,
то есть среднее арифметическое значение:

.

Арифметическая
середина обладает рядом свойств, из
которых можно выделить следующие:

1-е
свойство: при неограниченном увеличении
числа измерений n
арифметическая середина ℓ₀
стремится к истинному значению Х,
то есть является наиболее вероятнейшим
значением измеряемой величины.

+

просуммируем уравнения и разделим на
n

………………

│ 0=ℓ₀–Х.

↓
0 по свойству
компенсации.

Поэтому

,

.

2-е
свойство: сумма отклонений δ_i
измеренных значений ℓ_i
от арифметической середины ℓ₀
тождественно равна нулю.

+

Это вероятнейшие случайные ошибки.

но

поэтому

.

3-е
свойство: средняя квадратическая ошибка
М
арифметической середины в

раз меньше средней квадратической
ошибки результата отдельного измерения
m.

.

Рассматривая
эту формулу как функцию общего вида,
найдем:

.

Так
как измерения равноточные и

13.5. Оценка точности ряда измерений по вероятнейшим ошибкам

Истинные
случайные ошибки ∆ обычно остаются
неизвестны. Поэтому для оценки точности
используют вероятнейшие ошибки, то есть
отклонения отдельных результатов
измерений от арифметической середины.

Составим
уравнения истинных и вероятнейших
случайных ошибок:

Ур-я
ист. сл. ош. Ур-я вероятн.
сл. ош.

,

и

где
ℓ_i
– измеренные значения; ℓ
– истинное значение измеренной величины;
ℓ₀
– арифметическая середина.

Из
первой системы вычтем вторую:

,

где
М представляет собой случайную ошибку
арифметической середины.

Перепишем
равенства:

₂

Возведем
равенства в квадрат и сложим их;

||

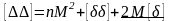
0 по второму свойству арифметической
середины.

Разделив
на n
полученное равенство, имеем:

.

Учтем,
что

.
Тогда формула Бесселя:

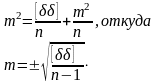
14. Задачи инженерной геодезии в строительстве

Геодезические
работы в строительстве регламентируются
следующими основными документами:

1.
СП 126.13330.2012 Геодезические работы в
строительстве. Актуализированная
редакция СНиП 3.01.03-84. В этом нормативном
документе содержатся требования к
геодезической разбивочной основе,
разбивочным работам, контролю точности
выполнения строительно-монтажных работ
и определяются условия обеспечения
точности геодезических измерений.

2.
СНиП 11-02-96 Инженерные изыскания для
строительства.

3.
СП 11-104-97 Инженерно-геодезические
изыскания для строительства.

4.
СНиП 3.03.01-87
Несущие и ограждающие конструкции.
Содержит сведения о точности выноса в
натуру и установки в проектное положение
несущих конструкций объектов.

5.
СНиП 3.02.01-87 Земляные сооружения. Основания
и фундаменты.

6.
ГОСТ 24846-2012
Грунты. Методы измерения деформаций
оснований зданий и сооружений.

В
них содержатся сведения о требованиях,
предъявляемых к инженерно-геодезическим
изысканиям: плотность пунктов
геодезической основы, методы ее создания,
требования к точности измерений и т.д.

Кроме
того, в практике производства геодезических
работ в строительстве используются
нормативные документы, ГОСТы, связанные
с применением геодезических приборов,
терминологии, технологией измерений.

Промышленное
и жилищное строительство, реконструкция
и благоустройство промышленных
предприятий и населенных мест
осуществляется по следующим стадиям:

1.
Изыскания.

2.
Проектирование.

3.
Строительство.

4.
Эксплуатация сооружения.

На
стадии изысканий геодезические работы
заключаются в получении планов или карт
территории строительства путем
топографических съемок местности
различными способами. Задача – дать
качественную топографическую основу
для проектирования строительства.

Геодезическими
работами на стадии проектирования
являются: вертикальная планировка
территории горизонтальной или вертикальной
плоскостями под строительство какого-либо
сооружения, построение продольного
профиля трассы и поперечных профилей
при проектировании сооружений линейного
типа, подготовка разбивочных данных
для выноса проекта сооружения на
местность и т.д. Все материалы проекта
планировки оформляются графически на
топографической основе в масштабах 1:5
000 – 1:10 000. К проекту прилагается
пояснительная записка.

При
строительстве крупных и сложных объектов
составляются генеральные планы на
каждый отдельный элемент: генеральный
план благоустройства, генеральный план
подземных сооружений и т.д. Генеральным
планом строительного объекта называют
основной чертеж (масштаб 1:500, 1: 2 000),
представляющий собой изображение на
бумаге границ объекта, всех зданий,
подземных, наземных и воздушных сооружений
и устройств, составляющих комплекс
проектируемого объекта, проектируемого
озеленения и сохраняющейся существующей
растительности, проектируемого вновь
и сохраняющегося естественного рельефа.
Он является неотъемлемой частью стадий
проектирования и строительства, отражает
сущность проекта и является основой
для воплощения последнего в натуре.

При
составлении генеральных планов
производится увязка существующих и
проектируемых объектов в смысле их
правильного размещения в горизонтальной
и вертикальной плоскостях. Все работы,
связанные с выявлением наиболее
рационального расположения проектируемых
объектов, их взаимной ориентировкой в
горизонтальной плоскости, отвода под
застройку участка определенных размеров,
называют горизонтальной планировкой.
В отличие от нее вертикальная планировка
есть размещение элементов строительного
объекта по высоте. Горизонтальная
планировка всегда предшествует
вертикальной, но неразрывно связана с
ней. Расчет горизонтальной планировки
может вестись либо графоаналитическим
способом (при отсутствии существующих
капитальных сооружений), либо аналитическим.
В последнем случае относительно зданий
и сооружений, положение которых в
процессе планировки площадки не
изменяется, аналитически рассчитывается
положение красных линий. Красной линией
застройки называется граница между
улицей и кварталом. Параллельно красной
линии на расстоянии 6 метров – для
магистральных улиц и 3 метров для жилых
улиц, располагается линия регулирования
застройки, за пределы которой не должны
выступать здания и сооружения. Промежуток
между красной линией и линией регулирования
застройки используется для озеленения
и прокладки подземных инженерных сетей.
В стесненных условиях эти линии совмещают.

В
натуре красные линии закрепляются
знаками, на которые передаются координаты
и абсолютная отметка. Впоследствии эти
знаки используются для выноса сооружения
в натуру.

Все
здания и сооружения на генеральном
плане, а затем и в натуре, задаются
характерными линиями, называемыми
осями. Различают три вида осей: главные,
основные и дополнительные (рис. 83).

Г₂
О₂

О₁

О₄

О₄

Д₁

Д₁

Г₁

Г₁

Д₂

Д₂

О₃

О₃

О₁

О₂

Г₂

главные
оси

основные оси

дополнительные оси

Рис.
83. Схема осей зданий и сооружений

Главные
оси– это
взаимно перпендикулярные прямые линии,
относительно которых здание или
сооружение располагается в основном
симметрично. Основные
оси – это
прямые линии, образующие внешний контур
здания или сооружения в плане. Это самый
распространенный в строительстве вид
осей. Взаимное расположение главных и
основных осей должно быть определено
с высокой точностью, так как они служат
основой детальной разбивки всего
сооружения. Дополнительные
оси – это
прямые линии, образующие очертания
частей и элементов зданий и сооружений,
оси фундаментов технологического
оборудования и др.

При
выносе осей в натуру соблюдается основной
принцип геодезических работ – переход
от общего к частному.
Разбиваются сначала главные и основные
оси, затем дополнительные, и только
потом разбивается запроектированное
здание или сооружение.

Подготовка
разбивочных данных для выноса проекта
сооружения в натуру может быть выполнена
одним из трех способов: аналитическим,
графическим и графо-аналитическим.
Рассмотрим графо-аналитический способ.

Пусть
требуется подготовить разбивочные
данные для выноса в натуру точки А
проектного сооружения (рис. 84). Вначале
определяют графически на генеральном
плане координаты точки А с учетом
деформации бумаги.

у_i
у_i+1

х_i+1

х_i+1

в

с
е

А

α_МN

а
β_N
α_NА

α_МА
β_М
α_NМ

М N

х_i
х_i

у_i
1:1 000

В 1 сантиметре 10
метров

Рис. 84. Фрагмент генерального плана

Измеряют
в сантиметрах расстояния а,
в, с, е – от
точки до линий сетки, затем выражают их
в метрах в масштабе плана и подставляют
в формулы:

;

.

Координаты
двух пунктов М
и N
строительной сетки берут в качестве
исходных и решают обратные геодезические
задачи для направлений МА,
NА,
МN.
В результате решения получают длины
(горизонтальные проложения этих
направлений) и их дирекционные углы –
α. Затем по разностям дирекционных углов
вычисляют разбивочные углы β_М
и β_N.

β_М=
α_МN–
α_МА;

β_N=
α_NА–
α_NМ.

Составляют
разбивочный чертеж в масштабе плана.
На нем подписывают все значения линейных
и угловых разбивочных данных для
вынесения проекта на местность разными
способами: прямоугольных координат,
линейных и угловых засечек, полярных
координат.

Подготовка
разбивочных данных аналитическим
способом аналогична предыдущему,
отличается тем, что все исходные данные
(в том числе проектные координаты)
имеются в проекте. При подготовке
графическим способом все разбивочные
данные получают графически с плана.
Погрешность линейных измерений составляет
при этом 0,2 мм в масштабе плана, а угловых
20′.

Стадия
строительства включает:

1.
Подготовительный период – геодезические
работы обеспечивают правильное
расположение на территории строительства
мест складирования стройматериалов и
элементов конструкций, временных сетей
водопровода, освещения и т.д.

2.
Начальный период (нулевой цикл) заключается
в перенесении осей сооружения в натуру,
контроль за возведением подземной
части.

3.
Период строительства – контроль за
соблюдением геометрических форм
сооружения, предусмотренных проектом.

4.
Завершающий период – исполнительные
съемки.

Геодезические
работы начинают с выноса проекта
сооружения в натуру, то есть на местность.
Такие работы называют разбивочными.

Соседние файлы в папке Учебники и пособия

• #
• #
• #
• #
• #
• #

Среднее арифметическое