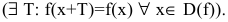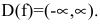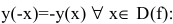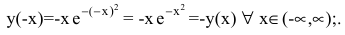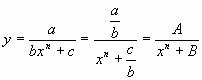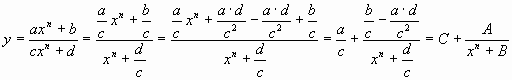Асимптоты графика функции. График дробно-линейной функции
Асимптоты графика функции. График дробно-линейной функции.
В этой статье мы рассмотрим, что такое асимптота графика функции, и как ее находить.
Асимптота – это прямая, к которой бесконечно близко приближается график функции.
Асимптоты бывают горизонтальные, вертикальные и наклонные.
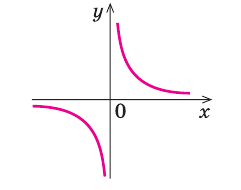
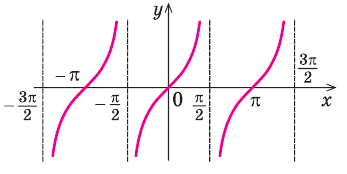
Если мы посмотрим на хорошо известный нам график функции 


В общем случае горизонтальная асимптота – это прямая, параллельная оси OX. Уравнение горизонтальной асимптоты имеет вид 




То есть 
Вертикальная асимптота – это прямая, параллельная оси OY. Уравнение вертикальной асимптоты имеет вид 




В некоторых случаях для построения графика функции бывает достаточно найти асимптоты графика.
Рассмотрим дробно-линейную функцию. В общем виде уравнение дробно-линейной функции имеет вид: 
График дробно-линейной функции – это гипербола. Как мы знаем, гипербола имеет две асимптоты: горизонтальную и вертикальную.
Заметим, что при 


Степень 





График дробно-линейной функции 
Для этого достаточно найти точки пересечения графика с осями координат.
Точка пересечения с осью OX (y=o): 
Точка пересечения с осью OY (x=0): 
Построим график функции 
Найдем горизонтальную и вертикальную асимптоты.
Уравнение горизонтальной асимптоты: 
уравнение вертикальной асимптоты (ноль знаменателя):
Найдем точки пересечения с осями координат:
С осью ОХ: 
с осью OY(x=0): 
То есть график функции 
И, наконец, наклонная асимптота. Наклонная асимптота – это к прямая, к кторой стремится график функции на бесконечности.
Уравнение наклонной асимптоты имеет вид 
Коэффициенты 

Найдем асимптоты графика функции
1. Начнем с области определения функции. Функция 


2. Степень числителя дроби 


3. Попробуем найти наклонную асимптоту.
(Предел функции равен отношению коэффициентов при максимальных степенях 


Итак, уравнение наклонной асимптоты:
График функции 
И.В. Фельдман, репетитор по математике.
Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты

Вертикальная асимптота 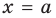
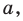
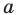
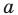
Примеры вертикальных асимптот графиков функций
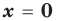
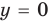
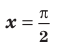
Наклонные и горизонтальные асимптоты
I. Если 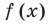
Примеры:
При 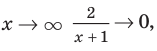
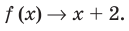
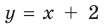
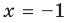
При 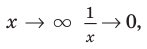
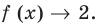
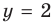
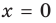
II. В общем случае уравнения наклонных и горизонтальных асимптот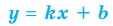
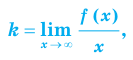
Понятие асимптоты
Если кривая 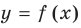
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
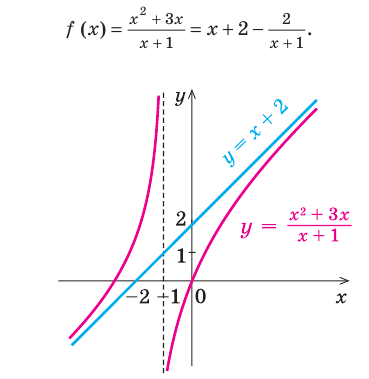
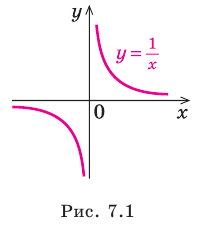
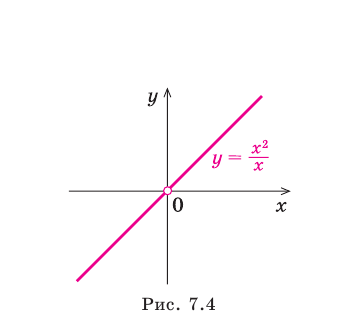
Например, для графика функции 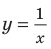
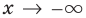
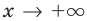
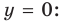
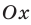
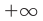
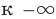
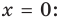
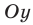
Если рассмотреть функцию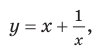
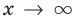
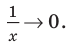
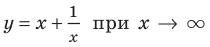
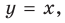
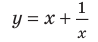
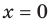
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая 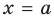
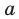

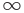
Например, у функции 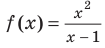
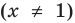

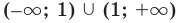

Аналогично
Таким образом, прямая 

Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция 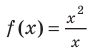
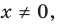
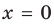
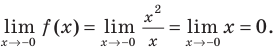
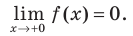
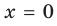
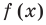
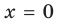
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
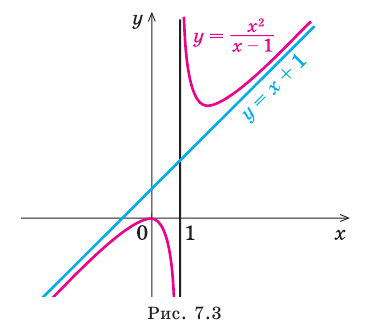
Например, еще раз рассмотрим функцию 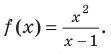
При 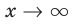
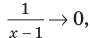
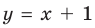
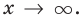
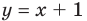
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции 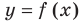

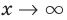
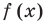
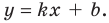
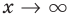
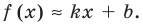
Эта равенство не нарушится, если обе его части разделить на 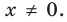
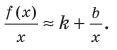
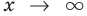
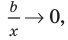
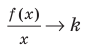
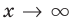
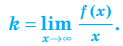
Возвращаясь к формуле (1), получаем, что при 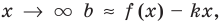
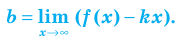
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции 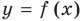
Отметим, что если у графика функции 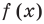
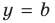
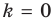
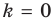
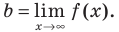
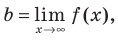
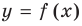
- Заказать решение задач по высшей математике
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции
Решение:
Будем искать наклонную асимптоту в виде 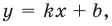
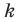
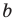
Асимптотой графика данной функции будет прямая 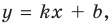
Пример:
Найдите асимптоты графика функции
Решение:
Область определения функции: 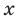
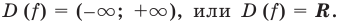
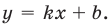
Таким образом, заданная функция имеет только горизонтальную асимптоту 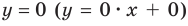
Иногда график функции 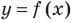
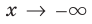
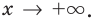
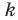
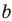
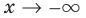
Как найти асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 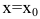
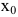
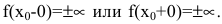
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции
Решение:
Функция 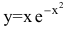
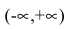
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность
нечетность
периодичность
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример:
Провести полное исследование функции 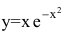
Решение:
Область определения функции – вся числовая прямая:
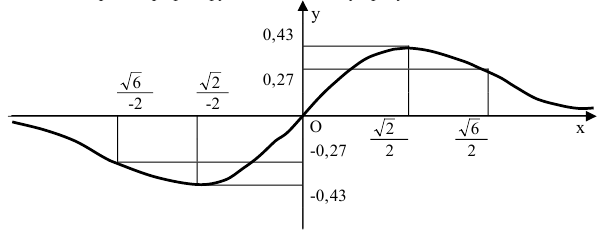
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для
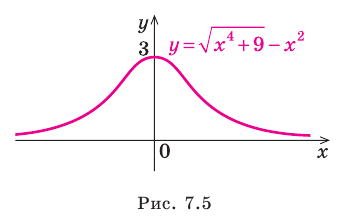
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 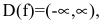
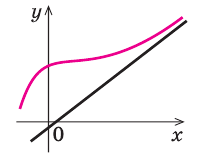
Строим график функции, используя результаты исследования.
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Иррациональные уравнения
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
Дро́бно-лине́йная фу́нкция — это числовая функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются линейные функции.
Дробно-линейная функция, отображающая в общем случае многомерное числовое пространство в одномерное числовое, представляет собой важный частный случай:
Формальное определение[править | править код]
Дробно-линейная функция — это числовая функция вида
где 






[1].
Возможно обобщение на кватернионы[2].
Вырожденные случаи[1]:
- если
-
- то дробно-линейная функция становится целой линейной функций;
- если ранг матрицы
-
- равен единице, то дробно-линейная функция вырождается в постоянную.
У собственно (невырожденной) дробно-линейной функции[1]:
- равен двум ранг матрицы
Вещественная дробно-линейная функция[править | править код]
Вещественная дробно-линейная функция — это числовая функция вида
где 




[1].
Функция одного переменного[править | править код]
В простейшем случае 
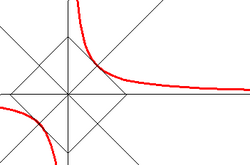
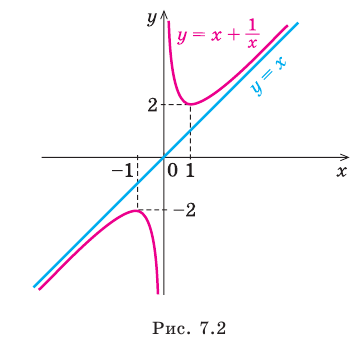
график дробно-линейной функции — равнобочная гипербола с асимптотами
и
параллельными осям координат:[1].
Асимптоты гиперболы[править | править код]
Пусть дробно-линейная функция одного переменного
несократима, то есть 


Теперь ясно, что график функции 

Таким образом, дробно-линейная функция одного переменного 



Также очевидно, что дробно-линейная функция одного переменного 
Производная
Неопределённый интеграл:
Каноническое уравнение гиперболы[править | править код]
Сначала приведём функцию
преобразованиями координат к виду
Для этого сделаем следующие замены:
получим требуемый вид функции[4].
Теперь повернём координатные оси на угол 
получим в новых координатах[4]:
Последнее уравнение есть каноническое уравнение равносторонней гиперболы с полуосями 
Функция двух переменных[править | править код]
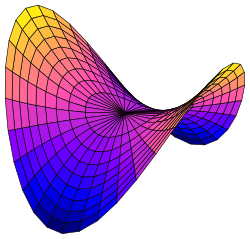
Гиперболический параболоид
В случае 








представляет собой гиперболический параболоид[1].
Комплексная дробно-линейная функция[править | править код]
Комплексная дробно-линейная функция — это числовая функция вида
где 




[1].
При 
—
аналитическая функция одной комплексной переменной всюду в расширенной комплексной плоскости 

При 
—
мероморфная функция в пространстве 

[1].
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 7 8 9 Математическая энциклопедия, т. 2, 1979, стб. 384.
- ↑ Alan F. Beardon. The geometry of discrete groups, 1983, p. 56.
- ↑ 1 2 3 Энциклопедия элементарной математики. Книга третья, 1952, с. 56—57.
- ↑ 1 2 3 Ефимов Н. В. Краткий курс аналитической геометрии, 2005, 119, с. 120.
Литература[править | править код]
- Ефимов Н. В. Краткий курс аналитической геометрии: Учебн. пособие. 13-е изд., стереот. М.: ФИЗМАТЛИТ, 2005. 238 с., ил. ISBN 5-9221-0252-4.
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д—Коо. М.: «Советская Энциклопедия», 1979. 1104 стб., ил.
- Энциклопедия элементарной математики. Книга третья. Функции и пределы (основы анализа) / Под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. М., Л.: Государственное издательство технико-теоретической литературы, 1952. 559 с., ил.
- Alan F. Beardon. The geometry of discrete groups. Berlin, Heidelberg, New York: Springer-Verlag, 1983. 337 p., 93 ill.
Дробно-рациональная функция – это такая
алгебраическая дробь, у которой числитель и
знаменатель представляют собой многочлены
некоторой степени.
Дробно-линейная функция представляет собой
частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая
алгебраическая дробь , у которой числитель и
знаменатель представляют собой линейные
функции.
Во всякой дробно-линейной функции можно
выделить целую часть.
Прямая линия называется асимптотой графика
функции, если график функции неограниченно
сближается с этой прямой при удалении точки
графика в бесконечность.
уравнение вертикальной асимптоты
уравнение горизонтальной асимптоты
уравнение наклонной асимптоты
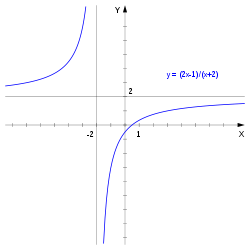
Пример 1. Построим график функции .
Преобразуем функцию с выделением целой части:
Дробно-линейная функция имеет две асимптоты:
горизонтальную и вертикальную.
горизонтальная асимптота
вертикальная асимптота, т.к.
Точки пересечения графика с осями координат:
при
, точка
при
, точка
Получаем график <Рисунок1>
Элементарная математика не располагает
средствами исследования всякой
дробно-рациональной функции общего вида. Однако
некоторые частные виды этих функций могут быть
исследованы средствами элементарной математики.
Если степень старшего члена числителя меньше
степени старшего члена знаменателя, то
рациональная алгебраическая дробь называется
правильной.
Если рациональная дробь неправильная, то
делением числителя на знаменатель можно ее
представить в виде суммы целого многочлена
(частное) и рациональной правильной дроби.
Методами элементарной математики могут быть
исследованы функции вида:
а)
б)
в)
г)
и некоторые другие.
Целая часть, полученная при делении числителя
на знаменатель, и будет либо горизонтальной
асимптотой (как в примере, разобранном выше), либо
наклонной асимптотой.
Пример 2 (стр. 141 учебника “Алгебра и начала
анализа 10-11 класс” Колмогоров А.Н.)
Построить график функции .
Преобразуем функцию с выделением целой части
1)
наклонная асимптота
2)
вертикальная асимптота
3)
функция ни четная, ни нечетная.
4) точки пересечения графика с осями координат:
при
, точка
с осью ординат график функции не пересекается,
т.к. эта ось есть асимптота.
5) ;
;
6)
7) Построим график <Рисунок2>.
Пример 3 (№295(г) учебника “Алгебра и начала
анализа 10-11 класс” Колмогоров А.Н.).
Построить график функции .
Преобразуем функцию с выделением целой части:
1)
наклонная асимптота
2)
вертикальная асимптота
3) функция ни четная, ни нечетная.
4) точки пересечения графика с осями координат:
при
, точка
с осью абсцисс график функции не пересекается,
т.к. эта ось есть асимптота.
5) ;
;
6)
7) Построим график <Рисунок3>.
Пример 4. Построить график функции .
Преобразуем функцию с выделением целой части:
1)
горизонтальная асимптота
2)
вертикальные асимптоты
3) четная, график функции симметричен
относительно оси ординат.
4) точки пересечения графика с осями координат:
при
, точка
при
, точки
и
.
5) ;
;
6)
7) Построим график <Рисунок4>.
Пример 5. Построить график функции .
Преобразуем функцию с выделением целой части:
1)
наклонная асимптота
2)
вертикальная асимптота
3) функция нечетная, график функции симметричен
относительно начала координат.
4) точки пересечения графика с осями координат:
при
, точки
и
с осью ординат график функции не пересекается.
5) ;
;
нет.
6)
7) Построим график <Рисунок5>.
Пример 6. Построить график функции .
Преобразуем функцию с выделением целой части:
1)
наклонная асимптота
2)
вертикальная асимптота
3) функция ни четная, ни нечетная.
4) точки пересечения графика с осями координат:
при
, точка
при
, точки
и
5) ;
;
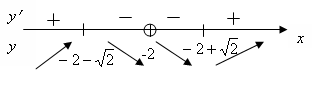
7) Построим график <Рисунок 6>.
Пример 7. Найти множество значений функции .
Преобразуем функцию с выделением целой части:
1)
горизонтальная асимптота
2)
3) функция ни четная, ни нечетная.
4) точки пересечения графика с осями координат:
при
, точка
при
, точки
и
5) 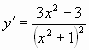
;

7) Построим график <Рисунок 7>.
Ответ:
Примеры 8–12.
(Приложение)
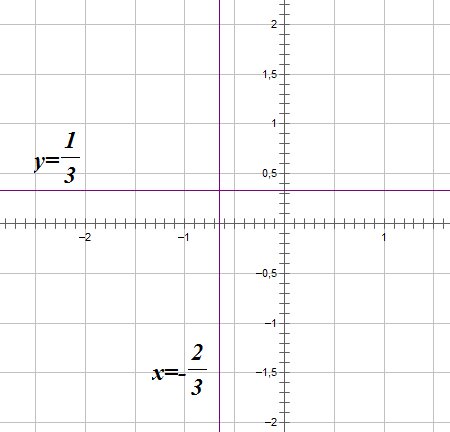
Вертикальная
асимптота.
Если выполнено
хотя бы одно из условий
,
,
то прямую
называют вертикальной асимптотой
графика функции
.
Невертикальная
асимптота.
Прямую
называют
невертикальной асимптотой графика
функции
при
,
если
.
Если
,
то асимптоту называют наклонной, а если
,
то асимптоту
называют горизонтальной.
Аналогично вводится
понятие асимптоты при
.
Для того чтобы
прямая
была асимптотой графика функции
при
,
необходимо и достаточно, чтобы существовали
конечные пределы

.
Аналогично находится
асимптота при
.
Исследование
асимптот при
и при
как правило проводят отдельно.
В некоторых частных
случаях возможно совместное исследование
асимптот при
и при
,
например, для
1) рациональных
функций;
2) четных и нечетных
функций, для графиков которых исследование
можно проводить на части области
определения.
Следует отметить,
что метод вычисления пределов для
нахождения асимптот не позволяет оценить
взаимное расположение графика функции
и его асимптоты. Для определения взаимного
положения графика и асимптоты можно
пользоваться следующими правилами.
1) Если функция
имеет асимптоту при
,
дифференцируема и строго выпукла вниз
на луче
,
то график функции лежит выше асимптоты.
2) Если функция
имеет асимптоту при
,
дифференцируема и строго выпукла вверх
на луче
,
то график функции лежит ниже асимптоты.
3) Могут быть другие
случаи поведения графика функции при
стремлении к асимптоте. Например,
возможно, что, график функции бесконечное
число раз пересекает асимптоту.
Аналогичное
утверждение справедливо и при
.
До исследования
свойств выпуклости графика функции
взаимное расположения графика функции
и его асимптоты можно определить по
знаку
в методе выделения главной части.
Метод выделения
главной части.
Для нахождения асимптоты выделяем
главную часть функции при
.
Аналогично при
.
Главную часть
дробно рациональной функции
удобно находить, выделяя целую часть
дроби.
Главную часть
иррациональной функции
при решении практических примеров
удобно находить используя методы
представления функции формулой Тейлора
при
.
Главную часть
иррациональных функций вида
и
удобно находить соответственно методом
выделения полного квадрата или полного
куба подкоренного выражения.
Примеры
5.1.
Найти асимптоты графика функции

Прямая
— вертикальная асимптота.
Наклонная асимптота.
Найдем угловой коэффициент
и свободный член
по формулам
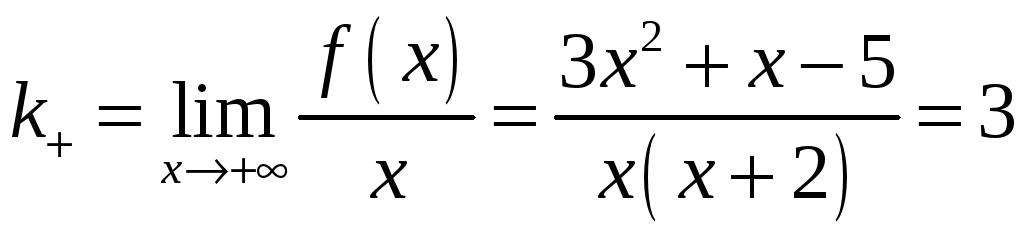
Таким образом,
прямая
— наклонная асимптота.
Найдем асимптоту
методом выделения главной части
дробно-рациональной функции. Выполняя
деление «столбиком», получаем
То есть,

Таким образом,
прямая
— наклонная асимптота.
5.2. Найти
асимптоты линии:

Вертикальных и
горизонтальных асимптот нет.
Выражая уравнение
линии в явном виде :.
Тогда

.
В итоге имеем 2
наклонных асимптоты:
.
5.3.
Найти асимптоты линии:
.
Выразим уравнение
линии в явном виде:
.
Так как

то прямая
– наклонная асимптота.
5.4. Найти
асимптоты функции:
Так как функция
не определена в точках
=
1,
то
– вертикальные асимптоты.
Найдём наклонную
асимптоту: угловой коэффициент прямой
и
число
найдём, применяя формулы:

.

Получили:
–
наклонная асимптота.
5.5. Найти
наклонную асимптоту графика функции

Так как

то по формуле
Тейлора получаем
и прямая
является искомой асимптотой. ◄
5.6. Найти
наклонные асимптоты графика функции
при
и
.
В подкоренном
выражении выделим полный квадрат
.
Так как график
функции
симметричен относительно прямой
и
то
при
.
Значит, прямая
является асимптотой при
,
а прямая
— асимптотой при
.
◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #













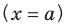
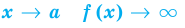
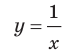
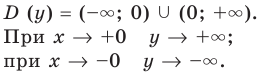
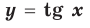
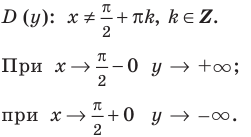
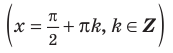
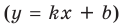
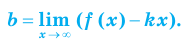
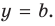
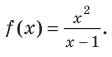
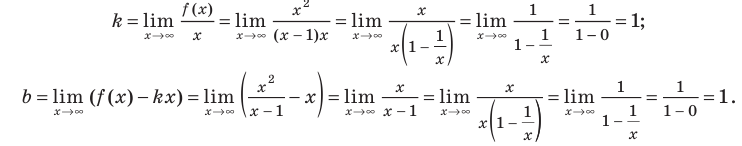
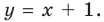
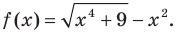
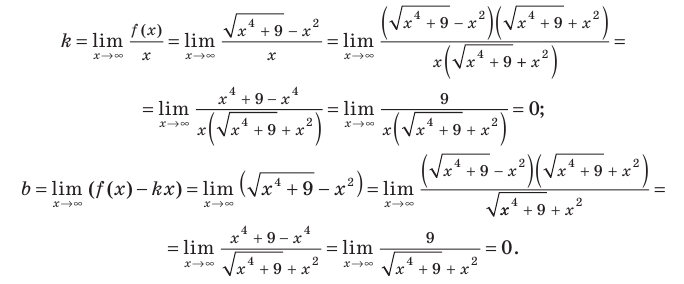
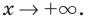
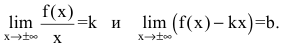
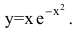
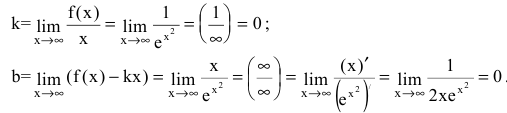
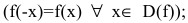 нечетность
нечетность 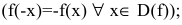 периодичность
периодичность