Бином Ньютона – формула
С натуральным n формула Бинома Ньютона принимает вид a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn, где имеем, что Cnk=(n)!(k)!·(n-k)!=n(n-1)·(n-2)·…·(n-(k-1))(k)!- биномиальные коэффициенты, где есть n по k, k=0,1,2,…,n, а “!” является знаком факториала.
В формуле сокращенного умножения a+b2=C20·a2+C21·a1·b+C22·b2=a2+2ab+b2
просматривается формула бинома Ньютона, так как при n=2 является его частным случаем.
Первая часть бинома называют разложением (a+b)n, а Сnk·an-k·bk – (k+1)-ым членом разложения, где k=0,1,2, …,n.
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
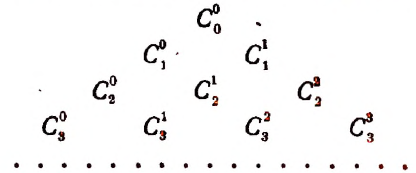
Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:
| Показатель степени | Биноминальные коэффициенты | ||||||||||
| 0 | C00 | ||||||||||
| 1 | C10 | C11 | |||||||||
| 2 | C20 | C21 | C22 | ||||||||
| 3 | C30 | C31 | C32 | C33 | |||||||
| ⋮ | … | … | … | … | … | … | … | … | … | ||
| n | Cn0 | Cn1 | … | … | … | … | … | Cnn-1 | Cnn |
При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||||
| 0 | 1 | ||||||||||||||
| 1 | 1 | 1 | |||||||||||||
| 2 | 1 | 2 | 1 | ||||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| n | Cn0 | Cn1 | … | … | … | … | … | … | … | … | … | Cnn-1 | Cnn |
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Доказательство формулы бинома Ньютона
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
- коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле Cnp=Cnn-p, где р=0, 1, 2, …, n;
- Cnp=Cnp+1=Cn+1p+1;
- биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть Cn0+Cn1+Cn2+…+Cnn=2n;
- при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.
Равенство вида a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn считается справедливым. Докажем его существование.
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
- Проверка справедливости разложения при n=3. Имеем, что
a+b3=a+ba+ba+b=a2+ab+ba+b2a+b==a2+2ab+b2a+b=a3+2a2b+ab2+a2b+2ab+b3==a3+3a2b+3ab2+b3=C30a3+C31a2b+C32ab2+C33b3 - Если неравенство верно при n-1, тогда выражение вида a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1
считается справедливым.
- Доказательство равенства a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1, основываясь на 2 пункте.
Выражению
a+bn=a+ba+bn-1==(a+b)Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1
Необходимо раскрыть скобки, тогда получимa+bn=Cn-10·an+Cn-11·an-1·b+Cn-12·an-2·b2+…+Cn-1n-2·a2·bn-2++Cn-1n-1·a·bn-1+Cn-10·an-1·b+Cn-11·an-2·b2+Cn-12·an-3·b3+…+Cn-1n-2·a·bn-1+Cn-1n-1·bn
Производим группировку слагаемых
a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1+Cn-1n-1·bn
Имеем, что Cn-10=1 и Cn0=1, тогда Cn-10=Cn0. Если Cn-1n-1=1 и Cnn=1, тогда Cn-1n-1=Cnn. При применении свойства сочетаний Cnp+Cnp+1=Cn+1p+1, получаем выражение вида
Cn-11+Cn-10=Cn1Cn-12+Cn-11=Cn2⋮Cn-1n-1+Cn-1n-2=Cnn-1
Произведем подстановку в полученное равенство. Получим, что
a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1=Cn-1n-1·bn
После чего можно переходить к биному Ньютона, тогда a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn.
Формула бинома доказана.
Бином Ньютона – применение при решении примеров и задач
Для полного понятия использования формулы рассмотрим примеры.
Разложить выражение (a+b)5 , используя формулу бинома Ньютона.
Решение
По треугольнику Паскаля с пятой степенью видно, что биноминальные коэффициенты – это 1, 5, 10, 10, 5, 1. То есть, получаем, что a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 является искомым разложением.
Ответ: a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида a+b10.
Решение
По условию имеем, что n=10, k=6-1=5. Тогда можно перейти к вычислению биномиального коэффициента:
Cnk=C105=(10)!(5)!·10-5!=(10)!(5)!·(5)!==10·9·8·7·6(5)!=10·9·8·7·61·2·3·4·5=252
Ответ: Cnk=C105=252
Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.
Доказать, что значение выражения 5n+28·n-1, при n, являющимся натуральным числом, делится на 16 без остатка.
Решение
Необходимо представить выражение в виде 5n=4+1n и воспользоваться биномом Ньютона. Тогда получим, что
5n+28·n-1=4+1n+28·n-1==Cn0·4n+Cn1·4n-1·1+…+Cnn-2·42·1n-2+Cnn-1·4·1n-1+Cnn·1n+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+n·4+1+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+32·n==16·(4n-2+Cn1·4n-3+…+Cnn-2+2·n)
Ответ: Исходя из полученного выражения, видно, что исходное выражение делится на 16.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 января 2022 года; проверки требуют 17 правок.
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
где 

В таком виде эта формула была известна ещё индийским и персидским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное действительное число (позднее она была распространена и на комплексные числа). В общем случае бином представляет собой бесконечный ряд[⇨].
Примеры:
Для быстрого разложения часто пользуются треугольником Паскаля.
Доказательство[править | править код]
Чтобы умножить скобки, нужно взять из каждой по одному слагаемому и все полученные произведения сложить. Для получения степени 











Доказательство
Докажем формулу бинома Ньютона индукцией по 
База индукции: 
Шаг индукции: Пусть утверждение для 
Тогда надо доказать утверждение для 
Начнём доказательство:
Извлечём из первой суммы слагаемое при 
Извлечём из второй суммы слагаемое при 
Теперь сложим преобразованные суммы:
Что и требовалось доказать.
■
Обобщения[править | править код]
Формула бинома Ньютона является частным случаем разложения функции 
где 
При этом ряд
сходится при 
В частности, при 

Переходя к пределу при 

которое именно таким образом было впервые получено Эйлером.
Мультиномиальная теорема[править | править код]
Бином Ньютона может быть обобщён до полинома Ньютона — возведения в степень суммы произвольного числа слагаемых:
где
суть Мультиномиальные коэффициенты. Сумма берётся по всем неотрицательным целым индексам 





Мультиномиальная теорема легко доказывается либо индукцией по 
При 

Полные полиномы Белла[править | править код]
Пусть 

История[править | править код]
Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке.
Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке, а также персидским математикам ат-Туси (XIII век) и аль-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.
Исаак Ньютон около 1665 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). На основе биномиального разложения Ньютон, а позднее Эйлер, выводили всю теорию бесконечных рядов.
В художественной литературе[править | править код]
В художественной литературе «бином Ньютона» часто фигурирует как синоним чего-то очень сложного (нередко иронически)[1]. Например, в романе «Мастер и Маргарита» М. А. Булгакова: «подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
В повести «Последнее дело Холмса» Шерлок Холмс рассказывает о профессоре Мориарти, в частности, следующее: «…когда ему исполнился 21 год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность…»
См. также[править | править код]
- Биномиальное распределение
- Биномиальный коэффициент
- Треугольник Паскаля
- Формулы сокращённого умножения многочленов — наиболее частые частные случаи бинома Ньютона
Примечания[править | править код]
- ↑ Успенский В. А. Предварение для читателей «Нового литературного обозрения» к семиотическим посланиям Андрея Николаевича Колмогорова // Новое литературное обозрение. — 1997. — № 24. Архивировано 14 июня 2011 года.
Литература[править | править код]
- Бином Ньютона // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Ньютона бином // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Произведение биномов, отличающихся только вторыми членами. Обыкновенным умножением находим:
(x+α) (x+b)=x²+ax+bx+ab=x²+(a+b) x+ab;
(x+a) (x+b) (x+c) = [x²+(a+b) x+ab] (x+c) =
= x³+(a+b) x2+abx+cx²+(ac+bc) x+abc=
= x³ + (a+b+c) x²+(ab+ac+bc) x+abc.
Подобно этому найдём:
(x+a) (х+b) (х+с) (x+d) = x⁴+(a +b+c+d) x³+
+ (ab+ac+ ad+bc+bd+cd) x²+(abc+abd+acd+bcd) x+abcd.
Рассматривая эти произведения, замечаем, что все они составлены по одному и тому же закону, а именно:
Произведение составляет многочлен, расположенный по убывающим степеням буквы х.
Показатель первого члена равен числу перемножаемых биномов; показатели при х в следующих членах убывают на 1; последний член не содержит х (содержит его в нулевой степени).
Коэффициент первого члена есть 1; коэффициент второго члена есть сумма всех вторых членов перемножаемых биномов; коэффициент третьего члена есть сумма всех произведений вторых членов, взятых по два; коэффициент четвёртого члена есть сумма всех произведений вторых членов, взятых по три. Последний член есть произведение всех вторых членов.
Докажем, что этот закон применим к произведению какого угодно числа биномов. Для этого предварительно убедимся, что если он верен для произведения m биномов:
(x+a) (x+b) (х+с) … (x+k),
то при этом предположении будет верен и для произведения (m+1) биномов:
(x+a) (x+b) (x+c) . .. (x+k) (х+l).
Итак, допустим, что верно следующее равенство:
(x+α) (x+b) (х+с)… (x+k) =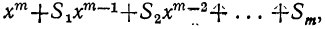
где для краткости мы положим: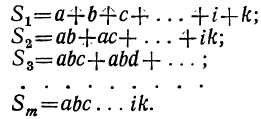
Умножим обе части допущенного равенства на бином x+l: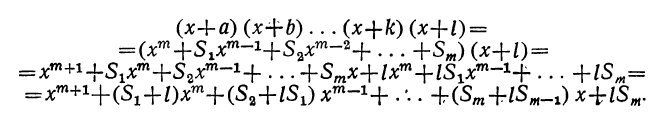
Рассматривая это новое произведение, убеждаемся, что оно подчиняется такому же закону, какой мы предположили верным для m биномов. Действительно, во-первых, этому закону следуют показатели буквы х; во-вторых, ему же следуют и коэффициенты, так как коэффициент второго члена S+l есть сумма всех вторых членов перемножаемых биномов, включая сюда и l; коэффициент третьего члена S₂+lS₁ есть сумма парных произведений всех вторых членов, включая сюда и l, и т. д.; наконец, 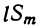 есть произведение всех вторых членов: abc… kl.
есть произведение всех вторых членов: abc… kl.
Мы видели, что закон этот верен для произведения двух, трёх и четырёх биномов; следовательно, по доказанному теперь, он должен быть верен и для произведения 4+1, т. е. для произведения пяти биномов, если же он верен для произведения пяти биномов, то он верен и для произведения 5+1, т. е. для произведения шести биномов, и т. д.
Изложенное рассуждение представляет так называемое „доказательство от m к m+1“. Оно называется также „математической индукцией» (или „совершенной индукцией»). Заметим, что в предыдущих главах этой книги неоднократно представлялся случай применить доказательство от m к m + 1 . Мы этого не делали только ради простоты изложения.

Формула бинома Ньютона
Предположим, что в доказанном нами равенстве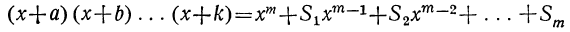
все вторые члены биномов одинаковы, т. е. что a=b=c= … =k. Тогда левая часть будет степень бинома 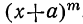 . Посмотрим, во что обратятся коэффициенты S₁, S₂, …,
. Посмотрим, во что обратятся коэффициенты S₁, S₂, …, 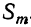 .
.
Коэффициент S₁, равный a+b+c+ … +k, обратится в та. Коэффициент S₂, равный ab+ac+ad+ …. обратится в число α², повторённое столько раз, сколько можно составить сочетаний из m элементов по 2, т. е. обратится в 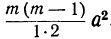 . Коэффициент S₃, равный abc+abd+…, обратится в число а³, повторённое столько раз, сколько можно составить сочетаний из т элементов по 3, т. е.
. Коэффициент S₃, равный abc+abd+…, обратится в число а³, повторённое столько раз, сколько можно составить сочетаний из т элементов по 3, т. е. 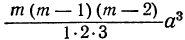 и т. д. Наконец, коэффициент
и т. д. Наконец, коэффициент 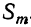 , равный abc...k, обратится в
, равный abc...k, обратится в 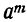 . Таким образом, мы получим:
. Таким образом, мы получим: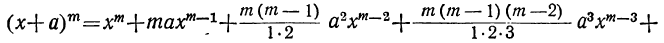
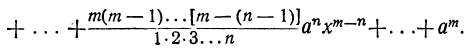
Это равенство известно как формула бинома Ньютона, причём многочлен, стоящий в правой части формулы, называется разложением бинома. Рассмотрим особенности этого многочлена.
Свойства формулы бинома Ньютона
Из этих свойств мы укажем следующие 10:
1) Показатели буквы х уменьшаются на 1 от первого члена к последнему, причём в первом члене показатель х равен показателю степени бинома, а в последнем он есть 0; наоборот, показатели буквы а увеличиваются на 1 от первого члена к последнему, причём в первом члене показатель при а есть 0; а в последнем он равен показателю степени бинома. Вследствие этого сумма показателей при х и а в каждом члене одна и та же, а именно: она равна показателю степени бинома.
2) Число всех членов разложения есть m+1, так как разложение содержит все степени а от 0 до m включительно.
3) Коэффициенты равны: у первого члена — единице, у второго члена — показателю степени бинома, у третьего члена — числу сочетаний из m элементов по 2, у четвёртого члена — числу сочетаний из m элементов по 3; вообще коэффициент (n+1)-ro члена есть число сочетаний из m элементов по n. Наконец, коэффициент последнего члена равен числу сочетаний из т элементов по m, т. е. 1.
Заметим, что эти коэффициенты называются биномиальными.
4) Обозначая каждый член разложения буквой T с цифрой внизу, указывающей номер места этого члена в разложении, т. е. первый член T₁, второй член T₂ и т. д., мы можем написать: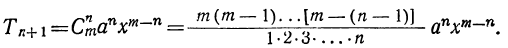
Эта формула выражает общий член разложения, так как из неё мы можем получить все члены (кроме первого), подставляя на место n числа: 1, 2, 3,…. m.
5) Коэффициент первого члена от начала разложения равен единице, коэффициент первого члена от конца тоже равен единице. Коэффициент второго члена от начала есть m, т. е. 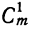 ; коэффициент второго члена от конца есть
; коэффициент второго члена от конца есть 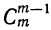 ; но так как
; но так как 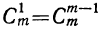 , то эти коэффициенты одинаковы. Коэффициент третьего члена от начала есть
, то эти коэффициенты одинаковы. Коэффициент третьего члена от начала есть 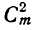 , а третьего члена от конца есть
, а третьего члена от конца есть 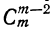 ; но
; но 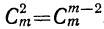 , поэтому и эти коэффициенты одинаковы и т. д. Значит:
, поэтому и эти коэффициенты одинаковы и т. д. Значит:
Коэффициенты членов, одинаково удалённых от концов разложения, равны между собой.
6) Рассматривая биномиальные коэффициенты: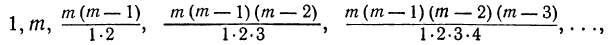
мы замечаем, что при переходе от одного коэффициента к следующему числители умножаются на числа, всё меньшие и меньшие (на m—1, на m — 2, на m — 3 и т. д.), а знаменатели умножаются на числа, всё большие и большие (на 2, на 3, на 4 и т. д.). Вследствие этого коэффициенты сначала возрастают (пока множители в числителе остаются большими соответственных множителей в знаменателе), а затем убывают. Так как коэффициенты членов, равно отстоящих от концов разложения, одинаковы, то наибольший коэффициент должен находиться посередине разложения. При этом, если число всех членов разложения нечётное (что бывает при чётном показателе бинома), то посередине будет один член с наибольшим коэффициентом; если же число всех членов чётное (что бывает при нечётном показателе бинома), то посередине должны быть два члена с одинаковыми наибольшими коэффициентами. Например:
(х+α)⁴=x⁴+4αx³+6α²x²+4α³x+α⁴;
(x+α)⁵=x⁵+5αx⁴+10α²x3+10α³x²+5α⁴x+α⁵∙
7) Из сравнения двух рядом стоящих членов: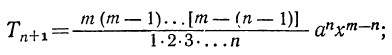
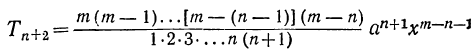
заключаем, что:
Для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы х в этом члене и разделить на число членов, предшествующих определяемому.
Пользуясь этим свойством, можно сразу писать, например, (x+a)⁷=x⁷+7ax⁶+…
Теперь берём 7, умножаем его на 6 и делим на 2, получаем 21: (x+a)⁷=x⁷+7ax⁶+21a²x⁵+… .
Теперь берём 21, умножаем на 5 и делим на 3, получаем 35:
(x+a)⁷ =х⁷+7ax⁶+21a²x⁵+35a³x⁴+….
Теперь уже выписаны члены до середины ряда, остальные получим, основываясь на свойстве пятом:
(х+а)⁷ =х⁷-7αx⁶+21α²x⁵+35α³x⁴+35α⁴x³+21α⁵x²+7α⁶x+α⁷.
8) Сумма всех биномиальных коэффициентов равна 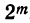 . Действительно, положив в формуле бинома x=a=1, получим:
. Действительно, положив в формуле бинома x=a=1, получим: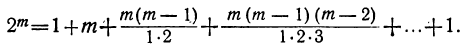
Например, сумма коэффициентов в разложении (х+a)⁷ равна
1+7+21+35+35 +21+7+1 = 128=2⁷.
9) Заменив в формуле бинома а на — а, получим: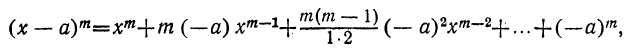
т. е. 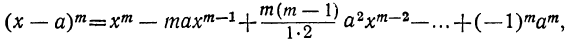
следовательно, знаки + и — чередуются.
10) Если в последнем равенстве положим x=α =1, то найдём: 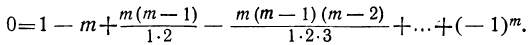
Сумма биномиальных коэффициентов, стоящих на нечётных местах, равна сумме биномиальных коэффициентов, стоящих на чётных местах.
Применение формулы бинома к многочлену
Формула бинома Ньютона позволяет возвышать в степень многочлен. Так:
(α+ b+c)⁴ = [(а+b)+с]⁴= (a+b)⁴+4c (а+b)³+6c² (а+b)²+4c³ (a+b)+c⁴.
Разложив (a+b)⁴, (a+b)³, (а+b)², окончательно получим:
(a+b+с)⁴=a⁴+4a³b+ 6a²b²+ 4ab³+ b⁴ +4a³c+12a²bc+
+12ab²c+4b³c+6a²c²+12abc²+6b²c²+ 4ac³ + 4bc³+с⁴.
Вывод формулы бинома ньютона
Очевидно, что
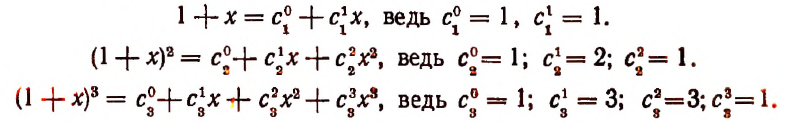
Возникает вопрос, будет ли закономерность, наблюдаемая в этих формулах, обладать общностью, т. е. будет ли справедливой формула
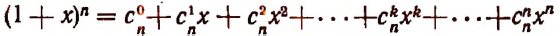
при всяком натуральном значении n?
Воспользуемся методом полной индукции. Допустим, что формула верна для произвольно взятого натурального числа р, т. е. предположим справедливым следующее равенство:
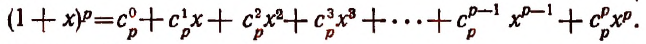
Умножим обе части этого предполагаемого равенства на 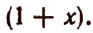
Тогда получим:
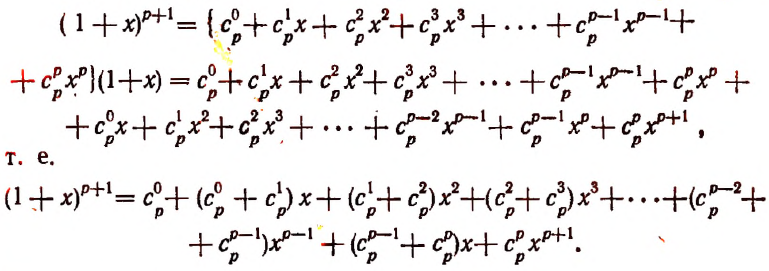
Пользуясь формулой
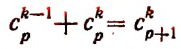
и приняв во внимание, что
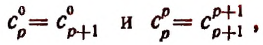
получим окончательно:
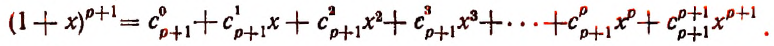
Из предположения, что формула верна при 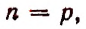 мы пришли к тому, что формула оказалась верной и при
мы пришли к тому, что формула оказалась верной и при 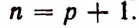 Но поскольку, кроме того, формула верна при
Но поскольку, кроме того, формула верна при 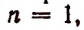 то она должна быть верна и при любом натуральном значении n.
то она должна быть верна и при любом натуральном значении n.
Теперь легко получить разложение и для 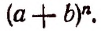
Действительно,
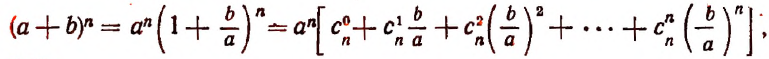
или
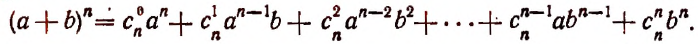
Последняя формула и называется формулой бинома Ньютона. Ее правая часть называется разложением степени бинома.
Числа  называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Свойства разложения бинома
В разложении бинома содержится членов на один больше, чем показатель степени бинома.
Все члены разложения имеют относительно букв а и b одно и то же измерение, равное показателю степени бинома. (Измерением одночлена относительно букв а и b называется сумма показателей степеней этих букв, входящих в этот одночлен.)
Поскольку все члены разложения имеют одинаковое измерение относительно букв а и b, то это разложение является однородным многочленом относительно букв а и b (см. стр. 450).
В разложении показатель степени буквы а последовательно понижается на единицу, начиная с показателя n, а показатель степени буквы b последовательно повышается на единицу, начиная с показателя, равного нулю.
Член разложения 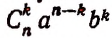 является
является 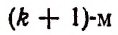 членом разложения и обозначается символом
членом разложения и обозначается символом 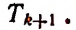
Формула
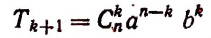
называется формулой общего члена разложения, так как, давая букве k целые значения от 0 до n, мы можем получить из нее любой член разложения.
Теперь напишем разложение для выражения 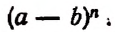
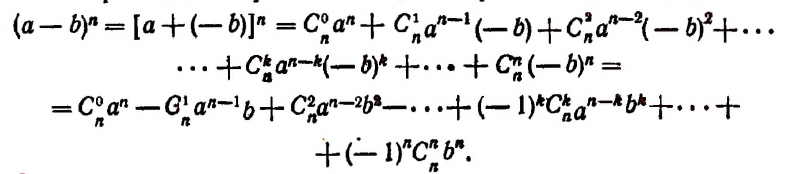
Здесь
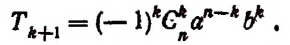
Свойства биномиальных коэффициентов
1. Биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны между собой. Действительно, по первому свойству числа сочетаний имеем:
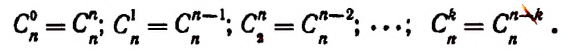
2. Сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома.
Доказательство:
Положим, в формуле бинома
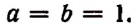
Тогда получим:
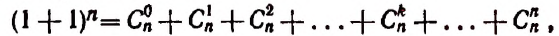
или
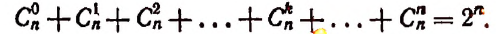
3. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме, биномиальных коэффициентов, стоящих на нечетных местах.
Доказательство:
Полагая в тождестве
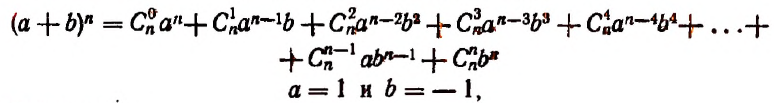
получим:
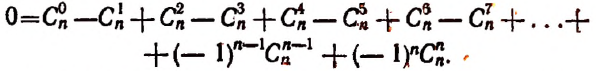
Перенеся все отрицательные члены в левую часть, получим:
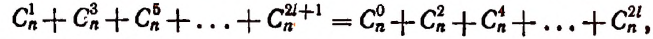
что и требовалось доказать.
Если вместо биномиальных коэффициентов 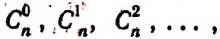
 подставить их значения, то формула бином Ньютона примет вид:
подставить их значения, то формула бином Ньютона примет вид:
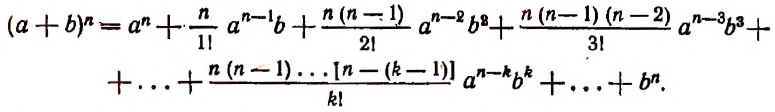
Формулу бинома Ньютона принято записывать ради краткости в следующем символическом виде:
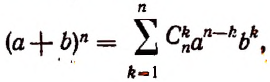
или
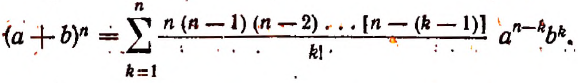
Читателю может показаться непонятным, почему столь элементарная формула
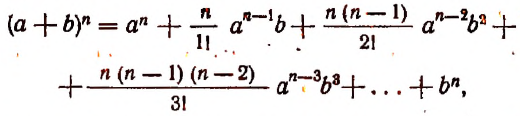
где n — целое положительное число, носит имя великого ученого Ньютона, тем более что эта формула была известна до Ньютона. Например, ее знал Аль-Каши (XV век) и она встречается в трудах Паскаля. Объясняется это тем, что именно Ньютоном была обобщена эта формула для любого действительного показателя.
Ньютон впервые показал, что выражение
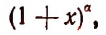
где 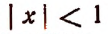 и
и 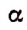 — любое действительное число, равняется сумме следующего сходящегося, ряда:
— любое действительное число, равняется сумме следующего сходящегося, ряда:
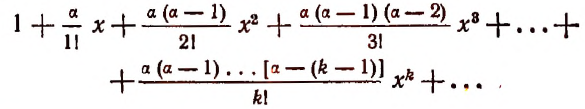
Например, если 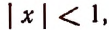 то
то
Арифметический треугольник, или треугольник паскаля
Написанная ниже таблица
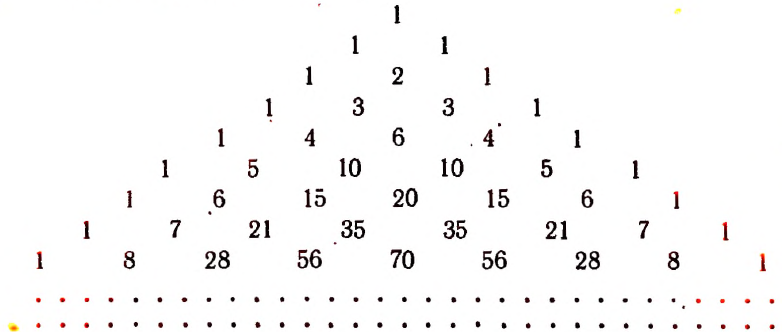
называется треугольником Паскаля *.
По боковым сторонам этой таблицы стоят единицы, внутри же стоят числа, получающиеся сложением двух соответствующих чисел предыдущей строки. Например, число 21 в 8-й строке получается сложением стоящих над ним чисел 6 и 15.
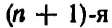 строка этой таблицы дает биномиальные коэффициенты разложения n-й степени бинома. Например:
строка этой таблицы дает биномиальные коэффициенты разложения n-й степени бинома. Например:
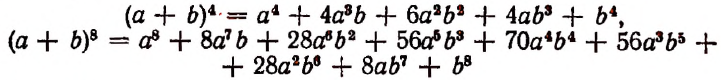
и так далее.
Треугольник Паскаля получается из следующей таблицы:
в силу того, что
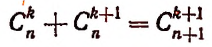
(см. стр. 662).
Треугольник Паскаля приведен в книге Паскаля «Трактат об арифметическом треугольнике», изданной после его смерти в 1665 году.
Примеры с решением на Бином Ньютона
1. В разложении 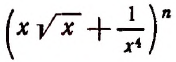 коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, т. е. член разложения, не зависящий от x (членом, не зависящим от х, будет тот, который содержит х в нулевой степени).
коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, т. е. член разложения, не зависящий от x (членом, не зависящим от х, будет тот, который содержит х в нулевой степени).
Решение:
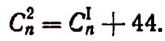 Отсюда
Отсюда 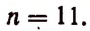
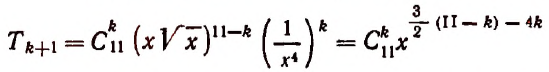
Приравняв показатель степени буквы х к нулю, получим:
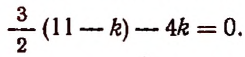 Отсюда
Отсюда 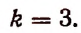
Искомым свободным членом будет четвертый, и он будет равен  т. е. 165.
т. е. 165.
2. Сколько рациональных членов содержится в разложении
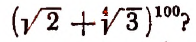
Решение:
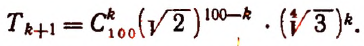
Для рациональности члена разложения необходимо, чтобы число k было кратно четырем. Но тогда 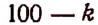 будет числом четным и
будет числом четным и 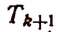 будет числом рациональным.
будет числом рациональным.
Число k может принимать целые значения 0, 1, 2….. 100. Среди этих чисел кратными четырем будут
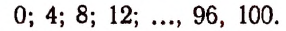
Пользуясь формулой 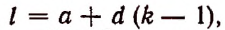 получим:
получим: 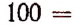
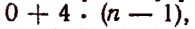 или
или  Следовательно, в разложении
Следовательно, в разложении 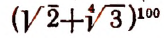 рациональных членов будет 26.
рациональных членов будет 26.
3. Доказать, что значение выражения
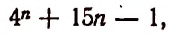
где n — натуральное число, делится на 9.
Доказательство:
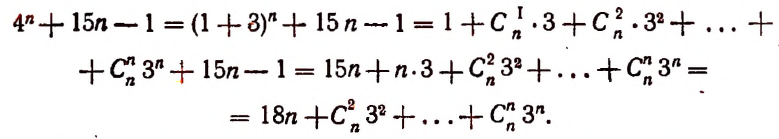
Каждое слагаемое последней суммы делится на 9, следовательно, и вся эта сумма, т. е. значение выражения 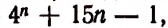 делится на 9, что и требовалось доказать.
делится на 9, что и требовалось доказать.
Дополнение к Бином Ньютону

Смотрите также:
- Решение задач по финансовой математике
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Бином Ньютона и треугольник Паскаля
18 декабря 2021
Сегодня мы детально разберём Бином Ньютона. Это формула, по которой можно раскрыть скобки ${{left( a+b right)}^{n}}$ и получить готовый многочлен. Сама формула выглядит так:
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $C_{n}^{k}$ — биноминальные коэффициенты (они же — «число сочетаний из $n$ по $k$»), которые считаются по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.
Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:
- Постановка задачи — в чём вообще проблема?
- Формула бинома Ньютона — что значат все эти значки?
- Знак суммы — чрезвычайно полезный материал для всех, кто хочет понять математику.
- Биноминальные коэффициенты — минутка комбинаторики.
- Треугольник Паскаля — лайфхак для быстрых вычислений.
- Доказательство Бинома Ньютона — для тех, кто хочет познать Истину.:)
Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!
1. Постановка задачи
Итак, мы хотим быстро раскрывать скобки в конструкциях вида ${{left( a+b right)}^{n}}$. Начнём с того, что мы и так знаем. Например:
[{{left( a+b right)}^{1}}=a+b]
Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:
[{{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]
И куб суммы:
[{{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}]
Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен…
Именно для нахождения этих коэффициентов придумали бином Ньютона.
2. Бином Ньютона
Пусть $nin mathbb{N}$. Тогда верно равенство
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $sum{left( … right)}$ — краткая запись суммы, $C_{n}^{k}$ — биноминальный коэффициент, который считается по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
В этой формуле прекрасно всё. Одних пугает знак суммы. Другие не понимают, что за $C_{n}^{k}$ такое (ещё раз: это объект из мира комбинаторики, читается «число сочетаний из $n$ по $k$»). Третьи более-менее понимают, о чём речь, но применить эту формулу на практике не могут.
Сегодня мы решим все эти проблемы. Начнём со знака суммы.
3. Знак суммы
Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:
[sumlimits_{k=a}^{k=b}{fleft( k right)}]
Формула $fleft( k right)$ задаёт общий вид однотипных слагаемых, а нижний и верхний индексы $k=a$ и $k=b$ (сверху вместо $k=b$ обычно пишут просто $b$) определяют диапазон значений, которые «пробегает» $k$ и которые нужно подставить в $fleft( k right)$. Например:
[sumlimits_{k=3}^{5}{2k}=2cdot 3+2cdot 4+2cdot 5]
Более привычный формат:
[sumlimits_{k=1}^{n}{fleft( k right)=fleft( 1 right)+fleft( 2 right)+…+fleft( n right)}]
То же самое с индексами:
[sumlimits_{k=1}^{n}{{{a}_{k}}={{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}]
Обратите внимание: если $k$ пробегает значения от $k=a$ до $k=b$, то всего таких слагаемых будет ровно $b-a+1$:
[sumlimits_{k=a}^{b}{fleft( k right)=underbrace{fleft( a right)+fleft( a+1 right)+ldots +fleft( b right)}_{b-a+1text{ слагаемых!}}}]
Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:
[frac{1}{1}+frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}=sumlimits_{n=1}^{5}{frac{1}{2n-1}}]
[frac{2}{3}+frac{4}{9}+frac{6}{27}+frac{8}{81}=sumlimits_{n=1}^{4}{frac{2n}{{{3}^{n}}}}]
В приложении к уроку — куча задач для самостоятельной тренировки.
Но вернёмся к биному Ньютона. Распишем его без знака суммы:
[begin{align} {{left( a+b right)}^{n}} & =C_{n}^{0}cdot {{a}^{n}}{{b}^{0}}+C_{n}^{1}cdot {{a}^{n-1}}{{b}^{1}}+ \ & +ldots +C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}+ldots + \ & +C_{n}^{n-1}cdot {{a}^{1}}{{b}^{n-1}}+C_{n}^{n}cdot {{a}^{0}}{{b}^{n}} end{align}]
В целом, всё понятно: степени буквы $a$ уменьшаются с ${{a}^{n}}$ до ${{a}^{0}}$; одновременно степени буквы $b$ растут с ${{b}^{0}}$ до ${{b}^{n}}$. Сумма степеней этих букв в каждом одночлене равна $n$. Но что такое $C_{n}^{k}$?
4. Биноминальные коэффициенты
Немного комбинаторики.
Определение. Число сочетаний из $n$ по $k$ — это число способов, которыми можно выбрать $k$ элементов среди $n$ элементов, если порядок выбора не имеет значения. Обозначается $C_{n}^{k}$ и считается по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
Обратите внимание: в числителе и знаменателе стоят факториалы. Стандартное определение: $n!$ — это произведение всех чисел от единицы до $n$:
[n!=1cdot 2cdot 3cdot …cdot n]
У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.
Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Очевидно, порядок кормления уток неважен. Покормить сначала утку №1, а затем №2 — это то же самое, что покормить сначала утку №2, затем №1. Результат один и тот же: накормлены лишь эти две утки, а остальные три — нет. Поэтому считаем $C_{5}^{2}$:
[begin{align} C_{5}^{2} & =frac{5!}{2!cdot 3!} \ & =frac{5cdot 4cdot 3cdot 2cdot 1}{2cdot 1cdot 3cdot 2cdot 1}= \ & =10 end{align}]
Вот и всё. Однако при больших $n$ и $k$ посчитать число сочетаний напрямую становится затруднительно. Тут на помощь приходит сокращение дробей.
Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Порядок вновь неважен, просто уток стало больше. Поэтому считаем $C_{150}^{2}$:
[begin{align} C_{150}^{2} & =frac{150!}{2!cdot 148!}= \ & =frac{150cdot 149cdot 148cdot …cdot 1}{2cdot 1cdot 148cdot …cdot 1}= \ & =frac{150cdot 149}{2cdot 1}= \ & =11175 end{align}]
Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.
4.1. Новое определение факториала
Стандартное определение мы уже привели выше:
[n!=1cdot 2cdot 3cdot …cdot n,quad nin mathbb{N}]
Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.
Определение. Пусть $nin mathbb{N}bigcup left{ 0 right}$ — целое неотрицательное число. Тогда факториал считается по формуле:
[n!=left{ begin{align} & 1,quad n=0 \ & ncdot left( n-1 right)!,quad n gt 0 \ end{align} right.]
В частности, $0!=1$ по определению.
Простейшие коэффициенты:
[begin{align} C_{n}^{0} & =frac{n!}{0!left( n-0 right)!}=frac{n!}{1cdot n!}=1; \ C_{n}^{1} & =frac{n!}{1!left( n-1 right)!}=frac{ncdot left( n-1 right)!}{1cdot left( n-1 right)!}=n; \ end{align}]
А вот ещё парочка весёлых примеров:
[begin{align} C_{7}^{3} & =frac{7cdot 6cdot 5cdot 4cdot ldots cdot 1}{3cdot 2cdot 1cdot 4cdot ldots cdot 1}=35 \ C_{8}^{2} & =frac{8cdot 7cdot 6cdot ldots cdot 1}{2cdot 1cdot 6cdot ldots cdot 1}=28 \ C_{64}^{3} & =frac{64cdot 63cdot 62cdot 61cdot ldots cdot 1}{3cdot 2cdot 1cdot 61cdot ldots cdot 1}= \ & =41664 end{align}]
5. Треугольник Паскаля
Посчитаем бином Ньютона для $n=0$, $n=1$, $n=2$, $n=3$:
[begin{align} & {{left( a+b right)}^{0}}=1 \ & {{left( a+b right)}^{1}}=1cdot a+1cdot b \ & {{left( a+b right)}^{2}}=1cdot {{a}^{2}}+2cdot ab+1cdot {{b}^{2}} \ & {{left( a+b right)}^{3}}=1cdot {{a}^{3}}+3cdot {{a}^{2}}b+3cdot a{{b}^{2}}+1cdot {{b}^{3}} \ end{align}]
Составим таблицу:
[begin{matrix} 1 \ 1quad 1 \ 1quad 2quad 1 \ 1quad 3quad 3quad 1 \ 1quad 4quad 6quad 4quad 1 \ end{matrix}]
Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:
[begin{align} & 3=1+2 \ & 4=1+3 \ & 6=3+3 \ end{align}]
И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.
Теорема. Биноминальные коэффициенты вычисляются по формуле
[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]
Доказывается напролом.
Распишем доказательство детально:
[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!}]
[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!} \ end{align}]
Заметим, что по определению факториала
[begin{align} & left( k+1 right)!=left( k+1 right)cdot k! \ & left( n-k right)!=left( n-k right)cdot left( n-k-1 right)! end{align}]
Поэтому знаменатели биноминальных коэффициентов можно переписать:
[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)left( n-k-1 right)!}+frac{n!}{left( k+1 right)k!left( n-k-1 right)!}]
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{n!}{k!left( n-k right)left( n-k-1 right)!}+ \ & +frac{n!}{left( k+1 right)k!left( n-k-1 right)!} end{align}]
Приведём к общему знаменателю:
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} end{align}]
[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ = & frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}=frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} \ end{align}]
Окончательно получим:
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( n+1 right)!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)!}{left( k+1 right)!left( n+1-left( k+1 right) right)!}= \ & = C_{n+1}^{k+1} end{align}]
Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.
6. Доказательство Бинома Ньютона
Итак, нужно доказать, что
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $C_{n}^{k}$ — биноминальные коэффициенты с теми чудесными свойствами, которые мы рассмотрели и доказали выше.
Будем доказывать по индукции.
6.1. База индукции
Рассмотрим $n=1$. Формула Бинома Ньютона для него:
[begin{align} {{left( a+b right)}^{1}} & =sumlimits_{k=0}^{1}{C_{1}^{k}{{a}^{1-k}}{{b}^{k}}}= \ & =C_{1}^{0}{{a}^{1}}{{b}^{0}}+C_{1}^{1}{{a}^{0}}{{b}^{1}}= \ & =a+bend{align}]
Очевидно, для $n=1$ формула верна. Переходим к индуктивному предположению.
6.2. Индуктивное предположение
Пусть Бином Ньютона верен для некоторого $n=t$:
[{{left( a+b right)}^{t}}=sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}]
Используя этот факт, докажем верность и для $n=t+1$, т.е. выполним индуктивный переход.
6.3. Индуктивный переход
Докажем, что бином Ньютона верен для $n=t+1$:
[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
Для этого сначала заметим, что
[{{left( a+b right)}^{t+1}}={{left( a+b right)}^{t}}cdot left( a+b right)]
Однако согласно индуктивному предположению, ${{left( a+b right)}^{t}}$ допускает разложение по Биному Ньютона, поэтому
[begin{align} left( a+b right)cdot {{left( a+b right)}^{t}} & =left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} end{align}]
[begin{align} & left( a+b right)cdot {{left( a+b right)}^{t}}= \ = & left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} \ end{align}]
Запишем отдельно первое слагаемое первой суммы и учтём, что $C_{t}^{0}=C_{t+1}^{0}=1$:
[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} & = C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ & = C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}= \ = & C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]
И последнее слагаемое последней второй суммы и учтём, что $C_{t}^{t}=C_{t+1}^{t+1}=1$:
[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Сейчас будет самая нетривиальная операция. Меняем индекс суммирования в последней сумме: выполняем подстановку $k=m-1$. При этом меняются и пределы суммирования:
[left[ begin{align} k & =m-1 \ k & =0Rightarrow m=1 \ k & =t-1Rightarrow m=t \ k+1 & =m \ t-k & =t+1-m \ end{align} right]]
В итоге последняя сумма перепишется так:
[sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]
[begin{align} & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ = & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Объединяем суммы вместе:
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+ \ + & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Заметим, что два знака суммы различаются лишь названием индекса и биноминальными коэффициентами. Всё остальное — диапазоны суммирования, степени буквы $a$ и буквы $b$ — всё идеально совпадает и никак не меняется, если написать вместо $k$ индекс $m$ или наоборот.
Такие суммы можно записать под единым знаком:
[C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]
[begin{align} & C_{t+1}^{0}cdot {{a}^{t+1}}+ \ + & sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+ \ + & C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Выражение под знаком суммы легко раскладывается на множители:
[begin{align} C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} & =left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ & =C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} end{align}]
[begin{align} & C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} \ end{align}]
Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:
[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]
Или, что то же самое
[C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}]
Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:
[ C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
[begin{align} C_{t+1}^{0}cdot {{a}^{t+1}} & +sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ & =sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]
Сопоставляя исходное выражение и конечное, получим
[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.
Смотрите также:
- Схема Горнера

- Теорема Безу и корни многочленов

- Знаки тригонометрических функций

- Уравнение касательной к графику функции

- Как представить обычную дробь в виде десятичной

- Сложные задачи B2 на проценты: вычисление полной стоимости

Рассмотрим многочлен
![]()
-й
степени
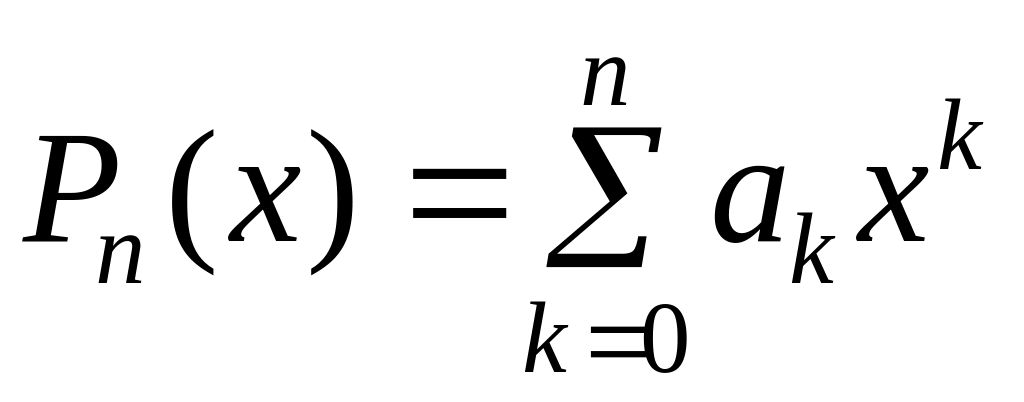
.
(1)
Представим этот
многочлен следующим образом:

![]()
. (2)
Неизвестные
коэффициенты
![]()
найдём следующим образом. Продифференцируем
(2)
раз. Получим
![]()
![]()
(3)
![]()
…………………………………………………………….
![]()
Полагая в (2) и (3)
,
найдём:
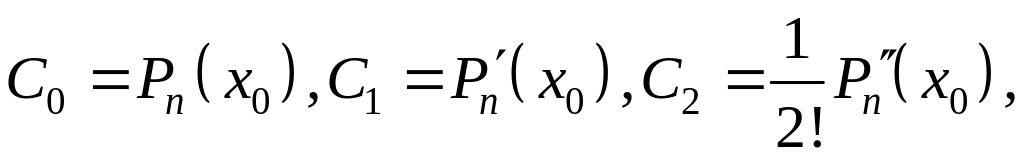
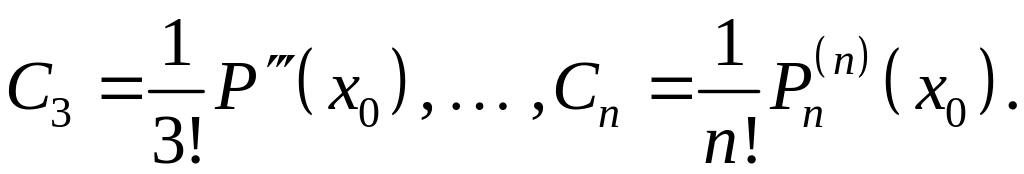
Ясно, что
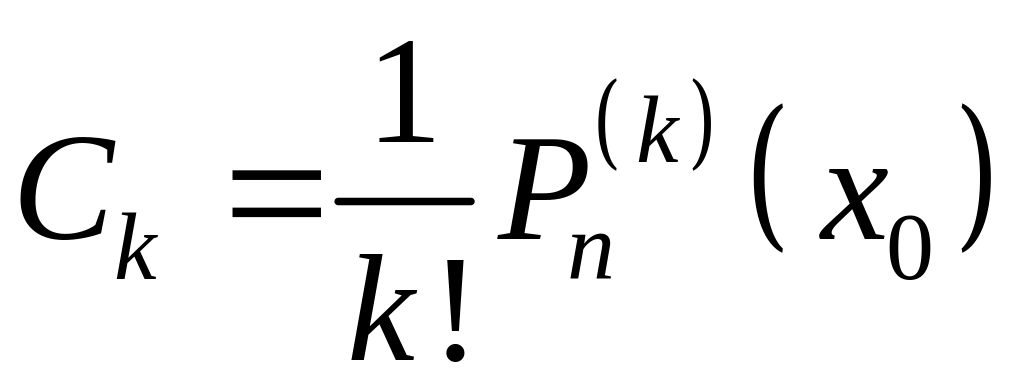
. (4)
Таким образом,
многочлен (2) примет вид
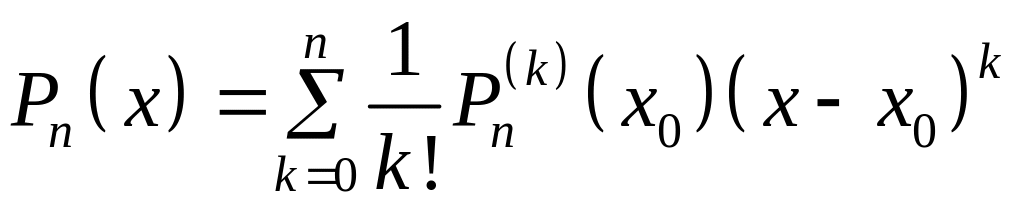
.
(5)
Многочлен (5)
называют многочленом Тейлора. Его
коэффициенты определяются соответствующей
производной многочлена в точке
.
Очевидно, что всякий многочлен является
многочленом Тейлора и задав значения
многочлена и его
производных в некоторой точке, мы
определим и сам многочлен.
Рассмотрим частный
случай
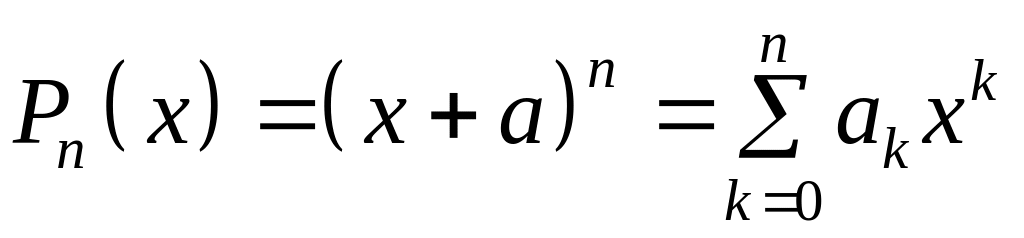
.
Коэффициенты
![]()
найдём по формуле (4) при
.
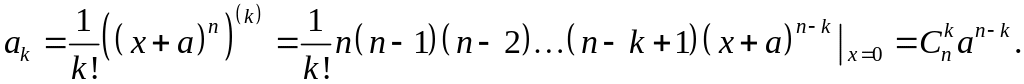
Таким образом, мы
получили формулу бинома Ньютона.
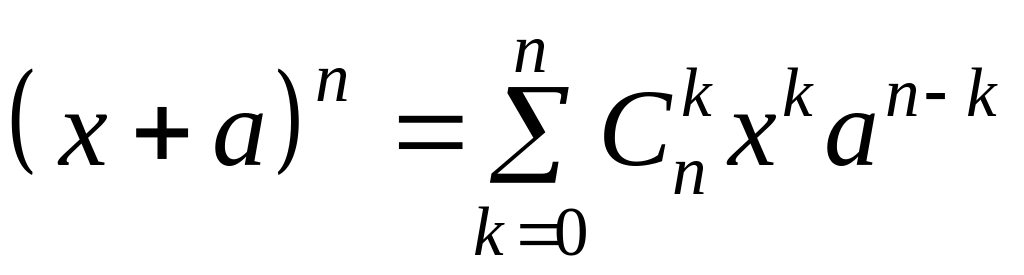
. (6)
§6. Формула Тейлора для функции
Пусть функция
дифференцируема
раз в окрестности точки
.
Запишем для неё многочлен Тейлора
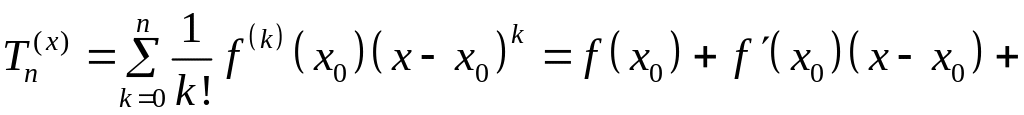
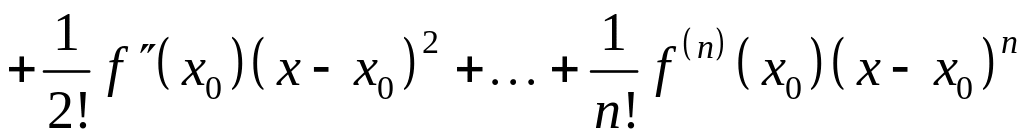
.
(1)
Как видно из (1)
значение функции
и
всех её
производных в точке
совпадает со значением и производными
многочлена Тейлора
![]()
![]()
![]()
. (2)
Однако, в точках
![]()
функция
может не совпадать с
многочленом
Тейлора. Поэтому положим
![]()
.
(3)
Величину
![]()
называют остаточным членом. Из (3) с
учётом (2) получим
![]()
. (4)
Докажем, что
остаточный член
является бесконечно малой высшего
порядка малости по сравнению с
![]()
,
то есть
![]()
или
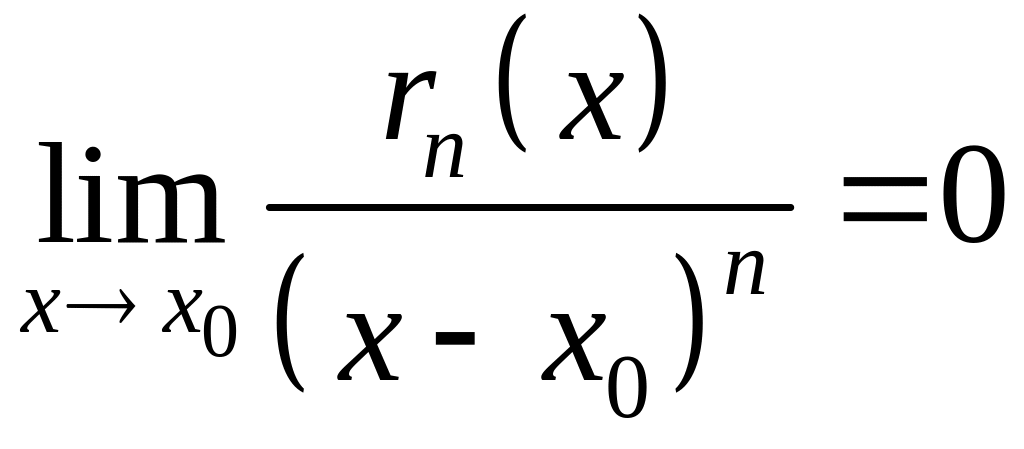
.
Применяя
раз правило Лопиталя и учитывая (4),
найдём:
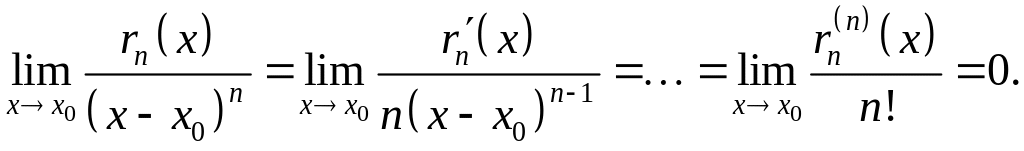
Что и требовалось
доказать.
Формулу
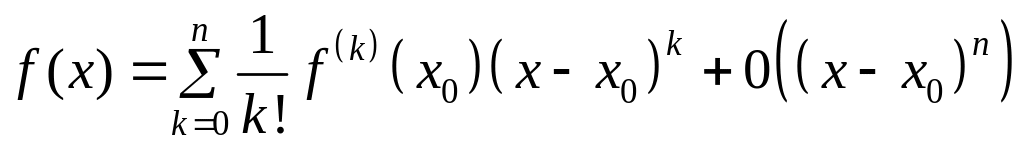
(3′)
называют формулой
Тейлора для функции
с остаточным
членом в форме Пеано, а многочлен Тейлора
(1) – многочленом
наилучшего приближения.
Заметим, что формула
(
)
является асимптотической (см. §6 гл. 4),
поэтому, заменяя функцию
на многочлен
Тейлора в окрестности точки
,
мы не можем указать допущенную ошибку,
а можем только указать порядок её
малости. Отсюда ясна необходимость
записать остаточный член в другой форме,
в которой можно оценить его величину.
Будем искать
остаточный член в виде
![]()
,
где
–
некоторая неизвестная постоянная.
Предположим теперь, что функция
имеет
-ю
непрерывную на отрезке
![]()
производную и
![]()
–ю
производную в каждой точке интервала
![]()
.
Перепишем формулу Тейлора (
)
в виде:
![]()
. (5)
Введём вспомогательную
функцию:
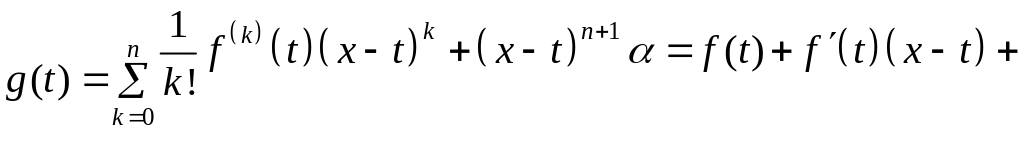

. (6)
Из (6) видно, что
при
![]()
![]()
,
а при
![]()
получим
![]()
то есть на концах
отрезка
функция
принимает равные значения. Поскольку
имеет
непрерывную n-ую
производную, то функция
непрерывна
на отрезке
,
а поскольку
имеет
![]()
-ю
производную, то функция
дифференцируема
на интервале
![]()
.
Как видно
удовлетворяет
теореме Ролля.
Найдём производную
функции
.
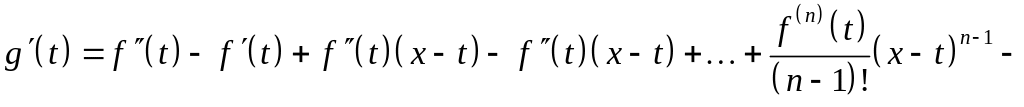
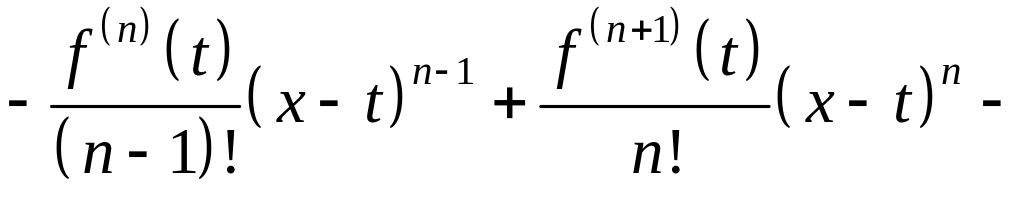
![]()
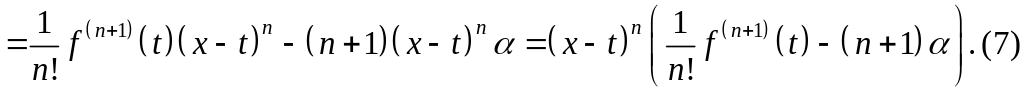
Согласно
теореме Ролля найдётся точка
![]()
такая, что
![]()
Тогда из (7) найдём
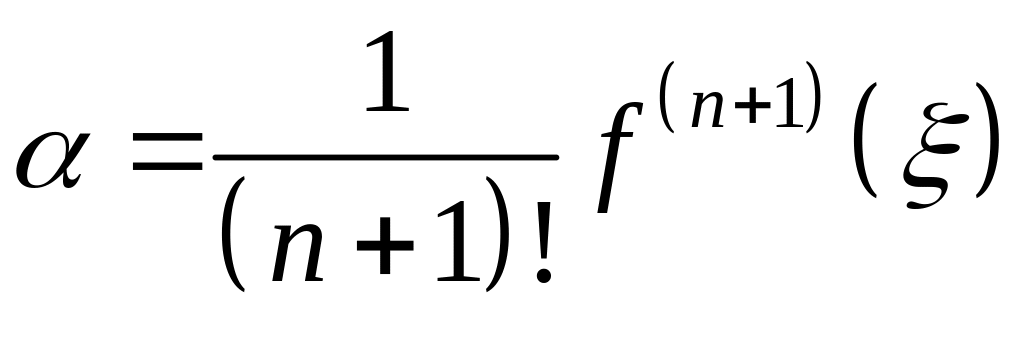
.
(8)
С учётом (8) формулу
(5) перепишем так:
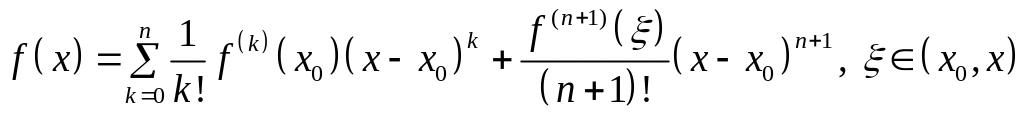
. (9)
Формулу (9) называют
формулой Тейлора с остаточным членом
в форме Лагранжа.
Если
![]()
ограничена в окрестности точки
,
то аппроксимируя функцию
многочленом
Тейлора, можно легко оценить возникающую
при этом погрешность, если остаточный
член формулы Тейлора записан в форме
Лагранжа.
Заметим, что иногда
точку
![]()
в (4) удобнее записать в виде
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


















