Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 июля 2022 года; проверки требует 1 правка.
| Биномиальное распределение | |
|---|---|
 Функция вероятности Функция вероятности |
|
 Функция распределения Функция распределения |
|
| Обозначение |
 |
| Параметры |
 — число «испытаний» — число «испытаний» — вероятность «успеха» — вероятность «успеха» |
| Носитель |
 |
| Функция вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
одно из  |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Биномиа́льное распределе́ние с параметрами 



Определение[править | править код]
Пусть 







имеет биномиальное распределение с параметрами 

Это записывается в виде:
.
Случайную величину 


Функция вероятности задаётся формулой:
где
— биномиальный коэффициент.
Функция распределения[править | править код]
Функция распределения биномиального распределения может быть записана в виде суммы:
,
где 

.
Моменты[править | править код]
Производящая функция моментов биномиального распределения имеет вид:
,
откуда
,
,
а дисперсия случайной величины.
.

Пример биноминального распределения
Свойства биномиального распределения[править | править код]
Связь с другими распределениями[править | править код]
См. также[править | править код]
- Треугольник Паскаля
- Локальная теорема Муавра — Лапласа
Задача 1
Прямоугольник
со сторонами l1 и l2 разделен на четыре равные
части, одна из которых заштрихована. На прямоугольник брошены три точки.
Попадание точки в любое место прямоугольника равновозможно. Дискретная случайная величина – число точек,
попавших на заштрихованную часть. Найти: закон распределения, числовые
характеристики, функцию распределения F(x). Построить график F(x).
Задача 2
Для
случайной величины X найти: а) закон распределения; б) функцию
распределения; в) математическое ожидание и дисперсию. При установившемся
технологическом процессе всей
производимой продукции станок-автомат выпускает 2/3 первым сортом и 1/3 – вторым. Случайным образом отбирается 5
изделий. X – число изделий первого сорта среди отобранных.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 3
Игральную
кость подбросили 3 раза. Найти математическое ожидание, дисперсию, среднее
квадратическое отклонение числа невыпадения единицы.
Задача 4
Монету
подбросили 4 раза. Найти математическое ожидание, дисперсию, среднее
квадратическое отклонение дискретной случайной величины X –
числа появлений герба.
Задача 5
В городе
имеется N=3 оптовых баз. Вероятность того, что требуемого сорта товар
отсутствует, на этих базах одинакова и равна p=0,2. Составить закон
распределения числа баз, на которых товар отсутствует в данный момент. Найти
математическое ожидание и среднее квадратическое отклонение.
Задача 6
Продавец
азартных игр объясняет, что в его лотерее 40% заклепок. Игрок покупает 5
билетов.
а) Какова
вероятность того, что он вытащит не более двух заклепок?
б)
Рассчитайте ожидаемое значение и интерпретируйте его
Задача 7
Случайные
величины ξ и η имеют биномиальные распределения с параметрами n=20 и p=0,2
для величины ξ и n=100 и p=0,1 для величины η.
Найти
математическое ожидание и дисперсию величины γ=10ξ-2η, если известен
коэффициент корреляции ρ(ξ,η)=-0,7.
Задача 8
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на второй
станке – 5%. На первом станке изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Производится
9 бомбометаний с вероятностью попадания при каждом 0,89. Какова вероятность при
более чем 4 бомбометаниях? Найти характеристики распределения случайной
величины.
Задача 10
Вероятность
того, что саженец абрикоса приживется в Новосибирской области, равна 0,6.
Посадили 5 саженцев. Записать закон распределения случайной величины X –
число прижившихся саженцев. Найти математическое ожидание и дисперсию
полученного распределения.
Задача 11
Из
курьерской службы отправились на объекты 5 курьеров. Каждый курьер с
вероятностью 0,3 независимо от других опаздывает на объект. Указать вид
распределения случайной величины X – числа опоздавших
курьеров. Построить ряд распределения случайной величины X.
Найти ее математическое ожидание и дисперсию. Найти вероятность того, что на
объекты опоздают не менее двух курьеров.
Задача 12
Проведено
5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 13
На складе
производителя электрических гирлянд, которые планируется поставлять на продажу,
проводится выборочная проверка их работоспособности. Известно, что у примерно
5% производимых гирлянд бывают неисправности различного рода. Предположим, были
отобраны 3 гирлянды для проверки их работоспособности. Найдите закон
распределения случайной величины
– число гирлянд без неисправностей среди
отобранных. Определите вероятность того, что более чем одна гирлянда будет
исправлена.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Торговый
агент в среднем контактирует с 4 потенциальными покупателями в день. Из опыта
ему известно, что вероятность того, что потенциальный покупатель совершит
покупку, равна 0,023. Составить закон распределения ежедневного числа продаж
для агента. Найти числовые характеристики этого распределения. Чему равна
вероятность того, что у агента будет хотя бы 2 продажи в течение дня?
Задача 15
Случайная
величина имеет биноминальное распределение с математическим ожиданием M(X)=3 и
дисперсией D(X)=1,2. Найти P(X≥2).
Задача 16
По мишени
производится 4 независимых выстрела с вероятностью попадания при каждом
выстреле p=0,9. Найти закон распределения дискретной
случайной величины X, равной числу попадания в мишень. Написать функцию
распределения.
Задача 17
Производится
4 независимых выстрела по некоторой цели. Вероятность попадания при одном
выстреле равна 0,25. Выписать ряд распределения для числа попаданий в цель.
Задача 18
Вероятность
попадания в цель одним выстрелом равна 0,5. Производят пять выстрелов. Найти:
а) Распределение вероятностей числа попаданий; б) Наивероятнейшее число
попаданий; в) Вероятность, что попаданий будет не более двух.
Задача 19
Клиенты
банка не возвращают полученный кредит в 12% случаев.
а)
составить ряд распределения числа не отдавших кредит клиентов из взятых наудачу
3-х.
б) найти
среднее число не отдавших кредит клиентов и отклонение от него.
Задача 20
При
установившемся технологическом процессе происходит в среднем 10 обрывов нити на
100 веретен в час. Найти закон распределения и математическое ожидание
случайного числа обрывов нити в течение часа среди трех веретен, работающих
независимо друг от друга.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Составить
закон распределения случайной величины Х и найти ее математическое ожидание,
дисперсию и среднее квадратическое отклонение:
Х – число
выигравших билетов лотереи, если куплено 3 билета, а выигрышные билеты
составляют в тираже 8%;
Задача 22
Производится
3 независимых опыта, в каждом из которых событие A появляется с вероятностью
0,4. Построить ряд распределения числа появлений события в 3-х опытах.
Найти F(X),M(X),D(X),σ(X),p(x≥1)
Задача 23
Построить
ряд распределения числа попаданий мячом в корзину при 4 бросках, если
вероятность попадания равна 0,7.
Задача 24
Производится
три независимых испытания, в каждом из которых вероятность появления события A равна
0,4. Составить закон распределения дискретной случайной величины X –
числа появления события A в указанных испытаниях.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 25
Запишите
таблицу для данного закона распределения случайной величины X,
постройте многоугольник распределения. Найдите числовые характеристики распределения
(M(X),D(X),σ(X)). Запишите функцию распределения и постройте ее график.
Ответьте на вопрос о вероятности описанного события.
Записи
страховой компании показали, что 30% держателей страховых полисов старше 50 лет
потребовали возмещения страховых сумм. Для проверки в случайном порядке было
отобрано 5 человек старше 50 лет, имеющих полисы. Случайная величина X –
количество требующих возмещения среди отобранных. Чему равна вероятность того,
что потребуют возмещения более трех человек?
Задача 26
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 27
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна 0,7. Для случайной величины X
элементов, безотказно работавших в одном опыте, построить закон распределения,
их графики, найти ее числовые характеристики.
Задача 28
В группе
студентов среднее число отличников составляет 20%. Составить закон распределения количества
отличников среди четырех студентов, отобранных случайным образом для участия в
деловой игре.
Задача 29
В урне 6
белых и 14 черных шара. Из урны извлекается один шар 4 раз подряд, причем
каждый раз вынутый шар возвращается в урну и шары перемешиваются. Приняв за
случайную величину Х число извлеченных белых шаров, составить закон
распределения этой случайной величины, найти ее математическое ожидание и
дисперсию.
Задача 30
Устройство состоит из трех
независимо работающих элементов. Вероятность отказа в одном опыте для каждого
элемента равна 0.1. Составить закон распределения случайного числа отказавших
элементов в одном опыте. Составить функцию распределения, построить ее график.
Задача 31
В
контрольной работе три задачи. Вероятность того, что задача будет решена, равна
0,9. Найти математическое ожидание случайной величины – числа решенных задач,
стандартное отклонение.
Задача 32
Известна
вероятность события A: p(A)=0,6. Дискретная случайная
величина ξ – число появлений A в трех опытах. Построить
ряд распределения случайной величины ξ. Найти математическое
ожидание mξ и дисперсию Dξ.
Не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает. Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом».
Эксперименты с такими данными называются схемой Бернулли, в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.
Переменная альтернативного признака
Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.
Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.
Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5. Такая вероятность традиционно обозначается латинской буквой p. Следовательно, вероятность наступления альтернативного события равна 1 — p, которую еще обозначают через q, то есть q = 1 – p. Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X.

Мы получили перечень возможных значений и их вероятности. Можно рассчитать математическое ожидание и дисперсию. Матожидание – это сумма произведений всех возможных значений на соответствующие им вероятности:
![]()
Вычислим матожидание, используя обозначения в таблицы выше.
![]()
Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p.
Теперь определим, что такое дисперсия альтернативного признака. Дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:
![]()
Отсюда дисперсия альтернативного признака:
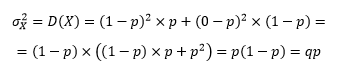
Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5).
Стандартное отклонение – корень из дисперсии:
![]()
Максимальное значение не превышает 0,5.
Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.
Биномиальное распределение случайной величины
Рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве бросков.
Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X, т.е. количеству единичных исходов.
![]()
Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 – все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.
Матожидание биномиальной переменной получить очень легко. Математическое ожидание суммы величин есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:
![]()
Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.
Теперь выведем формулу дисперсии биномиальной переменной. Дисперсия суммы независимых случайных величин есть сумма дисперсий. Отсюда
![]()
Стандартное отклонение, соответственно
![]()
Для 100 подбрасываний монеты стандартное отклонение количества орлов равно
![]()
И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k, где 0≤ k ≤n. Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?
Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга. Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка. Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:

Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке. Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Всего 6 вариантов.

Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.
Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно. Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k, где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:
![]()
Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).
Формулу для определения вероятности легко обобщить на любое количество n и k. В итоге формула биномиального распределения имеет следующий вид.
![]()
Количество подходящих под условие комбинаций умножить на вероятность одной из них.
Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:
![]()
Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.
Расчет вероятностей биномиального распределения в Excel
Если использовать только бумагу и калькулятор, то расчеты по формуле биномиального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков. Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.
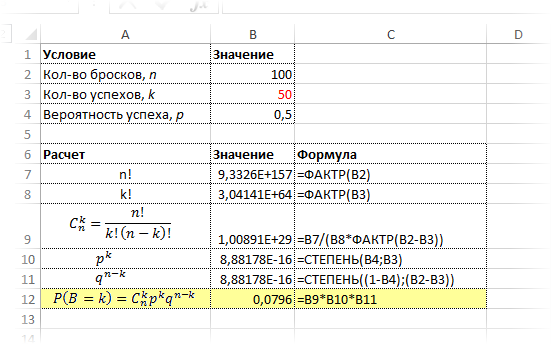
Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.
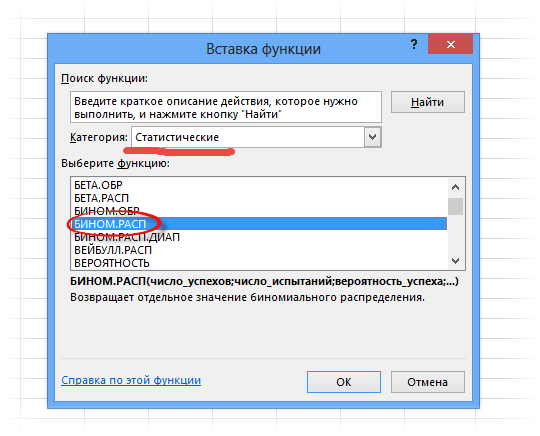
Синтаксис функции состоит из 4 аргументов:
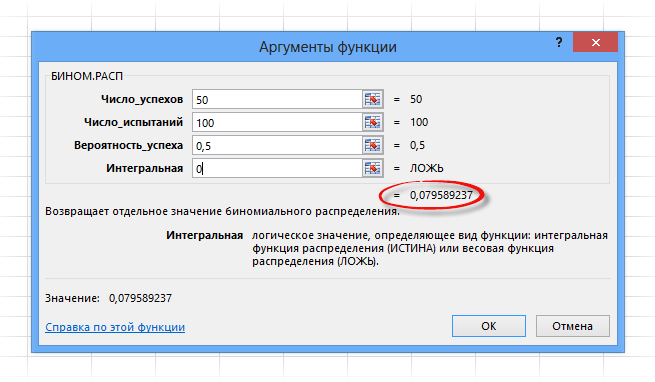
Поля имеют следующие назначения:
Число успехов – количество успешных испытаний. У нас их 50.
Число испытаний – количество бросков: 100 раз.
Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.
Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k); если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.
Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.
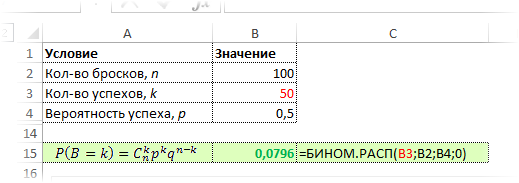
Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100. То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в следующей картинке. Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.
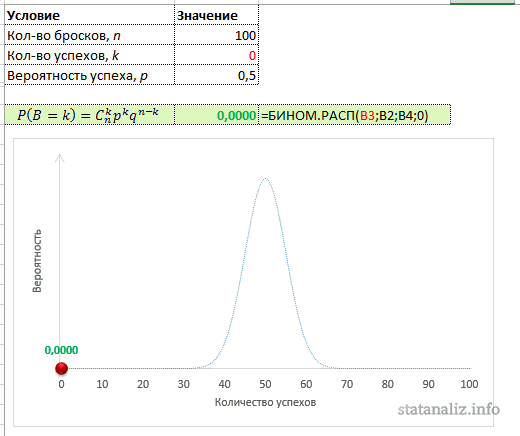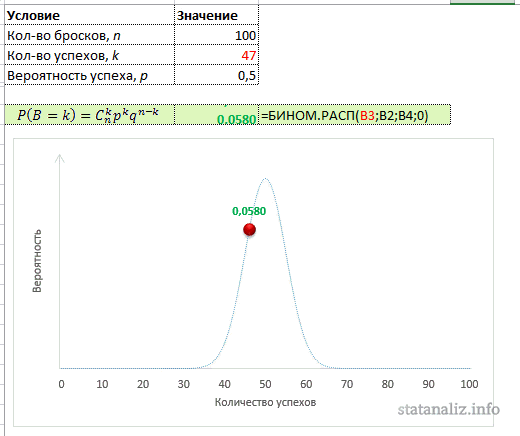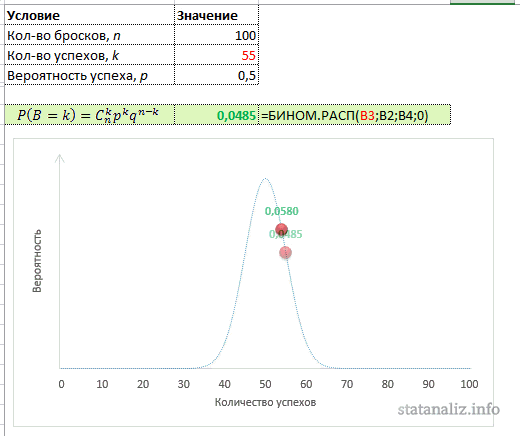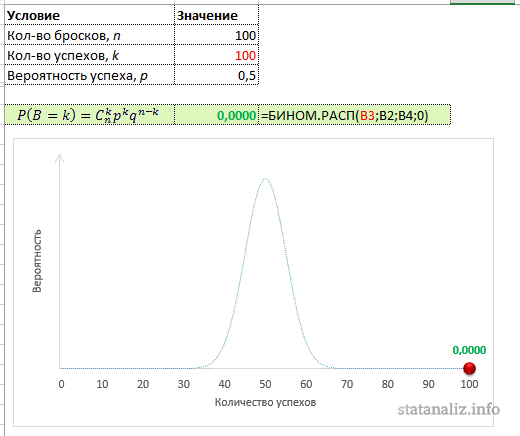
Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро.
Поделиться в социальных сетях:
|
Probability mass function
|
|
|
Cumulative distribution function
|
|
| Notation |
 |
|---|---|
| Parameters |
 – number of trials – number of trials![{displaystyle pin [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c) – success probability for each trial – success probability for each trial |
| Support |
 – number of successes – number of successes |
| PMF |
 |
| CDF |
 (the regularized incomplete beta function) (the regularized incomplete beta function) |
| Mean |
 |
| Median |
 or or  |
| Mode |
 or or  |
| Variance |
 |
| Skewness |
 |
| Ex. kurtosis |
 |
| Entropy |
 in shannons. For nats, use the natural log in the log. |
| MGF |
 |
| CF |
 |
| PGF |
![{displaystyle G(z)=[q+pz]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40494c697ce2f88ebb396ac0191946285cadcbdd) |
| Fisher information |
 (for fixed  ) ) |

Binomial distribution for
with n and k as in Pascal’s triangle
The probability that a ball in a Galton box with 8 layers (n = 8) ends up in the central bin (k = 4) is 
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success (with probability p) or failure (with probability 
The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and is widely used.
Definitions[edit]
Probability mass function[edit]
In general, if the random variable X follows the binomial distribution with parameters n ∈ 
for k = 0, 1, 2, …, n, where
is the binomial coefficient, hence the name of the distribution. The formula can be understood as follows: k successes occur with probability pk and n − k failures occur with probability 

In creating reference tables for binomial distribution probability, usually the table is filled in up to n/2 values. This is because for k > n/2, the probability can be calculated by its complement as
Looking at the expression f(k, n, p) as a function of k, there is a k value that maximizes it. This k value can be found by calculating
and comparing it to 1. There is always an integer M that satisfies[2]
f(k, n, p) is monotone increasing for k < M and monotone decreasing for k > M, with the exception of the case where (n + 1)p is an integer. In this case, there are two values for which f is maximal: (n + 1)p and (n + 1)p − 1. M is the most probable outcome (that is, the most likely, although this can still be unlikely overall) of the Bernoulli trials and is called the mode.
Example[edit]
Suppose a biased coin comes up heads with probability 0.3 when tossed. The probability of seeing exactly 4 heads in 6 tosses is
Cumulative distribution function[edit]
The cumulative distribution function can be expressed as:
where 
It can also be represented in terms of the regularized incomplete beta function, as follows:[3]
which is equivalent to the cumulative distribution function of the F-distribution:[4]
Some closed-form bounds for the cumulative distribution function are given below.
Properties[edit]
Expected value and variance[edit]
If X ~ B(n, p), that is, X is a binomially distributed random variable, n being the total number of experiments and p the probability of each experiment yielding a successful result, then the expected value of X is:[5]
This follows from the linearity of the expected value along with the fact that X is the sum of n identical Bernoulli random variables, each with expected value p. In other words, if 

The variance is:
This similarly follows from the fact that the variance of a sum of independent random variables is the sum of the variances.
Higher moments[edit]
The first 6 central moments, defined as ![{displaystyle mu _{c}=operatorname {E} left[(X-operatorname {E} [X])^{c}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c5ea3e05b674668550675c3c4593c725a1ec86b)
The non-central moments satisfy
and in general
[6]
[7]
where 



A simple bound
[8] follows by bounding the Binomial moments via the higher Poisson moments:
This shows that if 
![{displaystyle operatorname {E} [X^{c}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5989f9c9f5202059ad1c0a4026d267ee2a975761)
![{displaystyle operatorname {E} [X]^{c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d46bd564a6f77db38e12b156443bdbc3262cfb)
Mode[edit]
Usually the mode of a binomial B(n, p) distribution is equal to 

Proof: Let
For 









Let 
.
From this follows
So when 




Median[edit]
In general, there is no single formula to find the median for a binomial distribution, and it may even be non-unique. However, several special results have been established:
- If np is an integer, then the mean, median, and mode coincide and equal np.[10][11]
- Any median m must lie within the interval ⌊np⌋ ≤ m ≤ ⌈np⌉.[12]
- A median m cannot lie too far away from the mean: |m − np| ≤ min{ ln 2, max{p, 1 − p} }.[13]
- The median is unique and equal to m = round(np) when |m − np| ≤ min{p, 1 − p} (except for the case when p = 1/2 and n is odd).[12]
- When p is a rational number (with the exception of p = 1/2 and n odd) the median is unique.[14]
- When p = 1/2 and n is odd, any number m in the interval 1/2(n − 1) ≤ m ≤ 1/2(n + 1) is a median of the binomial distribution. If p = 1/2 and n is even, then m = n/2 is the unique median.
Tail bounds[edit]
For k ≤ np, upper bounds can be derived for the lower tail of the cumulative distribution function 

Hoeffding’s inequality yields the simple bound
which is however not very tight. In particular, for p = 1, we have that F(k;n,p) = 0 (for fixed k, n with k < n), but Hoeffding’s bound evaluates to a positive constant.
A sharper bound can be obtained from the Chernoff bound:[15]
where D(a || p) is the relative entropy (or Kullback-Leibler divergence) between an a-coin and a p-coin (i.e. between the Bernoulli(a) and Bernoulli(p) distribution):
Asymptotically, this bound is reasonably tight; see [15] for details.
One can also obtain lower bounds on the tail 
which implies the simpler but looser bound
For p = 1/2 and k ≥ 3n/8 for even n, it is possible to make the denominator constant:[17]
Statistical inference[edit]
Estimation of parameters[edit]
When n is known, the parameter p can be estimated using the proportion of successes:
This estimator is found using maximum likelihood estimator and also the method of moments. This estimator is unbiased and uniformly with minimum variance, proven using Lehmann–Scheffé theorem, since it is based on a minimal sufficient and complete statistic (i.e.: x). It is also consistent both in probability and in MSE.
A closed form Bayes estimator for p also exists when using the Beta distribution as a conjugate prior distribution. When using a general 
The Bayes estimator is asymptotically efficient and as the sample size approaches infinity (n → ∞), it approaches the MLE solution. The Bayes estimator is biased (how much depends on the priors), admissible and consistent in probability.
For the special case of using the standard uniform distribution as a non-informative prior, 
(A posterior mode should just lead to the standard estimator.) This method is called the rule of succession, which was introduced in the 18th century by Pierre-Simon Laplace.
When estimating p with very rare events and a small n (e.g.: if x=0), then using the standard estimator leads to 
Another method is to use the upper bound of the confidence interval obtained using the rule of three:
Confidence intervals[edit]
Even for quite large values of n, the actual distribution of the mean is significantly nonnormal.[19] Because of this problem several methods to estimate confidence intervals have been proposed.
In the equations for confidence intervals below, the variables have the following meaning:
Wald method[edit]
A continuity correction of 0.5/n may be added.[clarification needed]
Agresti–Coull method[edit]
[20]
Here the estimate of p is modified to
This method works well for 



Arcsine method[edit]
[23]
Wilson (score) method[edit]
The notation in the formula below differs from the previous formulas in two respects:[24]
-
[25]
Comparison[edit]
The so-called “exact” (Clopper–Pearson) method is the most conservative.[19] (Exact does not mean perfectly accurate; rather, it indicates that the estimates will not be less conservative than the true value.)
The Wald method, although commonly recommended in textbooks, is the most biased.[clarification needed]
[edit]
Sums of binomials[edit]
If X ~ B(n, p) and Y ~ B(m, p) are independent binomial variables with the same probability p, then X + Y is again a binomial variable; its distribution is Z=X+Y ~ B(n+m, p):[26]
A Binomial distributed random variable X ~ B(n, p) can be considered as the sum of n Bernoulli distributed random variables. So the sum of two Binomial distributed random variable X ~ B(n, p) and Y ~ B(m, p) is equivalent to the sum of n + m Bernoulli distributed random variables, which means Z=X+Y ~ B(n+m, p). This can also be proven directly using the addition rule.
However, if X and Y do not have the same probability p, then the variance of the sum will be smaller than the variance of a binomial variable distributed as 
Poisson binomial distribution[edit]
The binomial distribution is a special case of the Poisson binomial distribution, which is the distribution of a sum of n independent non-identical Bernoulli trials B(pi).[27]
Ratio of two binomial distributions[edit]
This result was first derived by Katz and coauthors in 1978.[28]
Let X ~ B(n,p1) and Y ~ B(m,p2) be independent. Let T = (X/n)/(Y/m).
Then log(T) is approximately normally distributed with mean log(p1/p2) and variance ((1/p1) − 1)/n + ((1/p2) − 1)/m.
Conditional binomials[edit]
If X ~ B(n, p) and Y | X ~ B(X, q) (the conditional distribution of Y, given X), then Y is a simple binomial random variable with distribution Y ~ B(n, pq).
For example, imagine throwing n balls to a basket UX and taking the balls that hit and throwing them to another basket UY. If p is the probability to hit UX then X ~ B(n, p) is the number of balls that hit UX. If q is the probability to hit UY then the number of balls that hit UY is Y ~ B(X, q) and therefore Y ~ B(n, pq).
Bernoulli distribution[edit]
The Bernoulli distribution is a special case of the binomial distribution, where n = 1. Symbolically, X ~ B(1, p) has the same meaning as X ~ Bernoulli(p). Conversely, any binomial distribution, B(n, p), is the distribution of the sum of n independent Bernoulli trials, Bernoulli(p), each with the same probability p.[29]
Normal approximation[edit]

If n is large enough, then the skew of the distribution is not too great. In this case a reasonable approximation to B(n, p) is given by the normal distribution
and this basic approximation can be improved in a simple way by using a suitable continuity correction.
The basic approximation generally improves as n increases (at least 20) and is better when p is not near to 0 or 1.[30] Various rules of thumb may be used to decide whether n is large enough, and p is far enough from the extremes of zero or one:
- One rule[30] is that for n > 5 the normal approximation is adequate if the absolute value of the skewness is strictly less than 0.3; that is, if
This can be made precise using the Berry–Esseen theorem.
- A stronger rule states that the normal approximation is appropriate only if everything within 3 standard deviations of its mean is within the range of possible values; that is, only if
-
- This 3-standard-deviation rule is equivalent to the following conditions, which also imply the first rule above.
The following is an example of applying a continuity correction. Suppose one wishes to calculate Pr(X ≤ 8) for a binomial random variable X. If Y has a distribution given by the normal approximation, then Pr(X ≤ 8) is approximated by Pr(Y ≤ 8.5). The addition of 0.5 is the continuity correction; the uncorrected normal approximation gives considerably less accurate results.
This approximation, known as de Moivre–Laplace theorem, is a huge time-saver when undertaking calculations by hand (exact calculations with large n are very onerous); historically, it was the first use of the normal distribution, introduced in Abraham de Moivre’s book The Doctrine of Chances in 1738. Nowadays, it can be seen as a consequence of the central limit theorem since B(n, p) is a sum of n independent, identically distributed Bernoulli variables with parameter p. This fact is the basis of a hypothesis test, a “proportion z-test”, for the value of p using x/n, the sample proportion and estimator of p, in a common test statistic.[31]
For example, suppose one randomly samples n people out of a large population and ask them whether they agree with a certain statement. The proportion of people who agree will of course depend on the sample. If groups of n people were sampled repeatedly and truly randomly, the proportions would follow an approximate normal distribution with mean equal to the true proportion p of agreement in the population and with standard deviation
Poisson approximation[edit]
The binomial distribution converges towards the Poisson distribution as the number of trials goes to infinity while the product np converges to a finite limit. Therefore, the Poisson distribution with parameter λ = np can be used as an approximation to B(n, p) of the binomial distribution if n is sufficiently large and p is sufficiently small. According to two rules of thumb, this approximation is good if n ≥ 20 and p ≤ 0.05, or if n ≥ 100 and np ≤ 10.[32]
Concerning the accuracy of Poisson approximation, see Novak,[33] ch. 4, and references therein.
Limiting distributions[edit]
- Poisson limit theorem: As n approaches ∞ and p approaches 0 with the product np held fixed, the Binomial(n, p) distribution approaches the Poisson distribution with expected value λ = np.[32]
- de Moivre–Laplace theorem: As n approaches ∞ while p remains fixed, the distribution of
- approaches the normal distribution with expected value 0 and variance 1. This result is sometimes loosely stated by saying that the distribution of X is asymptotically normal with expected value 0 and variance 1. This result is a specific case of the central limit theorem.
Beta distribution[edit]
The binomial distribution and beta distribution are different views of the same model of repeated Bernoulli trials. The binomial distribution is the PMF of k successes given n independent events each with a probability p of success.
Mathematically, when α = k + 1 and β = n − k + 1, the beta distribution and the binomial distribution are related by[clarification needed] a factor of n + 1:
Beta distributions also provide a family of prior probability distributions for binomial distributions in Bayesian inference:[34]
Given a uniform prior, the posterior distribution for the probability of success p given n independent events with k observed successes is a beta distribution.[35]
Random number generation[edit]
Methods for random number generation where the marginal distribution is a binomial distribution are well-established.[36][37]
One way to generate random variates samples from a binomial distribution is to use an inversion algorithm. To do so, one must calculate the probability that Pr(X = k) for all values k from 0 through n. (These probabilities should sum to a value close to one, in order to encompass the entire sample space.) Then by using a pseudorandom number generator to generate samples uniformly between 0 and 1, one can transform the calculated samples into discrete numbers by using the probabilities calculated in the first step.
History[edit]
This distribution was derived by Jacob Bernoulli. He considered the case where p = r/(r + s) where p is the probability of success and r and s are positive integers. Blaise Pascal had earlier considered the case where p = 1/2.
See also[edit]
- Logistic regression
- Multinomial distribution
- Negative binomial distribution
- Beta-binomial distribution
- Binomial measure, an example of a multifractal measure.[38]
- Statistical mechanics
- Piling-up lemma, the resulting probability when XOR-ing independent Boolean variables
References[edit]
- ^ Westland, J. Christopher (2020). Audit Analytics: Data Science for the Accounting Profession. Chicago, IL, USA: Springer. p. 53. ISBN 978-3-030-49091-1.
- ^ Feller, W. (1968). An Introduction to Probability Theory and Its Applications (Third ed.). New York: Wiley. p. 151 (theorem in section VI.3).
- ^ Wadsworth, G. P. (1960). Introduction to Probability and Random Variables. New York: McGraw-Hill. p. 52.
- ^ Jowett, G. H. (1963). “The Relationship Between the Binomial and F Distributions”. Journal of the Royal Statistical Society, Series D. 13 (1): 55–57. doi:10.2307/2986663. JSTOR 2986663.
- ^ See Proof Wiki
- ^ Knoblauch, Andreas (2008), “Closed-Form Expressions for the Moments of the Binomial Probability Distribution”, SIAM Journal on Applied Mathematics, 69 (1): 197–204, doi:10.1137/070700024, JSTOR 40233780
- ^ Nguyen, Duy (2021), “A probabilistic approach to the moments of binomial random variables and application”, The American Statistician, 75 (1): 101–103, doi:10.1080/00031305.2019.1679257, S2CID 209923008
- ^ D. Ahle, Thomas (2022), “Sharp and Simple Bounds for the raw Moments of the Binomial and Poisson Distributions”, Statistics & Probability Letters, 182: 109306, arXiv:2103.17027, doi:10.1016/j.spl.2021.109306
- ^ See also Nicolas, André (January 7, 2019). “Finding mode in Binomial distribution”. Stack Exchange.
- ^ Neumann, P. (1966). “Über den Median der Binomial- and Poissonverteilung”. Wissenschaftliche Zeitschrift der Technischen Universität Dresden (in German). 19: 29–33.
- ^ Lord, Nick. (July 2010). “Binomial averages when the mean is an integer”, The Mathematical Gazette 94, 331-332.
- ^ a b Kaas, R.; Buhrman, J.M. (1980). “Mean, Median and Mode in Binomial Distributions”. Statistica Neerlandica. 34 (1): 13–18. doi:10.1111/j.1467-9574.1980.tb00681.x.
- ^ Hamza, K. (1995). “The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions”. Statistics & Probability Letters. 23: 21–25. doi:10.1016/0167-7152(94)00090-U.
- ^ Nowakowski, Sz. (2021). “Uniqueness of a Median of a Binomial Distribution with Rational Probability”. Advances in Mathematics: Scientific Journal. 10 (4): 1951–1958. arXiv:2004.03280. doi:10.37418/amsj.10.4.9. ISSN 1857-8365. S2CID 215238991.
- ^ a b Arratia, R.; Gordon, L. (1989). “Tutorial on large deviations for the binomial distribution”. Bulletin of Mathematical Biology. 51 (1): 125–131. doi:10.1007/BF02458840. PMID 2706397. S2CID 189884382.
- ^ Robert B. Ash (1990). Information Theory. Dover Publications. p. 115. ISBN 9780486665214.
- ^ Matoušek, J.; Vondrak, J. “The Probabilistic Method” (PDF). lecture notes. Archived (PDF) from the original on 2022-10-09.
- ^ Razzaghi, Mehdi (2002). “On the estimation of binomial success probability with zero occurrence in sample”. Journal of Modern Applied Statistical Methods. 1 (2): 326–332. doi:10.22237/jmasm/1036110000.
- ^ a b Brown, Lawrence D.; Cai, T. Tony; DasGupta, Anirban (2001), “Interval Estimation for a Binomial Proportion”, Statistical Science, 16 (2): 101–133, CiteSeerX 10.1.1.323.7752, doi:10.1214/ss/1009213286, retrieved 2015-01-05
- ^ Agresti, Alan; Coull, Brent A. (May 1998), “Approximate is better than ‘exact’ for interval estimation of binomial proportions” (PDF), The American Statistician, 52 (2): 119–126, doi:10.2307/2685469, JSTOR 2685469, retrieved 2015-01-05
- ^ Gulotta, Joseph. “Agresti-Coull Interval Method”. pellucid.atlassian.net. Retrieved 18 May 2021.
- ^ “Confidence intervals”. itl.nist.gov. Retrieved 18 May 2021.
- ^ Pires, M. A. (2002). “Confidence intervals for a binomial proportion: comparison of methods and software evaluation” (PDF). In Klinke, S.; Ahrend, P.; Richter, L. (eds.). Proceedings of the Conference CompStat 2002. Short Communications and Posters. Archived (PDF) from the original on 2022-10-09.
- ^ Wilson, Edwin B. (June 1927), “Probable inference, the law of succession, and statistical inference” (PDF), Journal of the American Statistical Association, 22 (158): 209–212, doi:10.2307/2276774, JSTOR 2276774, archived from the original (PDF) on 2015-01-13, retrieved 2015-01-05
- ^ “Confidence intervals”. Engineering Statistics Handbook. NIST/Sematech. 2012. Retrieved 2017-07-23.
- ^ Dekking, F.M.; Kraaikamp, C.; Lopohaa, H.P.; Meester, L.E. (2005). A Modern Introduction of Probability and Statistics (1 ed.). Springer-Verlag London. ISBN 978-1-84628-168-6.
- ^
Wang, Y. H. (1993). “On the number of successes in independent trials” (PDF). Statistica Sinica. 3 (2): 295–312. Archived from the original (PDF) on 2016-03-03. - ^ Katz, D.; et al. (1978). “Obtaining confidence intervals for the risk ratio in cohort studies”. Biometrics. 34 (3): 469–474. doi:10.2307/2530610. JSTOR 2530610.
- ^ Taboga, Marco. “Lectures on Probability Theory and Mathematical Statistics”. statlect.com. Retrieved 18 December 2017.
- ^ a b Box, Hunter and Hunter (1978). Statistics for experimenters. Wiley. p. 130. ISBN 9780471093152.
- ^ NIST/SEMATECH, “7.2.4. Does the proportion of defectives meet requirements?” e-Handbook of Statistical Methods.
- ^ a b NIST/SEMATECH, “6.3.3.1. Counts Control Charts”, e-Handbook of Statistical Methods.
- ^ Novak S.Y. (2011) Extreme value methods with applications to finance. London: CRC/ Chapman & Hall/Taylor & Francis. ISBN 9781-43983-5746.
- ^ MacKay, David (2003). Information Theory, Inference and Learning Algorithms. Cambridge University Press; First Edition. ISBN 978-0521642989.
- ^ “Beta distribution”.
- ^ Devroye, Luc (1986) Non-Uniform Random Variate Generation, New York: Springer-Verlag. (See especially Chapter X, Discrete Univariate Distributions)
- ^ Kachitvichyanukul, V.; Schmeiser, B. W. (1988). “Binomial random variate generation”. Communications of the ACM. 31 (2): 216–222. doi:10.1145/42372.42381. S2CID 18698828.
- ^ Mandelbrot, B. B., Fisher, A. J., & Calvet, L. E. (1997). A multifractal model of asset returns. 3.2 The Binomial Measure is the Simplest Example of a Multifractal
Further reading[edit]
- Hirsch, Werner Z. (1957). “Binomial Distribution—Success or Failure, How Likely Are They?”. Introduction to Modern Statistics. New York: MacMillan. pp. 140–153.
- Neter, John; Wasserman, William; Whitmore, G. A. (1988). Applied Statistics (Third ed.). Boston: Allyn & Bacon. pp. 185–192. ISBN 0-205-10328-6.
External links[edit]
- Interactive graphic: Univariate Distribution Relationships
- Binomial distribution formula calculator
- Difference of two binomial variables: X-Y or |X-Y|
- Querying the binomial probability distribution in WolframAlpha
- Confidence (credible) intervals for binomial probability, p: online calculator available at causaScientia.org
@import url(‘https://fonts.googleapis.com/css?family=Droid+Serif|Raleway’);
words {
color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; padding-left: 100px; }
words label, input {
display: inline-block; vertical-align: baseline; width: 350px; }
#button { border: 1px solid; border-radius: 10px; margin-top: 20px; padding: 10px 10px; cursor: pointer; outline: none; background-color: white; color: black; font-family: ‘Work Sans’, sans-serif; border: 1px solid grey; /* Green */ }
#button:hover { background-color: #f6f6f6; border: 1px solid black; }
p, li { color:#000000; font-size: 19px; font-family: ‘Helvetica’; }
p a { color: #9b59b6 !important; } Биномиальное распределение является одним из самых популярных распределений в статистике. Чтобы понять биномиальное распределение, сначала нужно понять биномиальные эксперименты .
Биномиальные эксперименты
Биномиальный эксперимент — это эксперимент, обладающий следующими свойствами:
- Эксперимент состоит из n повторных попыток.
- Каждое испытание имеет только два возможных исхода.
- Вероятность успеха, обозначаемая p , одинакова для каждого испытания.
- Каждое испытание является независимым.
Наиболее очевидным примером биномиального эксперимента является подбрасывание монеты. Например, предположим, что мы подбрасываем монету 10 раз. Это биномиальный эксперимент, поскольку он обладает следующими четырьмя свойствами:
- Эксперимент состоит из n повторных попыток – всего 10 попыток.
- В каждом испытании есть только два возможных исхода — орел или решка.
- Вероятность успеха, обозначаемая p , одинакова для каждого испытания. Если мы определим «успех» как приземление орлом, то вероятность успеха для каждого испытания равна ровно 0,5.
- Каждое испытание является независимым — результат одного подбрасывания монеты не влияет на результат любого другого подбрасывания монеты.
Биномиальное распределение
Биномиальное распределение описывает вероятность достижения k успехов в n биномиальных экспериментах.
Если случайная величина X подчиняется биномиальному распределению, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = n C k * p k * (1-p) nk
куда:
- n: количество испытаний
- k: количество успехов
- p: вероятность успеха в данном испытании
- n C k : количество способов добиться k успехов в n испытаниях.
Например, предположим, что мы подбрасываем монету 3 раза. Мы можем использовать приведенную выше формулу, чтобы определить вероятность получения 0, 1, 2 и 3 решек во время этих 3 подбрасываний:
P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
P(X=1) = 3 C 1 * 0,5 1 * (1-0,5) 3-1 = 3 * 0,5 * (0,5) 2 = 0,375
P(X=2) = 3 C 2 * 0,5 2 * (1-0,5) 3-2 = 3 * 0,25 * (0,5) 1 = 0,375
P(X=3) = 3 C 3 * 0,5 3 * (1-0,5) 3-3 = 1 * 0,125 * (0,5) 0 = 0,125
Примечание. Мы использовали этот Калькулятор комбинаций для расчета n C k для каждого примера.
Мы можем создать простую гистограмму, чтобы визуализировать это распределение вероятностей:
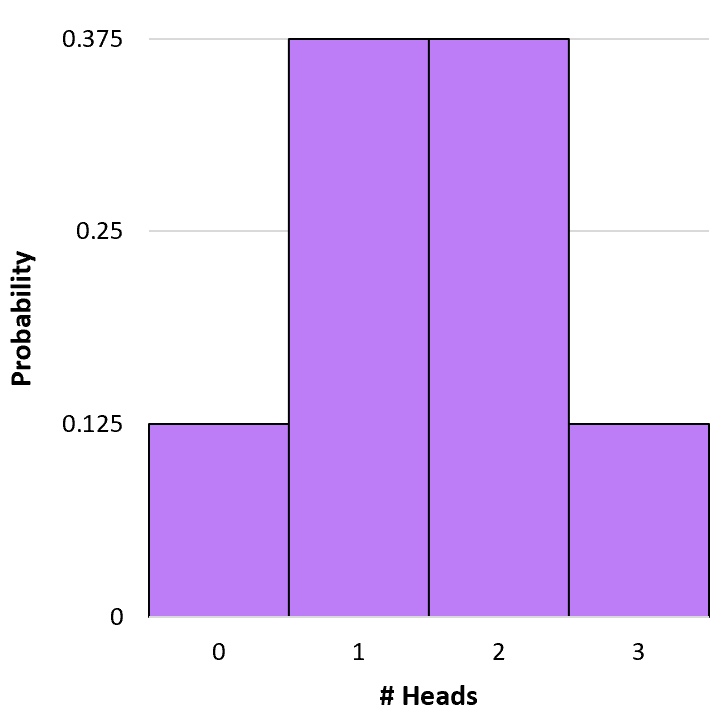
### Вычисление кумулятивных биномиальных вероятностей
Несложно рассчитать одну биномиальную вероятность (например, вероятность того, что монета выпадет орлом 1 раз из 3 бросков), используя приведенную выше формулу, но для расчета кумулятивных биномиальных вероятностей нам нужно сложить отдельные вероятности.
Например, предположим, что мы хотим узнать вероятность того, что монета выпадет орлом 1 или менее раз из 3 бросков. Мы будем использовать следующую формулу для расчета этой вероятности:
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
Это известно как кумулятивная вероятность , потому что она включает в себя добавление более одной вероятности. Мы можем рассчитать кумулятивную вероятность выпадения k или меньше орлов для каждого исхода, используя аналогичную формулу:
Р(Х≤0) = Р(Х=0) = 0,125 .
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .
Мы можем создать гистограмму, чтобы визуализировать это кумулятивное распределение вероятностей:
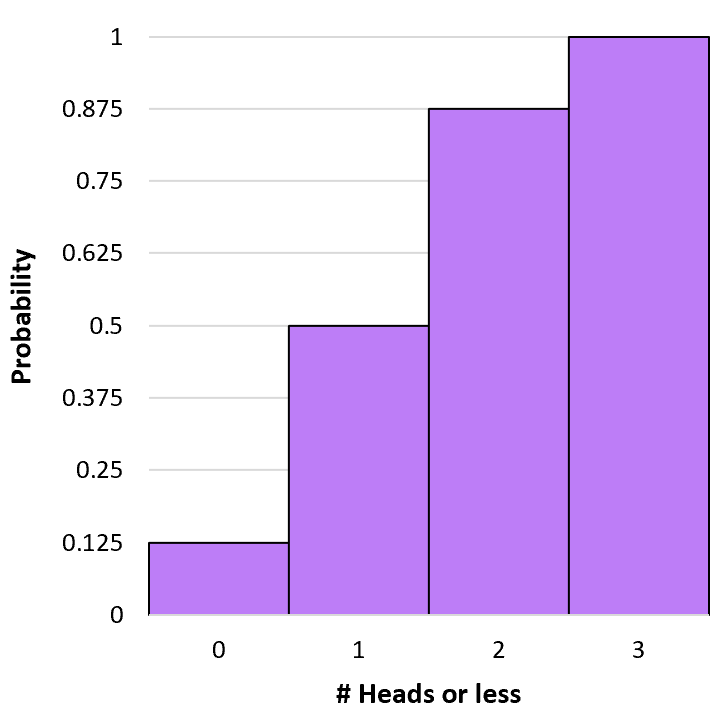
### Калькулятор биномиальной вероятности
Когда мы работаем с небольшими числами (например, 3 подбрасывания монеты), целесообразно рассчитать биномиальные вероятности вручную. Однако, когда мы работаем с большими числами (например, 100 бросков монеты), вычисление вероятностей вручную может оказаться затруднительным. В этих случаях может быть полезно использовать калькулятор биномиальной вероятности , подобный приведенному ниже.
Например, предположим, что мы подбрасываем монету n = 100 раз, вероятность того, что она выпадет орлом в данном испытании, равна p = 0,5, и мы хотим узнать вероятность того, что она выпадет орлом k = 43 раза или меньше:
p (вероятность успеха в данном испытании) n (количество испытаний) k (количество успехов) Р(Х= 43 ) = 0,03007
Р(Х< 43 ) = 0,06661
Р( Х≤43 ) = 0,09667
Р(Х > 43 ) = 0,90333
Р( Х≥43 ) = 0,93339
function pvalue() {
//get input values var p = document.getElementById(‘p’).value*1; var n = document.getElementById(‘n’).value*1; var k = document.getElementById(‘k’).value*1;
//assign probabilities to variable names var exactProb = jStat.binomial.pdf(k,n,p); var lessProb = jStat.binomial.cdf(k-1,n,p); var lessEProb = jStat.binomial.cdf(k,n,p); var greaterProb = 1-jStat.binomial.cdf(k,n,p); var greaterEProb = 1-jStat.binomial.cdf(k-1,n,p);
//output probabilities document.getElementById(‘k1’).innerHTML = k; document.getElementById(‘k2’).innerHTML = k; document.getElementById(‘k3’).innerHTML = k; document.getElementById(‘k4’).innerHTML = k; document.getElementById(‘k5’).innerHTML = k;
document.getElementById(‘exactProb’).innerHTML = exactProb.toFixed(5); document.getElementById(‘lessProb’).innerHTML = lessProb.toFixed(5); document.getElementById(‘lessEProb’).innerHTML = lessEProb.toFixed(5); document.getElementById(‘greaterProb’).innerHTML = greaterProb.toFixed(5); document.getElementById(‘greaterEProb’).innerHTML = greaterEProb.toFixed(5); } Вот как интерпретировать вывод:
- Вероятность того, что монета выпадет орлом ровно 43 раза, равна 0,03007 .
- Вероятность того, что монета выпадет орлом менее 43 раз, равна 0,06661 .
- Вероятность того, что монета выпадет орлом не более 43 раз, равна 0,09667 .
- Вероятность того, что монета выпадет орлом более 43 раз, равна 0,90333 .
- Вероятность того, что монета выпадет орлом 43 или более раз, равна 0,93339 .
Свойства биномиального распределения
Биномиальное распределение обладает следующими свойствами:
Среднее значение распределения равно µ = np
Дисперсия распределения равна σ 2 = np(1-p)
Стандартное отклонение распределения равно σ = √ np(1-p)
Например, предположим, что мы подбрасываем монету 3 раза. Пусть p = вероятность того, что монета выпадет орлом.
Среднее количество голов, которое мы ожидаем, равно μ = np = 3*.5 = 1.5 .
Ожидаемая дисперсия числа головок составляет σ 2 = np(1-p) = 3*,5*(1-,5) = 0,75 .
Проблемы практики биномиального распределения
Используйте следующие практические задачи, чтобы проверить свои знания о биномиальном распределении.
Проблема 1
Вопрос: Боб делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает ровно 10?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,6, n = 12 и k = 10, мы находим, что P(X=10) = 0,06385 .
Проблема 2
Вопрос: Джессика подбрасывает монету 5 раз. Какова вероятность того, что монета выпадет орлом 2 раза или меньше?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,5, n = 5 и k = 2, мы находим, что P(X≤2) = 0,5 .
Проблема 3
Вопрос: Вероятность того, что данный студент будет принят в определенный колледж, равна 0,2. Если подали заявки 10 студентов, какова вероятность того, что будут приняты более 4?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,2, n = 10 и k = 4, мы находим, что P(X>4) = 0,03279 .
Проблема 4
Вопрос: Вы подбрасываете монету 12 раз. Каково среднее ожидаемое количество выпавших орлов?
Ответ: Вспомните, что среднее биномиального распределения вычисляется как µ = np.Таким образом, µ = 12*0,5 = 6 голов .
Проблема 5
Вопрос: Марк совершает хоумран в 10% своих попыток. Если у него есть 5 попыток в данной игре, какова дисперсия количества хоум-ранов, которые он сделает?
Ответ: Напомним, что дисперсия биномиального распределения рассчитывается как σ 2 = np(1-p). Таким образом, σ 2 = 6*.1*(1-.1) = 0,54 .
Дополнительные ресурсы
Следующие статьи помогут вам научиться работать с биномиальным распределением в различных статистических программах:
- Как рассчитать биномиальные вероятности в Excel
- Как рассчитать биномиальные вероятности на калькуляторе ТИ-84
- Как рассчитать биномиальные вероятности в R
- Как построить биномиальное распределение в R













![{displaystyle operatorname {E} [X]=np.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f16b365410a1b23b5592c53d3ae6354f1a79aff)
![{displaystyle operatorname {E} [X]=operatorname {E} [X_{1}+cdots +X_{n}]=operatorname {E} [X_{1}]+cdots +operatorname {E} [X_{n}]=p+cdots +p=np.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f238d520c68a1d1b9b318492ddda39f4cc45bb8)


![{displaystyle {begin{aligned}operatorname {E} [X]&=np,\operatorname {E} [X^{2}]&=np(1-p)+n^{2}p^{2},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f2b3a9af52fc1ea633476400290069fc3ae7b4)
![{displaystyle operatorname {E} [X^{c}]=sum _{k=0}^{c}left{{c atop k}right}n^{underline {k}}p^{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db435ced7af59fa481fe26a023a1429d18a6a83a)
![{displaystyle operatorname {E} [X^{c}]leq left({frac {c}{log(c/(np)+1)}}right)^{c}leq (np)^{c}exp left({frac {c^{2}}{2np}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b86926254189719acfa57fcc1650caf698c292)


















![{begin{aligned}operatorname {P} (Z=k)&=sum _{i=0}^{k}left[{binom {n}{i}}p^{i}(1-p)^{n-i}right]left[{binom {m}{k-i}}p^{k-i}(1-p)^{m-k+i}right]\&={binom {n+m}{k}}p^{k}(1-p)^{n+m-k}end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38fc38e9a5e2c49743f45b4dab5dae6230ab2ad5)








