Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы

- Перпендикулярные прямые — определение и свойства

- Правила комбинаторики в задаче B6

- Метод координат в пространстве

- Четырехугольная пирамида: как найти координаты вершин

- Задача B4 про три дороги — стандартная задача на движение

Зависит ли угол, который образуют между собой биссектрисы смежных углов, от градусных мер этих углов?
Утверждение.
Биссектрисы смежных углов перпендикулярны.
 Дано: ∠AOD и ∠DOB — cмежные,
Дано: ∠AOD и ∠DOB — cмежные,
OF — биссектриса ∠AOD,
OK — биссектриса ∠DOB
Доказать:
![]()
Доказательство:
Так как сумма смежных углов равна 180º, то ∠AOD+∠DOB=180º.
Так как OF — биссектриса ∠AOD, то
![]()
Так как OK — биссектриса ∠DOB, то
![]()
Отсюда,
![]()
![]()
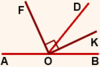 Таким образом, мы доказали, что угол между биссектрисами смежных углов не зависит от градусной меры смежных углов и всегда равен 90º, то есть, биссектрисы смежных углов перпендикулярны.
Таким образом, мы доказали, что угол между биссектрисами смежных углов не зависит от градусной меры смежных углов и всегда равен 90º, то есть, биссектрисы смежных углов перпендикулярны.
Задача.
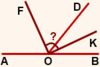 Найти угол между биссектрисами смежных углов, один из которых на 100º больше другого.
Найти угол между биссектрисами смежных углов, один из которых на 100º больше другого.
Решение:
Так как биссектрисы смежных углов перпендикулярны, ∠FOK=90º.
(Находить градусные меры смежных углов не требуется).
Ответ: 90º.
Опубликовано 3 года назад по предмету
Геометрия
от zmurshik
постройте биссектрисы смежных углов. найдите градусную меру угла между этими биссектрисами
-
Ответ
Ответ дан
TeoremaSinТак как смежные углы в сумме дают 180°, то градусная мера угла между ними будет равна 1/2 от первого угла + 1/2 от второго. И в сумме это всегда будет давать 90°.
Ответ: 90°
Самые новые вопросы
![]()
Математика – 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x – 5,21 = 9,54
![]()
Информатика – 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
![]()
География – 3 года назад
Почему япония – лидер по выплавке стали?
![]()
Математика – 3 года назад
Чему равно: 1*(умножить)х? 0*х?
![]()
Русский язык – 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Голосование за лучший ответ
Лев Ватлин
Знаток
(371)
9 лет назад
Если есть биссектриса самого угла, то биссектриса угла, смежного с ним, будем первой биссектрисе перпендикулярна
пятачок
Мастер
(1724)
9 лет назад
биссектрисы двух смежных углов взаимно перпендикулярны так что проводить надо под углом 90 градусов
ХУДОЖНИК
Искусственный Интеллект
(282695)
9 лет назад
Смотрите вот здесьhttp://pm298.ru/reshenie/febr.php
Биссектрисы смежных углов перпендикулярны
Анна Малкова
Пусть и
– смежные углы,
– биссектриса угла
,
– биссектриса угла
. Докажем, что
.

Смежные углы – это углы, имеющие общую сторону, и их сумма равна . Так как углы
и
– смежные,
.
,
.
Значит, , что и требовалось доказать.
Легко доказать также, что биссектрисы односторонних углов при параллельных прямых и секущей – перпендикулярны. Сделайте это самостоятельно.
Полезные следствия, применяемые в решении задач ЕГЭ:
Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны.
Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.
Задача ЕГЭ по теме «Биссектрисы односторонних углов»
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны. Угол между ними равен
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Биссектрисы смежных углов перпендикулярны» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023













