Как найти частоту звуковых колебаний
Звуком называют волны механических деформаций, распространяющиеся в любой достаточно упругой среде (жидкостях, твердых телах, газах). Как и другие волны, звук характеризуется, в частности, частотой колебаний. В зависимости от начальных условий найти частоту звука можно разными способами.

Вам понадобится
- – калькулятор;
- – физический справочник;
- – тахометр;
- – звуковой датчик;
- – осциллограф.
Инструкция
Найдите частоту звуковых колебаний, если известна длина их волн и скорость звука в среде, где они распространяются. Вычисления следует производить по формуле F=V/L. Здесь V – скорость звука в среде, а L – длина волны (известная величина). Значения скоростей звука для разных сред можно узнать из физических справочников. Так, для воздуха при нормальных условиях (температуре в районе 20°C и давлении, близком к атмосферному) это значение составляет 341 м/с. Поэтому, например, звуковые колебания в воздухе с длиной волны в 0,25 м будут иметь частоту 341/0,25=1364 Гц.
Найти частоту звуковых колебаний, зная их период, можно по простой формуле: F=1/T. Обратите внимание на то, что для получения корректных значений частоты, представленных в герцах, период T должен быть выражен системе СИ, то есть иметь размерность в секундах.
Для получения частоты звуковых колебаний, распространяющихся в реальной среде, осуществите физический эксперимент. Примените специализированное устройство – тахометр. Сегодня тахометры, как правило, имеют высокую точность измерений и отображают информацию в готовом виде на цифровом индикаторе.
При отсутствии тахометра для нахождения частоты звука можно воспользоваться микрофоном или другим звуковым датчиком с достаточной чувствительностью, а также осциллографом. Подключите датчик к осциллографу и создайте условия для получения сигнала (например, поместите датчик в исследуемую среду). Подберите чувствительность осциллографа так, чтобы колебания на экране отображались с достаточной амплитудой. Путем подстройки частоты развертки добейтесь отображения устойчивой картинки. Узнайте период звуковых колебаний, ориентируясь на шкалу прибора. Найдите частоту, используя способ, описанный во втором шаге.
Обратите внимание
При вычислениях, связанных с получением значений частоты звука, всегда переводите все известные значения в систему СИ.
Полезный совет
Если дополнительно требуется найти циклическую частоту звуковых колебаний, рассчитайте ее по формуле w=2*PI*F, где F – частота, выраженная в герцах, полученная одним из описанных способов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Звуковая волна – период, длина, частота и скорость распространения
Калькуляторы онлайн перевода длины звуковой, инфразвуковой или ультразвуковой
волны в частоту и наоборот. Таблица соответствия
нот полного звукоряда частотам.
Звуковая волна – это механические колебания, которые в результате колебаний молекул вещества распространяются в какой-либо
среде (в газе, жидкости или твёрдом теле) и, достигнув органов слуха человека, воспринимаются им как звук. Источник, создающий
возмущение (колебания воздуха), называется источником звука.
Как уже было сказано, для распространения звука необходима какая-либо упругая среда. Поэтому в вакууме ори, не ори – тебя никто не
услышит, по причине того, что звуковые волны распространяться не смогут, так как там нечему колебаться.., да и слушать там, по большому
счёту, тоже некому.
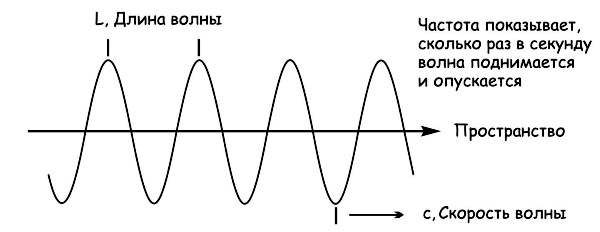
Так же, как и в случае с электромагнитными волнами, соотношение, связывающее длину звуковой волны с частотой колебаний,
в общем случае выглядит следующим образом:
λ (м) = V (м/сек) / F (Гц), где V (м/сек) – это скорость распространения
звука в среде.
Период колебаний также не претерпел никаких изменений и по-прежнему равен:
T(сек) = 1 / F (Гц) = λ (м) / V (м/сек).
Частота колебаний звукового сигнала F (Гц) – это параметр стабильный, практически не зависящий от среды распространения.
А вот скорость звука V (м/сек), а соответственно и длина звуковой волны – это величины, которые зависят
не только от плотности вещества, но и от его упругости, а в случае с жидкостями и газами ещё – и от температуры, и атмосферного
давления.
Зависимость скорости звуковой волны от свойств упругой среды легко прослеживается по следующей формуле:
V (м/сек) = √Eупр (паскаль) / ρ (кг/м3)
,
где Eупр представляет собой модуль объёмной упругости среды, а ρ – плотность среды.
Модуль упругости, так же как и плотность – это справочные величины, прописанные для конкретных материалов.
В качестве примера, ниже приведена таблица величины скорости распространения звука в различных средах:
| Среда | Скорость звука, м/сек |
| Воздух при 0° | 331 |
| Воздух при 30° | 350 |
| Вода | 1450 |
| Медь | 3800 |
| Дерево | 4800 |
| Железо | 4900 |
| Сталь | 5600 |
Для газов параметры модуля объёмной упругости и плотности имеют ярко выраженную зависимость от температуры и атмосферного давления.
Если углубиться, то скорость звука в газах можно вычислить по следующей формуле:
V (м/сек) = √γ*Ратм / ρ ,
где
γ = cp/сv – это отношение удельной теплоёмкости при постоянном давлении
к удельной теплоёмкости при постоянном объёме, а Pатм – атмосферное давление,
которое связано с температурой газообразной среды.
Поэтому, чтобы никого сильно не грузить, приведу и приближённую зависимость скорости звука (при нормальном
атмосферном давлении) от температуры среды:
V (м/сек) = (331 + 0,6 * T°), где 331 м/сек – это скорость звука при 0°С,
а T° – температура в градусах Цельсия.
Теперь можно совместить формулы и получить простое соотношение, связывающее длину звуковой волны с частотой колебаний с учётом
температуры среды:
λ (м) = (331 + 0,6 * T°) / F (Гц).
Всё это без лишнего напряга несложно посчитать при помощи листа бумаги или деревянных счёт, ну а для пущего упрощения жизни человека,
приведу и пару он-лайн считалок для перевода одного из параметров в другой.
Калькуляторы предполагают расчёты длины и частоты звуковой волны для воздушной среды при нормальном атмосферном
давлении (760 мм ртутного столба).
Онлайн калькулятор расчёта длины звуковой волны по частоте
|
Частота звуковых колебаний f |
|
|
Температура Т(°С) (по умолчанию 20°) |
||
Длина волны |
Онлайн калькулятор расчёта частоты по длине звуковой волны
|
Длина волны λ при заданной Т |
||
Температура Т(°С) (по умолчанию 20°) |
||
Частота колебаний |
Полный диапазон звуковых частот условно находится в пределах:
16…20 000 Гц.
Ниже ( 0,001…16Гц ) – инфразвук.
Выше ( 20…100кГц ) – низкочастотный ультразвук,
ещё выше (100кГц…1МГц) – высокочастотный ультразвук.
А для интересующихся приведу таблицу соответствия нот стандартного музыкального звукоряда частотам.
| Частота (Гц) | ||||||||||||
| Октава | Нота | |||||||||||
| До | До – диез | Ре | Ми – бемоль | Ми | Фа | Фа – диез | Си | Си- диез | Ля | Соль-бемоль | Соль | |
| C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B | |
| 0 | 16.35 | 17.32 | 18.35 | 19.45 | 20.60 | 21.83 | 23.12 | 24.50 | 25.96 | 27.50 | 29.14 | 30.87 |
| 1 | 32.70 | 34.65 | 36.71 | 38.89 | 41.20 | 43.65 | 46.25 | 49.00 | 51.91 | 55.00 | 58.27 | 61.74 |
| 2 | 65.41 | 69.30 | 73.42 | 77.78 | 82.41 | 87.31 | 92.50 | 98.00 | 103.8 | 110.0 | 116.5 | 123.5 |
| 3 | 130.8 | 138.6 | 146.8 | 155.6 | 164.8 | 174.6 | 185.0 | 196.0 | 207.7 | 220.0 | 233.1 | 246.9 |
| 4 | 261.6 | 277.2 | 293.7 | 311.1 | 329.6 | 349.2 | 370.0 | 392.0 | 415.3 | 440.0 | 466.2 | 493.9 |
| 5 | 523.3 | 554.4 | 587.3 | 622.3 | 659.3 | 698.5 | 740.0 | 784.0 | 830.6 | 880.0 | 932.3 | 987.8 |
| 6 | 1047 | 1109 | 1175 | 1245 | 1319 | 1397 | 1480 | 1568 | 1661 | 1760 | 1865 | 1976 |
| 7 | 2093 | 2217 | 2349 | 2489 | 2637 | 2794 | 2960 | 3136 | 3322 | 3520 | 3729 | 3951 |
| 8 | 4186 | 4435 | 4699 | 4978 | 5274 | 5588 | 5920 | 6272 | 6645 | 7040 | 7459 | 7902 |
Физика > Частота звуковых волн
Чему равна частота звуковой волны – частота, длина и скорость звука. Изучите единицу измерения, формулу частоты звуковой волны, что определяет, диапазон.
Частота – количество повторяющихся событий за временную единицу.
Задача обучения
- Объединить частоту, длину и скорость звука.
Основные пункты
- Частота основывается на длине и звуковой скорости:

- Период – длительность цикла повторяющегося события. Выступает обратной частоте.
- Единица измерения – Герц (количество циклов в секунду).
Термины
- Частота – количество периодического события за временную единицу: f = n/t.
- Герц – один период в секунду, единица частоты (Гц).
- Период – длительность цикла в повторяющемся событии.
Звуковые волны обладают частотой, то есть количеством вхождений повторяющегося события за временную единицу.
Частота колебаний звуковой волны основывается на длине волны и скорости звука: ![]()
Нижний рисунок демонстрирует связь частоты и длины.

Звуковая волна формируется из источника, вибрирующего на частоте (f), и распространяется при v на длине λ
Частота звуковой волны определяет и другие характеристики. Можно использовать частоту и длину, чтобы отыскать скорость волны. Не забывайте, что она зависит от того, в какой среде перемещается звук. Высокие показатели появляются в твердых веществах. Формула: vs = fλ.
Период – длительность цикла повторяющегося события. В анимации показаны различные частоты и периоды (от наименьшего к наивысшему).

Три мигающих огонька: от самой низкой частоты (сверху) до наивысшей (снизу). F – частота в Герцах. Т – период в секундах
Герц
Единица измерения – Герц (Гц). Это количество циклов в секунду: 100 Гц = 100 циклам.
Различные виды улавливают разные частотные диапазоны. Люди способны услышать 20 – 200000 Гц, а собаки до 60000 Гц. У летучих мышей диапазон вырастает до 120000 Гц. Последние применяют ультразвук, чтобы сориентироваться в пространстве или найти объекты. Звуковые волны отбиваются от предметов. Животное улавливает, сколько времени нужно на возврат, и понимает, какая дистанция образовалась. Это эхолокация.
From Wikipedia, the free encyclopedia
| Sound measurements | |
|---|---|
|
Characteristic |
Symbols |
| Sound pressure | p, SPL,LPA |
| Particle velocity | v, SVL |
| Particle displacement | δ |
| Sound intensity | I, SIL |
| Sound power | P, SWL, LWA |
| Sound energy | W |
| Sound energy density | w |
| Sound exposure | E, SEL |
| Acoustic impedance | Z |
| Audio frequency | AF |
| Transmission loss | TL |
|
|
|
|
An audio frequency or audible frequency (AF) is a periodic vibration whose frequency is audible to the average human. The SI unit of frequency is the hertz (Hz). It is the property of sound that most determines pitch.[1]
The generally accepted standard hearing range for humans is 20 to 20,000 Hz.[2][3][4] In air at atmospheric pressure, these represent sound waves with wavelengths of 17 metres (56 ft) to 1.7 centimetres (0.67 in). Frequencies below 20 Hz are generally felt rather than heard, assuming the amplitude of the vibration is great enough. Sound frequencies above 20 kHz are called ultrasonic.
Sound propagates as mechanical vibration waves of pressure and displacement, in air or other substances.[5] In general, frequency components of a sound determine its “color”, its timbre. When speaking about the frequency (in singular) of a sound, it means the property that most determines its pitch.[6] Higher pitches have higher frequency, and lower pitches are lower frequency.
The frequencies an ear can hear are limited to a specific range of frequencies. The audible frequency range for humans is typically given as being between about 20 Hz and 20,000 Hz (20 kHz), though the high frequency limit usually reduces with age. Other species have different hearing ranges. For example, some dog breeds can perceive vibrations up to 60,000 Hz.[7]
In many media, such as air, the speed of sound is approximately independent of frequency, so the wavelength of the sound waves (distance between repetitions) is approximately inversely proportional to frequency.
Frequencies and descriptions[edit]
| Frequency (Hz) | Octave | Description |
|---|---|---|
| 16 to 32 | 1st | The lower human threshold of hearing, and the lowest pedal notes of a pipe organ. |
| 32 to 512 | 2nd to 5th | Rhythm frequencies, where the lower and upper bass notes lie. |
| 512 to 2,048 | 6th to 7th | Defines human speech intelligibility, gives a horn-like or tinny quality to sound. |
| 2,048 to 8,192 | 8th to 9th | Gives presence to speech, where labial and fricative sounds lie. |
| 8,192 to 16,384 | 10th | Brilliance, the sounds of bells and the ringing of cymbals and sibilance in speech. |
| 16,384 to 32,768 | 11th | Beyond brilliance, nebulous sounds approaching and just passing the upper human threshold of hearing |

C5, an octave above middle C. The frequency is twice that of middle C (523 Hz).

C3, an octave below middle C. The frequency is half that of middle C (131 Hz).
| MIDI note | Frequency (Hz) | Description | Sound file |
|---|---|---|---|
| 0 | 8.17578125 | Lowest organ note | n/a (fundamental frequency inaudible) |
| 12 | 16.3515625 | Lowest note for tuba, large pipe organs, Bösendorfer Imperial grand piano | n/a (fundamental frequency inaudible under average conditions) |
| 24 | 32.703125 | Lowest C on a standard 88-key piano | |
| 36 | 65.40625 | Lowest note for cello | |
| 48 | 130.8125 | Lowest note for viola, mandola | |
| 60 | 261.625 | Middle C | |
| 72 | 523.25 | C in middle of treble clef | |
| 84 | 1,046.5 | Approximately the highest note reproducible by the average female human voice | |
| 96 | 2,093 | Highest note for a flute | |
| 108 | 4,186 | Highest note on a standard 88-key piano | |
| 120 | 8,372 | ||
| 132 | 16,744 | Approximately the tone that a typical CRT television emits while running. |
See also[edit]
- Absolute threshold of hearing
- Hypersonic effect, controversial claim for human perception above 20,000 Hz
- Loudspeaker
- Musical acoustics
- Piano key frequencies
- Scientific pitch notation
- Whistle register
References[edit]
- ^ Pilhofer, Michael (2007). Music Theory for Dummies. For Dummies. p. 97. ISBN 9780470167946.
- ^ “Hyperphysics”. Retrieved 19 September 2014.
- ^ Heffner, Henry; Heffner, Rickye (January 2007). “Hearing Ranges of Laboratory Animals”. Journal of the American Association for Laboratory Animal Science. 46 (1): 20–2. PMID 17203911. Retrieved 19 September 2014.
- ^ Rosen, Stuart (2011). Signals and Systems for Speech and Hearing (2nd ed.). BRILL. p. 163.
For auditory signals and human listeners, the accepted range is 20Hz to 20kHz, the limits of human hearing
- ^ “Definition of SOUND”. Retrieved 3 October 2016.
- ^ Pilhofer, Michael (2007). Music Theory for Dummies. For Dummies. p. 97. ISBN 978-0-470-16794-6.
- ^ Condon, Tim (2003). Elert, Glenn (ed.). “Frequency range of dog hearing”. The Physics Factbook. Retrieved 2008-10-22.
Очень часто походя употребляют такие вроде бы понятные термины, как спектр, фаза, частота и прочие. Но зачастую мы до конца не понимаем, что же это на самом деле такое. Что значат эти термины на самом деле, как можно “пощупать” их истинное значение? Можно пойти в библиотеку и почитать там книги по теории радиотехники и цифровой обработке сигналов, но времени постоянно не хватает даже на более важные дела. Поэтому автор попытался дать читателю выжимки из радиотехнических учебников, объясненные “на пальцах” и самый минимум формул (если кто-то заинтересовался более “математическим” изложением материала).
Волновая форма сигнала (звука). Период. Частота
Что такое звук? Это переменное звуковое (воздушное) давление на барабанную перепонку. Ухо воспринимает как звук только изменение давления. Когда звучит отдельная нота давление периодически то нарастает, то убывает и этот процесс циклически повторяется.
Период (T, сек) – длительность этого цикла.
Частота (f, Гц, Герц) – количество периодов, помещающихся в одной секунде. 1 Герц – это 1 период за секунду.
f = 1 / T (формула частоты)
Причем закон (форма) изменения звукового давления не изменяется от периода к периоду.
Если у нас звучит мелодия, то волны, порождаемые разными нотами (которые то появляются, то исчезают), складываются друг с другом в общую волну, которая уже не имеет периода (цикла повтора).
А что же такое шум?
Шум – это сигнал (волновая форма не имеет периода), который в любой момент времени имеет случайное значение звукового давления. Шум не имеет периода.
Звук, как известно распространяется с задержкой, которая зависит от расстояния от источника до человеческого уха. Как это происходит?
Длина волны
Механические колебания источника звука (музыкального инструмента или динамика колонки) сжимают/разрежают (выталкивают/притягивают) воздух около себя. Сжатый воздух начинает расширятся прочь от источника звука, сжимая в свою очередь соседнюю воздушную область. Таким образом область сжатого воздуха путешествует от источника звука к уху.
Расстояние, между областями одинакового сжатия воздуха называется длиной звуковой волны.
L = M / f (формула длины волны),
где
L – длина волны в метрах;
M – скорость звука (331,46 м/с) в метрах в секунду;
f – частота звука в Герцах.
Длина волны для:
20 Гц L20 = (331,46 м/с) / (20 Гц) = 16,5 м.
100 Гц L100 = (331,46 м/с) / (100 Гц) = 3,3 м.
1000 Гц L1000 = (331,46 м/с) / (1000 Гц) = 0,33 м = 33 см.
10000 Гц L10000 = (331,46 м/с) / (10000 Гц) = 0,033 м = 3,3 см.
20000 Гц L10000 = (331,46 м/с) / (20000 Гц) = 0,017 м = 1,7 см.
Чтобы “надавить” на ухо, область сжатого звука должна затратить некоторое время, чтобы пройти путь от музыкального инструмента до уха. Этим и объясняется задержка звука.
Расстояние вносит задержку распространения звука не зависящую от частоты, так как скорость звука на разных частотах одинакова.
Dt = l / M (формула задержки распространения звука),
где
Dt – задержка в секундах;
l – расстояние в метрах;
M – скорость звука (331,46 м/с) в метрах в секунду.
1 метр вносит задержку распространения звука
Dt= (1 м) / (331,46 м/с) = 0,003 секунды или 3 миллисекунды (мс).
Автор: Юрий Корзунов (2010)
ПРОДОЛЖЕНИЕ…>>
